Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) — результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | — |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
From Wikipedia, the free encyclopedia
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable 




Every probability distribution supported on the real numbers, discrete or «mixed» as well as continuous, is uniquely identified by a right-continuous monotone increasing function (a càdlàg function) ![{displaystyle Fcolon mathbb {R} rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c45b6faf38bb3fb300ab4678d3675afd172f56)


In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to 
Definition[edit]
The cumulative distribution function of a real-valued random variable 
|
|
(Eq.1) |
where the right-hand side represents the probability that the random variable 

The probability that 
![(a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

|
|
(Eq.2) |
In the definition above, the «less than or equal to» sign, «≤», is a convention, not a universally used one (e.g. Hungarian literature uses «<«), but the distinction is important for discrete distributions. The proper use of tables of the binomial and Poisson distributions depends upon this convention. Moreover, important formulas like Paul Lévy’s inversion formula for the characteristic function also rely on the «less than or equal» formulation.
If treating several random variables 






The probability density function of a continuous random variable can be determined from the cumulative distribution function by differentiating[3] using the Fundamental Theorem of Calculus; i.e. given 
as long as the derivative exists.
The CDF of a continuous random variable 

In the case of a random variable 

If 


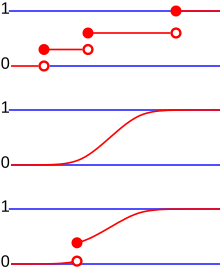
Properties[edit]
From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.
Example of a cumulative distribution function with a countably infinite set of discontinuities.
Every cumulative distribution function 
Every function with these four properties is a CDF, i.e., for every such function, a random variable can be defined such that the function is the cumulative distribution function of that random variable.
If 




If the CDF 




for all real numbers 




If 

and for any 
CDF plot with two red rectangles, illustrating 

as shown in the diagram.
In particular, we have
Examples[edit]
As an example, suppose 
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
Then the CDF of 
Suppose instead that 
Then the CDF of 
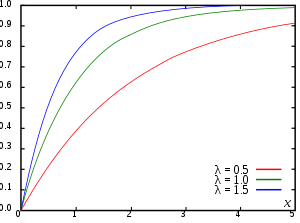
Suppose 

Here λ > 0 is the parameter of the distribution, often called the rate parameter.
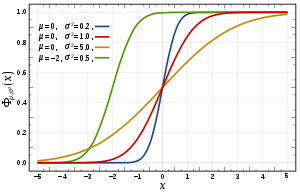
Suppose 

Here the parameter 

A table of the CDF of the standard normal distribution is often used in statistical applications, where it is named the standard normal table, the unit normal table, or the Z table.
Suppose 

Here 




Derived functions[edit]
Complementary cumulative distribution function (tail distribution)[edit]
Sometimes, it is useful to study the opposite question and ask how often the random variable is above a particular level. This is called the complementary cumulative distribution function (ccdf) or simply the tail distribution or exceedance, and is defined as
This has applications in statistical hypothesis testing, for example, because the one-sided p-value is the probability of observing a test statistic at least as extreme as the one observed. Thus, provided that the test statistic, T, has a continuous distribution, the one-sided p-value is simply given by the ccdf: for an observed value 
In survival analysis, 

- Properties
- For a non-negative continuous random variable having an expectation, Markov’s inequality states that[4]
- As
, and in fact
provided that
is finite.
Proof:[citation needed]
Assuminghas a density function
, for any
Then, on recognizing
and rearranging terms,
as claimed.
- For a random variable having an expectation,
and for a non-negative random variable the second term is 0.
If the random variable can only take non-negative integer values, this is equivalent to
Folded cumulative distribution[edit]
While the plot of a cumulative distribution 
where 
Inverse distribution function (quantile function)[edit]
If the CDF F is strictly increasing and continuous then ![F^{-1}(p),pin [0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89fe1b58ff06ad5647ba178886bb6704d8da846)


Some distributions do not have a unique inverse (for example if 


Some useful properties of the inverse cdf (which are also preserved in the definition of the generalized inverse distribution function) are:
is nondecreasing
if and only if
- If
has a
distribution then
is distributed as
. This is used in random number generation using the inverse transform sampling-method.
- If
is a collection of independent
-distributed random variables defined on the same sample space, then there exist random variables
such that
is distributed as
and
with probability 1 for all
.[citation needed]
The inverse of the cdf can be used to translate results obtained for the uniform distribution to other distributions.
Empirical distribution function[edit]
The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function[citation needed].
Multivariate case[edit]
Definition for two random variables[edit]
When dealing simultaneously with more than one random variable the joint cumulative distribution function can also be defined. For example, for a pair of random variables 

|
|
(Eq.3) |
where the right-hand side represents the probability that the random variable 



Example of joint cumulative distribution function:
For two continuous variables X and Y:
For two discrete random variables, it is beneficial to generate a table of probabilities and address the cumulative probability for each potential range of X and Y, and here is the example:[8]
given the joint probability mass function in tabular form, determine the joint cumulative distribution function.
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| X = 1 | 0 | 0.1 | 0 | 0.1 |
| X = 3 | 0 | 0 | 0.2 | 0 |
| X = 5 | 0.3 | 0 | 0 | 0.15 |
| X = 7 | 0 | 0 | 0.15 | 0 |
Solution: using the given table of probabilities for each potential range of X and Y, the joint cumulative distribution function may be constructed in tabular form:
| Y < 2 | 2 ≤ Y < 4 | 4 ≤ Y < 6 | 6 ≤ Y < 8 | Y ≥ 8 | |
| X < 1 | 0 | 0 | 0 | 0 | 0 |
| 1 ≤ X < 3 | 0 | 0 | 0.1 | 0.1 | 0.2 |
| 3 ≤ X < 5 | 0 | 0 | 0.1 | 0.3 | 0.4 |
| 5 ≤ X < 7 | 0 | 0.3 | 0.4 | 0.6 | 0.85 |
| X ≥ 7 | 0 | 0.3 | 0.4 | 0.75 | 1 |
Definition for more than two random variables[edit]
For 


|
|
(Eq.4) |
Interpreting the 

Properties[edit]
Every multivariate CDF is:
- Monotonically non-decreasing for each of its variables,
- Right-continuous in each of its variables,
-
Not every function satisfying the above four properties is a multivariate CDF, unlike in the single dimension case. For example, let 






The probability that a point belongs to a hyperrectangle is analogous to the 1-dimensional case:[9]
Complex case[edit]
Complex random variable[edit]
The generalization of the cumulative distribution function from real to complex random variables is not obvious because expressions of the form 

Complex random vector[edit]
Generalization of Eq.4 yields
as definition for the CDS of a complex random vector 
Use in statistical analysis[edit]
The concept of the cumulative distribution function makes an explicit appearance in statistical analysis in two (similar) ways. Cumulative frequency analysis is the analysis of the frequency of occurrence of values of a phenomenon less than a reference value. The empirical distribution function is a formal direct estimate of the cumulative distribution function for which simple statistical properties can be derived and which can form the basis of various statistical hypothesis tests. Such tests can assess whether there is evidence against a sample of data having arisen from a given distribution, or evidence against two samples of data having arisen from the same (unknown) population distribution.
Kolmogorov–Smirnov and Kuiper’s tests[edit]
The Kolmogorov–Smirnov test is based on cumulative distribution functions and can be used to test to see whether two empirical distributions are different or whether an empirical distribution is different from an ideal distribution. The closely related Kuiper’s test is useful if the domain of the distribution is cyclic as in day of the week. For instance Kuiper’s test might be used to see if the number of tornadoes varies during the year or if sales of a product vary by day of the week or day of the month.
See also[edit]
References[edit]
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. p. 181. ISBN 9781108455145.
- ^ a b c d e f Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
- ^ Montgomery, Douglas C.; Runger, George C. (2003). Applied Statistics and Probability for Engineers (PDF). John Wiley & Sons, Inc. p. 104. ISBN 0-471-20454-4. Archived (PDF) from the original on 2012-07-30.
- ^ Zwillinger, Daniel; Kokoska, Stephen (2010). CRC Standard Probability and Statistics Tables and Formulae. CRC Press. p. 49. ISBN 978-1-58488-059-2.
- ^ Gentle, J.E. (2009). Computational Statistics. Springer. ISBN 978-0-387-98145-1. Retrieved 2010-08-06.[page needed]
- ^
Monti, K. L. (1995). «Folded Empirical Distribution Function Curves (Mountain Plots)». The American Statistician. 49 (4): 342–345. doi:10.2307/2684570. JSTOR 2684570. - ^ Xue, J. H.; Titterington, D. M. (2011). «The p-folded cumulative distribution function and the mean absolute deviation from the p-quantile» (PDF). Statistics & Probability Letters. 81 (8): 1179–1182. doi:10.1016/j.spl.2011.03.014.
- ^ «Joint Cumulative Distribution Function (CDF)». math.info. Retrieved 2019-12-11.
- ^ «Archived copy» (PDF). www.math.wustl.edu. Archived from the original (PDF) on 22 February 2016. Retrieved 13 January 2022.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). «The Modified-Half-Normal distribution: Properties and an efficient sampling scheme». Communications in Statistics — Theory and Methods: 1–23. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
External links[edit]
Media related to Cumulative distribution functions at Wikimedia Commons
Кумулятивная функция распределения в нормально распределенных данных
Добавлено 30 августа 2020 в 11:43
В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.
Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.
Что мы знаем из предыдущих статей:
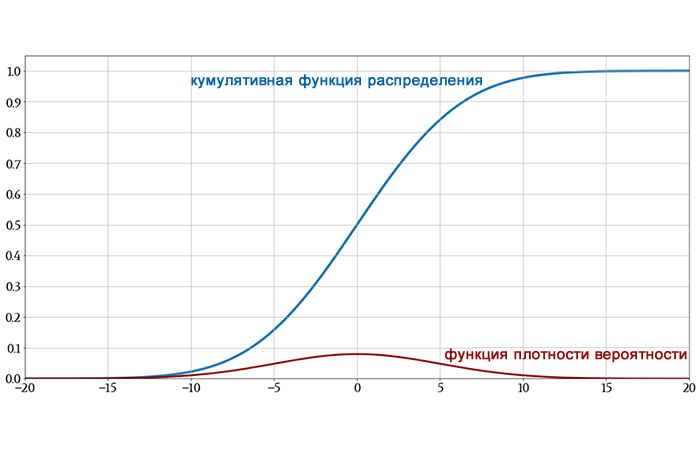
- мы можем получить функцию плотности вероятности нормально распределенных результатов измерений, вычислив стандартное отклонение и среднее значение набора данных;
- эта функция плотности вероятности является идеализированным математическим эквивалентом фигуры, которую мы наблюдаем на гистограмме набора данных;
- мы получаем вероятность (т.е. вероятность того, что определенные значения результатов измерений будут иметь место) путем интегрирования функции плотности вероятности по заданному интервалу.
Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.
Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.
Кумулятивная функция нормального распределения
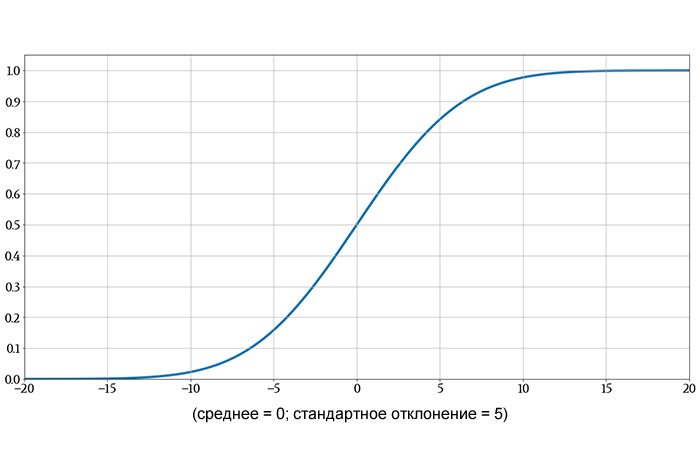
Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.
Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция (e^{-x^2}) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.
В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.
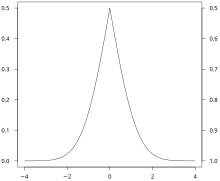
Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:
На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.
Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,
[Phi(z)=frac{1}{sqrt{2 pi}}int_{-infty}^{z}e^{-frac{x^2}{2}}dx]
Пример кумулятивной функции распределения
Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.
Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.
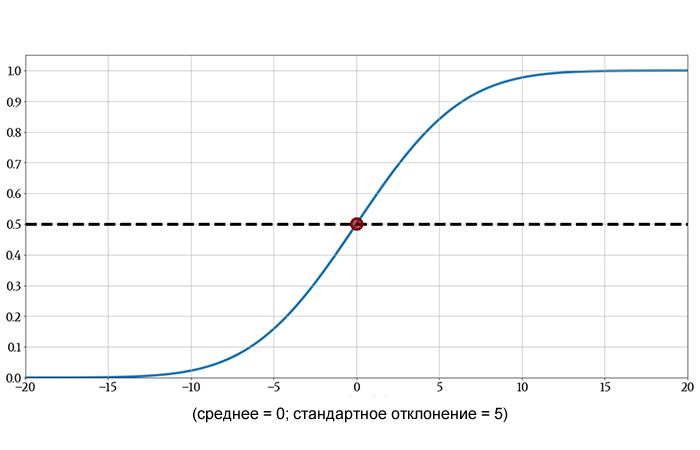
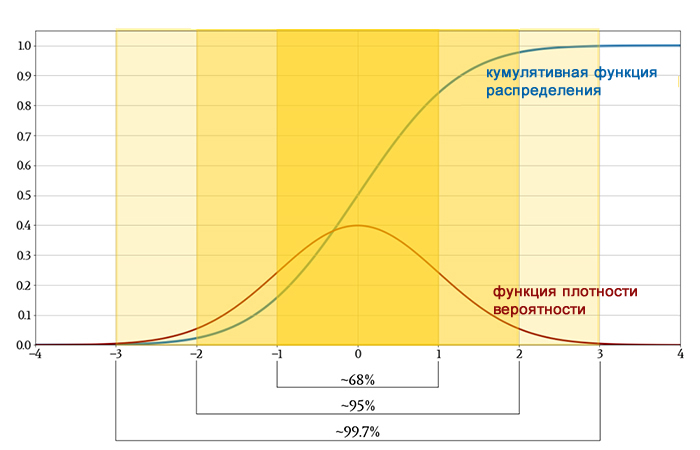
Например:
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.
Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z1 и z2, всё, что нам нужно сделать, это вычесть значение функции распределения в z2 из значения функции распределения в z1 (а затем при необходимости взять модуль полученного значения).
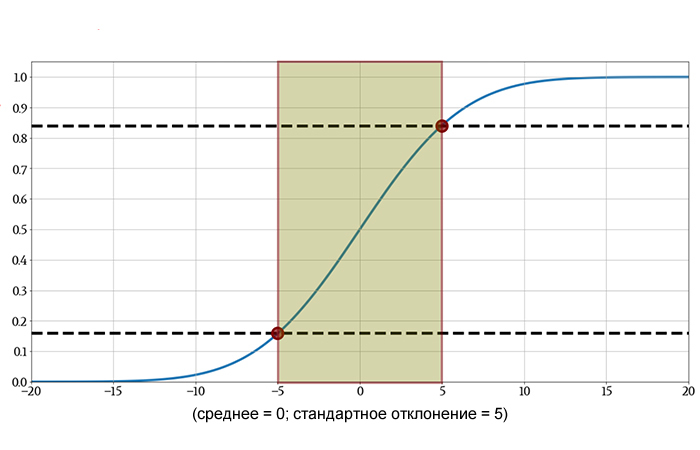
Вот еще один пример:
Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.
Вероятность и стандартное отклонение
Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).
Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:
- вероятность того, что измеренное значение будет в пределах двух стандартных отклонений от среднего, составляет 95,45%;
- вероятность того, что измеренное значение будет в пределах трех стандартных отклонений от среднего, составляет 99,73%.
Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.
Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.
Заключение
Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.
Теги
ВероятностьКумулятивная функция распределения / CDF (cumulative distribution function)Нормальное распределение / Гауссово распределениеСтандартное нормальное распределениеСтатистикаСтатистический анализФункция плотности вероятности
Кумулята
Теперь построим кумуляту — график накопленных относительных частот. Расположим его под гистограммой.
Кумулята — это экспериментальная оценка формы графика функции распределения. Теоретическая кривая будет красивой и гладкой — мы познакомились с ней в начале работы, обсуждая свой вариант задания. Экспериментальная оценка — ломаная линия, да ещё и с погрешностями. Эти случайные ошибки вызваны ограниченным, не бесконечным объёмом выборки. В любом случае, эти графики начинаются в нуле и постепенно растут до 100%.
Напомним, что значения накопленных частот должны быть привязаны к верхним границам интервалов — в соответствии со стандартами и здравым смыслом. Идея в том, что накопленная частота накапливается именно к концу интервала, а не к середине.
Построим график в виде ломаной линии:
Insert — Charts — Insert Scatter (X, Y) or Bubble Chart
Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму
Вставка графика Y (X)
Выбираем тип графика
Scatter — Scatter with Straight Lines
Точечная — Точечная с прямыми отрезками
Это просто ломаная линия без маркеров точек.
Ломаная линия
Выбираем данные для графика:
Select Data — Select Data Source — Legend Entries (Series) — Add
Выбрать данные — Выбор источника данных — Элементы легенды (ряды) — Добавить
В окне
Edit Series
Изменение ряда
выбираем следующие данные.
Столбец «иксов» — верхние границы:
Series X Values
Значения Х
Столбец «игреков» — накопленные частоты:
Series Y Values
Значения Y
Убираем заголовок диаграммы:
Chart Elements — Chart Title
Элементы диаграммы — Название диаграммы
Настраиваем цвет линии на графике.
Format Data Series — Series options — Fill & Line — Line
Формат ряда данных —Параметры ряда — Заливка и границы — Линия
Line — Solid line
Линия — Сплошная линия
Color — Black
Цвет — Чёрный
Width = 0.5 pt
Ширина — 0,5 пт
Если отрезков много, то ломаная линия выглядит как гладкая кривая.
Кумулята
Настроим числовые метки на вертикальной оси, чтобы выводились целые числа:
Format Axis — Axis Options — Number — Decimal places — 0
Формат оси — Параметры оси — Число — Число десятичных знаков — 0
Целочисленные метки
Установим диапазоны значений по осям.
Вертикальная ось — метки в процентах, а границы диапазона — числа. Поэтому пределы изменения будут от 0 до 1:
Category — Percentage
Категория — Процентный
Axis Options — Bounds
Параметры оси — Границы
Minimum — 0
Минимум — 0
Maximum — 1
Максимум — 1
Горизонтальная ось — в соответствии с интервалами группировки — от 190 до 310.
Кумулята
Подгоняем размеры графика и размещаем его под гистограммой. Можно сделать это вручную.
Если захочется особой точности, поработаем через меню параметров графика (числа условные).
Format Chart Area — Chart Options — Size & Properties — Size
Формат области диаграммы — Параметры диаграммы — Размер и свойства — Размер
Height — 1.8 in
Высота — 7,62 см
Width — 5.3 in
Ширина — 12,7 см
В английской версии пакета размеры измеряются в дюймах. В русской версии — в сантиметрах. Можем установить точные значения размеров вручную.
Размер диаграммы
Окончательно совмещаем маштаб гистограммы и кумуляты: начало первого интервала 190, конец последнего интервала 310. Положения этих двух меток на обоих графиках должны совпадать.
Проблемы с масштабом решаем так. Значение 190 находится в начале интервала, обозначенного 193. Значение 310 находится в конце интервала, следующего за 303.
Гистограмма и кумулята
















![{displaystyle mathbb {E} [X]=int _{-infty }^{infty }tdF_{X}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b8b269c99751edd630ab22c36aac1ffde3a4110)





















![{displaystyle F^{-1}(p)=inf{xin mathbb {R} :F(x)geq p},quad forall pin [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f8d361fa630d92216975a16f12756a137f3d84)





![U[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4a82b2a883d751cf53e5ac11ea12b9e36298f0)