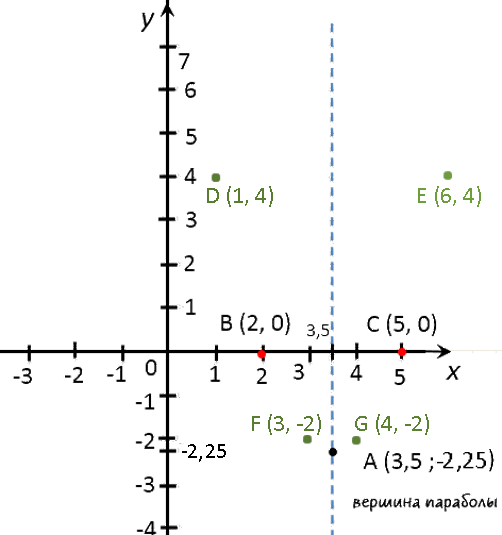Квадратичная функция как найти корни

Квадратичная функция

Adrien1018

Квадратичные функции

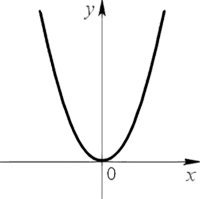
Квадратичная функция — это многочлен второй степени. Это означает, что он имеет вид ax ^ 2 + bx + c. Здесь a, b и c могут быть любым числом. Когда вы рисуете квадратичную функцию, вы получаете параболу, как вы можете видеть на картинке выше. Когда a отрицательно, эта парабола будет перевернута.

Что такое корни?

Корни функции — это точки, в которых значение функции равно нулю. Они соответствуют точкам, в которых график пересекает ось x. Поэтому, когда вы хотите найти корни функции, вы должны установить функцию равной нулю. Для простой линейной функции это очень просто. Например:

е (х) = х +3

Тогда корень x = -3, так как -3 + 3 = 0. Линейные функции имеют только один корень. Квадратичные функции могут иметь ноль, один или два корня. Вот простой пример:

е (х) = х ^ 2 — 1

Устанавливая x ^ 2-1 = 0, мы видим, что x ^ 2 = 1. Это верно как для x = 1, так и для x = -1.

Примером квадратичной функции только с одним корнем является функция x ^ 2. Он равен нулю только тогда, когда x равен нулю. Также может случиться так, что здесь нет корней. Так обстоит дело, например, с функцией x ^ 2 + 3. Затем, чтобы найти корень, мы должны иметь x, для которого x ^ 2 = -3. Это невозможно, если вы не используете комплексные числа. В большинстве практических ситуаций использование комплексных чисел имеет смысл, поэтому мы говорим, что решения нет.

Строго говоря, любая квадратичная функция имеет два корня, но вам может потребоваться использовать комплексные числа, чтобы найти их все. В этой статье мы не будем заострять внимание на комплексных числах, поскольку для большинства практических целей они бесполезны. Однако есть некоторые области, где они могут очень пригодиться. Если вы хотите узнать больше о комплексных числах, прочтите мою статью о них.

• Математика: как использовать комплексные числа и комплексную плоскость

Способы найти корни квадратичной функции

Факторизация

Чаще всего люди учатся определять корни квадратичной функции путем факторизации. Для многих квадратичных функций это самый простой способ, но также может быть очень трудно понять, что делать. У нас есть квадратичная функция ax ^ 2 + bx + c, но, поскольку мы собираемся установить ее равной нулю, мы можем разделить все члены на a, если a не равно нулю. Тогда у нас есть уравнение вида:

х ^ 2 + пикс + д = 0.

Теперь мы пытаемся найти такие факторы s и t, что:

(xs) (xt) = x ^ 2 + px + q

Если нам это удастся, мы знаем, что x ^ 2 + px + q = 0 истинно тогда и только тогда, когда (xs) (xt) = 0 истинно. (xs) (xt) = 0 означает, что либо (xs) = 0, либо (xt) = 0. Это означает, что x = s и x = t являются решениями, а значит, и корнями.

Если (xs) (xt) = x ^ 2 + px + q, то выполняется s * t = q и — s — t = p.

Числовой пример

х ^ 2 + 8x + 15

Затем мы должны найти такие s и t, что s * t = 15 и — s — t = 8. Итак, если мы выберем s = -3 и t = -5, мы получим:

х ^ 2 + 8х + 15 = (х + 3) (х + 5) = 0.

Следовательно, x = -3 или x = -5. Давайте проверим эти значения: (-3) ^ 2 + 8 * -3 +15 = 9-24 + 15 = 0 и (-5) ^ 2 + 8 * -5 +15 = 25-40 + 15 = 0. Итак действительно, это корни.

Однако найти такую ​​факторизацию может быть очень сложно. Например:

х ^ 2 -6x + 7

Тогда корни 3 — sqrt 2 и 3 + sqrt 2. Их не так просто найти.

Формула ABC

Другой способ найти корни квадратичной функции. Это простой метод, которым может воспользоваться каждый. Это просто формула, которую вы можете заполнить, которая дает вам корни. Формула для квадратичной функции ax ^ 2 + bx + c выглядит следующим образом:

(-b + sqrt (b ^ 2 -4ac)) / 2a и (-b — sqrt (b ^ 2 -4ac)) / 2a

Эта формула дает оба корня. Когда существует только один корень, обе формулы дадут одинаковый ответ. Если корней не существует, то b ^ 2 -4ac будет меньше нуля. Следовательно, квадратного корня не существует, и нет ответа на формулу. Число b ^ 2 -4ac называется дискриминантом.

Числовой пример

Давайте попробуем формулу на той же функции, которую мы использовали в примере факторизации:

х ^ 2 + 8x + 15

Тогда a = 1, b = 8 и c = 15. Следовательно:

(-b + sqrt (b ^ 2 -4ac)) / 2a = (-8 + sqrt (64-4 * 1 * 15)) / 2 * 1 = (-8 + sqrt (4)) / 2 = -6 / 2 = -3

(-b — sqrt (b ^ 2 -4ac)) / 2a = (-8-sqrt (64-4 * 1 * 15)) / 2 * 1 = (-8-sqrt (4)) / 2 = -10 / 2 = -5

Действительно, формула дает одни и те же корни.

Квадратичная функция

Завершение площади

Формула ABC составляется методом заполнения квадрата. Идея завершения квадрата заключается в следующем. У нас есть ax ^ 2 + bx + c. Мы предполагаем, что a = 1. Если это не так, мы могли бы разделить на a и получить новые значения для b и c. Другая часть уравнения равна нулю, поэтому, если мы разделим ее на a, она останется нулевой. Затем делаем следующее:

х ^ 2 + Ьх + с = (х + Ь / 2) ^ 2 — (Ь ^ 2/4) + с = 0.

Тогда (x + b / 2) ^ 2 = (b ^ 2/4) — c.

Следовательно, x + b / 2 = sqrt ((b ^ 2/4) — c) или x + b / 2 = — sqrt ((b ^ 2/4) — c).

Это означает, что x = b / 2 + sqrt ((b ^ 2/4) — c) или x = b / 2 — sqrt ((b ^ 2/4) — c).

Это равно ABC-формуле для a = 1. Однако это легче вычислить.

Числовой пример

Снова берем x ^ 2 + 8x + 15. Тогда:

х ^ 2 + 8х + 15 = (х + 4) ^ 2-16 + 15 = (х + 4) ^ 2-1 = 0.

Тогда x = -4 + sqrt 1 = -3 или x = -4 — sqrt 1 = -5.

Действительно, это дает то же решение, что и другие методы.

Резюме

Мы рассмотрели три различных метода нахождения корней квадратичной функции вида ax ^ 2 + bx + c. Первый — это факторизация, когда мы пытаемся записать функцию как (xs) (xt). Тогда мы знаем, что решениями являются s и t. Второй метод, который мы видели, — это формула ABC. Здесь вам просто нужно заполнить a, b и c, чтобы получить решения. Наконец, мы завершили метод квадратов, в котором мы пытаемся записать функцию как (xp) ^ 2 + q.

Квадратичные неравенства

Поиск корней квадратичной функции может возникнуть во многих ситуациях. Один из примеров — решение квадратичных неравенств. Здесь вы должны найти корни квадратичной функции, чтобы определить границы пространства решений. Если вы хотите узнать, как именно решить квадратичные неравенства, я предлагаю прочитать мою статью по этой теме.

• Математика: как решить квадратичное неравенство

Функции высшей степени

Определение корней функции степени выше двух — более сложная задача. Для функций третьей степени — функций вида ax ^ 3 + bx ^ 2 + cx + d — есть формула, аналогичная формуле ABC. Эта формула довольно длинная и не так проста в использовании. Для функций четвертой степени и выше доказано, что такой формулы не существует.

Это означает, что найти корни функции третьей степени возможно, но не так просто вручную. Для функций четвертой степени и выше это становится очень сложно, и поэтому лучше выполнять это с помощью компьютера.

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где  называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.

График  функции  имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если ,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3.  Если ,то уравнение  имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны  на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 

 

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение: 

,  

3.   Координаты  вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2.  Уравнение квадратичной функции имеет вид  — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции  , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение  графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат: 

Следовательно,  координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда 

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения  ,

— сдвига графика функции вдоль оси от значения  
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x2 − 7x + 9	a = 2 b = −7 с = 9
y = 3x2 − 1	a = 3 b = 0 с = −1
y = −3x2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Парабола выглядит следующим образом.

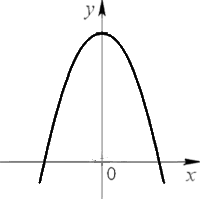
Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

1. Направление ветвей параболы

   Запомните!
   

   Если «a > 0», то ветви направлены вверх.
   

   Если «a < 0», то ветви направлены вниз.
   

   В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
   

2. Координаты вершины параболы

   Запомните!
   

   Чтобы найти «x₀»
   (координата вершины по оси «Ox»)
   нужно использовать формулу:

   Найдем «x₀» для нашей функции «y = x² −7x + 10».

   Теперь нам нужно найти «y₀»
   (координату вершины по оси «Oy»).
   Для этого нужно подставить найденное значение «x₀» в исходную функцию.
   Вспомнить, как найти значение функции можно в уроке
   «Как решать задачи на функцию» в подразделе
   «Как получить значение функции».

   y₀(3,5) =
   (3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

   −12,25 + 10 = −2,25

   Выпишем полученные координаты вершины параболы.

   (·) A (3,5; −2,25) — вершина параболы.

   Отметим вершину параболы на системе координат.
   Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
   относительно оси «Oy».

   

3. Нули функции

   Для начала давайте разберемся, что называют нулями функции.

   Запомните!
   

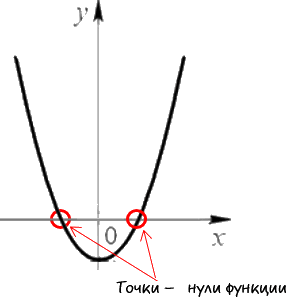
   Нули функции — это точки пересечения графика функции с осью «Ox»
   (осью абсцисс).

   Наглядно нули функции на графике выглядят так:

   

   Свое название нули функции получили из-за того, что у этих точек координата
   по оси «Oy» равна нулю.

   Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

   Запомните!
   

   Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
   «y = 0».

   Подставим в заданную функцию «y = x² −7x + 10»
   вместо «y = 0» и решим полученное
   квадратное уравнение
   относительно
   «x» .

   0 = x² −7x + 10
   x² −7x + 10 = 0

   x_1;2 =

   7 ± √49 − 4 · 1 · 10

   2 · 1

   x_1;2 =

   x_1;2 =

   x1 =	x2 =
   x1 =	x2 =
   x1 = 5	x2 = 2

   Мы получили два корня в уравнении, значит, у нас две точки пересечения
   с осью «Ox».
   Назовем эти точки и выпишем их координаты.

   • (·) B (5; 0)
   • (·) C (2; 0)

   Отметим полученные точки («нули функции») на системе координат.

   

4. Дополнительные точки для построения графика

   Возьмем четыре произвольные числовые значения для «x».
   Целесообразно брать целые числовые значения на оси «Ox»,
   которые наиболее близки к оси
   симметрии. Числа запишем в таблицу в порядке возрастания.

   x	1	3	4	6
   y

   Для каждого выбранного значения «x»
   рассчитаем «y».

   • y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
     4
   • y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
     −2

   • y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
     −2
   • y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
     4

   Запишем полученные результаты в таблицу.

   x	1	3	4	6
   y	4	−2	−2	4

   Отметим полученные точки графика на системе координат (зеленые точки).

   

   Теперь мы готовы построить график.
   На забудьте после построения подписать график функции.

   

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции
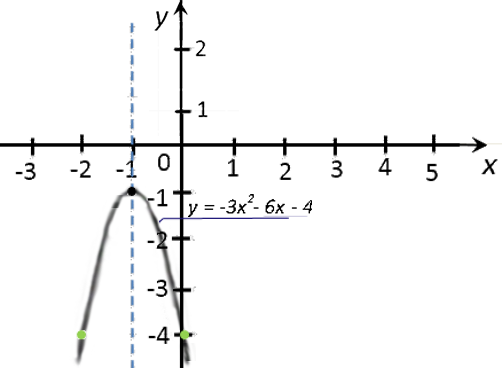
«y = −3x² − 6x − 4».

1. Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.


2. Координаты вершины параболы

   x₀ =
   x₀ = =

   = −1

   y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
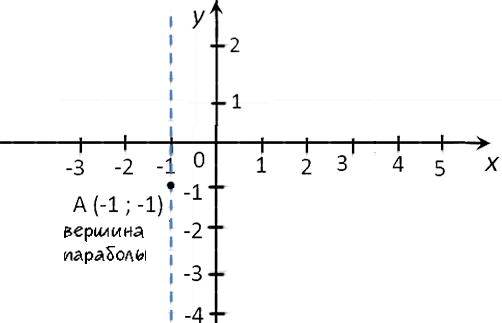
   −3 · 1 + 6 − 4 = −1

   (·) A (−1; −1)

   — вершина параболы.

   

3. Нули функции

   Точки пересечения с осью «Ox» (y = 0).

   0 = −3x² − 6x − 4

   −3x² − 6x − 4 = 0 |·(−1)

   3x² + 6x + 4 = 0

   x_1;2 =

   −6 ± √62 − 4 · 3 · 4

   2 · 1

   x_1;2 =

   x_1;2 =

   
   Ответ: нет действительных корней.

   Так как корней нет, значит, график функции не пересекает ось
   «Ox».

4. Вспомогательные точки для: «x = −3»;
   «x = −2»;
   «x = 0»;
   «x = 1». Подставим в исходную функцию
   «y = −3x² − 6x − 4».
   • y(−3) = −3 · (−3)² − 6 · (−3) − 4
     = −3 · 9 + 18 − 4 = −27 + 14 = −13
   • y(−2) = −3 · (−2)² − 6 · (−2) − 4
     = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

   • y(0) = −3 · 0² − 6 · 0 − 4
     = −4
   • y(1) = −3 · 1² − 6 · 1 − 4
     = −3 −6 − 4 = −13

   x	−3	−2	0	1
   y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

---

Ваши комментарии

Оставить комментарий:

---

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so «quadratic polynomial» and «quadratic function» were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as «quadratic».

For example, a univariate (single-variable) quadratic function has the form^[1]

where x is its variable. The graph of a univariate quadratic function is a parabola, a curve that has an axis of symmetry parallel to the y-axis.

If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros of the corresponding quadratic function.

The bivariate case in terms of variables x and y has the form

with at least one of a, b, c not equal to zero. The zeros of this quadratic function is, in general (that is, if a certain expression of the coefficients is not equal to zero), a conic section (a circle or other ellipse, a parabola, or a hyperbola).

A quadratic function in three variables x, y, and z contains exclusively terms x², y², z², xy, xz, yz, x, y, z, and a constant:

where at least one of the coefficients a, b, c, d, e, f of the second-degree terms is not zero.

A quadratic function can have an arbitrarily large number of variables. The set of its zero form a quadric, which is a surface in the case of three variables and a hypersurface in general case.

Etymology[edit]

The adjective quadratic comes from the Latin word quadrātum («square»). A term raised to the second power like x² is called a square in algebra because it is the area of a square with side x.

Terminology[edit]

Coefficients[edit]

The coefficients of a quadric function are often taken to be real or complex numbers, but they may be taken in any ring, in which case the domain and the codomain are this ring (see polynomial evaluation).

Degree[edit]

When using the term «quadratic polynomial», authors sometimes mean «having degree exactly 2», and sometimes «having degree at most 2». If the degree is less than 2, this may be called a «degenerate case». Usually the context will establish which of the two is meant.

Sometimes the word «order» is used with the meaning of «degree», e.g. a second-order polynomial. However, where the «degree of a polynomial» refers to the largest degree of a non-zero term of the polynomial, more typically «order» refers to the lowest degree of a non-zero term of a power series.

Variables[edit]

A quadratic polynomial may involve a single variable x (the univariate case), or multiple variables such as x, y, and z (the multivariate case).

The one-variable case[edit]

Any single-variable quadratic polynomial may be written as

where x is the variable, and a, b, and c represent the coefficients. Such polynomials often arise in a quadratic equation The solutions to this equation are called the roots and can be expressed in terms of the coefficients as the quadratic formula. Each quadratic polynomial has an associated quadratic function, whose graph is a parabola.

Bivariate and multivariate cases[edit]

Any quadratic polynomial with two variables may be written as

where x and y are the variables and a, b, c, d, e, f are the coefficients, and one of a, b and c is nonzero. Such polynomials are fundamental to the study of conic sections, as the implicit equation of a conic section is obtained by equating to zero a quadratic polynomial, and the zeros of a quadratic function form a (possibly degenerate) conic section.

Similarly, quadratic polynomials with three or more variables correspond to quadric surfaces or hypersurfaces.

Quadratic polynomials that have only terms of degree two are called quadratic forms.

Forms of a univariate quadratic function[edit]

A univariate quadratic function can be expressed in three formats:^[2]

The coefficient a is the same value in all three forms. To convert the standard form to factored form, one needs only the quadratic formula to determine the two roots r₁ and r₂. To convert the standard form to vertex form, one needs a process called completing the square. To convert the factored form (or vertex form) to standard form, one needs to multiply, expand and/or distribute the factors.

Graph of the univariate function[edit]

Regardless of the format, the graph of a univariate quadratic function is a parabola (as shown at the right). Equivalently, this is the graph of the bivariate quadratic equation .

• If a > 0, the parabola opens upwards.
• If a < 0, the parabola opens downwards.

The coefficient a controls the degree of curvature of the graph; a larger magnitude of a gives the graph a more closed (sharply curved) appearance.

The coefficients b and a together control the location of the axis of symmetry of the parabola (also the x-coordinate of the vertex and the h parameter in the vertex form) which is at

The coefficient c controls the height of the parabola; more specifically, it is the height of the parabola where it intercepts the y-axis.

Vertex[edit]

The vertex of a parabola is the place where it turns; hence, it is also called the turning point. If the quadratic function is in vertex form, the vertex is (h, k). Using the method of completing the square, one can turn the standard form

into

so the vertex, (h, k), of the parabola in standard form is

^{[citation needed]}

If the quadratic function is in factored form

the average of the two roots, i.e.,

is the x-coordinate of the vertex, and hence the vertex (h, k) is

The vertex is also the maximum point if a < 0, or the minimum point if a > 0.

The vertical line

that passes through the vertex is also the axis of symmetry of the parabola.

Maximum and minimum points[edit]

Using calculus, the vertex point, being a maximum or minimum of the function, can be obtained by finding the roots of the derivative:

x is a root of f ‘(x) if f ‘(x) = 0
resulting in

with the corresponding function value

so again the vertex point coordinates, (h, k), can be expressed as

Roots of the univariate function[edit]

Exact roots[edit]

The roots (or zeros), r₁ and r₂, of the univariate quadratic function

are the values of x for which f(x) = 0.

When the coefficients a, b, and c, are real or complex, the roots are

Upper bound on the magnitude of the roots[edit]

The modulus of the roots of a quadratic can be no greater than where is the golden ratio ^{[4][importance?]}

The square root of a univariate quadratic function[edit]

The square root of a univariate quadratic function gives rise to one of the four conic sections, almost always either to an ellipse or to a hyperbola.

If then the equation describes a hyperbola, as can be seen by squaring both sides. The directions of the axes of the hyperbola are determined by the ordinate of the minimum point of the corresponding parabola If the ordinate is negative, then the hyperbola’s major axis (through its vertices) is horizontal, while if the ordinate is positive then the hyperbola’s major axis is vertical.

If then the equation describes either a circle or other ellipse or nothing at all. If the ordinate of the maximum point of the corresponding parabola
is positive, then its square root describes an ellipse, but if the ordinate is negative then it describes an empty locus of points.

Iteration[edit]

To iterate a function , one applies the function repeatedly, using the output from one iteration as the input to the next.

One cannot always deduce the analytic form of , which means the n^th iteration of . (The superscript can be extended to negative numbers, referring to the iteration of the inverse of if the inverse exists.) But there are some analytically tractable cases.

For example, for the iterative equation

one has

where

and

So by induction,

can be obtained, where can be easily computed as

Finally, we have

as the solution.

See Topological conjugacy for more detail about the relationship between f and g. And see Complex quadratic polynomial for the chaotic behavior in the general iteration.

The logistic map

with parameter 2<r<4 can be solved in certain cases, one of which is chaotic and one of which is not. In the chaotic case r=4 the solution is

where the initial condition parameter is given by . For rational , after a finite number of iterations maps into a periodic sequence. But almost all are irrational, and, for irrational , never repeats itself – it is non-periodic and exhibits sensitive dependence on initial conditions, so it is said to be chaotic.

The solution of the logistic map when r=2 is

for . Since for any value of other than the unstable fixed point 0, the term goes to 0 as n goes to infinity, so goes to the stable fixed point

Bivariate (two variable) quadratic function[edit]

A bivariate quadratic function is a second-degree polynomial of the form

where A, B, C, D, and E are fixed coefficients and F is the constant term.
Such a function describes a quadratic surface. Setting equal to zero describes the intersection of the surface with the plane which is a locus of points equivalent to a conic section.

Minimum/maximum[edit]

If the function has no maximum or minimum; its graph forms a hyperbolic paraboloid.

If the function has a minimum if both A > 0 and B > 0, and a maximum if both A < 0 and B < 0; its graph forms an elliptic paraboloid. In this case the minimum or maximum occurs at where:

If and the function has no maximum or minimum; its graph forms a parabolic cylinder.

If and the function achieves the maximum/minimum at a line—a minimum if A>0 and a maximum if A<0; its graph forms a parabolic cylinder.

See also[edit]

• Quadratic form
• Quadratic equation
• Matrix representation of conic sections
• Quadric
• Periodic points of complex quadratic mappings
• List of mathematical functions

References[edit]

• Algebra 1, Glencoe, ISBN 0-07-825083-8
• Algebra 2, Saxon, ISBN 0-939798-62-X

External links[edit]

• Weisstein, Eric W. «Quadratic». MathWorld.