Благодаря прочтению этой статьи вы научитесь:
- Извлекать корни из разных чисел;
- Решать разнообразные задания по этой тематике;
- Применять удобные таблицы на практике.
А также пополните свой мозг новыми знаниями, что всегда хорошо и полезно! Приятным бонусом для вас будут задания для отработки материала с ответами, которые вы сможете найти в конце этой статьи. Что значит понятие: «Извлечение корня из числа»?
Определение
Извлечение корня из числа — это нахождение значения корня, т.е. действие, обратное возведению в степень.
Числа b и a равны, ведь при извлечении корня n-ной степени одного из чисел, мы, соответственно, находим и второе.
- n — натуральное число, являющиеся степенью корня.
- a — подкоренное значение.
Интересно
При помощи разложения функции в ряд можно показать, что сумма всех натуральных чисел равна:
1/12[18]
Когда следует извлекать корень? Если вы видите, что a можно представить в виде n-ной степени какого-либо числа b, то корень a можно извлечь.
Определение
Квадратный корень из числа — это неизвестное число, которое дает это же число при возведении его в квадрат.
Пример извлечения корня:
√25=5×5 — из этого становится ясно, что квадратный корень числа равен 5.
В обратной ситуации, когда нельзя представить корень n-ной степени из числа a, в виде n-ной степени числа b, корень не извлекается или находится лишь приближенное значение этого корня.
Пример:
√6≈√2,44949
Для этого используют различные виды решений, начиная с калькулятора, заканчивая формулами. Калькулятор хоть и посчитает все вместо нас, но не всегда мы можем его применить. Поэтому важно знать другие варианты нахождения приближенного значения корня.
Способы извлечения корня
Для того, чтобы найти значение корня, существуют такие способы извлечения корня, как:
- Применение различных таблиц.
- Разложение чисел или выражений на простые множители.
- Извлечение корней из дробных чисел.
- Извлечение отрицательного корня.
- Поразрядное нахождение значения корня.
Они основываются на свойствах корней. Далее рассмотрим таблицы, которые могут помочь в процессе извлечения корней.
Квадраты натуральных чисел
Основной является таблица квадратов натуральных чисел:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Она, пожалуй, самая распространенная среди школьников. Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:
- Чтобы быстро возвести в квадрат число, на конце которого 0, можно добавить к нему парочку нулей: 80×80=6400; 30×30=900. Т.е., первые цифры умножаем и дописываем два 0 к этому числу.
- Теперь возьмём какое-нибудь число так, чтобы вторая его цифра оканчивалась на 5. Так, например, число 75. Чтобы быстро возвести его в квадрат, прибавьте к первой цифре единицу, из чего получаются цифры 7 и 8.
- Умножаем их и приписываем в конец число 25 и получаем конечный результат в виде числа 5625.
Квадратные корни
Вторая таблица — это таблица квадратных корней:
| √x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 1,41421 | 1,73205 | 2 | 2,23607 | 2,44949 | 2,64575 | 2,82843 | 3 |
| 1 | 3,16228 | 3,31662 | 3,4641 | 3,60555 | 3,74166 | 3,87298 | 4 | 4,12311 | 4,24264 | 4,3589 |
| 2 | 4,47214 | 4,58258 | 4,69042 | 4,79583 | 4,89898 | 5 | 5,09902 | 5,19615 | 5,2915 | 5,38516 |
| 3 | 5,47723 | 5,56776 | 5,65685 | 5,74456 | 5,83095 | 5,91608 | 6 | 6,08276 | 6,16441 | 6,245 |
| 4 | 6,32456 | 6,40312 | 6,48074 | 6,55744 | 6,63325 | 6,7082 | 6,78233 | 6,85565 | 6,9282 | 7 |
| 5 | 7,07107 | 7,14143 | 7,2111 | 7,28011 | 7,34847 | 7,4162 | 7,48331 | 7,54983 | 7,61577 | 7,68115 |
| 6 | 7,74597 | 7,81025 | 7,87401 | 7,93725 | 8 | 8,06226 | 8,12404 | 8,18535 | 8,24621 | 8,30662 |
| 7 | 8,3666 | 8,42615 | 8,48528 | 8,544 | 8,60233 | 8,66025 | 8,7178 | 8,77496 | 8,83176 | 8,88819 |
| 8 | 8,94427 | 9 | 9,05539 | 9,11043 | 9,16515 | 9,21954 | 9,27362 | 9,32738 | 9,38083 | 9,43398 |
| 9 | 9,48683 | 9,53939 | 9,59166 | 9,64365 | 9,69536 | 9,74679 | 9,79796 | 9,84886 | 9,89949 | 9,94987 |
Числа в кубе
И, конечно же, третья — таблица кубов, при помощи которой осуществляется извлечение кубического корня.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175716 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Интересно
Название «Куб» приобрелось из-за того, что такая операция проводится для нахождения объема куба. Т.е., для этого нужно возвести длину ребра куба в третью степень.
Такие таблицы достаточно просты в использовании. Слева — десятки, а справа — единицы. С их помощью можно быстро и легко извлечь корень числа от 0 до 99. Это был один из методов извлечения корней, как мне кажется, самый простой после вычислительного средства — калькулятора, но, зачастую, мы не всегда можем им воспользоваться, как говорилось ранее. Так давайте же перейдем к другим интересным и сложным на первый взгляд вариантам решения.
Разложение подкоренного числа на простые множители
Двигаясь от наиболее удобного и быстрого способа к более сложному, давайте разберемся во втором из них — разложение подкоренного числа на простые множители.
Этот метод состоит в том, чтобы представить какое-либо число в виде степени с нужным нам показателем, из чего мы можем получить значение этого корня.
Пример 1:
Возьмём число 196. Для извлечения его квадратного корня, разложим это число на простые множители: √196=2×2×7×7=2²×7²
Теперь делаем следующие действия: 2×7=14.
Ответ: √196=14.
Объяснение:
Множители находятся так: 196 делим на 2, а полученное число 98 мы тоже делим на 2. Делим до тех пор, пока деление станет невозможным. Так, число 49 нельзя поделить пополам, поэтому мы действуем методом подбора. Находим такое число, которое делится. В данном случае — это 7. Два числа, что у нас получились (2 и 7), мы умножаем друг на друга, но уже без степени и получаем число 14, что есть извлечённый корень из числа 196.
Пример 2:
Для того, чтобы лучше понять, как раскладывать на множители, приведем ещё одно число и перейдем к действиям. Деление 441 на 2 невозможно, поэтому подбираем число. Оно делится на 3 два раза. Опять выходит число 49, которое мы делим 2 раза на 7. Из этого следует: √441=3×3×7×7=3²×7²
3×7=21. Значит, ответ: √441=21.
Объяснение:
3 мы умножили на 7, так как это два числа, имеющих 2 степень. Будь у одного из них 4 степень, например: 3⁴×7² — нужно было бы сделать так: 3×3×7. Проще сказать, что мы сокращаем степени ⁴ и ².
Интересно
Подкоренные числа, разложенные на простые множители, могут иметь лишь чётную степень.
Извлечение корней из дробных чисел
Перед тем, как начать вычисления, убедитесь, что дробное число представлено в виде обыкновенной дроби.
Перейдем к свойству корня из частного:
[sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}]
Далее нужно воспользоваться правилом извлечения корня из дроби, которое гласит: корень из дроби равен от деления корня числителя на корень знаменателя.
Пример 1:
Давайте возьмем любую десятичную дробь и на её примере посмотрим, как нужно извлекать корень.
Так, например, найдем кубический корень из 373,248.
Первый ход — это представление десятичной дроби в виде обыкновенной:
³√373248/³√1000. После этого найдем кубический корень в числе и знаменателе:
³√373248=2×2×2×2×2×2×2×2×2×3×3×3×3×3×3=2⁹×3⁶=72³
Эти действия происходят как с квадратными корнями, но здесь уже мы считаем числа 2 и 3 не по двойке, а тройке, т.е. 2⁹=2×2×2, а 3⁶=3×3. Или же сокращаем ⁹ и ⁶.
Проверим таким образом: из 9 вычитаем тройки до тех пор, пока не придем к 0: 9-3-3-3 – это значит, что двоек у нас будет именно 3. Так и с 3⁶. Если от 6 отнять 3 два раза, то будет 0. Выходит, что троек у нас именно две.
А 1000=10³.
Получается, ³√373248/³√1000=72/10=7,2.
Извлечение отрицательного корня
Существуют вещественные числа, из которых невозможно извлечь корень, т.е. решения нет. А вот из комплексных чисел можно извлекать корень. Для начала узнаем, что это за числа.
Определение
Вещественные (действительные) числа— это рациональные и иррациональные числа, которые можно записать в форме конечной или бесконечной десятичной дроби.
Комплексные числа — это выражение, в котором есть:
- вещественные числа a и b;
- i — мнимая единица.
Итак, чтобы извлечь корень из отрицательного числа, нужно помнить, что если знаменатель является нечётным, то число под знаком корня может оказаться отрицательным.
Далее, чтобы провести эту операцию с отрицательным числом, перейдем к следующим действиям:
- Извлекаем корень из противоположного ему положительного числа.
- Ставим перед полученным числом знак минус.
Пример 1:
1. Преобразуем выражение ⁵√-12 640/32 так, чтобы вместо отрицательного числа под корнем оказалось положительное:
⁵√-12 640/32 = -⁵√12 640/32
2. Избавимся от смешанного числа, заменив его обыкновенной дробью:
-⁵√12 640/32= -⁵√1024/32
3. С помощью правила извлечения корней из обыкновенной дроби, начнем извлекать:
-⁵√1024/32 = — ⁵√1024/⁵√32.
4. Теперь нужно вычислить корни в числителе и знаменателе:
— ⁵√1024/⁵√32 = — ⁵√4⁵/⁵√2⁵ = — 4/2 = -2.
Нет времени решать самому?
Наши эксперты помогут!
Поразрядное нахождение значения корня
Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.
Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.
Пример 1:
Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:
1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).
2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.
3. Значение сотых. По аналогии находим приближенное значение к 7.
2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.
Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.
Задания для отработки материала
1 задание
а)√324
б)√900
в)√1369
2 задание
а)³√531,441
б)³√166,375
3 задание
а) ⁵√-14 2471/1024
б) ⁵√-5 1182/3125
4 задание
а)Найдите квадратный корень из 3.
б)Найдите квадратный корень из 5.
в)Найдите квадратный корень из 9.
Ответы с решением
1 задание
а)√324
1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:
2)2×3×3=18. Получается, √324=18.
б)√900
1)2×2×3×3×5×5=2²×3²×5²=√900.
Извлекаем:
2)2×3×5=30. Мы получили √900=30.
в)√1369
1)37×37=37²=√1369.
А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.
2 задание
а)³√531441.
1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.
Разложили на простые множители, а теперь найдем квадратный корень.
2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.
3)1000=10³.
4)³√531441/³√1000=81/10=8,1.
б)³√166,375.
1) 5×5×5×11×11×11=5³×11³=³√166375.
2)5³×11³=55. Так как числа в кубе – они в степени 1.
3) 1000=10³.
4)³√166375/³√1000=55/10=5,5.
3 задание
а)
1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.
2) -⁵√14 2471/1024= -⁵√16801/1024.
3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.
4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.
б)
1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.
2) -⁵√5 1182/3125= -⁵√16807/3125.
3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.
4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.
4 задание
а)√3≈1,73.
б√5≈2,23.
в)√8≈2,82.
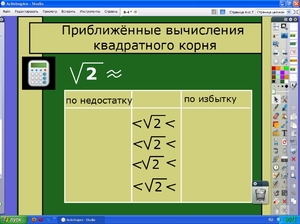
Определение «Корень»
Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √64 = 8 (√64 равно числу 8).
Формула: √a2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечение корней: примеры
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).
Например, извлечь корень из 64 – значит найти √64.
Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
- Разложение подкоренного выражения (числа) на простые множители.
Порядок нахождения корня в этом случае будет следующим:
1. Разложение подкоренного значения на простые множители,
2. Объединение одинаковых множителей и их представление в виде степени с необходимым показателем.
Например, √144 = √2х2х2х2х3х3 = √(2х2)х(2х2)х(3х3) = √22х22х32 = √122 = 12
3. В случае, если невозможно найти корень из числа, то можно упростить подкоренное выражение (число). В этом случае применяется следующее правило: корень из произведения чисел равен произведению корней этих чисел.
Например, √72 = √2х2х2х3х3 = √(2х2)х2х(3х3) = √22х2х32 = √62х2 = 6√2 - Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Например, √130=√13х5х2 – упростить нельзя.
- Извлечение корня из дроби. В этом случае применяются следующие правила:
1. дробное число должно быть записано в виде обыкновенной дроби;
2. корень из дроби равен частному от деления корня числителя на корень знаменателя.
Например, √3,24 = √324/100 = √81/25 = √81 / √25 = 9/5 = 1,8. - Извлечение нечетной степени из отрицательных чисел. Чтобы извлечь корень нечетной степени из отрицательного числа необходимо извлечь его из положительного числа и поставить перед ним знак минус.
Например, чтобы найти корень третьей степени из (-125), нужно найти корень третьей степени из 125 (будет 5) и подставить знак минуса (будет -5).
Приведение корней с разными показателями
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n√an.
Например, есть квадратный корень (второй степени √2 ) и кубический корень (третьей степени 3√3).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n√an: √2 = 2√2 = 6√23 = 6√8; 3√3 = 6√32 = 6√9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Корень: сложение и вычитание корней
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√3 + 3√3 = 5√3
2√3 + 2√4 – не выполняется.
При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√3 + 3√12 = 2√3 + 3√2х2х3 = 2√3 + 3√ 22х3 = 2√3 + 6√3 = 8√3.
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Корень: умножение
Умножение корней без множителей
Произведение корней из чисел равно корню из произведения этих чисел.
√a*b=√a*√b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√2 х √3 = √6
√6 х √3 = √18 = √3х3х2 = 3√2
Умножение корней с множителями
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√2 х √5 = (3х1) √(2*5) = 3√10
4√2 х 3√3 = (3х4) √(2х3) = 12√6
Корень: деление
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√a:b=√a:√b
В процессе деления квадратных корней дроби упрощаются.
Деление корней без множителей
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √21:√3=√21:3=√7
Деление квадратных корней с множителями
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√32 : 6√16 = (12:6) √(32:16) = 2√2.
Примеры для практики
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Извлечение квадратного корня при помощи таблицы квадратов
Один из простейших способов вычисления корней заключается в использовании специальной таблицы. Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:
√R = √a + (R — a) / 2√a,
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода:
10,55² = 111,3025.
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
10,536² = 111,0073.
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора.
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
- Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n <30.
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
- Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Видео
Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.
Соколов Лев Владимирович, учащийся 8 класса МКОУ «Тугулымская В(С)ОШ»
Цель работы:
найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.
Скачать:
Предварительный просмотр:
Районная научно-практическая конференция
обучающихся Тугулымского городского округа
Извлечение квадратных корней из больших чисел без калькулятора
Исполнитель: Лев Соколов,
МКОУ «Тугулымская В(С)ОШ»,
8 класс
Руководитель: Сидорова Татьяна
Николаевна
р.п. Тугулым, 2016 г.
Введение 3
Глава 1. Способ разложения на простые множители 4
Глава 2. Извлечение квадратного корня уголком 4
Глава 3. Способ использования таблицы квадратов двузначных чисел 6
Глава 4. Формула Древнего Вавилона 6
Глава 6. Канадский метод 7
Глава 7. Метод подбора угадыванием 8
Глава 8 . Метод вычетов нечётного числа 8
Заключение 10
Список литературы 11
Приложение 12
Введение
Актуальность исследования,
когда я изучал тему квадратные корни в этом учебном году, то меня заинтересовал вопрос, как можно извлечь квадратный корень из больших чисел без калькулятора.
Я заинтересовался и решил изучить этот вопрос глубже, чем он изложен в школьной программе, а также приготовить мини-книжечку с наиболее простыми способами извлечения квадратных корней из больших чисел без калькулятора.
Цель работы:
найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.
Задачи:
- Изучить литературу по данному вопросу.
- Рассмотреть особенности каждого найденного способа и его алгоритм.
- Показать практическое применение полученных знаний и оценить
Степень сложности в использовании различных способов и алгоритмов.
- Создать мини-книжечку по самым интересным алгоритмам.
Объект исследования:
математические символы – квадратные корни.
Предмет исследования:
особенности способов извлечения квадратных корней без калькулятора.
Методы исследования:
- Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
- Сравнение найденных способов.
- Анализ полученных способов.
Все знают, что извлечь квадратный корень без калькулятора — это очень сложная
задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Например, таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, извлечь корень из 75, 37,885,108,18061 и другие даже приблизительно.
Также часто на экзаменах ОГЭ и ЕГЭ пользование калькулятором запрещено и нет
таблицы квадратов целых чисел, а надо извлечь корень из 3136 или 7056 и т.д.
Но изучая литературу по данной теме, я узнал, что извлекать корни из таких чисел
возможно и без таблицы и калькулятора, люди научились задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.
Глава 1. Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.
Таким способом принято пользоваться при решении заданий с корнями в школе.
3136│2 7056│2
1568│2 3528│2
784│2 1764│2
392│2 882│2
196│2 441│3
98│2 147│3
49│7 49│7
7│7 7│7
√3136 = √2²∙2²∙2²∙7² = 2∙2∙2∙7 = 56 √3136 = √2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84
Многие применяют его успешно и считают единственным. Извлечение корня разложением на множители — трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 209764? Разложение на простые множители дает произведение 2∙2∙52441. А как быть дальше? С этой задачей сталкиваются все, и спокойно в ответе записывают остаток от разложения под знак корня. Методом проб и ошибок, подбором разложение, конечно, можно сделать, если быть уверенным в том, что получится красивый ответ, но практика показывает, что очень редко предлагаются задания с полным разложением. Чаще мы видим, что корень до конца не извлечь.
Поэтому, этот способ лишь частично решает проблему извлечения без калькулятора.
Глава 2. Извлечение квадратного корня уголком
Для извлечения квадратного корня уголком и
рассмотрим алгоритм:
1-й шаг. Число 8649 разбиваем на грани справа налево; каждая из которых должна содержать две цифры. Получаем две грани:
.
2-й шаг. Извлекаем квадратный корень из первой грани 86, получаем
с недостатком. Цифра 9 –это первая цифра корня.
3-й шаг. Число 9 возводим в квадрат (9
2
= 81) и число 81 вычитаем из первой грани, получаем 86- 81=5. Число 5 – первый остаток.
4-й шаг. К остатку 5 приписываем вторую грань 49, получаем число 549.
5-й шаг
. Удваиваем первую цифру корня 9 и, записывая слева, получаем-18
К числу нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Это цифра 3. Она находится путем подбора: количество десятков числа 549, то есть число 54 делится на 18, получаем 3, так как 183 ∙ 3 = 549. Цифра 3 – это вторая цифра корня.
6-й шаг. Находим остаток 549 – 549 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 93.
Пприведу еще пример: извлечь √212521
|
Шаги алгоритма |
Пример |
Комментарии |
|
|
Разбить число на группы по 2 цифры в каждой справа налево |
21’ 25’ 21 |
Общее число образовавшихся групп определяет количество цифр в ответе |
|
|
Для первой группы цифр подобрать цифру, квадрат которой будет наибольшим, но не превосходящим числа первой группы |
1 группа – 21 4 цифра — 4 |
Найденная цифра записывается в ответе на первом месте |
|
|
Из первой группы цифр вычесть найденный на шаге 2 квадрат первой цифры ответа |
21’ 25’ 21 |
||
|
К остатку, найденному на шаге 3, приписать справа (снести) вторую группу цифр |
21’ 25’ 21 16__ |
||
|
К удвоенной первой цифре ответа приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходила числа, найденного на шаге 4 |
4*2=8 цифра – 6 86*6=516 |
Найденная цифра записывается в ответе на втором месте |
|
|
Из числа, полученного на шаге 4 вычесть число, полученное на шаге 5. Снести к остатку третью группу |
21’ 25’ 21 |
||
|
К удвоенному числу, состоящему из первых двух цифр ответа, приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру был наибольшим, но не превосходило числа, полученного на шаге 6 |
46*2=92 цифра 1 921*1=921 |
Найденная цифра записывается в ответе на третьем месте |
|
|
Записать ответ |
√212521=461 |
Глава 3. Способ использования таблицы квадратов двузначных чисел
Про этот способ я узнал из Интернета. Способ очень простой и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора. Одно условие для этого метода – наличие таблицы квадратов чисел до 99.
(Она есть во всех учебниках алгебры 8 класса, и на экзамене ОГЭ предлагается в качестве справочного материала.)
Откройте таблицу и проверьте скорость нахождения ответа. Но сначала несколько рекомендаций: самый левый столбик – это будут в ответе целые, самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее подкоренное число, и далее действуйте по правилам этой таблицы.
Рассмотрим на примере. Найдём значение √87.
Закрываем две последние цифры у всех чисел в таблице и находим близкие для 87 – таких только два
86
49 и
88
37. Но 88 – это уже много.
Значит, остаётся только одно – 8649.
Левый столбик даёт ответ 9 (это целых), а верхняя строчка 3 (это десятых). Значит √87≈ 9,3. Проверим на МК √87 ≈ 9,327379.
Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Глава 4. Формула Древнего Вавилона
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а
2
+b, где а
2
ближайший к числу х точный квадрат натурального числа а (а
2
. (1)
Извлечем с помощью формулы (1) корень квадратный, например из числа 28:
Результат извлечения корня из 28 с помощью МК 5,2915026.
Как видим способ вавилонян дает хорошее приближение к точному значению корня.
Глава 5. Способ отбрасывания полного квадрата
(только у четырехзначных чисел)
Сразу стоит уточнить, что этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.
- Извлечение корней до числа 75
2
= 5625
Например: √¯3844 = √¯
37
00 + 144 = 37 + 25 = 62.
Число 3844 представим в виде суммы, выделив из этого числа квадрат 144, затем выделенный квадрат отбрасываем, к
числу сотен первого слагаемого
(37)
прибавляем
всегда 25
. Получим ответ 62.
Так можно извлекать только квадратные корни до числа 75
2
=5625!
2)
Извлечение корней после числа 75
2
= 5625
Как же устно извлечь квадратные корни из чисел больше 75
2
=5625?
Например: √7225 = √
70
00 + 225 = 70 + √225 = 70 + 15 = 85.
Поясним,7225 представим в виде суммы 7000 и выделенного квадрата 225. Затем
к числу сотен прибавить квадратный корень
из 225, равный 15.
Получим ответ 85.
Этот способ нахождения очень интересен и в какой – то мере оригинален, но в ходе моего исследования встретился только один раз в работе пермского преподавател.
Возможно, он мало изучен или имеет какие – то исключения.
Он достаточно сложен в запоминании из – за двойственности алгоритма и применим только для четырёхзначных чисел точных корней, но я проработал множество примеров и убедился в его правильности. Кроме всего этот способ доступен тем, кто уже запомнил наизусть квадраты чисел от 11 до 29, ведь без их знания он будет бесполезен.
Глава 6. Канадский метод
√ X = √ S + (X — S) / (2 √ S), гдеX — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Давайте попробуем извлечь квадратный корень из 75
√ 75 = 9 + (- 6/18) = 9 — 0,333 = 8,667
При детальном изучении этого метода легко можно доказать его сходство с вавилонским и поспорить за авторские права изобретения этой формулы, если такие есть в действительности. Метод несложный и удобный.
Глава 7. Метод подбора угадыванием
Этот метод предлагают английские студенты математического колледжа Лондона, но каждый в своей жизни хоть раз непроизвольно пользовался этим методом. Он основан на подборе разных значений квадратов близких чисел путём сужения области поиска. Овладеть этим способом может каждый, но вот пользоваться вряд ли, потому что он требует многократного вычисления произведения столбиком не всегда правильно угаданных чисел. Этот способ проигрывает и в красоте решения, и по времени. Алгоритм прост:
Предположим, вы хотите извлечь квадратный корень из 75.
Так как 8
2
= 64 и 9
2
= 81, вы знаете, ответ находится где-то между ними.
Попробуйте возвести 8,5
2
и вы получите 72,25 (слишком мало)
Теперь попробуйте 8,6
2
и вы получите 73,96 (слишком небольшой, но все ближе)
Теперь попробуйте 8,7
2
и вы получите 75,69 (слишком большая)
Теперь вы знаете, ответ находится между 8,6 и 8,7
Попробуйте возвести 8,65
2
и вы получите 74,8225 (слишком мало)
Теперь попробуйте 8,66
2
… и так далее.
Продолжайте, пока не получите ответ достаточно точный для вас.
Глава 8.
Метод вычетов нечётного числа
Многие знают метод извлечения квадратного корня разложением числа на простые множители. В своей работе представлю ещё один способ, с помощью которого можно узнать целую часть квадратного корня числа. Способ очень простой. Заметим, что для квадратов чисел верны следующие равенства:
1=1
2
1+3=2
2
1+3+5=3
2
1+3+5+7=4
2
и т.д.
Правило: узнать целую часть квадратного корня числа можно вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий.
Например, чтобы получить квадратный корень из 36 и 121 это:
Общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6.
Общее количество вычитаний = 11, поэтому √121 = 11.
Еще пример: найдём √529
Решение: 1)_529
2)_528
3)_525
4)_520
5)_513
6)_504
7)_493
8)_480
9)_465
10)_448
11)_429
12)_408
13)_385
14)_360
15)_333
16)_304
17)_273
18)_240
19)_205
20)_168
21)_129
22)_88
23)_45
Ответ: √529 = 23
Ученые называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень — очень длинный в решёнии.
Заключение
Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от калькулятора.
В результате проведённого исследования я пришел к выводу: различные способы извлечения квадратного корня без калькулятора необходимы в школьном курсе математики, чтобы развивать навыки вычислений.
Теоретическая значимость исследования – систематизированы основные методы извлечения квадратных корней.
Практическая значимость:
в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами (Приложение1).
Литература и сайты Интернета:
- И.Н. Сергеев, С.Н. Олехник, С.Б.Гашков «Примени математику». – М.: Наука, 1990
- Керимов З., «Как найти целый корень?» Научно-популярный физико-математический журнал «Квант» №2, 1980
- Петраков И.С. «математические кружки в 8-10 классах»; Книга для учителя.
–М.:Просвещение,1987
- Тихонов А.Н., Костомаров Д.П. «Рассказы о прикладной математики».- М.: Наука. Главная редакция физико- математической литературы, 1979
- Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
- Жохов В.И., Погодин В.Н. Справочные таблицы по математике.-М.: ООО «Издательство «РОСМЭН-ПРЕСС», 2004.-120 с.
- http://translate.google.ru/translate
- http://www.murderousmaths.co.uk/books/sqroot.htm
- http://ru.wikipedia.ord /wiki /teorema/
Добрый день, уважаемые гости!
Меня зовут Лев Соколов, я учусь в 8 классе в вечерней школе.
Представляю вашему вниманию работу на тему: «
Извлечение квадратных корней из больших чисел без калькулятора».
При изучении темы
квадратные корни в этом учебном году, меня заинтересовал вопрос, как можно извлечь квадратный корень из больших чисел без калькулятора и я решил изучить его глубже, так как на следующий год мне предстоит сдавать экзамен по математике.
Цель моей работы:
найти и показать способы извлечения квадратных корней без калькулятора
Для достижения цели я решал следующие
задачи:
1. Изучить литературу по данному вопросу.
2. Рассмотреть особенности каждого найденного способа и его алгоритм.
3. Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов.
4.Создать
мини-книжечку
по самым интересным алгоритмам.
Объектом моего исследования стали
квадратные корни.
Предмет исследования:
способы извлечения квадратных корней без калькулятора.
Методы исследования:
1. Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
2. Сравнение и анализ найденных способов.
Я нашел и изучил 8 способов извлечения квадратных корней без калькулятора и отработал их на практике. Название найденных способов приведены на слайде.
Я остановлюсь на тех из них, которые мне понравились.
Покажу на примере, как можно способом разложения на простые множители извлечь квадратный корень из числа 3025.
Основной недостаток этого способа
— он занимает много времени.
С помощью формулы Древнего Вавилона я извлеку квадратный корень из этого же числа 3025.
Способ удобен только для малых чисел.
Из этого же числа 3025 извлекаем квадратный корень уголком.
На мой взгляд, это самый универсальный способ, он применим к любым числам.
В
современной науке известно много способов извлечения квадратного корня без калькулятора, но я изучил не все.
Практическая значимость моей работы:
в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами.
Результаты моей работы могут успешно применяться на уроках математики, физики и других предметах, где требуется извлечение корней без калькулятора.
Спасибо за внимание!
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Извлечение квадратных корней из больших чисел без калькулятора Исполнитель: Лев Соколов, МКОУ « Тугулымская В(С)ОШ»,8 класс Руководитель: Сидорова Татьяна Николаевна I категория, учитель математики р.п. Тугулым
Правильному применению методов можно научиться, применяя и на разнообразных примерах. Г. Цейтен Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора. Задачи: — Изучить литературу по данному вопросу. — Рассмотреть особенности каждого найденного способа и его алгоритм. — Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов. — Создать мини-книжечку по самым интересным алгоритмам.
Объект исследования: квадратные корни Предмет исследования: способы извлечения квадратных корней без калькулятора. Методы исследования: Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора. Сравнение найденных способов. Анализ полученных способов.
Способы извлечения квадратного корня: 1. Способ разложения на простые множители 2. Извлечение квадратного корня уголком 3. Способ использования таблицы квадратов двузначных чисел 4. Формула Древнего Вавилона 5. Способ отбрасывания полного квадрата 6. Канадский метод 7. Метод подбора угадыванием 8. Метод вычетов нечётного числа
Способ разложения на простые множители Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения. 3136│2 7056│2 209764│2 1568│2 3528│2 104882│2 784│2 1764│2 52441│229 392│2 882│2 229│229 196│2 441│3 98│2 147│3 √209764 = √2∙2∙52441 = 49│7 49│7 = √2²∙229² = 458. 7│7 7│7 √3136 = √ 2²∙2²∙2²∙7² = 2∙2∙2∙7 = 56. √7056 = √2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84. Не всегда легко можно разложить, чаще до конца не извлекается, занимает много времени.
Формула Древнего Вавилона (Вавилонский метод) Алгоритм извлечения квадратного корня древневавилонским способом. 1 . Представить число с в виде суммы а ² + b , где а ² ближайший к числу с точный квадрат натурального числа а (а ² ≈ с); 2. Приближенное значение корня вычисляется по формуле: Результат извлечения корня с помощью калькулятора равен 5,292.
Извлечение квадратного корня уголком Способ почти универсальный, так как применим к любым числам, но составление ребуса (угадывание цифры на конце числа) требует логики и хороших вычислительных навыков столбиком.
Алгоритм извлечения квадратного корня уголком 1. Разбиваем число (5963364) на пары справа налево (5`96`33`64) 2. Извлекаем квадратный корень из первой слева группы (- число 2). Так мы получаем первую цифру числа. 3. Находим квадрат первой цифры (2 2 =4). 4. Находим разность первой группы и квадрата первой цифры (5-4=1). 5.Сносим следующие две цифры (получили число 196). 6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4). 7.Теперь необходимо найти вторую цифру числа: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 — вторая цифра числа &. 8. Находим разность (196-176=20). 9. Сносим следующую группу (получаем число 2033). 10. Удваиваем число 24, получаем 48. 11. 48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа. Далее процесс повторяется.
Метод вычетов нечётного числа (арифметический способ) Алгоритм извлечения квадратного корня: Вычитать нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитать количество выполненных действий – это число есть целаячасть числа извлекаемого квадратного корня. Пример 1: вычислить 1. 9 − 1 = 8; 8 − 3 = 5; 5 − 5 = 0. 2. Выполнено 3 действия
36 — 1 = 35 — 3 = 32 — 5 = 27 — 7 = 20 — 9 = 11 — 11 = 0 общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6. 121 – 1 = 120 — 3 = 117- 5 = 112 — 7 = 105 — 9 = 96 — 11 = 85 – 13 = 72 — 15 = 57 – 17 = 40 — 19 = 21 — 21 = 0 Общее количество вычитаний = 11, поэтому квадратный корень из 121 = 11. 5963364 = ??? Российские учёные «за глаза» называют его «методом черепахи» из-за его медлительности. Он неудобен для больших чисел.
Теоретическая значимость исследования – систематизированы основные методы извлечения квадратных корней. Практическая значимость: в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами.
Спасибо за внимание!
Предварительный просмотр:
При решении некоторых задач потребуется извлечь квадратный корень из крупного числа. Как это сделать?
Метод вычетов нечётного числа.
Способ очень простой. Заметим, что для квадратов чисел верны следующие равенства:
1=1
2
1+3=2
2
1+3+5=3
2
1+3+5+7=4
2
и т.д.
Правило:
узнать целую часть квадратного корня числа можно вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий.
Например,
чтобы получить квадратный корень из 36 и 121 это:
36 —
1
= 35 —
3
= 32 —
5
= 27 —
7
= 20 —
9
= 11 —
11
= 0
Общее количество вычитаний = 6, поэтому квадратный корень из
36 = 6.
121 —
1
= 120 —
3
= 117-
5
= 112 —
7
= 105 —
9
= 96 —
11
= 85 –
13
= 72 —
15
= 57 –
17
= 40 —
19
= 21 —
21
= 0
Общее количество вычитаний = 11, поэтому
√121 = 11.
Канадский метод.
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула:
√ X = √ S + (X — S) / (2 √ S), где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Пример.
Извлечь квадратный корень из 75.
X = 75, S = 81. Это означает, что √ S = 9.
Просчитаем по этой формуле √75: √ 75 = 9 + (75 — 81) / (2∙ 9)
√ 75 = 9 + (- 6/18) = 9 — 0,333 =
8,667
Способ извлечения квадратного корня уголком.
1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)
2. Извлекаем квадратный корень из первой слева группы ( — число 2). Так мы получаем первую цифру числа.
3. Находим квадрат первой цифры (2
2
=4).
4. Находим разность первой группы и квадрата первой цифры (5-4=1).
5.Сносим следующие две цифры (получили число 196).
6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).
7.Теперь необходимо найти вторую цифру числа: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 — вторая цифра числа &.
8. Находим разность (196-176=20).
9. Сносим следующую группу (получаем число 2033).
10. Удваиваем число 24, получаем 48.
11.48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа.
Действие
извлечения корня квадратного
обратно действию возведения в квадрат.
√81= 9 9
2
=81.
Метод подбора.
Пример:
Извлечь корень из числа 676
.
Замечаем, что 20
2
= 400, а 30
2
= 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4
2
и 6
2
.
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24
2
= 576, 26
2
= 676.
Ответ:
√
676 = 26.
Еще
пример:
√6889
.
Так как 80
2
= 6400, а 90
2
= 8100, то 80 Цифру 9 дают 3
2
и 7
2
, то √6889 равен либо 83, либо 87.
Проверяем: 83
2
= 6889.
Ответ:
√6889 = 83
.
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например,
найти √893025
.
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3
6
∙5
2
∙7
2
= 3
3
∙5 ∙7 = 945.
Вавилонский метод.
Шаг №1.
Представить число х в виде суммы: х=а
2
+ b, где а
2
ближайший к числу х точный квадрат натурального числа а.
Шаг №2.
Использовать формулу:
Пример.
Вычислить
.
Арифметический метод.
Вычитаем из числа все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитав количество выполненных действий, определяем, целую часть квадратного корня из числа.
Пример.
Вычислить целую часть числа
.
Решение.
12 — 1 = 11; 11 — 3 = 8; 8 — 5 = 3; 3 3 — целая часть числа
. Итак,
.
Метод (известный как метод Ньютона)
заключается в следующем.
Пусть
а
1
— первое приближение числа
(в качестве а
1
можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего
.
Указанный способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.
Метод оценки.
Шаг №1.
Выяснить диапазон, в котором лежит исходный корень (100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000).
Шаг №2
.
По последней цифре определить на какую цифру заканчивается искомое число.
|
Цифра единиц числа х |
||||||||||
|
Цифра единиц числа х |
Шаг №3.
Возвести в квадрат предполагаемые числа и определить из них искомое число.
Пример 1.
Вычислить
.
Решение.
2500 50
2
2
50
= *2 или
= *8.
52
2
= (50 +2)
2
= 2500 + 2 · 50 · 2 + 4 = 2704;
58
2
= (60 − 2)
2
= 3600 − 2 · 60 · 2 + 4 = 3364.
Следовательно,
=
58.
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень
. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней
.
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа
.
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
На кружке показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм запомнился, а вопросы остались. Непонятно было, откуда взялся метод и почему он дает верный результат. В книжках этого не было, а может, просто не в тех книжках искала. В итоге, как и многое из того, что на сегодняшний день знаю и умею, вывела сама. Делюсь своим знанием здесь. Кстати сказать, до сих пор не знаю, где приведено обоснование алгоритма)))
Итак, сначала на примере рассказываю, “как работает система”, а потом объясняю, почему она на самом деле работает.
Возьмем число (число взято “с потолка”, только что в голову пришло).
1.
Разбиваем его цифры на пары: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Получаем .
2.
Извлекаем квадратный корень из первой группы цифр слева — в нашем случае это (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число . Записываем в ответ — это старшая цифра корня.
3.
Возводим число, которое стоит уже в ответе — это — в квадрат и вычитаем из первой слева группы цифр — из числа . В нашем случае остается .
4.
Приписываем справа следующую группу из двух цифр: . Число , которое уже стоит в ответе, умножаем на , получаем .
5.
Теперь следите внимательно. Нам нужно к числу справа приписать одну цифру , и число умножить на , то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к , но опять-таки не больше этого числа. В нашем случае это будет цифра , ее записываем в ответ рядом с , справа. Это следующая цифра в десятичной записи нашего квадратного корня.
6.
Из вычитаем произведение , получаем .
7.
Далее повторяем знакомые операции: приписываем к справа следующую группу цифр , умножаем на , к полученному числу > приписываем справа одну цифру, такую, чтобы при умножении на нее получилось число, меньшее , но наиболее близкое к нему –– это цифра –– следующая цифра в десятичной записи корня.
Вычисления запишутся следующим образом:
А теперь обещанное объяснение. Алгоритм основан на формуле
Комментариев: 50
-
2 Антон:
Слишком сумбурно и запутано. Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом.
-
5 Юлия:
-
6 :
Юлия, 23 на данный момент записано справа, это две первые (слева) уже полученные цифры корня, стоящие в ответе. Умножаем на 2 согласно алгоритму. Повторяем действия, описанные в пункте 4.
-
7 zzz:
ошибка в “6. Из 167 вычитаем произведение 43 * 3 = 123 (129 нада), получаем 38.”
непонятно как после запятой получилось 08… -
9 Федотов Александр:
А ещё в докалькуляторную эпоху нас в школе учили не только квадратный, но и кубический корень в столбик извлекать, но это более нудная и кропотливая работа. Проще было таблицами Брадиса воспользоваться или логарифмической линейкой, которую мы уже в старших классах изучали.
-
10 :
Александр, Вы правы, можно извлекать в столбик и корни больших степеней. Я собираюсь написать как раз о том, как находить кубический корень.
-
12 Сергей Валентинович:
Уважаемая Елизавета Александровна! Мной в конце 70-х разработана схема автоматического (т.е. не подбором) вычисления квадр. корня на арифмометре “Феликс”. Если заинтересуетесь, могу выслать описание.
-
14 Vlad aus Engelsstadt:
(((Извлечение квадратного корня в столбик)))
Алгоритм упрощается, если использовать 2-ную систему счисления, которую изучают в информатике, но полезно и в математике. А.Н. Колмогоров в популярных лекциях для школьников приводил этот алгоритм. Его статью можно найти в “Чебышёвском сборнике” (Математический журнал, ищите ссылку на него в интернете)
К случаю сказать:
Г.Лейбниц в свое время носился с идеей о переходе от 10-ной системы счисления к двоичной из-за ее простоты и доступности для начинающих (младших школьников). Но устоявшиеся традиции ломать это все равно что лбом ломать крепостные ворота: можно, но бесполезно. Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых.До следующих встреч.
-
15 Vlad aus Engelsstadt:
))Сергей Валентинович, да, мне интересно…((
Бьюсь об заклад, что это вариация под “Феликс” Вавилонского метода извлечения коня квадратного методом последовательных приближений. Этот алгоритм был перекрыт методом Ньютона (метод касательных)
Интересно, не ошибся ли я в прогнозе?
-
18 :
2Vlad aus Engelsstadt
Да, алгоритм в двоичной системе должен быть проще, это довольно очевидно.
О методе Ньютона. Может, оно и так, но все равно интересно
-
20 Кирилл:
Спасибо большое. А алгоритма так и нету, неизвестно откуда он взялся, но результат правильный получается. СПАСИБО БОЛЬШОЕ! Долго искал это)
-
21 Александр:
А каким образом пойдёт извлечение корня из числа, где вторая слева-направо группа весьма мала? к примеру, любимое всеми число 4 398 046 511 104 . после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.
-
22 Алексей:
Да, знаю этот способ. Я, помню, вычитал его в книге “Алгебра” какого-то старого издания. Тогда еще по аналогии сам вывел, как так же в столбик извлекать кубический корень. Но там уже сложнее: каждая цифра определяется уже не в одно (как для квадратного), а в два вычитания, да еще там каждый раз надо перемножать длинные числа.
-
23 Артем:
В примере извлечения квадратного корня в столбик из 56789,321 имеются опечатки. Группа цифр 32 приписана дважды к числам 145 и 243, в числе 2388025 вторую 8 необходимо заменить на 3. Тогда последнее вычитание следует записать так: 2431000 – 2383025 = 47975.
Дополнительно, при делении остатка на увеличенное в два раза значение ответа (без учета запятой), получим добавочное количество значащих цифр (47975/(2*238305) = 0.100658819…), которые следует дописать к ответу (√56789,321 = 238,305… = 238,305100659). -
24 Сергей:
По всей видимости алгоритм пришел из книги Исаака Ньютона “Всеобщая арифметика или книга о арифметических синтезе и анализе”. Вот выдержка из неё:
ОБ ИЗВЛЕЧЕНИИ КОРНЕЙ
Чтобы извлечь из числа квадратный корень, прежде всего следует поставить над его цифрами через одну, начиная с единиц, точки. Затем следует в частном или в корне написать цифру, квадрат которой равен или ближайший по недостатку к цифрам или цифре, предшествующим первой точке. После вычитания этого квадрата остальные цифры корня будут последовательно найдены посредством деления остатка на удвоенную величину уже извлеченной части корня и вычитания всякий раз из остатка квадрата последней найденной цифры и ее удесятеренного произведения на названный делитель.
-
25 Сергей:
Поправьте ещё название книги “Всеобщая арифметика или книга оБ арифметических синтезе и анализе”
-
26 Александр:
Спасибо за интересный материал. Но мне этот метод представляется несколько более сложным, чем нужно, например, школьнику. Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
sqrt(x)= A1+A2-A3, где
А1 – целое число, квадрат которого ближе всего к х;
А2 – дробь, в числителе х-А1, в знаменателе 2*А1.
Для большинства чисел, встречающихся в школьном курсе, этого достаточно, чтобы получить результат с точностью до сотых.
Если нужен более точный результат, берем
А3 – дробь, в числителе А2 в квадрате, в знаменателе 2*А1+1.
Конечно, для применения нужна таблица квадратов целых чисел, но это в школе не проблема. Запомнить эту формулу достаточно просто.
Меня, правда, смущает, что А3 я получил опытным путем в результате экспериментов с электронной таблицей и не вполне понимаю, почему этот член имеет такой вид. Может, подскажете? -
27 Александр:
Да, я тоже рассматривал эти соображения, но дьявол кроется в деталях. Вы пишете:
“поскольку a2 и b отличаются уже довольно мало”. Вопрос именно стоит, насколько мало.
Эта формула хорошо работает на числах второго десятка и гораздо хуже (не до сотых, только до десятых) на числах первого десятка. Почему так происходит уже трудно понять без привлечения производных. -
28 Александр:
Я уточню, в чем я вижу преимущество предложенной мной формулы. Она не требует не вполне естественного разбиения чисел на пары цифр, которое, как показывает опыт, часто выполняется с ошибками. Смысл ее очевиден, а для человека, знакомого с анализом, тривиален. Хорошо работает на числах от 100 до 1000, наиболее часто встречающихся в школе.
-
29 Александр:
Кстати, я немного покопался и нашел точное выражение для А3 в моей формуле:
А3= А22 /2(A1+A2) -
30 vasil stryzhak:
В наше время, повсеместного использования вычислительной техники, вопрос извлечения квадратного коня из числа с практической точки зрения не стоит. Но для любителей математики, несомненно, представляют интерес различные варианты решения данной задачи. В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям.
Существенным недостатком предлагаемого Александром способа является использование таблицы квадратов целых чисел. Каким большинством чисел встречающихся в школьном курсе она ограничена автор умалчивает. Что касается формулы, то в целом она мне импонирует в виду относительно высокой точностью вычисления. -
31 Александр:
для 30 vasil stryzhak
Я ни о чем не умолчал. Таблица квадратов предполагается до 1000. В мое время в школе ее просто заучивали наизусть и она была во всех учебниках математики. Я в явном виде назвал этот интервал.
Что до вычислительной техники, то она не применяется, в основном, на уроках математики, если только не идет специально тема применения калькулятора. Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ. -
32 vasil stryzhak:
Александр, спасибо за разъяснение!Я считал,что для предлагаемого метода теоретически необходимо помнить или пользоваться таблицей квадратов всех двузначных чисел.Тогда для подкоренных чисел не входящих в интервал от 100 до 10000 можно использовать прием их увеличения или уменьшения на необходимое количество порядков переносом запятой.
-
33 vasil stryzhak:
-
39 АЛЕКСАНДР:
МОЯ ПЕРВАЯ ПРОГРАММА НА ЯЗЫКЕ “ЯМБ” НА СОВЕТСКОЙ МАШИНЕ “ИСКРА 555″ БЫЛА НАПИСАНА ДЛЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА ПО АЛГОРИТМУ ИЗВЛЕЧЕНИЯ В СТОЛБИК! а сейчас забыл как извлекать в ручную!
Рассмотрим этот алгоритм на примере. Найдем
1-й шаг. Число под корнем разбиваем на грани по две цифры (справа налево):
2-й шаг. Извлекаем квадратный корень из первой грани, т. е. из числа 65, получаем число 8. Под первой гранью пишем квадрат числа 8 и вычитаем. К остатку приписываем вторую грань (59):
(число 159 — первый остаток).
3-й шаг. Удваиваем найденный корень и пишем результат слева:
4-й шаг. Отделяем в остатке (159) одну цифру справа, слева получаем число десятков (оно равно 15). Затем делим 15 на удвоенную первую цифру корня, т. е. на 16, так как 15 на 16 не делится, то в частном получается нуль, который записываем как вторую цифру корня. Итак, в частном получили число 80, которое опять удваиваем, и сносим следующую грань
(число 15 901 — второй остаток).
5-й шаг. Отделяем во втором остатке одну цифру справа и полученное число 1590 делим на 160. Результат (цифру 9) записываем как третью цифру корня и приписываем к числу 160. Полученное число 1609 умножаем на 9 и находим следующий остаток (1420):
В дальнейшем действия выполняются в той последовательности, которая указана в алгоритме (корень можно извлекать с нужной степенью точности).
Замечание. Если подкоренное выражение — десятичная — дробь, то ее целую часть разбивают на грани по две цифры справа налево, дробную часть — по две цифры слева направо и извлекают корень по указанному алгоритму.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
1. Извлеките квадратный корень из числа: а) 32; б) 32,45; в) 249,5; г) 0,9511.
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
- Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
- В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18. - Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
- В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Как вычислять корни без Калькулятора ЕГЭ
3 способа как вычислять квадратные корни без калькулятора на ЕГЭ
ЗАПИСАТЬСЯ НА КУРСЫ http://extraege.ru
https://vk.com/extra_maths Группа
https://vk.com/dmitry_sinyaev Страница вк
Глава первая.
Извлечение из данного целого числа наибольшего целого квадратного корня.
170. Предварительные замечания.
а)
Так как мы будем говорить об извлечении только квадратного корня, то для сокращения речи в этой главе мы вместо „квадратный» корень будем говорить просто „корень».
б)
Если возвысим в квадрат числа натурального ряда: 1,2,3,4,5 . . . , то получим такую таблицу квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,121,144. .,
Очевидно, имеется очень многo целых чисел, которые в этой таблице не находятся; из таких чисел, конечно, нельзя извлечь целый корень. Поэтому, если требуется извлечь корень из какого-нибудь целого числа, напр. требуется найти √4082
, то мы условимся это требование понимать так: извлечь целый корень из 4082, если это возможно; если же нельзя, то мы должны найти наибольшее
целое число, квадрат
которого заключается в 4082 (такое
число есть 63, так как 63 2 = 39б9, а 64 2 = 4090).
в)
Если данное число меньше 100, то корень из него находится по таблице умножения; так, √60
будет 7, так как семью 7 равно 49, что меньше 60, а восемью 8 составляет 64, что больше 60.
171. Извлечение корня из числа, меньшего 10000, но большего 100.
Пусть надо найти √4082
. Так как это число меньше 10 000, то корень из него меньше √l0 000
= 100. С другой стороны, данное число больше 100; значит, корень из него больше (или равен 10) . (Если бы, напр., требовалось найти √
120
, то хотя число 120
> 100, однако √
120
равен 10, т.к. 11
2
= 121.)
Но всякое число, которое больше 10, но меньше 100, имеет 2 цифры; значит, искомый корень есть сумма:
десятки + единицы,
и поэтому квадрат его должен равняться сумме:
Сумма эта должна быть наибольшим квадратом, заключающимся в 4082.
Возьмем из них наибольший, 36, и допустим,что квадрат десятков корня будет равен именно этому наибольшему квадрату. Тогда число десятков в корне должно быть 6. Проверим теперь, что это всегда должно быть так, т. е. всегда число десятков корня равно наибольшему целому корню из числа сотен подкоренного числа.
Действительно, в нашем примере число десятков корня не может быть больше 6, так как (7 дес.) 2 = 49 сотен, что превосходит 4082. Но оно не может быть и меньше 6, так как 5 дес. (с единицами) меньше 6 дес, а между тем (6 дес.) 2 = 36 сотен, что меньше 4082. А так как мы ищем наибольший целый корень, то мы не должны брать для корня 5 дес, когда и 6 десятков оказывается не много.
Итак, мы нашли число десятков корня, именно 6. Пишем эту цифру направо от знака =, запомнив, что она означает
десятки корня. Возвысив ее в квадрат, получим 36 сотен. Вычитаем эти 36 сотен из 40 сотен подкоренного числа и сносим две остальные цифры данного числа. В остатке 482 должны содержаться 2 (6 дес.) (ед.) + (ед.)2. Произведение (6 дес.) (ед.) должно составлять десятки; поэтому удвоенное произведение десятков на единицы надо искать в десятках остатка, т. е. в 48 (мы получим число их, отделив в остатке 48″2 одну цифру справа). Удвоенные десятки корня составляют 12. Значит, если 12 умножим на единицы корня (которые
пока неизвестны), то мы должны получить число, содержащееся в 48. Поэтому мы разделим 48 на 12.
Для этого налево от остатка проводим вертикальную черту и за нею (отступив от черты на одно место влево для цели, которая сейчас обнаружится) напишем удвоенную первую цифру корня, т. е. 12, и на нее разделим 48. В частном получим 4.
Однако, заранее нельзя ручаться, что цифру 4 можно принять за единицы корня,
так как мы сейчас разделили на 12 все число десятков остатка, тогда как некоторая часть из них может и не принадлежать удвоенному произведению десятков на единицы, а входит в состав квадрата единиц. Поэтому цифра 4 может оказаться велика. Надо ее испытать
. Она, очевидно, годится в том случае, если сумма 2 (6 дес.) 4 + 4 2 окажется не больше
остатка 482.
В результате
получаем сразу сумму того и другого. Полученное произведение оказалось 496, что больше остатка 482; значит, цифра 4 велика. Тогда испытаем таким же образом следующую меньшую цифру 3.
Примеры.
В примере 4-м при делении 47 десятков остатка на 4, мы получаем в частном 11. Но так как цифра единиц корня не может быть двузначным числом 11 или 10, то надо прямо испытать цифру 9.
В примере 5-м после вычитания из первой грани квадрата 8 остаток оказывается 0, и следующая грань тоже состоит из нулей. Это показывает, что искомый корень состоит только из 8 десятков, и потому на место единиц надо поставить нуль.
172. Извлечение корня из числа, большего 10000
. Пусть требуется найти √35782
. Так как подкоренное число превосходит 10 000, то корень из него больше √10000
= 100 и, следовательно, он состоит из 3 цифр или более. Из скольких бы цифр он ни состоял, мы можем его всегда рассматривать как сумму только десятков и единиц. Если, напр., корень оказался бы 482, то мы можем его считать за
сумму 48 дес. + 2 ед. Тогда квадрат корня будет состоять
из 3 слагаемых:
(дес.) 2 + 2 (дес.) (ед.) + (ед.) 2 .
Теперь мы можем рассуждать совершенно так же, как и при нахождении √4082
(в предыдущем параграфе). Разница будет только та, что для нахождения десятков корня из 4082 мы должны были извлечь корень из 40, и это можно было сделать по таблице умножения; теперь же для получения десятков√35782
нам придется извлечь корень из 357, что по таблице умножения нельзя выполнить. Но мы можем найти√357
тем приемом, который был описан в предыдущем параграфе, так как число 357
Далее поступаем так, как мы поступали при нахождении √4082
, a именно: налево от остатка 3382 проводим вертикальную черту и за нею пишем (отступив от черты на одно место) удвоенное число найденных десятков корня, т. е. 36 (дважды 18). В остатке отделяем одну цифру справа и делим число десятков остатка, т. е. 338, на 36. В частном получаем 9. Эту цифру испытываем, для чего
ее приписываем к 36 справа и на нее же умножаем. Произведение оказалось 3321, что меньше остатка. Значит, цифра 9 годится, пишем ее в корне.
Вообще, чтобы извлечь квадратный корень из какого угодно целого числа, надо сначала извлечь корень из числа его сотен; если это число более 100, то придется искать корень из числа сотен этих сотен, т. е. из десятков тысяч данного числа; если и это число более 100, придется извлекать корень из числа сотен десятков тысяч, т. е. из миллионов данного числа, и т. д.
Примеры.
В последнем примере, найдя первую цифру и вычтя квадрат ее, получаем в остатке 0. Сносим следующие 2 цифры 51. Отделив десятки, мы получаем 5 дес, тогда как удвоенная найденная цифра корня есть 6. Значит, от деления 5 на 6 мы получаем 0. Ставим в корне 0 на втором месте и к остатку сносим следующие 2 цифры; получаем 5110. Далее продолжаем как обыкновенно.
В этом примере искомый корень состоит только из 9 сотен, и потому на месте десятков и на месте единиц надо поставить нули.
Правило.
Чтобы, извлечь квадратный корень из данною целого числа, разбивают его, от правой руки к левой, на грани, по 2 цифры в каждой, кроме последней, в которой может быть и одна цифра.
Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят
вторую грань и число десятков получившегося числа делят
на
удвоенную первую цифру корня; полученное целое число подвергают испытанию.
Испытание это производится так: за вертикальной чертой (налево от остатка) пишут удвоенное ранее найденное число корня и к нему, с правой стороны, приписывают испытуемую цифру, получившееся, после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, большее остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
Следующие,
цифры корня находятся по тому же приему.
Если после снесения грани число десятков получившегося числа окажется меньше делителя, т. е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
173. Число цифр корня.
Из рассмотрения процесса нахождения корня следует, что в корне столько цифр, сколько в подкоренном числе заключается граней по 2 цифры каждая (в левой грани может быть и одна цифра).
Глава вторая.
Извлечение приближенных квадратных корней из целых и дробных чисел
.
Извлечение квадратного корня из многочленов см. в дополнениях ко 2-й части § 399 и след.
174. Признаки точного квадратного корня.
Точным квадратным корнем из данного числа называется такое число, квадрат которого в точности равняется данному числу. Укажем некоторые признаки, по которым можно судить, извлекается ли из данного числа точный корень, или нет:
а)
Если из данного целого числа не извлекается точный целый корень (получается при извлечении остаток), то из такого числа нельзя найти и дробный точный корень, так как всякая дробь, не равная целому числу, будучи умножена сама на себя, дает в произведении тоже дробь, а не целое число.
б)
Так как корень из дроби равен корню из числителя, деленному на корень из знаменателя, то точный корень из несократимой дроби не может быть найден в том случае, если его нельзя извлечь из числителя или из знаменателя. Напр, из дробей 4 / 5 , 8 / 9 и 11 / 15 нельзя извлечь точный корень, так как в первой дроби нельзя его извлечь из знаменателя,
во второй — из числителя и в третьей — ни из числителя, ни из знаменателя.
Из таких чисел, из которых нельзя извлечь точный корень, можно извлекать лишь приближенные корни.
175. Приближенный корень с точностью до 1
. Приближенным квадратным корнем с точностью до 1 из данного числа (целого или дробного — все равно) называется такое целое число, которое удовлетворяет следующим двум требованиям:
1) квадрат этого числа не больше данного числа; 2) но квадрат этого числа увеличенного на 1, больше данного числа. Другими словами, приближенным квадратным корнем с точностью до 1 называется наибольший целый квадратный корень из данного числа,
т. е.тот корень, который мы научились находить в предыдущей главе. Корень этот называется приближенным с точностью
до 1, потому что для получения точного корня к этому приближенному корню надо было бы добавить еще некоторую дробь, меньшую 1, так что если вместо неизвестного точного корня мы возьмем этот приближенный, то сделаем ошибку, меньшую 1.
Правило.
Чтобы извлечь приближенный квадратный корень с точностью до 1, надо извлечь наибольший целый корень из целой части данного числа.
Найденное по этому правилу число есть приближенный корень с недостатком
, так как в нем недостает до точного корня некоторой дроби (меньшей 1). Если этот корень увеличим на 1, то получим другое число, в котором есть некоторый избыток над точным корнем, и избыток этот меньше 1. Этот увеличенный на 1 корень можно назвать тоже приближенным корнем с точностью до 1, но с избытком. (Названия:
„с недостатком» или „с избытком» в некоторых математических книгах заменены другими равносильными: „по недостатку» или „по избытку».)
176. Приближенный корень с точностью до 1 / 10
. Пусть требуется найти √2,35104
с точностью до 1 / 10 . Это значит, что требуется найти такую десятичную дробь, которая состояла бы из целых единиц и десятых долей и которая удовлетворяла бы двум следующим требованиям:
1) квадрат этой дроби не превосходит 2,35104, но 2) если увеличим ее на 1 / 10 , то квадрат этой увеличенной дроби превосходит 2,35104.
Чтобы найти такую дробь, мы сначала нaйдем приближенный корень с точностью до 1, т. е. извлечем корень только из целого числа 2. Получим 1 (и в остатке 1). Пишем в корне цифру1 и ставим после нее запятую. Теперь будем искать цифру десятых. Для этого сносим к остатку 1 цифры 35, стоящие направо от запятой, и продолжаем извлечениетак, как будто мы извлекали корень из целого числа 235. Полученную цифру 5 пишем в корне на месте десятых. Остальные цифры подкоренного числа (104)
нам не нужны. Что полученное число 1,5 будет действительно приближенный корень с точностью до 1 / 10 видно из следующего. Если бы мы находили наибольший целый корень из 235 с точностью до 1, то получили бы 15. Значит:
15 2 235, но 16 2 >235.
Разделив все эти числа на 100, получим:
Значит, число 1,5 есть та десятичная дробь, которую мы назвали приближенным корнем с точностью до 1 / 10 .
Найдем еще этим приемом следующие приближенные корни с точностью до 0,1:
177. Приближенный квадратный корень с точностью до 1 / 100 до 1 / 1000 и т. д.
Пусть требуется найти с точностью до 1 / 100 приближенный √248
. Это значит: найти такую десятичную дробь, которая состояла бы из целых, десятых и сотых долей и которая удовлетворяла бы двум требованиям:
1) квадрат ее не превосходит 248, но 2) если увеличим эту дробь на 1 / 100 то квадрат этой увеличенной дроби превосходит 248.
Такую дробь мы найдем в такой последовательности: сначала отыщем целое число, потом цифру десятых, затем и цифру сотых. Корень
из целого числа будет 15 целых. Чтобы получить цифру десятых, надо как мы видели, снести к остатку 23 еще 2 цифры, стоящие направо от запятой. В нашем примере этих цифр нет вовсе, ставим на их место нули. Приписав их к остатку и продолжая действие так, как будто находим корень из целого числа 24 800, мы найдем цифру десятых 7. Остается найти цифру сотых. Для этого приписываем к остатку 151 еще 2 нуля и продолжаем извлечение, как будто мы находим корень из целого числа 2 480 000. Получаем 15,74. Что это
число действительно есть приближенный корень из 248 с точностью до 1 / 100 видно из следующего. Если бы мы находили наибольший целый квадратный корень из целого числа 2 480 000, то получили бы 1574; значит:
1574 2 2 480 000, но 1575 2 > 2 480 000.
Разделив все числа на 10 000 (= 100 2), получим:
Значит, 15,74 есть та десятичная дробь, которую мы назвали приближенным корнем с точностью до 1 / 100 из 248.
Применяя этот прием к нахождению приближенного корня с точностью до 1 / 1000 до 1 / 10000 и т. д. найдем следующее.
Правило.
Чтобы извлечь из данного целою числа или из данной десятичной дроби приближенный корень с точностью до 1 / 10 до 1 / 100 до 1 / 100 и т. д., находят сначала приближенный корень с точностью до 1, извлекая корень из целого числа (если его нет, пишут о корне 0 целых).
Потом находят цифру десятых. Для этого к остатку сносят,2 цифры подкоренного числа, стоящие направо от запятой (если их нет, приписывают к остатку два нуля), и продолжают извлечение так, как это делается при извлечении корня из целого числа. Полученную цифру пишут в корне на месте десятых.
Затем находят цифру сотых. Для этого к остатку сносят снова две цифры, стоящие направо от тех, которые были только что снесены, и т. д.
Таким образом, при извлечении корня из целого числа с десятичной дробью, надо делить на грани по 2 цифры в каждой, начиная от запятой, как влево (в целой части числа), так и вправо, (в дробной части).
Примеры.
1) Найти до 1 / 100 корни: а) √2
; б) √0,3
;
В последнем примере мы обратили дробь 3 / 7 в десятичную, вычислив 8 десятичных знаков, чтобы образовались 4 грани, потребные для нахождения 4 десятичных знаков корня.
178. Описание таблицы квадратных корней.
В конце этой книги приложена таблица квадратных корней, вычисленных с четырьмя цифрами. По этой таблице можно быстро находить квадратный корень из целого числа (или десятичной дроби), которое выражено не более, чем четырьмя цифрами. Прежде чем объяснить, как эта таблица устроена, заметим, что первую значащую цифру искомого корня мы всегда можем найти без помощи таблиц по одному взгляду на подкоренное число; мы легко
также определим, какой десятичный разряд означает первая цифра корня и, следовательно, где в корне, когда найдем его цифры, надо поставить запятую. Приведем несколько примеров:
1)
√5″27,3
.
Первая цифра будет 2, так как левая грань подкоренного числа есть 5; а корень из 5 равен 2. Кроме того, так как в целой части подкоренного числа всех граней только 2, то в целой части искомого корня должно быть 2 цифры и, следовательно, первая его цифра 2 должна означать десятки.
2)
√9,041
. Очевидно, в этом корне первая цифра будет 3 простые единицы
.
3)
√0,00″83″4
. Первая значащая цифра есть 9, так как грань, из которой пришлось бы извлекать корень для получения первой значащей цифры, есть 83, а корень из 83 равен 9. Так как в искомом числе не будет ни целых, ни десятых, то первая цифра 9 должна означать сотые.
4)
√0,73″85
. Первая значащая цифра есть 8 десятых
.
5) √0,00″00″35″7
. Первая значащая цифра будет 5 тысячных
.
Сделаем еще одно замечание. Положим, что требуется извлечь корень из такого числа, которое, после отбрасывания в нем занятой, изображается рядом таких цифр: 5681. Корень этот может быть один из слелуюших:
Если возьмем корни, подчеркнутые нами одной чертою, то все они будут выражены одним и тем же рядом цифр, именно теми цифрами, которые получаются при извлечении корня из 5681 (это будут цифры 7, 5, 3, 7). Причина этому та, что грани, на которые приходится разбивать подкоренное число при нахождении цифр корня, будут во всех этих примерах одни и те же, поэтому и цифры для каждого корня окажутся одинаковые (только положение запятой будет, конечно, различное). Точно так же
во всех корнях, подчеркнутых нами двумя чертами, должны получиться одинаковые цифры, именно те, которыми выражается √568,1
(эти цифры будут 2, 3, 8, 3), и по той же причине. Таким образом, цифры корней из чисел, изображаемых (по отбрасывании запятой) одним и тем же рядом цифр 5681, будут двоякого (и только двоякого) рода: либо это ряд 7, 5, 3, 7, либо ряд 2, 3, 8, 3. То же самое, очевидно, может быть сказано о всяком другом ряде цифр. Поэтому, как мы сейчас
увидим,
в таблице каждому ряду цифр подкоренного
числа соответствуют 2 ряда цифр для корней.
Теперь мы можем объяснить устройство таблицы и способ ее пользования. Для ясности объяснения мы изобразили здесь начало первой страницы таблицы.
Таблица эта расположена на нескольких страницах. На каждой из них в первой слева колонке помещены числа 10, 11, 12… (до 99). Эти числа выражают первые 2 цифры числа, из которого ищется квадратный корень. В верхней горизонтальной строчке (а также и в нижней) размещены числа: 0, 1, 2, 3… 9, представляющие собою 3-ю цифру данного числа, а затем далее направо помещены цифры 1, 2, 3 . . . 9, представляющие собою4-ю цифру данного числа. Во всех
других горизонтальных строчках помещены по 2 четырехзначных числа, выражающие квадратные корни из соответствующих чисел.
Пусть требуется найти квадратный корень из какого-нибудь числа, целого или выраженного десятичною дробью. Прежде всего находим без помощи таблиц первую цифру корня и ее разряд. Затем отбросим в данном числе запятую, если она есть. Положим сначала, что после отбрасывания запятой останутся только 3 цифры, напр. 114. Находим в таблицах в левой крайней колонке первые 2 цифры, т. е. 11, и продвигаемся от них
направо по горизонтальной строке до тех пор, пока не дойдем до вертикальной колонки, наверху (и внизу) которой стоит 3-я цифра числа, т. е. 4. В этом месте мы находим два четырехзначных числа: 1068 и 3376. Которое из этих двух чисел надо взять и где поставить в нем запятую, это определяется первою цифрою корня и ее разрядом, которые мы нашли раньше. Так, если надо найти √0,11″4
, то первая цифра корня есть 3 десятых, и потому мы должны
взять для корня 0,3376. Если бы требовалось
найти √1,14
, то первая цифра корня была бы 1, и мы взяли бы тогда 1,068.
Таким образом мы легко найдем:
√5,30
= 2,302; √7″18
= 26,80; √0,91″6
= 0,9571 и т.п.
Положим теперь, что требуется найти корень из числа, выраженного (по отбрасывании запятой) 4 цифрами, напр.√7″45,6
. Заметив, что первая цифра корня есть 2 десятка, находим для числа 745 так, как сейчас было объяснено, цифры 2729 (это число только замечаем пальцем, но его не записываем). Потом продвигаемся от этого числа еще направо до тех пор, пока в правой части таблицы (за последнею жирною чертою) не встретим ту вертикальную
колонку, которая отмечена наверху (и внизу)
4-й цифрой данного числа, т. е. цифрой 6, и находим там число 1. Это будет поправка, которую надо приложить (в уме) к ранее найденному числу 2729; получим 2730. Это число записываем и ставим в нем запятую на надлежащем месте: 27,30.
Таким путем найдем, напр:
√44,37
= 6,661; √4,437
= 2,107; √0,04″437
=0,2107 и т.д.
Если подкоренное число выражается только одной или двумя цифрами, то мы можем предположить, что после этих цифр стоит один или два нуля, и затем поступать так, как было объяснено для трехзначного числа. Напр.√2,7
=√2,70
=1,643; √0,13
= √0,13″0
= 0,3606 и т.п..
Наконец, если подкоренное число выражено более, чем 4 цифрами, то из них мы возьмем только первые 4, а остальные отбросим, причем для уменьшения ошибки, если первая из отбрасцваемых цифр есть 5 или более 5, то мы увеличим на l четвертую из удержанных цифр. Так:
√357,8|
3
|
= 18,91; √0,49″35|7 |
= 0,7025; и т.п.
Замечание.
В таблицах указан приближенный квадратный корень иногда с недостатком, иногда же с избытком, а именно тот из этих приближенных корней, который ближе подходит к точному корню.
179. Извлечение квадратных корней из обыкновенных дробей.
Точный квадратный корень из несократимой дроби можно извлечь лишь тогда, когда оба члена дроби точные квадраты . В этом случае достаточно извлечь корень из числителя и знаменателя отдельно, напр.:
Приближенный квадратный корень из обыкновенной дроби c какою-нибудь десятичною точностью проще всего можно находить, если предварительно обратим обыкновенную дробь в десятичную, вычислив в этой дроби такое число десятичных знаков после запятой, которое было бы вдвое больше числа десятичных знаков в искомом корне.
Впрочем можно поступать и иначе. Объясним это на следующем примере:
Найти приближенный √ 5 / 24
Сделаем знаменатель точным квадратом. Для этого достаточно было бы умножить оба члена дроби на знаменатель 24; но в этом примере можно поступить иначе. Разложим 24 на простые множители: 24 = 2 2 2 3. Из этого разложения видно, что если 24 умножить на 2 и еще на 3, то тогда в произведении каждый простой множитель будет повторяться четное число раз, и, следовательно, знаменатель сделается квадратом:
Остается вычислить √30
с какой-нибудь точностью и результат разделить на 12. При этом надо иметь в виду, что от деления на 12 уменьшится и дробь, показывающая степень точности. Так, если найдем √30
с точностью до 1 / 10 и результат разделим на 12, то получим приближенный корень из дроби 5 / 24 с точностью до 1 / 120 (а
именно
54 / 120 и 55 / 120)
Глава третья.
График функции
х = √
y
.
180. Обратная функция.
Пусть дано какое-нибудь уравнение, определяющее у
как функцию от х
, напр, такое: у = х
2
. Мы можем сказать, что оно определяет не только у
как функцию от х
, но и, обратно, определяет х
как функцию от у
, хотя и неявным образом. Чтобы сделать эту функцию явной, надо решить данное уравнение относительно х
,
принимая у
за известное число; так, из взятого нами уравнения находим: у = х
2
.
Алгебраическое выражение, полученное для x после решения уравнения, определяющего у как функцию от x, называется функцией, обратной той, которая определяет у.
Значит, функция, х = √
y
обратна функции у = х
2
. Если, как это принято, независимое переменное обозначим х
, а зависимое у
, то полученную сейчас обратную функцию можем выразить так: y = √
x
. Таким образом, чтобы получить функцию, обратную данной (прямой), надо из уравнения, определяющего эту данную функцию, вывести х
в зависимости от y
и в полученном выражении заменить y
на x
, а х
на y
.
181. График функции
y = √
x
. Функция эта невозможна при отрицательном значении х
, но ее возможно вычислить (с любою точностью) при всяком положительном значении x
, причем для каждого такого значения функция получает два различных значения с одинаковой абсолютной величиной, но с противоположными знаками. Если знаком √
будем обозначать только арифметическое
значение квадратного корня, то эти два значения функции можем выразить так: y =
±
√
x
Для построения графика этой
функции надо предварительно составить таблицу ее значений. Всего проще эту таблицу составить из таблицы значений прямой функции:
у = х
2
.
если значения у
примем за значения х
, и наоборот:
y =
±
√
x
Нанеся все эти значения на чертеже, получим следующий график.
На том же чертеже мы изобразили (прерывистой линией) и график прямой функции у = х
2
. Сравним эти два графика между собою.
182. Соотношение между графиками прямой и обратной функций.
Для составления таблицы значений обратной функции y =
±
√
x
мы брали для х
те числа, которые в таблице прямой функции у = х
2
служили значениями для у
, а для у
брали те числа; которые в этой таблице были значениями для x
. Из этого следует, что оба графика одинаковы, только график прямой функции так расположен относительно оси у
— ов, как график обратной функции расположен относительно оси х
— ов. Вследствие этого, если мы перегнем чертеж вокруг прямой ОА
, делящей пополам прямой угол xОу
, так, чтобы часть чертежа, содержащая полуось Оу
, упала
на ту часть, которая содержит полуось Ох
, то Оу
совместится с Ох
, все деления Оу
совпадут c делениями Ох
, и точки параболы у = х
2
совместятся с соответствующими точками графика y =
±
√
x
. Напр, точки М
и N
, у которых ордината 4
, а абсциссы 2
и —2
, совпадут с точками М»
и N»
, у которых абсцисса 4
, а ординаты 2
и —2
. Если же эти точки совпадут, то это значит, что прямые ММ»
и NN»
перпендикулярны к ОА
и делятся этою прямою пополам. То же самое можно сказать о всех других соответствующих точках обоих графиков.
Таким образом, график обратной функции должен быть такой же, как и грaфик прямой функции, но расположены эти графики различно, а именно симметрично друг с другом относительно биссектрисы угла хОу
. Можно сказать, что график обратной функции есть отображение (как в зеркале) графика прямой функции относительно биссектрисы угла хОу
.
Как извлечь корень
из числа. В этой статье мы будем учиться извлекать квадратный корень из четырехзначных и пятизначных чисел.
Давайте, для примера, извлечем квадратный корень из числа 1936.
Следовательно, .
Последняя цифра в числе 1936 — цифра 6. На 6 заканчивается квадрат числа 4 и числа 6. Следовательно, 1936 может быть квадратом числа 44 или числа 46. Осталось проверить с помощью умножения.
Значит,
Извлечем квадратный корень из числа 15129.
Следовательно, .
Последняя цифра в числе 15129 — цифра 9. На 9 заканчивается квадрат числа 3 и числа 7. Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
Значит,
Как извлечь корень — видео
А теперь предлагаю вам посмотреть видео Анны Денисовой — «Как извлечь корень
«, автора сайта » Простая физика
«, в котором она рассказывает, как извлекать квадратные и кубические корни без калькулятора.
В видео рассматривается несколько способов извлечения корней:
1. Самый простой способ извлечения квадратного корня.
2. Подбором, используя квадрат суммы.
3. Вавилонский способ.
4. Способ извлечения квадратного корня в столбик.
5. Быстрый способ извлечения кубического корня.
6. Способ извлечения кубического корня в столбик.
Пришло время разобрать способы извлечения корней
. Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0
до 99
включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Таблицы кубов, таблицы четвертых степеней чисел от 0
до 99
и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n
-ой степени из числа a
, при этом число a
содержится в таблице n
-ых степеней. По этой таблице находим число b
такое, что a=b n
. Тогда , следовательно, число b
будет искомым корнем n
-ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683
. Находим число 19 683
в таблице кубов, из нее находим, что это число является кубом числа 27
, следовательно, .
Понятно, что таблицы n
-ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем
: после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a
извлекается корень n
-ой степени, и его значение равно b
. В этом случае верно равенство a=b n
. Число b
как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m
в виде p 1 ·p 2 ·…·p m
, а подкоренное число a
в этом случае представляется как (p 1 ·p 2 ·…·p m) n
. Так как разложение числа на простые множители единственно, то разложение подкоренного числа a
на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n
, что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a
не может быть представлено в виде (p 1 ·p 2 ·…·p m) n
, то корень n
-ой степени из такого числа a
нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144
.
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2
, откуда понятно, что квадратный корень из 144
равен 12
.
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144
на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3
. На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2
. Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243
имеет вид 243=3 5
. Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2
. Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7
не кратна трем. Следовательно, кубический корень из числа 285 768
не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q
. Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби
: корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169
.
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5
, а квадратный корень из знаменателя равен 13
. Тогда 
завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552
.
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000
. Тогда 
(2·3·13) 3 =78 3
и 1 000=10 3
, то и
. Осталось лишь завершить вычисления

Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел
: чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: 



Приведем краткую запись решения: 
Ответ:

Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n
-ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n
числа 0, 10, 100, …
до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n
на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, …
и возводим их в квадрат, пока не получим число, превосходящее 5
. Имеем 0 2 =05
, значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9
. При этом параллельно вычисляются n
-ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9
.
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23
. И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, …
.
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100
и т.д. пока не получим число, превосходящее 2 151,186
. Имеем 0 3 =02 151,186
, таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Извлечение корня из большого числа. Дорогие друзья!
В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.
Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:
Вычисляем:
Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Суть рассматриваемого нами метода
—
это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.
Извлечём корень из 190969.
Сначала определим — между какими числами (кратными ста) лежит наш результат.
Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500,
так как
400 2
=160000 и 500 2
=250000
Действительно:
посредине, ближе к 160 000 или к 250 000?
Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
Действительно, он меньше 450, так как 190 969
Теперь проверим число 440:
Значит наш результат меньше 440, так как
190 969
Проверяем число 430:
Мы установили, что результат данного корня лежит в пределах от 430 до 440.
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце.
Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце.
Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце.
Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце.
Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце.
Например, 17 на 17 равно 289.
Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.
*Только они при возведении в квадрат могут дать 9 в конце.
Проверяем:
Значит результат корня будет равен 437.
То есть, мы как бы «нащупали» верный ответ.
Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.
Извлеките самостоятельно корень из 148996
Такой дискриминант получается в задаче:
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Посмотреть решение
Результат корня находится между числами 300 и 400:
300 2 =90000 400 2 =160000
Действительно, 90000
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.
Вычислим разности
148996
—
90000=58996 и 160000
—
148996=11004.
Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.
Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Вы
хотите хорошо сдать ЕГЭ по математике? Тогда вам просто необходимо
уметь считать быстро, правильно и без калькулятора. Ведь главная причина
потери баллов на ЕГЭ по математике – вычислительные ошибки.
По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по
математике не разрешено. За использование калькулятора или мобильного
телефона может быть начислен штраф в размере от трех до десяти тысяч
рублей.
На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи
решаются без него. Главное – внимание, аккуратность и некоторые
секретные приемы, о которых мы расскажем.
1
. Начнем с главного правила. Если какое-то вычисление можно упростить – упростите его.
Вот, например, такое «дьявольское уравнение»:
666 2 
Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле b 2 4ac
, после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на 333
. Получится
2 2 
Какой способ проще?
2
. Многие школьники не любят умножение в
«столбик». Никому не нравилось в четвертом классе решать скучные
«примеры». Однако перемножить числа во многих случаях можно и без
«столбика», в строчку. Это намного быстрее.
385 7 300 7 




18 17 18 10 





Обратите внимание, что мы начинаем не с меньших разрядов, а с бoльших. Это удобно.
3
. Теперь – деление. Нелегко «в столбик» разделить 9450
на 2100
. Но вспомним, что знак деления: и дробная черта – одно и то же. Запишем 9450: 2100
в виде дроби и сократим дробь:
Другой пример.
4
. Как быстро и без всяких столбиков возвести в квадрат двузначное число? Применяем формулы сокращенного умножения:
(а+b) 2 а 2 

23 2 (20+3) 2 20 2 



39 2 (30 




44 2 (40 




Иногда удобно использовать и другую формулу:
(а-b) 2 = а 2 — 2ab 
78 2 = (80 – 2) 2 = 6400 – 320 
89 2 = (90 – 1) 2 = 8100 – 180 
5
. Числа, оканчивающиеся на 5
, в квадрат возводятся моментально.
Допустим, надо найти квадрат числа А5
(А
— не обязательно цифра, любое натуральное число). Умножаем А
на А+1
и к результату приписываем 25
. Всё!
Например: 45 2 2025
(4 5 20
и приписали 25
).
65 2 4225
(6 7 42
и приписали 25
).
125 2 15625
(12 13 156
и приписали 25
).
Этот способ полезен не только для возведения в квадрат, но для извлечения квадратного корня из чисел, оканчивающихся на 25
.
6
. А как вообще извлечь квадратный корень без калькулятора? Покажем два способа.
Первый способ – разложение подкоренного выражения на множители.
Например, найдем
Число 6561
делится на 3
(так как сумма его цифр делится на 3
). Разложим 6561
на множители:
6561 3 3 3 3 81 81 81
81
Найдем . Это число делится на 2
. На 3
оно тоже делится. Раскладываем 2916
на множители.
Еще пример.
Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.
Например, надо найти . Число под корнем – нечетное, оно не делится на 3
, не делится на 5
, не делится на 7
… Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
Очевидно, что в квадрат возводили двузначное число, которое находится между числами 70
и 80
, поскольку 70 2 4900, 80 2 6400
, а число 5041
находится между ними. Первую цифру в ответе мы уже знаем, это 7
.
Последняя цифра в числе 5041
равна 1
. Поскольку 1 2
1
, 9 2
81
, последняя цифра в ответе – либо 1
, либо 9
. Проверим:
71 2 (70 


. Получилось!
Найдем .
50 2 2500, 60 2 3600
. Значит, первая цифра в ответе – пятерка.
В числе 2809
последняя цифра – девятка. 3 2 9
, 7 2 49
. Значит, последняя цифра в ответе – либо 3
, либо 9
.
Проверим:
53 2 (50 


.
Если число, из которого надо извлечь квадратный корень, заканчивается на 2, 3, 7
или 8
– значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на 2, 3, 7
или 8
.
Помните, что в задачах части В вариантов ЕГЭ по математике ответ должен
быть записан в виде целого числа или конечной десятичной дроби, то есть
должен являться рациональным числом.
7
. Квадратные уравнения встречаются нам в задачах В5
, В12
и В13
вариантов ЕГЭ, а также в части С
.
В них нужно считать дискриминант, а затем извлекать из него корень. И
совсем не обязательно искать корни из пятизначных чисел. Во многих
случаях дискриминант удается разложить на множители.
Например, в уравнении
8
. Иногда дискриминант удается посчитать по известной формуле сокращенного умножения: a 2 b 2 (ab)(a
. Вот, например, такое уравнение вполне может получиться при решении задачи В12
:
9
. Еще одна ситуация, в которой выражение под корнем можно разложить на множители, взята из задачи В4
.
Гипотенуза прямоугольного треугольника равна 39
, один из катетов равен 36
, найти второй катет.
По теореме Пифагора, он равен . Можно долго считать в столбик, но проще применить формулу сокращенного умножения.
А теперь расскажем самое интересное — из-за чего все-таки выпускники
теряют на ЕГЭ драгоценные баллы. Ведь ошибки в вычислениях возникают не
просто так.
1
.
Верный путь к потере баллов — неаккуратные вычисления, в которых что-то
исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите
на свои черновики. Возможно, они выглядят так же?
Пишите разборчиво! Не экономьте бумагу. Если что-то неправильно – не исправляйте одну цифру на другую, лучше напишите заново.
2
. Почему-то многие школьники, считая в
столбик, стараются сделать это 1) очень-очень быстро, 2) очень мелкими
цифрами, в уголке тетради и 3) карандашом. В результате получается вот
что:
Разобрать что-либо невозможно. Что ж тогда удивляться, что оценка за ЕГЭ ниже, чем ожидали?
3
. Многие школьники привыкли игнорировать скобки в выражениях. Иногда встречается и такое:
Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.

4
. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что .
Здесь нарисован «гамбургер», то есть многоэтажная дробь. Крайне сложно при таком способе получить правильный ответ.
Подведем итоги.
Проверка заданий части В
– автоматическая.
Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет.
Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому в
ваших интересах научиться считать быстро, правильно и без калькулятора.
Задания части С
проверяет эксперт. Позаботьтесь о нем! Пусть ему будет понятен и ваш почерк, и логика решения.
SHARES
Этот список нескольких малоизвестных математических трюков покажет вам как быстро считать в уме в случаях, посложнее чем 5 умножить на 10. Умение быстро считать создает представление о вас, как о человеке умном и надежном.
1. Умножаем на 11
Все мы знаем, как быстро умножить число на 10, нужно лишь добавить ноль в конце, но знаете ли вы, что есть фишка как легко умножить двузначное число на 11? Узнать все фишки…
Допустим, нам нужно умножить 63 на 11. Возьмите двузначное число, которое нужно умножить на 11 и представьте между его двумя цифрами место:
6_3
Теперь сложите первую и вторую цифру этого числа и поместите в это место:
6_(6+3)_3
И наш результат умножения готов:
63*11=693
Если же результат сложения первой и второй цифры двузначное число, вставляйте только вторую цифру, а к первой цифре исходного числа прибавляйте единицу:
79*11=
7_(7+9)_9
(7+1)_6_9
79*11=869
2. Быстрое возведение в квадрат числа, оканчивающегося на 5
Если вам нужно возвести в кадрат двузначное число, заканчивающееся на 5, то вы можете сделать это очень просто в уме. Умножьте первую цифру числа на саму себя плюс единица и добавьте в конце 25, и это всё:
45*45=4*(4+1)_25=2025
3. Умножение на 5
Вам нужно взять это число и разделить на 2. Если результат целое число, то добавьте к нему 0 в конце, если нет, отбросьте остаток и добавьте 5 в конце:
1248*5=(1248/2)_(0 или 5)=624_(0 или 5)=6240 (результат деления на 2 целое число)
4469*5=(4469/2)_(0 или 5)=(2234.5)_(0 или 5)=22345 (результат деления на 2 число с остатком)
4. Умножение на 4
Это очень простая и, с первого взгляда, очевидная фишка умножения любого числа на 4, но насмотря на это люди не догадываются о ней в нужный момент. Чтобы просто умножить любое число на 4, нужно уножить его на 2, а потом снова умножить на 2:
67*4=67*2*2=134*2=268
5. Вычислить 15%
Если вам нужно в уме вычислить 15% от какого-либо числа, то есть простой способ, как это сделать. Возьмите 10% от числа (разделив число на 10) и добавьте к этому числу половину от полученных 10%.
15% от 884 рублей=(10% от 884 рублей)+((10% от 884 рублей)/2)=88.4 рубля + 44.2 рубля = 132.6 рублей
6. Умножение больших чисел
Если вам нужно перемножить большие числа в уме и одно из них четное, то вы можете воспользоваться методом упрощения множителей, уменьшя четно число в два раза, а второе увеличивая в два раза:
32*125 это
16*250 это
8*500 это
4*1000=4000
7. Деление на 5
Разделить большое число на 5 в голове очень просто. Всё что нужно, это умножить число на 2 и сместить запятую на один знак назад:
175/5
Умножаем на 2: 175*2=350
Смещаем на один знак: 35.0 или 35
1244/5
Умножаем на 2: 1244*2=2488
Смещаем на один знак: 248.8
8. Вычитание из 1000
Чтобы вычесть большое число из тысячи, следуйте простой технике, отнимайте все цифры числа от 9, кроме последней, а последнее цифру числа отнимите от 10:
1000-489=(9-4)_(9-8)_(10-9)=511
Разумеется, чтобы научиться быстро считать в уме, нужно много раз попрактиковаться в использовании этих приемов, чтобы довести их до автоматизма, одноразовое прочтение оставит только нули в вашей голове.
Для большинства людей умножение на 5 не составляет труда для небольших чисел, но как быстро считать в уме большие числа, умноженные на 5?
В данной статье мы предлагаем вам подборку простых математических приёмов, многие из которых довольно актуальны в жизни и позволяют считать быстрее.
«Чистая математика является в своём роде поэзией логической идеи».
Альберт Эйнштейн
Быстрое вычисление процентов
Пожалуй, в эпоху кредитов и рассрочек наиболее актуальным математическим навыком можно назвать виртуозное вычисление процентов в уме. Самым быстрым способом вычислить определённый процент от числа является умножение данного процента на это число с последующим отбрасыванием двух последних цифр в получившемся результате, ведь процент есть не что иное, как одна сотая доля.
Сколько составляют 20% от 70? 70 × 20 = 1400. Отбрасываем две цифры и получаем 14. При перестановке множителей произведение не меняется, и если вы попробуете вычислить 70% от 20, то ответ также будет 14.
Данный способ очень прост в случае с круглыми числами, но что делать, если надо посчитать, к примеру, процент от числа 72 или 29? В такой ситуации придётся пожертвовать точностью ради скорости и округлить число (в нашем примере 72 округляется до 70, а 29 до 30), после чего воспользоваться тем же приёмом с умножением и отбрасыванием двух последних цифр.
Быстрая проверка делимости
Можно ли поровну поделить 408 конфет между 12 детьми? Ответить на этот вопрос легко и без помощи калькулятора, если вспомнить простые признаки делимости, которые нам преподавали ещё в школе.
Число делится на 2, если его последняя цифра делится на 2.
Число делится на 3, если сумма цифр, из которых состоит число, делится на 3. Например, возьмём число 501, представим его как 5 + 0 + 1 = 6. 6 делится на 3, а значит, и само число 501 делится на 3.
Число делится на 4, если число, образованное его последними двумя цифрами, делится на 4. Например, берём 2 340. Последние две цифры образуют число 40, которое делится на 4.
Число делится на 5, если его последняя цифра 0 или 5.
Число делится на 6, если оно делится на 2 и 3.
Число делится на 9, если сумма цифр, из которых состоит число, делится на 9. Например, возьмём число 6 390, представим его как 6 + 3 + 9 + 0 = 18. 18 делится на 9, а значит, и само число 6 390 делится на 9.
Число делится на 12, если оно делится на 3 и 4.
Быстрое вычисление квадратного корня
Квадратный корень из 4 равен 2. Это посчитает любой. А как насчёт квадратного корня из 85?
Для быстрого приблизительного решения находим ближайшее к заданному квадратное число, в данном случае это 81 = 9^2.
Теперь находим следующий ближайший квадрат. В данном случае это 100 = 10^2.
Корень квадратный из 85 находится где-то в интервале между 9 и 10, а поскольку 85 ближе к 81, чем к 100, то квадратный корень этого числа будет 9 с чем-то.
Быстрое вычисление времени, через которое денежный вклад под определённый процент удвоится
Хотите быстро узнать время, которое потребуется, чтобы ваш денежный вклад с определённой процентной ставкой удвоился? Тут также не нужен калькулятор, достаточно знать «правило 72».
Делим число 72 на нашу процентную ставку, после чего получаем приблизительный срок, через который вклад удвоится.
Если вклад сделан под 5% годовых, то потребуется 14 с небольшим лет, чтобы он удвоился.
Почему именно 72 (иногда берут 70 или 69) ? Как это работает? На эти вопросы развёрнуто ответит «Википедия».
Быстрое вычисление времени, через которое денежный вклад под определённый процент утроится
В данном случае процентная ставка по вкладу должна стать делителем числа 115.
Если вклад сделан под 5% годовых, то потребуется 23 года, чтобы он утроился.
Быстрое вычисление почасовой ставки
Представьте, что вы проходите собеседования с двумя работодателями, которые не называют оклад в привычном формате «рублей в месяц», а говорят о годовых окладах и почасовой оплате. Как быстро посчитать, где платят больше? Там, где годовой оклад составляет 360 000 рублей, или там, где платят 200 рублей в час?
Для расчёта оплаты одного часа работы при озвучивании годового оклада необходимо отбросить от названной суммы три последних знака, после чего разделить получившееся число на 2.
360 000 превращается в 360 ÷ 2 = 180 рублей в час. При прочих равных условиях получается, что второе предложение лучше.
Продвинутая математика на пальцах
Ваши пальцы способны на гораздо большее, нежели простые операции сложения и вычитания.
С помощью пальцев можно легко умножать на 9, если вы вдруг забыли таблицу умножения.
Пронумеруем пальцы на руках слева направо от 1 до 10.
Если мы хотим умножить 9 на 5, то загибаем пятый палец слева.
Теперь смотрим на руки. Получается четыре несогнутых пальца до согнутого. Они обозначают десятки. И пять несогнутых пальцев после согнутого. Они обозначают единицы. Ответ: 45.
Если мы хотим умножить 9 на 6, то загибаем шестой палец слева. Получим пять несогнутых пальцев до согнутого пальца и четыре после. Ответ: 54.
Таким образом можно воспроизвести весь столбик умножения на 9.
Быстрое умножение на 4
Существует чрезвычайно лёгкий способ молниеносного умножения даже больших чисел на 4. Для этого достаточно разложить операцию на два действия, умножив искомое число на 2, а затем ещё раз на 2.
Посмотрите сами. Умножить 1 223 сразу на 4 в уме сможет не каждый. А теперь делаем 1223 × 2 = 2446 и далее 2446 × 2 = 4892. Так гораздо проще.
Быстрое определение необходимого минимума
Представьте, что вы проходите серию из пяти тестов, для успешной сдачи которых вам необходим минимальный балл 92. Остался последний тест, а по предыдущим результаты таковы: 81, 98, 90, 93. Как вычислить необходимый минимум, который нужно получить в последнем тесте?
Для этого считаем, сколько баллов мы недобрали/перебрали в уже пройденных тестах, обозначая недобор отрицательными числами, а результаты с запасом — положительными.
Итак, 81 − 92 = −11; 98 − 92 = 6; 90 − 92 = −2; 93 − 92 = 1.
Сложив эти числа, получаем корректировку для необходимого минимума: −11 + 6 − 2 + 1 = −6.
Получается дефицит в 6 баллов, а значит, необходимый минимум увеличивается: 92 + 6 = 98. Дела плохи.
Быстрое представление значения обыкновенной дроби
Примерное значение обыкновенной дроби можно очень быстро представить в виде десятичной дроби, если предварительно приводить её к простым и понятным соотношениям: 1/4,1/3, 1/2 и 3/4.
К примеру, у нас есть дробь 28/77, что очень близко к 28/84 = 1/3, но поскольку мы увеличили знаменатель, то изначальное число будет несколько больше, то есть чуть больше, чем 0,33.
Трюк с угадыванием цифры
Можно немного поиграть в Дэвида Блэйна и удивить друзей интересным, но очень простым математическим трюком.
Попросите друга загадать любое целое число.
Пусть он умножит его на 2.
Затем прибавит к получившемуся числу 9.
Теперь пусть отнимет 3 от получившегося числа.
А теперь пусть разделит получившееся число пополам (оно в любом случае разделится без остатка).
Наконец, попросите его вычесть из получившегося числа то число, которое он загадал в начале.
Ответ всегда будет 3.
Да, очень тупо, но часто эффект превосходит все ожидания.
Метки:
The syntax here is horrible! Double check your textbook for the rules for constructing well formed formulae. Also you have used «2» which isn’t in your official vocabulary. But most basically, your quantifiers haven’t got the right «scope», i.e. aren’t governing what you need them to govern.
It greatly helps to take translations in stages, using «Loglish» as a half way house as you go along. So you want to render
The square root of an odd number is odd
And you understand that as a universal generalization, so
(For any number $x$)(if $x$ is the square root of an odd number, then x is odd)
Which unpacks as
(For any number $x$)(if there is an odd number $y$ where $x cdot x = y$, then $x$ is odd)
Let’s now make things simpler by explicitly assuming that the domain is (natural?) numbers, so we needn’t explicitly type the variables. That seems to be assumed in the question, as you aren’t given a symbol for «is a number». Then we have, more simply
(For any $x$)(if (there exists $y$)($y$ is odd and $x cdot x = y$), then $x$ is odd).
Now putting in the quantifier, conjunction and conditional symbols we get
($forall x$)(($exists y$)($y$ is odd $land$ $x cdot x = y$) $to x$ is odd).
Note the bracketing. So now you just need to translate «$x$ is odd», «$y$ is odd» given your available apparatus.
«$w$ is odd» can be rendered something like this: $(exists z)(w = (z + z) + 1)$
or equally
«$w$ is odd» can be rendered something like this: $(exists z)(w = (1 + 1)cdot z + 1)$
So now plug in this sort of thing, and you are done! Though your official syntax may not need brackets round quantifiers, and I’ve been a bit sloppy with brackets in the last two formulae (where?).
Now, I’m not suggesting that you write down all the Loglish mash-ups — but it is worth writing down some when faced with this sort of translation excercse. Thinking in stages like this will keep you on track!
If your library has a copy of P-t-r Sm-th’s Introduction to Formal Logic, check out the (short but quite good!) chapters 22- 24 for more along these lines.
Арифметический корень натуральной степени
Арифметическим корнем натуральной степени $n ge 2$ из неотрицательного числа $a ge 0$ называется неотрицательное число, n-я степень которого равна a.
Поиск корня n-й степени называют извлечением корня n-й степени.
Эта операция является обратной возведению в n-ю степень.
Например:
$ sqrt[3]{27} = 3, т.к. 3^3 = 27 $
$ sqrt[4]{625} = 5, т.к. 5^4 = 625 $
Корень нечётной степени из отрицательного числа
Если степень n нечётная, то корнем нечётной степени n из отрицательного числа $a lt 0$ называют такое отрицательное число, n-я степень которого равна a.
Например:
$ sqrt[3]{-27} = -3, т.к. (-3)^3 = -27 $
$ sqrt[5]{-32} = -2, т.к. (-2)^5 = -32 $
Решение уравнений $x^n = a$
Решим уравнения:
$$ x^2 = 16 iff x^2-16 = 0 iff (x+4)(x-4) = 0 iff left[ begin{array}{cc} x_1 = -4 \ x_2 = 4 end{array} right. $$
$$ x^2 = -9 lt 0 iff x in varnothing, решений quad нет$$
$$ x^4 = 81 iff x^4-81 = 0 iff (x^2+9)(x^2-9) = 0 iff $$
$$ iff (x^2+9)(x+3)(x-3) = 0 iff left[ begin{array}{cc} x_1 = -3 \ x_2 = 3 end{array} right. $$
$$ x^3 = 27 iff x^3-27 = 0 iff (x-3)(x^2+3x+9) = 0 iff x = 3 $$
$$ x^3 = -27 iff x^3+27 = 0 iff (x+3)(x^2-3x+9) = 0 iff x = -3 $$
Делаем вывод:
Если n – чётно и $a ge 0$, уравнение $x^n = a$ имеет два решения: $x = pm sqrt[n]{a}$
Если n – чётно и $a lt 0$, уравнение $x^n = a$ решений не имеет.
Если n — нечётно, уравнение $x^n = a$ имеет одно решение $x = sqrt[n]{a}$ при любом $a in Bbb R$.
Свойства арифметических корней натуральной степени
$$ sqrt[n]{ab} = sqrt[n]{a} cdot sqrt[n]{b}, quad a ge 0, b ge 0, n in Bbb N $$
$$ sqrt[n]{frac{a}{b}} = frac{sqrt[n]{a}}{sqrt[n]{b}}, quad a ge 0, b gt 0, n in Bbb N $$
$$ sqrt[n]{a^m} = (sqrt[n]{a})^m, quad a ge 0, n in Bbb N, m in Bbb N $$
$$ sqrt[n]{a^m} = sqrt[np]{a^{mp}}, quad a ge 0, n in Bbb N, m in Bbb N, p in Bbb N $$
$$ sqrt[m]{sqrt[n]{a}} = sqrt[mn]{a}, quad a ge 0, n in Bbb N, m in Bbb N $$
$$ sqrt[n]{a^n} = (sqrt[n]{a})^n = a, quad a ge 0, n in Bbb N $$
Примеры
Пример 1. Упростите выражение:
$ а) sqrt[3]{64b^6 z^9} = sqrt[3]{(4b^2 z^3)^3} = 4b^2 z^3 $
$ б) sqrt[4]{3a^2 b} cdot sqrt[4]{27a^6 b^3} = sqrt[4]{3a^2 b cdot 27a^6 b^3} = sqrt[4]{81a^8 b^4} = sqrt[4]{(3a^2 b)^4} = 3a^2 b $
$ в) sqrt[5]{32x^6 y} : sqrt[5]{xy^{11}} = sqrt[5]{frac{32x^6 y}{xy^11}} = sqrt[5]{(frac{32x^5}{y^{10}})} = sqrt[5]{(frac{2x}{y^2})^5} = frac{2x}{y^2} $
$ г) (sqrt{sqrt[3]{7a^2 b^5}})^6 = (sqrt[2 cdot 3]{7a^2 b^5})^6 = 7a^2 b^5 $
Пример 2. Вычислите:
$ а) sqrt[3]{1 frac{2}{3}} cdot sqrt[3]{2 frac{7}{9}} = sqrt[3]{frac{5}{3} cdot frac{25}{9}} = sqrt[3]{( frac{5}{3} )^3} = frac{5}{3} = 1 frac{2}{3} $
$ б) sqrt[5]{64} : sqrt[5]{2} + sqrt[6]{27^2} — sqrt[3]{sqrt{64}} = sqrt[5]{frac{64}{2}} + sqrt[6]{(3^3 )^2} — sqrt[{3 cdot 2}]{64} = sqrt[5]{2^5} + sqrt[6]{3^6} — sqrt[6]{2^6} = $
= 2+3-2 = 3
$ в) sqrt[3]{13- sqrt{44}} cdot sqrt[3]{13 + sqrt{44}} = sqrt[3]{(13- sqrt{44})(13+ sqrt{44})} = sqrt[3]{13^2-44} = sqrt[3]{125} = 5 $
$ г) (sqrt[3]{7} — sqrt[3]{5})(sqrt[3]{49} + sqrt[3]{35} + sqrt[3]{25}) = (sqrt[3]{7}-sqrt[3]{5})((sqrt[3]{7})^2 + sqrt[3]{7} cdot sqrt[3]{5} + (sqrt[3]{5})^2 ) = $
$ = (sqrt[3]{7})^3 — (sqrt[3]{5})^3 = 7-5 = 2 $
Пример 3. Сравните числа:
$ а) sqrt[3]{14} и sqrt[3]{17} $
$ 14 lt 17 Rightarrow sqrt[3]{14} lt sqrt[3]{17} $
$ б) sqrt[3]{-14} и sqrt[3]{-17} $
$ -14 gt -17 Rightarrow sqrt[3]{-14} gt sqrt[3]{-17} $
$ в) sqrt[3]{-14} и sqrt{5} $
$ sqrt[3]{-14} lt 0 lt sqrt{5} Rightarrow sqrt[3]{-14} lt sqrt{5} $
$ г) sqrt[3]{29} и sqrt[4]{78} $
$ sqrt[3]{29} gt sqrt[3]{27} = 3, sqrt[4]{78} lt sqrt[4]{81} = 3 $
$ sqrt[4]{78} lt 3 lt sqrt[3]{29} Rightarrow sqrt[3]{29} gt sqrt[4]{78} $
Пример 4. Найдите область определения функции:
$ а) y = — sqrt[4]{frac{x+3}{x-1}} $
Выражение под чётным корнем должно быть неотрицательным:
$ frac{x+3}{x-1} ge 0 Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x+3 ge 0 \ x-1 gt 0 end{array} right.} \ {left{ begin{array}{c} x+3 le 0 \ x -1 lt 0 end{array} right.} end{array} right. Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x ≥ -3 \ x gt 1 end{array} right.} \ {left{ begin{array}{c} x le -3 \ x lt 1 end{array} right.} end{array} right. Rightarrow left[ begin{array}{cc} x gt 1 \ x le -3 end{array} right. Rightarrow x le -3 cup x gt 1 $
Область определения: $x in (-infty;-3] cup (1;+infty)$
$ б) y = frac{2}{x+3} — sqrt[5]{frac{x}{x-8}} $
Выражение под нечётным корнем может иметь любой знак.
Ограничения области определения связаны только с делением на 0:
$ {left{ begin{array}{c} x+3 neq 0 \ x-8 neq 0 end{array} right.} Rightarrow {left{ begin{array}{c} x neq -3 \ x neq 8 end{array} right.} $
Область определения: $x in (-infty;-3) cup (-3;8) cup (8;+infty)$
Пример 5. Решите уравнение:
$а) x^5=32$
$ x = sqrt[5]{32} = sqrt[5]{2^5} = 2 $
$б) x^6 = 64$
$ x = pm sqrt[6]{64} = pm sqrt[6]{2^6} = pm 2 $
$ в) x^3 = -27 $
$ x = sqrt[3]{-27} = sqrt[3]{(-3)^3} = -3 $
$ г) x^4 = -81 $
$ x in varnothing$ — решений нет
Пример 6*. Найдите значение выражения $sqrt[3]{9+sqrt{80}} +sqrt[3]{9-sqrt{80}}$
Обозначим $A = sqrt[3]{9+sqrt{80}} +sqrt[3]{9-sqrt{80}}$
Найдём:
$$ A^3 = Biggl( sqrt[3]{9+sqrt{80}} +sqrt[3]{9-sqrt{80}} Biggr)^3= $$
$$ = Biggl( sqrt[3]{9+sqrt{80}} Biggr)^3+3 Biggl(sqrt[3]{9+sqrt{80}} Biggr)^2 sqrt[3]{9-sqrt{80}} +3 sqrt[3]{9+sqrt{80}} Biggl( sqrt[3]{9-sqrt{80}} Biggr)^2+ Biggl( sqrt[3]{9-sqrt{80}} Biggr)^3= $$
$$ = 9+sqrt{80}+9-sqrt{80}+3sqrt[3]{(9+sqrt{80})(9-sqrt{80})} Biggl( underbrace{sqrt[3]{9+sqrt{80}} +sqrt[3]{9-sqrt{80}}}_{= A} Biggr) = $$
$$ = 18+3 underbrace{sqrt[3]{9^2-80}}_{= 1} cdot A = 18+3A = 3(A+6) $$
Мы получили уравнение: $A^3 = 3(A+6)$ или $ frac{A^3}{3} = A+6$. Решим его графически:
A = 3 — искомое значение выражения
Ответ: 3