Линия симметрии как найти

The line of symmetry is the axis or imaginary line that passes through the center of an object and divides it into identical halves. If we cut an equilateral triangle into two halves, then it forms two right-angled triangles. Similarly, rectangle, square, circle are examples of a line of symmetry. The line of symmetry is also called an axis of symmetry. Also, it is named a mirror line where it forms two reflections of an image. A basic definition of a line of symmetry is it divides an object into two halves.

There are mainly two types considered in Lines of Symmetry concepts. They are
1. Vertical Line of Symmetry
2. Horizontal Line of Symmetry

Vertical Line of Symmetry:  If the axis of the shape cuts it into two equal halves vertically then it is called a Vertical Line of Symmetry. The mirror image of the one half appears in a vertical or straight standing position. Examples for vertical Line of Symmetry are H, M, A, U, O, W, V, Y, T.
Horizontal Line of Symmetry: If the axis of the shape cuts it into two equal halves horizontally, then it is called as Horizontal Line of Symmetry. The mirror image of the one half appears as the other similar half. Examples of Horizontal Line of Symmetry are C, B, H, E.
Three Lines of Symmetry: An equilateral triangle is an example of three lines of symmetry. This is symmetrical along its three medians.
Four Lines of Symmetry: A square is an example of Four Lines of Symmetry. The symmetrical lines are two along the diagonals and two along with the midpoints of the opposite sides.
Five Lines of Symmetry: A regular pentagon is an example of Five Lines of Symmetry. The symmetrical lines are joining a vertex to the mid-point of the opposite side.
Six Lines of Symmetry: A regular hexagon is an example of Six Lines of Symmetry. The symmetrical lines are 3 joining the opposite vertices and 3 joining the mid-points of the opposite sides.
Infinite Lines of Symmetry: A circle is an example of Infinite Lines of Symmetry. It has infinite or no lines of symmetry. It is symmetrical along all its diameters.

Line of Symmetry Examples

Check out some of the examples of Line of Symmetry and learn completely with clear details.

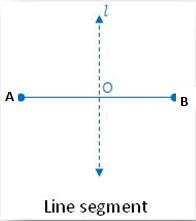
1. Line segment:

From the figure, there is one line of symmetry. line of symmetry of a Line segment passes through its center. There may infinite line passes through the line segment and forms different angles. But we only consider a line as a line of symmetry that cuts the line segment into two equal halves. The Line segment AB is symmetric along the perpendicular bisector l.

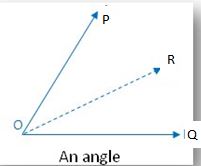
2. An angle:

From the figure, there is one line of symmetry. An angle measures the amount of ‘turning’ between two straight lines that meet at a point. The figure is symmetric along the angle bisector OC.

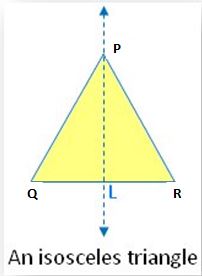
3. An isosceles triangle:

From the figure, there is one line of symmetry. The isosceles triangle figure is symmetric along the bisector of the vertical angle. The Median PL. If the isosceles triangle is also an equilateral triangle, then it has three lines of symmetry. An isosceles triangle has exactly two sides of equal length. Therefore, it has only 1 line of symmetry that passes from the vertex between the two sides of equal length to the midpoint of the side opposite that vertex.

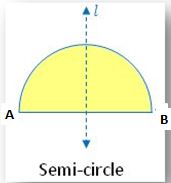
4. Semi-circle:

From the figure, there is one line of symmetry. The Semi-circle figure is symmetric along the perpendicular bisector l. of the diameter AB. A semi-circle does not have any rotational symmetry.

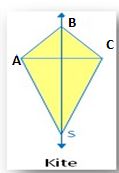
5. Kite:

From the figure, there is one line of symmetry. The Kite is symmetric along with the diagonal BS. A kite is a quadrilateral with two different pairs of adjacent sides that are equal in length and also have only one line of symmetry.

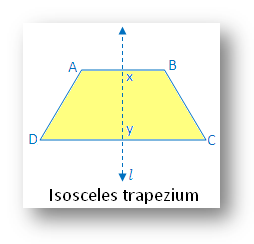
6. Isosceles trapezium:

From the figure, there is one line of symmetry. The Isosceles trapezium figure is symmetric along the line l joining the midpoints of two parallel sides AB and DC. The isosceles trapezium is a convex quadrilateral consists a pair of non-parallel sides that are equal and another pair of sides is parallel but not equal.

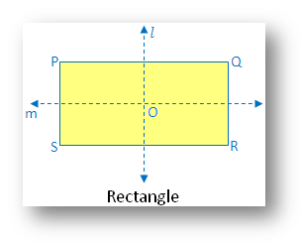
7. Rectangle:

From the figure, there are two lines of symmetry. The Rectangle figure is symmetric along the lines l and m joining the midpoints of opposite sides. There are 2 symmetry lines of a rectangle which are from its length and breadth. They cut the rectangle into two equal halves. They appear mirror to each other.

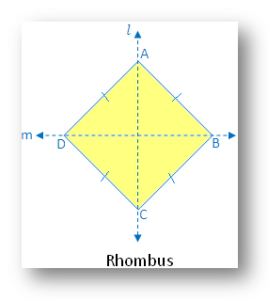
8. Rhombus:

From the figure, there are two lines of symmetry. The Rhombus figure is symmetric along the diagonals AC and BD of the figure. Both the lines of symmetry in a rhombus are from its diagonals. So, it can also say the rhombus lines of symmetry are both diagonals.

Lines of Symmetry in Alphabets

Have a look at the letters that have the line of symmetry.
One Line of symmetry: The letters consist of One line of symmetry are A B C D E K M T U V W Y.
Vertical Line of symmetry: The letters consist of a Vertical line of symmetry is A M T U V W Y.
Horizontal Line of symmetry: The letters consist of a Horizontal line of symmetry is B C D E K.
Two Lines of Symmetry: The letters consist of Two lines of symmetry are H I X. These are having both horizontal and vertical lines of symmetry.
No Lines of Symmetry: The letters consist of No lines of symmetry are F G J L N P Q R S Z. These have neither horizontal nor vertical lines of symmetry.
Infinite Lines of Symmetry: The letter having Infinite lines of symmetry is O.

ВИДЕОУРОК

Симметрия – слово греческого происхождения. Оно означает соразмерность, наличие
определённого порядка, закономерности в расположении частей.

Люди с давних времён
использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре,
художестве, строительстве.

Симметрия широко распространена и в природе, где
не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и
цветов растений, в расположении различных органов животных, в форме кристаллических
тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Симметрия
в геометрии – свойство геометрических фигур.

Рассмотрим две симметрии на плоскости относительно точки и прямой.

ОСЕВАЯ СИММЕТРИЯ

Ось симметрии.

Две
точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по
разные стороны и на одинаковом расстоянии от неё, называются симметричными
относительно этой плоскости (или прямой). Фигура (плоская или пространственная)
симметрична относительно прямой (оси симметрии) или плоскости (плоскости
симметрии), если её точки попарно обладают указанным свойством.

Фигура симметрична
относительно прямой, если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре. Прямая – ось симметрии фигуры, а фигура обладает
осевой симметрией.

Фигура, обладающая
осевой симметрией – это неразвёрнутый угол, который имеет одну ось симметрии –
прямую на которой расположена биссектриса угла.

Осевая симметрия – это симметрия относительно проведённой
прямой (оси).

Две точки  А 
и  В 
симметричны относительно прямой  а (оси симметрии), если эта прямая проходит через середину отрезка
АВ  и перпендикулярна
к нему.

Проведем прямую 
ЕF  через
середины  Е  и  F  сторон  АВ  и  СD  прямоугольника  АВСD.

Эта прямая делит прямоугольник пополам. Если прямоугольник перегнуть по этой
прямой, то обе две половины совпадут. Говорят, что прямоугольник симметричный относительно
прямой  ЕF, а прямую  ЕF  называют осью симметрии прямоугольника. У
прямоугольника  АВСD  есть другая ось симметрии – прямая  NК.

Вообще, фигуру называют симметричной относительно прямой  l, если эта прямая делит фигуру на две части, которые совпадают при перегибании
по этой прямой. Прямую  l  называют осью симметрии этой фигуры.

Две
точки  А  и  В, которые совпадают при перегибании плоскости по
прямой  l, называют симметричными относительно этой
прямой. Если точки  А  и  В  симметричные относительно прямой  l, то:

1) отрезок  АВ 
перпендикулярен прямой  l.

2) прямая  l  делит этот отрезок пополам.

Окружность имеет бесконечное количество осей симметрии. Любая прямая, которая
проходит через центр окружности, будет его осью симметрии.

Ось симметрии имеют изображения многих фигур (предметов), которые часто
встречаются в природе и технике.

Каждая точка прямой  а  симметрична самой себе.

ПРИМЕР:

АО
= ОВ, АВ ⊥
а.

Точка  А 
симметрична сама себе.

Фигура симметрична относительно прямой – если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре.

Прямая – ось симметрии фигуры, а
фигура обладает осевой симметрией.

Фигуры, симметричные относительно прямой, равны.

Иногда у фигур несколько осей симметрии.

Фигуры, обладающие осевой симметрией.

ПРИМЕР:

Неразвёрнутый угол имеет одну ось симметрии –
прямую, на которой расположена биссектриса угла.

Равнобедренный
треугольник имеет одну ось симметрии.

Равносторонний
треугольник имеет три оси симметрии.

Квадрат имеет четыре оси
симметрии.

Прямоугольник имеет две
оси симметрии

Ромб имеет две оси
симметрии

Окружность имеет
бесконечно много осей симметрии – любая прямая, проходящая через центр,
является осью симметрии.

Примером фигур, у которых нет ни одной оси симметрии, являются
параллелограмм и треугольник, все стороны которого различны.

Алгоритм построения фигуры, симметричной относительно некоторой прямой.

ПРИМЕР:

Построим треугольник  А₁В₁С₁, симметричный треугольнику  АВС 
относительно красной прямой линии (ось симметрии).

Для этого проведём из вершины
треугольника  АВС  прямые,
перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.

Измерим расстояние от вершин треугольника
до получившихся точек на прямой и отложим с другой стороны прямой такие же
расстояния.

Соединим получившиеся точки отрезками и
получим треугольник  А₁В₁С₁, симметричный данному треугольнику  АВС.

ЗАДАЧА:

Дан отрезок  АВ.
Построить его симметрию относительно прямой 
l,
не пересекающий данный отрезок.

РЕШЕНИЕ:

Изобразим схематически условие задачи.

Так как осевая симметрия
является движением, то отрезок  АВ 
отобразится на равный ему отрезок 
А’В’.

Для его построения сделаем
следующее: проведём через точки  А  и  В  прямые  m  и  n  перпендикулярно
прямой  l.
Пусть 

m ∩ l = Х, n ∩ l = Y.

Далее проведём отрезки 

А’Х
= АХ  и 
В’Y = ВY.

ЗАДАЧА:

Построить симметричный
треугольник для данного треугольника относительно какой-либо его стороны.

РЕШЕНИЕ:

Пусть нам дан треугольник  АВС. Будем строить его
симметрию относительно стороны  ВС.

Сторона  ВС  при осевой симметрии перейдёт в саму себя (следует из
определения). Точка  А  перейдёт в точку  А₁  следующим образом:

АА₁ ⊥ ВС, АН = НА₁.

Треугольник  АВС  перейдёт в треугольник  А₁ВС.

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Симметрию относительно точки называют центральной
симметрией.

Две точки  А  и  В 
симметричны относительно точки  О, если  О – середина отрезка  АВ. Точка  О  называется центром симметрии.

Точка  О  симметрична самой
себе.

Фигура
симметрична относительно точки (центр симметрии), если её точки попарно лежат
на прямых, проходящих через центр симметрии, по разные стороны и на равных
расстояниях от него.

Фигура симметрична относительно точки, если для каждой точки фигуры симметричная ей точка
относительно данной точки также принадлежит этой фигуре. Данная точка – центр симметрии фигуры, а фигура обладает центральной симметрией.

Фигуры, симметричные относительно некоторой точки, равны.

Фигуры, обладающие центром симметрии.

ПРИМЕР:

Окружность, центр окружности
является её центром симметрии.

Параллелограмм, его центром
симметрии является точка пересечения диагоналей.

Прямая имеет бесконечно много
центров симметрии, так как любая точка прямой является её центром симметрии.

Примером фигуры, не имеющей центра симметрии, является треугольник.

Алгоритм построения центрально-симметричных фигур.

ПРИМЕР:

Построим треугольник  А₁В₁С₁, симметричный треугольнику  АВС 
относительно центра (точки)  О.

Для этого соединим точки  А,В,С  с центром  О  и продолжим эти отрезки.

Измерим отрезки  АО,
ВО, СО  и отложим с
другой стороны от точки  О  равные им отрезки 

АО
= ОА₁, ВО = ОВ₁, СО = ОС₁.

Соединим получившиеся точки
отрезками и получим треугольник  

А₁В₁С₁, симметричный данному треугольнику  АВС.

ЗАДАЧА:

Дан отрезок  АВ.
Построить его симметрию относительно точки 
С, лежащей на прямой  l.

РЕШЕНИЕ:

Изобразим схематически условие задачи.

Так как центральная симметрия
является движением, то отрезок  АВ 
отобразится на равный ему отрезок 
А»В».

Для его построения сделаем
следующее: проведём прямые  АС  и  ВС. Далее проведём отрезки  

х‘ =
х,

у‘ =
–у.

3) При повороте на  90°  вокруг начала координат ось  Ох 
переходит в ось  Оу  так, что положительное направление переходит
в положительное, а ось  Оу  отображается на ось  Ох  так, что
положительное направление переходит в отрицательное. Поэтому  Р(х, у)  отображается на
точку  Р’

с координатами:

х‘ =
–у,

у‘ =
х.

4) При центральной симметрии

каждая из осей координат
отображается на себя, но так, что положительное направление оси переходит в
отрицательное и наоборот: отрицательное в положительное. Поэтому

Объединим результаты в таблицу

Линия симметрии, базовая геометрическая концепция, делит форму на две одинаковые части. Учителя вводят основную концепцию еще в начальной школе, а классы средней школы и даже колледжа используют симметрию. Поиск линии симметрии может быть полезен при проектировании объектов от поздравительных открыток до ландшафтных проектов.

Ищите середины в форме. Если вы рассматриваете большую область, например, двор, измерьте ее и нарисуйте ее в масштабе на листе миллиметровки, чтобы найти середины.

Используйте линейку, чтобы нарисовать прямую линию от предполагаемой средней точки до фигуры.

Сложите форму пополам, чтобы увидеть, совпадают ли обе стороны. Если они совпадают, вы нашли линию симметрии.

Проверьте все углы формы (если она содержит углы), чтобы найти все возможные линии симметрии.

Держите небольшое зеркало перпендикулярно возможной линии симметрии. Если форма в зеркале совпадает с формой на бумаге, вы нашли правильную линию симметрии.

подсказки

• Некоторые формы могут иметь несколько линий симметрии, в то время как некоторые неправильные формы не имеют линий симметрии.