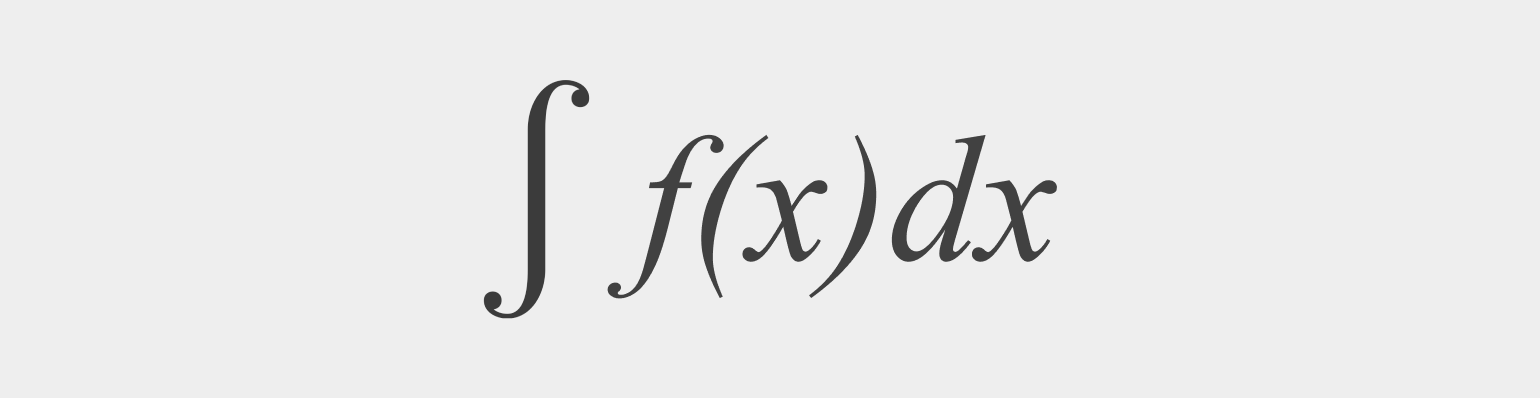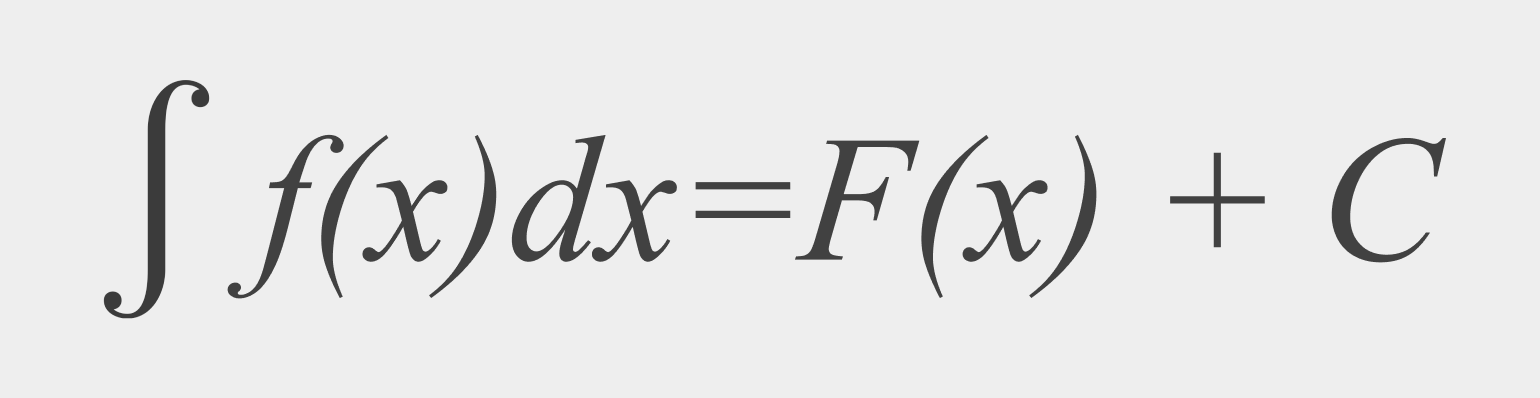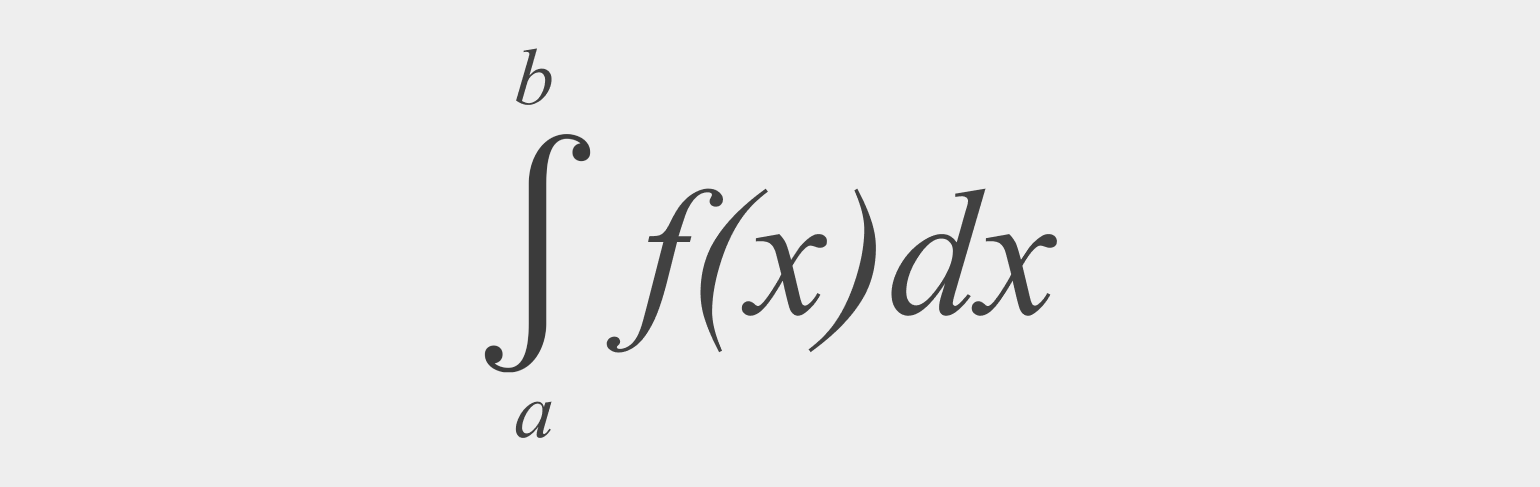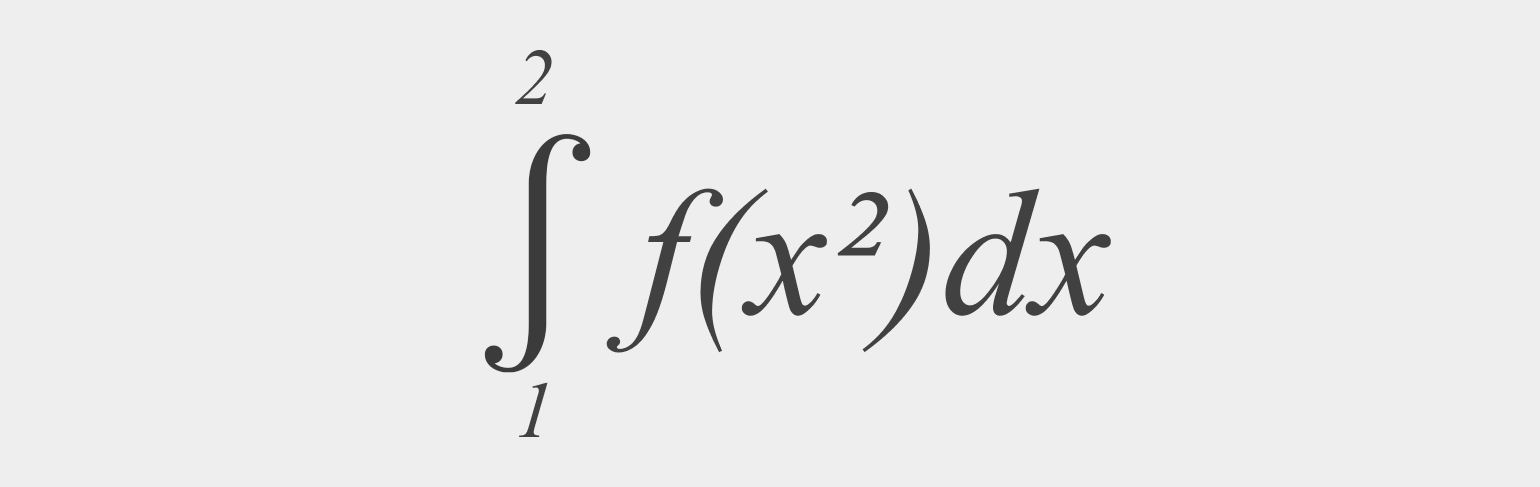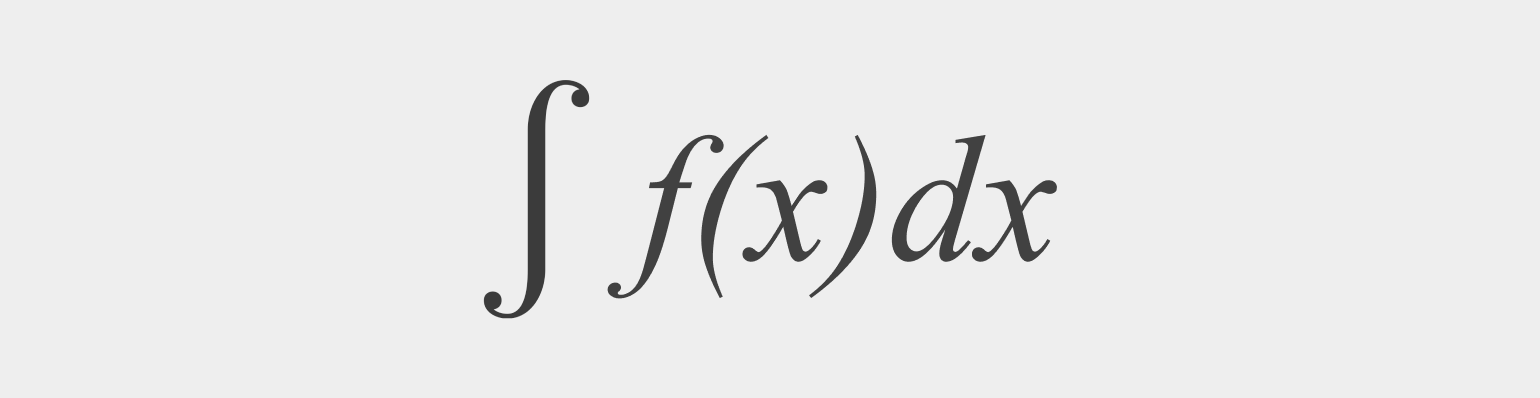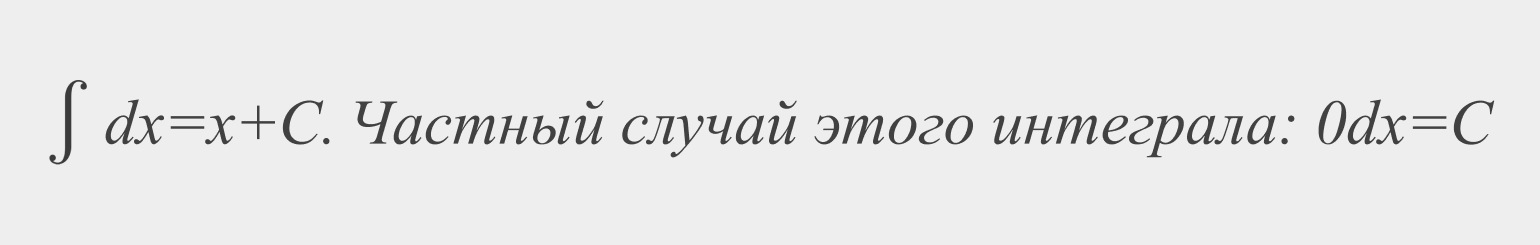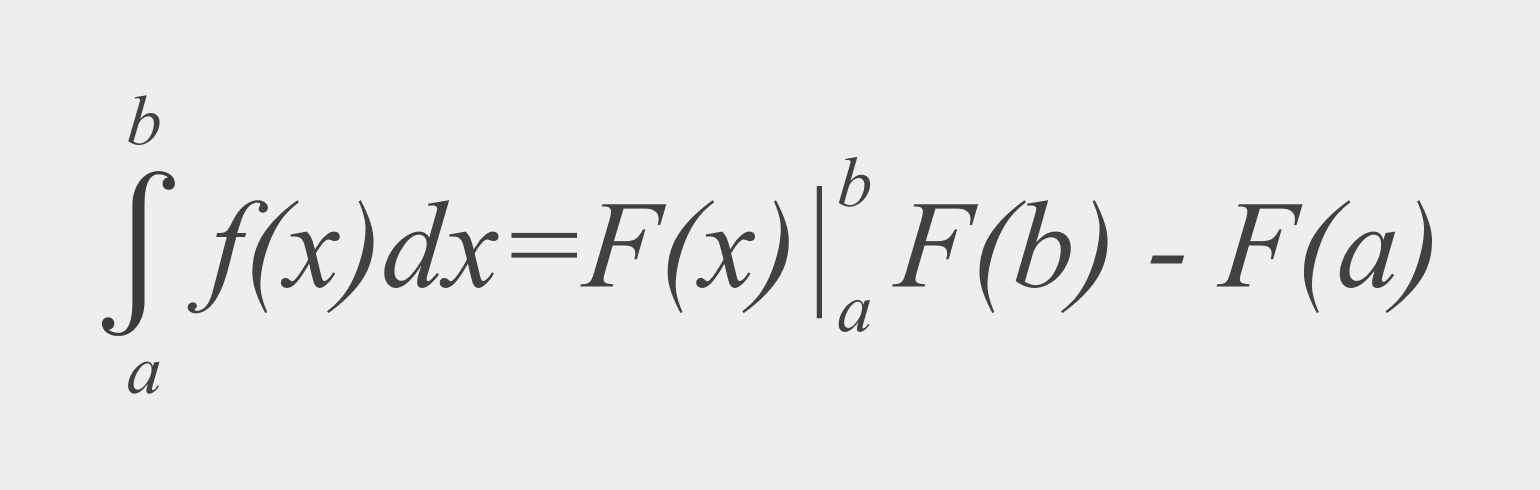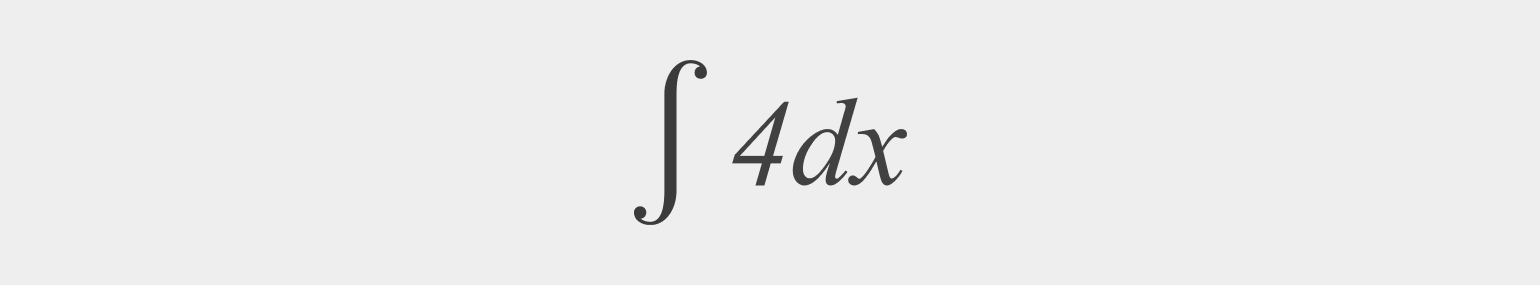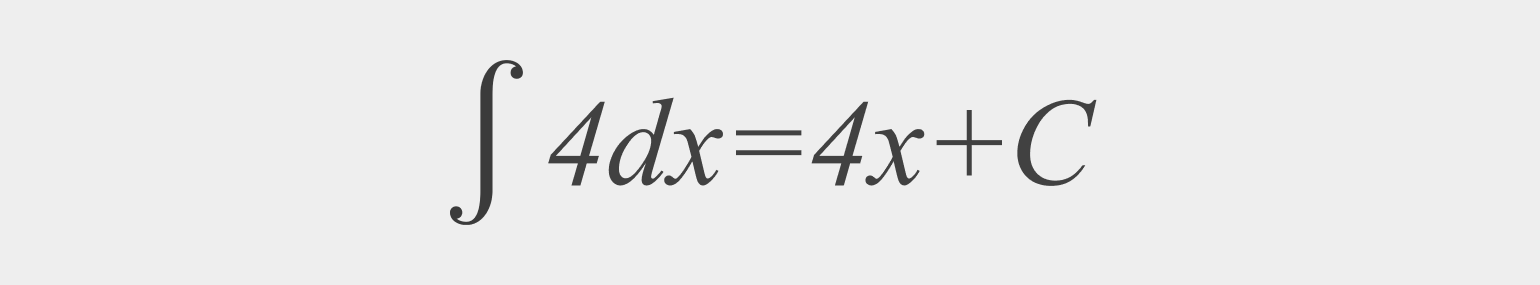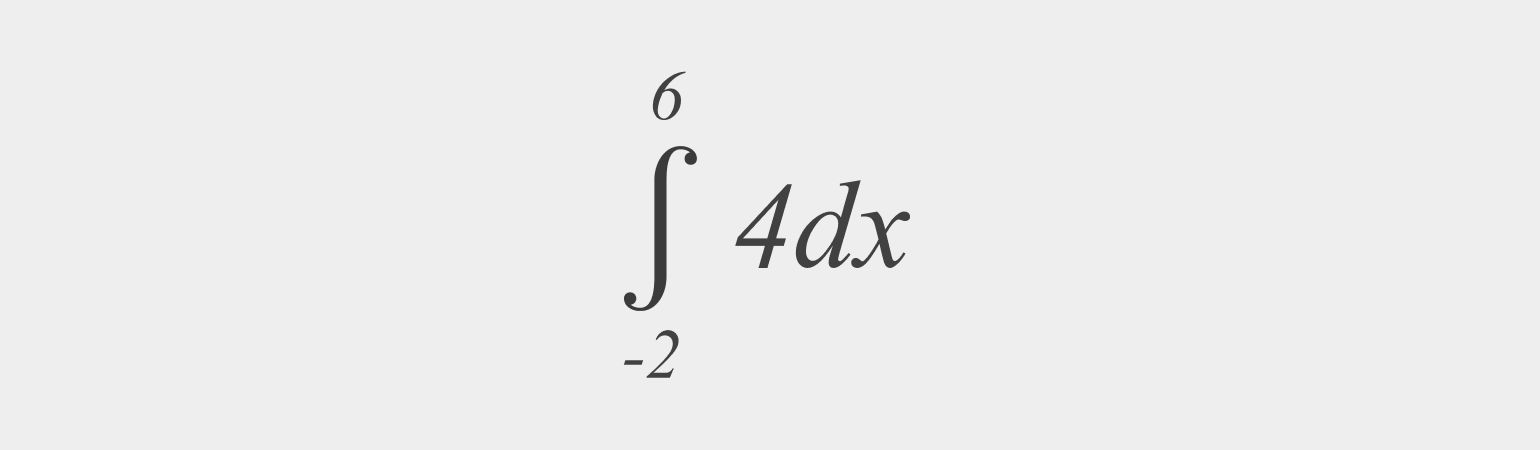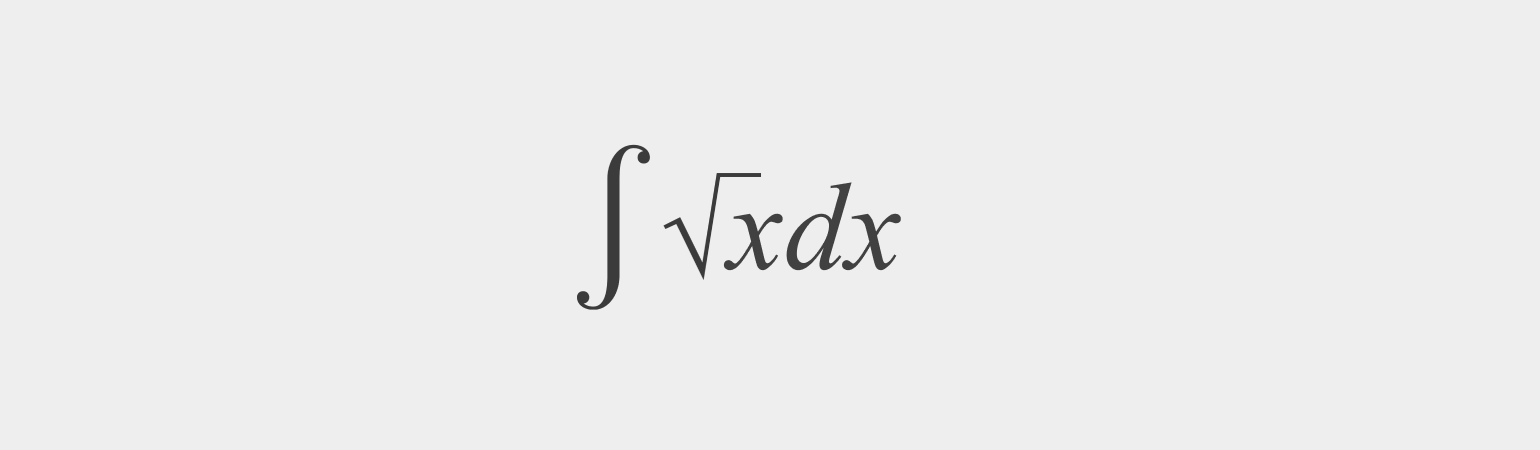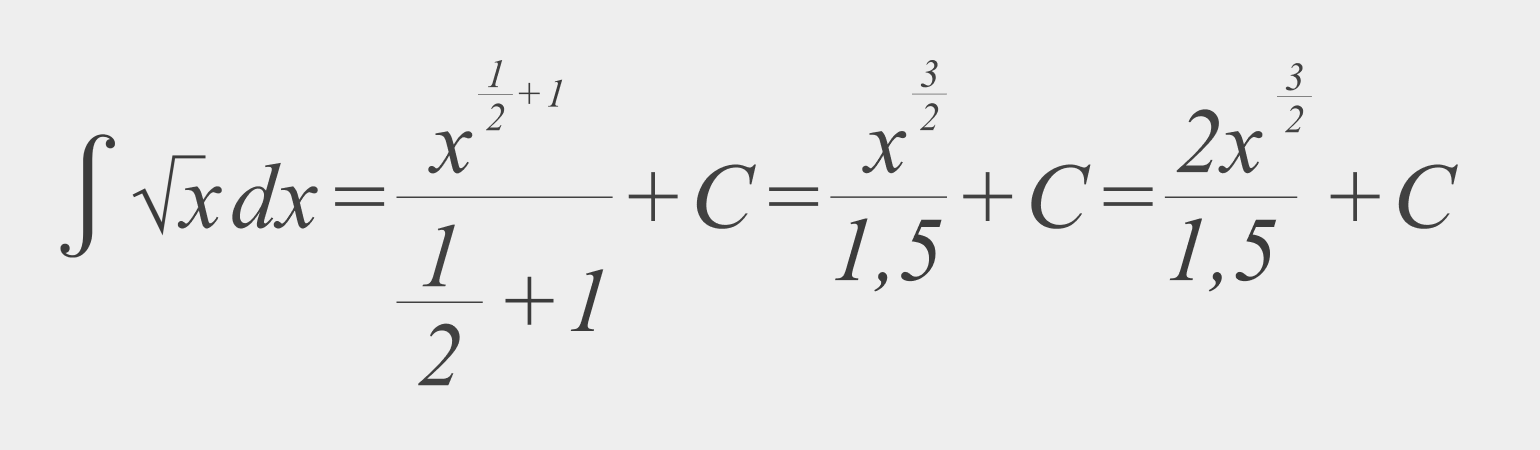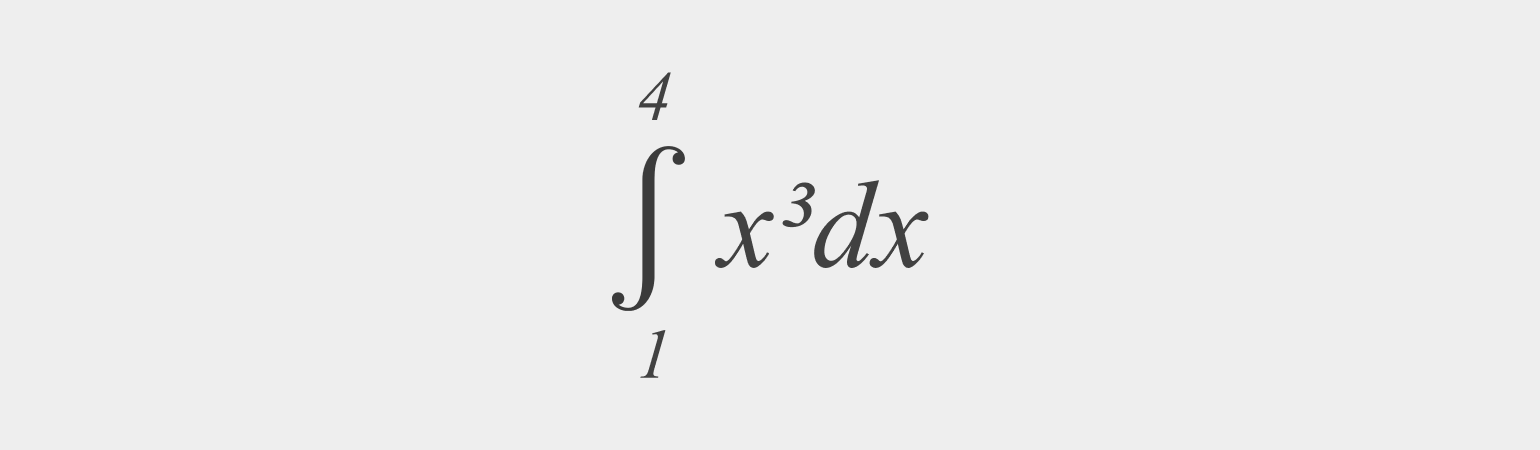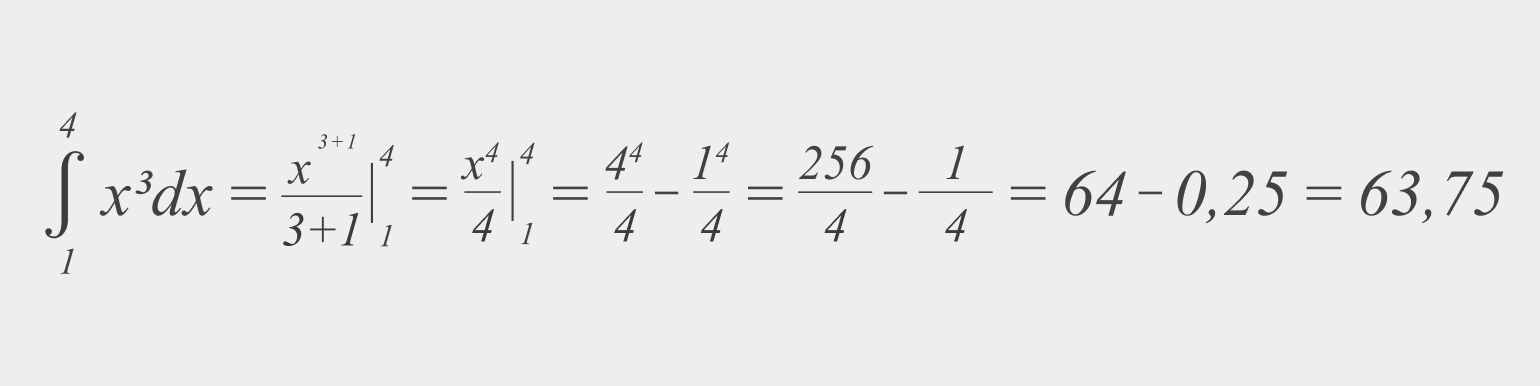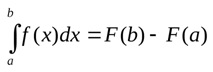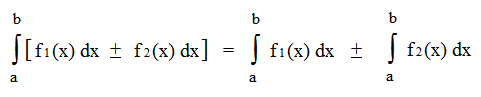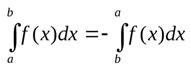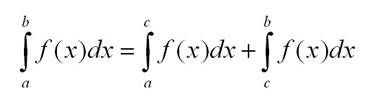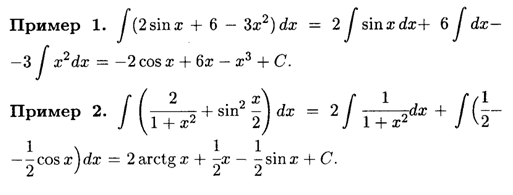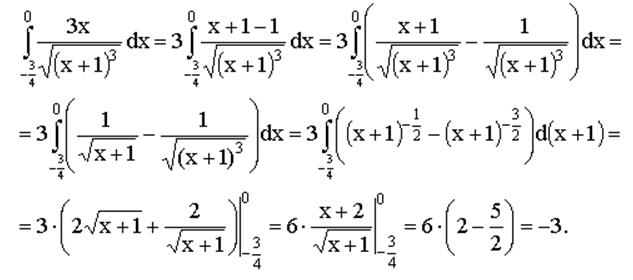Математический анализ как найти интеграл

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

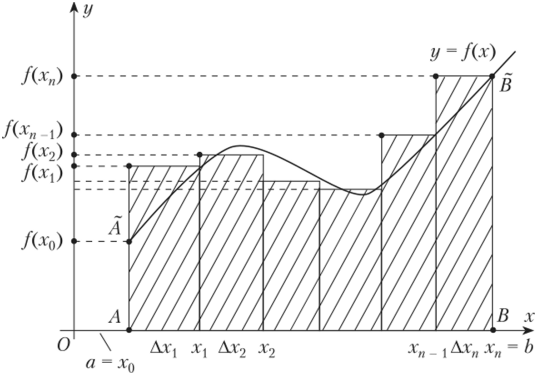
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иллюстрация: Оля Ежак для Skillbox Media

Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.

Интегральное исчисление — мудрёный на первый взгляд раздел математического анализа, который оперирует такими понятиями, как «первообразная», «производная», «дифференцирование» и «предел». Оно описывается кучей формул, в которых легко заблудиться, особенно если зайти в тему без должной математической подготовки.

На самом деле в сути интегрирования нет ничего сложного: нужно лишь провести множество операций умножения нескольких слагаемых, а затем сложить результаты этих умножений друг с другом. Идеальный (то есть без погрешностей) интеграл работает с бесконечными величинами.

Если сказать простыми словами, интеграл — это сумма бесконечного количества умножений, проведённых с бесконечно малыми слагаемыми.

В природе практически не существует ничего прямого и постоянного: процессы изменяют свою скорость, а материальные объекты сплошь и рядом неправильной формы. Это сильно затрудняет вычисление и описание реальности, но математики научились с этим справляться.

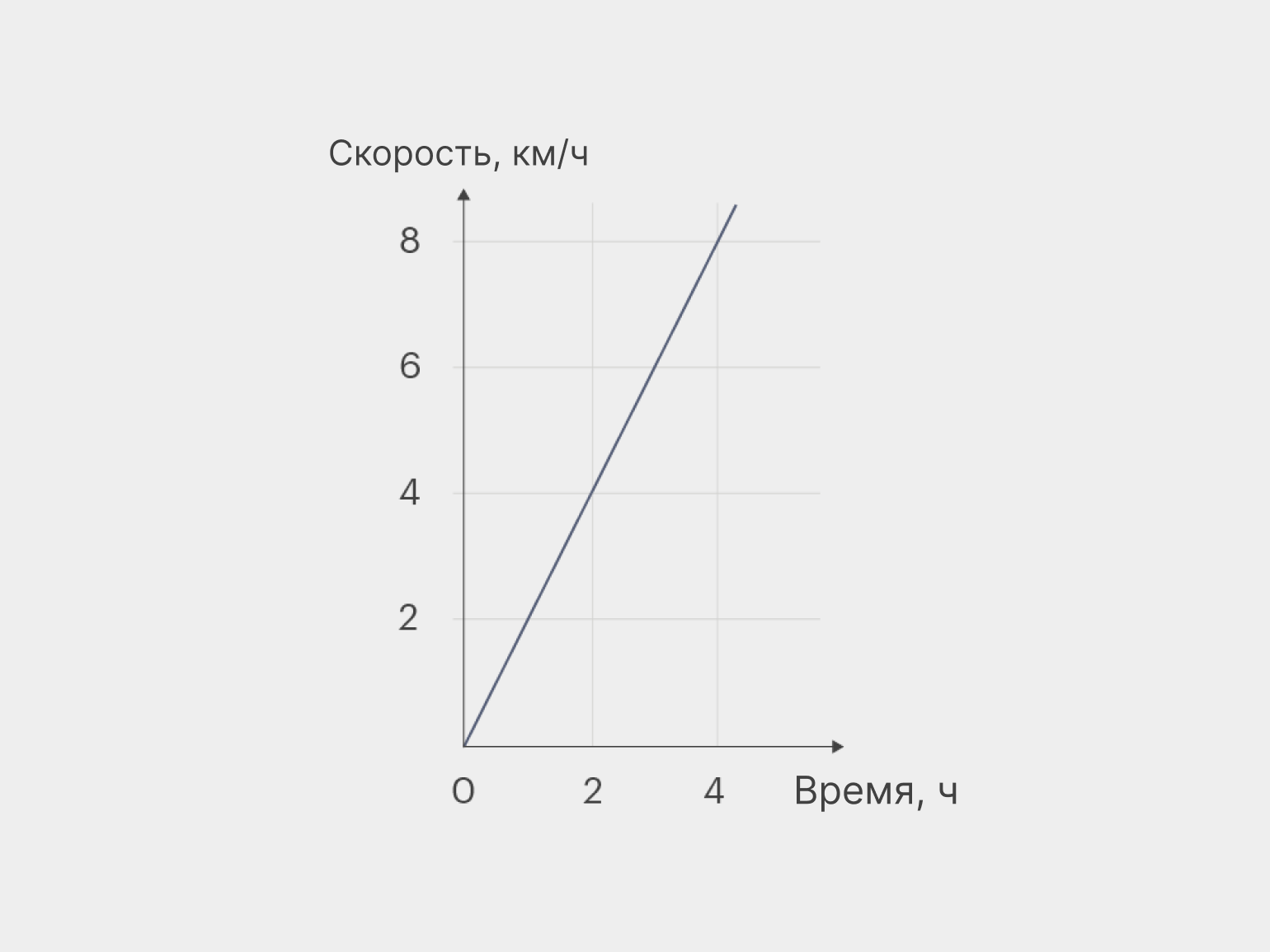
Представьте, что у вас есть велосипед со спидометром, который не только показывает вашу скорость, но и записывает её в каждый момент времени, а затем выдаёт график вашего движения.

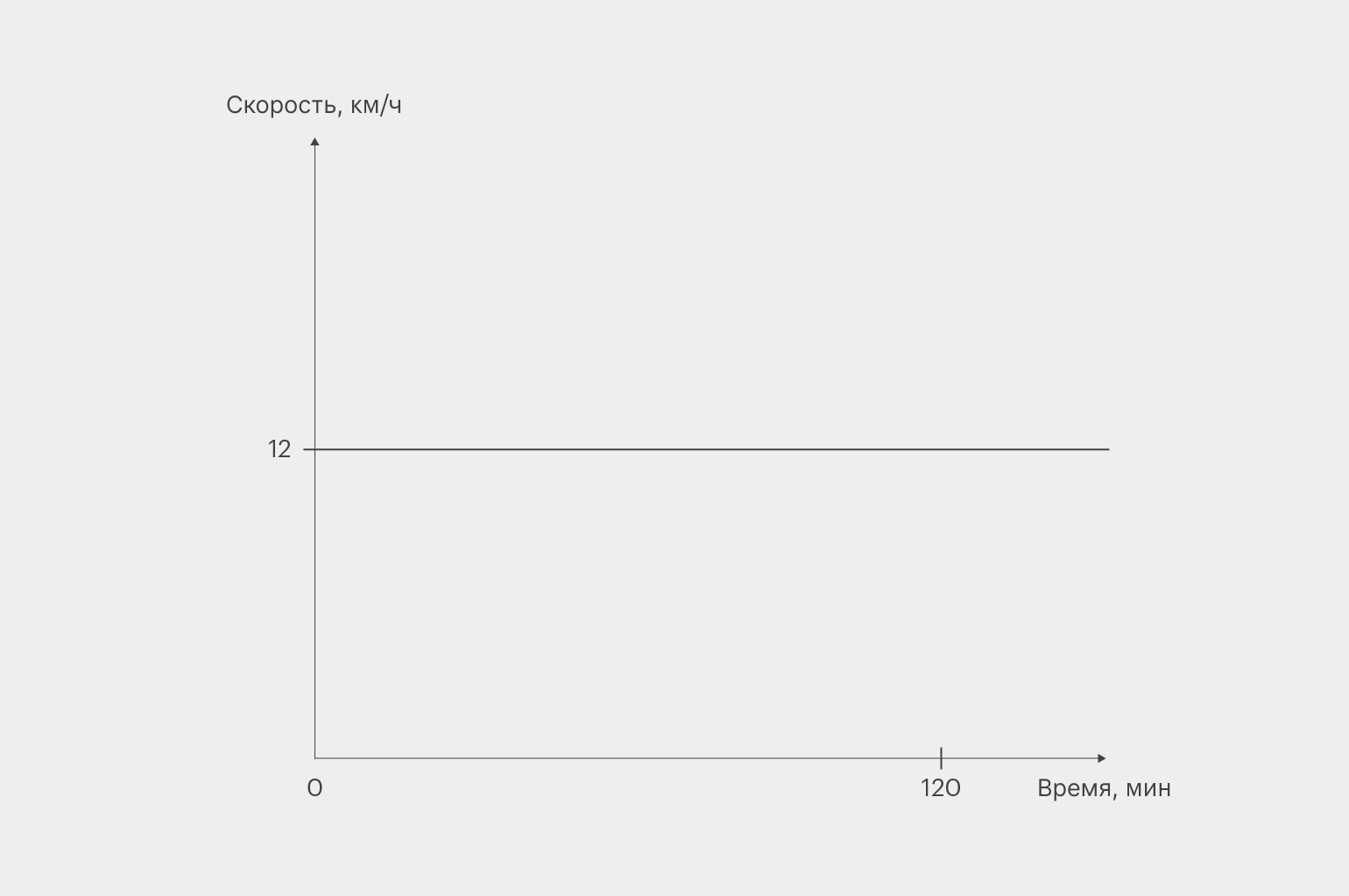
Вы выехали из точки А в точку Б и два часа двигались со средней скоростью 12 км/ч. Так вам казалось, во всяком случае. То есть график вашего движения, по вашему мнению, выглядел как-то так:

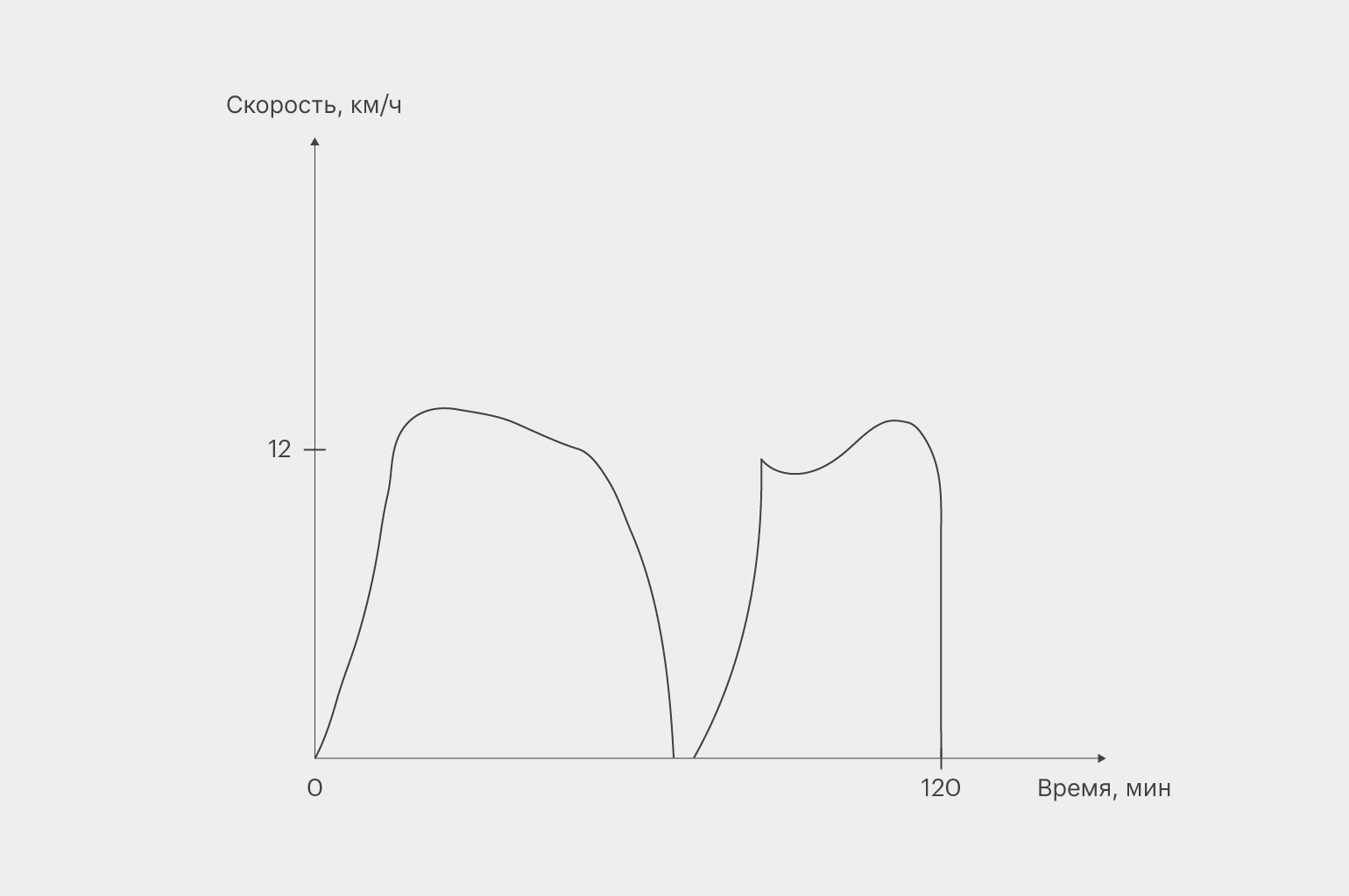
Но в реальности всё было иначе. Сначала вы колесили не спеша, потом разогнались, потом замедлились на подъёме в горку, затем вообще встали на светофоре, после чего снова пришлось разогнаться. То есть реальный график вашего движения был таким:

Скорость менялась, и в разные периоды времени вы проделывали разный путь. Как же посчитать, сколько вы накрутили в итоге?

Очень просто: нужно поделить всё время на равные промежутки — и посчитать, с какой примерно скоростью вы ехали в каждый из них. Возьмём промежутки по 15 минут, умножим их на примерную среднюю скорость, получим расстояние — и представим всё это в таблице.

Время, мин	Скорость, км/ч	Расстояние, км
0–15	~7	~1,75
15–30	~13	~3,25
30–45	~12	~3
45–60	~8	~2
60–75	~4	~1
75–90	~7	~1,75
90–105	~12	~3
105–120	~11	~2,75

Теперь сложим все расстояния и получим приблизительно 18,5 км. Но это всё ещё не точный результат: скорость-то мы оценивали примерно.

Чтобы посчитать точнее, нужно взять как можно большее количество промежутков — по минуте, секунде, наносекунде и так далее. Чем короче будет каждый промежуток, тем ближе к реальности окажется результат.

В идеале наш график можно поделить на число промежутков, стремящееся к бесконечности, а размер каждого из них будет стремиться, соответственно, к нулю. Затем произвести умножение во всех промежутках и сложить результаты — в общем, сделать то же, что и раньше. Только табличка получится безразмерная. Это и есть интеграл нашей функции, который математически, если кто не помнит, записывается так:

∫ — значок интеграла. Выбран неслучайно: так как интеграл представляет собой сумму, то и обозначается вытянутой буквой S.

f(x) — это функция, которую мы интегрируем. В нашем примере мы задали функцию вручную, а не формулой, но математики работают именно с формулами.

dx — это обозначение того, что каждый промежуток является бесконечно малой величиной. Читается как «дельта икс».

У интегрирования есть ещё один математический смысл. Это операция, обратная дифференцированию. Давайте разберёмся, что это значит.

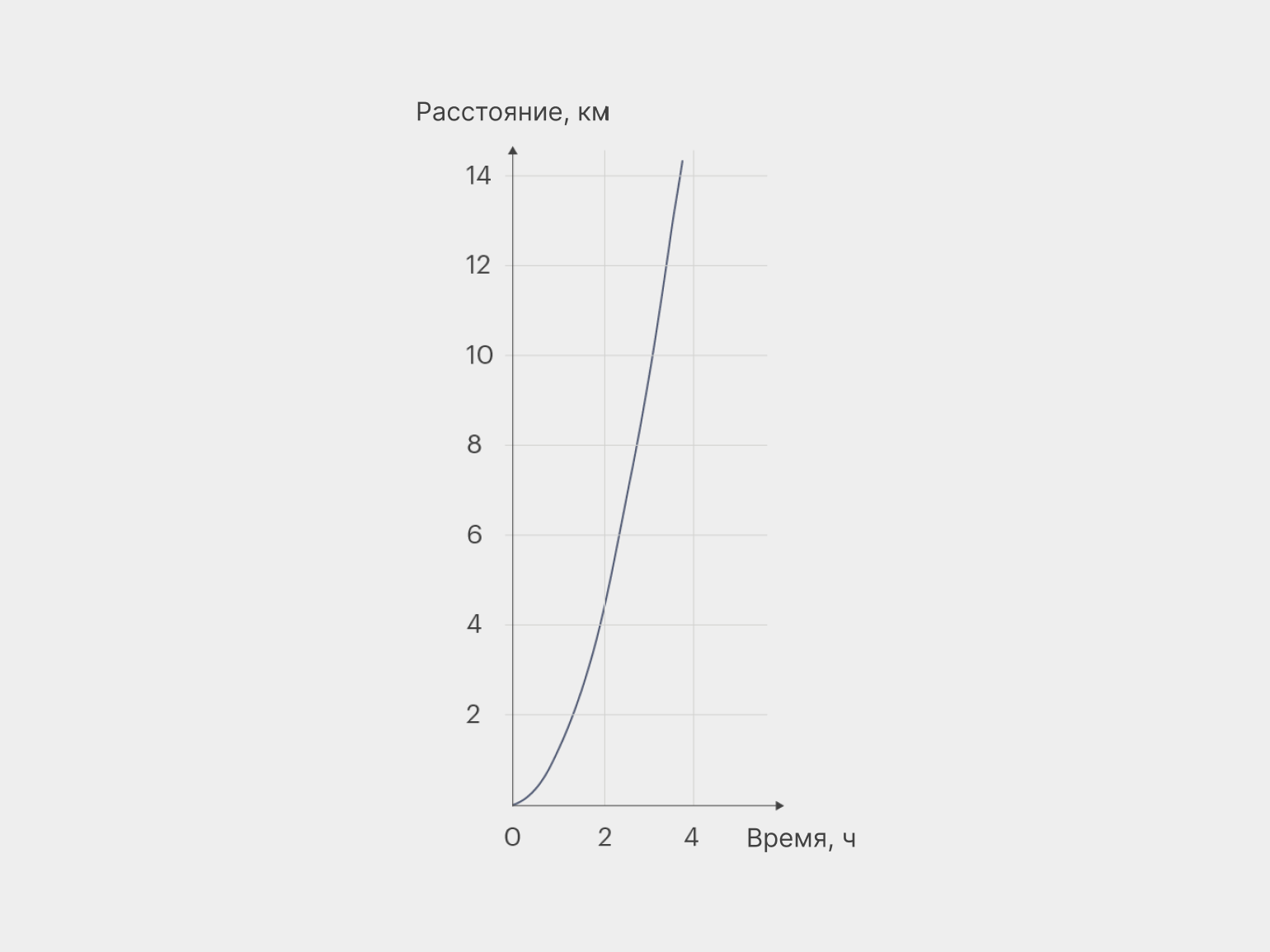
Представьте, что вы выпускаете в космосе аппарат, который удаляется от вас по формуле y = x², где y — расстояние от вас в километрах, а x — время в часах. Причём x может принимать только положительные значения.

Вот график движения этого аппарата:

Наша функция растёт неравномерно: скорость её роста увеличивается, причём по определённому принципу.

Чтобы найти эту скорость, или, математически выражаясь, производную нашей функции, придумали дифференцирование. Производной от функции f(x²) будет F(2x). Физически она будет показывать не положение аппарата в пространстве, а скорость, с которой движется аппарат:

Сравните саму функцию и её производную (то есть скорость изменения этой функции). Она растёт — её производная принимает положительные значения. Она начинает расти быстрее — её производная принимает более высокие значения.

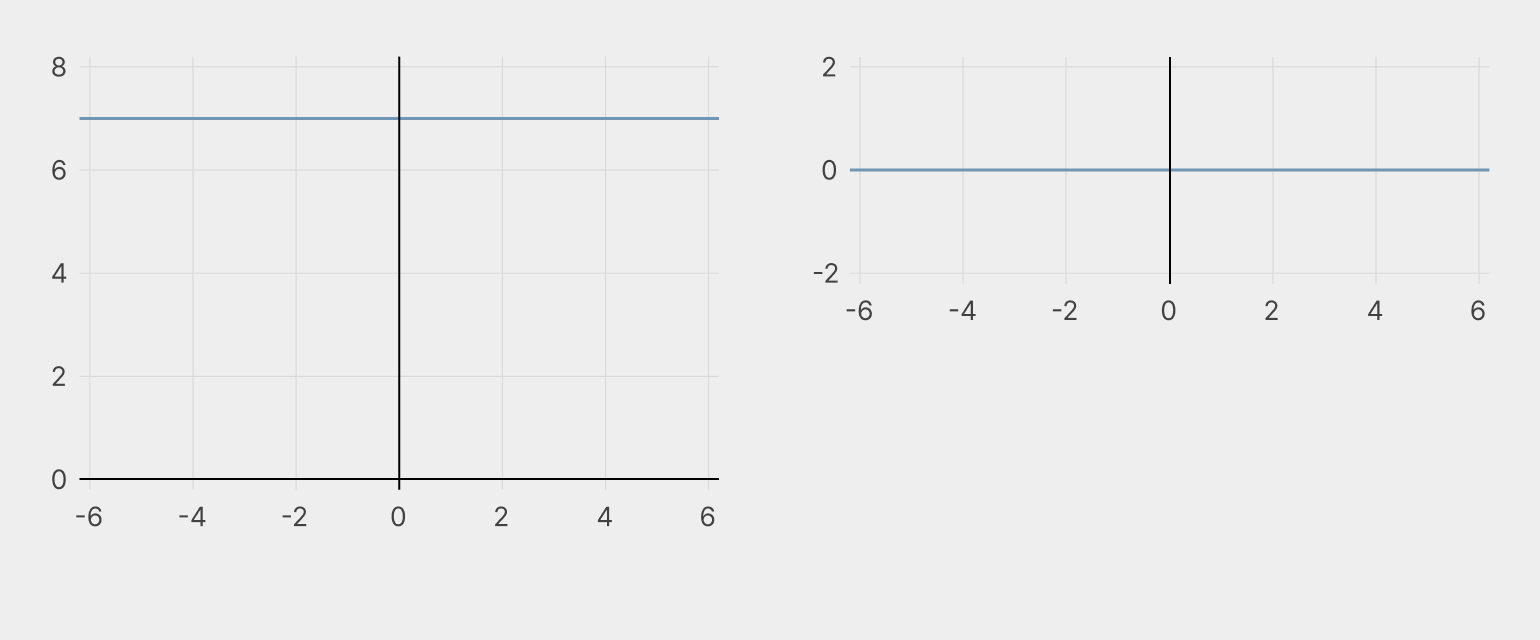
Чтобы лучше понять смысл производной, посмотрите на графики функций и их производных и попробуйте понять связь между ними:

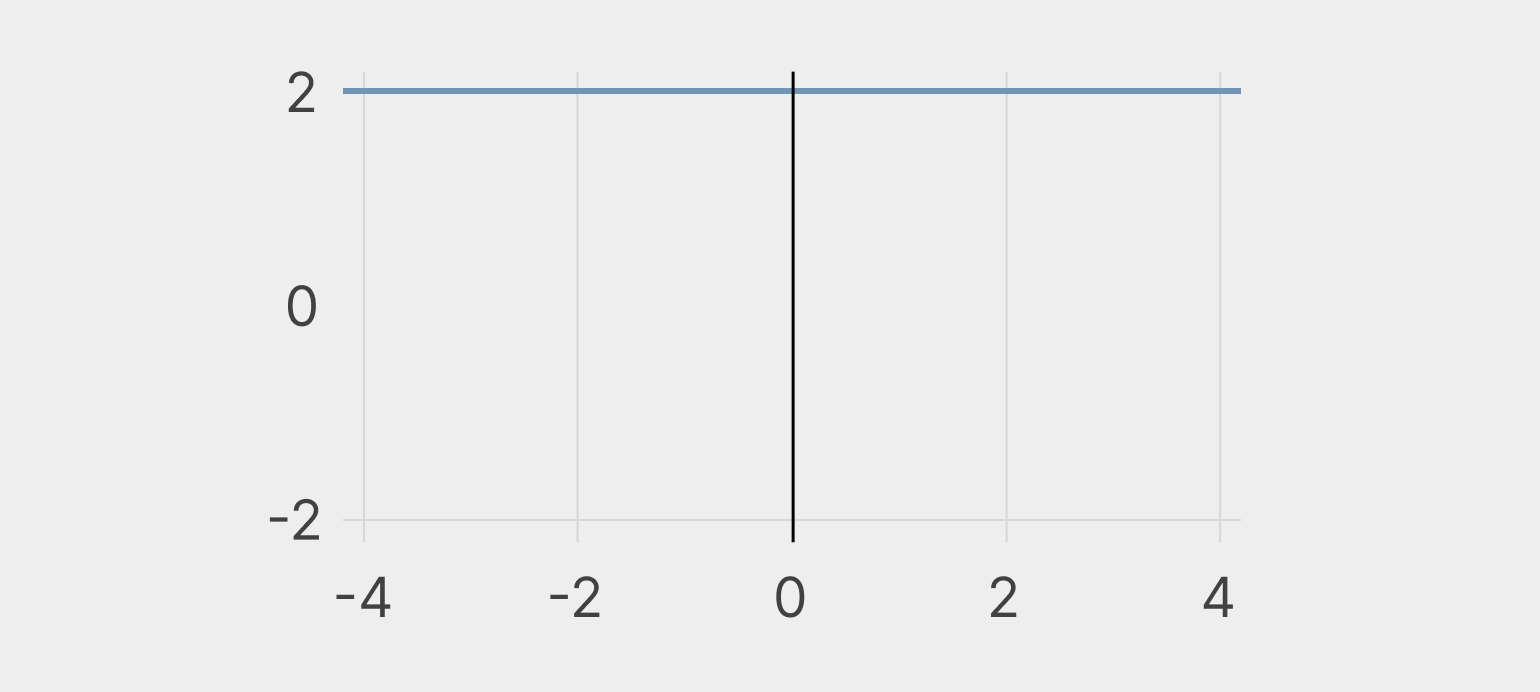
Слева — y = 8, справа — производная y = 0. Так как функция не растёт и не убывает, то и её производная отражает отсутствие изменений в левом графике.

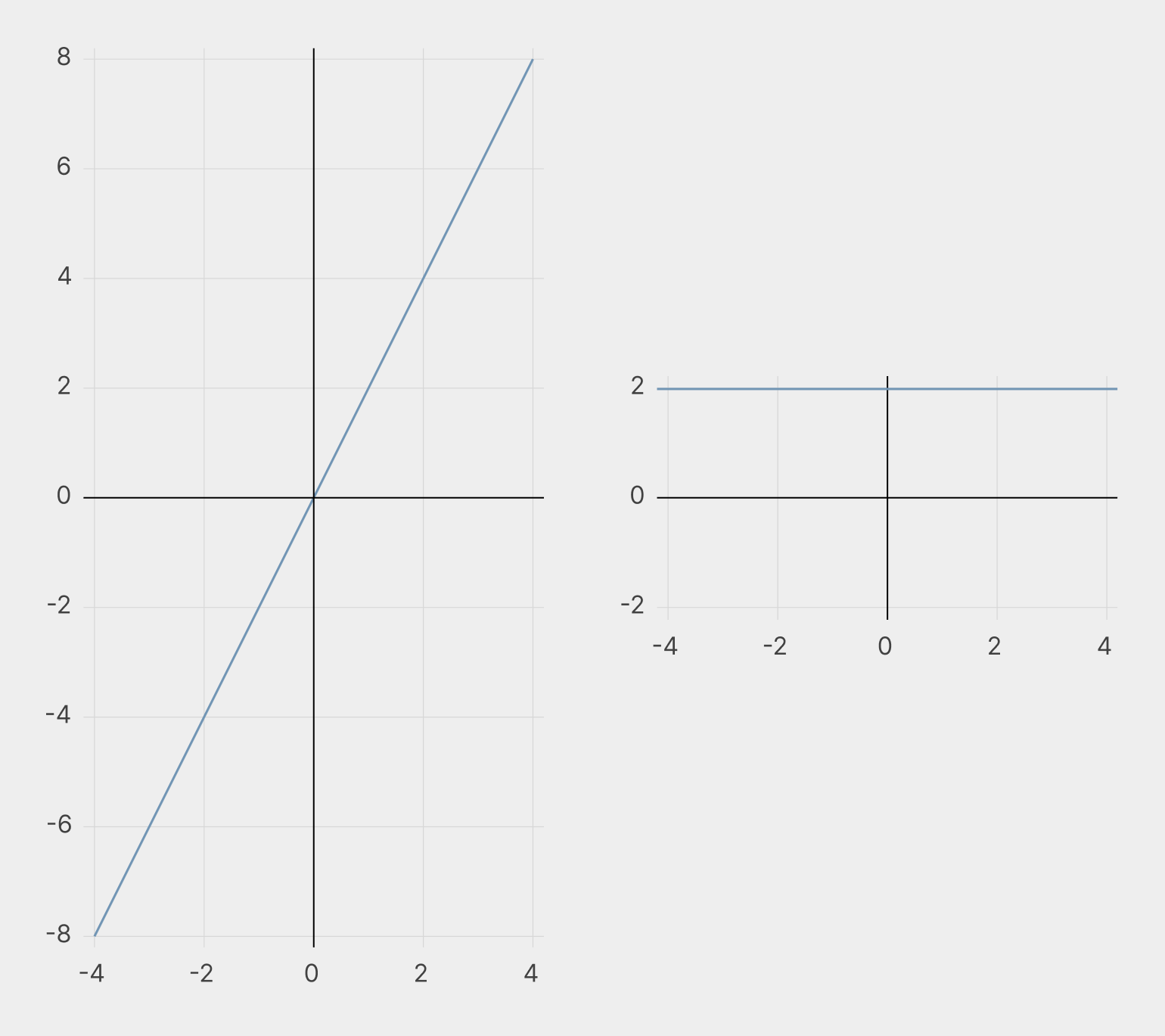
Слева — y = 2x, справа — производная y = 2. Функция равномерно растёт в течение всего своего существования. Её производная отражает наличие роста и то, что этот рост неизменен: за каждый шаг x к функции всегда прибавляются два шага y.

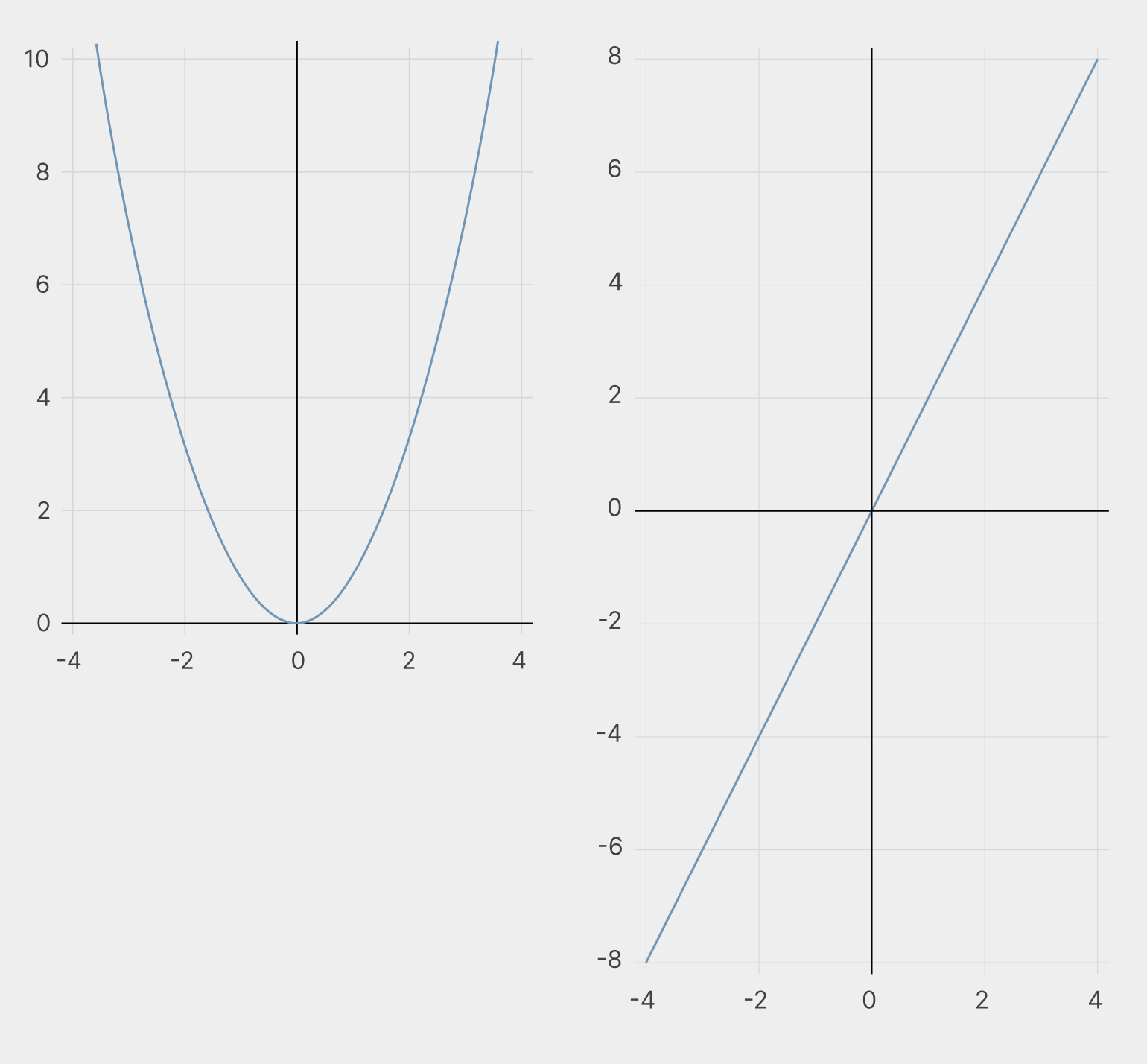
Слева — y = x², справа — производная y = 2x. Чтобы лучше понять связь, рассмотрим графики по частям.

На промежутке от минус бесконечности до нуля функция убывает. Следовательно, её производная принимает отрицательные значения.

Чем дальше, тем медленнее убывает левый график. На промежутке x от −3 до −2 он уменьшается с 9 до 4 — сразу на пять делений. А на промежутке от −2 до −1 уменьшается с 4 до 2 — всего на два деления. Так и производная, приближаясь к нулю, показывает, что функция убывает всё медленнее и медленнее.

В точке x = 0 функция не растёт и не убывает. Следовательно, в этой точке её производная равна нулю.

На промежутке от нуля до плюс бесконечности левый график растёт. Следовательно, производная принимает положительные значения.

Чем дальше, тем рост быстрее — по аналогии с предыдущим промежутком. Вместе с тем и производная увеличивает свои значения и этим показывает всё ускоряющийся рост функции. Всё это нужно понять, потому что интегрирование — это операция, обратная дифференцированию.

А теперь вернёмся к нашим интегралам. Если при дифференцировании мы ищем производную и превращаем левый график в правый, то при интегрировании поступаем наоборот: ищем первообразную и превращаем правый график в левый.

Вернёмся к аппарату, который мы запустили в космос. Мы знали расстояние, на котором он был от нас в каждый момент времени, и с помощью дифференцирования построили график его скорости.

Если же мы знаем скорость аппарата в каждый момент времени, то можем сделать наоборот и с помощью интегрирования построить график его перемещения.

Итак, мы выяснили, что с помощью интегралов можем воспроизвести функцию, зная только её производную. Такая восстановленная функция называется первообразной, а интеграл, который её ищет, — неопределённым. Для него выбрали такое имя, потому что он представляет собой не конкретное число, а целую функцию.

У неопределённого интегрирования есть интересная особенность — оно возвращает не одну первообразную, а целое их семейство.

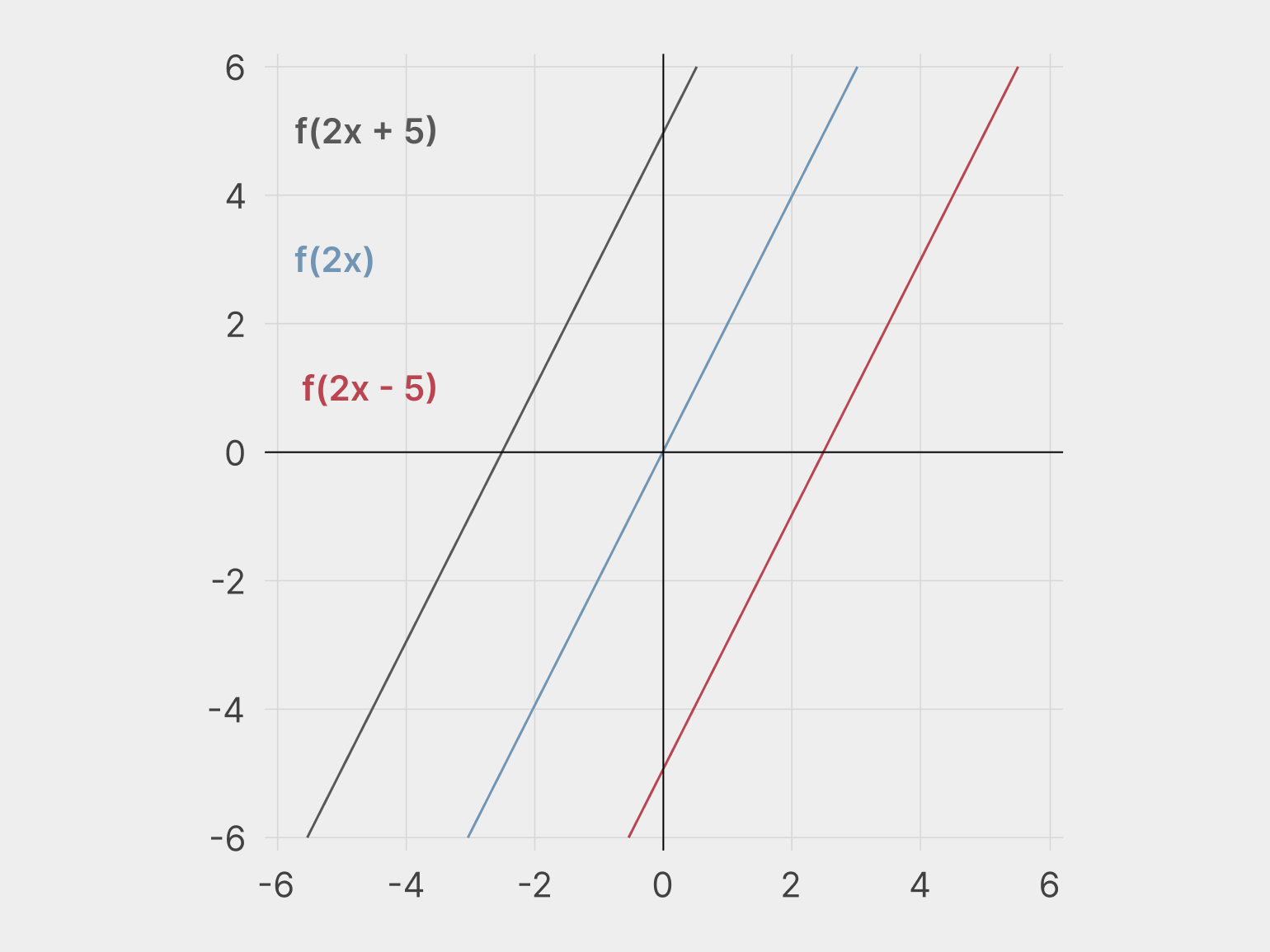
Возьмём три первообразные: f(2x), f(2x + 5) и f(2x − 5). Вот их графики.

Теперь продифференцируем функции и найдём производную для каждой из них. Во всех трёх случаях получается F(2), то есть y = 2.

Так получается, потому что каждая из этих функция растёт с одинаковой скоростью: за один шаг в «иксе» они прибавляют два шага в «игреке». Следовательно, и производная у них одна и та же.

Интегрирование — обратная операция. Когда мы берём интеграл от F(2), то можем получить и f(2x), и f(2x + 5), и f(2x − 5), бесконечное количество других функций того же типа. Это дополнительное число называется произвольной постоянной.

Поэтому, когда мы берём неопределённый интеграл, то указываем в результате эту произвольную постоянную: f(2x + C).

В общем виде неопределённый интеграл выглядит так:

Определённый интеграл отличается от неопределённого тем, что его результатом является не формула (семейство первообразных), а конкретное число.

Когда мы считали, сколько проехали на велосипеде за два часа, то брали именно определённый интеграл. Его запись отличается от записи неопределённого интеграла и выглядит так:

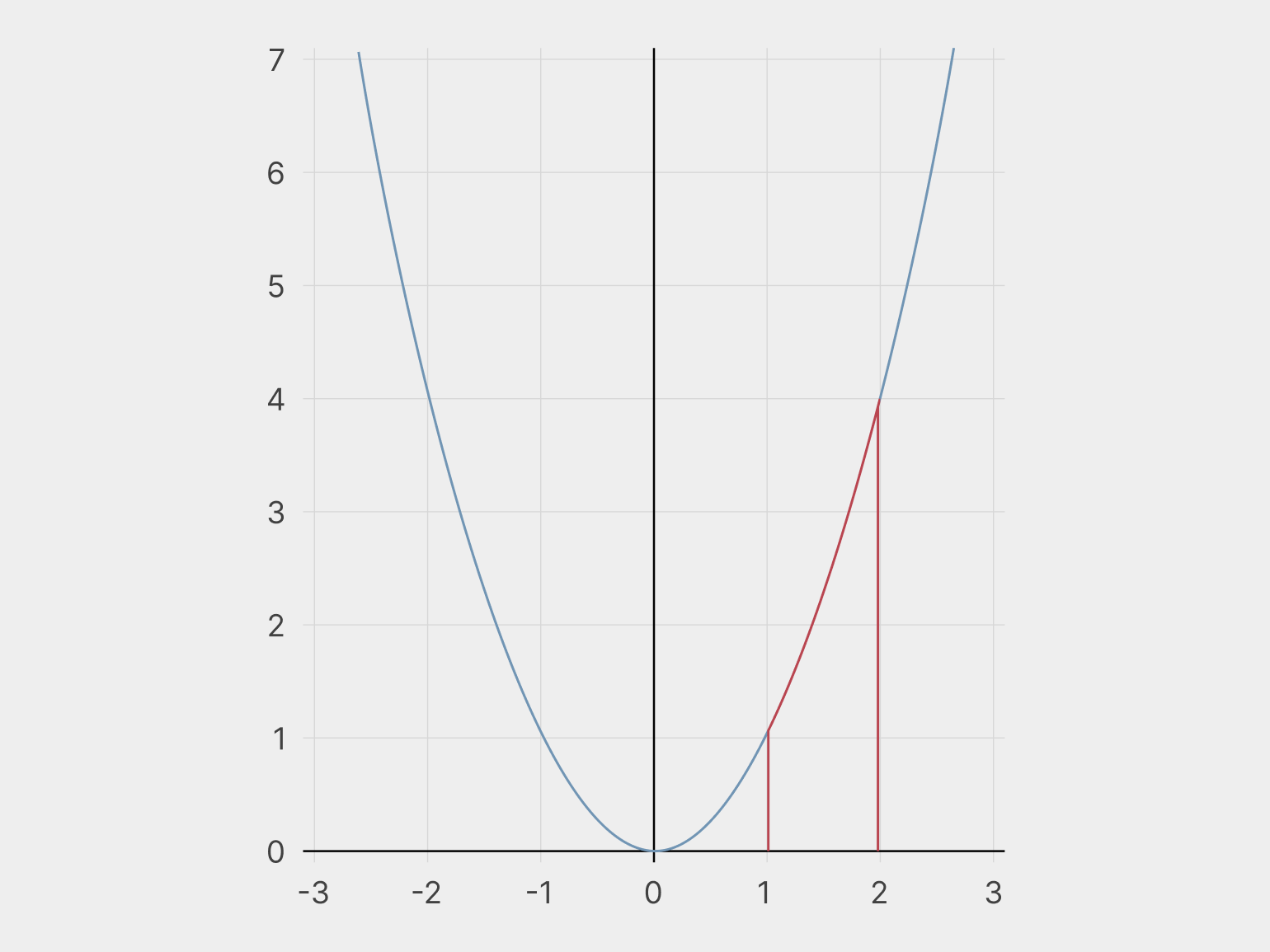
a здесь обозначает начало интегрируемого промежутка, b — его окончание. Таким образом, если мы берём интеграл:

То нас интересует только вот этот кусок параболы:

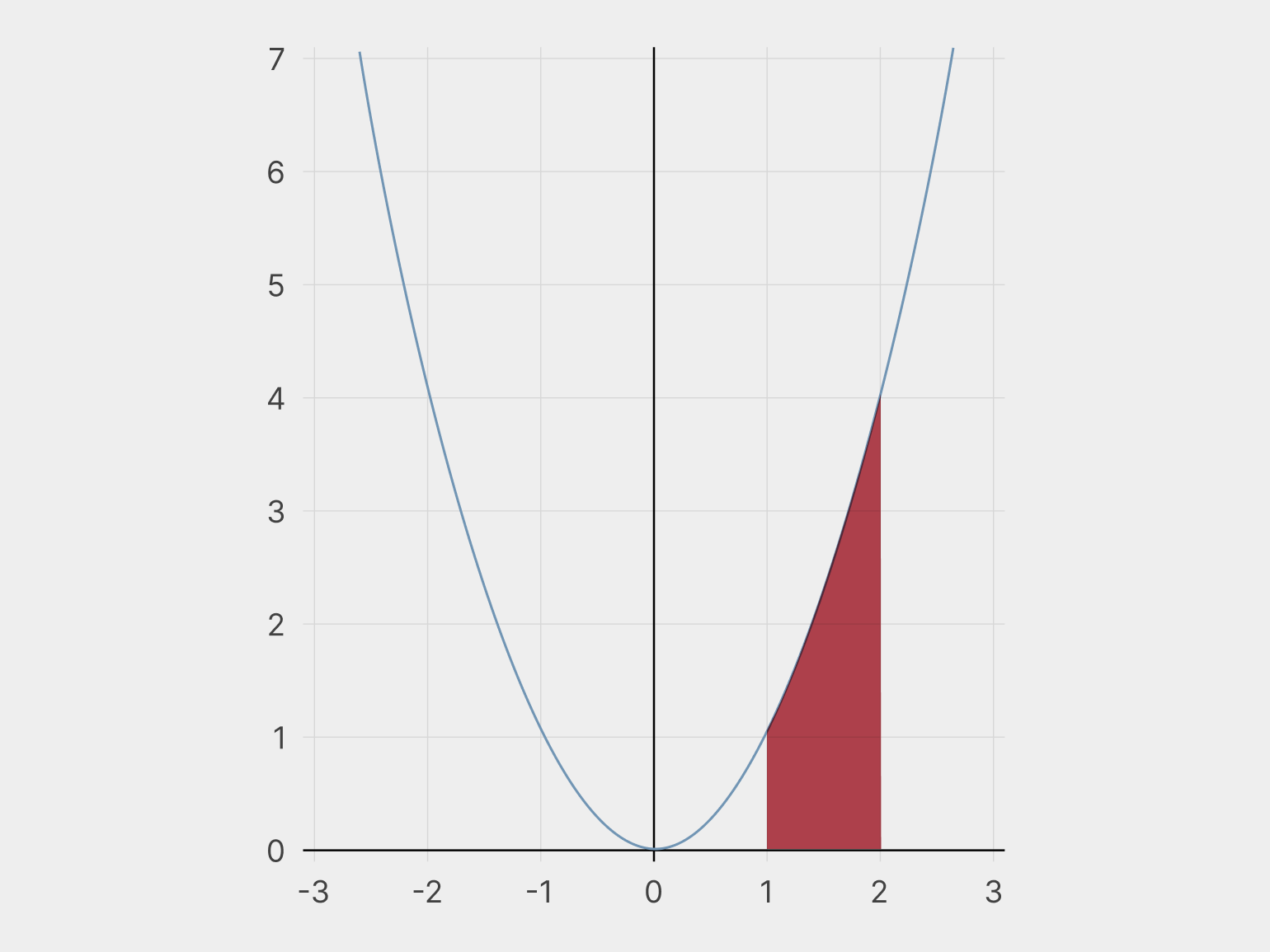
Наши красные линии вам ничего не напоминают? Это же криволинейная трапеция! А так как интеграл представляет собой сумму маленьких умножений x на y в каждой возможной точке, то в результате интегрирования у нас получается площадь красной фигуры.

Именно поэтому интеграл часто описывают как «площадь фигуры под кривой» — это одно из его геометрических проявлений.

Теперь давайте посмотрим, как посчитать интеграл

Если интеграл сложный, то сначала его нужно преобразовать, пользуясь методами интегрирования. Этих методов не очень много, но они сложные и комплексные, поэтому мы не рассматриваем их в этой статье.

Примечание. Интегрировать можно не каждую функцию. Это возможно только в тех случаях, когда она определена и непрерывна в области интегрирования.

После того как подынтегральная функция приведена в элементарный вид, нужно найти её первообразную. Чтобы сделать это, следует воспользоваться таблицей неопределённых интегралов.

Вот список основных и самых простых (но далеко не всех) интегралов:

Если вы считали неопределённый интеграл, то вуаля: подставляете значения в формулу, и ответ готов — очень просто. Если же вы ищете определённый интеграл, нужно воспользоваться формулой Ньютона — Лейбница.

Как видим, для нахождения определённого интеграла необходимо провести два преобразования.

Сначала, как и в случае с неопределённым интегралом, мы находим первообразную F (x). Константа C в этом случае не добавляется. 

Этот символ значит, что мы работаем со значениями этой первообразной от a до b.

Затем мы должны подставить значения a и b в найденную первообразную, посчитать результат и найти разность этих результатов. Это и будет определённый интеграл.

Чтобы было нагляднее и понятнее, закрепим алгоритм интегрирования несколькими простыми примерами.

---

Найдите неопределённый интеграл:

Решение

---

Найдите определённый интеграл:

Решение

---

Найдите неопределённый интеграл:

Решение

Обратите внимание, что если построить график функции и её первообразной, то в обоих случаях x будет принимать значения от нуля до плюс бесконечности.

---

Найдите определённый интеграл:

Решение

Научитесь: Профессия Data Engineer
Узнать больше

Одно из самых значимых понятий в математике — интеграл. Термин часто можно встретить при решении задач по математике и физике. С помощью интеграла существенно упрощается поиск площади под кривой, пройденного пути объекта, движущегося неравномерно, массы неоднородного тела, функции по производной.

Что такое интеграл — понятие и определение

Интеграл представляет собой аналог суммы для бесконечного числа бесконечно малых слагаемых.

Интеграл является эффективным инструментом для решения задач из математического анализа. Слово «интеграл» происходит от латинского «integer», то есть «целый». Впервые это понятие ввел Иоганн Бернулли.

Разобраться в определении интеграла можно, если рассмотреть понятный график функции:

Исходя из графика, можно сделать вывод, что интегралом является сумма малых частей, которые составляют в целом рассматриваемый объект. Компоненты складываются в какую-то геометрическую фигуру. При сложении этих частей можно определить, какова ее площадь. Таким образом, пояснение для интеграла заключается в следующем: интеграл является площадью какой-то фигуры, расположенной под линией функции.

Данное понятие относится к определенному интегралу. Он определен на отрезке между точками а и b. В верхней части в качестве ограничения выступает некоторый график функции, как представлено на рисунке:

Математическая запись интеграла:

(int_{a}^{b}{f(x)dx})

где f(x) является той самой функцией, график которой ограничивает фигуру в верхней части;

a и b представляют собой пределы;

x соответствует направлению, вдоль которого построены столбцы на графике.

Процесс интегрирования является обратным дифференцированию. В том случае, когда требуется определить минимальный промежуток заданной функции, целесообразно взять от нее производную. Это объясняется тем, что производная или дифференциал являются быстрым методом поиска части чего-либо. Можно наглядно определить с помощью рисунка, что минимальная фигура, которая является частью целого, при таком числе составляющих компонентов не повторяет форму кривой функции. Таким образом, требуется уменьшить габариты таких частей, чтобы они максимально точно совпадали с графиком. Площадь наименьшего компонента фигуры будет стремиться к нулевому значению. Точность повышается с уменьшением размеров рассматриваемой части. Площадь геометрической фигуры состоит из суммы таких частей, которые стремятся к нулю. Записать это можно с помощью уравнения:

(P=lim_{Delta x_{i}rightarrow 0}sum{y_{i}Delta x_{i}})

Подробно полученное выражение можно рассмотреть на графике:

Площадь малой части фигуры определяется так же, как площадь прямоугольника. Значение Y нужно помножить на значение ΔХ. Так как фигура представляет собой совокупность малых частей, то их требуется сложить. Следует учитывать, что каждый компонент фигуры ΔХ стремится к нулевому значению. Поэтому формула, которая представлена выше, включает это условие и позволяет определить результат максимально точно.

Если обозначить количество частей ΔХ, стремящихся к бесконечности, то можно определить, что существует предел интегральной суммы, которая состоит из таких компонентов, стремящихся к нулю и к бесконечности по числу таких частей. Таким образом, правая граница фигуры, изображенной на графике, является пределом. В этом выражается геометрический смысл определенного интеграла.

Физический смысл интеграла состоит в том, что это сумма бесконечно малых величин на бесконечно большом интервале. Исходя из этого, можно определить любую величину, которая изменяется, согласно функции. К примеру, рассчитать общий путь по закону изменения скорости. Необходимость в интеграле возникла, когда потребовалось рассчитать площади каких-либо фигур и объем любых тел, выбранных произвольно.

В том случае, когда расчеты подразумевают наличие постоянной характеристики, к примеру, скорости, найти путь можно с помощью произведения этой постоянной скорости и времени. Этот же момент можно проверить при вычислении интеграла от такой функции и записи уравнения прямой. Но скорость в процессе движения может меняться. Данное изменение можно представить в виде зависимости. Тогда следует вписать граничные условия, например, в случае пути — это время, в интеграл скорости по времени. Полученное выражение будет равно площади трапеции, которая расположена под функцией скорости, что является физическим смыслом определенного интеграла.

Свойства, которыми обладает определенный интеграл:

1. Когда функции f и g интегрируются на интервале [a, b], то для любых чисел (alpha) и (beta (alpha in R, beta in R)) функция (varphi(x) = alpha f(x) + beta g(x)) также интегрируема на отрезке [a, b]. Справедливо равенство: (intlimits_a^b (alpha f(x) + beta g(x)) dx = alpha intlimits_a^b f(x) dx + beta intlimits_a^b g(x) dx.label{ref1})
2. Если функции f и g интегрируемы на отрезке [a, b], то функция (varphi(x) = f(x)g(x)) также интегрируема на этом отрезке.
3. В том случае, когда функция f(x) интегрируема на отрезке (Delta = [a, b]) она интегрируема на любом отрезке (Delta_{1} subset Delta.)
4. При функции f(x), интегрируемой на отрезке [a, b] и a < c  < b, будет работать формула: (intlimits_a^b f(x) dx = intlimits_a^c f(x) dx + intlimits_c^b f(x) dx)
5. При функции f, интегрируемой на отрезке [a, b] и если (c_{1}, c_{2}, c_{3}) являются любыми точками данного интервала, то (intlimits_{c_{1}}^{c_{3}} f(x) dx = intlimits_{c_{1}}^{c_{2}} f(x) dx + intlimits_{c_{2}}^{c_{3}} f(x) dx)

Термин «неопределенный интеграл» применим в ситуациях, когда требует найти площадь криволинейной трапеции, путь в соответствии с известной скоростью тела, которое движется неравномерно, и для решения других подобных задач.

Свойства, которыми характеризуется неопределенный интеграл:

1. Константу можно выносить за знак интеграла: (int kf(x) dx = kint f(x) dx)
2. Интеграл разности или суммы функций соответствует разности или сумме интегралов от этих функций: (int ( f(x) pm g(x) ) dx = int f(x) dx pm int g(x) dx)
3. Производная интеграла определяется как выражение, находящееся под знаком интеграла: (bigg (int f(x) dx bigg )’ = f(x))
4. Интеграл от производной функции равен сумме этой функции и постоянной: (int F'(x) dx = F(x) + C)
5. Интеграл дифференциала функции равен сумме этой функции и постоянной интегрирования: (int df(x) dx = f(x) + C)

Таблица интегралов для студентов

Такие формулы позволяют упростить решение многих задач. Основные интегралы:

(int 0dx=C)

(int dx=int 1dx=x+C)

(int x^n dx = frac{x^{n+1}}{n+1}+C)

(int frac{dx}{x}=ln |x|+C)

(int a^x dx = frac{a^x}{ln a} + C)

(int e^x dx = e^x + C)

(int sin x dx = -cos x + C)

(int cos x dx = sin x+C)

(int frac{dx}{sin^2 x}=-ctgx + C)

(int frac{dx}{cos^2 x}=tgx+C)

(int frac{dx}{sqrt{a^2-x^2}}=arcsin frac{x}{a}+C)

(int frac{dx}{a^2+x^2}=frac{1}{a}arctgfrac{x}{a}+C)

(int frac{dx}{a^2-x^2}=frac{1}{2a} ln|frac{a+x}{a-x}|+C)

(int frac{dx}{sqrt{x^2pm a^2}}=ln|x+sqrt{x^2pm a^2}|)

Методы решения интегралов

Данные методики позволяют преобразовать сложные уравнения в простые формы, решения которых можно найти в таблице. Также к преобразованным выражениям можно применять свойства интегралов.

Непосредственное интегрирование

Данный метод целесообразно применять, когда в интеграле имеются табличные простейшие функции, либо функции, которые можно представит в таком виде по результатам элементарных действий. К примеру, когда требуется вынести константу за знак интеграла, разбить интеграл на слагаемые в виде интегралов, чтобы в подынтегральном выражении присутствовала готовая функция для интегрирования. Можно привести простой пример:

Необходимо определить интеграл непосредственным интегрированием:

(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx)

Исходя из свойства суммы интегралов, получим:

(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = int x^3 dx + int frac{3 dx}{2sqrt{x}} + int frac{2 dx}{x})

Первый интеграл записан в табличном виде. В таком случае можно воспользоваться непосредственным интегрированием:

(int x^3 dx = frac{x^{3+1}}{3+1} = frac{x^4}{4} + C)

Второй интеграл обладает константой, которую допустимо вынести за знак. Затем интеграл будет преобразован в табличную форму:

(int frac{3dx}{2sqrt{x}} = 3 int frac{dx}{2sqrt{x}} = 3 sqrt{x} + C)

В третьем интеграле можно вынести константу. Далее необходимо воспользоваться методом непосредственного интегрирования:

(int frac{2dx}{x} = 2int frac{dx}{x} = 2 ln x + C)

Полученные выражения необходимо представить в виде одной записи:

(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x + C)

Ответ: (int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x+ C)

Метод подведения под знак дифференциала

Решить некоторые типы интегралов можно с помощью этого способа. Он заключается в вынесении под знак интеграла. Таким образом получается интеграл табличной формы. Формула имеет следующий вид:

(f'(x) dx = d( f(x) ))

В том случае, когда подынтегральная функция содержит произведение пары функций, одна из которых представляет собой дифференциал другой, нужно внести под знак дифференциала нужную функцию. Данное действие можно записать таким образом:

(int f(varphi(x)) varphi'(x) dx = int f(varphi(x)) d(varphi(x))=int f(u) du)

(u=varphi(x))

Воспользоваться способом подведения основных функций можно при знании таблицы производных и интегрирования. Из них следуют следующие уравнения:

(dx = d(x+c) )

(c=const)

(-sin x dx=d(cos x))

(dx=frac{1}{a} d(ax))

(cos x dx = d(sin x))

(xdx=frac{1}{2} d(x^2+a) )

(frac{dx}{x} = d(ln x))

(-frac{dx}{x^2}= d(frac{1}{x}))

(frac{dx}{cos^2 x} = d(tg x))

(int f(kx+b)dx = frac{1}{k} int f(kx+b)d(kx+b) = frac{1}{k} F(kx+b) + C)

В качестве примера можно решить задачу на нахождение интеграла, обладающего таким видом:

(int sin x cos x dx)

В этом случае допустимо заносить под знак дифференциала любую из указанных функций. Целесообразно занести (cos x) из-за удобства смены знаков. Применяя формулы, получим:

(int sin x cos xdx = int sin x d(sin x) = frac{1}{2} sin^2 x + C)

Ответ: (int sin x cos x dx = frac{1}{2} sin^2 x + C)

Метод интегрирования по частям

Данная методика применима, когда требуется решить интегралы от произведения двух простейших функций. Одна из них достаточно просто дифференцируется, а вторая — интегрируется. В данном случае справедлива методика для неопределенных и определенных интегралов. Неопределенный интеграл характеризуется уравнением:

(int udv = uv — int vdu)

Определенный интеграл соответствует формуле:

(int limits_{a}^{b} udv = uv bigg |_{a}^{b} — int limits_{a}^{b} vdu)

В качестве примера можно определить интеграл:

(int xe^xdx)

Заметим, что в состав подынтегральной функции входит пара функций. Одна из них путем дифференцирования преобразуется в единицу, а вторая достаточно просто интегрируется. Поэтому в данном случае справедлив метод интегрирования по частям. Можно предположить, что:

(u = x rightarrow du=dx)

(dv = e^x dx rightarrow v=e^x)

Далее необходимо подставить полученные значения в первую формулу интегрирования:

(int xe^x dx = xe^x — int e^x dx = xe^x — e^x + C)

Ответ: (int xe^x dx = xe^x — e^x + C)

Метод замены переменной или метод подстановки

Этот способ нахождения интегралов применим в задачах, где одна функция — это производная второй функции. Допустим, что интеграл записан так:

(int f(x) dx)

Можно заменить (x=phi(t)). При этом функция (phi(t)) является дифференцируемой, поэтому можно найти (dx = phi'(t) dt.)

Далее следует подставить (begin{vmatrix} x = phi(t) \ dx = phi'(t) dt end{vmatrix}) в интеграл. Таким образом:

(int f(x) dx = int f(phi(t)) cdot phi'(t) dt)

Полученное выражение является формулой замены переменной в неопределенном интеграле.

При условиях задачи, которая содержит интеграл (int f(phi(x)) cdot phi'(x) dx), целесообразно заменить переменную на новую:

(t = phi(x))

(dt = phi'(t) dt)

Таким образом, интеграл преобразуется в форму, которую легко рассчитать с помощью основных методов интегрирования:

(int f(phi(x)) cdot phi'(x) dx = int f(t)dt)

Следует помнить, что по итогам расчетов требуется вернуть замененную переменную назад к x.

Например, можно рассмотреть задачу, по условиям которой необходимо вычислить неопределенный интеграл с помощью замены переменной:

(int e^{3x} dx)

Замена переменной будет выполнена следующим образом:

(t = 3x)

(dt = 3dx)

Таким образом:

(int e^{3x} dx = int e^t frac{dt}{3} = frac{1}{3} int e^t dt =frac{1}{3} e^t + C = frac{1}{3} e^{3x} + C)

Ответ: (int e^{3x} dx = frac{1}{3} e^{3x} + C)

Примеры решения

Задача 1

Требуется рассчитать определенный интеграл:

(int_0^1 frac{x}{x^4+1} dx)

Решение

Требуется заменить (t = x^2)

Таким образом, (dt = 2xdx)

Далее необходимо пересчитать пределы интегрирования для переменной t. Для этого нужно подставить 0 и 1 в замену (t = x^2)

В данной задаче они остались прежними. После манипуляций с подстановками получим:

(int_0^1 frac{x}{x^4+1}dx = int_0^1 frac{1}{2} frac{dt}{t^2+1})

Можно найти интеграл по таблице:

(int_0^1 frac{1}{2} frac{dt}{t^2+1}=frac{1}{2} arctg t bigg |_0^1)

Используя формулу Ньютона-Лейбница, запишем решение:

(frac{1}{2} arctg t bigg |_0^1 =frac{1}{2} arctg 1 — frac{1}{2} arctg 0 = frac{1}{2} cdot frac{pi}{4} = frac{pi}{8})

Ответ: (int_0^1 frac{x}{x^4+1} dx = frac{pi}{8})

Задача 2

Необходимо решить определенный интеграл:

(int_0^pi (x+5)sin x dx)

Решение

Можно заметить произведение двух функций, которое находится под интегралом. В этом случае целесообразно воспользоваться методом интегрирования по частям:

(int udv = uv — int vdu)

(int_0^pi (x+5) sin x dx = begin{vmatrix} u = x+5 & du = dx \ dv = sin x dx & v = -cos x end{vmatrix})

Нужно подставить в уравнение интегрирования по частям рассчитанные данные из вертикальных скобок:

(-(x+5)cos x bigg |_0^pi&nbsp;+ int_0^pi&nbsp;cos x dx)

С помощью формулы Ньютона-Лейбница для вычисления определенного интеграла запишем ответ:

(-(x+5)cos x bigg |_0^pi + int_0^pi cos x dx = -(pi+5) cdot (-1) + 5 + sin x bigg |_0^pi = pi + 10 + sin pi — sin 0 = pi + 10)

Ответ:  (int_0^pi (x+5)sin x dx = pi + 10)

Задача 3

Требуется найти определенны интеграл, записанный в виде:

(int_0^2 (x^3 + 2x + 2) dx)

Решение

Используя способ разложения интеграла на простейшие, после получения промежуточного результата необходимо интегрировать каждый интеграл индивидуально:

(int_0^2 (x^3+2x+2) dx = int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx)

В случае первых двух интегралов целесообразно воспользоваться правилом:

(x^p = frac{x^{p+1}}{p+1})

Третий интеграл содержит константу. Таким образом:

(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )

Далее следует подставить пределы интегрирования в каждую функцию и записать ответ:

(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )

Ответ: (int_0^2 (x^3 + 2x + 2) dx = 12)

Задача 4

Необходимо найти решение интеграла:

(int 3cos x dx)

Решение

Требуется вынести константу по первому свойству за знак интеграла и записать ответ:

(int 3cos x dx = 3 int cos x dx = 3 sin x + C)

Ответ: (int 3cos x dx = 3 sin x + C)

Задача 5

Необходимо определить интеграл:

(int (e^x + sin x) dx)

Решение

Исходя из первого свойства неопределенного интеграла, интеграл суммы равен сумме интегралов:

(int (e^x + sin x) dx = int e^x dx + int sin x dx = e^x — cos x)

Ответ: (int (e^x + sin x) dx = e^x — cos x)

Задача 6

Требуется определить производную от интеграла:

( int ln x dx)

Решение

Согласно третьему свойству неопределенного интеграла, производная неопределенного интеграла определяется, как подынтегральная функция:

(bigg (int ln x dx bigg )’ = ln x)

Ответ: (bigg (int ln x dx bigg )’ = ln x)

Задача 7

Требуется доказать следующее выражение:

( int (x^2+x)’ = x^2+x+C)

Решение

В первую очередь необходимо определить производную подынтегральной функции:

( (x^2+x)’ = (x^2)’ + (x)’ = 2x + 1)

Исходя из первого и второго свойства неопределенного интеграла, получим ответ:

(int (2x+1) dx = int 2x dx + int 1 dx = 2 int x dx + int 1 dx =2 cdot frac{x^2}{2} + x + C = x^2 + x + C)

Ответ: выражение доказано.

Благодаря теоретическим знаниям и практическим навыкам решения задач с интегралами, можно с легкостью осваивать самые сложные темы по физике и математическому анализу. Главное — уметь пользоваться таблицей с основными формулами и свойствами определенного и неопределенного интегралов. Если в процессе изучения материала возникают трудности, то в любое время можно открыть сервис Феникс.Хелп. 

Время на прочтение
10 мин

Количество просмотров 49K

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

1. использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

2. логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

3. последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

4. высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

1. Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

2. Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

3. Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

4. Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

5. Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

6. Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

7. Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «… Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый — отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй — подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т.д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

• В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

• В случае с вещественными числами.

  • Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

  • Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

  • В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.

• В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

• Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

• Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

1. Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

• Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).

• Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение

• Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).

• Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при , , а значение . Если. Тогда, при , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов