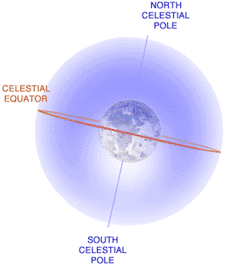
Небесная сфера разделена небесным экватором.
Небе́сная сфе́ра — воображаемая вспомогательная сфера произвольного радиуса, на которую проецируются небесные светила: служит для решения различных астрометрических задач. За центр небесной сферы, как правило, принимают глаз наблюдателя. Для находящегося на поверхности Земли наблюдателя вращение небесной сферы воспроизводит суточное движение светил на небе. Площадь небесной сферы с учетом непостоянства значения размеров дуги равных склонений составляет 41252.96 кв. градусов.
Радиус небесной сферы может быть принят каким угодно: в целях упрощения геометрических соотношений его полагают равным единице. В зависимости от решаемой задачи центр небесной сферы может быть помещен в место:
- где находится наблюдатель (топоцентрическая небесная сфера),
- в центр Земли (геоцентрическая небесная сфера),
- в центр той или иной планеты (планетоцентрическая небесная сфера),
- в центр Солнца (гелиоцентрическая небесная сфера) или в любую др. точку пространства.
Каждому светилу на небесной сфере соответствует точка, в которой её пересекает прямая, соединяющая центр небесной сферы со светилом (с его центром). При изучении взаимного расположения и видимых движений светил на небесной сфере выбирают ту или иную систему координат), определяемую основными точками и линиями. Последние обычно являются большими кругами небесной сферы. Каждый большой круг сферы имеет два полюса, определяющиеся на ней концами диаметра, перпендикулярного к плоскости данного круга.
Содержание
- 1 История
- 2 Названия важнейших точек и дуг на небесной сфере
- 2.1 Отвесная линия и связанные с ней (производные) понятия
- 2.1.1 Отвесная линия
- 2.1.2 Зенит и надир
- 2.1.3 Математический горизонт
- 2.2 Вращение небесной сферы и связанные (производные) понятия
- 2.2.1 Ось мира
- 2.2.2 Полюсы мира
- 2.2.3 Небесный экватор
- 2.3 Термины, рождаемые в пересечениях понятий «Отвесная линия» и «Вращение небесной сферы»
- 2.3.1 Точки востока и запада
- 2.3.2 Небесный меридиан
- 2.3.3 Полуденная линия
- 2.3.4 Точки севера и юга
- 2.4
- 2.4.1 Эклиптика
- 2.4.2 Точки равноденствия
- 2.4.3 Точки солнцестояния
- 2.4.4 Ось эклиптики
- 2.4.5 Полюсы эклиптики
- 2.5 Галактические полюсы и галактический экватор
- 2.1 Отвесная линия и связанные с ней (производные) понятия
- 3 Названия дуг на небесной сфере, связанные с положением светил
- 3.1 Альмукантарат
- 3.2 Вертикальный круг
- 3.3 Суточная параллель
- 3.4 Круг склонения
- 3.5 Круг эклиптической широты
- 3.6 Круг галактической широты
- 4 Любопытные факты
- 5 См. также
История
Представление о Небесной сфере возникло в глубокой древности; в основу его легло зрительное впечатление о существовании куполообразного небесного свода. Это впечатление связано с тем, что в результате огромной удалённости небесных светил человеческий глаз не в состоянии оценить различия в расстояниях до них, и они представляются одинаково удалёнными. У древних народов это ассоциировалось с наличием реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды. Таким образом, в их представлении небесная сфера была важнейшим элементом Вселенной. С развитием научных знаний такой взгляд на небесную сферу отпал. Однако заложенная в древности геометрия небесной сферы в результате развития и совершенствования получила современный вид, в котором и используется в астрометрии.
Названия важнейших точек и дуг на небесной сфере
Отвесная линия и связанные с ней (производные) понятия
Отвесная линия
Отве́сная ли́ния (или вертика́льная ли́ния) — прямая, проходящая через центр небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения. Для наблюдателя, находящегося на поверхности Земли, отвесная линия проходит через центр Земли и точку наблюдения.
Зенит и надир
Отвесная линия пересекается с поверхностью небесной сферы в двух точках — зени́те, над головой наблюдателя, и нади́ре — диаметрально противоположной точке.
Математический горизонт
Математи́ческий горизо́нт — большой круг небесной сферы, плоскость которого перпендикулярна к отвесной линии. Математический горизонт делит поверхность небесной сферы на две половины: видимую для наблюдателя, с вершиной в зените, и невидимую, с вершиной в надире. Математический горизонт, вообще говоря, не совпадает с видимым горизонтом вследствие неровности поверхности Земли и различной высотой точек наблюдения, а также искривления лучей света в атмосфере.
Вращение небесной сферы и связанные (производные) понятия
Ось мира
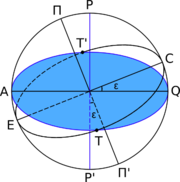
P,P’ — полюсы мира, T,T’ — точки равноденствия, E,C — точки солнцестояния, П,П’ — полюса эклиптики, PP’ — ось мира, ПП’ — ось эклиптики, ATQT’- небесный экватор, ETCT’ — эклиптика
Ось ми́ра — воображаемая линия, пересекающая небесную сферу в северном и южном полюсах (вокруг неё происходит вращение небесной сферы).
Полюсы мира
Ось мира пересекается с поверхностью небесной сферы в двух точках — се́верном по́люсе ми́ра и ю́жном по́люсе ми́ра. Северным полюсом называется тот, со стороны которого вращение небесной сферы происходит по часовой стрелке, если смотреть на сферу извне.
Если смотреть на небесную сферу изнутри, (что мы обычно и делаем, наблюдая звёздное небо), то в окрестности северного полюса мира её вращение происходит против часовой стрелки, а в окрестности южного полюса мира —- по часовой стрелке.
Небесный экватор
Небе́сный эква́тор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира. Небесный экватор делит поверхность небесной сферы на два полушария: се́верное полуша́рие, с вершиной в северном полюсе мира, и ю́жное полуша́рие, с вершиной в южном полюсе мира.
Термины, рождаемые в пересечениях понятий «Отвесная линия» и «Вращение небесной сферы»
Точки востока и запада
Небесный экватор пересекается с математическим горизонтом в двух точках: то́чке восто́ка и то́чке за́пада. Точкой востока называется та, в которой точки вращающейся небесной сферы пересекают математический горизонт, переходя из невидимой полусферы в видимую.
Небесный меридиан
Небе́сный меридиа́н — большой круг небесной сферы, плоскость которого проходит через отвесную линию и ось мира. Небесный меридиан делит поверхность небесной сферы на два полушария — восто́чное полуша́рие, с вершиной в точке востока, и за́падное полуша́рие, с вершиной в точке запада.
Полуденная линия
Полу́денная ли́ния — линия пересечения плоскости небесного меридиана и плоскости математического горизонта.
Точки севера и юга
Небесный меридиан пересекается с математическим горизонтом в двух точках: то́чке се́вера и то́чке ю́га. Точкой севера называется та, которая ближе к северному полюсу мира.
Эклиптика
Экли́птика — большой круг небесной сферы, пересечение небесной сферы и плоскости орбиты центра масс системы Земля — Луна. С большой точностью по эклиптике происходит видимое годовое движение Солнца по небесной сфере. Плоскость эклиптики пересекается с плоскостью небесного экватора под углом ε = 23°26′. Северный полюс эклиптики находится в созвездии Дракона с экваториальными координатами: R.A. = 18h00m, Dec = +66°33′. Примечательно, что недалеко от северного полюса эклиптики расположена планетарная туманность Кошачий Глаз (NGC6543).
Точки равноденствия
Эклиптика пересекается с небесным экватором в двух точках — то́чке весе́ннего равноде́нствия и то́чке осе́ннего равноде́нствия. Точкой весеннего равноденствия называется та, в которой Солнце, в результате своего годового движения, переходит из южного полушария небесной сферы в северное. В точке осеннего равноденствия Солнце переходит из северного полушария небесной сферы в южное.
Точки солнцестояния
Точки эклиптики, отстоящие от точек равноденствия на 90°, называются то́чкой ле́тнего солнцестоя́ния (в северном полушарии) и то́чкой зи́мнего солнцестоя́ния (в южном полушарии).
Ось эклиптики
Ось экли́птики — диаметр небесной сферы, перпендикулярный плоскости эклиптики.
Полюсы эклиптики
Ось эклиптики пересекается с поверхностью небесной сферы в двух точках — се́верном по́люсе экли́птики, лежащем в северном полушарии, и ю́жном по́люсе экли́птики, лежащем в южном полушарии.
Галактические полюсы и галактический экватор
Точка небесной сферы с экваториальными координатами
α = 192,85948° β = 27,12825°
или
R.A.=12h51m26s Dec.=+27°07’42»
называется се́верным галакти́ческим по́люсом, а диаметрально противоположная ей точка — ю́жным галакти́ческим по́люсом.
Большой круг небесной сферы, плоскость которого перпендикулярна линии, соединяющей галактические полюсы, называется галакти́ческим эква́тором.
Названия дуг на небесной сфере, связанные с положением светил
Альмукантарат
Альмукантара́т — араб. круг равных высот
Альмукантарат светила — малый круг небесной сферы, проходящий через светило, плоскость которого параллельна плоскости математического горизонта.
Вертикальный круг
Круг высоты́ или вертика́льный круг или вертика́л светила — большой полукруг небесной сферы, проходящий через зенит, светило и надир.
Суточная параллель
Су́точная паралле́ль светила — малый круг небесной сферы, проходящий через светило, плоскость которого параллельна плоскости небесного экватора. Видимые суточные движения светил совершаются по суточным параллелям.
Круг склонения
Круг склоне́ния светила — большой полукруг небесной сферы, проходящий через полюсы мира и светило.
Круг эклиптической широты
Круг эклипти́ческой широты́, или просто круг широты светила — большой полукруг небесной сферы, проходящий через полюсы эклиптики и светило.
Круг галактической широты
Круг галакти́ческой широты́ светила — большой полукруг небесной сферы, проходящий через галактические полюсы и светило.
Любопытные факты
Слово зенит пришло к нам из арабского языка, где оно произносится как замт. Переписанное латинскими буквами как zamt, оно было впоследствии искажено переписчиками, превратившись в zanit, а затем и в зенит.
См. также
- Системы небесных координат
- Армиллярная сфера
Wikimedia Foundation.
2010.
Обновлено: 27.05.2023
бы находящимися на внутренней поверхности некоторой сферы произвольного радиуса.
Поэтому видимые, положения светил можно определять только направлениями, а их
взаимное расположение — углами между этими направлениями, или соответствующими
дугами больших кругов на сфере, из центра которой исходят все направления.
Воображаемая сфера произвольного радиуса с центром в произвольной точке
пространства, на поверхности которой расположены светила так, как они видны на
небе в некоторый момент времени из дачной точки пространства, называется
Таким образом, воображаемый наблюдатель, находящийся в центре небесной сферы,
должен видеть положения светил на ее поверхности точно в таком же взаимном
расположении, в каком реальный наблюдатель видит реальные светила на небе.
Вращение небесной сферы повторяет вращение небесного свода.
Небесная сфера служит для изучения видимых положений и движений небесных тел.
Для этого на ее поверхности фиксируются основные линии и точки, по отношению к
которым и производятся соответствующие измерения.
Прямая ZOZ’ ( 4), проходящая через центр О небесной сферы и совпадающая с
направлением нити отвеса в месте наблюдения, называется отвесной или
Отвесная линия пересекается с поверхностью небесной сферы в двух точках: в
зените Z, над головой наблюдателя, и в диаметрально противоположной точке —
Большой круг небесной сферы (SWNE), плоскость которого перпендикулярна к
отвесной линии, называется математическим или истинным горизонтом.
Математический горизонт делит поверхность небесной сферы на две половины:
видимую для наблюдателя, с вершиной в зените Z, и невидимую, с вершиной в надире
Математический горизонт следует отличать от видимого горизонта (линии, вдоль
которой «небо сходится с Землей»). Видимый горизонт на суше — неправильная
линия, точки которой лежат то выше, то ниже истинного горизонта. В открытом море
видимый горизонт всегда малый круг, плоскость которого параллельна плоскости
Малый круг небесной сферы (аМа), проходящий через светило М и плоскость которого
параллельна плоскости математического горизонта, называется альмукантаратом
Большой полукруг небесной сферы ZMZ’, проходящий через зенит, светило М и надир,
называется кругом высоты, вертикальным кругом, или просто вертикалом светила.
Диаметр РР’ ( 5) вокруг которого происходит вращение небесной сферы,
называется осью мира. Ось мира пересекается с поверхностью небесной сферы в двух
точках: в северном полюсе мира Р и южном полюсе мира Р’. Северный полюс тот, со
стороны которого вращение небесной сферы происходит по часовой стрелке, если
смотреть на сферу извне. Большой круг небесной сферы QWQ’E, плоскость которого
перпендикулярна к оси мира, называется небесным экватором. Небесный экватор
делит поверхность небесной сферы на два полушария: северное, с северным полюсом
мира Р, и южное, с южным полюсом мира Р’.
Малый круг небесной сферы (bМb), плоскость которого параллельна плоскости
небесного экватора, называется небесной или суточной параллелью светила М.
Видимые суточные движения светил совершаются по суточным параллелям.
Большой полукруг небесной сферы РМР’, проходящий через полюсы мира и через
светило М, называется часовым кругом или кругом склонения светила.
Небесный экватор пересекается с математическим горизонтом в двух точках: в точке
востока Е и в точке запада W. Круги высот, проходящие через точки востока и
запада, называются первыми вертикалами — восточным и западным.
Большой круг небесной сферы PZQSP’Z’Q’N, плоскость которого проходит через
отвесную линию и ось мира, называется небесным меридианом.
Небесный меридиан делит поверхность небесной сферы на два полушария: восточное,
с точкой востока Е, и западное, с точкой запада W.
Плоскость небесного меридиана и плоскость математического горизонта пересекаются
по прямой линии NOS, которая называется полуденной линией.
Небесный меридиан пересекается с математическим горизонтом в двух точках: в
точке севера N и в точке юга S. Точкой севера называется та, которая ближе к
северному полюсу мира. Точка юга — ближе к южному полюсу мира.
Небесный меридиан пересекается с небесным экватором также в двух точках: в
верхней точке экватора Q, которая ближе к зениту, и в нижней точке экватора Q’,
которая ближе к надиру.
Дуга небесного меридиана PZQSP’ является его верхней частью, а дуга PNQ’Z’P’ —
Люди в древности считали, что все звезды располагаются на небесной сфере, которая как единое целое вращается вокруг Земли. Уже более 2.000 лет тому назад астрономы стали применять способы, которые позволяли указать расположение любого светила на небесной сфере по отношению к другим космическим объектам или наземным ориентирам. Представлением о небесной сфере удобно пользоваться и теперь, хотя мы знаем, что этой сферы реально не существует.
Небесная сфера — воображаемая шаровая поверхность произвольного радиуса, в центре которой находится глаз наблюдателя, и на которую мы проецируем положение небесных светил.
Понятием небесной сферы пользуются для угловых измерений на небе, для удобства рассуждений о простейших видимых небесных явлениях, для различных расчетов, например вычисления времени восхода и захода светил.
Построим небесную сферу и проведем из ее центра луч по направлению к звезде А.
Там, где этот луч пересечет поверхность сферы, поместим точку А1 изображающую эту звезду. Звезда В будет изображаться точкой В1. Повторив подобную операцию для всех наблюдаемых звезд, мы получим на поверхности сферы изображение звездного неба – звездный глобус. Ясно, что если наблюдатель находится в центре этой воображаемой сферы, то для него направление на сами звезды и на их изображения на сфере будут совпадать.
- Что является центром небесной сферы? (Глаз наблюдателя)
- Каков радиус небесной сферы? (Произвольный)
- Чем отличаются небесные сферы двух соседей по парте? (Положением центра).
Для решения многих практических задач расстояния до небесных тел не играют роли, важно лишь их видимое расположение на небе. Угловые измерения не зависят от радиуса сферы. Поэтому, хотя в природе небесной сферы и не существует, но астрономы для изучения видимого расположение светил и явлений, которые можно наблюдать на небе в течении суток или многих месяцев, применяют понятие Небесная сфера. На такую сферу и проецируются звезды, Солнце, Луна, планеты и т.д, отвлекаясь от действительных расстояний до светил и рассматривая лишь угловые расстояние между ними. Расстояния между звездами на небесной сфере можно выражать только в угловой мере. Эти угловые расстояния измеряются величиной центрального угла между лучами, направленными на одну и другую звезду, или соответствующими им дугами на поверхности сферы.
Для приближенной оценки угловых расстояний на небе полезно запомнить такие данные: угловое расстояние между двумя крайними звездами ковша Большой Медведицы (α и β) составляет около 5°, а от α Большой Медведицы до α Малой Медведицы (Полярной звезды) – в 5 раз больше – примерно 25°.
Простейшие глазомерные оценки угловых расстояний можно провести также с помощью пальцев вытянутой руки.
Только два светила – Солнце и Луну – мы видим как диски. Угловые диаметры этих дисков почти одинаковы – около 30′ или 0,5°. Угловые размеры планет и звезд значительно меньше, поэтому мы их видим просто как светящиеся точки. Для невооруженного глаза объект не выглядит точкой в том случае, если его угловые размеры превышают 2–3′. Это означает, в частности, что наш глаз различает каждую по отдельности светящуюся точку (звезду) в том случае, если угловое расстояние между ними больше этой величины. Иначе говоря, мы видим объект не точечным лишь в том случае, если расстояние до него превышает его размеры не более чем в 1700 раз.
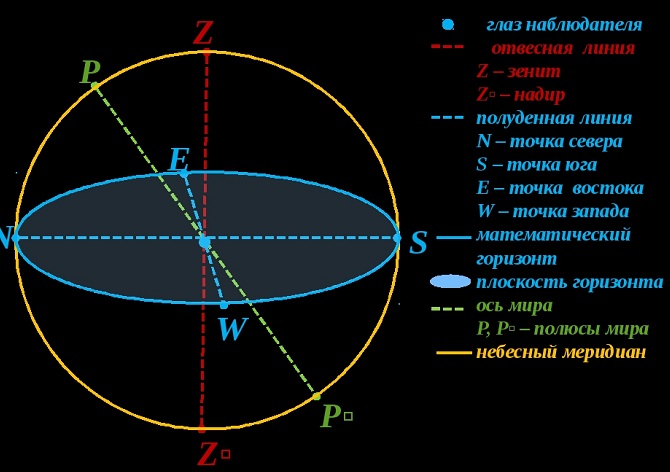
Отвесная линия Z,Z’, проходящая через глаз наблюдателя (точка С), находящегося в центре небесной сферы, пересекает небесную сферу в точках Z — зенит, Z’ — надир.
Зенит — эта наивысшая точка над головой наблюдателя.
Надир — противоположная зениту точка небесной сферы.
Плоскость, перпендикулярная отвесной линии, называется горизонтальной плоскостью (или плоскостью горизонта).
Математическим горизонтом называется линия пересечения небесной сферы с горизонтальной плоскостью, проходящей через центр небесной сферы.
Невооруженным глазом на всем небе можно видеть примерно 6000 звезд, но мы видим лишь половину из них, потому что другую половину звездного неба закрывает от нас Земля. Движутся ли звезды по небосводу? Оказывается, движутся все и притом одновременно. В этом легко убедиться, наблюдая звездное небо (ориентируясь по определенным предметам).
Вследствие ее вращения вид звездного неба меняется. Одни звезды только еще появляются из-за горизонта (восходят) в восточной его части, другие в это время находятся высоко над головой, а третьи уже скрываются за горизонтом в западной стороне (заходят). При этом нам кажется, что звездное небо вращается как единое целое. Теперь каждому хорошо известно, что вращение небосвода — явление кажущееся, вызванное вращением Земли.
Картину того, что в результате суточного вращения Земли происходит со звездным небом, позволяет запечатлеть фотоаппарат.
На полученном снимке каждая звезда оставила свой след в виде дуги окружности . Но есть и такая звезда, передвижение которой в течение всей ночи почти незаметно. Эту звезду назвали Полярной. Она в течение суток описывает окружность малого радиуса и всегда видна почти на одной и той же высоте над горизонтом в северной стороне неба. Общий центр всех концентрических следов звезд находится на небе неподалеку от Полярной звезды. Эта точка, в которую направлена ось вращения Земли, получила название северный полюс мира. Дуга, которую описала Полярная звезда, имеет наименьший радиус. Но и эта дуга, и все остальные — независимо от их радиуса и кривизны — составляют одну и ту же часть окружности. Если бы удалось сфотографировать пути звезд на небе за целые сутки, то на фотографии получились бы полные окружности — 360°. Ведь сутки — это период полного оборота Земли вокруг своей оси. За час Земля повернется на 1/24 часть окружности, т. е. на 15°. Следовательно, длина дуги, которую звезда опишет за это время, составит 15°, а за полчаса — 7,5°.
Звезды в течение суток описывают тем большие окружности, чем дальше от Полярной звезды они находятся.
Ось суточного вращения небесной сферы называют осью мира (РР’).
Точки пересечения небесной сферы с осью мира называют полюсами мира (точка Р — северный полюс мира, точка Р’ — южный полюс мира).
Полярная звезда расположена вблизи северного полюса мира. Когда мы смотрим на Полярную звезду, точнее, на неподвижную точку рядом с ней — северный полюс мира, направление нашего взгляда совпадает с осью мира. Южный полюс мира находится в южном полушарии небесной сферы.
Плоскость ЕАWQ, перпендикулярная оси мира РР’ и проходящая через центр небесной сферы, называется плоскостью небесного экватора, а линия пересечения ее с небесной сферой — небесным экватором.
Небесный экватор – линия окружности, полученная от пересечения небесной сферы с плоскостью проходящая через центр небесной сферы перпендикулярно к оси мира.
Небесный экватор делит небесную сферу на два полушария: северное и южное.
Ось мира, полюса мира и небесный экватор аналогичны оси, полюсам и экватору Земли, так как перечисленные названия связаны с видимым вращением небесной сферы, а оно является следствием действительного вращения земного шара.
Плоскость, проходящая через точку зенита Z, центр С небесной сферы и полюс Р мира, называют плоскостью небесного меридиана, а линия пересечения ее с небесной сферой образует линию небесного меридиана.
Небесный меридиан – большой круг небесной сферы, проходящий через зенит Z, полюс мира Р, южный полюс мира Р’, надир Z’
В любом месте Земли плоскость небесного меридиана совпадает с плоскостью географического меридиана этого места.
Полуденная линия NS — это линия пересечения плоскостей меридиана и горизонта. N – точка севера, S – точка юга
Она названа так потому, что в полдень тени от вертикальных предметов падают по этому направлению.
- Каков период вращения небесной сферы? (Равен периоду вращения Земли – 1 сутки).
- В каком направлении происходит видимое (кажущееся) вращение небесной сферы? (Противоположно направлению вращения Земли).
- Что можно сказать о взаимном расположении оси вращения небесной сферы и земной оси? (Ось небесной сферы и земная ось будут совпадать).
- Все ли точки небесной сферы участвуют в видимом вращении небесной сферы? (Точки, лежащие на оси, покоятся).
Земля движется по орбите вокруг Солнца. Ось вращения Земли наклонена к плоскости орбиты на угол 66,5°. Вследствие действия сил тяготения со стороны Луны и Солнца ось вращения Земли смещается, в то время как наклон оси к плоскости земной орбиты остается постоянным. Ось Земли как бы скользит по поверхности конуса. (то же происходит с осью у обыкновенного волчка в конце вращения).
Это явление было открыто еще в 125 г. до н. э. греческим астрономом Гиппархом и названо прецессией.
Один оборот земная ось совершает за 25 776 лет – этот период называется платоническим годом. Сейчас вблизи Р – северного полюса мира находится Полярная звезда – α Малой Медведицы. Полярной называется та звезда, которая на сегодняшний день находится вблизи Северного полюса мира. В наше время, примерно с 1100 года, такой звездой является альфа Малой Медведицы – Киносура. Раньше титул Полярной поочередно присваивался π, η и τ Геркулеса, звездам Тубан и Кохаб. Римляне вовсе не имели Полярной звезды, а Кохаб и Киносуру (α Малой Медведицы) называли Стражами.
На начало нашего летоисчисление – полюс мира был вблизи α Дракона – 2000 лет назад. В 2100 г полюс мира будет всего в 28′ от Полярной звезды – сейчас в 44′. В 3200г полярным станет созвездие Цефей. В 14000 г – полярной будет Вега (α Лиры).
Как найти в небе Полярную звезду?
Чтобы найти Полярную звезду, нужно через звезды Большой Медведицы (первые 2 звезды «ковша») мысленно провести прямую линию и отсчитать по ней 5 расстояний между этими звездами. В этом месте рядом с прямой мы увидим звезду, почти одинаковую по яркости со звездами «ковша» – это и есть Полярная звезда.
В созвездии, которое нередко называют Малый Ковш, Полярная звезда является самой яркой. Но так же, как и большинство звезд ковша Большой Медведицы, Полярная — звезда второй величины.
А вот так выглядит звездное небо на 15 сентября, 21 час.
Летний (летне-осенний) треугольник = звезда Вега (α Лиры, 25,3 св. лет), звезда Денеб (α Лебедя, 3230 св. лет), звезда Альтаир (α Орла, 16,8 св. лет)
Небесные координаты
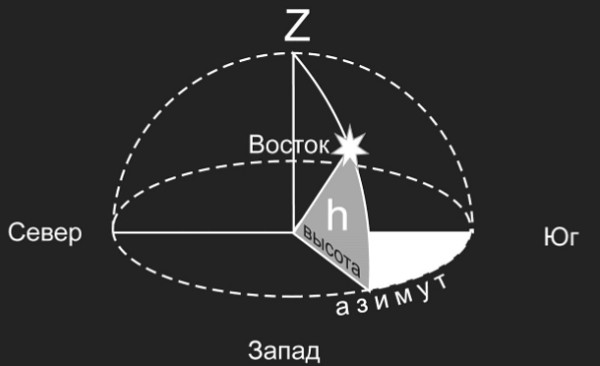
Чтобы отыскать на небе светило, надо указать, в какой стороне горизонта и как высоко над ним оно находится. С этой целью используется система горизонтальных координат – азимут и высота. Для наблюдателя, находящегося в любой точке Земли, нетрудно определить вертикальное и горизонтальное направления.
Первое из них определяется с помощью отвеса и изображается на чертеже отвесной линией ZZ’, проходящей через центр сферы (точку О).
Точка Z, расположенная прямо над головой наблюдателя, называется зенитом.
Плоскость, которая проходит через центр сферы перпендикулярно отвесной линии, образует при пересечении со сферой окружность – истинный, или математический, горизонт.
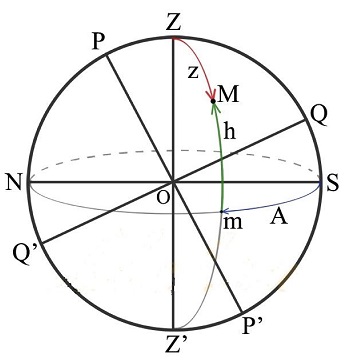
Высота светила отсчитывается по окружности, проходящей через зенит и светило, и выражается длиной дуги этой окружности от горизонта до светила. Эту дугу и соответствующий ей угол принято обозначать буквой h.
Высота светила, которое находится в зените, равна 90°, на горизонте – 0°.
Положение светила относительно сторон горизонта указывает его вторая координата – азимут, обозначаемый буквой А. Азимут отсчитывается от точки юга в направлении движения часовой стрелки, так что азимут точки юга равен 0°, точки запада – 90° и т. д.
Горизонтальные координаты светил непрерывно меняются с течением времени и зависят от положения наблюдателя на Земле, потому что по отношению к мировому пространству плоскость горизонта в данном пункте Земли вращается вместе с ней.
Горизонтальные координаты светил измеряют для определения времени или географических координат различных пунктов на Земле. На практике, например в геодезии, высоту и азимут измеряют специальными угломерными оптическими приборами – теодолитами.
Чтобы создать звездную карту, изображающую созвездия на плоскости, надо знать координаты звезд. Для этого нужно выбрать такую систему координат, которая вращалась бы вместе со звездным небом. Для указания положения светил на небе используют систему координат, аналогичную той, которая используется в географии, — систему экваториальных координат.
Система экваториальных координат сходна с системой географических координат на земном шаре. Как известно, положение любого пункта на земном шаре можно указать с помощью географических координат — широты и долготы.
Географическая широта — это угловое расстояние пункта от земного экватора. Географическая широта (φ) отсчитывается по меридианам от экватора к полюсам Земли.
Долгота — угол между плоскостью меридиана данного пункта и плоскостью начального меридиана. Географическая долгота (λ) отсчитывается вдоль экватора от начального (Гринвичского) меридиана.
Так, например, Москва имеет следующие координаты: 37°30′ восточной долготы и 55°45′ северной широты.
Введем систему экваториальных координат, которая указывает положение светил на небесной сфере относительно друг друга.
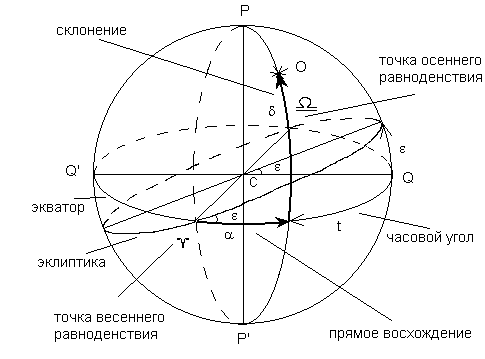
Проведем через центр небесной сферы линию, параллельную оси вращения Земли, — ось мира. Она пересечет небесную сферу в двух диаметрально противоположных точках, которые называются полюсами мира — Р и Р΄. Северным полюсом мира называют тот, вблизи которого находится Полярная звезда. Плоскость, проходящая через центр сферы параллельно плоскости экватора Земли, в сечении со сферой образует окружность, называемую небесным экватором. Небесный экватор (подобно земному) делит небесную сферу на два полушария: Северное и Южное. Угловое расстояние светила от небесного экватора называется склонением. Склонение отсчитывается по кругу, проведенному через светило и полюса мира, оно аналогично географической широте.
Склонение — угловое расстояние светил от небесного экватора. Склонение обозначают буквой δ. В северном полушарии склонения считают положительными, в южном — отрицательными.
Вторая координата, которая указывает положение светила на небе, аналогична географической долготе. Эта координата называется прямым восхождением. Прямое восхождение отсчитывается по небесному экватору от точки весеннего равноденствия γ, в которой Солнце ежегодно бывает 21 марта (в день весеннего равноденствия). Оно отсчитывается от точки весеннего равноденствия γ против часовой стрелки, т. е. навстречу суточному вращению неба. Поэтому светила восходят (и заходят) в порядке возрастания их прямого восхождения.
Прямое восхождение — угол между плоскостью полукруга, проведенного из полюса мира через светило (круга склонения), и плоскостью полукруга, проведенного из полюса мира через лежащую на экваторе точку весеннего равноденствия (начального круга склонений). Прямое восхождение обозначается буквой α
Склонение и прямое восхождение (δ, α) называют экваториальными координатами.
Склонение и прямое восхождение удобно выражать не в градусах, а в единицах времени. Учитывая, что Земля делает один оборот за 24 ч, получаем:
360° — 24 ч, 1 ° — 4 мин;
15° — 1 ч, 15′ —1 мин, 15″ — 1 с.
Следовательно, прямое восхождение, равное, например, 12 ч, составляет 180°, а 7 ч 40 мин соответствует 115°.
Если не нужна особая точность, то небесные координаты для звезд можно считать неизменными. При суточном вращении звездного неба вращается и точка весеннего равноденствия. Поэтому положения звезд относительно экватора и точки весеннего равноденствия не зависят ни от времени суток, ни от положения наблюдателя на Земле.
Экваториальная система координат изображена на подвижной карте звездного неба.
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Лекция № 2. Небесная сфера, её основные точки.
1. Горизонтальные и экваториальные системы небесных координат.
2. Прямое восхождение. Склонение светила.
3. Проведение вечерних астрономических наблюдений звёздного неба.
Небесная сфера. Основные точки, линии и круги на небесной сфере
Небесной сферой называют сферу любого радиуса с центром в произвольной точке пространства. За ее центр, в зависимости от постановки задачи, принимают глаз наблюдателя, центр инструмента, центр Земли и т. д.
Рассмотрим основные точки и круги небесной сферы, за центр О которой принят глаз наблюдателя (рис. 72). Через центр небесной сферы проведем отвесную линию. Точки пересечения отвесной линии со сферой называют зенитом Z и надиром п.
Рис. 72.
Плоскость, проходящую через центр небесной сферы перпендикулярно отвесной линии, называют плоскостью истинного горизонта. Эта плоскость, пересекаясь с небесной сферой, образует окружность большого круга, называемую истинным горизонтом. Последний делит небесную сферу на две части: надгоризонтную и подгоризонтную.
Прямую, проходящую через центр небесной сферы параллельно земной оси, называют ось ю мира . Точки пересечения оси мира с небесной сферой называются полюсами мира. Один из полюсов, соответственно полюсам Земли, называют северным полюсом мира и обозначают Pn, другой — южным полюсом мира Ps.
Плоскость QQ’, проходящую через центр небесной сферы перпендикулярно оси мира, называют плоскостью небесного экватора. Эта плоскость, пересекаясь с небесной сферой, образует окружность большого круга — небесный экватор, который делит небесную сферу на северную и южную части.
Большой круг небесной сферы, проходящий через полюсы мира, зенит и надир, называют меридианом наблюдателя PN nPsZ. Ось мира делит меридиан наблюдателя на полуденную PN ZPs и полуночную PN nPs части.
Меридиан наблюдателя пересекается с истинным горизонтом в двух точках: точке севера N и точке юга S. Прямую, соединяющую точки севера и юга, называют полуденной линией.
Если из центра сферы смотреть в точку N, то справа будет точка востока O st , а слева — точка запада W. Малые круги небесной сферы аа’, параллельные плоскости истинного горизонта, называют альмукантаратами; малые bb’ параллельные плоскости небесного экватора, — небесными параллелями.
Круги небесной сферы Zon, проходящие через точки зенита и надира, называют вертикалами. Вертикал, проходящий через точки востока и запада, называют первым вертикалом.
Круги небесной сферы PNoPs, проходящие через полюсы мира, называют кругами склонения.
Меридиан наблюдателя является одновременно вертикалом и кругом склонения. Он делит небесную сферу на две части — восточную и западную.
Полюс мира, расположенный над горизонтом (под горизонтом), называют повышенным (пониженным) полюсом мира. Наименование повышенного полюса мира всегда одноименно с наименованием широты места.
Ось мира с плоскостью истинного горизонта составляет угол, равный географической широте места.
Положение светил на небесной сфере определяют при помощи сферических координатных систем. В мореходной астрономии применяются горизонтная и экваториальная системы координат.
Представление о небесной сфере возникло в глубокой древности; в основу его легло зрительное впечатление о существовании куполообразного небесного свода. Это впечатление связано с тем, что в результате огромной удалённости небесных светил человеческий глаз не в состоянии оценить различия в расстояниях до них, и они представляются одинаково удалёнными. У древних народов это ассоциировалось с наличием реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды. Таким образом, в их представлении небесная сфера была важнейшим элементом Вселенной. С развитием научных знаний такой взгляд на небесную сферу отпал. Однако заложенная в древности геометрия небесной сферы в результате развития и совершенствования получила современный вид, в котором и используется в астрометрии.
Элементы небесной сферы
Отвесная линия и связанные с ней понятия
Диаграмма, показывающая соотношение зенита , надира и горизонта (в различных определениях). Заметим, что зенит противоположен надиру.
Отвесная линия — прямая, проходящая через центр небесной сферы и точку наблюдения на поверхности Земли. Отвесная линия пересекается с поверхностью небесной сферы в двух точках — зените над головой наблюдателя и надире под ногами наблюдателя.
Истинный (математический) горизонт — большой круг небесной сферы, плоскость которого перпендикулярна к отвесной линии. Истинный горизонт делит поверхность небесной сферы на две полусферы: видимую полусферу с вершиной в зените и невидимую полусферу с вершиной в надире. Истинный горизонт не совпадает с видимым горизонтом вследствие приподнятости точки наблюдения над земной поверхностью, а также по причине искривления лучей света в атмосфере.
Суточное вращение небесной сферы и связанные с ним понятия
Ось мира — воображаемая линия, проходящая через центр мира, вокруг которой происходит вращение небесной сферы. Ось мира пересекается с поверхностью небесной сферы в двух точках — северном полюсе мира и южном полюсе мира . Вращение небесной сферы происходит против часовой стрелки вокруг северного полюса, если смотреть на небесную сферу изнутри.
Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и проходит через центр небесной сферы. Небесный экватор делит небесную сферу на два полушария: северное и южное .
Круг склонения светила — большой круг небесной сферы, проходящий через полюсы мира и данное светило.
Суточная параллель — малый круг небесной сферы, плоскость которого параллельна плоскости небесного экватора. Видимые суточные движения светил совершаются по суточным параллелям. Круги склонения и суточные параллели образуют на небесной сфере координатную сетку, задающую экваториальные координаты светила.
Небесный экватор пересекается с математическим горизонтом в точке востока и точке запада . Точкой востока называется та, в которой точки вращающейся небесной сферы восходят из-за горизонта. Полукруг высоты, проходящий через точку востока, называется первым вертикалом .
Небесный меридиан — большой круг небесной сферы, плоскость которого проходит через отвесную линию и ось мира. Небесный меридиан делит поверхность небесной сферы на два полушария: восточное полушарие и западное полушарие .
Полуденная линия — линия пересечения плоскости небесного меридиана и плоскости математического горизонта. Полуденная линия и небесный меридиан пересекают математический горизонт в двух точках: точке севера и точке юга . Точкой севера называется та, которая ближе к северному полюсу мира.
Годовое движение Солнца по небесной сфере и связанные с ним понятия
P,P’ — полюсы мира, T,T’ — точки равноденствия, E,C — точки солнцестояния, П,П’ — полюса эклиптики, PP’ — ось мира, ПП’ — ось эклиптики, ATQT’- небесный экватор, ETCT’ — эклиптика
Эклиптика — большой круг небесной сферы, по которому происходит видимое годовое движение Солнца . Плоскость эклиптики пересекается с плоскостью небесного экватора под углом ε = 23°26′.
Две точки, в которых эклиптика пересекается с небесным экватором, называются точками равноденствия . В точке весеннего равноденствия Солнце в своём годовом движении переходит из южного полушария небесной сферы в северное; в точке осеннего равноденствия — из северного полушария в южное. Две точки эклиптики, отстоящие от точек равноденствия на 90° и тем самым максимально удалённые от небесного экватора, называются точками солнцестояния . Точка летнего солнцестояния находится в северном полушарии, точка зимнего солнцестояния — в южном полушарии. Эти четыре точки обозначаются символами зодиака , соответствующими созвездиям , в которых они находились во времена Гиппарха (в результате предварения равноденствий эти точки сместились и ныне находятся в других созвездиях): весеннего равноденствия — знаком Овна ( ♈ ), осеннего равноденствия — знаком Весов ( ♎ ), зимнего солнцестояния — знаком Козерога ( ♑ ), летнего солнцестояния — знаком Рака ( ♋ )
Ось эклиптики — диаметр небесной сферы, перпендикулярный плоскости эклиптики. Ось эклиптики пересекается с поверхностью небесной сферы в двух точках — северном полюсе эклиптики , лежащем в северном полушарии, и южном полюсе эклиптики , лежащем в южном полушарии. Северный полюс эклиптики имеет экваториальные координаты R.A. = 18h00m, Dec = +66°33′, и находится в созвездии Дракона , а южный полюс — R.A. = 6h00m, Dec = −66°33′ в созвездии Золотой Рыбы .
Круг эклиптической широты , или просто круг широты — большой полукруг небесной сферы, проходящий через полюсы эклиптики.
Для определения видимого положения небесных тел и изучения их движения в астрономии вводится понятие небесная сфера. Сфера имеет произвольные размеры и произвольный центр. В её центр в точке О помещён наблюдатель, а вращение сферы повторяет вращение небесного свода. Прямая ZOZ′ обозначает отвесную линию для наблюдателя, где бы он не находился. Верхняя точка над головой наблюдателя Z называется Зенит, а противоположная её точка Z′ — называется Надир. Большой круг SWNE перпендикулярен отвесной линии называется истинным горизонтом или математический горизонт. Математический горизонт делит сферу на две половины, видимую и невидимую для наблюдателя. Линия РР′ — называется ось мира, вокруг этой оси происходит вращение небесной сферы. Плоскость ЕQWQ′ перпендикулярна к оси мира называется небесный экватор. Он делит небесную сферу на два полушария – северное и южное. Большой круг небесной сферы PZQSP′Z′Q′N называется небесным меридианом. Небесный меридиан делит небесную сферу на Восточное и Западное полушарие. Линия NOS называется полуденной линией.
Положение основных элементов небесной сферы относительно друг друга зависит от географической широты места наблюдателя. Под углом к плоскости математического горизонта расположена ось мира РР′. Положения светил на небе определяется по отношению к основным плоскостям и связанным с ними линиями и точками небесной сферы и выражается количественно двумя величинами (центральными углами или дугами больших кругов) которые называются небесными координатами.
2 Горизонтальная система координат
Основной плоскостью горизонтальной системы координат является математический горизонт NWSE , а отчёт ведётся от Z зенита и от одной из точек математического горизонта. Одной координатной является зенитное расстояние z (Зенитное расстояние к югу zв = φ – δ; к северу zн = 180 — φ – δ) или высота светила над горизонтом h . Высотой h светила М называется высота вертикального круга mМ от математического горизонта до светила, или центральный угол mOM между плоскостью математического горизонта и направлением на светило М. Высоты отсчитываются от 0 до 90 к зениту и от 0 до -90 к надиру. Зенитным расстоянием светила называется дуга вертикального круга ZM от светила до зенита. z + h = 90 (1). Положение самого вертикального круга определяется дугой координатной – азимутом А. Азимутом А называется дуга математического горизонта Sm от точки юга S до вертикального круга, проходящего через светило. Азимуты отсчитывается в сторону вращения небесной сферы, т.е. к западу от точки юга, в пределах от 0 до 360. Система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов.
3 Первая экваториальная система координат
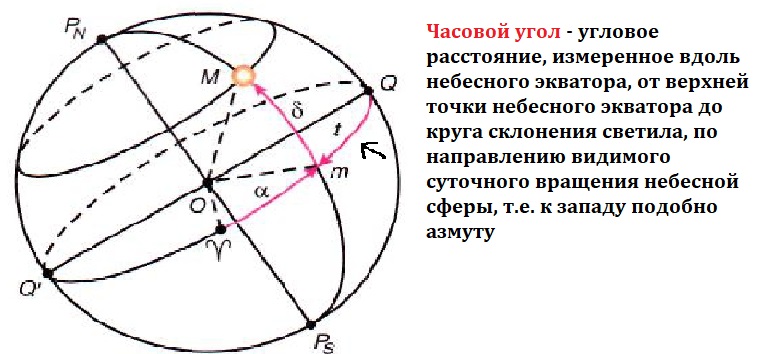
Начало отсчёта – точка небесного экватора Q. Одной координатной является склонение. Склонением называется дуга mM часового круга PMmP′ от небесного экватора до светила. Отсчитываются от 0 до +90 к северному полюсу и от 0 до -90 к южному. p + = 90 . Положение часового круга определяется часовым углом t. Часовым углом светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового круга PMmP′, проходящего через светило. Часовые углы отсчитываются в сторону суточного обращения небесной сферы, к западу от Q в пределах от 0 до360 или от 0 до 24 часов. Система координат используется в практической астрономии для определения точного времени и суточного вращения неба. Определяет Суточное движение Солнца, Луны и других светил.
4 Вторая экваториальная система координат
Одной координатной является склонение , другой прямое восхождение α. Прямое восхождение α светила М называется дуга небесного экватора ♈m от точки весеннего равноденствия ♈ до часового круга, проходящего через светило. Отсчитывается в сторону противоположную суточному вращению в пределах от 0 до до 360 или от 0 до 24 часов. Система используется для определения звёздных координат и составления каталогов. Определяет годичное движение Солнца и других светил.
5 Высота полюса мира над горизонтом, высота светила в меридиане
Высота полюса мира над горизонтом всегда равна астрономической широте места наблюдателя:
- Если склонение светила меньше географической широты, то оно кульминирует к югу от зенита на z= φ – δ или на высоте h= 90– φ + δ
- Если склонение светила равно географической широте, то оно кульминирует в зените и z= 0, а h= + 90
- Если склонение светила больше географической широты, то оно кульминирует к северу от зенита на z=с – φ или на высоте h= 90+ φ – с
6 Условия для восхода и заката светил
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
Читайте также:
- Ошибки при подаче в волейболе кратко
- Химический состав организма кратко
- Опишите закономерность изменения скорости при движении планеты вокруг солнца кратко
- Возвратный лизинг это кратко
- Приготовление блюд из субпродуктов кратко
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Занимаясь исследованиями космоса и неба, учёные установили, что всё вокруг находится в движении.
История возникновения системы координат началась ещё в древности.
Прежде всего, разработка системы координат связана с потребностью ориентирования на местности, и пониманием структуры небесной поверхности.
Для определения расположения и перемещения объектов человечество разработало целую систему методов и способов. Более того, придумали специальные числовые и символичные обозначения.
На самом деле, систем, определяющих точки положения объектов, несколько. Главным образом отличаются они выбором главной плоскости и пунктом отсчёта.
Так как, наблюдая с Земли, мы видим небо в виде сферы, то координаты в астрономии тоже сферические. Кроме того, они представляют некие дуги кругов сферы. Стоит отметить, что исчисляются они в градусах, иногда в часах.
Горизонтальная система координат
В ней математический горизонт выступает главной плоскостью. А полюса составляют зенит и надир.
Горизонтальной системой координат пользуются для наблюдений с Земли. Это возможно и невооружённым глазом, и с помощью телескопа. Наблюдают за звёздами и перемещением объектов на небе. Разумеется, что в рамках Солнечной системы.
Разумеется, наблюдение и измерение происходит постоянно. Потому как движение небесных тел происходит непрерывно.
Некоторые определения системы координат
Отвесная линия представляет собой прямую, проходящую через центр неба. К тому же она совпадает с течением нити отвеса относительно точки наблюдения. Для наблюдателя данная прямая вертикально пересекает центр планеты и место наблюдения.
Зенит и надир это две противоположности. Как известно, отвесная линия пересекается с небом над головой наблюдателя-это и есть зенит. Собственно, надир оказывается полярной по диаметру точкой.
Математический горизонт является огромным кругом небесной сферической поверхности. Его область перпендикулярна отвесной линии. Что важно, он делит всю поверхность неба пополам. Более того, эти части называют видимой и невидимой для наблюдателя. Первая имеет верхнюю точку в зените, а вторая в надире.
В то же время, математический горизонт никогда не соответствует видимому горизонту. Так как, во-первых, поверхность Земли неровная. Как следствие, высшая точка наблюдения разная. А во-вторых, по причине искривления лучей в атмосфере нашей планеты.
Горизонтальные координаты в астрономии составляют высота светила и зенитное расстояние. Помимо этого, есть ещё азимут.
Высота светила это дуга его вертикала от математического горизонта до направления на само светило. Границы высоты к зениту равны от 0° до +90°.и наоборот к надиру, то есть от 0° до — 90°.
Стоит отметить, что зенитное расстояние это дуга вертикала от зенита до светила. Кстати, рассчитывают зенитный отрезок от зенита к надиру в пределах от 0° до 180°.
Азимут, то есть дуга математического горизонта от южной точки до вертикали светила.
Притом азимут отсчитывают к западу от южной точки в пределах от 0° до 360°. А именно в сторону суточного вращения небесной сферы.
Первая экваториальная система координат
За плоскую область в этой системе берётся поверхность экватора неба, а точка отчёта — Q. Помимо того, координаты представляют склонение и часовой угол.
Что такое склонение вы можете узнать тут.
Часовым углом является дуга, которая расположена посередине небесного меридиана и кругом склонения. Граница его измерения от 0° до 360°.
Надо сказать, что применяется первая экваториальная система координат в связи с постоянным движением нашей планеты в течение суток. В связи с этим, местом отсчёта установили точку весеннего равноденствия. Так как она является постоянной относительно звёзд.
Вторая экваториальная система координат
Что интересно, главная плоскость и точка отчёта аналогичны предыдущей системе. Но её координатами выступают склонение и прямое восхождение.
Подразумевается, что восхождение это дуга экватора неба, которая проходит от точки весеннего равноденствия до круга светила. Кроме того, измерение проходит в часовой мере. Однако, её отсчёт ведётся противоположно часовой стрелки.
Между тем, вторая система координат, характеризуется постоянными координатами звёзд. В противовес первой системе, движение Земли за сутки не влияет на них. Применяется она для определения перемещения небесных тел за год.
Важно понимать, что координаты могут быть всегда разными. Поэтому существует множество задач. Их решение возможно с применением, подходящей отдельной ситуации, системой. Вообще, для решения задач и определении координат, очень часто чередуют системы.
Создание систем координат позволило учёным составить карту звёздного неба. Кроме того, обрисовалась определённая структура небесной системы. Что, в значительной мере, способствовало развитию астрономии и астрологии. Помимо того, экваториальные системы координат применяются во многих областях научной деятельности.
Очевидно, что разработка и внедрение определённых систем, составляет основу исследования космического пространства. Мы стараемся максимально приблизиться к его пониманию. Конечно, множество уже применяемых приёмов, расчётов и методов способствует расширению нашего кругозора.
Положение светила
на небе, или вообще какой-либо точки на
сфере, однозначно определяется по
отношению к основным плоскостям и
связанным с ними линиям и точкам небесной
сферы и выражается количественно двумя
величинами (центральными углами или
дугами больших кругов), которые называются
небесными
координатами.
Для решения
разнообразных задач астрономии пользуются
различными системами небесных координат.
Системы эти отличаются одна от другой
выбором основной плоскости и началом
отсчета.
Горизонтальная
система координат.
Основной плоскостью в этой системе
является плоскость математического
горизонта,
а отсчет ведется от зенита и от одной
из точек математического горизонта
(рис. 1.3).

Рис. 1.3.
Горизонтальная система координат.
Одной координатой
является высота
светила над горизонтом h
или зенитное
расстояние z.
Высотой
h
светила М
называется дуга круга высоты mМ
от математического горизонта до светила
или центральный угол mОМ
между плоскостью математического
горизонта и направлением на светило М.
Высоты отсчитываются
в пределах от 0° до +90° к зениту (если
светило находится в видимой части
небесной сферы) и от 0° до 90°
к надиру (если светило находится в
невидимой части небесной сферы).
Зенитным
расстоянием
z
светила М
называется дуга круга высоты ZM
от зенита до светила или центральный
угол ZOM
между отвесной линией и направлением
на светило М.
Зенитные
расстояния отсчитываются в пределах
от 0° до 180° в направлении от зенита к
надиру. Светила, находящиеся в видимой
части небесной сферы, имеют z
90°, а в невидимой части
z
>
90°.
Между
зенитным расстоянием и высотой одного
и того же светила всегда справедливо
соотношение
|
z |
(1.1) |
Светила, находящиеся
на одном альмукантарате, имеют одинаковые
высоты и одинаковые зенитные расстояния.
Положение самого
круга высоты на небесной сфере определяется
другой координатой — азимутом
А. Азимутом
А светила
М
называется дуга математического
горизонта Sm
от точки юга S
до круга высоты, проходящего через
светило, или центральный угол SOm.
Азимуты отсчитываются
в сторону суточного вращения небесной
сферы, т.е. к западу от точки юга S,
в пределах от 0° до 360°. Иногда азимуты
отсчитываются от 0° до +180° к западу
(западные азимуты) и от 0° до 180°
(восточные азимуты).
Светила, находящиеся
на одном круге высоты, имеют одинаковые
азимуты.
Первая экваториальная
система координат.
Основной плоскостью в этой системе
является плоскость небесного экватора
QQ‘,
а началом отсчета — точки небесного
экватора и северный полюс мира (рис.
1.4).
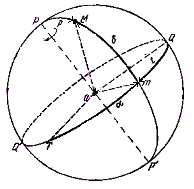
Рис. 1.4.
Экваториальные системы координат.
Одной координатой
является склонение
светила .
Склонением
светила М
называется дуга mМ
круга склонения от небесного экватора
до светила, или центральный угол mОМ
между
плоскостью небесного экватора и
направлением на светило.
Склонения
отсчитываются в пределах от 0° до + 90° к
северному полюсу мира (светило находится
в северном, полушарии небесной сферы)
и от 0° до 90°
к южному полюсу мира (светило находится
в южном полушарии сферы).
Иногда, но весьма
редко, склонение
заменяется полярным
расстоянием
р, т.е. дугой
РМ
круга склонения от северного полюса
мира до светила, или центральным углом
РОМ
между осью мира и направлением на
светило. Полярные расстояния отсчитываются
в пределах от 0° до 180° от северного
полюса мира к южному. Светила, находящиеся
в северном полушарии небесной сферы,
имеют р
< 90°, а в южном полушарии р
> 90°.
Между полярным расстоянием и склонением
одного и того же светила всегда справедливо
соотношение
|
p |
(1.2) |
Светила, находящиеся
на одной суточной параллели, имеют
одинаковые склонения
и одинаковые полярные расстояния р.
Положение самого
круга склонения на небесной сфере
определяется другой координатой —
часовым углом
t.
Часовым углом
t
светила М
называется дуга небесного экватора Qm
от верхней точки Q
небесного экватора до круга склонения,
проходящего через светило, или центральный
угол QOm.
Часовые углы
отсчитываются в сторону суточного
вращения небесной сферы, т.е. к западу
от верхней точки Q
небесного экватора, в пределах от 0° до
360° (в градусной мере) или от 0h
до 24h
(в часовой мере). Иногда часовые углы
отсчитываются от 0° до +180° (от 0h
до +12h)
к западу (западные часовые углы) и от 0°
до 180°
(от 0h
до 12h)
к востоку (восточные часовые углы).
Светила, находящиеся
на одном круге склонения, имеют одинаковые
часовые углы.
Вторая экваториальная
система координат.
Основной плоскостью в этой системе
является также плоскость небесного
экватора, а одной координатой — склонение
(реже — полярное расстояние р).
Другой же координатой,
определяющей положение часового круга
светила, является прямое
восхождение .
Прямым
восхождением
светила М
называется дуга небесного экватора m
(см. рис. 1.4) от точки весеннего равноденствия
до круга склонения, проходящего через
светило, или центральный угол Оm.
Прямые восхождения
отсчитываются в сторону, противоположную
суточному вращению небесной сферы, в
пределах от 0° до 360° (в градусной мере)
или от 0h
до 24h
(в часовой мере).
Светила, находящиеся
на одном круге склонения, имеют одинаковые
прямые восхождения.
Горизонтальные
координаты (z,
h,
А) и часовой
угол светила t
непрерывно изменяются вследствие
суточного вращения небесной сферы, так
как они отсчитываются от неподвижных
точек, не участвующих в этом вращении.
Экваториальные
координаты светила (прямое восхождение
и склонение )
из-за суточного вращения небесной сферы
не меняются, так как они отсчитываются
от точек небесного экватора, которые
сами участвуют в суточном вращении, и
следовательно, положение светила
относительно этих точек не изменяется.
Горизонтальная
система координат используется для
непосредственных определений видимых
положений светил с помощью угломерных
инструментов.
Первая экваториальная
система (склонение и часовой угол)
используется преимущественно при
определении точного времени — одной
из основных задач практической астрономии.
Вторая экваториальная
система является основной при решении
задач фундаментальной астрометрии. В
этой системе составляются списки
звездных положений (звездные каталоги)
и звездные карты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #