1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 1. Страница 86. Номер №8
Решение 1
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
.
Решение 2
Способ 1.
AB = CD = 5 см;
BC = AD = 2 см;
S
A
B
C
D
=
A
B
∗
A
D
=
5
∗
2
=
10
(
с
м
2
)
.
Способ 2.
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
;
S
A
B
C
D
=
S
B
C
K
E
+
S
A
E
K
D
=
4
+
6
=
10
(
с
м
2
)
.
Периметр данного многоугольника можно найти сложив длинны всех его сторон, но для начала придётся найти длинны двух сторон — АВ и АК:
АВ = CD + EK = 2 + 1 = 3 см
AK = BC + DE = 4 + 2 = 6 см
Теперь можно найти периметр всей фигуры:
Р = AB + BC + CD + DE + EK + AK = 3 + 4 + 2 + 2 + 1 + 6 = 18 см
Площадь же многоугольника можно найти, как минимум пятью способами ( правда не уверен, что в третьем классе уже умеют находить площадь трапеций по длинам оснований и высоте — в данном случае трапеции ABCD и ADEK ). Для того, чтобы проще описать способы решения я добавил на чертёж ещё три точки ( впрочем, для разных вариантов решения не все точки потребуются одновременно ).
Вот такой чертёжик у меня получился
Проще всего найти площадь этой фигуры так
S = S(ABEK) — S(CDEH) = AB * AK — CD * DE = 3 * 6 — 2 * 2 = 18 — 4 = 14 см²
Второй способ:
S = S(ABCG) + S(DEGK) = AB * BC + DE * EK = 3 * 4 + 2 * 1 = 12 + 2 = 14 см²
Третий способ:
S = S(BCDF) + S(AFEK) = BC * CD + AK * EK = 4 * 2 + 6 * 1 = 8 + 6 = 14 см²
Четвёртый способ:
S = S(BCDF) + S(AFDG) + S(DEKG) = BC * CD + AG * AF + DE * EK = 4 * 2 + 4 * 1 + 2 * 1 = 8 + 4 + 2 = 14 см²
Ну, и, наконец, пятый способ с трапециями ( извиняюсь, забыл провести на чертеже ещё и AD, впрочем в решении его величина не важна ):
S = S(ABCD) + S(ADEK) = BC * ( AB + CD )/2 + EK * ( DE + AK )/2 = 4 * ( 3 + 2 )/2 + 1 * ( 2 + 6 )/2 = 10 + 4 = 14 см²
Ответ: периметр многоугольника равен 18 см, а его площадь — 14 см²
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
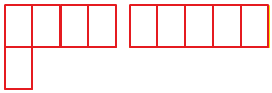
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
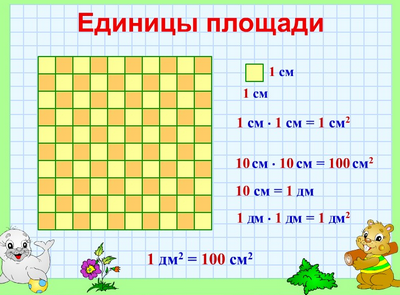
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
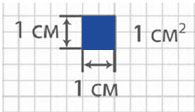
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
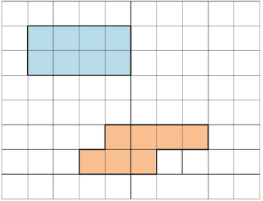
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
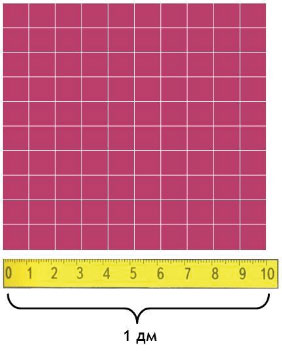
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
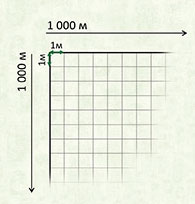
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
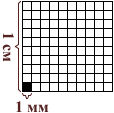
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
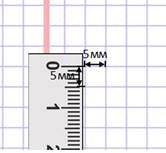
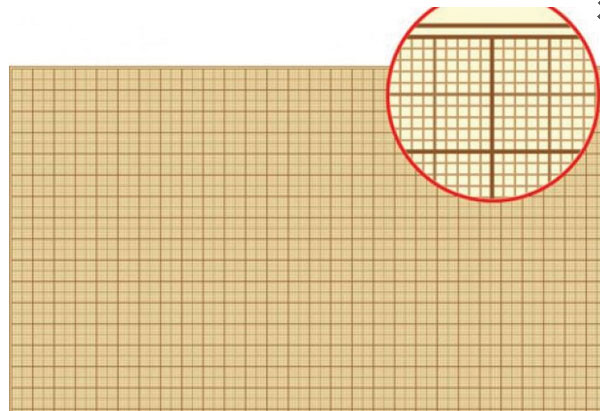
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 40. Урок 16,
Петерсон, Учебник, часть 2
Страница 41. Урок 16,
Петерсон, Учебник, часть 2
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 65. Урок 26,
Петерсон, Учебник, часть 2
Страница 79. Урок 32,
Петерсон, Учебник, часть 2
Страница 85. Урок 35,
Петерсон, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 3
Страница 33. Урок 11,
Петерсон, Учебник, часть 3
Страница 51. Урок 17,
Петерсон, Учебник, часть 3
Страница 52. Урок 18,
Петерсон, Учебник, часть 3
3 класс
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 111,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 11. Урок 5,
Петерсон, Учебник, часть 2
Страница 87. Урок 38,
Петерсон, Учебник, часть 2
Страница 70. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 58. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 115,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 70,
Моро, Волкова, Рабочая тетрадь, часть 2
Математика, 3 класс
Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр
Перечень вопросов, рассматриваемых в теме:
— что такое площадь фигуры?
— какие есть способы сравнения фигур по площади?
— что такое квадратный сантиметр?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
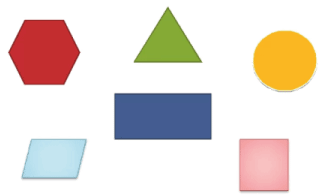
Сравним фигуры и расставим их в порядке убывания их площади.
Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.
В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».
Сравним фигуры и выясним, площадь какой фигуры больше.
Способом сравнения на глаз, определить площадь какой фигуры невозможно.
Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.
Сравним две фигуры.
Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.
Посчитаем количество мерок в фигурах: в синей фигуре содержится 6 мерок, в красной-5 мерок, следовательно, площадь синей фигуры больше площади красной, т. к. в синей фигуре 6 мерок-квадратов, а в красной — 5.
В математике мерка- квадрат. А квадрат со стороной 1 см называется квадратный сантиметр и обозначается см2..
Задания тренировочного модуля:
1.Выберите правильное высказывание:
Площадь фигуры — это…..
1. сумма длин всех сторон
2. внутренняя часть фигуры
Правильный ответ:
2. внутренняя часть фигуры
2. Выделите фигуры с одинаковой площадью.
Правильный ответ:
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5