- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 
и 
— члены отношения; число — предыдущий член отношения; — последующий член отношения.
Например:
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
— отношение числа 
к числу 
;
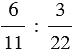
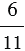
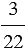
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и 
.
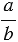
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
.
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
.
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб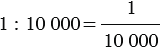 
, то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 
длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 5
10 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 578,
Мерзляк, Полонский, Якир, Учебник
Номер 581,
Мерзляк, Полонский, Якир, Учебник
Номер 608,
Мерзляк, Полонский, Якир, Учебник
Номер 665,
Мерзляк, Полонский, Якир, Учебник
Номер 740,
Мерзляк, Полонский, Якир, Учебник
Номер 792,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 729,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1230,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 230,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 846,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.
(a:b=frac{a}{b}) – так записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член.
Например: отношение 75 к 25 можно записать в виде: (75:25=frac{75}{25}=3).
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Процентное отношение
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: (52:400cdot100%=13 %).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Примеры.
Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий – это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 – 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 (Rightarrow 1100:1200cdot100%=91,7%).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 (Rightarrow 2300:1200cdot100%=191,7%).
2) На сколько процентов перевыполнен план?
(191,7%-100%=91,7%).
Ответ: на 91,7%.
Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение:
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
(150:500cdot 100%=frac{150}{500}cdot 100% )(=frac3{10}cdot 100%=0,3cdot 100%=30%).
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение:
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах: (45:36cdot 100%=1,25cdot 100%=125%).
Онлайн калькулятор для вычисления процентного соотношения чисел.
Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.
Находится по формуле: R%= N1/N2×100%
Пример вычисления процентного соотношение между двумя числами:
Число 540 составляет 49.09% от числа 1100
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
Проценты
- Нахождение процентов от числа
- Нахождение числа по его процентам
- Процентное отношение двух чисел
- Перевод процентов в десятичную дробь
Процент — это одна сотая часть числа. Отсюда следует, что два процента — это две сотых, двадцать процентов — двадцать сотых и так далее.
Слово процент
обозначается знаком %
. Так, 43% какого либо числа означает 43 процента, то есть 
этого числа. Однако стоит обратить внимание, что в вычислениях знак %
не пишется, он может быть записан в условии задачи и в окончательном результате.
Величина, от которой вычисляются проценты (например, цена, длина, количество конфет и т. д.), составляет 100 своих сотых долей, то есть 100%.
Чтобы найти один процент от числа, надо разделить это число на 100.
Пример 1. Найти один процент от числа 300.
Решение:
300 : 100 = 3.
Ответ: Один процент от 300 равен 3.
Пример 2. Найти один процент от числа 27,5.
Решение:
27,5 : 100 = 0,275.
Ответ: Один процент от 27,5 равен 0,275.
Нахождение процентов от числа
Чтобы найти некоторое число процентов от данного числа, нужно данное число разделить на 100 и умножить на число процентов.
Задача 1. В том году в магазине к новому году купили 200 ёлок. В этом году количество купленных ёлок увеличилось на 120%. Сколько ёлок купили в этом году?
Решение: Сначала надо найти 120% от 200, для этого 200 надо разделить на 100, так мы найдём 1%, а затем полученный результат умножить на 120:
(200 : 100) · 120 = 240.
Число 240 — это 120% от 200. Значит, в этом году количество проданных ёлок увеличилось на 240 штук. То есть, количество ёлок, проданных в этом году равно:
200 + 240 = 440 (ёлок).
Ответ: В этом году купили 440 ёлок.
Задача 2. В коробке 28 конфет, 25% конфет с клубничной начинкой. Сколько конфет с клубничной начинкой в коробке?
Решение:
Ответ: В коробке 7 конфет с клубничной начинкой.
Нахождение числа по его процентам
Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на 100.
Задача. Цена метра сукна снизилась на 24 руб., что составило 15% цены. Сколько стоил метр сукна до снижения?
Решение:
Ответ: Метр сукна стоил 160 рублей.
Процентное отношение двух чисел
Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Задача. Завод по годовому плану должен выпустить продукции на сумму 1 250 000 руб. За 1-ый квартал он выпустил её на сумму 450 000 руб. На сколько процентов выполнен заводом годовой план за 1-ый квартал?
Решение:
Ответ: За 1-ый квартал план выполнен на 36%.
Перевод процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на 100.
Пример 1. Представить 25% в виде десятичной дроби.
Решение:
25 : 100 = 0,25.
Ответ: 25% — это 0,25.
Пример 2. Выразить 100% десятичной дробью.
Решение:
100 : 100 = 1.
Ответ: 100% — это 1.
Пример 3. Выразить 230% десятичной дробью.
Решение:
230 : 100 = 2,3.
Ответ: 230% — это 2,3.
Из данных примеров следует, что для перевода процентов в десятичные дроби, надо в числе, стоящем перед знаком %
, перенести запятую на два знака влево.