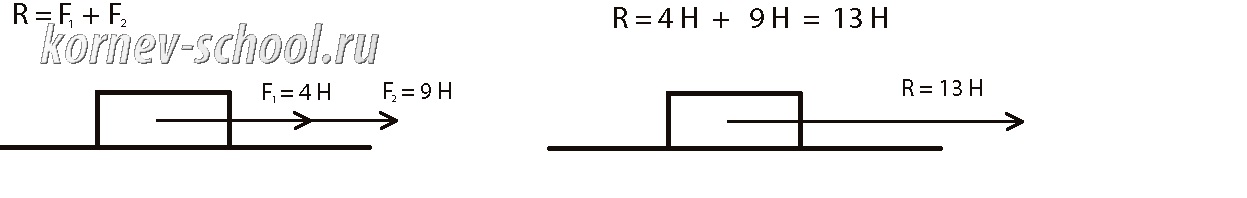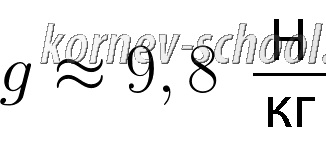Вопрос о том, как найти центростремительную силу, часто задают. Ответ на него таков: центростремительная сила — это сила, которая в основном требуется для приведения тела в движение по круговой траектории.
В этой статье мы увидим, как найти центростремительную силу, которая отвечает за круговое движение тела. Когда тело сталкивается с круговым движением, оно поддерживается центростремительной силой, которая регулируется центром оси вращения.
Допустим, мяч движется по прямолинейному пути и воспринимает нормальную силу и ускорение, необходимые для движения вперед. Когда он испытывает кривая в пути он автоматически будет иметь действие другой силы.
Нормальная сила в линейном движении эквивалентна весу объекта, который включает в себя массу и влияние гравитации. Но когда говорят, что тело движется по круговой траектории, потребуются дополнительные количества, которые способствуют этому движению.
Компания величина нормальной силы будет больше на криволинейном пути по сравнению с линейным путем. центростремительная сила будет иметь нормальную силу вместе с ней, которая имеет значение больше, чем у линейного движения.
Компания влияние гравитации при круговом движении происходит из-за наличия центростремительной силы. Эта центростремительная сила всегда действует внутрь. Когда солнце находится в движении, оно всегда направлено внутрь, к орбите и оси вращения.
Как найти формулу центростремительной силы?
Мы должны знать, что на самом деле означает сила, а затем погрузиться в тему центростремительной силы. Сила – это величина, необходимая для приведения тела в движение.
Формула общей силы фактически получена из второго закона Ньютона. То есть ф=ма. Сила — это просто произведение массы на ускорение.
Центростремительная сила не какая-то новая сила, а существующая сила в виде нескольких других сил в различных аспектах. Формула центростремительной силы имеет много факторов, которые ей помогают.
Во-первых, поскольку это круговое движение, тело совершает обороты. Теперь число оборотов называют частотой. Эта революция также рассчитывается с точки зрения периода времени.
Один оборот рассчитывается по периоду времени и равен обратной частоте. Итак, число оборотов = частота; период времени одного оборота t= 1/частота.
Когда все факторы собраны вместе, мы получаем полную формулу для центростремительной силы как fc=мв2/r, где m=масса; v= скорость; г = радиус.
Радиус на самом деле определяется окружностью кругового пути, который аналогичен расстоянию и смещению при прямолинейном движении.
Как найти центростремительную силу с массой и радиусом?
Из обычной формулы для центростремительной силы мы знаем, что масса, скорость и радиус являются факторами, влияющими на центростремительную силу.
Центростремительная сила находится в прямой зависимости от массы объекта, скорости его движения при круговом движении и радиуса кругового движения. При прямолинейном движении значение нормальной силы меньше, чем при круговом движении.
Масса в нормальной силе удерживается гравитацией и кажется меньше по сравнению с круговым движением. Когда тело привязано к веревке в центре оси масса также должна тянуться таким же образом.
Компания равнодействующая сила действуя на тело, заставит другую силу, подобную этой, действовать на тело. Когда тело тянут круговым движением, оно образует почти идеальный круг, и это только если смотреть сверху.
Когда это движение образует правильную окружность, длина окружности дает расстояние и перемещение, аналогичное линейному движению. От чего образуется диаметр, в свою очередь находится и радиус поворота.
Теперь мы можем найти центростремительную силу, используя массу и радиус с массой и радиусом, и формула будет такой же, как и обычная,
Fc= мв2/r
Давайте рассмотрим несколько задач, в которых масса и радиус играют главную роль в определении центростремительной силы.
1 задачи:
Кривая траектории имеет радиус кривизны 0.5 м при массе тела 2 кг. Приравняйте центростремительную силу всей системы, если скорость равна 5 м/с.
Решение:
Fc=мв2/r
Fc= 100 Н
2 задачи:
Мяч имеет радиус 2.5 м и весит 10 кг. Мяч вращается со скоростью 12 м/с. Найдите центростремительную силу, с которой он движется.
Решение:
Fc=мв2/r
Fc= 576 Н
Как найти центростремительную силу без массы?
Вообще существует ошибочное мнение, что центростремительная одна отдельная сила, которая приводит тело в движение по круговой траектории.
Центростремительная — это сила притяжения к центру кругового движения, которая может быть любой формой силы, скажем, силой гравитации, силой натяжения и так далее. Эта сила представляет собой всего лишь усилие, прикладываемое к объекту для того, чтобы он оставался в круговом движении.
Допустим, мяч привязан к веревке, прикрепленной к гвоздю. Когда мяч совершает круговое движение, его фактически вызывает струна, и в струне создается натяжение. Но сила направлена внутрь так сила натяжения в этом случае рассматривается центростремительная сила.
Идеология центростремительной силы состоит в том, что это просто сила, которая изображает работу другой силы, когда линейное движение. Для пример когда масса привязан к центру оси вращения, на него будет действовать сила.
Когда масса совершает круговое движение, она образует правильную окружность, и на нее действует сила, которую можно измерить. сила натяжения так как струна имеет натяжение. Тогда он будет иметь направленную вверх силу, так как его притягивает сила гравитации.
Следовательно, центростремительную силу можно найти без массы через силу натяжения. гравитационный сила, сила трения.
Как найти центростремительную силу без скорости?
Как мы уже обсуждали в предыдущей подтеме относительно определения центростремительной силы без учета массы.
Если объект совершает круговое движение, на него будет действовать сила, обеспечиваемая нормальной силой, аналогичной линейному движению. Когда объект привязан к центру вращения, его движение вызывается силой, действующей на элемент, удерживающий объект в целости.
Теперь эта сила может быть тангенциальной силой, потому что существует струна, действующая как система поддержки объекта, которая удерживает его в движении по круговой траектории. Поскольку сила натяжения действует по касательной к движущемуся объекту, она рассматривается как центростремительная сила.
На пути, по которому движется тело, совершая круговое движение, трение будет меньше или равно нулю. Таким образом, учитывая силу натяжения системы, центростремительную силу можно найти без скорости, соответственно.
Рассмотрим пример, когда центростремительная сила находится без учета скорости. Объект движется с постоянной скоростью по круговой траектории. Центростремительная сила находится через силу натяжения, и это значение должно быть найдено. Значение массы 2 кг.
Когда масса движется по кругу, она также управляется сила гравитации быть неразрывным с движением. Т=мг; Т= 2х9.8; Т= 19.6 Н. Вот как решается простая задача с использованием формулы силы натяжения для расчета центростремительной силы.
Как найти центростремительную силу с угловой скоростью?
При любом круговом движении нам нужно знать факторы или величины, которые помогают в самом круговом движении.
Угловая скорость также известна как радиальная скорость, которая приводит тело в движение. Это в основном будет определять количество оборотов в секунду, а также количество оборотов, совершаемых в секунду.
Центростремительная сила и угловая скорость идут рука об руку, когда тело движется по окружности. Отсюда мы можем легко узнать, как найти центростремительную силу с угловой силой.
Сначала нужно вывести формулу центростремительной силы, которая ФК=МВ2/r. Здесь фактор v2/r это центростремительное ускорение что аналогично формуле ж=мА; fc=m (а); ФК=МВ2/r. Расширив эту формулу, мы получим часть угловой скорости.
С v2/r это центростремительное ускорение мы можем разбить формулу дальше с точки зрения скорости. Формула для центростремительное ускорение ас=v2/r. расширяя это, мы получаем формулу угловой скорости, то есть ас=rω2, (ω=vr).
Теперь, когда мы знаем, как найти центростремительную силу через угловой скорости легче определить центростремительное ускорение также в таких случаях.
Как найти центростремительную силу по радиусу?
Формула для центростремительной силы с точки зрения радиуса дается как fc=mv2/r. В этом случае радиус определяется окружностью кругового пути.
Мы разработаем несколько примеров, где радиус находится при заданной центростремительной силе. Мы также увидим, как на центростремительную силу влияют радиус и масса объекта.
Когда радиус кругового пути мал, кривая клятвы будет острой и образует изгиб шпильки в виде кривой.
1 задачи:
Мотоцикл массой 200 кг тащит вокруг столба высотой 12 м со скоростью 10 м/с. 12 м также можно считать радиусом кругового движения, если столб согнут и ровно стоит на земле. Рассчитайте центростремительную силу по приведенным выше значениям?
Решение:
Fc=mv2/r
Fc= 1666.6 Н
2 задачи:
Шарик массой 5 кг привязан к нити, которая образует радиус 0.25 м от окружности кругового движения. Сила, действующая на мяч, вызывает его движение по окружности со скоростью 9 м/с. Определите центростремительную силу, действующую внутрь, а также действующую как сила притяжения.
Решение:
Fc=mv2/r
Fс=1620Н
Часто задаваемые вопросы
Как рассчитать центростремительную силу с радиусом и временем?
Радиус вызывает определенное количество силы, которая помогает телу двигаться. Разбивая формулу (fc=mv2/r), мы придем к периоду времени движения.
Например, скажем, что объект массой 10 кг движется со скоростью 2 м/с по круговой траектории радиусом 0.6 м, и ответом на это будет 66.6 Н. Теперь, нарушая формулу, мы приходим к центростремительное ускорение ac=v2/r, далее разбивая формулу на несколько шагов, мы окончательно приходим к формуле периода времени (t=1/f). Частота – это, по сути, мера количества оборотов, совершаемых телом при круговом движении..
Что вызывает центростремительную силу?
Компания круговое движение любого объекта вызовет центростремительное заставить действовать.
Центростремительная сила — это в основном сила притяжения, которая действует радиально внутрь окружности. Это не какая-то особая сила, а форма любых других сил, которые действуют по касательной к объекту при круговом движении.
Куда направлена центростремительная сила?
Направление центростремительной силы всегда направлено к оси вращения.
Центростремительная сила всегда направлена к оси вращения кругового движения, другими словами, она действует радиально внутрь. Эта сила также соответствует второму закону Ньютона, где сила определяется произведением массы на ускорение.
Модуль равнодействующей силы
Четверг, 24 декабря, 2015
В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.
Как найти модуль равнодействующей силы
Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.
Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.
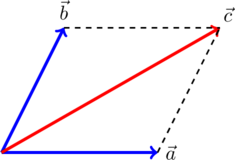
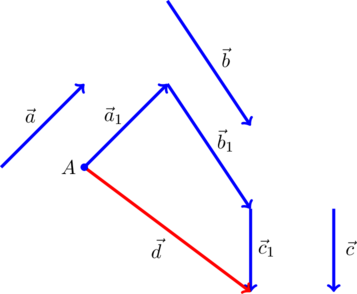
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и
. Суммарный вектор есть вектор
:
Если векторы и
не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор
заменен на равный ему вектор
, и
:
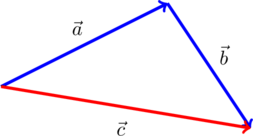
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы и
. В сумме получается вектор
:
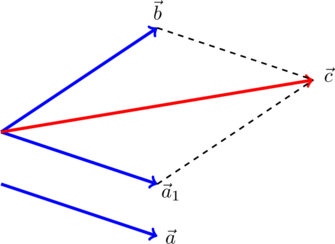
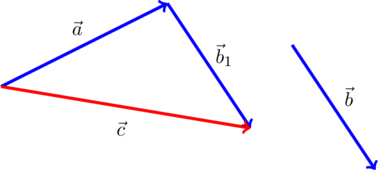
Если вектор отложен не от конца вектора
, нужно заменить его равным и отложенным от конца вектора
, после чего воспользоваться правилом треугольника. Например, на рисунке вектор
заменен равным ему вектором
, и
:
3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки
в конец последнего отложенного вектора. На рисунке
:
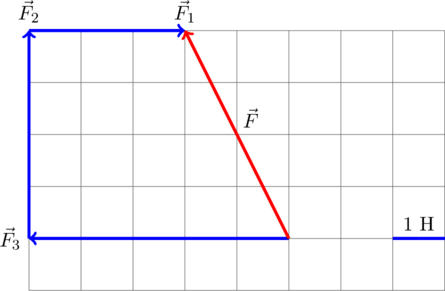
Задача на нахождение модуля равнодействующей силы
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.
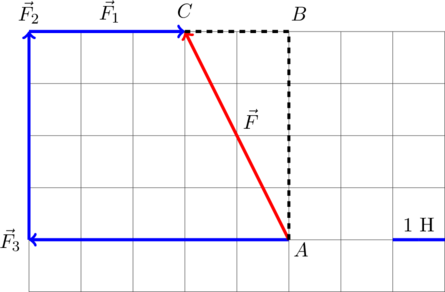
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:
Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :
Требуется найти гипотенузу этого треугольника. «По клеточкам» находим длину катетов:
Н,
Н. Тогда по теореме Пифагора для этого треугольника получаем:
Н. То есть искомый модуль равнодействующей сил равен
Н.
Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич
В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.
Что такое равнодействующая
Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.
Результат сложения может дать:
- вектор, имеющий длину,
- или вектор, не имеющий длины.
Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.
Длина вектора содержит сумму квадратов всех его проекций на оси.
В частности, для вектора ускорения (vec{a}), лежащего на плоскости xOy, длина вычисляется так
[ large left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2}} ]
Где ( a_{x} ) и ( a_{y} ) — это проекции вектора (ссылка) ( vec{a} ) на оси Ox и Oy.
Когда вектор равен нулю, равна нулю каждая его проекция на осях.
Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.
Прочитайте подробнее о параметрах векторов.
Левая часть силового уравнения
В левой части силового уравнения записываем силы, действующие на тело.
Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.
Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».
Правая часть силового уравнения
В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.
Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.
Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.
Тогда в правой части уравнения запишем:
- (ma), если ускорение направлено туда же, куда направлена ось;
- (- ma), если ускорение направлено противоположно оси;
А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.
В правой части уравнения запишем ноль (0 = ускорения нет).
Векторы сил параллельны
В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.
Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.
Рис. 1. Парашютист спускается на парашюте, векторы сил направлены вдоль единственной оси
Проведем на рисунке ось, направим ее вверх.
Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.
Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:
[large F_{text{сопр}} — m cdot g ]
Сила ( F_{text{сопр}}) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.
В правую часть уравнения поместим равнодействующую.
Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.
Математики запишут, что ускорение есть, но оно – нулевое (vec{a}=0).
То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.
Примечания:
- На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec{v_{0}}). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
- На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.
Итоговое силовое уравнение имеет вид:
[large F_{text{сопр}} — m cdot g = 0 ]
Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.
Векторы сил не параллельны
Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.
Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).
Рис. 2. Равнозамедленное движения тела по горизонтальной шероховатой поверхности
Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.
Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.
Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.
Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.
Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.
Так выглядит уравнение для горизонтальной оси
[large -F_{text{трен}} = -m cdot a_{x} ]
Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.
Для вертикальной оси уравнение выглядит так:
[large N — m cdot g = 0 ]
Система, пригодная для решения задачи, состоит из двух уравнений
[ large boxed{ begin{cases} -F_{text{трен}} = -m cdot a_{x} \ N — m cdot g = 0 end{cases} } ]
Куда направить оси
Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).
Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.
Рис. 3. Большая часть векторов не лежит на осях, такие векторы придется раскладывать на проекции, чтобы составить силовые уравнения
Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.
Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.
Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.
Рис. 4. Большая часть векторов лежит на осях, раскладывать на проекции нужно только один вектор, силовые уравнения будут иметь простой вид
При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.
Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.
Выводы:
- Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
- Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.
Движение по наклонной плоскости
Составим систему уравнений для решения такой задачи:
Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.
Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.
Выражение для ускорения
Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)
Рис. 5. Велосипедист едет в гору по инерции, отмечены силы, действующие на велосипедиста, видно, что при таком выборе осей необходимо разложить вектор mg на проекции
Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.
Пользуясь осями координат, составляем теперь уравнения в проекциях.
Уравнение для проекций векторов на ось Ox:
[ large — F_{text{трен}} – m cdot g_{x} = — m cdot a ]
Уравнение для проекций векторов на ось Oy:
[ large N – m cdot g_{y} = 0 ]
Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.
[ large begin{cases} m cdot g_{y} = mg cdot cos left(alpha right) \ m cdot g_{x} = mg cdot sin left(alpha right) end{cases} ]
Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений
[ large begin{cases} — F_{text{трен}} – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end{cases} ]
Дополним эту систему выражением для силы трения.
[ large F_{text{трен}} = mu cdot N ]
Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.
[ large begin{cases} N = mg cdot cos left(alpha right) \ F_{text{трен}} = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end{cases} ]
Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:
[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]
Выражение для пройденного пути
Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:
[ large begin{cases} 0 = v_{0} — a cdot t \ S = v_{0} cdot t — a cdot frac{t^2}{2} end{cases} ]
Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.
[ large begin{cases} t = frac{v_{0}}{a} \ S = v_{0} cdot frac{v_{0}}{a} — a cdot frac{1}{2} cdot frac{v_{0}}{a} cdot frac{v_{0}}{a} end{cases} ]
Упрощенная система для решения задачи теперь включает всего два уравнения
[ large begin{cases} mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_{0} cdot frac{v_{0}}{a} — frac{v_{0}}{2} cdot frac{v_{0}}{a} end{cases} ]
Подставив в эту систему известные значения начальной (v_{0}) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.
Сила обозначается буквой F
Сила измеряется в Ньютонах [Н]
Равнодействующая сила это сила, которой можно заменить
действие нескольких сил.
Если силы сонаправлены, то равнодействующая равна
их сумме R = F1 + F2
На рисунке две силы 4Н и 9Н заменены одной силой 13Н
Если силы разнонаправлены, то равнодействующая равна разности этих сил R = F1 — F2
Равнодействующая направлена в сторону большей силы
Сила тяжести

g это ускорение свободного падения, в расчетах будем округлять до 10
1. На тело действуют вправо две силы: F1 = 3Н и F2 = 8Н.
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
2. На тело действует вправо сила F1 = 7Н и влево сила F2 = 3Н .
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
3. На автомобиль действует сила тяги F1 = 700Н и сила
сопротивления воздуха F2 = 700Н .
Сделать рисунок с расстановкой сил, определить
равнодействующую силу.
Показать решение
4. На тело вдоль одной прямой действуют три силы: F1 = 7Н ,
F2 = 3Н и F3 =10Н.
Чему может быть равна равнодействующая сила ?
Сделать рисунки с расстановкой сил для всех вариантов,
определить
равнодействующие силы.
Показать решение
Загрузить PDF
Загрузить PDF
Сила – это физический термин, который определяется как воздействие, заставляющее объект изменять свою скорость, направление движения или вращаться. Сила может ускорять объект под действием толчка или тяги. Отношение между силой, массой и ускорением было определено Исааком Ньютоном во втором законе движения, который гласит: сила, действующая на объект, равна произведению его массы на ускорение. Если вы хотите узнать, как измерить силу, следуйте данной пошаговой инструкции.
-
1
Разберитесь в соотношении между силой, массой и ускорением. Сила, действующая на объект – это произведение его массы на ускорение. Это соотношение можно представить в виде следующей формулы: Сила = Масса x Ускорение. Далее приведены другие положения, которые нужно иметь в виду при расчете силы:[1]
- Стандартная единица измерения массы — килограммы (кг).
- Стандартная единица измерения ускорения — м/с2.
- Стандартная единица измерения силы – ньютон (Н). Ньютон – это производная стандартная единица измерения. 1N = 1 кг x 1м/с2.
-
2
Измерьте массу заданного объекта. Масса объекта – это количество содержащейся в нем материи. Масса объекта всегда неизменна, неважно на какой планете он находится, тогда как вес меняется в зависимости от силы притяжения; ваша масса одинакова и на Земле, и на Луне.[2]
В метрической системе массу можно выражать в граммах в граммах или килограммах. Скажем, объект, с которым мы имеем дело – это грузовик, масса которого – 1000 кг.- Чтобы найти массу заданного объекта, поместите его на тройные рычажные или двойные чашечные весы. При этом будет получена масса в килограммах или граммах.
- В английской системе единиц измерения масса может быть выражена в фунтах. Поскольку сила также может быть выражена в фунтах, с целью уточнения использования данной величины был придуман термин «фунт-масса». Однако если вы нашли массу объекта с использованием фунтов в английской системе, то будет лучше перевести ее в метрическую систему. Зная массу объекта в фунтах, вы можете перевести ее в килограммы просто умножив значение на 0,45.
-
3
Измерьте ускорение объекта. В физике ускорение определяется как изменение скорости, т.е. скорость в определенном направлении в единицу времени. Кроме общепринятого определения ускорения как повышения скорости, оно также может подразумевать замедление объекта или изменение направления его движения. Подобно измерению скорости с помощью спидометра, ускорение можно измерить акселерометром. Пусть ускорение грузовика массой 1000 кг, с которым мы имеем дело, составляет 3м/с2.
- В метрической системе скорость выражается в сантиметрах в секунду или в метрах в секунду, а ускорение – в сантиметрах в секунду за секунду (сантиметрах в секунду в квадрате) или в метрах в секунду за секунду (метрах в секунду в квадрате).
- В английской системе единиц измерения одним из способов выражения скорости являются футы в секунду, т.е. ускорение будет выражаться в футах в секунду в квадрате.
-
4
Умножьте массу объекта на ускорение. В результате вы получите значение силы. Просто подставьте известные числа в уравнение и вы узнаете силу объекта. Не забудьте указать ответ в ньютонах (Н).[3]
- Сила = Масса x Ускорение
- Сила = 1000 кг x 3м/с2
- Сила = 3000Н
Реклама
-
1
Найдите массу, зная силу и ускорение. Если вы знаете силу и ускорение объекта, то просто подставьте их в ту же формулу и найдете массу объекта. Вот как это сделать:
- Сила= Масса x Ускорение
- 3Н = Масса x 3м/с2
- Масса = 3Н/3м/с2
- Масса = 1 кг
-
2
Найдите ускорение, зная силу и массу. Если вы знаете силу и массу объекта, просто подставьте их в ту же формулу, чтобы найти ускорение объекта. Вот как это сделать:
- Сила= Масса x Ускорение
- 10Н = 2 кг x Ускорение
- Ускорение = 10Н/2кг
- Ускорение = 5м/с2
-
3
Найдите ускорение объекта. Если вы хотите найти силу объекта, вы можете вычислить его ускорение, зная массу. Все, что вам нужно сделать – это воспользоваться формулой для нахождения ускорения объекта.[4]
Формула имеет вид (Ускорение = Конечная скорость — Начальная скорость)/Время.- Пример: Бегун развивает скорость 6 м/с за десять секунд. Каково его ускорение?
- Конечная скорость составляет 6 м/с. Начальная скорость равна 0 м/с. Время равно 10 с.
- Ускорение = (6 м/с — 0 м/с)/10с = 6м/с/10с = 0,6м/с2
Реклама
Советы
- Если вы работаете с английскими единицами, то разделите ответ на коэффициент пересчета. Как было отмечено выше, в английской системе «фунт» может быть единицей измерения как силы, так и массы. Когда фунт используется в качестве единицы силы, его называют «фунт-сила». Коэффициент пересчета равен 32,174 фунт-футов делить на фунт-силу за секунду в квадрате; 32,174 – это ускорение свободного падения на Земле в футах в секунду в квадрате. (Для упрощения вычислений, мы округлим это значение до 32)
- Обратите внимание, что взаимосвязь силы, массы и ускорения означает, что объект с малой массой и высоким ускорением может обладать такой же силой, что и объект с большой массой и низким ускорением.
- Массу можно выражать в слагах. Один слаг равен 32,174 фунтов массы. Слаг – это количество массы, которую сила в 1 фунт ускоряет на 1 фут в секунду в квадрате. При умножении массы в слагах на ускорение в футах в секунду в квадрате коэффициент перевода не используется.
- Масса 20 г, движущаяся с ускорением 5 сантиметров в секунду в квадрате, несет силу 20 умножить на 5, или 100 грамм-сантиметров в секунду в квадрате. (Грамм-сантиметр на секунду в квадрате называется диной).
- Так, масса 640 фунтов массы, движущаяся с ускорением 5 футов в секунду в квадрате несет силу приблизительно 640 умножить на 5 поделить на 32 или 100 фунтов силы.
- Вес – это выражение массы, на которую действует ускорение свободного падения. У поверхности Земли это ускорение примерно равно 9,8 метров в секунду в квадрате (9,80665), или 32 футов в секунду в квадрате (32,174). Так, в метрической системе 100 килограмм массы весят около 980 ньютонов, а 100 грамм массы – около 980 дин. В английской системе масса и вес могут быть выражены одной и той же единицей, поэтому 100 фунтов массы весят 100 фунтов силы. Поскольку пружинные весы измеряют силу притяжения объекта, они фактически измеряют вес, а не массу. (В повседневном обиходе разницы между этими понятиями нет, пока единственной силой притяжения в рассматриваемом вопросе является таковая на поверхности Земли).
- Масса 150 килограмм, движущаяся с ускорением 10 метров в секунду в квадрате несет силу 150 умножить на 10, или 1500 килограмм-сантиметров в секунду в квадрате. (Килограмм-метр в секунду в квадрате называется ньютон).
- Силы могут иметь специальные названия в зависимости от того, как они действуют на объект. Сила, которая ускоряет объект, называется тягой, тогда как сила, замедляющая объект, носит название торможения. Сила, изменяющая то, как объект вращается вокруг своей оси, называется моментом.
Реклама
Что вам понадобится
- Рычажные или пружинные весы
- Акселерометр
- Карандаш и бумага или калькулятор
Об этой статье
Эту страницу просматривали 35 246 раз.