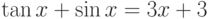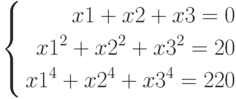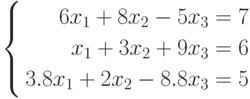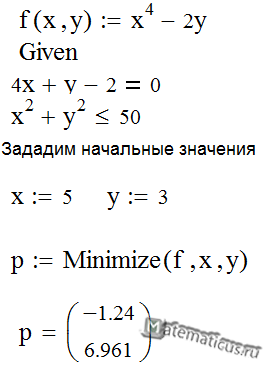4.4. Задачи оптимизации
В программе MathCAD с успехом решаются задачи оптимизации. Задача оптимизации (линейного программирования) — определение значений аргументов функции, при которых функция имеет экстремальное (минимальное, максимальное) значение. Условия, налагаемые на аргументы функции — заданные ограничения. Используется методика решения системы уравнений помощью блока Given. При этом вместо функции Find используется функция Maximize(), если определяется максимум, и функция Minimize() , если определяется минимум оптимизируемой функции. Последовательность действий следующая:
- ввести оптимизируемую функцию,
- определить начальные значения аргументов,
- в блоке Given ввести уравнения (неравенства) ограничений,
- ввести функцию Maximize () (Minimaze() ),
- определить решение.
Задача решается в алгебраическом и матричном виде. В матричном виде начальное значение корней, ограничения задаются в виде матриц. Решение в обоих случаях получается в виде матрицы.
Пример 4.11
Найти максимум функции
при ограничениях
Листинги решения в алгебраическом и матричном виде.
Оптимизируемая функция – поиск максимума,
Начальные значения:
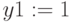
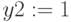
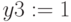
Ограничения:
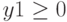
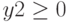
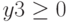
Решение:
Максимальное значение функции:
Матрица коэффициентов функции:
Матрица левых частей ограничений:
Матрица правых частей ограничений:
Начальные значения:
Решение:
Максимальное значение функции:
Основные итоги
В лекции представлены методы численного решения уравнений и систем уравнений с использованием функций MathCAD. Рассмотрены функция Root (), функция для поиска корней полинома polyroots(), вычислительные блоки Given .Find() и Given Minerr().. Описано численное решение систем линейных уравнений, а также способы аналитического решения : с помощью матриц, функции lsolve(), символьного оператора solve. Показано решение задач оптимизации.
Задания для самостоятельного выполнения
- Построить графики функций. Решить уравнения с применением функции root()
а)
для
б)
в)
(2 корня)
- Решить с применением функции polyroots() следующие уравнения
а)
б)
- Решить системы уравнений с использованием блока Given Find(.)
а)
найти 3 корня
б)
найти 2 корня
в)
г)
д)
- Решить систему уравнений тремя способами.
Ключевые термины
root() – функция для численного решения нелинейного уравнения с одним неизвестным. Возвращает с заданной точностью значение переменной, при котором функция равна нулю.
polyroot() — функция для численного поиска корней полинома. Возвращает вектор длиной n+1 всех корней полинома степени n.
Given Find() – вычислительный блок для численного решения нелинейных уравнений и систем уравнений.
Given Minerr() вычислительный блок для приближенного численного решения нелинейных уравнений и систем уравнений.
Maximize () – функция для поиска значений переменных функции, при которых функция имеет максимальное значение.
Minimaze() — , функция для поиска значений переменных функции, при которых функция имеет минимальное значение.
lsolve(A,B) — функция аналитического решения системы линейных уравнений, представленной в виде AX=B.
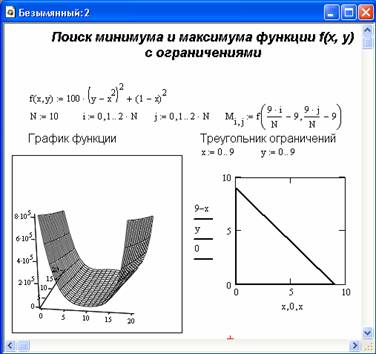
Теперь рассмотрим решение задачи на поиск минимума и максимума с применением функций Maximize и Minimize. Первая часть документа, реализующая решение данной задачи, представлена на рисунке 4.2. Здесь показано задание самого уравнения, построение графика функции и геометрическое представление ограничительных условий. Тут полезно особо отметить, что решение задачи оптимизации с ограничениями в принципе намного сложнее, чем без таковых. Алгоритм решения данной задачи с применением средств Mathcad показан на рисунке 4.3. Следует отметить, что функция Minimize (или Maximize) может вычислять минимум (или максимум) как при отсутствии ограничений, так и при их наличии.
Рис. 4.2 Начало документа с решением задачи поиска минимума и максимума функции с учетом ограничений
Объективности ради надо заметить, что результаты решения сильно зависят от выбора начальных значений переменных и далеко не всегда имеют устраивающую пользователя погрешность.
Рис. 4.3 Конец документа с решением задачи поиска минимума и максимума функции с учетом ограничений
Пример решения задачи оптимизации в программе Mathcad
Пример
Дана нелинейная целевая функция
f(x,y)=x4–2y→min
Ограничения
4x+y–2=0
x2+y2≤50
Решение
Для поиска минимального или максимального значения функции в Mathcad имеются функции:
Minimize(f, x1, x2, …xn)
Maximize(f, x1, x2, …xn)
f — функция без аргументов для максимизации и минимизации значений;
x1, x2, …xn — скалярные переменные, найденные в системе уравнений.
Записываем решение в пакете Mathcad
3073
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
В самом обширном смысле под оптимизацией понимается поиск наилучшего решения из числа данных. Определение «оптимальный» чаще всего понимают как благоприятный, максимальный (минимальный), наиболее результативный и др. Каждый из нас ежедневно, решает вопрос: как достичь наилучшего результата, обладая ограниченными ресурсами. В современном мире образовались математические модели, с помощью которых описывают различные ситуации на языке математики. Единым для всех моделей являлось то, что в них поиск наилучших вариантов сводился к поиску экстремального значения функции. Данные модели стали назваться экстремальными задачами, а функции – оптимизируемые.
Известный ученый И. Бернулли дал основание исследованию экстремальных задач – вариационному исчислению. В вариационном исчислении исследуется отбор экстремумов функционалов, установленных на множестве непрерывных функций. Главный труд в решение задач на условный экстремум, привнес известный ученый Ж. Лагранж. Его принцип популярен и в наше время, как в практических, так и в теоретических исследованиях. Сформулированы универсальные способы решения задач линейного программирования [3].
Изучение математических моделей оптимизации производится в разной вариации. Использование этих методов в первую обуславливается от вида самой модели, ее размерности и т.д. Математическая модель – это совокупность соотношений описывающих данную задачу, ее ограничения, целевую функцию. На практике применяют разные способы решения экстремальных задач. Основные способы анализа моделей оптимизации: численное моделирование, аналитический способ, методы случайного поиска.
Аналитический метод, предоставляет наглядную картину процесса и его характеристик. Создание модели – сложная задача. Цель исследователя заключается в том, чтобы в ходе выстраивания математической модели можно было ее исследовать аналитическими методами. Изучение при помощи численных методов и ЭВМ менее наглядно. По сравнению с аналитическими, класс моделей, подходящих для анализа численными методами, существеннее обширней. Итоги изучений очень громоздкие в сравнении с аналитическими методами нуждаются большой вычислительной деятельности. В связи с внедрением компьютеров и современного программного обеспечения данный способ находит все большее использование. Из числа численных методов широкое использование приобрели методы дихотомии, золотого сечения, Фибоначчи, методы покоординатного спуска и т.д. Анализ при помощи методов случайного поиска подразумевает моделирование различных явлений без изменения их логической структуры и расположения во времени с применением случайных процессов и величин.Рассмотрено решение некоторых оптимизационных задач, в том числе и задач линейного программирования, в средах математического пакета Mathсad. А так же табличный процессор Excel имеющий развитые средства, позволяющие решать разнообразные задачи оптимизации, с помощью встроенной функции: поиск решения.
1. Общая задача оптимизации
1.1 Классификация задач оптимизации
С учетом типа целевой функции и соотношения ограничений выделяют различные задачи оптимизации.
1. По типу параметров задачи оптимизации. Выделяют непрерывные задачи оптимизации дискретные и целочисленные.
2. По условию размерности допустимого множества параметров D. Задачи оптимизации по этому условию делятся на задачи одномерной и многомерной оптимизации.
3. По условию наличия или отсутствия ограничений на вероятное множество D. Различают задачи условной и безусловной оптимизации. Данный показатель классификации может относиться, как к одномерным, так и к многомерным задачам оптимизации.
4. По характеру ограничений. Различают детерминированную оптимизацию и стохастическую. Если множество допустимых значений включает случайные компоненты, то имеет место стохастическое программирование. При этом стохастическая оптимизация можно отнести и к дискретной задаче.
5. По виду целевой функции и виду ограничений. Выделяют линейное и нелинейное программирование. Задача одномерной безусловной оптимизации.
Ограничения отсутствуют, т.е. задача без ограничений с одномерным вектором. Вид f(x) произвольный.
Задача многомерной безусловной оптимизации
.
Ограничений нет, – любого вида.
Задача условной многомерной оптимизации
.
Задача линейного программирования
Целевая функция – линейна, ограничения тоже линейны. Наиболее известные классические задачи линейного программирования: транспортная задача, задача о диете и другие.
Задача целочисленного программирования.
В задачах целочисленного программирования компоненты вектора {x} принимают только целые значения. В зависимости от ограничений и вида целевой функции различают задачи оптимизации, классификация которых показана на рисунке 1.
Рисунок 1 – Классификация задач оптимизации
Задачи нелинейного программирования подразделяются так, как показано на рисунке 2.
.
Рисунок 2 – Классификация задач нелинейного программирования
Эта классификация выполнена по виду нелинейности целевой функции, при этом предполагалось, что ограничения f(x) – линейны.
.
1.2 Постановка задач оптимизации
Чтобы решить оптимизационную задачу необходимо найти наилучшее решение среди возможных вариантов. Объекты оптимизации – различные устройства, процессы и ситуации, согласно к которым необходимо решить задачу оптимизации. Методы оптимизации занимаются построением оптимальных решений для математических моделей, при этом сам вид модели определяется методом, используемым для построения оптимального решения. Для решения любой задачи достаточно представить объект оптимизации в виде математической модели. Математическая модель – модель, которая определена с поддержкой математических формализмов, сама модель не является точной, а является идеализацией. Для постановки задач оптимизации необходимо учитывать заданную последовательность:
Первый пункт – установление границ. Система это отдельная часть внешнего мира. Параметры системы задают пределы, которые ограничивают ее от внешнего мира. При этом подразумевается, что взаимосвязи с внешним миром закреплены. С целью получения адекватного решения необходимо дополнить в систему дополнительные подсистемы, однако это приведет к росту размерности задачи. Необходимо стремиться к представлению системы в виде отдельных подсистем.
Второй пункт – подбор количественного условия. Он дает возможность выявить лучший вариант, называемый характеристическим условием. Условия бывают технологического или экономического характера. Условие, установленное в качестве характеристического, должно принимать максимальное (или минимальное) значение для самого лучшего варианта. Условий может быть
любое количество, тогда задача становится многокритериальной. Для приведения многокритериальных задач к однокритериальной достаточно одного из условий выбрать как первичным, а остальные оставить вторичными. Изначальное условие используется как характеристическое, а вторичные формируют ограничения задачи.
Третий пункт – определение внутрисистемных переменных. Через них проявляется характеристическое условие. Подбор переменных происходит с учетом рекомендаций. Следует разбить переменные, которые меняются на большом интервале и переменные, которые статичны или изменяется слабо. Первые – это независимые переменные, а вторые – параметры задачи. Параметры задачи разделяют на фиксированные, которые испытывают случайное отклонение под воздействием вешней среды. Необходимо выбрать только те переменные, которые оказывают наибольшее воздействие на характеристический критерий.
Четвертый пункт – создание модели. Модель будет описываться как взаимосвязь внутри системных переменных, а сама модель системы представляет связь между переменными и отображает степень воздействия этих переменных на характеристическое условие. В модель входят главные уравнения материальных и энергетических балансов; уравнения, описывающие физически значений переменных.
Характеристики оптимизации – это изменение при оптимизации величины, входящие в математическую модель объекта оптимизации, а сами соотношения, устанавливающие пределы возможного изменения этих параметров – ограничениями, ограничения задаются в форме равенств или неравенств [1].
Несмотря на разнообразные постановки задачи, структура оптимизационной задачи однотипна и включает следующие компоненты:
1. Целевая функция – мерного векторного аргумента
т.е.
2. Ограничения в виде неравенств
3. Ограничения в виде равенств
4. Область допустимых значений
Задача оптимизации в общем виде: ;
Ограничения первого рода ;
Ограничения второго рода ; .
2 Линейное программирование
Линейное программирование – это раздел прикладной математики, посвященный способам нахождения наибольших или наименьших значений линейной функции многих переменных, т.е. функций вида:
Причем переменных должны удовлетворять дополнительным условиям, имеющим вид линейного уравнения
или линейных неравенств вида:
Или
,
где – действительные числа.
Обычно в задачах линейного программирования на переменные налагаются еще условия не отрицательности: .
Линейная функция zназывается целевой функцией или функцией цели, а дополнительное условие называются ограничениями. Построение математической модели задачи выполняются в следующем порядке:
1. Вводятся переменные величины задачи, т.е. такие величины, заданием числовых значений которых однозначно определяется один из вариантов исследуемого процесса.
2. Основываясь на условия задачи, выводятся ограничения, которым должны соответствовать введенные значения, при этом нужно учитывать, чтобы каждое условие было учтено.
3. Создается целевая функция, то есть линейная функция переменных задачи, которая в математической форме выражает условие выбора оптимального варианта.
Переменные величины задачи задаются не единственным способом. От их выбора зачастую зависит сложность математической модели, вследствие этого и удобство ее анализа. В элементарных задачах, подбор переменных вытекает из условий задачи
.
1.2 Графический метод решения задачи линейного программирования
Графическим методом можно решать задачу с двумя переменными с ограничениями в виде неравенств. Пусть требуется решить задачу
(2.1)
(2.2)
(2.3)
Т.е. найти такие значения , которые удовлетворяют системе ограничений, и максимизирует линейную функцию (2.1).
Каждое неравенство определяет в плоскости полуплоскость с граничной прямой т.е. точки , лежащие в этой полуплоскости, удовлетворяют данному неравенству, которое представлено на рисунке 3.
Рисунок 3
Неравенство определяют соответственно правую и верхнюю полуплоскости.
Область допустимых решений образуется целым рядом точек пересечения полуплоскостей, которые представлены на рисунке 4. Любая точка данного многоугольника будет являться решением системы ограничений или планом задачи линейного программирования. Область допустимых решений может быть как ограниченной областью, так и неограниченной или даже выражаться прямой, либо точкой [10].
Рисунок 4
В случае если система ограничений несовместима, то область допустимых
значений пустая, отсюда, при пересечении полуплоскостей, не образуется общей, для всей области. Любое решение графической задачи начинают с построения многоугольника решений, который представлен на рисунке 5. После того, как многоугольник построен – находится такая его точка , которая дает целевую функцию z, достигающую максимума.
Рисунок 5
При фиксированном значении равенство
Представляет собой уравнение прямой . Так называемой линией уровня, для всех точек которой функция принимает одно и то же значение .
Если перемещать эту прямую в направлении вектора , являющегося градиентом функции , то соответствующее значение функции будет возрастать. В случае ограниченного многоугольника решений линия уровня при ее перемещении дважды становится опорной по отношению к многоугольнику. Главная прямая для многоугольника – это прямая, которая содержит одну или несколько точек пересечения с многоугольником, а все оставшиеся точки многоугольника лежат по одну сторону этой прямой. Одна из этих главных прямых соответствует минимуму функции z ,а другая – максимум
z в области допустимых решений.
Оптимальным планом называется точка . Это и есть результат решения задачи линейного программирования. Главная прямая всегда проходит хотя бы через одну угловую точку решений многоугольника, отсюда, оптимальному плану будет удовлетворять угловая точка. Линия уровня, которая подходит оптимальному плану, иногда совпадает со стороной многоугольника решений. В таком случае оптимальное решение не уникально – здесь имеет место альтернативный оптимум.
2.2 Задача линейного программирования
Предприятие химической промышленности выпускает соляную и серную кислоту. Выпуск одной тонны соляной кислоты – 25 денежных единиц выпуск одной тонны серной кислоты – 40 денежных единиц. Для выполнения государственного заказа необходимо выпустить не менее 200 т соляной и не менее 100 т серной кислоты. Кроме того, необходимо учитывать, что выпуск кислот связан с образованием опасных отходов. При выпуске одной тонны соляной кислоты образуется 0,5 т опасных отходов, при выпуске одной тонны серной кислоты – 1,2 т опасных отходов. Общее количество опасных отходов не должно превышать 600 т, так как превышение этого ограничения приведет к выплате предприятием крупного штрафа. Требуется определить, сколько соляной и серной кислоты должно выпустить предприятие, чтобы получить максимальную прибыль.
1. Составим математическую модель задачи. Для этого введем переменные. Обозначим через — количество выпускаемой соляной кислоты, через – количество серной кислоты.
2. В данной задаче требуется определить производство кислот, при котором доход будет максимальным. Доход от выпуска одной тонны соляной кислоты составляет 25 денежных единиц. Следовательно, доход от выпуска соляной кислоты составит денежных единиц. Доход от выпуска серной кислоты составит денежных единиц. Таким образом, общая прибыль от выпуска кислот составит денежных единиц. Необходимо найти такие значения переменных , при которых эта величина будет максимальной. Таким образом, целевая функция для данной задачи будет иметь следующий вид:
3. Составим ограничения, связанные с необходимостью выполнения государственного заказа.
А. Предприятию необходимо выпустить не менее 200 тонн соляной кислоты и 100 тонн серной кислоты. Это ограничение можно записать следующим образом:
.
Б. Переменные по своему физическому смыслу не могут принимать отрицательных значений, так как они обозначают количество выпускаемых кислот. Поэтому необходимо учитывать ограничения не отрицательности:
.
В. Составим ограничение на небезопасные отходы. При выпуске одной тонны соляной кислоты образуется 0,5 тонн опасных отходов; значит, общее количество опасных отходов при выпуске соляной кислоты составит тонн. При выпуске серной кислоты образуется тонн опасных отходов. Таким образом, общее количество опасных отходов будет иметь вид:
.
Таким образом, целевая функция и ограничения образуют математическую модель рассматриваемой задачи.
На рисунках представлено аналитическое и графическое решение задачи линейного программирования. Оптимизационные задачи решаются в Mathcad с помощью встроенных функций: Given, Maximize, Minimize, а в MS EXCEL с помощью надстройки поиск решения.
Рисунок 6 – Mathcad-документ решения ЗЛП
Рисунок 7 – Excel-документ аналитическое решение ЗЛП
Рисунок 8 Excel-документ графическое решение ЗЛП
3 Классические методы нахождение экстремума
3.1 Условия существования экстремума
Функция f(x) определенна на множестве D, достигает своего глобального минимума в точке в том и только в том случае, если
Если можно указать ℇ — окрестность точки, в которой выполняется условие то говорят, что функция f(x) имеет на множестве D локальный минимум. Локальных экстремумов на интервале D может быть несколько.
Функция является унимодальной на отрезке , если любой её локальный минимум на отрезке одновременно является и глобальным.
Функция f(x), определенная на интервале , называется выпуклой, когда для любых двух точек выполняется неравенство Иенсена, которое представлено на рисунке 9. Прямая соединяющая две точки лежит выше всех значений функции .
Рисунок 9 – Геометрическая иллюстрация неравенства Иенса
Свойства выпуклых функций:
1. Хорда, соединяющая две любые точки выпуклой функции, проходит выше графика функций в интервале между этими точками.
2. Производная возрастает при увеличении .
3. .
4. Для выпуклой функции локальный экстремум всегда является глобальным.
5. Функция f(x) является вогнутой на интервале тогда и только тогда, когда – f(x) есть выпуклая функция на этом интервале.
6. Касательная – в любой точке интервала лежит ниже графика функции f(x).
Если функция имеет несколько экстремумов, то она является мульти модальной.
Стационарной точкой функции называется точка , в которой:
Бывает несколько видов стационарных точек, которые представлены на рисунке 10.
Рисунок 10 – Типы стационарных точек
Необходимые условия экстремума.
Для того, чтобы дифференцируемая на функция имела в точке локальный экстремум необходимо, чтобы точка являлась стационарной.
Достаточные условия экстремума.
Пусть в точке производные функции f(x) обращаются в нуль, а производная порядка отлична от нуля, тогда:
Если n – нечетное, то — точка перегиба;
Если n – четное, то — точка локального экстремума, и если эта производная больше нуля, то — локальный минимум, а если эта производная меньше нуля, то — локальный максимум.
Методика нахождения экстремума на интервале. На основании сказанного можно сформулировать следующий алгоритм для исследования дифференцируемой функции на максимум и минимум:
1. Ищем первую производную функции
2. Находим критические точки первого порядка; для этого:
а) приравниваем первую производную нулю и находим действительные корни полученного уравнения .
б) находим значения х, при которых производная терпит разрыв.
3. Исследуем знак производной слева и справа от критических точек.
4. Вычисляем значение функции f(x) при каждом критическом значении аргумента, при переходе которого производная меняет свой знак, находя экстремальные значения [5].
Ниже на рисунке 11 приведен пример нахождения экстремума функции одной переменной с помощью пакета Matchad.
Рисунок 11 – Mathcad-документ нахождение экстремумов функции одной переменной
3.2Наибольшее и наименьшее значение функции на отрезке
Функция принимает свой максимум и минимум, только в том случае, когда она определена и непрерывна на отрезке . Считается, что на отрезке эта функция содержит конечное число критических точек. Когда максимум достигается внутри отрезка , то значение подразумевается одним из максимумов функции – наибольшим максимумом. Также может быть, что минимум достигается на одном из концов отрезка. Функция на отрезке может достигать наибольшее значение на одном из концов этого отрезка или во внутренней точке этого отрезка, которая является точкой максимума. Подобное можно сказать и о наименьшем значении функции: оно достигается или на одном из концов данного отрезка, или во внутренней точке этого отрезка, которая является точкой минимума. Чтобы найти наибольшее и наименьшее значение на
отрезке необходимо:
1. Найти первую производную функции .
2. Найти все критические точки первого порядка .
3. Установить значения функции в критических точках, принадлежащих отрезку .
4. Определить значения функции на концах отрезка.
5. Из всех полученных выше значений функции подобрать наибольшее и наименьшее – они и будут представлять собой наибольшее и наименьшее значения функции на отрезке .
На рисунке 12 показан способ нахождения наибольшего и наименьшего значения функции одной переменной в пакете Mathcad.
Рисунок 12 – Mathcad-документ наибольшее и наименьшее значение на заданном отрезке
3.3 Безусловный экстремум функции многих переменных
1. Необходимое условие экстремума.
Говорят, что функция нескольких переменных , определенная в некоторой окрестности точки ,имеет в этой точке локальный максимум(минимум),если существует такая проколотая окрестность точки a,что для любой точки выполнено неравенство
.
Понятия локального минимума и локального максимума функции объединяют под общим названием экстремум функции.
Если неравенства являются строгими, то говорят о строгом экстремуме функции.
2. Необходимое условие экстремума функции.
Пусть функция нескольких переменных имеет в точке экстремум. Если функция имеет в точке а частную производную первого порядка по переменному то эта частная производная равна нулю:
Пусть рассмотрим действительную функцию одного действительного переменного t, которая получается, если у функции закреплены все переменные, кроме i, равногоt. Функция в точке имеет локальный экстремум. В самом деле, пусть, например, имеет в точке, а локальный минимум. Тогда существует такая проколотая окрестность точки а, что при
Но в таком случае что соответствует определению локального максимума функции одного переменного. Функция дифференцируема в точке , так как функция имеет в точке а частную производную по переменному . При этом Согласно необходимому условию локального экстремума для функции действительного переменного, выполнено равенство , следовательно, .
Пусть функция нескольких переменных имеет в точке экстремум, тогда:
Если в точке, а определен градиент функции , то он равен нулю: .
Если функция дифференцируема в точке а, то .
Из сказанного выше вытекает, что точки экстремума функции нескольких переменных надо искать либо среди точек, в которых стационарных точек, либо среди точек, в которых градиент не определен. Все точки, в которых градиент функции равен нулю или не определен, называют критическими точками.
3. Достаточное условие экстремума.
Для того, чтобы произвести изучение стационарных точек на экстремум нужно проанализировать дифференциал второго порядка. Дифференциал второго порядка функции для нескольких переменных является квадратичной формой касательно приращений независящих друг от друга переменных.
4. Достаточное условие экстремума функции.
Пусть функция нескольких переменных определена в окрестности точки a, дважды непрерывно дифференцируема в тогда:
Если квадратичная форма в точке, а положительно определенная, то в этой точке функция имеет строгий локальный минимум.
Если квадратичная форма в точке, а отрицательно определенная, то в этой точке функция имеет строгий локальный максимум.
Если квадратичная форма в точке, а знакопеременная, то в этой точке функция не имеет экстремума.
Вид квадратичной формы определяется критерием Сильвестра или приведением к каноническому виду. Если функция двух переменных, то условие экстремума вместе с критерием Сильвестра приводят к элементарным правилам проверки
Предположим, что функция дважды дифференцируема в окрестности точки и в этой же точке выполнено необходимое условие экстремума функции, т.е.
В точке матрица Гессе
Для частных производных в фиксированной точке часто используют обозначения:
При помощи этих обозначений дифференциал второго порядка функции и матрица Гессе записывается следующим образом:
5. Достаточное условие экстремума для функции двух переменных.
Пусть функция определена в окрестности дважды непрерывно дифференцируема в тогда:
Еслито в точке функция имеет строгий локальный минимум.
Еслито в точке функция имеет строгий локальный максимум.
Если , то функция не имеет в точке экстремума.
По критерию Сильвестра, второй дифференциал является положительно определенной квадратичной формой.
Если и второй дифференциал является отрицательно определенной квадратичной формой.
Если . То в итоге, квадратичная форма вырождена,
Если , в этом случае квадратичная форма вырождена, но сохраняет знак, так как квадратичный трехчлен
По переменному или переменному имеет нулевой дискриминант и поэтому представляет собой полный квадрат.
Например: при имеем
Исследование функций на экстремум.
Задачу исследования функции нескольких переменных на экстремум часто записывают в виде
Решение таких задач делят на два этапа:
Этап первый: происходит отбор критических точек на основании необходимых условий экстремума.
Этап второй: каждая отобранная точка исследуется на экстремум. Исследование проводиться при достаточных условиях экстремума или при помощи прямого анализа функции в пределах исследуемой точки.
На рисунке 13 представлено решение по нахождению безусловного экстремума функции двух переменных в пакете Matchad с помощью встроенных функций Given и Find.
1. Определим функцию z(x,y)и найдем производные первого порядка.
2. Найдем стационарные точки с помощью служебного слова Given.
3. Найдем частные производные второго порядка и их значение в стационарных точках и .
4. Найдем значение дискриминанта в стационарных точках.
Рисунок 13 – Mathcad-документ нахождение экстремума функции двух переменных
3.4Условный экстремум
Понятие условного экстремума.
Рассмотрим функцию двух переменных . При отыскании экстремумов данной функции иногда необходимо найти их не на всей области определения ,а только на некотором ее подмножестве, например на линии .
Таким образом, перед нами становится задача поиска на линии Gточки . В этой точке значение функции считается наибольшим или наименьшим согласно с ее значениями в других точках линии G,находящихся вблизи точки .
Рассмотрим функцию при условии, что ее аргументы являются связанными между собой соотношениями, которые называются уравнениями связи.
(3.1)
И пусть координаты точки удовлетворяют данной системе уравнений.
Считают, что функция имеет в точке условный минимум(максимум) при условиях связи (3.1) ,если существует такая – окрестность точки ,что для любой точки , координаты которой удовлетворяют уравнениям (3.1), выполняется неравенство
В отличие от безусловной точки экстремума, значение функции в точке условного экстремума сравнивается с ее значениями не во всех точках некоторой – окрестности точки , а только в тех ее точках, которые
связаны между собой условиями связи.
1. Метод исключения части переменных.
Далее рассматривается задача нахождения условного экстремума для функции двух переменных. Предположим, что требуется отыскать локальный экстремум функции с условием, что x и y соответствуют уравнению связи .
Если уравнение связи разрешается относительно y, то есть y выражается как , то функция принимает . Далее вычисляется значение x, при котором достигает экстремума, затем определяется y из уравнения связи. После этого находятся точки условного экстремума. Аналогичный ответ получится, если уравнение можно решить относительно переменной x, т.е. x вывести как функцию y.
Если условие связи задается параметрическими уравнениями . Подставляя x и y в аналитическое выражение функции , приходим к задаче отыскания экстремума функции одной переменной. Однако если уравнение связи нельзя разрешить относительно какой-либо одной из переменных и представить параметрическими уравнениями, данная задача значительно усложняется.
1. Метод множителей Лагранжа.
Рассмотрим задачу нахождения условного экстремума функции , не разрешая уравнение связи относительно x или y. Для этого используем метод множителей Лагранжа.
Введем вспомогательную функцию, называемую функцией Лагранжа:
,
— левая часть уравнения связи, λ — неопределенный постоянный множитель, называемый множителем Лагранжа.
Функция может иметь максимум или минимум при тех значениях x , при которых производная обращается в нуль.
Учитывая, что уравнение разрешимо относительно найдем полную производную функции которая в точках экстремума обращается в нуль:
Продифференцировав уравнение связи по x , получим
отсюда
. (3.2)
Этому равенству удовлетворяют все точки x , y , лежащие на линииG, задаваемой уравнением связи . Умножив все члены этого равенства на неизвестный коэффициент λ и сложив их с соответствующими членами равенства (3.2), получим:
или
(3.3)
Равенство (3.3) выполняется во всех точках локального экстремума, лежащих на линии G. Подберем неопределенный множитель λ так, чтобы для значений x и y , соответствующих экстремуму функции , коэффициент обратился в нуль. Тогда выражение тоже обратится в нуль. Таким образом, точки локального экстремума, лежащие на линии G , задаваемой уравнением связи , должны удовлетворять следующим условиям:
(3.4)
.
Из уравнений видно, что левые части уравнений являются частными производными функции по переменным x , y , λ .Решив систему (3.4), найдем критические точки и вспомогательное число λ.
Система уравнений (3.4) представляет собой необходимые условия существования условного экстремума: не любая критическая точка координаты которой удовлетворяют системе уравнений (3.4), будет точкой условного экстремума. Для изучения характера критической точки необходимо провести дополнительный анализ знака приращения в окрестности критической точки , лежащей на линии G.
Правило нахождения точек условного экстремума. Для того чтобы определить точки условного экстремума функции , удовлетворяющие уравнению связи , необходимо:
1. Составить функцию Лагранжа
2. Вычислить частные производные функции Лагранжа по переменным x, y, λ;
3. Приравняв нулю найденные производные, составить систему уравнений (4); решив ее, можно определить координаты критических точек P возможного условного экстремума;
4. Определить знак приращения в окрестностях критических точек по тем точкам окрестности, которые удовлетворяют уравнению , т.е. лежат на линии L.
Если выполняется условие,то
— точка условного минимума.
Есливыполняется условие е
— точка условного максимума.
На рисунке 14 показано решение по нахождению условного экстремума в пакете Matchad с помощью встроенной функции Given.
Рисунок 14 – Mathcad-документ нахождение условного экстремума функции двух переменных
3.5 Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Пусть, функция определена и непрерывна в замкнутой области D. Отсюда в этой области функция достигает максимум и минимум своих значений. Эти значения могут достигаться или в самой области D, или на ее границе. Точки максимума и минимума также называют точками абсолютного или глобального экстремума. Когда максимум или минимум находятся внутри области, их называют точками локального экстремума функции Следовательно, функция z принимает максимум или минимум, то ее точки считаются или точками локального экстремума, или граничными точками. Для того, чтобы найти максимум и минимум функции в замкнутой области D надо:
1. Вычислить значения функции в точках возможного экстремума, принадлежащих области D.
2. Найти наибольшее и наименьшее значения на ее границе.
3. Сравнить найденные значения и выбрать наибольшее и наименьшее.
Допустим, что граница области D задана уравнением . Задача нахождения наибольшего и наименьшего значений функции на границе области D сводится к отысканию наибольшего и наименьшего значений функции одной переменной, так как уравнение границы области D связывает переменные x и y между собой. Следовательно, если разрешить это уравнение относительно одной из переменных или представить его в параметрическом виде и подставить выражения в уравнение , то придем к задаче нахождения наибольшего и наименьшего значений функции одной переменной. Если же уравнение нельзя разрешить ни относительно x , ни относительно y , а также невозможно представить его параметрическими уравнениями, то задача сводится к отысканию условного экстремума[3].
ЗАКЛЮЧЕНИЕ
Предметом данной курсовой работы служат классические методы нахождения экстремума. В процессе выполнения работы обоснованы актуальность использования методов оптимизации, классических методов нахождения экстремума и специализированных математических пакетов при решении задачи линейного программирования, определены цели и задачи исследования, предмет и объект исследования. Подробно рассмотрен безусловный экстремум функции многих переменных. Для каждого метода приведен пример с подробным решением в средах математического пакета Mathcad. А так же табличный процессор Excel имеющий развитые средства, позволяющие решать разнообразные задачи оптимизации, с помощью встроенной функции: поиск решения.
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ
1. Аверьянова С.Ю., Растеряев Н.В. Содержательные задачи линейного программирования и их решение с помощью ЭТ MS EXCEL и пакета MATHCAD: учебное пособие/ Южный федеральный университет. – Ростов-на-Дону: Издательство ЮФУ, 2014. – 132 с.
2. Растеряев, Н.В., Герасименко Ю.Я. Решение оптимизационных задач в среде MATHCAD и EXCEL: Учеб. пособие – Новочеркасск: Южно-российский гос. тех. ун-т (НПИ), 2004.- 100 с.
3. Шадрина, Н.И. Решение задач оптимизации в Microsoft Excel 2010 : учеб. пособие / Н.И. Шадрина, Н.Д. Берман. – Хабаровск : Издательство Тихоокеан. гос. университета, 2016. – 101 с.
4. Пантелеев, А.В. Методы оптимизации в примерах и задачах: Учеб. пособие/ А.В. Пантелеев, Т.А. Летова. – 2-е изд., исправл. – М.: Высш. шк., 2005. – 544 с.
5. Семенкин, Е.С. Методы оптимизации: Учеб. пособие по циклу практических знаний. Красноярск 2007. – 105 с.
6. Кочегурова, Е.А. Теория и методы оптимизации / Е.А. Кочегурова; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2012. – 157 с.
7. [Электронный ресурс] – Режим доступа: – 2011. – Режим доступа: http://www.optimiz.ru/catalog/poisk, свободный.
8. Аббасов, М.Э. Методы оптимизации: Учеб. пособие / Аббасов М.Э. – СПб.: Издательство «ВВМ», 2014. – 64 с.
9. Бирюков, Р.С., Городецкий С.Ю., Григорьева С.А . Методы оптимизации в примерах и задачах : Учебно — методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2010. – 101 с.
10. Габасов Р., Кириллова Ф. Качественная теория оптимальных процессов. М.: Наука, 1971. — 508 с.
11. [Электронный ресурс] – Режим доступа: 2011. – Режим доступа: http://www.alest.info/catalog/f1/, свободный.


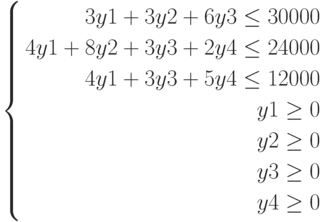

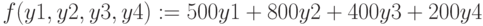


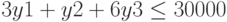

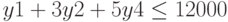
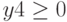

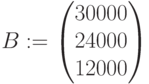
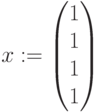
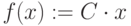



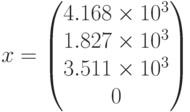
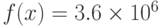
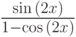 для
для 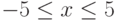
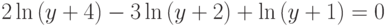
 (2 корня)
(2 корня)
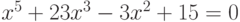
 найти 3 корня
найти 3 корня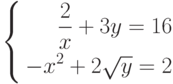 найти 2 корня
найти 2 корня