В статье рассмотрены основные возможности mathcad 15 для работы с матрицами
- Ввод матриц
- Перемножение матриц
- Транспонирование матриц
- Обратные матрицы
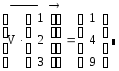
- Выделение строки и столбца матрицы
Ввод матрицы
Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку «Matrix or vector». В появившемся окне нужно ввести количество строк и столбцов и нажать OK
Рис. 1. Ввод матрицы
Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2
Рис. 2. Заполнение матрицы
Перемножение матриц
Как известно, перемножение матриц осуществляется по правилу «строка на столбец». Введем 2 матрицы 3 х 3 с именами M и N. Перемножение матриц осуществляется с помощью стандартной операции умножения. На рис. 3 смотрите синтаксис записи
Рис. 3. Перемножение матриц
Транспонирование матриц
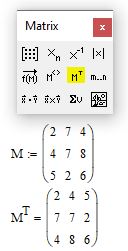
Как известно, при транспонировании матрицы ее строки становятся столбцами. В mathcad есть функция, которая позволяет выполнить транспонирование. Введите имя матрицы, которую хотите транспонировать, и на панели Matrix нажмите кнопку «Matrix transpose». На рис. 4 смотрите синтаксис для записи этой операции.
Рис. 4. Транспонирование матрицы
Обратные матрицы
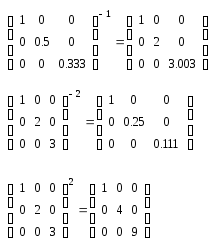
Как известно, обратной матрицей M^-1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку «Invers». на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы
Рис. 5. Обратная матрица
Выделение столбца и строки из матрицы
Для того чтобы «вытащить» столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с «нуля»
Рис. 6. Выделение столбца матрицы
Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать. При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7
Рис. 7. Выделение строки матрицы
Обратите внимание, что если при перемножении матриц их размерность «не совпадает» то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы
Поиск обратной
матрицы возможен, если матрица квадратная,
и ее определитель не равен нулю.
Произведение исходной матрицы на
обратную по определению является
единичной матрицей. Для ввода оператора
поиска обратной матрицы используется
кнопка Обратная
матрица (Inverse)
на палитре Матрицы
(Matrix).
Задание
10. Для
матрицы A
получите обратную матрицу:
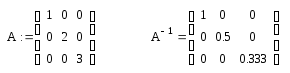
Получите единичную
матрицу, умножив исходную матрицу на
обратную:
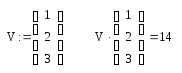
1.10. Возведение матрицы в степень
К квадратным
матрицам можно формально применить
операцию возведения в степень n.
Для этого n
должно быть целым числом. Выполнение
этой операции организуется с помощью
кнопки Возведения
в степень (Raise
to
Power)
на палитре Арифметика
(Calculator).
Задание
11.
Реализуйте
следующие примеры:
1.11. Векторизация массивов
Векторная алгебра
MathCAD
включает несколько необычный оператор,
который называется оператором
векторизации. Этот оператор предназначен
для работы с массивами. Он позволяет
провести однотипную операцию над всеми
элементами массива, упрощая тем самым
программирование циклов. (Например,
когда требуется умножить каждый элемент
одного массива на соответствующий
элемент другого). Непосредственно такой
операции в MathCAD
нет, но ее легко осуществить с помощью
векторизации.
Задание
12.
-
Получите скалярное
произведение:
-
С помощью кнопки
Задать вектор
(Factorize)
на палитре Матрица
(Matrix)
проведите векторизацию:
-
Проанализируйте
полученные результаты.
Оператор векторизации
можно использовать только с векторами
и матрицами одинакового размера.
1.12. Символьные
операции с матрицами
Все матричные и
векторные операторы допустимо использовать
в символических вычислениях. Мощь
символьных операций заключается в
возможности проводить их не только над
конкретными числами, но и над переменными.
Задание
13. Реализуйте
следующие примеры. Запишите название
каждой операции.
2. Матричные функции
Эти встроенные
функции предназначены для облегчения
работы с векторами и матрицами. Их можно
использовать для создания матриц,
слияния, и выделения части матриц,
получения основных свойств матриц и
т.д.
2.1. Функции создания
матриц
Самым наглядным
способом создания матрицы или вектора
является использования палитры Матрицы
(Matrix).
Однако в ряде случаев, в частности при
программировании сложных процессов,
удобнее создавать массивы с помощью
встроенных функций.
2.1.1. Определение
элементов матрицы через функцию
Для создания
матрицы можно использовать встроенную
функцию
matrix(M,N,f)
– создание матрицы размера M×N,
каждый i,j
элемент которой есть функция f(i,j).
Обратиться к этой функции можно из
диалогового окна Встроенные
функции,
которое появляется, ели на панели
инструментов Стандартные
выбрать команду Вставить
функцию.
Задание
14. Построить
матрицу, содержащую две строки и три
столбца:
Для создания матриц
имеются еще две специфические функции,
применяемые, в основном, для быстрого
и эффективного представления каких-либо
зависимостей в виде трехмерных графиков
(типа поверхности или пространственной
кривой).
Функция
СreateSpace(F(или
f1,f2,f3),
t0,
t1,
tgrid,
fmap)
— для создания вложенного массива,
представляющего x,
y
и z
координаты
параметрической пространственной
кривой, заданной функцией F:
-
F(t)
– векторная
функция из трех элементов, заданная
параметрически относительно единого
аргумента
t; -
f1(t),
f2(t),
f3(t)
– скалярные
функции; -
t0
– нижний
предел t
(по умолчанию -5); -
t1
– верхний
предел t
(по умолчанию 5); -
tgrid
– число
точек сетки по переменной t
(по умолчанию 20); -
fmap
– векторная
функция от трех аргументов, задающая
преобразование координат.
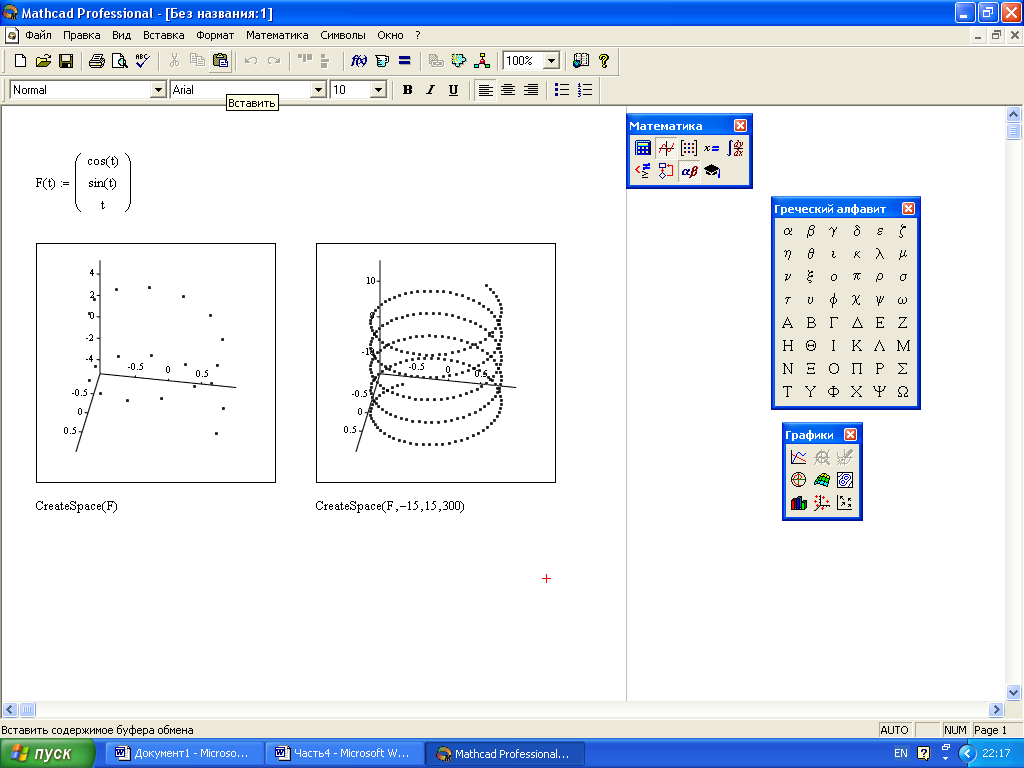
Задание
15. Реализуйте
примеры, приведенные на рис.35, используя
встроенную функцию СreateSpace.
Для этого выполните следующие операции:
-
Запишите векторную
функцию F(t). -
На палитре Графики
выберите трехмерный точечный график. -
В местозаполнитель
графика введите встроенную функцию
СreateSpace(F). -
Повторите построение
графика верхний и нижний пределы
аргумента и число точек.
Рис.
36. Использование функции СreateSpace
с разными наборами параметров
Функция создания
матрицы для графика трехмерной поверхности
устроена совершенно аналогично, за тем
исключением, что для определения
поверхности требуется не одна, а две
переменных.
СreateMesh(F(или
g,
или f1,f2,f3),
s0,
s1,
t0,
t1,
sgrid,
tgrid,
fmap)
— для создания вложенного массива,
представляющего x,
y
и z
координаты
параметрической пространственной
кривой, заданной функцией F:
-
F(s,t)
– векторная
функция из трех элементов, заданная
параметрически относительно двух
аргументов s
и t; -
g(s,t)
— скалярная
функция; -
f1(s,t),
f2(s,t), f3(s,t) –
скалярные
функции; -
s0,
t0
– нижние
пределы аргументов s,
t
(по умолчанию -5); -
s1,
t1
– верхние
пределы аргументов s,
t
(по умолчанию 5); -
sgrid,
tgrid
– число
точек сетки по переменным s
и t
(по умолчанию 20); -
fmap
– векторная
функция от трех аргументов, задающая
преобразование координат.
Задание
16. Реализуйте
примеры, приведенные на рис.35, используя
встроенную функцию СreateMesh.
Для получения поверхностного графика
необходимо в диалоговом окне Формат
3-D
графика
на вкладке Общие
выбрать переключатель Поверхностный
график.
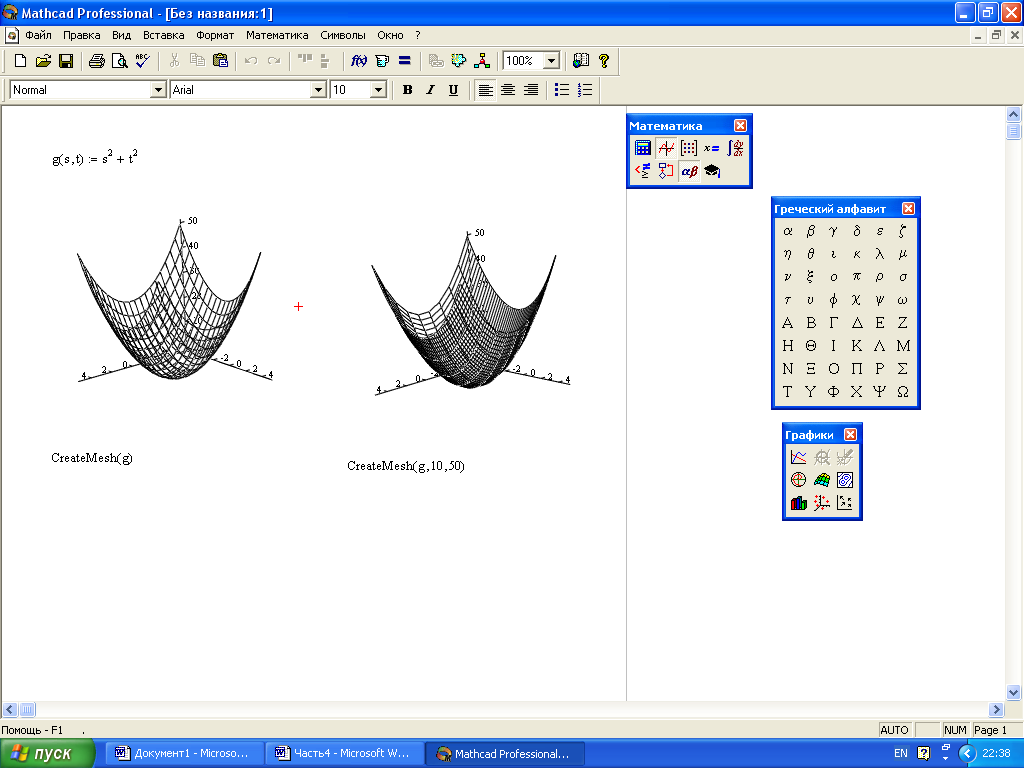
Рис.
37. Использование функции СreateMesh
с разным набором параметров
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация
Схемотехника
CAD / CAM
Статьи
MathCAD 12
MatLab
OrCAD
P CAD
AutoCAD
MathCAD 8 — 11
- Главная
- База знаний
- CAD / CAM
- org/Breadcrumb»>MathCAD 12
/
/
/
- Линейная алгебра
- 7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
- 7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
- 7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
- 7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7.
4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы
Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку
Inverse (Обратная матрица) на панели инструментов Matrix (Матрица). В листинге 7.16 приведен пример поиска обратной матрицы и последующая проверка правильности ее вычисления.
Листинг 7.16. Вычисление обратной матрицы
Теги MathCad
САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9922 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6945 0
Глава 2 Работа с файлами Mathcad 11
12401 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте
Использование материалов
Контакты
Новости
Статьи
База знаний
Радиомастер
© 2005–2022 radiomaster.
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2245 s
МЕТОД ОБРАТНОЙ МАТРИЦЫ В MATHCAD
Пример 1. Данасистемалинейныхалгебраических уравнений
Решить СЛАУ методом обратной матрицы
1. Задаем массив коэффициентов СЛАУ и вектор правых
|
частей: 1 |
2 |
3 |
4 |
30 |
|||
|
A |
1 2 |
3 |
4 |
f |
10 |
||
|
1 |
1 |
||||||
|
0 |
1 |
3 |
|||||
|
1 |
1 |
1 |
1 |
10 |
6
МЕТОД ОБРАТНОЙ МАТРИЦЫ В MATHCAD
2.
3. Находим обратную матрицу A–1:
|
1 |
1 |
3 |
||||||||
|
A |
1 |
0.75 |
1.25 |
4 |
||||||
|
0.5 |
0.5 |
1 |
||||||||
|
4. Находим решение: |
0. |
0.75 |
2 |
|||||||
|
1 |
||||||||||
|
x A |
1 |
f |
2 |
|||||||
|
3 |
||||||||||
|
30 |
4 |
|||||||||
|
5. |
||||||||||
|
A x |
10 |
|||||||||
|
3 |
||||||||||
|
10 |
A 4
3
21
1
7
РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА
Пусть det A 0
Построим m вспомогательных матриц
|
a |
11 |
. |
f |
1 |
… | ||
|
A i |
a |
21 |
… |
f 2 |
… |
||
|
… |
… |
… |
|||||
|
… |
i-й столбец |
||||||
|
… |
f m |
… |
|||||
|
am1 |
Решения находим по формулам:
|
xi |
det Ai |
i=1,2,…m. |
|
|
det A |
|||
Метод используется для решения небольших систем, т.к. нахождение определителей –
трудоемкая операция
8
МЕТОД КРАМЕРА В MATHCAD
Пример 2. Данасистемалинейныхалгебраических уравнений
Решить СЛАУ методом Крамера
1.По умолчанию элементы массива нумеруются с нуля. Для того, чтобы элементы нумеровались с единицы:
ORIGIN 1
9
Как быстро начать свое математическое образование с PTC Mathcad
Давайте посмотрим правде в глаза. В реальном мире немногие ученые или инженеры до сих пор используют калькуляторы и миллиметровую бумагу для решения важных уравнений. Они обращаются к программному обеспечению, которое может не только проверить их работу, но и четко передать ее.
Преподаватели любого уровня могут помочь своим ученикам повысить профессиональный уровень, заранее внедрив такое же мощное математическое программное обеспечение.
Если вы учитель, которому нужна помощь в начале освоения учебной программы, или если вы учитесь самостоятельно во время летних каникул, вот несколько советов, которые помогут вам начать работу:
Ресурсы
Начать изучая эти бесплатные ресурсы.
- PTC Mathcad Express . Вам понадобится хорошее программное обеспечение для инженерной математики. И хотя некоторые профессионалы STEM используют электронные таблицы для сложных расчетов, общение через Excel может привести к ошибкам и недоразумениям. PTC предлагает PTC Mathcad Express бесплатно, и вы можете сохранить большую часть функций на всю жизнь. [Обратите внимание, что многие студенты имеют право на академическую лицензию. Узнайте больше об академическом издании здесь.]
- Библиотека электронного обучения PTC Mathcad. Каждая библиотека предлагает комплексные учебные курсы.
С помощью этих руководств по PTC Mathcad вы можете узнать о обширных функциях PTC Mathcad Prime, таких как открытие файлов Mathcad и работа с ними, навигация по рабочим пространствам, определение переменных и выражений и решение уравнений.
- Обучающий соединитель PTC. Для учебных пособий и самостоятельного обучения, а также других справочных документов. Все это вы найдете прямо в программном обеспечении PTC Mathcad:
Пробные примеры
Теперь проработайте эти примеры. Мы начнем с задачи и покажем, как ее решить в PTC Mathcad. В других случаях мы просто покажем проблему и решение в PTC Mathcad, потому что, на мой взгляд, программное обеспечение лучше всего справляется с сообщением о сложных проблемах.
Пример 1
Решение в PTC Mathcad:
Пример 2
Проверьте, являются ли числа 50 и 17 взаимно простыми (подсказка: PTC Mathcad использует gcd для наибольшего общего делителя).
Решение в PTC MathCad:
Пример 3
Найдите наименьшее количество чисел: 3, 5, 10.
Решение в PTC Mathcad:
Пример 40003
Пример 4.
Вычислите скалярное произведение и косинус угла между следующими векторами:
Problem and solution in PTC Mathcad:
Example 5
Find the eigen vectors and the eigen values of the following matrix:
Problem and solution in PTC Mathcad:
Пример 6
Вычислить определитель, транспонирование и символьную обратную для следующей матрицы:
Задача и решение в PTC Mathcad:
Пример 7
Рассчитайте производную в данной точке:
Решение в PTC Mathcad:
Пример 8
Рассчитайте частичное производство или второй заказ: следующая функция Пример
Проблема и решение в PTC MathCad:
Пример 10
Упростить следующую сумму:
Решение в PTC MathCad:
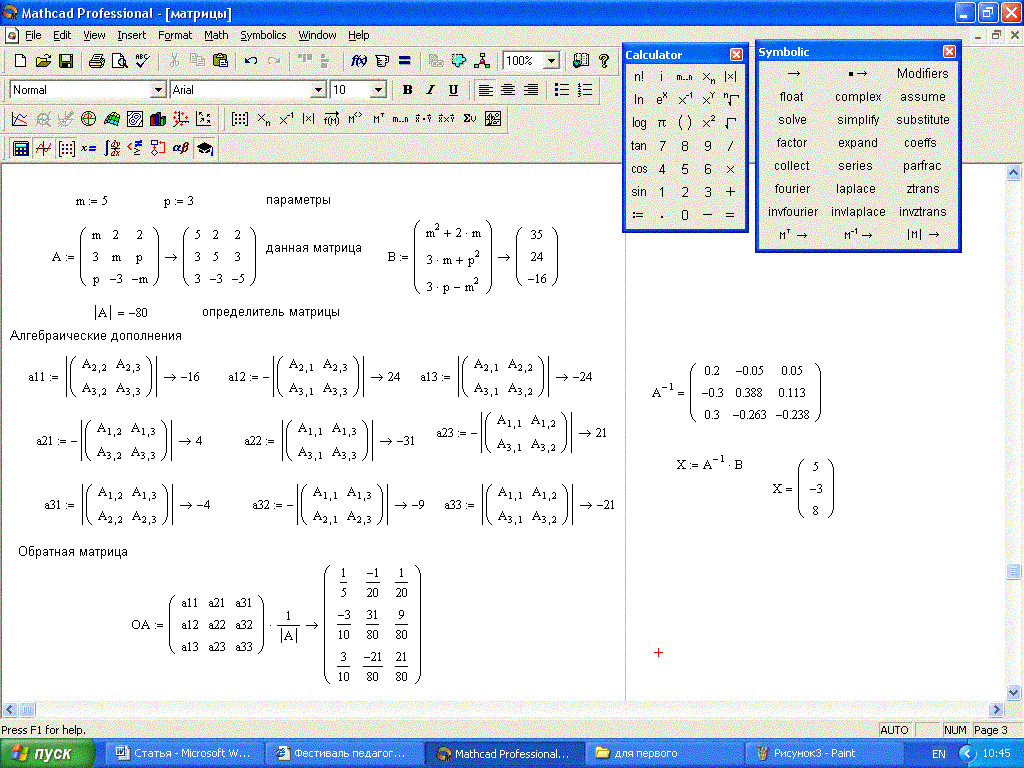
Пример
Фактор:
.
Пример 12
Определите коэффициенты полинома:
Решение в PTC MathCad:
Пример 13
Создайте графическое представление следующей функции:
в PTC MathCD.
Пример 14
Создайте графическое представление следующей функции:
Решение в PTC Mathcad:
После того, как вы просмотрите этот список, вы можете перейти к использованию других экспериментальных функций, которые требуют лучшего понимания математики. На самом деле вы можете найти несколько примеров в справке PTC Mathcad, доступной по нажатию F1.
Займитесь математикой
Хотите изучить сложные математические вопросы? Если вы еще этого не сделали, загрузите PTC Mathcad Express, выберите вариант полной функциональности на 30 дней, и вы получите доступ к полной версии PTC Mathcad на 30 дней.
Что означает эта строка mathcad?
спросил
7 лет, 3 месяца назад
Изменено
7 лет, 2 месяца назад
Просмотрено
165 раз
A — набор действительных чисел.
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Бредун А.Н.
1
Часов К.В.
1
1 Армавирский механико-технологический институт (филиал) ФГБОУ ВО «Кубанский государственный технологический университет»
В статье рассматривается вопрос методики изучения понятия «обратная матрица». Данная проблема возникает по причине неочевидности и высокой степени непонятности процесса вычисления. Приведён процесс получения интерактивного обучающего документа, подготавливаемого самим обучающимся, в котором он повторяет уже известные ему факты из теории. Исследование в математической среде MathCAD процесса вычисления обратной матрицы с помощью символьных вычислений приводит к результату, который получает преподаватель на доске, пытаясь пояснить, почему именно так, а не иначе нужно проводить вычисления. Наглядно полученный результат показывает применение уже знакомых студенту формул и правил (в частности, правило Саррюса, вычисление алгебраических дополнений к элементам исходной матрицы). Тем самым, математическая среда становится интерактивным учителем, обучение и самоучение становится активным и интерактивным.
математическая среда MathCAD
вычисления обратной матрицы
интерактивный обучающий документ
активное и интерактивное обучение
1. Вандина А.И., Часов К.В. Использование в& образовательной среде кафедры учебных пособий нового типа& // Международный журнал экспериментального образования.& – 2014.& – № 7-1.& – С. 98-100.
2. Горовенко Л.А. Создание электронного учебно-методического комплекса дисциплины как один из методов перехода от традиционной методики обучения к& обучению, основанному на самостоятельной работе студента// Инновационные процессы в& высшей школе: материалы XV юбилейной Всероссийской научно-практической конференции& – Краснодар: Изд.ГОУ ВПО КубГТУ, 2009. С. 211-213.
3. Кендюхов В.С., Часов К.В. Операция деления матрицы на матрицу (квадратные). Сборник студенческих работ, отмеченных наградами XIV студенческой научной конференции АМТИ.& – Армавир: Изд-во АМТИ.& – Вып.1, 2008, С.& 46-48.
4. Колупаев И.А., Часов К.В. Нестандартная методика деления (слева и& справа) квадратных матриц одного размера в& среде MathCAD // Успехи современного естествознания.& – 2012.& – № 5.& – С. 53-55; URL: http://natural-sciences.ru/ru/article/viewid=30077 (дата обращения: 02.02.2017).
5. Часов К.В. К вопросу об интерактивности в& обучении& // VIII Международная конференция «Стратегия качества в& промышленности и& образовании». Варна, Болгария, 2012. Международный научный журнал Acta Universitatis Pontica Euxinus.& – № S1. 2012. С. 344-346
6. Часов К.В., Зинченко О.И. Учебные материалы нового типа& // Международный студенческий научный вестник.& – 2016.& – № 5-3.& – С. 350-350; URL: http://eduherald.ru/ru/arti cle/viewid=15941 (дата обращения: 28.01.2017).
7. Часов К.В., Филимонов В.В. Интерактивный обучающий документ в& среде MathCAD // Международный студенческий научный вестник.& – 2016.& – № 5-3.& – С. 361-361; URL: https://eduherald.ru/ru/article/viewid=15947 (дата обращения: 28.01.2017).
Из педагогической практики преподавателей математики (высшей математики) известно, что изучение вопроса об обратных матрицах зачастую вызывает затруднения у студентов. Затруднения возникают в связи с тем, что сам процесс получения обратной матрицы представляется обучающимся надуманным. Указанное является причиной того, что большая часть студентов во время решения систем линейных уравнений (n×n) стараются не использовать метод решения систем матричным способом, всё чаще используя, если появляется возможность, электронные помощники – математические редакторы, «интернет-решатели» на доступных сайтах.
Один из авторов статьи (Часов К.В.) со своими студентами ещё с 2007 года начал исследование вопроса решения систем линейных уравнений, когда после изучения темы об обратных матрицах и их применении один из студентов (Кендюхов В.С.) заявил ([3]), что может решать системы без вычисления обратной матрицы. И, хотя анализ решения на занятии выявил большое количество ошибок и практически нерешённость примера, идея была признана удачной. Так учебно-исследовательская работа по решению домашней задачи перешла в разряд научно-исследовательской. Была опубликована статья ([3]), проект направлялся на внешние конкурсы.
Работа над методами решения систем линейных уравнений без использования обратной матрицы была продолжена в работе студента Колупаева И.А. ([4]), который с одним из авторов статьи (Часов К.В.) разработал программу в математической среде MathCAD, реализующая идею Кендюхова В.С. для деления «слева» и «справа» квадратных матриц одного размера.
В случае стандартного подхода к изучению теории матриц, решение систем линейных уравнений приходится проводить с использованием обратных матриц. Некоторым студентам процесс вычисления обратной матрицы приходится просто заучивать. К примеру, дана матрица 3-го порядка, для которой требуется получить обратную матрицу. Вычисляют определитель. Если он отличен от нуля, то далее…
– для чего-то вычисляются алгебраические дополнения к каждому элементу исходной матрицы;
– алгебраические дополнения располагаются в матрице 3-го порядка в том же порядке, в каком и были записаны сами элементы (что практически не вызывает вопросов у обучающихся);
– матрица транспонируется (а это вообще непонятно достаточно многим студентам – для чего?).
То, что каждый элемент полученной матрицы делится на определитель исходной матрицы, конечно же, понятно, как и само существование обратной матрицы зависит от того, что исходная матрица не вырожденная. В результате получается искомая обратная матрица. Но в совокупности указанные шаги не складываются в мышлении обучающихся в единую картину. Очевидно, что там, где нет наглядности, там исчезает смысл и, следовательно, пропадает понимание. Кроме того, необходимо учитывать высокий уровень абстракции при выполнении операции вычисления обратной матрицы.
Совершенно другая ситуация возникнет, если обучающийся сам произведёт вполне определённые выкладки в среде MathCAD, введённые в интерактивный обучающий документ [1, 5], которые в этом случае просто наглядны, но всё равно остаются «вещью в себе». Но при этом студент будет всё-таки «доверять» электронному, бездушному помощнику, который при этом не сможет объяснить студенту: а почему так, а не иначе(?). По этой причине в интерактивный обучающий документ вводимый в текстовом редакторе Word необходимо включать соответствующие комментарии по каждому этапу выкладок или вычислений.
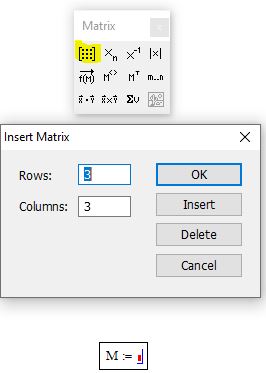
Задаём исходную матрицу в математической среде в общем виде (символьное представление), выделяем всю матрицу и в системном меню выбирает пункт «Символы», в выпавшем меню строку «Матрица >», в котором появляется своё выпавшее меню, в котором выбираем строку «Инвертировать». Ниже появится матрица очень большого размера (рисунок).
а) первый столбец обратной матрицы
б) второй столбец обратной матрицы
в) третий столбец обратной матрицы
Вычисление обратной для матрицы, заданной в символьном виде, в математической среде MathCAD
Очевидно, что в каждом знаменателе полученной матрицы находится определитель исходной матрицы, вычисленный с помощью правила Саррюса, которое обучающиеся уже знают и легко могут проверить указанный факт. Проверка должна происходить вручную. При необходимости, если студент не очень понимает почему вычисления производятся таким образом, он должен включить в документ соответствующий поясняющий комментарий. Необходимо отметить, что при изучении определителей, обучающиеся также не имеют чёткого представления об этом понятии. И только решение систем линейных уравнений помогает студентам понять необходимость ввода понятия определитель. Для небольшой части группы студентов это понятие всё-таки остаётся «вещью в себе» и они просто заучивают соответствующее определение, собственно как и некоторые операции с матрицами (а для чего они нужны?).
В получившейся матрице в числителях первого столбца (рисунок, а)) – алгебраические дополнения для элементов первой строки исходной матрицы, аналогично и для второго и третьего столбцов (рисунок, б), в)). Вследствие этого, если перемножить исходную матрицу и полученную, получим единичную, как этого и требует определение обратной матрицы. Только указанное действие придётся выполнять вручную, т.к. исходная матрица задана в символьном виде – её элементы не заданы и математическая среда не поддерживает подобные вычисления. Проведённые операции вручную ещё предстоит студентам ввести в интерактивный обучающий документ. Здесь преследуется следующая цель – кроме мыслительной деятельности и запоминания действует зрительная и мышечная память.
Приведённые выше вычисления, решения задач на определение обратных матриц, в том числе задач с системами, решаемых матричным способом, а так же, как упоминалось и ручные выкладки, обучающиеся сводят в интерактивный обучающий документ ([7]), располагающийся в информационной обучающей среде кафедры [1, 2]. Из всего многообразия предложенных вариантов отбираются наилучшие результаты, которые дополняются наиболее удачным содержанием из других документов, что решается совместно всеми обучающимися группы.
Самостоятельно анализируя указанный в статье фрагмент (рисунок), обучающиеся, не разобравшиеся на лекции с получением обратной матрицы, начинают понимать – зачем нужно вычислять соответствующие алгебраические дополнения, почему их нужно располагать в матрице именно так, а не иначе. Но, правда, необходимо, чтобы студент всё-таки желал и был мотивирован изучить проблему, хотя бы с точки зрения своей учебной работы.
Подводя итог, укажем, что при указанном способе изучения информация визуализируется, перестаёт быть для студента «вещью в себе». Становится очевидным, что учебно-исследовательская деятельность студентов по освоению обратных матриц проходит в активной и интерактивной формах, что и было целью преподавателя [6], а сама математическая среда MathCAD в указанном случае становится интерактивным помощником (и, в каком-то смысле, учителем). Несомненно, что учебно-исследовательская деятельность студентов перерастает в научно-исследовательскую деятельность.
Библиографическая ссылка
Бредун А.Н., Часов К.В. ИССЛЕДОВАНИЕ ВЫЧИСЛЕНИЯ ОБРАТНОЙ МАТРИЦЫ В MATHCAD // Международный студенческий научный вестник. – 2017. – № 4-6.
;
URL: https://eduherald.ru/ru/article/view?id=17561 (дата обращения: 30.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)


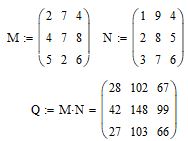

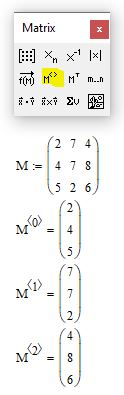
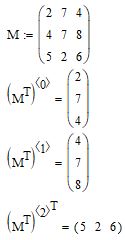



 4.3. Сортировка элементов матриц
4.3. Сортировка элементов матриц 25
25 Проверка решения:
Проверка решения: ..
..
 С помощью этих руководств по PTC Mathcad вы можете узнать о обширных функциях PTC Mathcad Prime, таких как открытие файлов Mathcad и работа с ними, навигация по рабочим пространствам, определение переменных и выражений и решение уравнений.
С помощью этих руководств по PTC Mathcad вы можете узнать о обширных функциях PTC Mathcad Prime, таких как открытие файлов Mathcad и работа с ними, навигация по рабочим пространствам, определение переменных и выражений и решение уравнений. 

