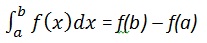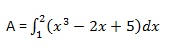Матлаб как найти интеграл

If f is a symbolic expression, then

attempts to find another symbolic expression, F, so that
diff(F) = f. That is,
int(f) returns the indefinite integral or antiderivative of
f (provided one exists in closed form). Similar to
differentiation,

uses the symbolic object v as the variable of integration, rather than
the variable determined by symvar. See how int works by
looking at this table.

Mathematical Operation

MATLAB® Command

∫xndx={log(x)if n=−1xn+1n+1otherwise.

int(x^n) or
int(x^n,x)

∫0π/2sin(2x)dx=1

int(sin(2*x), 0, pi/2) or int(sin(2*x), x,
0, pi/2)

g  =  cos(at +
b)

∫g(t)dt=sin(at+b)/a

g = cos(a*t + b) int(g) or int(g,
t)

∫J1(z)dz=−J0(z)

int(besselj(1, z)) or int(besselj(1, z),
z)

In contrast to differentiation, symbolic integration is a more complicated task. A number
of difficulties can arise in computing the integral:

  • The antiderivative, F, may not exist in closed form.

  • The antiderivative may define an unfamiliar function.

  • The antiderivative may exist, but the software can’t find it.

  • The software could find the antiderivative on a larger computer, but runs out of time
    or memory on the available machine.

Nevertheless, in many cases, MATLAB can perform symbolic integration successfully. For example, create the symbolic
variables

The following table illustrates integration of expressions containing those
variables.

f

int(f)

 
syms x n
f = x^n;
 
int(f)
ans =
piecewise(n == -1, log(x), n ~= -1,...
 x^(n + 1)/(n + 1))
 
syms y
f = y^(-1);
 
int(f)
ans =
log(y)
 
syms x n
f = n^x;
 
int(f)
ans =
n^x/log(n)
 
syms a b theta
f = sin(a*theta+b);
 
int(f)
ans =
-cos(b + a*theta)/a
 
syms u
f = 1/(1+u^2);
 
int(f)
ans =
atan(u)
 
syms x
f = exp(-x^2);
 
int(f)
ans =
(pi^(1/2)*erf(x))/2

In the last example, exp(-x^2), there is no formula for the integral
involving standard calculus expressions, such as trigonometric and exponential functions. In
this case, MATLAB returns an answer in terms of the error function erf.

If MATLAB is unable to find an answer to the integral of a function f,
it just returns int(f).

Definite integration is also possible.

Definite Integral

Command

∫abf(x)dx

int(f, a, b)

∫abf(v)dv

int(f, v, a, b)

Here are some additional examples.

f

a, b

int(f, a, b)

 
syms x
f = x^7;
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
1/8
 
syms x
f = 1/x;
 
a = 1;
b = 2;
 
int(f, a, b)
ans =
log(2)
 
syms x
f = log(x)*sqrt(x);
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
-4/9
 
syms x
f = exp(-x^2);
 
a = 0;
b = inf;
 
int(f, a, b)
ans =
pi^(1/2)/2
 
syms z
f = besselj(1,z)^2;
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
hypergeom([3/2, 3/2],...
          [2, 5/2, 3], -1)/12

For the Bessel function (besselj) example, it is possible to compute a
numerical approximation to the value of the integral, using the double function. The commands

syms z
a = int(besselj(1,z)^2,0,1)

return

a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12

and the command

returns

Integration with Real Parameters

One of the subtleties involved in symbolic integration is the “value” of
various parameters. For example, if a is any positive real number, the
expression

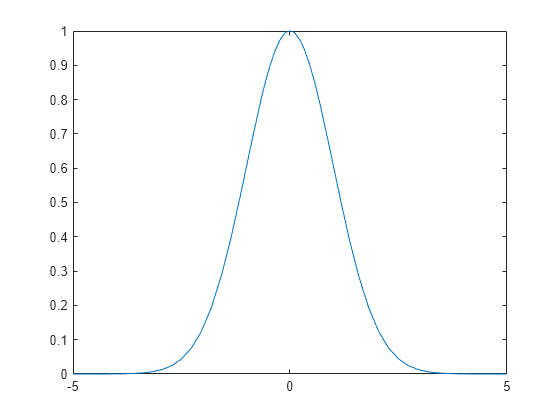
is the positive, bell shaped curve that tends to 0 as x tends to ±∞. You can create an example of this curve, for a = 1/2.

syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)

Figure contains an axes object. The axes object contains an object of type functionline.

However, if you try to calculate the integral

without assigning a value to a, MATLAB assumes that a represents a complex number, and therefore
returns a piecewise answer that depends on the argument of a. If you are
only interested in the case when a is a positive real number, use
assume to set an assumption on a:

Now you can calculate the preceding integral using the commands

syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)

This returns

Integration with Complex Parameters

To calculate the integral

for complex values of a, enter

syms a x 
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)

Use syms to clear all the assumptions on variables. For more
information about symbolic variables and assumptions on them, see Delete Symbolic Objects and Their Assumptions.

The preceding commands produce the complex output

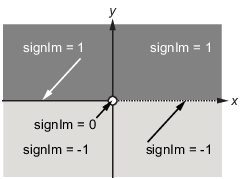
The function signIm is defined as:

Cartesian representation of a complex number z, showing regions where signIm has a value of 1, 0, and -1

To evaluate F at a = 1 + i, enter

High-Precision Numerical Integration Using Variable-Precision Arithmetic

High-precision numerical integration is implemented in the vpaintegral function of the Symbolic Math Toolbox™. vpaintegral uses variable-precision arithmetic in
contrast to the MATLAB
integral function, which uses
double-precision arithmetic.

Integrate besseli(5,25*u).*exp(-u*25) by using both
integral and vpaintegral. The
integral function returns NaN and issues a
warning while vpaintegral returns the correct result.

syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);

usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)

Warning: Infinite or Not-a-Number value encountered. 
usingIntegral =
   NaN

usingVpaintegral =
0.688424

For more information, see vpaintegral.

See Also

int | diff | vpaintegral

External Websites

  • Calculus Integrals (MathWorks Teaching Resources)
Источник

Доброго времени суток! Мы продолжаем говорить о численных методах. И сегодня мы поговорим о реализации численных методов интегрирования в среде Matlab.

Геометрический смысл интегрирования — это нахождение площади, которая находится под интегрируемой функцией.Геометрический смысл интегрирования На рисунке показана площадь для определённого интеграла, ограниченного a и b.

Численное интегрирование не только в Matlab, но и в других средах, строится именно на нахождении площади. Для начала мы разберем простые методы:

Методы прямоугольников

  • метод правых прямоугольников
  • метод левых прямоугольников
  • метод средних прямоугольников

Суть их в построение под кривой прямоугольников одинаковый ширины и нахождение их суммарной площади.Методы левых/правых/средних прямоугольниковКак видите, они различаются только точкой соприкосновения с кривой. Методы достаточны простые в реализации. Однако, погрешности данных методов весьма высоки. Точнее говоря, методы прямоугольников имеют первый порядок точности. Это означает, что ошибка пропорциональна шагу и накапливается со временем. Соответственно, чем меньше шаг, тем меньшую ошибку мы получим.

Также, следует отметить, что метод средних прямоугольников является более точным и предпочтительно использовать именно этот метод численного интегрирования, если у вас стоит выбор из этих трех методов. Эту точность можно доказать с помощью разложения в ряд Тейлора.

  • Пример 1

Необходимо посчитать интеграл функции f(x) = xesin(x)x с шагом разбиения h = 0.02 на интервале от 0 до 1.

f=inline('x.*exp((sin(x)).^x)');
a=0;
b=1;
h=0.02;
N=((b-a)/h)+1;
i=1:N; %количество шагов
x=a:h:b; %вычисление координат узлов сетки
y=feval(f,x); %вычисление значений функции в узлах сетки
m=2:N;
y1(m-1)=y(m);
Fr=sum(h*y1)

Вывод:

Fr =
    1.0825

Функция feval (родственник функции eval) — интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции, однако, в отличии от eval, интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции.

Метод трапеций

Метод трапецийЕщё одни популярный и в тоже время простой метод — метод трапеций. Аналогично методу прямоугольников строятся трапеции под кривой и находится их суммарная площадь. Данный метод имеет второй порядок точности (ошибка пропорциональна шагу в квадрате).

В Matlab метод трапеций реализован двумя функциями:

  • cumtrapz()
  • trapz()

Первую функцию обычно используют при работе с табличными данными или векторами. Откликом функции является n-интегралов, где n — число элементов вектора или элементов в каждом столбце матрицы. Следующие примеры отображают работу этой функции.

  • Пример 2

Пусть функция y(x) имеет значения, представленные в виде следующего вектора: y = [1,2,3,4,5,6,7,8,9,10]. Необходимо вычислить:

int_{a}^{b} y(x)dx

При этом a = 1; b = 1, 2, 3, 4 …,10.
Пишем в Matlab:

y=[1,2,3,4,5,6,7,8,9,10];
cumtrapz(y)

В выводе:

ans =
0    1.5000    4.0000    7.5000   12.0000   17.5000   24.0000   31.5000   40.0000   49.5000
  • Пример 3

Теперь рассмотрим вариант работы с вектором и матрицей:
Функция y(x) задана в виде матрицы y(x) = [1 3 5; 3 5 7; 4 6 8; 4 7 9; 5 7 10]. При этом аргумент представляет собой вектор: x = [1,3,7,9,10].

y = [1 3 5; 3 5 7; 4 6 8; 4 7 9; 5 7 10];
x = [1,3,7,9,10];
cumtrapz(x,y)

ans =
         0         0         0
    4.0000    8.0000   12.0000
   18.0000   30.0000   42.0000
   26.0000   43.0000   59.0000
   30.5000   50.0000   68.5000

Вторая функция для интегрирования, работающая по методу трапеций Matlab — trapz(). Наиболее используемая студентами, так как позволяет работать не только с векторами и матрицами, но и с аналитической формой подынтегральной функции. Выглядит это примерно так:

  • Пример 4

Необходимо вычислить определённый интеграл в диапазоне от 1 до 10 с шагом 0.5 для заданной функции:

y(x)= xe^{x} + ln(x) + 1

x = 1:0.5:10;
y = x.*exp(x) + log(x) +1;
trapz(y)

Вывод:

ans =
  4.0657e+005

Как видите, ничего сложного. А иногда даже удобнее некоторых онлайн сервисов для расчёта интегралов.

Метод Симпсона

Метод СимпсонаПреимущество этого метода в том, что точки, взятые на каждом шаге на кривой, интерполируются полиномом второй степени. Проще говоря, соединяются параболой. Это даёт методу четвёртый порядок точности.

 На рисунке красная кривая (1) - функция, зелёная(2) - полином.

В Matlab интегрирование с помощью метода Симпсона производит функция quad. Сразу разберем пример.

  • Пример 5

Вычислить определённый интеграл с точностью 10-4 методом Симпсона.

int_{0}^{10} (xe^{-x} + ln(x) + 1)dx

%стандартным оператором

quad('x.*exp(-x)+log(x)+1',0.001,10,1e-4) %зададим погрешность 10*-4

ans =

24.0323

Точность вычислений задается 4 параметром функции quad. Также, следует отметить, что в задании нижним пределом является 0, а мы использовали число 0.001. Это связано с тем, что при подстановке 0 функция не определена, а точнее, натуральный логарифм не существует.

% не стандартным оператором

F = @(x) x*exp(-x)+log(x)+1; %функция

a=0.01; %пределы интегрирования

b=10;

n=100; %количество частей деления

h=(b-a)/n; %определяем шаг

integ = F(a);

for i=1:1:((n/2)-1) %сам алгоритм Симпсона

x=a+2*h*i;

integ=integ+2*F(x)+4*F(x+h);

end

integ=h*integ/3;

24.091

Ну и реализация этого метода вручную приведена здесь для общего развития. Этим я хочу подчеркнуть, что практически любой метод или алгоритм возможно написать самому, а не пользоваться стандартными методами Matlab.

Символьное интегрирование в Matlab

Часто нам необходимо найти интеграл от какой либо функции, не зная пределов интегрирования. Тогда нам нужно взять интеграл в общем или символьном виде. В Matlab за символьное интегрирование отвечает функция int. Она принимает как минимум 2 параметра: 1 — функция, 2 — имя переменной по которой берется интеграл. int(fun, var). Рассмотрим короткий пример:

  • Пример 6

Вычислить неопределённый интеграл:

int_{}^{} (a^{x}e^{-x})dx

syms x %Определение переменной

f=sym('a^x*e^(-x)'); %Определение функции

int(f,x) %Вычисление неопределенного интеграла

ans =

1/(log(a)-log(e))*a^x*e^(-x)

Следует отметить, что функция int также может считать и определенные интегралы, для этого нужно задать пределы интегрирования в 3 и 4 параметры функции соответственно.

Заключение

На этом я хочу закончить сегодняшнюю тему «Интегрирование в Matlab». Не забывайте, что Matlab позволяет программировать сложные алгоритмы, а не только использовать встроенный функционал. Любой численный метод можно реализовать и вызывать как функцию. Если у вас остались вопросы, то задавайте их в комментариях.

В этот раз без исходников, примеры небольшие.

Источник

Интегрирование

Если f символьное выражение, затем

попытки найти другое символьное выражение, F, так, чтобы diff(F) = f. Таким образом, int(f) возвращает неопределенный интеграл или антипроизводную f (если каждый существует в закрытой форме). Подобно дифференцированию,

использует символьный объект v когда переменная интегрирования, а не переменная определяется symvar. Смотрите как int работает путем рассмотрения этой таблицы.

Математическая операция

MATLAB® Команда

∫xndx={log(x)если n=−1xn+1n+1в противном случае.

int(x^n) или int(x^n,x)

∫0π/2sin(2x)dx=1

int(sin(2*x), 0, pi/2) или int(sin(2*x), x, 0, pi/2)

g = because(at + b)

∫g(t)dt=sin(at+b)/a

g = cos(a*t + b) int(g) или int(g, t)

∫J1(z)dz=−J0(z)

int(besselj(1, z)) или int(besselj(1, z), z)

В отличие от дифференцирования, символьное интегрирование является более сложной задачей. Много трудностей могут возникнуть в вычислении интеграла:

  • Антипроизводная, F, может не существовать в закрытой форме.

  • Антипроизводная может задать незнакомую функцию.

  • Антипроизводная может существовать, но программное обеспечение не может найти его.

  • Программное обеспечение могло найти антипроизводную на более крупном компьютере, но заканчивается время или память на доступной машине.

Тем не менее, во многих случаях, MATLAB может выполнить символьное интегрирование успешно. Например, создайте символьные переменные

Следующая таблица иллюстрирует интегрирование выражений, содержащих те переменные.

f

int (f)

 
syms x n
f = x^n;
 
int(f)
ans =
piecewise(n == -1, log(x), n ~= -1,...
 x^(n + 1)/(n + 1))
 
syms y
f = y^(-1);
 
int(f)
ans =
log(y)
 
syms x n
f = n^x;
 
int(f)
ans =
n^x/log(n)
 
syms a b theta
f = sin(a*theta+b);
 
int(f)
ans =
-cos(b + a*theta)/a
 
syms u
f = 1/(1+u^2);
 
int(f)
ans =
atan(u)
 
syms x
f = exp(-x^2);
 
int(f)
ans =
(pi^(1/2)*erf(x))/2

В последнем примере, exp(-x^2), нет никакой формулы для интеграла включающих стандартных выражений исчисления, таких как тригонометрические и показательные функции. В этом случае MATLAB дает ответ в терминах функции ошибок erf.

Если MATLAB не может найти ответ на интеграл функционального f, это только возвращает int(f).

Определенное интегрирование также возможно.

Определенный интеграл

Команда

∫abf(x)dx

int(f, a, b)

∫abf(v)dv

int(f, v, a, b)

Вот некоторые дополнительные примеры.

f

a, B

int (f, a, b)

 
syms x
f = x^7;
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
1/8
 
syms x
f = 1/x;
 
a = 1;
b = 2;
 
int(f, a, b)
ans =
log(2)
 
syms x
f = log(x)*sqrt(x);
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
-4/9
 
syms x
f = exp(-x^2);
 
a = 0;
b = inf;
 
int(f, a, b)
ans =
pi^(1/2)/2
 
syms z
f = besselj(1,z)^2;
 
a = 0;
b = 1;
 
int(f, a, b)
ans =
hypergeom([3/2, 3/2],...
          [2, 5/2, 3], -1)/12

Для Функции Бесселя (besselj) пример, возможно вычислить числовое приближение к значению интеграла, с помощью double функция. Команды

syms z
a = int(besselj(1,z)^2,0,1)

возврат

a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12

и команда

возвращается

Интеграция с действительными параметрами

Одна из тонкости, вовлеченной в символьное интегрирование, является “значением” различных параметров. Например, если a является каким-либо положительным вещественным числом, выражением

положительная, кривая, имеющая форму звонка, которая стремится к 0, как x стремится к ± ∞. Можно создать пример этой кривой для a = 1/2.

syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)

Figure contains an axes object. The axes object contains an object of type functionline.

Однако, при попытке вычислить интеграл

не присваивая значение a, MATLAB принимает, что a представляет комплексное число, и поэтому дает кусочный ответ, который зависит от аргумента a. Если вы только интересуетесь случаем, когда a является положительным вещественным числом, используйте assume установить предположение на a:

Теперь можно вычислить предыдущий интеграл с помощью команд

syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)

Это возвращается

Интеграция с комплексными параметрами

Вычислить интеграл

для комплексных чисел a, войти

syms a x 
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)

Используйте syms очистить все предположения на переменных. Для получения дополнительной информации о символьных переменных и предположениях на них, смотрите, Удаляют Символьные Объекты и Их Предположения.

Предыдущие команды производят комплексный выход

Функция signIm задан как:

Оценивать F в a = 1 + i, войти

Численное интегрирование высокой точности Используя арифметику Переменной Точности

Численное интегрирование высокой точности реализовано в vpaintegral функция Symbolic Math Toolbox™. vpaintegral арифметика переменной точности использования в отличие от MATLAB integral функция, которая использует арифметику с двойной точностью.

Интегрируйте besseli(5,25*u).*exp(-u*25) при помощи обоих integral и vpaintegral. integral функция возвращает NaN и выдает предупреждение в то время как vpaintegral возвращает правильный результат.

syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);

usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)

Warning: Infinite or Not-a-Number value encountered. 
usingIntegral =
   NaN

usingVpaintegral =
0.688424

Для получения дополнительной информации смотрите vpaintegral.

Источник

Main Content

Quadratures, double and triple integrals, and multidimensional derivatives

Numerical integration functions can approximate the value of an integral whether or not
the functional expression is known:

  • When you know how to evaluate the function, you can use integral to calculate integrals with specified bounds.

  • To integrate an array of data where the underlying equation is unknown, you can use
    trapz, which performs trapezoidal integration
    using the data points to form a series of trapezoids with easily computed areas.

For differentiation, you can differentiate an array of data using gradient, which uses a finite difference formula to calculate numerical
derivatives. To calculate derivatives of functional expressions, you must use the
Symbolic Math Toolbox™
.

Functions

expand all

Integrate Functional Expressions

integral Numerical integration
integral2 Numerically evaluate double integral
integral3 Numerically evaluate triple integral
quadgk Numerically evaluate integral — Gauss-Kronrod quadrature
quad2d Numerically evaluate double integral — tiled method

Integrate Numeric Data

cumtrapz Cumulative trapezoidal numerical integration
trapz Trapezoidal numerical integration

Finite Difference Derivatives

del2 Discrete Laplacian
diff Differences and approximate derivatives
gradient Numerical gradient

Polynomials

Topics

  • Integration to Find Arc Length

    This example shows how to parametrize a curve and
    compute the arc length using integral.

  • Complex Line Integrals

    This example shows how to calculate complex line integrals using the 'Waypoints' option of the integral function.

  • Singularity on Interior of Integration Domain

    This example shows how to split the integration domain to place a singularity on the boundary.

  • Analytic Solution to Integral of Polynomial

    This example shows how to use the polyint function to integrate polynomial expressions analytically.

  • Integration of Numeric Data

    This example shows how to integrate a set of discrete velocity data numerically to approximate the distance traveled.

  • Calculate Tangent Plane to Surface

    This example shows how to approximate gradients of a function by finite differences.

Источник

Интеграция имеет дело с двумя принципиально разными типами проблем.

  • В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .

  • Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .

В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .

Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .

Определенные интегралы используются для определения площади, объема, центра тяжести, момента инерции, работы, выполняемой силой, и во многих других приложениях.

Поиск неопределенного интеграла с помощью MATLAB

По определению, если производная функции f (x) есть f ‘(x), то мы говорим, что неопределенный интеграл от f’ (x) по x равен f (x). Например, поскольку производная (по x) x 2 равна 2x, мы можем сказать, что неопределенный интеграл от 2x равен x 2 .

В символах –

f ‘(x 2 ) = 2x , следовательно,

∫ 2xdx = x 2 .

Неопределенный интеграл не является уникальным, потому что производная x 2 + c для любого значения константы c также будет 2x.

Это выражается в символах как –

∫ 2xdx = x 2 + c .

Где c называется «произвольной константой».

MATLAB предоставляет команду int для вычисления интеграла выражения. Чтобы вывести выражение для неопределенного интеграла функции, мы пишем – 

int(f);

Например, из нашего предыдущего примера – 

syms x 
int(2*x)

MATLAB выполняет приведенный выше оператор и возвращает следующий результат – 

ans =
   x^2

Пример 1

В этом примере давайте найдем интеграл некоторых часто используемых выражений. Создайте файл сценария и введите в нем следующий код – 

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Когда вы запускаете файл, он показывает следующий результат – 

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Пример 2

Создайте файл сценария и введите в нем следующий код – 

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))

int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))

int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Обратите внимание, что функция pretty возвращает выражение в более читаемом формате.

Когда вы запускаете файл, он показывает следующий результат – 

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Нахождение определенного интеграла с помощью MATLAB

По определению, определенный интеграл в основном является пределом суммы. Мы используем определенные интегралы, чтобы найти области, такие как область между кривой и осью x и область между двумя кривыми. Определенные интегралы могут также использоваться в других ситуациях, где требуемое количество может быть выражено как предел суммы.

Функция int может использоваться для определенной интеграции, передавая пределы, по которым вы хотите вычислить интеграл.

Вычислять

Определенный Интеграл

мы пишем, 

int(x, a, b)

Например, для расчета стоимости 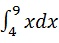пример мы пишем – 

int(x, 4, 9)

MATLAB выполняет приведенный выше оператор и возвращает следующий результат – 

ans =
   65/2

Ниже приведен октавный эквивалент приведенного выше расчета – 

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат – 

Area: 

   32.500

Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом: 

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат – 

Area: 
   32.500

Пример 1

Вычислим площадь, заключенную между осью x и кривой y = x 3 -2x + 5 и ординатами x = 1 и x = 2.

Требуемая площадь определяется как –

Расчет площади

Создайте файл сценария и введите следующий код – 

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Когда вы запускаете файл, он показывает следующий результат – 

a =
23/4
Area: 
   5.7500

Ниже приведен октавный эквивалент приведенного выше расчета – 

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат – 

Area: 

   5.7500

Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом: 

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат – 

Area: 
   5.7500

Пример 2

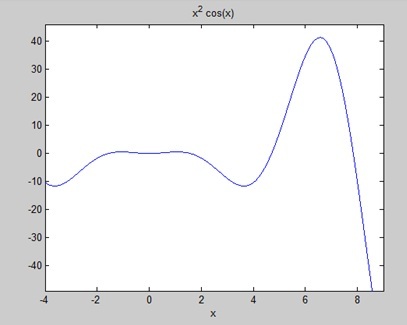
Найдите площадь под кривой: f (x) = x 2 cos (x) для −4 ≤ x ≤ 9.

Создайте файл сценария и напишите следующий код – 

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Когда вы запускаете файл, MATLAB строит график –

Определенный Интеграл

Выход дан ниже – 

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Ниже приведен октавный эквивалент приведенного выше расчета –

Источник

Понравилась статья? Поделить с друзьями:
  • Как составить монографию по книге
  • Что такое концентрация вещества как найти
  • Как найти друг друга в крафтсман
  • Как по татарски будет нашел
  • Как найти работу в росатом