Матлаб как найти угол между векторами

So why doesn’t matlab give us a function for that instead of having us look endlessly on forums?

This topic has been discussed many times on the Newsgroup forum … if I looked hard enough I’m sure I could find several Roger Stafford posts from many years ago on this. E.g., here is one of them:

The basic acos formula is known to be inaccurate for small angles. A more robust method is to use both the sin and cos of the angle via the cross and dot functions. E.g.,

An extreme case to clearly show the difference:

This does the same thing, also capable of determining the angle of higher (than one) dimensional subspaces.

will give you the same answer.

Just a note on how to vectorize the whole thing: (semicolons purposely omitted to see the intermediate results)

or in short (the hard to read variant)

Coordinates of two vectors xb,yb and xa,ya .

angle(vector.b,vector.a)=pi/2*((1+sgn(xa))*(1-sgn(ya^2))-(1+sgn(xb))*(1-sgn(yb^2)))

function angle_in_degrees = vector2angle(u,v)

a= sqrt(u(1)^2+u(2)^2+u(3)^2);

b=sqrt(v(1)^2+v(2)^2+v(3)^2);

c=0;

for i=1:1:numel(u)

c=c+u(i)*v(i);

end

angle_in_degrees=acos(c/(a*b))*180/pi

end

Currently, there is no built-in MATLAB function to calculate the angle between two vectors. However, you can use dot product property of two vectors to find the angle:

Hi, i would like to update the answer:

The subspace Function was added 2006a.

function theta = calcAngleBetweenVectors(u, v)

dotUV = dot(u, v);
normU = norm(u);
normV = norm(v);

theta = acos(dotUV/(normU * normV));

2

 theta = atan2(norm(cross(a,b)),dot(a,b));

2

Глава 4. Элементы матричной алгебры

вительного в этом ничего нет, поскольку для любой квадратной матрицы ˆ

A

На заметку

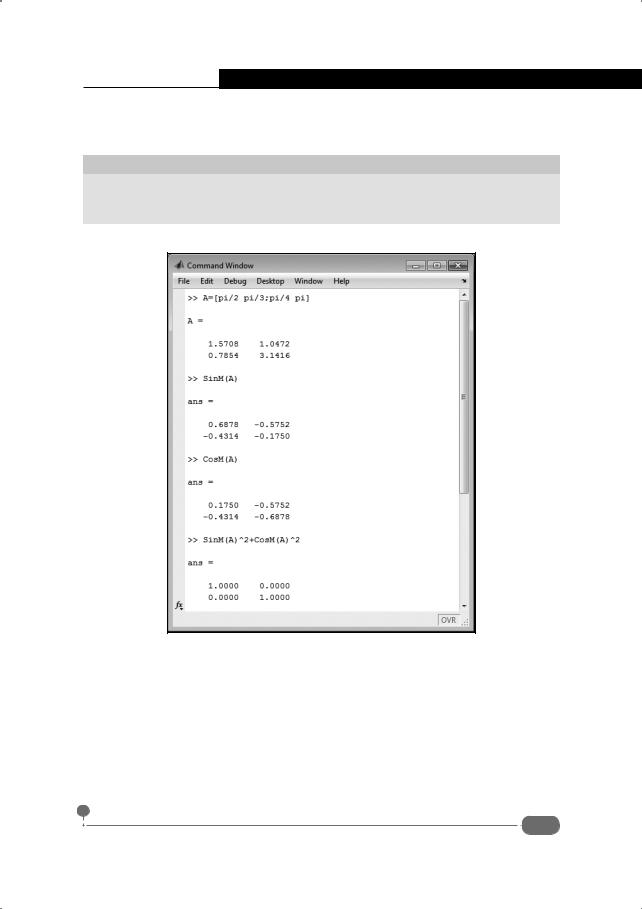
Операции SinM(A)^2 и CosM(A)^2 имеют смысл, поскольку SinM(A) и CosM(A) – квадратные матрицы, и к ним, как к обычным матрицам, применим оператор ^ возведения в целочисленную степень.

Результат вычислений показан в документе на рис. 4.25.

Рис. 4.25. Вычисление матричного синуса и косинуса

Справедливости ради следует отметить, что приведенный способ вычисления матричного синуса и косинуса далеко не единственный. Существуют и более простые пути. Например, можно воспользоваться формулой Эйлера для экспоненты в комплексной степени: exp(ix) = cos(x) + i sin(x), где i — мнимая единица, для которой по определению i2 = −1 . Таким образом, cos(x) = Re(exp(ix)) и sin(x) = Im(exp(ix)) . Здесь через Re(z)

и Im(z) обозначены соответственно действительная и мнимая части комплексного числа z . Мы могли бы, например, определить матричный синус

Самоучитель Matlab

как ˆ = ˆ , а матричный косинус как ˆ = ˆ . sin(A) Im(exp(iA)) cos(A) Re(exp(iA))

Примеры таких вычислений приведены ниже:

>>real(expm(A*i)) ans =

0.1750 -0.5752 -0.4314 -0.6878

>>imag(expm(A*i)) ans =

0.6878 -0.5752 -0.4314 -0.1750

Несложно заметить, что данный способ вычисления синуса и косинуса от матричного аргумента дает такой же результат (в пределах точности вычислений), что и с использованием ряда Тейлора.

На заметку

В вычислениях использовалась встроенная функция expm() для расчета матричной экспоненты. Она справляется с задачей, даже если аргумент комплексный. Действительная часть вычисляется с помощью функции real(), а мнимая – с помощью функции imag().

Окно с результатами вычислений показано на рис. 4.26.

Рис. 4.26. Альтернативный способ вычисления матричного синуса и косинуса

Как пример использования блочных матриц рассмотрим такую задачу. Предположим, есть три вектора в декартовом трехмерном пространстве

= ( , , ), индекс k = 1,2, 3 . Предполагаем также, что эти векторы ak ak1 ak2 ak 3

линейно-независимы и образуют базис. Задача состоит в том, чтобы разло-

жить по этому базису некоторый известный вектор b = (b1,b2,b3).

Глава 4. Элементы матричной алгебры

шением и воспользуемся для вычисления координат вектора в новом базисе. Рассмотрим приведенный ниже командный код (жирным шрифтом выделен ввод пользователя):

>>a1=[1 3 1];

>>a2=[-2 1 0];

>>a3=[0 -1 2];

>>b=[1 3 -2];

>>A=[a1;a2;a3]

A =

>> x=b/A x =

0.6250 -0.1875 -1.3125 >> x*A

ans =

13 -2

Сначала мы создаем три вектора для нового базиса (значения записываются в переменные a1, a2 и a3), а также вектор (переменная b), который необходимо разложить по базису. Командой A=[a1;a2;a3] на основе векторов нового базиса создается блочная матрица. С помощью этой матрицы, воспользовавшись командой x=b/A, вычисляем вектор координат вектора b в базисе векторов a1, a2 и a3. Проверить, корректно ли вычислен результат, можно, воспользовавшись командой x*A. В результате должны получить вектор b, что, собственно, и происходит (рис. 4.27).

Самоучитель Matlab

Рис. 4.27. Вычисление координат вектора в новом базисе

На заметку

Для умножения вектора b справа на обратную матрицу к A мы использовали оператор /. Хотя реальный алгоритм вычисления результата в этом случае на самом деле несколько сложнее, в принципе, можно полагать, что команда b/A вычисляется так: вектор b справа умножается на матрицу, которая обратна к матрице A.

Классической стала задача о вычислении угла между двумя векторами в пространстве. В Matlab эта задача решается исключительно просто. Рас-

косинус угла, можно вычислить сам угол с помощью функции арккосинуса.

На заметку

В Matlab для вычисления арккосинуса имеется функция acos(). Однако здесь есть один специфический момент. Дело в том, что если известен косинус угла,

Глава 4. Элементы матричной алгебры

то сам угол восстанавливается неоднозначно. Арккосинус дет значение в пределах от 0 до p. Поэтому важно четко представлять, что же именно мы вычисляем. В данном случае вычисляется абсолютное значение угла между векторами – в плоскости векторов меньший из двух смежных углов между линиями, вдоль которых направлены векторы.

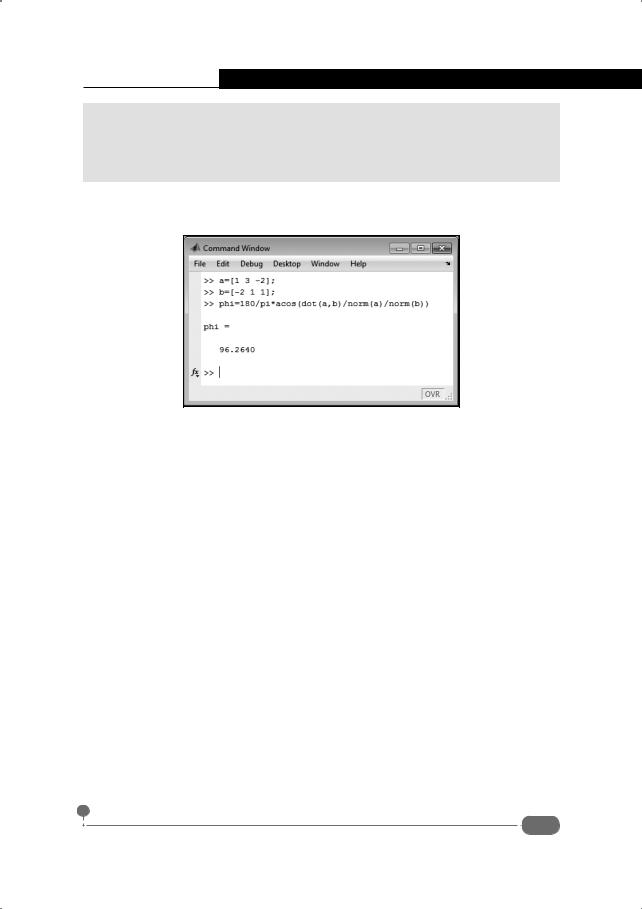
Пример вычисления угла между векторами представлен в документе на рис. 4.28.

Рис. 4.28. Вычисление угла между векторами

Собственно, для вычисления угла между векторами a и b, помимо команд инициализации векторов, используется всего одна команда phi=180/ pi*acos(dot(a,b)/norm(a)/norm(b)). Угол вычисляется в градусах, поэтому результат, возвращаемый арккосинусом, умножается на 180 и делится на π. Скалярное произведение векторов вычисляем с помощью функции dot(), а модуль вектора вычисляется функцией norm().

Похожая в известном смысле задача – вычисление площади и периметра пространственного треугольника. Задача формулируется так. Заданы три точки в пространстве. Они образуют треугольник. Необходимо найти площадь этого треугольника и его периметр.

AC . С другой стороны, если вычислить векторное произведение AB ×AC ,

то результатом будет вектор, и его модуль равен | AB || AC | sin(ϕ), то есть в два раза больше площади треугольника.

Самоучитель Matlab

На заметку

Если заданы начальная и конечная точка вектора, то координаты вектора можно рассчитать путем вычитания из координат конечной точки соответствующих координат начальной точки.

Ниже приведен командный код, с помощью которого вычисляется площадь и периметр треугольника (жирным шрифтом выделен ввод пользователя).

>>A=[1 2 1];

>>B=[-2 3 -1];

>>C=[1 -1 2];

>>AB=B-A

AB =

-3 1 -2 >> AC=C-A

AC =

0 -3 1 >> BC=C-B

BC =

3 -4 3

>>P=norm(AB)+norm(AC)+norm(BC)

P = 12.7349

>>S=norm(cross(AB,AC))/2

S=

5.3619

Командами A=[1 2 1], B=[-2 3 -1] и C=[1 -1 2] создаются точки – вершины треугольника. Затем с помощью команд AB=B-A, AC=C-A и BC=C-B вычисляются векторы, которые нам нужны для вычисления периметра и площади треугольника. Периметр вычисляем командой

P=norm(AB)+norm(AC)+norm(BC). Площадь вычисляем командой

S=norm(cross(AB,AC))/2, в которой для вычисления векторного произведения использована встроенная функция cross(). Результат вычислений показан на рис. 4.29.

Обращаем внимание, что точки представляются в виде списков из трех элементов. Это позволяет достаточно просто на основании известных точек вычислить соответствующие им векторы.

Еще одной классической является задача о решении системы линейных ал-

гебраических уравнений. В общем случае задача формулируется так. Не-

n

обходимо решить систему уравнений ∑aijxj = bi (индекс i = 1,2,…,n )

j =1

относительно неизвестных x1 , x2 , …, xn при условии, что параметры aij

Глава 4. Элементы матричной алгебры

Рис. 4.29. Вычисление периметра и площади треугольника

и bi (индексы i, j = 1,2,…,n ) заданы. Именно этой задачей и займемся. Всякие экзотические случаи, наподобие системы без решений, исследовать не будем. Предполагаем, что у системы уравнений решение есть, и оно единственно.

Исходную систему уравнений удобно представить в матричном виде, вве-

зом, для решения системы уравнений достаточно знать матрицу коэффици-

ˆ

ентов A и вектор правых частей уравнений b . Данный подход реализован в коде, представленном ниже:

Самоучитель Matlab

>> A=[1 2 3;-1 1 2;1 -2 5]

A =

1 2 3 -1 1 2 1 -2 5

>>b=[10;1;4]

b =

10

1

4

>>x=Ab

x =

3

2

1

Матрица коэффициентов задается командой A=[1 2 3;-1 1 2;1 -2 5]. Вектор коэффициентов правых частей задается командой b=[10;1;4]. Таким образом, решается следующая система уравнений:

Система имеет единственное решение x1 = 3 , x2 = 2 и x3 = 1. Именно его попытаемся найти. Для этого используем команду x=Ab, в результате чего

иполучаем нужное решение (рис. 4.30).

На заметку

Вместо вычисления обратной матрицы к матрице A и умножения ее (слева) на вектор b мы использовали оператор .

Важная задача, которая встречается достаточно часто, связана с диагонализацией матриц. Вначале краткая предыстория о том, откуда такая задача

вообще может возникнуть. Допустим, мы вместо одного векторного базиса

вводим другой. Единичные орты исходного базиса обозначим как a1 , a2 и a3 .

На заметку

Далее, если явно не указано, подразумевается, что речь идет о векторахстолбцах, а все матрицы квадратные размера 3×3 (хотя изложенное далее без особых проблем применимо и к более общему случаю квадратных матриц произвольного размера).

Глава 4. Элементы матричной алгебры

Рис. 4.30. Решение системы линейных уравнений

и ничто не запрещают нам записать новые орты через старые орты. Это бу-

хода. У этой матрицы есть ряд интересных свойств. Так, несложно показать, что для матрицы перехода Sˆ′ = Sˆ−1 — то есть транспонированная матрица

равна обратной. Определитель матрицы ˆ (по модулю) равен единице. Для

S

преобразования базиса достаточно задать матрицу перехода ˆ. Все необ-

S

ходимые преобразования вычисляются на основе этой матрицы. Так, если

в старом базисе задан некоторый вектор x , то в новом базисе получим век-

= ˆ

тор y Sx. Это следует непосредственно из способа определения матрицы перехода.

Самоучитель Matlab

На заметку

Если в старом базисе задана некоторая матрица ˆ, то в новом базисе эта

A

матрица вычисляется как ˆ = ˆˆ ˆ−1.

B SAS

На заметку

Очень часто задача состоит в том, чтобы выполнить преобразование базиса,

при котором некоторая матрица (например, ˆ) принимает наиболее про-

A

стой вид. А что может быть проще диагональной матрицы? Другими словами, задача может быть сформулирована, например, следующим образом.

Задана симметричная матрица ˆ. Необходимо найти матрицу перехода ˆ

A S

такую, чтобы матрица ˆ = ˆˆ ˆ−1 была диагональной.

B SAS

На заметку

К диагональному виду матрицу ˆ можно привести, если все ее собственные

A

числа различны. В противном случае удается свести матрицу к жорданову виду, когда матрица «почти диагональная». Более того, матрица перехода будет удо-

да S , то свести к диагональному виду можно только симметричную матрицу A

сразными собственными числами.

ВMatlab есть несколько встроенных функций, с помощью которых может решаться описанная выше задача (или идейно близкая к ней). Здесь остановимся на уже известной функции вычисления собственных чисел eig() и функции выполнения жорданова преобразования jordan(). Функция eig() уже описывалась. Что касается функции jordan(), то ее аргументом указывается исходная, преобразуемая, матрица. В качестве результата возвращается две матрицы. Первая матрица – это матрица, с помощью которой выполняется преобразование (аналог матрицы перехода, но только аналог!). Вторая матрица — диагональная или «почти диагональная» (жор-