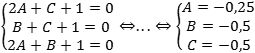Метод координат как найти координаты вектора

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

Разность векторов:

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1.  В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2.  В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и :

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму.

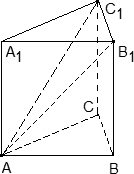
3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

.

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

;

.

Выразим C и B через A и подставим в третье уравнение:

.

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

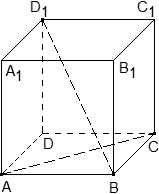
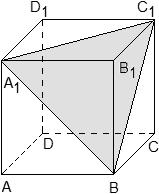
4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Упростим систему:

.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор  или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

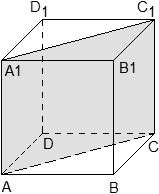
6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

  

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Система координат

С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.

Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции ( y=ax+b), например, ( y=2{x}-3).

Напомню, ты строил ее по точкам. Помнишь?

Ты выбирал произвольное число ( x), подставлял ее в формулу ( y=2{x}-3) и вычислял таким образом ( y).

Например, если ( x=0), то ( y=2cdot 0-3=-3), если же ( x=1), то ( y=2cdot 1-3=-1)и т. д.

Что же ты получал в итоге?

А получал ты точки с координатами: ( Aleft( 0,-3 right)) и ( Bleft( 1,-1 right)).

Далее ты рисовал «крестик» (систему координат ( X0Y)), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции ( y=2{x}-3).

Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:

• Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке;
• Принято, что ось ( displaystyle X) идет слева направо, а ось ( displaystyle Y) – cнизу вверх;
• Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой ( displaystyle O);
• В записи координаты точки, например ( displaystyle Aleft( 0,-3 right)), слева в скобках стоит координата точки по оси ( displaystyle X), а справа, по оси ( displaystyle Y). В частности, ( displaystyle Aleft( 0,-3 right)) просто означает, что у точки ( displaystyle A) ( displaystyle x=0,~y=-3.);
• Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа);
• Для любой точки, лежащей на оси ( displaystyle Ox,), ( displaystyle y=0.);
• Для любой точки, лежащей на оси ( displaystyle Oy), ( displaystyle x=0.);
• Ось ( displaystyle Ox) называется осью абсцисс;
• Ось ( displaystyle Oy) называется осью ординат.

Векторы

Теперь давай с тобой сделаем следующий шаг: отметим две точки ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).

Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки ( displaystyle A) к точке ( displaystyle B):

То есть мы сделаем наш отрезок направленным!

Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!

Вектором называется направленный отрезок, имеющий начало и конец.

Таким образом, если мы соединим точку ( displaystyle A) c точкой ( displaystyle B), причем началом у нас будет точка A, а концом – точка B, то мы получим вектор ( displaystyle overrightarrow{AB}).

Это построение ты тоже делал в 8 классе, помнишь?

Координаты вектора

Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора.

Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты?

Оказывается, что да! И делается это очень просто:

Координаты вектора = координаты точки конца – координаты точки начала.

Таким образом, так как в векторе ( displaystyle overrightarrow{AB}) точка ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) – начало, а ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)) – конец, то вектор ( displaystyle overrightarrow{AB}) имеет следующие координаты:

Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке ( displaystyle B), а конец – в точке ( displaystyle A).

Тогда:

Единственное их отличие – это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:

Еще больше о векторах и проекциях (эту тему мы непременно затронем) ты можешь прочитать в статье по физике «Большая теория по векторам» 🙂

Действия с векторами

Что еще можно делать с векторами?

Да почти все то же самое, что и с обычными числами:

• Векторы можно складывать друг с другом;
• Векторы можно вычитать друг из друга;
• Векторы можно умножать (или делить) на произвольное ненулевое число;
• Векторы можно умножать друг на друга.

Что же происходит при выполнении этих действий с координатами векторов?

1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты.

То есть:

2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:

( kcdot vec{a}left( {{x}_{1}},{{y}_{1}} right)=vec{b}left( k{{x}_{1}},k{{y}_{1}} right))

Например:

Най­ди­те сумму ко­ор­ди­нат век­то­ра ( vec{a}+vec{b}).

Вектор растягивается или сжимается или меняет направление при умножении или делении на число:

Давай вначале найдем координаты каждого из векторов.

Оба они имеют одинаковое начало – точку начала координат. Концы у них разные.

Тогда ( vec{a}left( 2-0,6-0 right)=vec{a}left( 2,6 right)), ( vec{b}left( 8-0,4-0 right)=vec{b}left( 8,4 right)).

Теперь вычислим координаты вектора ( vec{c}=vec{a}+vec{b}=vec{c}left( 2+8,4+6 right)=vec{c}left( 10,10 right))

Тогда сумма координат полученного вектора равна ( 20).

Ответ: ( 20)

Теперь реши сам следующую задачу:

Найти сумму координат вектора ( 3vec{a}-2vec{b})

Проверяем:

• ( vec{a}=vec{a}left( 4-2,10-4 right)=vec{a}left( 2,6 right));
• ( vec{b}=vec{b}left( 10-2,6-2 right)=vec{b}left( 8,4 right));
•  ( vec{c}=3vec{a}-2vec{b}=3vec{a}left( 2,6 right)-2vec{b}left( 8,4 right)=left( 6,18 right)-left( 16,8 right)=vec{c}left( -10,10 right)); 
• ( -10+10=0).

Ответ: ( 0)

Расстояние между двумя точками на координатной плоскости

Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?

Пусть первая точка будет ( {{P}_{1}}({{x}_{1}},{{y}_{1}})), а вторая ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).

Обозначим расстояние между ними через ( d). Давай сделаем для наглядности следующий чертеж:

Что я сделал?

Я, во-первых, соединил точки ( {{P}_{1}}left( {{x}_{1}},{{y}_{1}} right)) и ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).

А также из точки ( {{P}_{1}}) провел линию, параллельную оси ( Ox), а из точки ( {{P}_{2}}) провел линию, параллельную оси ( Oy).

Они пересеклись в точке ( R), образовав при этом замечательную фигуру. Чем она замечательна?

Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!

Искомый отрезок – это гипотенуза этого треугольника, а отрезки ( {{P}_{1}}R,~{{P}_{2}}R) – катеты.

Чему равны координаты точки ( R)?

Да, их несложно найти по картинке: ( Rleft( {{x}_{2}},{{y}_{1}} right).~)

( {{d}^{2}}=text{ }!!~!!text{ }left| {{P}_{1}}{{P}_{2}} right|=text{ }!!~!!text{ }{{left| {{P}_{1}}R right|}^{2}}+{{left| {{P}_{2}}R right|}^{2}}=({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}~)

( d=~sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})

Таким образом, расстояние между двумя точками – это корень из суммы квадратов разностей из координат. 

Или же – расстояние между двумя точками – это длина отрезка, их соединяющего.

Легко заметить, что расстояние между точками не зависит от направления.

Тогда:

( d=left| overrightarrow{{{P}_{1}}{{P}_{2}}} right|=left| overrightarrow{{{P}_{2}}{{P}_{1}}} right|=sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})

Отсюда делаем три вывода:

• Длина вектора = корень из суммы квадратов его координат;
• Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
• Длины векторов, соединяющих две точки в разном направлении, равны.

Давай немного поупражняемся в вычислении расстояния между двумя точками:

Например, если ( Aleft( 1,2 right),~Bleft( 3,4 right)), то расстояние между ( A) и ( B) равно

Теперь немного потренируйся сам:

Задание. Найти расстояние между указанными точками:

• ( Aleft( 2,sqrt{3} right),~Bleft( 5,2sqrt{3} right));
• ( Cleft( 2,4 right),~Dleft( 1,-5 right));
• ( Fleft( sqrt{12},1 right),~Gleft( sqrt{3},-1 right)).

Проверяем:

• ( d=sqrt{{{left( 5-2 right)}^{2}}+{{left( 2sqrt{3}-sqrt{3} right)}^{2}}}=sqrt{9+3}=sqrt{12}=2sqrt{3});
• ( displaystyle d=sqrt{{{left( 1-2 right)}^{2}}+{{left( -5-4 right)}^{2}}}=sqrt{1+81}=sqrt{82});
• ( displaystyle d=sqrt{{{left( sqrt{3}-sqrt{12} right)}^{2}}+{{left( -1-1 right)}^{2}}}=sqrt{left( 3-2sqrt{3}sqrt{12}+12 right)+4}=); ( displaystyle=sqrt{3-2sqrt{36}+12+4}=sqrt{3-12+12+4}=sqrt{7}).

Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:

1. Най­ди­те квад­рат длины век­то­ра ( vec{a}-vec{b}).

2. Най­ди­те квад­рат длины век­то­ра ( overrightarrow{AB})

Я так думаю, ты с ними без труда справился? Проверяем:

1. А это на внимательность) Мы уже нашли координаты векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}) ранее: ( displaystyle vec{a}left( 2,6 right),~vec{b}left( 8,4 right)). Тогда вектор ( displaystyle vec{a}-vec{b}) имеет координаты ( displaystyle left( 2-8,6-4 right)=left( -6,2 right)). Квадрат его длины будет равен:

Тогда квадрат его длины равен

Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.

Задача 1. Най­ди­те синус угла на­кло­на от­рез­ка, со­еди­ня­ю­ще­го точки ( displaystyle Oleft( 0;~0 right)),( displaystyle Aleft( 6;~8 right)) с осью абсцисс.

Как мы будем поступать здесь?

Нужно найти синус угла между ( displaystyle OA) и осью ( displaystyle Ox).

А где мы умеем искать синус? Верно, в прямоугольном треугольнике.

Так что нам нужно сделать? Построить этот треугольник!

Поскольку координаты точки ( displaystyle A-6) и ( displaystyle 8), то отрезок ( displaystyle OB) равен ( displaystyle 6), а отрезок ( displaystyle AB-8).

Нам нужно найти синус угла ( displaystyle angle AOB).

Напомню тебе, что синус – это отношение противолежащего катета к гипотенузе, тогда

Найти гипотенузу.

Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!).

Я пойду вторым путем:

Следующая задача покажется тебе еще проще. Она – на координаты точки.

Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки ( displaystyle A) до осей координат.

Задача – вообще элементарная, если знать, что такое расстояние от точки до осей.

Ты знаешь?

Я надеюсь, но все же напомню тебе:

Расстояние от точки до осей координат – это длины перпендикуляров, опущенных из точки к осям.

Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр. К какой он оси?

К оси ( displaystyle Ox).

И чему же равна тогда его длина?

Она равна ( displaystyle 8).

Теперь сам проведи перпендикуляр к оси ( displaystyle Oy) и найди его длину. Она будет равна ( displaystyle 6), ведь так?

Тогда их сумма равна ( displaystyle 14).

Ответ: ( displaystyle 14).

Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке ( displaystyle A) относительно оси абсцисс.

Решение:

Я думаю, тебе интуитивно ясно, что такое симметрия?

Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д.

Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой.

А что тогда такое ось?

Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии – прямая ( displaystyle l)):

Теперь давай вернемся к нашей задаче.

Нам известно, что мы ищем точку, симметричную относительно оси ( displaystyle Ox).

Тогда эта ось – ось симметрии.

Значит, нам нужно отметить такую точку ( displaystyle {{A}_{1}}), чтобы ось ( displaystyle Ox) разрезала отрезок ( displaystyle A{{A}_{1}}) на две равные части.

Попробуй сам отметить такую точку. А теперь сравни с моим решением:

У тебя получилось так же?

Хорошо! У найденной точки нас интересует ордината.

Она равна ( displaystyle -8)

Ответ: ( displaystyle -8)

Теперь задачка на параллелограмм:

Задача 5. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Cleft( 0;~6 right)~) яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки ( displaystyle B).

Можно решать эту задачу двумя способами: логикой и методом координат. 

Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.

Совершенно ясно, что абсцисса точки ( displaystyle B) равна ( displaystyle 6). (она лежит на перпендикуляре, проведенной из точки ( displaystyle A) к оси абсцисс).

Нам нужно найти ординату.

Воспользуемся тем, что наша фигура – параллелограмм, это значит, что ( displaystyle CA=OB).

Найдем длину отрезка ( displaystyle CA), используя формулу расстояния между двумя точками:

Опускаем перпендикуляр, соединяющий точку ( B) с осью ( Ox).

Точку пересечения обозначу буквой ( D).

Длина отрезка ( OD) равна ( 6). (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка ( BD) по теореме Пифагора:

Ответ: ( 2).

Другое решение (я просто приведу рисунок, который его иллюстрирует)

Ход решения:

• Провести ( CE);
• Найти координаты точки ( E) и длину ( AE);
• Доказать, что ( BD=AE).

Еще одна задачка на длину отрезка:

Точки ( Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 8;~2 right)) яв­ля­ют­ся вер­ши­на­ми тре­уголь­ни­ка. Най­ди­те длину его сред­ней линии ( CD), па­рал­лель­ной ( OA).

Ты помнишь, что такое средняя линия треугольника?

Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника – это линия, которая соединяет середины противоположных сторон.

Она параллельна основанию и равна его половине.

Основание – это отрезок ( OA).

Его длину нам приходилось искать ранее, оно равно ( 10).

Тогда длина средней линии вдвое меньше и равна ( 5).

Ответ: ( 5).

Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.

А пока – вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!

1. Точки ( Oleft( 0;~0 right),~Aleft( 10;~0 right),~Bleft( 8;~6 right),~Cleft( 2;~6 right)) яв­ля­ют­ся вер­ши­на­ми тра­пе­ции. Най­ди­те длину ее сред­ней линии ( DE).

2. Точки ( Oleft( 0;~0 right),~Bleft( 8;~2 right),~Cleft( 2;~6 right)) и ( A) яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки ( A).

3. Най­ди­те длину от­рез­ка, со­еди­ня­ю­ще­го точки ( Aleft( 6 ;~8 right)) и ( Bleft( -2;~2 right).)

4. Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры на ко­ор­ди­нат­ной плос­ко­сти.

5. Окруж­ность с цен­тром в на­ча­ле ко­ор­ди­нат про­хо­дит через точку ( displaystyle Pleft( 8;text{ }6 right)). Най­ди­те ее ра­ди­ус.

6. Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около пря­мо­уголь­ни­ка ( displaystyle ABCD), вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты со­от­вет­ствен­но ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right).)

Решения:

1. Известно, что средняя линия трапеции равна полусумме ее оснований.

Основание ( displaystyle CB) равно ( displaystyle 6), а основание ( displaystyle OA-10).

Тогда ( displaystyle ED=frac{CB+OA}{2}=frac{16}{2}=8)

Ответ: ( displaystyle

2. Проще всего решить эту задачу так: заметить, что ( displaystyle overrightarrow{OA}=overrightarrow{OC}+overrightarrow{OB}) (правило параллелограмма).

Тогда ( displaystyle overrightarrow{OA}) имеет координаты ( displaystyle left( 10,8 right)).

Эти же координаты имеет и точка ( displaystyle A), поскольку начало вектора ( displaystyle overrightarrow{OA}) – это точка с координатами ( displaystyle left( 0,0 right)).

Нас интересует ордината. Она равна ( displaystyle 8).

Ответ: ( displaystyle

3. Действуем сразу по формуле расстояния между двумя точками:

4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область?

Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького.

Сторона маленького квадрата – это отрезок, соединяющий точки ( displaystyle left( 0,2 right)) и ( displaystyle left( 2,0 right).) Его длина равна

Его длина равна

5. Если окружность имеет в качестве центра начало координат и проходит через точку ( displaystyle P), то ее радиус ( displaystyle R) будет в точности равен длине отрезка ( displaystyle OP) (сделай рисунок и ты поймешь, почему это очевидно).

6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали.

Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)

Ну что, ты со всем справился?

Было не очень сложно разобраться, ведь так? Правило здесь одно – уметь сделать наглядную картинку и просто «считать» с нее все данные.

Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить:

• как найти координаты середины отрезка и

Координаты середины отрезка

Давай попробуем решить вот такую нехитрую задачку.

Пусть даны две точки ( displaystyle Aleft( {{x}_{1}},{{x}_{2}} right)~) и ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).

Найти координаты середины отрезка ( displaystyle AB). Решение этой задачки следующее: пусть точка ( displaystyle D) – искомая середина, тогда ( displaystyle D) имеет координаты:

( displaystyle Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2} right))

То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.

Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:

1. Най­ди­те ор­ди­на­ту се­ре­ди­ны от­рез­ка, со­еди­ня­ю­ще­го точки ( displaystyle Aleft( 6,~8 right)~) и ( displaystyle Bleft( -2,~2 right).)

2. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 6;~2 right),~Cleft( 0;~6 right)) яв­ля­ют­ся вер­ши­на­ми че­ты­рех­уголь­ни­ка. Най­ди­те ор­ди­на­ту точки ( displaystyle P) пе­ре­се­че­ния его диа­го­на­лей.

3. Най­ди­те абс­цис­су цен­тра окруж­но­сти, опи­сан­ной около пря­мо­уголь­ни­ка ( displaystyle ABCD), вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты со­от­вет­ствен­но ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right)).

Решения:

1. Первая задачка – просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты ( displaystyle left( frac{6-2}{2},~frac{8+2}{2} right)=left( 2,5 right)).

Ордината равна ( displaystyle 5).

Ответ: ( displaystyle 5)

2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой.

Что я знаю про параллелограмм?

Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей – это что?

Это середина любой из диагоналей!

Выберу, в частности диагональ ( displaystyle OA). Тогда точка ( displaystyle P) имеет координаты ( displaystyle left( frac{6+0}{2},frac{8+0}{2} right)=left( 3,4 right).)

Ордината точки ( displaystyle P) равна ( displaystyle 4).

Ответ: ( displaystyle 4)

3. С чем совпадает центр описанной около прямоугольника окружности?

Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника?

Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей.

Возьму, например, диагональ ( displaystyle AC). Тогда если ( displaystyle P) – центр описанной окружности, то ( displaystyle P) – середина ( displaystyle AC).

Ищу координаты: ( displaystyle Pleft( frac{-2+6}{2},frac{-2+4}{2} right)=Pleft( 2,1 right).) Абсцисса равна ( displaystyle 2).

Ответ: ( displaystyle 2)

Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.

1. Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)

2. Най­ди­те ор­ди­на­ту цен­тра окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)

3. Ка­ко­го ра­ди­у­са долж­на быть окруж­ность с цен­тром в точке ( displaystyle Pleft( 8;~6 right),) чтобы она ка­са­лась оси абс­цисс?

4. Най­ди­те ор­ди­на­ту точки пе­ре­се­че­ния оси ( displaystyle Oy) и от­рез­ка, со­еди­ня­ю­ще­го точки ( displaystyle Aleft( 6;text{ }8 right)) и ( displaystyle Bleft( -6;text{ }0 right).)

Ответы:

• ( displaystyle 5);
• ( displaystyle 3);
• ( displaystyle 6);
• ( displaystyle 4).

Умножение векторов

Все удалось? Очень на это надеюсь! Теперь – последний рывок.

Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат, но также встречается повсеместно и в задачах повышенной сложности.

Какое из своих обещаний я еще не сдержал?

Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл?

Забыл! Забыл объяснить, что значит умножение векторов.

Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:

• Скалярное произведение (результат – число);
• Векторное произведение (результат – вектор).

Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим чуть позже. А пока мы остановимся на скалярном произведении.

Есть аж два способа, позволяющих нам его вычислить:

• Через координаты векторов;
• Через длины векторов и угол между ними.

Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:

Най­ди­те ска­ляр­ное про­из­ве­де­ние век­то­ров ( displaystyle {vec{a}}) и ( displaystyle {vec{b}})

Справился? Может, и подвох небольшой заметил? Давай проверим:

( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)) – координаты векторов, как в прошлой задаче! Ответ: ( displaystyle 40).

Скалярное произведение через длины векторов и косинус угла между ними

Помимо координатного, есть и другой способ вычислить скалярное произведение, а именно, через длины векторов и косинус угла между ними:

( displaystyle left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|coswidehat{vec{a},~vec{b}})

( displaystyle widehat{vec{a},~vec{b}}) – обозначает угол между векторами ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}).

То есть скалярное произведение равно произведению длин векторов на косинус угла между ними.

Зачем же нам эта вторая формула, если у нас есть первая, которая намного проще, в ней по крайней мере нет никаких косинусов?

А нужна она для того, что из первой и второй формулы мы с тобой сможем вывести, как находить угол между векторами!

Пусть ( displaystyle vec{a}left( {{x}_{1}},{{y}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}} right).) Тогда вспоминай формулу для длины вектора!

У нас теперь есть формула, позволяющая вычислять угол между двумя векторами! Иногда ее для краткости записывают еще и так:

( displaystyle coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|})

Решение:

1. Эти вектора – наши старые знакомые. Их скалярное произведение мы уже считали и оно было равно ( displaystyle 40).

Координаты у них такие: ( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)). Тогда найдем их длины:

Ответ: ( 45)

Ну а теперь сам реши вторую задачу, а потом сравним! Я приведу лишь очень краткое решение:

2. ( vec{a}+vec{b}) имеет координаты ( left( 10,10 right)), ( vec{a}-vec{b}) имеет координаты ( left( -6,2 right)).

Метод координат (продвинутый уровень)

Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:

• Находить координаты вектора;
• Находить длину вектора (альтернативно: расстояние между двумя точками);
• Складывать, вычитать векторы. Умножать их на вещественное число;
• Находить середину отрезка;
• Вычислять скалярное произведение векторов;
• Находить угол между векторами.

Конечно, в эти 6 пунктов не укладывается весь координатный метод.

Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!

Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.

Когда стоит применять метод координат

Итак, я бы стал применять метод координат, если ставятся вопросы:

• Найти угол между двумя плоскостями;
• Найти угол между прямой и плоскостью;
• Найти угол между двумя прямыми;
• Найти расстояние от точки до плоскости;
• Найти расстояние от точки до прямой;
• Найти расстояние от прямой до плоскости;
• Найти расстояние между двумя прямыми.

Подходящими фигурами для метода координат являются:

• Куб;
• Прямоугольный параллелепипед;
• Прямая призма (треугольная, шестиугольная…);
• Пирамида (треугольная, четырехугольная, шестиугольная);
• Тетраэдр (одно и то же, что и треугольная пирамида).

Неподходящими фигурами для метода координат являются тела вращения:

• шар;
• цилиндр;
• конус

По моему опыту, нецелесообразно использовать метод координат для:

• Нахождения площадей сечений;
• Вычисления объемов тел.

Однако следует сразу отметить, что три «невыгодные» для метода координат ситуации на практике достаточно редки.

В большинстве же задач он может стать твоим спасителем, особенно если ты не очень силен в трехмерных построениях (которые порою бывают довольно замысловатыми).

Как применять метод координат

Какими являются все перечисленные мною выше фигуры?

Они уже не плоские, как, например, квадрат, треугольник, окружность, а объемные! Соответственно, нам нужно рассматривать уже не двухмерную, а трехмерную систему координат.

Строится она достаточно легко: просто помимо оси абсцисс и ординат, мы введем еще одну ось, ось аппликат. На рисунке схематично изображено их взаимное расположение:

Все они являются взаимно перпендикулярными, пересекаются в одной точке ( displaystyle O), которую мы будем называть началом координат.

Ось абсцисс, как и прежде, будем обозначать ( Ox), ось ординат – ( Oy), а введенную ось аппликат – ( Oz).

Если раньше каждая точка на плоскости характеризовалась двумя числами – абсциссой и ординатой, то каждая точка в пространстве уже описывается тремя числами – абсциссой, ординатой, аппликатой.

Например:

Соответственно абсцисса точки ( displaystyle P) равна ( displaystyle 1), ордината – ( displaystyle 2), а аппликата – ( displaystyle 3).

Иногда абсциссу точки еще называют проекцией точки на ось абсцисс, ординату – проекцией точки на ось ординат, а аппликату – проекцией точки на ось аппликат. Соответственно, если задана точка ( Aleft( x,y,z right)) то, точку с координатами:

( Aleft( x,y,0 right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxy)

( Aleft( x,0,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxz)

( Aleft( 0,y,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oyz)

Встает естественный вопрос: справедливы ли все формулы, выведенные для двухмерного случая, в пространстве?

Ответ утвердительный, они справедливы и имеют тот же самый вид. За маленькой деталью. Я думаю, ты уже сам догадался, за какой именно.

Во все формулы мы должны будем добавить еще один член, отвечающий за ось аппликат.

Формулы метода координат для трехмерных фигур

1. Если заданы две точки: ( Aleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), ( Aleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:

• Координаты вектора ( overrightarrow{AB}): ( overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} right));
• Расстояние между двумя точками (или длина вектора ( overrightarrow{AB})) ( d=left| overrightarrow{AB} right|=sqrt{{{left( {{x}_{2}}-{{x}_{1}} right)}^{2}}+{{left( {{y}_{2}}-{{y}_{1}} right)}^{2}}+{{left( {{z}_{2}}-{{z}_{1}} right)}^{2}}});
• Середина ( D) отрезка ( AB) имеет координаты
• ( Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2},frac{{{z}_{1}}+{{z}_{2}}}{2} right)).

2. Если дано два вектора: ( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)) и ( vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:

• Их скалярное произведение равно: ( left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|cosoverset{}{widehat{vec{a},~vec{b}}},) или ( left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}});
• Косинус угла между векторами равен:
• ( cosoverset{}{widehat{vec{a},~vec{b}}},=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}}).

Плоскость — как «обобщение» прямой

Однако с пространством не все так просто.

Как ты понимаешь, добавление еще одной координаты вносит существенное разнообразие в спектр фигур, «живущих» в этом пространстве. И для дальнейшего повествования мне потребуется ввести некоторое, грубо говоря, «обобщение» прямой.

Этим «обобщением» будет плоскость. Что ты знаешь про плоскость? Попробуй ответить на вопрос, а что такое плоскость? Очень сложно сказать.

Однако мы все интуитивно представляем, как она выглядит:

Грубо говоря, это некий бесконечный «лист», засунутый в пространство. «Бесконечность» следует понимать, что плоскость распространяется во все стороны, то есть ее площадь равна бесконечности.

Однако, это объяснение «на пальцах» не дает ни малейшего представления о структуре плоскости. А нас будет интересовать именно она.

Давай вспомним одну из основных аксиом геометрии: через две различные точки на плоскости проходит прямая, притом только одна.

Или ее аналог в пространстве: через три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.

Уравнение прямой в плоскости и пространстве

Конечно, ты помнишь, как по двум заданным точкам вывести уравнение прямой, это совсем нетрудно: если первая точка имеет координаты: ( Aleft( {{x}_{0}},{{y}_{0}} right)) а вторая ( Bleft( {{x}_{1}},{{y}_{1}} right)), то уравнение прямой будет следующим:

Это следует понимать вот как: точка ( Dleft( x,y,z right)) лежит на прямой, если ее координаты удовлетворяют следующей системе:

Направляющий вектор прямой

Направляющий вектор прямой – любой ненулевой вектор, лежащий на данной прямой или параллельный ей.

Например, оба вектора ( overrightarrow{{{M}_{0}}{{M}_{1}}}), ( vec{s}) являются направляющими векторами прямой ( l). Пусть ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)) – точка, лежащая на прямой, а ( vec{p}left( m,n,q right)) – ее направляющий вектор.

Тогда уравнение прямой можно записать в следующем виде:

Еще раз: это ЛЮБОЙ ненулевой вектор, лежащий на прямой, или параллельный ей.

Уравнение плоскости

Вывести уравнение плоскости по трем заданным точкам уже не так тривиально, и обычно этот вопрос не рассматривается в курсе средней школы.

А зря!

Этот прием жизненно необходим, когда мы прибегаем к методу координат для решения сложных задач. Однако, я предполагаю, что ты полон желания научиться чему-то новому?

Более того, ты сможешь поразить своего преподавателя в ВУЗе, когда выяснится, что ты уже умеешь с методикой, которую обычно изучают в курсе аналитической геометрии. Итак, приступим.

Уравнение плоскости не слишком отличается от уравнения прямой на плоскости, а именно оно имеет вид:

Как видишь, уравнение плоскости не очень отличается от уравнения прямой (линейной функции). Однако, вспомни, что мы с тобой утверждали? Мы говорили, что если у нас есть три точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), не лежащие на одной прямой, то уравнение плоскости однозначно по ним восстанавливается.

Но как? Попробую тебе объяснить.

Поскольку уравнение плоскости имеет вид:

Дилемма! Однако всегда можно предполагать, что ( D=1) (для этого нужно разделить ( ~Ax+By+Cz+D=0) на ( D)).

Таким образом, мы получим три уравнения с тремя неизвестными ( displaystyle A,B,C):

Уравнение плоскости, проходящей через три заданные точки

Однако объект, который ты видишь перед собой не имеет ничего общего с модулем. Этот объект называется определителем третьего порядка.

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

Причем под первым индеком ( displaystyle i) мы понимаем номер строки, а под индеком ( displaystyle j) – номер столбца.

Например, ( {{a}_{23}}) означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

• Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
• Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
• Тогда определитель равен разности значений, полученных на шаге ( displaystyle 1) и ( displaystyle 2).

Если записать все это цифрами, то мы получим следующее выражение:

Давай проиллюстрируем метод треугольников на примере:

Метод треугольников на примере

1. Вычислить определитель: ( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right|)

Давай разбираться, что мы складываем, а что – вычитаем.

Слагаемые, которые идут с «плюсом»:

Это главная диагональ: произведение элементов равно 

( 2cdot 21cdot 9=378)

Первый треугольник, «перпендикулярный главной диагонали: произведение элементов равно 

( 3cdot left( -5 right)cdot 4=-60)

Второй треугольник, «перпендикулярный главной диагонали: произведение элементов равно 

( 11cdot 6cdot left( -1 right)=-66)

Складываем три числа: ( 378-60-66=252)

Слагаемые, которые идут с «минусом»:

Это побочная диагональ: произведение элементов равно 

( left( -1 right)cdot 21cdot 4=-84)

Первый треугольник, «перпендикулярный побочной диагонали: произведение элементов равно 

( 3cdot 11cdot 9=297)

Второй треугольник, «перпендикулярный побочной диагонали: произведение элементов равно 

( 6cdot left( -5 right)cdot 2=-60)

Складываем три числа:

Теперь попробуй самостоятельно вычислить:

• Главная диагональ: ( 2cdot 2cdot 2=8);
• Первый треугольник, перпендикулярный главной диагонали: ( left( -2 right)cdot 5cdot 1=-10);
• Второй треугольник, перпендикулярный главной диагонали: ( 3cdot 2cdot 4=24);
• Сумма слагаемых с плюсом: ( 8-10+24=22);
• Побочная диагональ: ( 1cdot 2cdot 4=8);
• Первый треугольник, перпендикулярный побочной диагонали: ( 2cdot 5cdot 2=20);
• Второй треугольник, перпендикулярный побочной диагонали: ( left( -2 right)cdot 3cdot 2=-12);
• Сумма слагаемых с минусом: ( 8+20-12=16);
• Сумма слагаемых с плюсом минус сумма слагаемых с минусом: ( 22-16=6).

Вывод:

( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right| = 6)

Вот тебе еще пара определителей, вычисли их значения самостоятельно и сравни с ответами:

• ( left| {begin{array}{*{20}{c}}1&3&{ — 1}\0&4&2\{ — 3}&2&0end{array}} right|);
• ( left| {begin{array}{*{20}{c}}3&1&7\6&2&{14}\{ — 1}&0&8end{array}} right|).

Ответы:

• ( displaystyle -34);
• ( displaystyle 0).

Ну что, все совпало?

Отлично, тогда можно двигаться дальше! Если же есть затрудения, то совет мой таков: в интернете есть куча программ вычисления определителя онлайн.

Все, что тебе нужно – придумать свой определитель, вычислить его самостоятельно, а потом сравнить с тем, что посчитает программа.

И так до тех пор, пока результаты не начнут совпадать. Уверен, этот момент не заставит себя долго ждать!

Теперь давай вернемся к тому определителю, который я выписал, когда говорил про уравнение плоскости, проходящей через три заданные точки:

Естественно, поскольку ( displaystyle x,y,z) – переменные, то ты получишь некоторое выражение, от них зависящее.

Именно это выражение и будет уравнением плоскости, проходящей через три заданные точки, не лежащие на одной прямой!

1. Построить уравнение плоскости, проходящей через точки

( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right))

Cоставляем для этих трех точек определитель:

Теперь попробуй решить одну задачку самостоятельно, а потом мы ее обсудим:

Составляем определитель:

Теперь две задачи для самоконтроля:

• Построить уравнение плоскости, проходящей через три точки: ( Kleft( 2,3,4 right),~Lleft( 6,-3,4 right),~Mleft( -4,6,-4 right).);
• Построить уравнение плоскости, проходящей через три точки:
• ( Aleft( 5,-1,3 right),~Bleft( 2,2,0 right),~Cleft( -1,1,1 right).).

Проверим:

• ( 6x+4y-3z-12=0);
• ( y+z-2=0).

Все совпало?

Опять-таки, если есть определенные затруднения, то мой совет таков: берешь из головы три точки (с большой степенью вероятности они не будут лежать на одной прямой), строишь по ним плоскость.

А потом проверяешь себя онлайн. Например, на сайте:

http://www.webmath.ru/web/prog9_1.php

Однако при помощи определителей мы будем строить не только уравнение плоскости. 

Вспомни, я говорил тебе, что для векторов определено не только скалярное произведение. Есть еще векторное, а также смешанное произведение.

Векторное произведение векторов

И если скалярным произведением двух векторов и будет число, то векторным произведением двух векторов ( vec{a}) и ( vec{b}) будет вектор ( ~vec{c}=vec{a}cdot vec{b}), причем данный вектор будет перпендикулярен к заданным:

Причем его модуль будет равен площади параллелограмма, построенного на векторах ( vec{a}) и ( vec{b}).

Данный вектор понадобится нам для вычисления расстояния от точки до прямой. Как же нам считать векторное произведение векторов ( vec{a}) и ( vec{b}), если их координаты заданы?

На помощь к нам опять приходит определитель третьего порядка.

Однако, прежде чем я перейду к алгоритму вычисления векторного произведения, я вынужден сделать небольшое лирическое отступление.

Данное отступление касается базисных векторов.

Базисными векторами в трехмерном пространстве называются три вектора:

Как ты думаешь, а почему они называется базисными? Дело в том, что любой вектор в трехмерном пространстве можно представить через сумму трех базисных векторов:

Справедливость этой формулы очевидна, ведь:

( vec{a}left( x,y,z right)=xcdot vec{i}+ycdot vec{j}+zcdot vec{k}=left( x,0,0 right)+left( 0,y,0 right)+left( 0,0,z right)=left( x,y,z right)=vec{a}.)

Смешанное произведение трех векторов

Последняя конструкция, которая мне понадобится – это смешанное произведение трех векторов. 

Оно, как и скалярное, является числом. Есть два способа его вычисления. ( displaystyle 1) – через определитель, ( displaystyle 2) – через смешанное произведение.

А именно, пусть у нас даны три вектора:

( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right),~vec{c}left( {{x}_{3}},{{y}_{3}},{{z}_{3}} right)), тогда смешанное произведение трех векторов, обозначаемое через ( (vec{a},vec{b},vec{c})) можно вычислить как:

1. ( left( vec{a},vec{b},vec{c} right)=left( vec{a},vec{b}cdot vec{c} right)) – то есть смешанное произведение – это скалярное произведения вектора на векторное произведение двух других векторов

И опять – два примера для самостоятельного решения:

• ( vec{a}left( 1,2,3 right),~vec{b}left( 1,1,1 right),~vec{c}left( 1,2,1 right));
• ( vec{a}left( 1,2,3 right),~vec{b}left( 1,-1,1 right),~vec{c}left( 2,0,-1 right)).

Ответы:

• ( displaystyle 2);
• ( displaystyle 1).

Выбор системы координат

Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.

Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.

Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.

Я напомню, что в этом разделе мы рассматриваем следующие фигуры:

• куб;
• Прямоугольный параллелепипед;
• Прямая призма (треугольная, шестиугольная…);
• Пирамида (треугольная, четырехугольная);
• Тетраэдр (одно и то же, что и треугольная пирамида).

Для каждой из фигур я дам практические рекомендации, как выбирать систему координат.

Я неслучайно расположил задачи в таком порядке. Пока ты еще не успел начать ориентироваться в методе координат, я сам разберу наиболее «проблемные» фигуры, а тебе предоставлю разобраться с простейшим кубом!

Постепенно тебе предстоит научиться работать со всеми фигурами, сложность задач я буду увеличивать от теме к теме.

Приступаем к решению задач:

1. Рисуем тетраэдр, помещаем его в систему координат так, как я предлагал ранее. Поскольку тетраэд правильный – то все его грани (включая основание) – правильные треугольники.

Поскольку нам не дана длина стороны, то я могу принять ее равной ( 1). Я думаю, ты понимаешь, что угол на самом деле не будет зависеть от того, насколько наш тетраэдр будет «растянут»?

Также проведу в тетраэдре высоту и медиану ( displaystyle BM).

Попутно я нарисую его основание (оно нам тоже пригодится).

Мне нужно найти угол между ( displaystyle DH) и ( displaystyle BM). Что нам известно?

Нам известна только координата точки ( displaystyle B). Значит, надо найти еще координаты точек ( displaystyle D,H,M).

Теперь думаем: точка ( displaystyle H) – это точка пересечения высот (или биссектрисс или медиан) треугольника ( displaystyle ABC).

А точка ( displaystyle D) – это приподнятая точка ( displaystyle H).

Точка же ( displaystyle M) – это середина отрезка ( displaystyle AD).

Тогда окончательно нам надо найти: координаты точек: ( displaystyle A,D,H,M).

Начнем с самого простого: координаты точки ( displaystyle A).

Смотри на рисунок: Ясно, что аппликата точки ( displaystyle A) равна нулю (точка лежит на плоскости ( displaystyle Oxy)).

Её ордината равна ( displaystyle 0,5) (так как ( displaystyle AK) – медиана).

Сложнее найти ее абсциссу. Однако это легко делается на основании теоремы Пифагора: Рассмотрим треугольник ( displaystyle BAS). Его гипотенуза ( displaystyle BA) равна ( displaystyle 1), а один из катетов ( displaystyle AS) равен ( displaystyle 0,5)

Тогда:

( BS=sqrt{B{{A}^{2}}-A{{S}^{2}}}=sqrt{1-frac{1}{4}}=frac{sqrt{3}}{2})

Окончательно имеем: ( Aleft( frac{sqrt{3}}{2},frac{1}{2},0 right)).

Теперь найдем координаты точки ( displaystyle H).

Ясно, что ее аппликата опять равна нулю, а ее ордината такая же, как у точки ( displaystyle A), то есть ( 0,5).

Найдем ее абсциссу. Это делается достаточно тривиально, если помнить, что высоты равностороннего треугольника точкой пересечения делятся в пропорции ( displaystyle mathbf{2}:mathbf{1}), считая от вершины. Так как: ( AK=BS=frac{sqrt{3}}{2}), то искомая абсцисса точки, равная длине отрезка ( displaystyle KH), равна: ( KH=frac{AK}{3}=frac{sqrt{3}}{6}). Т

аким образом, координаты точки ( displaystyle H) равны:

( Hleft( frac{sqrt{3}}{6},frac{1}{2},0 right).)

Найдем координаты точки ( displaystyle D).

Ясно, что ее абсцисса и ордината совпадают с абсциссой и ординатой точки ( displaystyle H). А аппликата равна длине отрезка ( displaystyle DH). ( displaystyle DH) – это один из катетов треугольника ( displaystyle DAH). Гипотенуза треугольника ( displaystyle DAH) – это отрезок ( AD=AB=1.) ( displaystyle AH) – катет.

Он ищется из соображений, которые я выделил жирным шрифтом:

( AH=frac{2}{3}cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{3})

Тогда:

( DH=sqrt{1-{{left( frac{sqrt{3}}{3} right)}^{2}}}=sqrt{frac{2}{3}})

Отсюда:

( Dleft( frac{sqrt{3}}{6},frac{1}{2},sqrt{frac{2}{3}} right).)

Точка ( M) – это середина отрезка ( AD). Тогда нам нужно вспомнить формулу координат середины отрезка:

( Mleft( frac{frac{sqrt{3}}{2}+frac{sqrt{3}}{6}}{2},~frac{frac{1}{2}+frac{1}{2}}{2},frac{0+sqrt{frac{2}{3}}}{2} right)=Mleft( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right).~)

Ну все, теперь мы можем искать координаты направляющих векторов:

( overrightarrow{BM}left( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right))

( overrightarrow{DH}left( 0,0,-sqrt{frac{2}{3}} right))

Ну что, все готово: подставляем все данные в формулу:

( displaystyle cosvarphi =frac{left| frac{1}{sqrt{6}}cdot left( -sqrt{frac{2}{3}} right) right|}{sqrt{{{left( frac{sqrt{3}}{3} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}+{{left( frac{1}{sqrt{6}} right)}^{2}}}cdot sqrt{{{left( -sqrt{frac{2}{3}} right)}^{2}}}}=frac{frac{1}{3}}{sqrt{frac{19}{36}}cdot sqrt{frac{2}{3}}}=frac{frac{1}{3}}{sqrt{frac{19}{54}}}=frac{sqrt{54}}{3sqrt{19}}=sqrt{frac{6}{19}})

Таким образом, ( varphi =arccossqrt{frac{6}{19}}.)

Ответ: ( varphi =arccossqrt{frac{6}{19}}.)

Тебя не должны пугать такие «страшные» ответы: для задач С2 это обычная практика. Я бы скорее удивился «красивому» ответу в этой части. Также, как ты заметил, я практически не прибегал ни к чему, кроме как к теореме Пифагора и свойству высот равностороннего треугольника. То есть для решения стереометрической задачи я использовал самый минимум стереометрии. Выигрыш в этом частично «гасится» достаточно громоздкими вычислениями. Зато они достаточно алгоритмичны!

2. Изобразим правильную шестиугольную пирамиду вместе с системой координат, а также ее основание:

Нам нужно найти угол между прямыми ( displaystyle SB) и ( displaystyle CD).

Таким образом, наша задача сводится к поиску координат точек: ( displaystyle S,B,C,D).

Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины ( displaystyle S) найдем через координату точки ( displaystyle O).

Работы навалом, но надо к ней приступать!

a) Координата ( displaystyle D): ясно, что ее аппликата и ордината равны нулю.

Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник ( displaystyle EDP). Увы, в нем нам известна только гипотенуза, которая равна ( displaystyle 1). Катет ( displaystyle DP) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета ( displaystyle DP) даст нам абсциссу точки ( displaystyle D)).

Как же нам ее искать?

Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.

А что это значит? Это значит, что у него все стороны и все углы равны. Надо бы найти один такой угол. Есть идеи?

Идей масса, но есть формула:

Сумма углов правильного n-угольника равна ( left( n-2 right)cdot 180{}^circ ).

Таким образом, сумма углов правильного шестиугольника равна ( displaystyle 720) градусов. Тогда каждый из углов равен:

( frac{720{}^circ }{6}=120{}^circ )

Вновь смотрим на картинку.

Ясно, что отрезок ( displaystyle EB) – биссектрисса угла ( displaystyle DEF). Тогда угол ( displaystyle DEP) равен ( displaystyle 60) градусам.

Тогда:

( sin60{}^circ =frac{sqrt{3}}{2}=frac{DP}{ED}=frac{DP}{1}=DP)

Тогда ( DP=frac{sqrt{3}}{2}), откуда ( DF=2DP=sqrt{3}).

Таким образом, ( displaystyle D) имеет координаты ( Dleft( sqrt{3},0,0 right))

b) Теперь легко найдем координату точки ( C): ( Cleft( sqrt{3},1,0 right)).

c) Найдем координаты точки ( displaystyle B).

Так как ее абсцисса совпадает с длиной отрезка ( FP) то она равна ( frac{sqrt{3}}{2}).

Найти ординату тоже не очень сложно: если мы соединим точки ( displaystyle C) и ( displaystyle A) а точку пересечения прямой ( displaystyle AC) обозначим, скажем за ( displaystyle M). (сделай сам несложное построение). Тогда ( BM=EP.)

Таким образом, ордината точки B равна сумме длин отрезков ( PM+MB). Вновь обратимся к треугольнику ( displaystyle DEP).

Тогда

( frac{1}{2}=cos60{}^circ =frac{EP}{ED}=EP)

Тогда так как ( PM=DC=1,~mo~PB=1+frac{1}{2}=frac{3}{2}.) Тогда точка ( B) имеет координаты ( Bleft( frac{sqrt{3}}{2},frac{3}{2},0 right).)

d) Теперь найдем координаты точки ( displaystyle O).

Рассмотри прямоугольник ( displaystyle ACDF) и докажи, что ( PO=frac{1}{2}.)

Таким образом, координаты точки ( displaystyle O): ( Oleft( frac{sqrt{3}}{2},frac{1}{2},0 right).)

e) Осталось найти координаты вершины ( S). Ясно, что ее абсцисса и ордината совпадает с абсциссой и ординатой точки ( O).

Найдем аппликату. Так как ( FC=EB=2), то ( OF=1). Рассмотрим прямоугольный треугольник ( displaystyle OFS). По условию задачи боковое ребро ( FS=2). Это гипотенуза моего треугольника.

Тогда высота пирамиды ( displaystyle OS) – катет.

( OS=sqrt{F{{S}^{2}}-O{{F}^{2}}}=sqrt{4-1}=sqrt{3})

Тогда точка ( S) имеет координаты: ( Sleft( frac{sqrt{3}}{2},frac{1}{2},sqrt{3} right).)

Ну все, у меня есть координаты всех интересующих меня точек. Ищу координаты направляющих векторов прямых:

( overrightarrow{SB}left( frac{sqrt{3}}{2}-frac{sqrt{3}}{2},frac{1}{2}-frac{3}{2},sqrt{3}-0 right)=overrightarrow{SB}left( 0,-1,sqrt{3} right).)

( overrightarrow{CD}left( sqrt{3}-sqrt{3},0-1,0 right)=overrightarrow{CD}left( 0,-1,0 right).)

Ищем угол между этими векторами:

( cosvarphi =frac{left| 0+left( -1 right)cdot left( -1 right)+sqrt{3}cdot 0 right|}{sqrt{{{left( -1 right)}^{2}}+{{left( sqrt{3} right)}^{2}}}cdot sqrt{{{left( -1 right)}^{2}}}}=frac{1}{2})

Тогда ( varphi =arccos left( frac{1}{2} right)=60{}^circ )

Ответ: ( 60{}^circ )

Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.

3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице. 

Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.

Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:

Ищем угол между ( displaystyle BM) и ( displaystyle PH).

Я буду делать очень краткие выкладки, когда буду заниматься поиском координат точек. Тебе необходимо будет «расшифровать» их:

a) ( Bleft( 0,1,0 right))

b) ( displaystyle H) – середина отрезка ( displaystyle AC). Её координаты:

( Hleft( frac{1}{2},frac{1}{2},0 right))

c) Длину отрезка ( displaystyle AH) я найду по теореме Пифагора в треугольнике ( displaystyle AHD). ( AH=frac{sqrt{2}}{2}.) Найду ( displaystyle PH) по теореме Пифагора в треугольнике ( displaystyle AHP).

( PH=sqrt{1-frac{1}{2}}=frac{1}{sqrt{2}})

Координаты ( P): ( Pleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).)

d) ( M) – середина отрезка ( AP). Ее координаты равны ( Mleft( frac{1}{4},frac{1}{4},frac{1}{2sqrt{2}} right).)

e) Координаты вектора ( overrightarrow{PH}:~overrightarrow{PH}left( 0,0,-frac{1}{sqrt{2}} right).~)

f) Координаты вектора ( overrightarrow{BM}:~overrightarrow{BM}left( frac{1}{4},-frac{3}{4},frac{1}{2sqrt{2}} right).)

g) Ищем угол: ( cosvarphi =frac{frac{1}{4}}{frac{1}{sqrt{2}}cdot frac{sqrt{3}}{2}}=frac{1}{sqrt{6}})

h) Ответ: ( arccosfrac{1}{sqrt{6}})

Куб – простейшая фигура. Я уверен, что с ней ты разберешься самостоятельно. Ответы к задачам 4 и 5 следующие:

4. ( arccosfrac{4}{sqrt{30}})

5. ( arccosfrac{1}{sqrt{15}})

Нахождение угла между прямой и плоскостью

Ну что, время простых задачек окончено!

Теперь примеры будут еще сложнее. Для отыскания угла между прямой и плоскостью мы будем поступать следующим образом:

• По трем точкам строим уравнение плоскости: ( Ax+By+Cz+D=0), используя определитель третьего порядка;
• По двум точкам ищем координаты направляющего вектора прямой: ( vec{s}left( l,m,n right));
• Применяем формулу для вычисления угла между прямой и плоскостью: ( sinvarphi =frac{left| Al+Bm+Cn right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}~}cdot sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}})

Как видишь, эта формула очень похожа на ту, что мы применяли для поиска углов между двумя прямыми.

Структура правой части просто одинакова, а слева мы теперь ищем синус, а не косинус, как раньше. Ну и добавилось одно противное действие – поиск уравнения плоскости.

Опять я решу первые две задачи подробно, третью – кратко, а последние две оставляю тебе для самостоятельного решения.

К тому же тебе уже приходилось иметь дело с треугольной и четырехугольной пирамидами, а вот с призмами – пока что нет.

Решения:

1. Изобразим призму, а также ее основание. Совместим ее с системой координат и отметим все данные, которые даны в условии задачи:

Извиняюсь за некоторое несоблюдение пропорций, но для решения задачи это, по сути, не так важно. Плоскость ( BC{{C}_{1}}) – это просто «задняя стенка» моей призмы. Достаточно просто догадаться, что уравнение такой плоскости имеет вид:

( x=0)

Однако, это можно показать и непосредственно:

Выберем произвольные три точки на этой плоскости: например, ( Bleft( 0,0,0 right),~Cleft( 0,8,0 right),~{{B}_{1}}left( 0,0,3 right)).

Составим уравнение плоскости:

( left| {begin{array}{*{20}{c}}x&0&0\y&8&0\z&0&3end{array}} right| = 0)

Упражнение тебе: самостоятельно вычислить этот определитель. У тебя получилось ( 24x)? Тогда уравение плоскости имеет вид:

( 24x=0)

Или просто

( x=0)

Таким образом, ( A=1,B=0,C=0,D=0.)

Для решения примера мне нужно найти координаты направляющего вектора прямой ( B{{A}_{1}}).

Так как точка ( B) cовпала с началом координат, то координаты вектора (overrightarrow{B{{A}_{1}}}) просто совпадут с координатами точки ( {{A}_{1}}.)

Для этого найдем вначале координаты точки ( displaystyle A).

Для этого рассмотрим треугольник ( displaystyle ABC).

Проведем высоту (она же – медиана и биссектрисса) из вершины ( displaystyle A).

Так как ( BC=8), то ордината точки ( displaystyle A) равна ( displaystyle 4).

Для того, чтобы найти абсциссу этой точки, нам нужно вычислить длину отрезка ( displaystyle AT).

По теореме Пифагора имеем:

( AT=sqrt{A{{B}^{2}}-B{{T}^{2}}}=sqrt{25-16}=3.)

Тогда точка ( displaystyle A) имеет координаты:

( Aleft( 3,4,0 right))

Точка ( {{A}_{1}})– это «приподнятая» на ( displaystyle 3) точка ( displaystyle A):

( {{A}_{1}}left( 3,4,3 right))

Тогда координаты вектора ( overrightarrow{B{{A}_{1}}}):

( overrightarrow{B{{A}_{1}}}left( 3,4,3 right).)

( sinvarphi =frac{left| 3cdot 1+4cdot 0+3cdot 0 right|}{sqrt{{{1}^{2}}+{{0}^{2}}+{{0}^{2}}}cdot sqrt{{{3}^{2}}+{{4}^{2}}+{{3}^{2}}}}=frac{3}{sqrt{34}}.)

( varphi =arcsinfrac{3}{sqrt{34}}.)

Ответ: ( arcsinfrac{3}{sqrt{34}}.)

Как видишь, ничего принципиально сложного при решении таких задач нет. На самом деле процесс еще немного упрощает «прямота» такой фигуры, как призма.

Теперь давай перейдем к следующему примеру:

2. Рисуем параллелепипед, проводим в нем плоскость и прямую, а также отдельно вычерчиваем его нижнее основание:

Вначале найдем уравнение плоскости: Координаты трех точек, лежащих в ней:

( Aleft( 0,0,0 right),~Bleft( 0,2,0 right),{{C}_{1}}left( 1,2,1 right)) (первые две координаты получены очевидным способом, а последнюю координату ты легко найдешь по картинке из точки ( C)). Тогда составляем уравнение плоскости:

( left| {begin{array}{*{20}{c}}x&0&1\y&2&2\z&0&1end{array}} right| = 0)

Вычисляем:

( 2x-2z=0,~x-z=0)

Тогда ( A=1,B=0,C=-1,D=0.)

Ищем координаты направляющего вектора ( overrightarrow{A{{B}_{1}}}): Ясно, что его координаты совпадают с координатами точки ( {{B}_{1}}), не правда ли?

Как найти координаты ( {{B}_{1}})?

Это же координаты точки ( B), приподнятые по оси аппликат на единицу! ( {{B}_{1}}left( 0,2,1 right)). Тогда ( overrightarrow{A{{B}_{1}}}left( 0,2,1 right).)

Ищем искомый угол:

( sinvarphi =frac{left| 1cdot 0+0cdot 2+left( -1 right)cdot 1 right|}{sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}+{{0}^{2}}~}cdot sqrt{0+{{2}^{2}}+{{1}^{2}}}}=frac{1}{sqrt{10}}.)

( ~varphi =arcsinfrac{1}{sqrt{10}}.)

Ответ: ( arcsinfrac{1}{sqrt{10}}.)

3. Рисуем правильную шестиугольную призму, а затем проводим в ней плоскость и прямую.

Тут даже плоскость нарисовать проблемно, не говоря уже о решении этой задачи, однако методу координат все равно! Именно в его универсальности и заключается его основное преимущество!

Плоскость проходит через три точки: ( A,C,{{D}_{1}}). Ищем их координаты:

1) ( Aleft( 0,0,0 right),~left( frac{sqrt{3}}{2},frac{3}{2},0 right), {{D}_{1}}left( sqrt{3},1,1 right)). Сам выведи координаты для последних двух точек. Тебе пригодится для этого решение задачи с шестиугольной пирамидой!

2) Строим уравнение плоскости:

( left| {begin{array}{*{20}{c}}x&{frac{{sqrt 3 }}{2}}&{sqrt 3 }\y&{frac{3}{2}}&1\z&0&1end{array}} right| = 0)

( -sqrt{3}x+y+2z=0)

( A=-sqrt{3},B=1,C=2,D=0.)

Ищем координаты вектора ( overrightarrow{A{{C}_{1}}}): ( text{ }!!~!!text{ }overrightarrow{A{{C}_{1}}}left( frac{sqrt{3}}{2},frac{3}{2},1 right)). (снова смотри задачу с треугольной пирамидой!)

3) Ищем угол:

( sinvarphi =frac{left| -sqrt{3}cdot frac{sqrt{3}}{2}+frac{3}{2}+2 right|}{sqrt{{{left( frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{3}{2} right)}^{2}}+{{1}^{2}}~}cdot sqrt{{{left( -sqrt{3} right)}^{2}}+{{1}^{2}}+{{2}^{2}}}}=frac{2}{2sqrt{8}}=frac{1}{2sqrt{2}}.)

Ответ: ( arcsinfrac{1}{2sqrt{2}}.)

Как видишь, ничего сверхъестественно сложного в этих задачах нет. Нужно лишь быть очень внимательным с корнями. К последним двум задачам я дам лишь ответы:

4. ( text{arcsin}frac{12}{sqrt{193}}~)

5. ( text{arcsin}frac{1}{sqrt{6}}~)

Как ты мог убедиться, техника решения задач везде одинаковая: основная задача найти координаты вершин и подставить их в некие формулы. Нам осталось рассмотреть еще один класс задач на вычисление углов, а именно: вычисление углов между двумя плоскостями.

Решения задач:

1. Сто­ро­на ос­но­ва­ния пра­виль­ной тре­уголь­ной приз­мы ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) равна ( 2), а диа­го­наль бо­ко­вой грани равна ( sqrt{5}). Най­ди­те угол между плос­ко­стью ( {{A}_{1}}BC) и плос­ко­стью ос­но­ва­ния приз­мы.

Рисую правильную (в основании – равносторонний треугольник) треугольную призму и отмечаю на ней плоскости, которые фигурируют в условии задачи:

Нам нужно найти уравнения двух плоскостей: ( ABC~и~BC{{A}_{1}}.) Уравнение основания получается тривиально: ты можешь составить соответствующий определитель по трем точкам, я же составлю уравнение сразу:

( z=0.)

То есть:

( {{A}_{1}}=0, {{B}_{1}}=0, {{C}_{1}}=1, {{D}_{1}}=0.)

Теперь найдем уравнение ( BC{{A}_{1}}.) Точка ( B) имеет координаты ( Bleft( 0,0,0 right).) Точка ( C) – ( Cleft( 0,1,0 right).)

Так как ( AO) – медиана и высота треугольника ( ABC), то ( BO=OC=1.) ( AO) легко находится по теореме Пифагора в треугольнике ( BAO:) ( AO=sqrt{4-1}=sqrt{3}).

Тогда точка ( A) имеет координаты: ( Aleft( sqrt{3},1,0 right).)

Найдем аппликату точки ( {{A}_{1}}.) Для этого рассмотрим прямоугольный треугольник ( {{A}_{1}}AC.~)

( A{{A}_{1}}=sqrt{{{A}_{1}}{{C}^{2}}-A{{C}^{2}}}=1.)

Тогда получаем вот такие координаты: ( {{A}_{1}}left( sqrt{3},1,1 right).) Cоставляем уравнение плоскости ( BC{{A}_{1}}).

( left| {begin{array}{*{20}{c}}x&0&{sqrt 3 }\y&1&1\z&0&1end{array}} right| = 0.)

( x+sqrt{3}z-sqrt{3}z-sqrt{3}y=0)

( x-sqrt{3}z=0)

Тогда

( {{A}_{2}}=1, {{B}_{2}}=0, {{C}_{2}}=-sqrt{3}, {{D}_{2}}=0.)

Вычисляем угол между плоскостями:

( cosvarphi =frac{left| -sqrt{3} right|}{sqrt{1+{{left( -sqrt{3} right)}^{2}}}}=frac{sqrt{3}}{2}.)

Отсюда

( varphi =30{}^circ .)

Ответ: ( 30{}^circ .)

2. В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де ( displaystyle SABCD), все ребра ко­то­рой равны ( displaystyle 1), най­ди­те синус угла между плос­ко­стью ( displaystyle SAD) и плос­ко­стью, про­хо­дя­щей через точку ( displaystyle A) пер­пен­ди­ку­ляр­но пря­мой ( displaystyle BD).

Делаем рисунок:

Самое сложное – это понять, что это такая за таинственная плоскость, проходящая через точку ( A) перпендикулярно ( DB).

Ну что же, главное, это что? Главное – это внимательность! В самом деле, прямая ( AC) перпендикулярна ( BD). Прямая ( OS) также перпендикулярна ( BD).

Тогда плоскость, проходящая через эти две прямые, будет перпендикулярна прямой ( BD), и, кстати, проходить через точку ( A). Эта плоскость также проходит через вершину пирамиды.

Тогда искомая плоскость – ( SAC.) А плоскость ( SAD) нам уже дана. Ищем координаты точек ( displaystyle S,A,C,D).

• ( displaystyle Aleft( 0,1,0 right))
• ( displaystyle Cleft( 1,0,0 right))
• ( displaystyle Dleft( 0,0,0 right))

Координату точки ( S) найдем через точку ( O). Из маленького рисунка легко вывести, что координаты у точки ( O) будут такие: ( Oleft( frac{1}{2},frac{1}{2},0 right).~)

Что теперь осталось найти, чтобы найти координаты вершины пирамиды?

Еще нужно вычислить ее высоту.

Это делается при помощи все той же теоремы Пифагора: вначале докажи, что ( OB=frac{sqrt{2}}{2}) (тривиально из маленьких треугольничков, образующих квадрат в основании).

Так как по условию ( SB=1), то имеем:

( OS=sqrt{1-{{left( frac{sqrt{2}}{2} right)}^{2}}}=frac{1}{sqrt{2}}.)

Теперь все готово: координаты вершины:

( Sleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).~)

Составляем уравнение плоскости ( displaystyle DAS):

( left| {begin{array}{*{20}{c}}x&0&{frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)

Ты уже спец в вычислении определителей. Без труда ты получишь:

( frac{1}{sqrt{2}}x-frac{1}{2}z=0)

Или иначе (если домножим обе части на корень из двух)

( x-frac{1}{sqrt{2}}z=0.)

Теперь найдем уравнение плоскости ( displaystyle SAC):

( left| {begin{array}{*{20}{c}}{x — 1}&{ — 1}&{ — frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)

(ты ведь не забыл, как мы получаем уравнение плоскости, правда?

Если ты не понял, откуда взялась эта минус единица, то вернись к определению уравнения плоскости! Просто всегда до этого оказывалось так, что моей плоскости принадлежало начало координат!)

Вычисляем определитель:

( begin{array}{l}frac{x-1}{sqrt{2}}-frac{1}{2}z+frac{1}{2}z+frac{y}{sqrt{2}}=0\frac{x-1}{sqrt{2}}+frac{y}{sqrt{2}}=0\x+y-1=0end{array}).

(Ты можешь заметить, что уравнение плоскости совпало с уравнением прямой, проходящей через точки ( displaystyle A) и ( displaystyle C)! Подумай, почему!)

Теперь вычисляем угол:

( cosvarphi =frac{left| 1+1cdot 0-frac{1}{sqrt{2}}cdot 0 right|}{sqrt{1+{{left( -frac{1}{sqrt{2}} right)}^{2}}}cdot sqrt{{{1}^{2}}+{{1}^{2}}}~~}=frac{1}{sqrt{3}}.)

Нам же нужно найти синус:

( sinvarphi =sqrt{1-{{cos }^{2}}varphi }=sqrt{1-frac{1}{3}}=sqrt{frac{2}{3}}).

Ответ: ( sqrt{frac{2}{3}}.)

3. В правильной че­ты­рех­уголь­ной призме ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) сто­ро­ны ос­но­ва­ния равны ( displaystyle 1), а бо­ко­вые ребра равны ( displaystyle 5). На ребре ( A{{A}_{1}}) от­ме­че­на точка ( displaystyle E) так, что ( AE:E{{A}_{1}}=2:3). Найдите угол между плос­ко­стя­ми ( ABC) и ( BE{{D}_{1}}.)

Каверзный вопрос: а что такое прямоугольная призма, как ты думаешь? Это же всего-то навсего хорошо известный тебе параллелепипед! Сразу же делаем чертеж! Можно даже отдельно не изображать основание, пользы от него здесь немного:

Плоскость ( ABC), как мы уже раньше заметили, записывается в виде уравнения:

( z=0.)

Теперь составляем плоскость ( BE{{D}_{1}}.)

( Bleft( 0,0,0 right),~Eleft( 1,0,2 right),~{{D}_{1}}left( 1,1,5 right).)

Cразу же составляем уравнение плоскости:

( left| {begin{array}{*{20}{c}}x&1&1\y&0&1\z&2&5end{array}} right| = 0)

( begin{array}{l}2y+z-2x-5y=0\-2x-3y+z=0\2x+3y-z=0end{array})

Ищем угол:

( cosvarphi =frac{1}{sqrt{4+9+1}}=frac{1}{sqrt{14}})

Ответ: ( arccos frac{1}{sqrt{14}}~~)

Теперь ответы к последним двум задачам:

4. ( arccosfrac{2}{3})

5. ( sqrt{frac{2}{3}})

Ну что же, теперь самое время немного передохнуть, ведь мы с тобой молодцы и проделали огромную работу!

Вычисление расстояния от точки до плоскости

Что нам потребуется для решения этой задачи?

• Координаты точки ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
• Уравнение плоскости ( Ax+By+Cz+D=0.)

Итак, как только мы получим все необходимые данные, то применяем формулу:

( d=frac{left| A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}})

Как мы строим уравнение плоскости тебе уже должно быть известно из предыдущих задач, которые я разбирал в прошлой части. Давай сразу приступим к задачам.

Схема следующая: 1, 2 –я помогаю тебе решать, причем довольно подробно, 3, 4 – только ответ, решение ты проводишь сам и сравниваешь. Начали!

Решения:

1. Рисуем кубик с единичными ребрами, строим отрезок и плоскость, середину отрезка ( B{{C}_{1}}) обозначим буквой ( M)

Вначале давай начнем с легкого: найдем координаты точки ( displaystyle M). Так как ( displaystyle Bleft( 0,1,0 right),~{{C}_{1}}left( 1,1,1 right),~) то ( displaystyle Mleft( frac{1}{2},1,frac{1}{2} right).) (вспомни координаты середины отрезка!)

Теперь составляем уравнение плоскости по трем точкам ( displaystyle Aleft( 0,0,0 right),~{{B}_{1}}left( 0,1,1 right),~{{D}_{1}}left( 1,0,1 right).)

(left| {begin{array}{*{20}{c}}x&0&1\y&1&0\z&1&1end{array}} right| = 0)

( displaystyle x+y-z=0.)

( displaystyle A=1,B=1,C=-1,~D=0.)

Теперь я могу приступать к поиску расстояния:

( displaystyle d=frac{left| frac{1}{2}+1-frac{1}{2} right|}{sqrt{1+1+1}}=frac{1}{sqrt{3}})

Ответ: ( displaystyle frac{1}{sqrt{3}})

2. Вновь начинаем с чертежа, на котором отмечаем все данные!

Для пирамиды было бы полезно отдельно рисовать ее основание.

Даже тот факт, что я рисую как курица лапой, не помешает нам с легкостью решить эту задачу!

1. ( AO=OC=frac{1}{2}AC=frac{sqrt{{{2}^{2}}+{{2}^{2}}}}{2}=sqrt{2}).

Тогда ( OS=sqrt{S{{C}^{2}}-O{{C}^{2}}}=sqrt{3}.)

Теперь легко найти координаты точки ( S.)

Так как координаты точки ( O:Oleft( 1,1,0 right),~), то ( Sleft( 1,1,sqrt{3} right).)

2. Так как координаты точки ( C:) ( Cleft( 2,2,0 right),) а ( M) – середина отрезка ( SC), то

( Mleft( frac{3}{2},frac{3}{2},frac{sqrt{3}}{2} right).)

Без проблем найдем и координаты еще двух точек на плоскости ( ADM.) ( Dleft( 1,0,0 right),~Aleft( 0,0,0 right).) Составляем уравнение плоскости и упростим его:

(left| {left| {begin{array}{*{20}{c}}x&1&{frac{3}{2}}\y&0&{frac{3}{2}}\z&0&{frac{{sqrt 3 }}{2}}end{array}} right|} right| = 0)

( frac{3}{2}z-frac{sqrt{3}}{2}y=0)

( sqrt{3}y-3z=0)

( y-sqrt{3}z=0.)

Так как точка ( B) имеет координаты: ( Bleft( 0,2,0 right)), то вычисляем расстояние:

( d=frac{2}{sqrt{1+3}}=1.)

Ответ (очень редкий!): ( 1)

Ну что, разобрался?

Мне кажется, что здесь все так же технично, как и в тех примерах, что мы рассматривали с тобой в предыдущей части. Так что я уверен, что если ты овладел тем материалом, то тебе не составит труда решить оставшиеся две задачи.

Я лишь приведу ответы:

• ( frac{3sqrt{39}}{4})
• ( frac{sqrt{3}}{2})

Вычисление расстояния от прямой до плоскости

На самом деле, здесь нет ничего нового. Как могут располагаться прямая и плоскость друг относительно друга?

У них есть всего ( 2) возможности: пересечься, или прямая параллельна плоскости. Как ты думаешь, чем равно расстояние от прямой до плоскости, с которой данная прямая пересекается?

Мне кажется, что тут ясно, что такое расстояние равно нулю. Неинтересный случай.

Второй случай хитрее: тут уже расстояние ненулевое. Однако, так как прямая параллельна плоскости, то каждая точка прямой равноудалена от этой плоскости:

Таким образом:

Расстояние от плоскости до параллельной ей прямой равно расстоянию от любой точки прямой до плоскости.

А это значит, что моя задача свелась к предыдущей: ищем координаты любой точки на прямой, ищем уравнение плоскости, вычисляем расстояние от точки до плоскости.

На самом деле, такие задачи в ЕГЭ встречаются крайне редко. Мне удалось найти лишь одну задачу, и то данные в ней были такими, что метод координат к ней был не очень-то и применим!

Теперь перейдем к другому, гораздо более важному классу задач:

Вычисление расстояния точки до прямой

Что нам потребуется?

• Координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
• Координаты любой точки, лежащей на прямой ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
• Координаты направляющего вектора прямой ( vec{s}left( m,n,p right))

Какую применяем формулу?

Ответ: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})

Что означает знаменатель данной дроби тебе и так должно быть ясно: это длина направляющего вектора прямой. Здесь очень хитрый числитель!

Выражение ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|) означает модуль (длина) векторного произведения векторов ( overrightarrow{{{M}_{0}}{{M}_{1}}}) и ( vec{s}.)

Как вычислять векторное произведение, мы с тобой изучали в предыдущей части работы. Освежи свои знания, нам они сейчас очень пригодятся!

Таким образом, алгоритм решения задач будет следующий:

• Ищем координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
• Ищем координаты любой точки на прямой, до которой мы ищем расстояние: ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
• Строим вектор ( overrightarrow{{{M}_{0}}{{M}_{1}}}:) ( overrightarrow{{{M}_{0}}{{M}_{1}}}left( {{x}_{1}}-{{x}_{0}},{{y}_{1}}-{{y}_{0}},{{z}_{1}}-{{z}_{0}} right).)
• Строим направляющий вектор прямой ( vec{s}left( m,n,p right))
• Вычисляем векторное произведение ( overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s})
• Ищем длину полученного вектора: ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|)
• Вычисляем расстояние: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})

Работы у нас много, а примеры будут достаточно сложными! Так что теперь сосредоточь все внимание!

1. Дана пра­виль­ная тре­уголь­ная пи­ра­ми­да ( DABC) с вер­ши­ной ( D). Сто­ро­на ос­но­ва­ния пи­ра­ми­ды равна ( sqrt{6}), вы­со­та равна ( sqrt{30}).

Най­ди­те рас­сто­я­ние от се­ре­ди­ны бо­ко­во­го ребра ( BD) до пря­мой ( MT), где точки ( M) и ( T) — се­ре­ди­ны ребер ( AC) и ( AB) со­от­вет­ствен­но.

2. Длины ребер ( AB,A{{A}_{1}}) и ( AD) пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) равны со­от­вет­ствен­но ( 12,text{ }16~) и ( 15.)

Най­ди­те рас­сто­я­ние от вер­ши­ны ( {{A}_{1}}) до пря­мой ( B{{D}_{1}}.)

3. В пра­виль­ной ше­сти­уголь­ной приз­ме ( ABCDEF{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}{{E}_{1}}{{F}_{1}}) все ребра ко­то­рой равны ( 1) най­ди­те рас­сто­я­ние от точки ( B) до пря­мой ( {{E}_{1}}{{F}_{1}}.)

Решения:

1. Делаем аккуратный чертеж, на котором отмечаем все данные:

Ну что же, работы нам предстоит немало! Принимаемся за нее, засучив рукава!

1. Чтобы найти координаты высоты пирамиды, нам нужно знать координаты точки ( displaystyle O.) Её аппликата равна нулю, а ордината равна ( displaystyle frac{sqrt{6}}{2}.)

Абсцисса ее равна длине отрезка ( displaystyle OS.) ( displaystyle AS=sqrt{A{{B}^{2}}-S{{B}^{2}}}=sqrt{6-frac{6}{4}}=frac{3}{sqrt{2}}.~)

Так как ( displaystyle AS) – высота равностороннего треугольника ( displaystyle ABC), то она делится в отношении ( displaystyle 2:1), считая от вершины, отсюда ( displaystyle OS=frac{3}{3sqrt{2}}=frac{1}{sqrt{2}}).

Окончательно, получили координаты:

( displaystyle Oleft( frac{1}{sqrt{2}},frac{sqrt{6}}{2},0 right).)

Тогда ( displaystyle D(left( frac{1}{sqrt{2}},frac{sqrt{6}}{2},sqrt{30} right)).

Координаты точки ( displaystyle A:Aleft( frac{3}{sqrt{2}},frac{sqrt{6}}{2},0 right).)

2. ( displaystyle K) – середина отрезка ( displaystyle BD:)

( displaystyle Kleft( frac{1}{2sqrt{2}},frac{sqrt{6}}{4},frac{sqrt{30}}{2} right).~)

3. ( displaystyle M) – середина отрезка ( displaystyle AC:)

( displaystyle Mleft( frac{3}{2sqrt{2}},~frac{frac{sqrt{6}}{2}+sqrt{6}}{2},0 right)=Mleft( frac{3}{2sqrt{2}},~frac{3sqrt{6}}{4},0 right).)

( displaystyle T) – середина отрезка ( displaystyle AB)

( displaystyle Tleft( frac{3}{2sqrt{2}},~frac{sqrt{6}}{4},0 right).~)

4. Координаты( displaystyle overrightarrow{KT}:overrightarrow{KT}left( frac{3}{2sqrt{2}}-frac{1}{2sqrt{2}},frac{sqrt{6}}{4}-frac{sqrt{6}}{4},~0-frac{sqrt{30}}{2} right)=overrightarrow{KT}left( frac{1}{sqrt{2}},~0,~-frac{sqrt{30}}{2} right).)

Координаты вектора ( displaystyle overrightarrow{TM}:)

( displaystyle overrightarrow{TM}left( 0,frac{3sqrt{6}}{4}-frac{sqrt{6}}{4},0 right)=overrightarrow{TM}left( 0,~frac{sqrt{6}}{2},0 right).)

5. Вычисляем векторное произведение:

( displaystyle overrightarrow{KT}times overrightarrow{TM}=frac{1}{sqrt{2}}cdot frac{sqrt{6}}{2}cdot overrightarrow{k}-frac{sqrt{30}}{2}cdot frac{sqrt{6}}{2}cdot vec{i}=frac{3sqrt{5}}{2}vec{i}+frac{sqrt{3}}{2}overrightarrow{k}=left( frac{3sqrt{5}}{2},0,~frac{sqrt{3}}{2} right).)

6. Длина вектора ( displaystyle TM): проще всего заменить, что отрезок ( displaystyle TM) – средняя линия треугольника ( displaystyle ABC), а значит, он равен половине основания ( displaystyle BC). Так что ( displaystyle left| text{ }!!~!!text{ }overrightarrow{TM} right|=frac{sqrt{6}}{2}).

7. Считаем длину векторного произведения:

( displaystyle left| overrightarrow{KT}times overrightarrow{TM} right|=sqrt{{{left( frac{3sqrt{5}}{2} right)}^{2}}+{{left( frac{sqrt{3}}{2} right)}^{2}}}=2sqrt{3}.)

8. Наконец, находим расстояние:

( displaystyle d=frac{left| overrightarrow{KT}times overrightarrow{TM} right|}{text{ }!!~!!text{ }left| text{ }!!~!!text{ }overrightarrow{TM} right|}=frac{2sqrt{3}}{frac{sqrt{6}}{2}}=2sqrt{2})

Уф, ну все!

Честно тебе скажу: решение этой задачи традиционными методами (через построения), было бы намного быстрее.

Зато здесь я все свел к готовому алгоритму!

Я так думаю, что алгоритм решения тебе ясен? Поэтому попрошу тебя решить оставшиеся две задачи самостоятельно. Сравним ответы?

2. ( displaystyle 12)

3. ( displaystyle 2)

Опять-таки повторюсь: эти задачи проще (быстрее) решать через построения, а не прибегая к координатному методу.

Я продемонстрировал такой способ решения лишь затем, чтобы показать тебе универсальный метод, который позволяет «ничего не достраивать».

Наконец, рассмотрим последний класс задач: Вычисление расстояния между скрещивающимися прямыми.

Вычисление расстояния между скрещивающимися прямыми

Здесь алгоритм решения задач будет схож с предыдущим. Что у нас есть:

• Направляющий вектор первой прямой: ( overrightarrow{{{a}_{1}}(}{{x}_{1}},{{y}_{1}},{{z}_{1}}).)
• Направляющий вектор второй прямой: ( overrightarrow{{{a}_{2}}(}{{x}_{2}},{{y}_{2}},{{z}_{2}}).)
• Любой вектор, соединяющий точки первой и второй прямой: ( overrightarrow{{{a}_{3}}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right))

Как мы ищем расстояние между прямыми?

Формула следующая:

( d=frac{left| left( overrightarrow{{{a}_{3}}},~overrightarrow{{{a}_{1}}},overrightarrow{{{a}_{2}}} right) right|}{left| overrightarrow{{{a}_{1}}}times overrightarrow{{{a}_{2}}} right|})

Числитель – это модуль смешанного произведения (мы его вводили в предыдущей части), а знаменатель – как и в предыдущей формуле (модуль векторного произведения направляющих векторов прямых, расстояние между которыми мы с тобой ищем).

Я напомню тебе, что

тогда формулу для расстояния можно переписать в виде:

[d = frac{{left| begin{array}{l}begin{array}{*{20}{c}}{{x_0}}&{{y_0}}&{{z_0}}end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}{{left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}]

Этакий определитель делить на определитель! Хотя, если честно, мне здесь совсем не до шуток!

Данная формула, на самом деле, очень громоздка и приводит к достаточно сложным вычислениям. На твоем месте я бы прибегал к ней только в самом крайнем случае!

Давай попробуем решить несколько задач, используя изложенный выше метод:

• В пра­виль­ной тре­уголь­ной приз­ме ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}), все рёбра ко­то­рой равны ( 1), най­ди­те рас­сто­я­ние между пря­мы­ми ( A{{A}_{1}}) и ( B{{C}_{1}}).
• Дана пра­виль­ная тре­уголь­ная приз­ма ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) все рёбра ос­но­ва­ния ко­то­рой равны ( 2sqrt{7}) Се­че­ние, про­хо­дя­щее через бо­ко­вое ребро ( A{{A}_{1}}) и се­ре­ди­ну ( M) ребра ( {{B}_{1}}{{C}_{1}}) яв­ля­ет­ся квад­ра­том. Най­ди­те рас­сто­я­ние между пря­мы­ми ( {{A}_{1}}B) и ( AM.)

Первую решаю я, а опираясь на нее, вторую решаешь ты!

1. Рисую призму и отмечаю прямые ( A{{A}_{1}}) и ( B{{C}_{1}}.)

Координаты точки С: ( C:Cleft( frac{sqrt{3}}{2},frac{1}{2},0 right),) тогда ( {{C}_{1}}left( frac{sqrt{3}}{2},frac{1}{2},1 right).~)

Координаты точки ( B:Bleft( 0,1,0 right).~)

Координаты вектора ( overrightarrow{B{{C}_{1}}}:~overrightarrow{B{{C}_{1}}}left( frac{sqrt{3}}{2},-frac{1}{2},1 right).)

Координаты точки ( {{A}_{1}}:{{A}_{1}}left( 0,0,1 right).)

Координаты вектора ( overrightarrow{A{{A}_{1}}}:~overrightarrow{A{{A}_{1}}}left( 0,0,1 right).)

Координаты вектора ( overrightarrow{AB}left( 0,1,0 right).)

[left( {B,overrightarrow {A{A_1}} overrightarrow {B{C_1}} } right) = left| {begin{array}{*{20}{l}}{begin{array}{*{20}{c}}0&1&0end{array}}\{begin{array}{*{20}{c}}0&0&1end{array}}\{begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}}end{array}} right| = frac{{sqrt 3 }}{2}]

Считаем векторное произведение между векторами ( AA) и ( overrightarrow{B{{C}_{1}}}:)

[overrightarrow {A{A_1}} cdot overrightarrow {B{C_1}} = left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}0&0&1end{array}\begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}end{array} right| — frac{{sqrt 3 }}{2}overrightarrow k + frac{1}{2}overrightarrow i ]

Теперь считаем его длину:

( left| overrightarrow{A{{A}_{1}}}times overrightarrow{B{{C}_{1}}} right|=sqrt{{{left( -frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}}=1)

Тогда

( d=frac{frac{sqrt{3}}{2}}{1}=frac{sqrt{3}}{2}.)

Ответ: ( frac{sqrt{3}}{2}.)

Теперь постарайся аккуратно выполнить вторую задачу. Ответом на нее будет: ( frac{sqrt{6}}{2}).

Метод координат в пространстве

30 мая 2011

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

1. Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

   

2. Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
3. Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB₁ = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Ответ: L = (0,5; 0,5; 1)

Смотрите также:

1. Введение системы координат
2. Четырехугольная пирамида в задаче C2
3. В 2012 году ЕГЭ по математике станет двухуровневым?
4. Сводный тест по задачам B12 (1 вариант)
5. Симметрия корней и оптимизация ответов в тригонометрии
6. ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

План урока:

Разложение векторов

Координаты векторов

Сложение и вычитание векторов

Признак коллинеарности векторов

Разложение векторов

Заметим, что если два вектора a и b коллинеарны, то обязательно найдется такое число k, для которого будет справедливо равенство:

Длина а составляет 6 клеток, а длина b – 9 клеток, при этом они сонаправлены. Получается, что b длиннее a в 9/6 = 1,5 раза, а потому можно записать:

Мы смогли выразить b через а. Иначе можно сказать, что мы разложили вектор b по вектору a. Можно и наоборот, выразить b через a:

Теперь посмотрим на вектора с и d. Их длины составляют 4 и 8 клеток, то есть отличаются в 2 раза, при этом они противоположно направлены. Поэтому эти вектора можно выразить так:

Обратите внимание, что выразить, например, а через с не удастся. Действительно, предположим, что есть такое число k, что

Тогда, по определению операции умножения вектора на число, вектора а и c должны быть коллинеарными, но они таковыми не являются.

Вектор можно раскладывать не на один, а на два вектора, которые ему не коллинеарны. Покажем это на примере:

Здесь вектора р, а и b не коллинеарны, при этом р выражен через а и b:

В данном случае говорят, что р разложен на вектора а и b, а числа 2 и 4 именуют коэффициентами разложения.

Верно следующее утверждение:

Продемонстрируем, как можно осуществить такое разложение. Пусть заданы вектора с, а и b, и требуется разложить c на а и b:

На первом шаге просто отложим все три вектора от одной точки. Далее построим прямые, проходящие через вектора а и b:

Далее через конец вектора с проведем прямые, параллельные построенным на предыдущем шаге прямым. В результате у нас получится некоторый параллелограмм АВСD:

Заметим, что вектор с оказался диагональю в этом параллелограмме. Тогда, согласно правилу параллелограмма, можно записать:

Ясно, что вектора АВ и b коллинеарны, так как лежат на одной и той же прямой. Тогда найдется такое число k, для которого будет верно отношение:

Конкретно в данном случае видно по рисунку, что АВ вдвое длиннее вектора b, поэтому

Аналогично коллинеарными являются вектора а и АD, поэтому существует число m, при котором справедливо равенство:

Понятно, что числа k и m определяются единственным образом. В общем случае они могут быть не только целыми, но и дробными (в том числе иррациональными) и даже отрицательными числами. Проще говоря, они могут быть любыми действительными числами.

Задание. Найдите коэффициенты разложения вектора d на вектора e и f:

Решение. Отложим все три вектора от одной точки. Далее проведем прямые, на которых лежат вектора e и f:

Теперь через конец d проводим ещё две прямые, параллельные двум уже построенным прямым, и в результате получаем параллелограмм:

Вектор d можно представить в виде суммы:

Особняком стоит случай, когда раскладываемый вектор коллинеарен одному из тех векторов, на которые он раскладывается. В этом случае один из коэффициентов разложения оказывается равным нулю. Например, пусть с надо разложить на а и b:

Строить параллелограмм в данном случае не нужно. Так как а и с коллинеарны, то найдется некоторое число k, при котором будет выполняться равенство:

Координаты векторов

Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:

Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.

Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.

Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:

Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:

Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:

Можно записать равенство:

Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:

Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i. Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.

В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).

Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.

Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:

Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:

После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:

После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты {1; – 3}.

Выполним построение и для с:

Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют {3,5; 0}.

Осталось рассмотреть d:

Здесь координаты вектора будут равны {– 2,5; – 2,5}, так как такие же координаты имеет точка D.

Ответ: а{4;3}; b{1; – 3}; с{3,5; 0}; d{– 2,5; – 2,5}.

Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.

Задание. Даны координаты вектора:

Постройте по три вектора, имеющие заданные координаты.

Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:

Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:

Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:

Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:

Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).

Сложение и вычитание векторов

Пусть у нас есть векторы a{x₁; у₁} и b{x₂; у₂}. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:

Эта запись означает, что с имеет координаты {х₁ + х₂; у₁ + у₂}. В результате мы можем сформулировать правило сложения векторов:

Проиллюстрируем правило на примере. Пусть надо сложить вектора а {2; 3} и b {4; 5}. Понятно, что в результате получится новый вектор, который мы обозначим как с {х; у}. Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:

x = 2 + 4 = 6

Для нахождения второй координаты складываем соответственно вторые координаты векторов:

y = 3 + 5 = 8

В итоге получился вектор с {6; 8}.

Задание. Сложите вектора, имеющие координаты:

Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):

Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a{x₁; у₁} и b{x₂; у₂}. Снова запишем их разложение на единичные вектора:

Теперь мы можем сформулировать правило вычитания векторов:

Например, пусть надо вычесть из вектора а{5; 3} вектор b{2;1}. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:

x = 5 — 2 = 3

Аналогично вычисляем и координату у:

y = 3 — 1 = 2

В итоге получили вектор с координатами {3; 2}.

Задание. Вычтите из вектора а вектор b, если известны их координаты:

Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):

Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х₁и у₁ можно разложить на орты следующим образом:

Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.

Например, есть вектор а{3; 7}, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:

x = 5*3 = 15

y = 5*7 = 35

В результате получился вектор {15; 35}.

Задание. Умножьте вектор а на число k, если известно, что:

Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:

Признак коллинеарности векторов

Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что 

Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:

x₁ = k * x₂

y₁ = k * y₂

Если числа х₂ и у₂ не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:

Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.

Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.

Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:

24:8 = 3

Получили число 3. Далее поделим и координаты у:

15:5 = 3

Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:

В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:

Естественно, снова получилось одинаковое число.

Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у₁}, причем у₁≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x₂; у₂} составят:

Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у₂ и у₁ могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие

y₂ = ky₁

Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,

Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:

Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.

Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.

Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:

Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:

Числа различны, поэтому вектора НЕ коллинеарны.

В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.

е) {0; 5} и {0; 12}

У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.

ж) {0; 3} и {2; 6}

У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.

з) {9; 0} и {4; 0}

У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.

и) {0; 3} и {12; 0}

Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.

к) {0; 0} и {5; 8}

Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.

Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.

Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.

Вопросы
занятия:

· 
вспомнить, как определяют координаты векторов;

·  рассмотреть
три вспомогательные задачи: определение координат середины отрезка, вычисление
длины вектора по его координатам и определение расстояния между точками.

Материал урока

Итак, построим прямоугольную систему
координат. От точки О начала координат отложим единичные векторы  и . Т.е.
векторы длины, которых равны единице.

Причём, направление вектора  совпадает
с направлением оси , а
направление вектора  совпадает
с направлением оси .

Векторы  называются
координатными векторами.

Понятно, что
любой вектор  можно
разложить по векторам .
Причём коэффициенты разложения, числа ,
определяются единственным образом.

Коэффициенты
разложения вектора  по
координатным векторам называют координатами вектора  в
данной системе координат.

Напомним, что
координаты вектора записывают в фигурных скобках через точку с запятой. При
этом первым указывают коэффициент разложения , а
вторым — .

Задание.

Записать
координаты векторов, указанных на экране.

Решение.

Обратите
внимание, что такие координаты данные векторы будут иметь только в конкретной
системе координат и при конкретных координатных векторах .

Коэффициенты
разложения нулевого вектора по векторам  и  равны
нулю.

Тогда получаем,
что нулевой вектор имеет координаты ,
причём в любой системе координат и при любых координатных векторах.

Если векторы
равны, то их разложения по векторам  и  также
будут равны, а значит, равны будут и коэффициенты разложения.

Таким образом,
получаем, что координаты равных векторов соответственно равны.

Вспомним ещё один
особенный случай — противоположные векторы. Их разложения противоположны.

Значит,
противоположны будут и соответственные координаты.

Задание.

Разложить векторы по координатным векторам  и  и указать их координаты.

Решение.

Задание.

Построить векторы
по их координатам.

Координатами
вектора  являются
числа 8 и –1. Значит, чтобы переместиться из точки О на вектор ,
сначала нужно переместиться на вектор , а
затем на вектор . Соединив
точку О с конечной точкой, получим вектор .

Далее изобразим
вектор . Для
этого из точки О переместимся на вектор . Тем
самым получим искомый вектор .

Чтобы из точки О
переместиться на вектор ,
сначала переместимся на вектор , а
затем на вектор .
Проведём вектор из точки О в конечную точку. Так мы получили вектор .

Теперь давайте
вспомним правила, позволяющие по координатам векторов находить
координаты их суммы, разности и произведения вектора на число.

Сначала
рассмотрим сумму двух векторов  и ,
координаты которых равны:

Пользуясь их
координатами, можем записать разложения данных векторов по координатным
векторам  и .

Сложим полученные
равенства. Пользуясь свойствами сложения векторов и произведения вектора на
число, получаем, что координаты вектора суммы векторов  и  равны:

Сформулируем правило.

Каждая
координата суммы двух и более векторов равна сумме соответствующих координат этих
векторов.

Задание.

Найти координаты
векторов суммы, если , , , .

Координаты
вектора суммы  равны:

Координаты
вектора суммы  равны:

Перейдём к
разности векторов  и .

Из разложения
вектора  вычтем
разложение вектора .

Получаем, что
координаты вектора разности равны:

Сформулируем правило.

Каждая координата
разности двух векторов равна разности соответствующих координат данных векторов.

Задание.

Найти координаты
векторов разности, если , , , .

Разность векторов
 имеет
координаты:

Разность векторов
 имеет
координаты:

Далее получим
координаты произведения вектора  на
число .

Получаем, что
координаты произведения равны:

Сформулируем правило.

Каждая
координата произведения вектора на число равна произведению соответствующей
координаты вектора на это число.

Задание.

Найти координаты
произведения вектора на число.

Координаты
вектора . Они
равны:

Координаты
вектора  равны:

Вектор  имеет
координаты:

Ну, а вектор  имеет координаты:

Рассмотрим прямоугольную систему
координат и какую-нибудь точку .

Проведём вектор из точки О к точке М.
Такой вектор  называют
радиус-вектором точки М.

Давайте докажем,
что координаты точки М равны соответствующим координатам её радиус-вектора .

Понятно, что
вектор  по
правилу параллелограмма. Теперь необходимо доказать, что вектор , а
вектор . Тем
самым мы докажем, что вектор .

Если , то
длина отрезка . А так
как векторы  и  сонаправлены,
то вектор , а
длина .

Если же , то
длина отрезка . Так
как векторы  и  противоположно
направлены, можно записать, что вектор . А .

Ну, и если , то
точка М лежит на оси  и
вектор . Тогда
его можно выразить как . А это
значит, что справедливо равенство .

Абсолютно
аналогично проводят доказательство того, что вектор .

Итак, мы
доказали, что вектор . То
есть координаты вектора , так
же как и у точки М.

Что и требовалось
доказать.

Задание.

Назвать
координаты вектора.

Решение.

Итак, мы
доказали, что координаты точки М равны соответствующим координатам её
радиус-вектора.

Радиус-вектором
точки называют вектор, начало которого совпадает с точкой начала координат, а
конец — с данной точкой.

Пользуясь этим
утверждением, выразим координаты вектора  через
координаты его начала и конца. Пусть точка А имеет координаты , а
точка В имеет координаты .

Вектор . А они
в свою очередь являются радиус-векторами точек В и А соответственно. А это
значит, что координаты вектора , а
координаты вектора . Можем
найти координаты вектора разности: . Понятно,
что эти значения и будут координатами вектора .

Так мы доказали,
что каждая координата вектора равна разности соответствующих координат его
конца и начала.

Задание.

По координатам
точек  и  найти
координаты вектора

.

Решение.

Теперь
давайте рассмотрим три вспомогательных задачи, которые используют при
решении геометрических задач методом координат.

Первой
решим задачу на определение координат середины отрезка.

Пусть
точка  и
точка  —
некоторые точки координатной плоскости. Точка  —
середина отрезка . И нам
необходимо определить её координаты.

Воспользуемся
ранее доказанным утверждением и на основании того, что  —
середина отрезка ,
запишем, что вектор .

Векторы
 и  являются
радиус-векторами точек А и В соответственно. Значит, координаты вектора , а
координаты вектора .

Вектор
их суммы будет иметь координаты .

Координаты
вектора их полусуммы равны .

Эти
значения и будут координатами вектора ,
который в свою очередь является радиус-вектором точки С. А это значит, что
координаты точки  равны
соответствующим координатам её радиус-вектора.

Таким
образом, мы получили, что каждая координата середины отрезка равна полусумме
соответствующих координат его концов.

Далее
рассмотрим вторую вспомогательную задачу — задачу на вычисление длины
вектора по его координатам.

От
начала координат отложим вектор .
Проведём перпендикуляры  и  к
осям.

Если
точка , то и
её радиус-вектор . При
этом координаты вектора , ведь
векторы .

Итак,
можно сказать, что длина отрезка , а
длина отрезка . Длину
отрезка  можем
выразить из прямоугольного треугольника  по
теореме Пифагора, как

Но
ведь векторы , а
значит, . Получаем,
что длина вектора равна корню квадратному из суммы квадратов его координат,
причём от какой бы точки он не был отложен.

Далее
решим последнюю вспомогательную задачу — задачу на определение расстояния
между двумя точками.

Пусть
точка , а точка
. Выразим
расстояние  между
этими точками через их координаты.

Для
начала рассмотрим вектор . Его
координаты равны разностям соответствующих координат конца М₂ и
начала М₁.

Тогда
длина этого вектора равна корню квадратному из суммы квадратов его координат.

Но
с другой стороны, длина вектора . Отсюда
получаем, что расстояние между двумя точками находят, как корень квадратный из
суммы квадратов разностей соответствующих координат данных точек.

Итоги урока

На этом уроке мы
поговорили о «методе координат». Вспомнили, как определяют координаты
векторов. Рассмотрели три вспомогательные задачи: определение координат
середины отрезка, вычисление длины вектора по его координатам и определение
расстояния между точками.