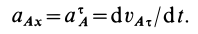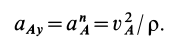Мгновенный центр вращения:
Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.
Рис. 71
Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение. Можно ввести угловую скорость вращения вокруг мгновенного центра вращения или, точнее, вокруг мгновенной оси, проходящей через мгновенный центр вращения и перпендикулярной плоскости движения.
При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой,— подвижной центроидой. Для каждого плоского движения фигуры существуют свои две центроиды: подвижная и неподвижная. Очевидно, что точка плоской фигуры, с которой в рассматриваемый момент совпадает мгновенный центр вращения, имеет скорость, равную нулю; следовательно, она является в то же время мгновенным центром скоростей.
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
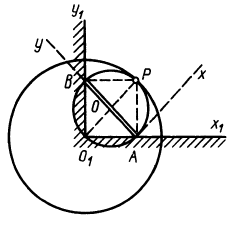
Центроиды нашли применение в некоторых вопросах кинематики механизмов. Рассмотрим пример нахождения центроид.
Пример:
Стержень
Решение. Скорость точки 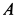
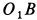
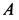
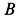
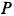
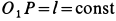
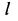
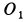
На подвижной плоскости 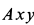
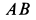
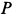
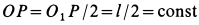
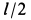
При качении подвижной окружности по неподвижной концы 
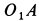
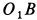
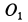
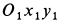
- Заказать решение задач по теоретической механике
Таким образом убеждаемся, что все точки подвижной окружности движутся по прямым линиям, проходящим через центр неподвижной окружности 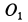
Рис. 72
В общем случае движения плоской фигуры мгновенный центр скоростей— точка 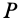
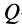
Выберем точку 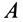
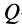
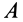
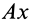
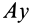
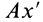
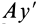
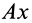
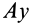
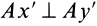
и 
Точка 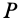
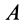
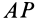
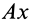
Ось 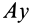
Если 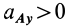
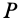
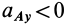
Кажется, что у точки 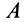
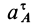
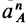
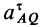
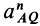
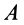
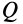
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
From Wikipedia, the free encyclopedia
Sketch 1: Instantaneous center P of a moving plane
The instant center of rotation (also, instantaneous velocity center,[1] instantaneous center, or instant center) is the point fixed to a body undergoing planar movement that has zero velocity at a particular instant of time. At this instant, the velocity vectors of the other points in the body generate a circular field around this point which is identical to what is generated by a pure rotation.
Planar movement of a body is often described using a plane figure moving in a two-dimensional plane. The instant center is the point in the moving plane around which all other points are rotating at a specific instant of time.
The continuous movement of a plane has an instant center for every value of the time parameter. This generates a curve called the moving centrode. The points in the fixed plane corresponding to these instant centers form the fixed centrode.
The generalization of this concept to 3-dimensional space is that of a twist around a screw. The screw has an axis which is a line in 3D space (not necessarily through the origin), and the screw also has a finite pitch (a fixed translation along its axis corresponding to a rotation about the screw axis).
Pole of a planar displacement[edit]
Sketch 2: Pole of a planar displacement
The instant center can be considered the limiting case of the pole of a planar displacement.
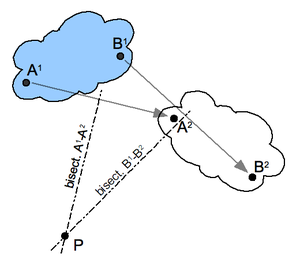
The planar displacement of a body from position 1 to position 2 is defined by the combination of a planar rotation and planar translation. For any planar displacement there is a point in the moving body that is in the same place before and after the displacement. This point is the pole of the planar displacement, and the displacement can be viewed as a rotation around this pole.
Construction for the pole of a planar displacement: First, select two points A and B in the moving body and locate the corresponding points in the two positions; see the illustration. Construct the perpendicular bisectors to the two segments A1A2 and B1B2. The intersection P of these two bisectors is the pole of the planar displacement. Notice that A1 and A2 lie on a circle around P. This is true for the corresponding positions of every point in the body.
If the two positions of a body are separated by an instant of time in a planar movement, then the pole of a displacement becomes the instant center. In this case, the segments constructed between the instantaneous positions of the points A and B become the velocity vectors VA and VB. The lines perpendicular to these velocity vectors intersect in the instant center.
The algebraic construction of the Cartesian coordinates 

has the Cartesian coordinates
and the midpoint between 

The two angles from 



taking the correct branches of the tangent. Let the center 



Rewrite this as a 4 × 4 inhomogeneous system of linear equations with 4 unknowns (the two distances 

The coordinates of the center of the rotation are the first two components of the solution vector
Pure translation[edit]
If the displacement between two positions is a pure translation, then the perpendicular bisectors of the segments A1B1 and A2B2 form parallel lines. These lines are considered to intersect at a point on the line at infinity, thus the pole of this planar displacement is said to «lie at infinity» in the direction of the perpendicular bisectors.
In the limit, pure translation becomes planar movement with point velocity vectors that are parallel. In this case, the instant center is said to lie at infinity in the direction perpendicular to the velocity vectors.
Instant center of a wheel rolling without slipping[edit]
Instant centre of rotation of a rolling wheel broken down into points. By breaking down the rolling wheel into several points, it can be more easily seen how all points of the wheel rotate around a single point at each instant. This point is the instant centre of rotation, shown in black.
Consider the planar movement of a circular wheel rolling without slipping on a linear road; see sketch 3. The wheel rotates around its axis M, which translates in a direction parallel to the road. The point of contact P of the wheel with road does not slip, which means the point P has zero velocity with respect to the road. Thus, at the instant the point P on the wheel comes in contact with the road it becomes an instant center.
The set of points of the moving wheel that become instant centers is the circle itself, which defines the moving centrode. The points in the fixed plane that correspond to these instant centers is the line of the road, which defines the fixed centrode.
The velocity vector of a point A in the wheel is perpendicular to the segment AP and is proportional to the length of this segment. In particular, the velocities of points in the wheel are determined by the angular velocity of the wheel in rotation around P. The velocity vectors of a number of points are illustrated in sketch 3.
The further a point in the wheel is from the instant center P, the proportionally larger its speed. Therefore, the point at the top of the wheel moves in the same direction as the center M of the wheel, but twice as fast, since it is twice the distance away from P. All points that are a distance equal to the radius of the wheel ‘r’ from point P move at the same speed as the point M but in different directions. This is shown for a point on the wheel that has the same speed as M but moves in the direction tangent to the circle around P.
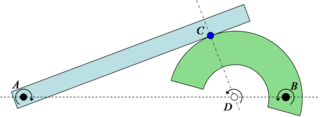
Relative center of rotation for two contacting planar bodies[edit]
Sketch 4: Example relative center of rotation. Two bodies in contact at C, one rotating about A and the other about B must have a relative center of rotation somewhere along the line AB. Since the parts cannot interpenetrate the relative rotation center must also be along the normal direction to the contact and through C. The only possible solution is if the relative center is at D.
If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in involute gear design as the pitch point, where there is no relative sliding between the gears. In fact, the gearing ratio between the two rotating parts is found by the ratio of the two distances to the relative center. In the example in Sketch 4 the gearing ratio is 
Instant center of rotation and mechanisms[edit]
Sketch 1 above shows a four-bar linkage where a number of instant centers of rotation are illustrated. The rigid body noted by the letters BAC is connected with links P1-A and P2-B to a base or frame.
The three moving parts of this mechanism (the base is not moving) are: link P1-A, link P2-B, and body BAC. For each of these three parts an instant center of rotation may be determined.
Considering first link P1-A: all points on this link, including point A, rotate around point P1. Since P1 is the only point not moving in the given plane it may be called the instant center of rotation for this link. Point A, at distance P1-A from P1, moves in a circular motion in a direction perpendicular to the link P1-A, as indicated by vector VA.
The same applies to link P2-B: point P2 is the instant center of rotation for this link and point B moves in the direction as indicated by vector VB.
For determining the instant center of rotation of the third element of the linkage, the body BAC, the two points A and B are used because its moving characteristics are known, as derived from the information about the links P1-A and P2-B.
The direction of speed of point A is indicated by vector VA. Its instant center of rotation must be perpendicular to this vector (as VA is tangentially located on the circumference of a circle). The only line that fills the requirement is a line colinear with link P1-A. Somewhere on this line there is a point P, the instant center of rotation for the body BAC.
What applies to point A also applies to point B, therefore this instant center of rotation P is located on a line perpendicular to vector VB, a line colinear with link P2-B. Therefore, the instant center of rotation P of body BAC is the point where the lines through P1-A and P2-B cross.
Since this instant center of rotation P is the center for all points on the body BAC for any random point, say point C, the speed and direction of movement may be determined: connect P to C. The direction of movement of point C is perpendicular to this connection. The speed is proportional to the distance to point P.
Continuing this approach with the two links P1-A and P2-B rotating around their own instant centers of rotation the centrode for instant center of rotation P may be determined. From this the path of movement for C or any other point on body BAC may be determined.
Examples of application[edit]
In biomechanical research the instant center of rotation is observed for the functioning of the joints in the upper and lower extremities.[2]
For example, in analysing the knee,[3][4][5]
ankle,[6] or shoulder joints.[7][8]
Such knowledge assists in developing artificial joints and prosthesis, such as elbow [9] or finger joints.[10]
Study of the joints of horses: «…velocity vectors determined from the instant centers of rotation indicated that the joint surfaces slide on each other.»[11]
Studies on turning a vessel moving through water.[12]
The braking characteristics of a car may be improved by varying the design of a brake pedal mechanism.[13]
Designing the suspension of a bicycle,[14] or of a car.[15]
In the case of the coupler link in a four-bar linkage, such as a double wishbone suspension in front view, the perpendiculars to the velocity lie along the links joining the grounded link to the coupler link. This construction is used to establish the kinematic roll center of the suspension.
See also[edit]
- Angular velocity
- Burmester’s theory
- Centrode
- Rigid body
- Roll center
- Rotation around a fixed axis
- Screw axis
References[edit]
- ^ Illustrated Dictionary of Mechanical Engineering: English, German, French, Dutch, Russian (Springer Science & Business Media, 17 Apr. 2013 — 422 pages)
- ^ «Muscle Physiology — Joint Moment Arm».
- ^ Knee joint motion description and measurement[permanent dead link]
- ^ Moorehead JD, Montgomery SC, Harvey DM (Sep 2003). «Instant center of rotation estimation using the Reuleaux technique and a Lateral Extrapolation technique». J Biomech. 36 (9): 1301–7. doi:10.1016/S0021-9290(03)00156-8. PMID 12893038.
- ^ Hollman JH, Deusinger RH, Van Dillen LR, Matava MJ (Aug 2003). «Gender differences in surface rolling and gliding kinematics of the knee». Clin Orthop Relat Res. 413 (413): 208–21. doi:10.1097/01.blo.0000072902.36018.fe. PMID 12897612. S2CID 45191914.
- ^ Maganaris CN, Baltzopoulos V, Sargeant AJ (Aug 1998). «Changes in Achilles tendon moment arm from rest to maximum isometric plantarflexion: in vivo observations in man». Journal of Physiology. 510 (Pt 3): 977–85. doi:10.1111/j.1469-7793.1998.977bj.x. PMC 2231068. PMID 9660906. Archived from the original on 2012-09-08.
- ^ Biomechanics of shoulder
- ^ Poppen NK, Walker PS (Mar 1976). «Normal and abnormal motion of the shoulder». J Bone Joint Surg Am. 58 (2): 195–201. doi:10.2106/00004623-197658020-00006. PMID 1254624.
- ^ US 5030237 Elbow prosthesis
- ^ «Pyrocarbon Finger Joint Implant» (PDF). Archived from the original (PDF) on 2011-07-21. Retrieved 2008-08-22.
- ^ Colahan P, Piotrowski G, Poulos P (Sep 1988). «Kinematic analysis of the instant centers of rotation of the equine metacarpophalangeal joint». Am J Vet Res. 49 (9): 1560–5. PMID 3223666.
- ^ «PART VI Vessel Navigation and Manoeuvering» (PDF). Archived from the original (PDF) on 2009-12-15. Retrieved 2008-08-22.
- ^ GB 1443270 Variable Mechanical Ratio Brake Pedal Mounts — General Motors, 1976
- ^ US 7100930 Bicycle rear suspension system
- ^ Reza N. Jazar (2008). Vehicle Dynamics: Theory and Application. Berlin: Springer. ISBN 978-0-387-74243-4.
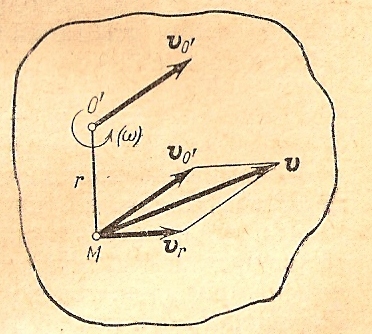
Зная скорость
поступательного движения
и угловую скорость ω вращательного
движения, можно определить скорость
любой точки М фигуры (рис.15.4)
Рис.15.4.
Скорость точки М на
основании теоремы о сложении скоростей
будет равна векторной сумме скоростей,
которые точка М имеет в каждом из этих
двух движений – переносном и относительном.
Переносное движение поступательное,
поэтому переносная скорость любой точки
фигуры равна
,
а скорость точки М во вращательном
(относительном) движении, которую
обозначим через
,
перпендикулярна к радиусу вращения
r=О’М и равна по
модулю rω, в дальнейшем под ω будем
понимать абсолютное значение угловой
скорости
.
Следовательно, диагональ параллелограмма,
построенного на этих двух скоростях,
определяет по модулю и направлению
искомую скорость
точки М фигуры.
Скорость всякой точки
М движущейся плоской фигуры равна
векторной сумме двух скоростей:
-
Скорости
произвольно выбранной точки О’ этой
фигуры -
Скорости
точки М во вращательном движении вокруг
точки О’.
Точка, для которой
переносная и относительная скорости
равны по модулю и противоположны по
направлению, имеет скорость равную
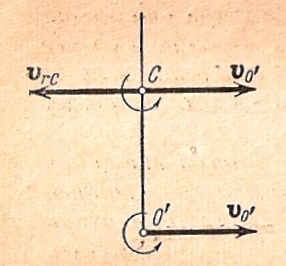
нулю. Найдем эту точку (рис.15.5):
рис.
15.5.
Повернем полупрямую
по
,
по которой направлена скорость на 90
вокруг точки О’ в
направлении вращения фигуры. Затем на
этой полупрямой отложим отрезок
.
Отрезок равный отношению переносной
поступательной скорости к угловой
скорости фигуры. Тогда точка С будет
искомой точкой. В самом деле, абсолютная
скорость точки С равна векторной сумме
переносной скорости
и относительной скорости во вращательном
движении вокруг точки О’.
Вращательная скорость перпендикулярна
к О’С и по модулю равна
.
Как видно из рисунка 15.5 эти две скорости
направлены по одной прямой в противоположные
стороны, поэтому модуль абсолютной
скорости точки С равен их алгебраической
сумме:
Таким образом, скорость
точки С фигуры в данный момент равна
нулю. Эта точка С называется мгновенным
центром скоростей.
При разложении движения
плоской фигуры на поступательное и
вращательное точку О’
можно выбрать произвольно. Если при
разложении мы вместо точки О’ выберем
точку С, то для скорости любой точки М
фигуры будем иметь:
где
обозначает скорость точки М во вращательном
движении фигуры вокруг точки С. Но
,
поэтому
,
т.е скорость любой
точки фигуры в данный момент равна по
модулю и направлению той скорости,
которую имеет в тот же момент эта точка
во вращательном движении фигуры вокруг
точки С.
Угловая скорость фигуры
не зависит от выбора точки О’,
поэтому угловая скорость фигуры в ее
вращении вокруг центра С равна той же
угловой скорости ω, с которой фигура
вращается вокруг точки О’.
При движении плоской
фигуры в ее плоскости в каждый данный
момент имеется мгновенный центр вращения
фигуры, так что скорости всех ее точек
в этот момент определяются как вращательные
скорости вокруг этого центра.
Положение мгновенного
центра вращения не остается неизменным
на неподвижной плоскости, по которой
перемещается фигура, так же как и
положение мгновенного центра скоростей
на плоскости самой движущейся фигуры.
Различным моментам
времени соответствуют различные точки
данной фигуры, которые являются в эти
моменты центрами скоростей, т.е. различные
положения мгновенного центра вращения
фигуры.
Таким образом, движение
плоской фигуры можно представить как
непрерывный ряд последовательных
вращений вокруг мгновенных центров,
занимающих в разные моменты времени
различные, но вполне определенные
положения как на неподвижной плоскости
так и на плоскости движущейся фигуры.
В дальнейшем мгновенный центр скорости
и совпадающий с ним в данный момент
мгновенный центр вращения фигуры мы
будем обозначать через
.
Если положение
мгновенного центра вращения в данный
момент найдено и угловая скорость фигуры
в этот момент известна, то скорость
любой точки фигуры будет равна по модулю
и направлению вращательной скорости
этой точки вокруг мгновенного центра
скоростей
.
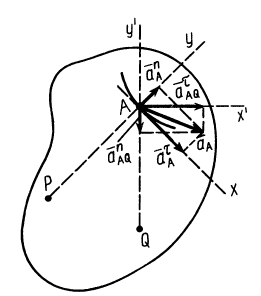
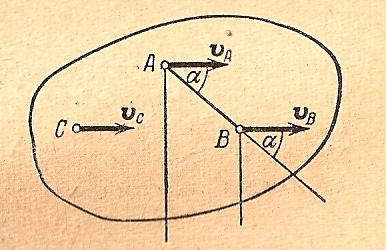
Например, для точек А
и В движущейся фигуры рис.15.6 будем иметь:
Рис.15.6.
и
,
и
Отсюда следует, что
1 – мгновенный центр
вращения фигуры лежит в точке пересечения
перпендикуляров, восстановленных в
двух точках фигуры к скоростям этих
точек
2 —
— скорости точек движущейся фигуры по
модулю пропорциональны расстояниям
этих точек от мгновенного центра вращения
фигуры.
Если нам известна по
модулю и направлению скорость одной
точки фигуры и направление скорости
другой точки фигуры, то мы можем найти
модуль этой второй скорости. Поэтому
нельзя задавать произвольно по модулю
и направлению скорости двух точек
фигуры. Эти скорости находятся между
собой в определенной зависимости,
которая устанавливается следующей
теоремой.
Теорема: Проекции
скоростей двух точек фигуры на прямую,
соединяющую эти точки равны между собой.
Рис.15.7.
Пусть скорости точек
А и В фигуры равны
и
.
Рассматривая
движение фигуры как сложное, которое
можно разложить на поступательное
движение со скоростью
и вращательное
вокруг точки А с угловой скоростью ω,
заключаем, что скорость точки В равна
векторной сумме двух скоростей: скорости
поступательного переносного движения
и скорости этой точки В в относительном
вращательном движении вокруг точки А.
Если обозначим вторую скорость
,
то эта зависимость выразится векторным
равенством
Причем скорость
равна по модулю
АВω и направлена перпендикулярно к АВ.
Проектируя скорости
и
на прямую АВ и
обозначая их проекции через Аа и Вb, из
равенства треугольников АКа и ВLb получим,
что Аа= Вb. Чтд.
Предположим, что
скорости двух точек А и В плоской фигуры
в данный момент параллельны, причем эти
скорости образуют с прямой АВ некоторый
угол α, не равный 90 рис.15.8.
Рис.15.8.
На основании теоремы
о равенстве проекций этих скоростей на
направление АВ, имеем:
или
и, следовательно,
Поэтому из равенства
следует, что
,
или
,
откуда
.
Если рассмотрим какую-нибудь третью
точку С фигуры, то ее скорость равна
,
где
обозначает скорость точки С во вращательном
движении фигуры вокруг точки А и,
следовательно,
,
а потому
.
Таким образом, скорости
всех точек фигуры в данный момент равны
как по модулю, так и по направлению, т.е.
в данном случае мы имеем такое же
распределение скоростей в движущейся
плоской фигуре, как и при поступательном
движении этой фигуры.
Если в точках А и В
восставим перпендикуляры к скоростям
этих точек, то они будут параллельны.
Поэтому мгновенный центр вращения
фигуры, находящийся в точке пересечения
этих перпендикуляров, оказывается в
данном случае бесконечно удаленным.
В тот момент, когда
мгновенный центр скоростей вращения
фигуры оказывается бесконечно удаленным,
угловая скорость фигуры равна нулю, а
скорости всех ее точек равны по модулю
и имеют одно и то же направление.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мгновенный центр вращения
2017-02-17
Когда колесо катится без проскальзывания, его движение складывается из поступательного и вращательного. Скорость нижней точки колеса в таком движении всегда равна нулю, и эта точка является мгновенным центром вращения.
Другие видеоуроки по физика:
- Видео
- Конспект
- Задачи
Измерить вес тела можно также пружинными весами (рис. 3). Груз давит на дно чаши и сжимает пружину внутри весов. Чем больше вес тела, тем больше сжатие пружины. Чтобы измерять вес, пружинные весы нужно предварительно проградуировать, используя эталонные грузы.
Как возникает действие груза на пружинные весы? Известно, что все тела притягиваются Землей силой тяжести. Груз давит на чашу весов силой, равной по величине силе тяжести, которая уравновешивается пружиной. Эту силу называют весом тела.
Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
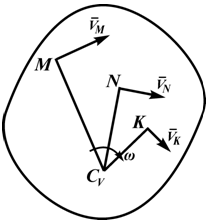
Рисунок 2.16
При определении положения МЦС скорость любой точки может быть записана: VM = VCv + VMCv , где точка CV выбрана за полюс. Поскольку это МЦС и VCv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:
VM=VCv+ VMCv=VMCv , VM=VMCv=ω∙CVM,
VN=VCv+ VNCv=VNCv , VN =VNCv=ω∙CVN,
VK=VCv+ VKCv=VKCv , VK=VKCv=ω∙CVK.
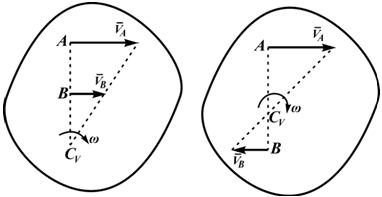
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:
VM/CVM=VN/CVN=VK/CVK=ω
Рисунок 2.17
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
- CV совпадает с точкой B, VB=0. Шатун вращается вокруг точки B,
ωAB=VA/ACV=VA/AB; - VA/ACV=VB/BCV=ωAB;
- МЦС лежит в «бесконечности»:
VA/∞=VB/∞=ωAB=0, VB=VA; - VA/ACV=VB/BCV=ωAB.
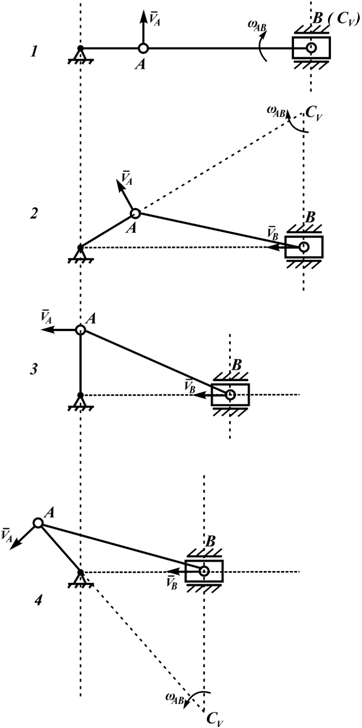
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.
VA/ACV=VB/BCV=ω
Рисунок 2.18
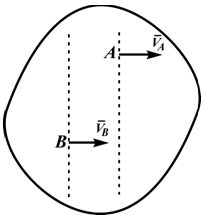
VB||VA
В этом случае МЦС находится в «бесконечности», т.е.
ω=VA/∞=VB/∞=ωAB=0, VB=VA
Рисунок 2.19
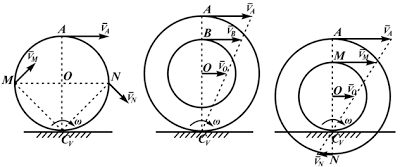
Рисунок 2.20
- VA/2R=V0/R=VM/(R√2)=ω,
- VA/2R=V0/R=VB/(R+r)=ω,
- VA/(R+r)=V0/r=VN/(R-r)=ω
Формулы справедливы при отсутствии проскальзывания в точке CV.
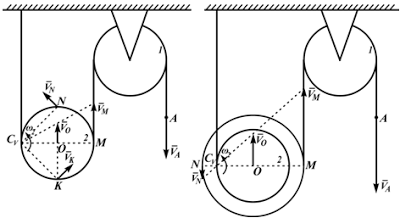
а б
Рисунок 2.21
Для «а»:
VM=VA
VM/MCV=V0/OCV=VN/NCV=VK/KCV=ω2
Для «б»:
VA=VM
VM/MCV=V0/OCV=VN/NCV=ω2
Примеры решения задач >
Ускорение точки в плоскопараллельном движении >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее