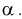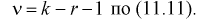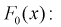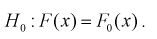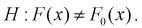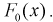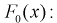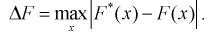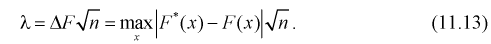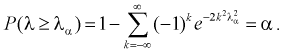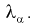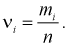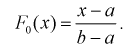Мощность критерия при проверке гипотезы о значении генеральной средней
Если известна
генеральная дисперсия
,
то при проверке гипотезыиспользуется нормальное распределение.
Для вычисления мощности критерия при
односторонней конкурирующей гипотезе
применяется формула
,
(11)
где
находится из уравнения
.
Если генеральная
дисперсия неизвестна, то мощность
критерия определяется по формулам:
(12)
где
.
Мощность критерия при проверке гипотезы о значении генеральной дисперсии
При проверке
гипотезы
,
то мощность критерия вычисляется с
использованием распределения Пирсона.
Если критическая
область левосторонняя, то

Если критическая
область правосторонняя, то

(14)
Пример 2.
По данным 12 рейсов установлено, что в
среднем машина затрачивает на поездку
до хлебоприёмного пункта
минуты. Допустив,
что время поездки есть нормальная
случайная величина, на уровне значимости
0,05 проверить гипотезу
мин:
а) при конкурирующей
гипотезе
мин, если известно, что
мин;
б) при конкурирующей
гипотезе
мин, если выборочное среднее квадратическое
отклонение равномин;
в) для условий а)
и б) вычислить мощность критерия.
Решение:
а) Для проверки
гипотезы
мин, при
мин, выбирают
левостороннюю критическую область
,
тогда
из уравнения
находим
.
Рассчитаем
наблюдаемое значение статистики
критерия:
Так как
— то нулевая гипотеза отвергается с
вероятностью ошибки.
б) Для проверки
нулевой гипотезы, если
неизвестно, а
мин,
наблюдаемое значение статистики критерия
рассчитывают по формуле:
Границу критической
области находим по таблице Стьюдента:
Поскольку
,
гипотезане отвергается, т.е.
мин не противоречит наблюдениям.
в) Мощность критерия
для случая а) рассчитаем по формуле
(11):
Мощность критерия
в случае б) вычислим по формуле (12):
Пример 3.
По результатам 7 независимых измерений
диаметра поршня одним и тем же прибором
в предположении, что ошибки измерения
имеют нормальное распределение, была
проверена на уровне значимости 0,05
гипотеза
мм2
при конкурирующей гипотезе
мм2.
Гипотеза
не отвергнута. Вычислить мощность
критерия.
Решение:
Согласно
строится правосторонняя критическая
область.
По таблице
—
распределения на уровне значимостии при числе степеней свободы
определяем критическую границу
.
Вычисляем в формуле
(14)
По таблице
—
распределения находим
.
Лекция 4 Гипотезы о виде закона распределения генеральной совокупности
Одной из важнейших
задач математической статистики является
установление теоретического закона
распределения случайной величины по
её эмпирическому распределению,
представляющему вариационный ряд.
Для этого на основе
анализа опытных данных, общих теоретических
предпосылок и особенностей известных
распределений подбирают среди них такой
закон, который лучше других отражает
опытное распределение случайной
величины.
Существенную
помощь при выборе закона распределения
могут оказать кривые распределения и
сравнение их с графическим изображением
опытного распределения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Методика проверки статистических гипотез
- 2 Альтернативная методика на основе достигаемого уровня значимости
- 3 Типы критической области
- 4 Ошибки первого и второго рода
- 5 Свойства статистических критериев
- 6 Типы статистических гипотез
- 7 Типы статистических критериев
- 7.1 Критерии согласия
- 7.2 Критерии сдвига
- 7.3 Критерии нормальности
- 7.4 Критерии однородности
- 7.5 Критерии симметричности
- 7.6 Критерии тренда, стационарности и случайности
- 7.7 Критерии выбросов
- 7.8 Критерии дисперсионного анализа
- 7.9 Критерии корреляционного анализа
- 7.10 Критерии регрессионного анализа
- 8 Литература
- 9 Ссылки
Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.
Методика проверки статистических гипотез
Пусть задана случайная выборка — последовательность
объектов из множества
.
Предполагается, что на множестве существует некоторая неизвестная вероятностная мера
.
Методика состоит в следующем.
- Формулируется нулевая гипотеза
о распределении вероятностей на множестве
. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая
и альтернативная
. Иногда альтернатива не формулируется в явном виде; тогда предполагается, что
означает «не
». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.
- Задаётся некоторая статистика (функция выборки)
, для которой в условиях справедливости гипотезы
выводится функция распределения
и/или плотность распределения
. Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика
. Вывод функции распределения
при заданных
и
является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для
; в статистических пакетах имеются готовые вычислительные процедуры.
- Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число
. На практике часто полагают
.
- На множестве допустимых значений статистики
выделяется критическое множество
наименее вероятных значений статистики
, такое, что
. Вычисление границ критического множества как функции от уровня значимости
является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
- Собственно статистический тест (статистический критерий) заключается в проверке условия:
Итак, статистический критерий определяется статистикой
и критическим множеством , которое зависит от уровня значимости
.
Замечание.
Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна.
Тому есть две причины.
Альтернативная методика на основе достигаемого уровня значимости
Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.
Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия
где
— критическая область критерия.
Другая интерпретация:
достигаемый уровень значимости — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем
Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается.
В частности, его можно сравнивать с фиксированным уровнем значимости;
тогда альтернативная методика будет эквивалентна классической.
Типы критической области
Обозначим через значение, которое находится из уравнения
, где
— функция распределения статистики
.
Если функция распределения непрерывная строго монотонная,
то есть обратная к ней функция:
-
.
Значение называется также
—квантилем распределения
.
На практике, как правило, используются статистики с унимодальной (имеющей форму пика) плотностью распределения.
Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения.
Поэтому чаще всего возникают критические области одного из трёх типов:
- Левосторонняя критическая область:
-
- определяется интервалом
.
- пи-величина:
- определяется интервалом
- Правосторонняя критическая область:
-
- определяется интервалом
.
- пи-величина:
- определяется интервалом
- Двусторонняя критическая область:
-
- определяется двумя интервалами
- пи-величина:
- определяется двумя интервалами
Ошибки первого и второго рода
- Ошибка первого рода или «ложная тревога» (англ. type I error,
error, false positive) — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода:
- Ошибка второго рода или «пропуск цели» (англ. type II error,
error, false negative) — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:
| Верная гипотеза | |||
|---|---|---|---|
| |
|
||
| Результат применения критерия |
|
|
(Ошибка второго рода) |
| |
(Ошибка первого рода) |
|
Свойства статистических критериев
Мощность критерия:
— вероятность отклонить гипотезу
, если на самом деле верна альтернативная гипотеза
.
Мощность критерия является числовой функцией от альтернативной гипотезы .
Несмещённый критерий:
для всех альтернатив
или, что то же самое,
для всех альтернатив .
Состоятельный критерий:
при
для всех альтернатив
.
Равномерно более мощный критерий.
Говорят, что критерий с мощностью является равномерно более мощным, чем критерий с мощностью
, если выполняются два условия:
;
для всех рассматриваемых альтернатив
, причём хотя бы для одной альтернативы неравенство строгое.
Типы статистических гипотез
- Простая гипотеза однозначно определяет функцию распределения на множестве
. Простые гипотезы имеют узкую область применения, ограниченную критериями согласия (см. ниже). Для простых гипотез известен общий вид равномерно более мощного критерия (Теорема Неймана-Пирсона).
- Сложная гипотеза утверждает принадлежность распределения к некоторому множеству распределений на
. Для сложных гипотез вывести равномерно более мощный критерий удаётся лишь в некоторых специальных случаях.
Типы статистических критериев
В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.
Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.
- Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.
- Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.
Критерии согласия
Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.
- Критерий Колмогорова-Смирнова
- Критерий хи-квадрат (Пирсона)
- Критерий омега-квадрат (фон Мизеса)
Критерии сдвига
Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.
- Критерий Стьюдента
- Критерий Уилкоксона-Манна-Уитни
Критерии нормальности
Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.
- Критерий Шапиро-Уилка
- Критерий асимметрии и эксцесса
Критерии однородности
Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.
Критерии симметричности
Критерии симметричности позволяют проверить симметричность распределения.
- Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
- Критерий знаков
- Коэффициент асимметрии
Критерии тренда, стационарности и случайности
Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.
Критерии выбросов
Критерии дисперсионного анализа
Критерии корреляционного анализа
Критерии регрессионного анализа
Литература
- Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
- Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006. — 816 с.
Ссылки
- Statistical hypothesis testing — статья в англоязычной Википедии.
Содержание:
Теория статистической проверки гипотез
Пусть имеется выборка
Тогда нулевой гипотезой 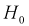
Альтернативной (конкурирующей, противоположной) гипотезой Н называется гипотеза, которая принимается тогда, когда отвергается нулевая.
Целью статистической проверки гипотез является выбор критерия по выборке 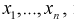
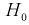
- Отклонение
, когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости.
- Принятие
когда она на самом деле не верна — ошибка второго рода, вероятность ошибки —
.
Чем серьезнее будут последствия ошибки первого рода, тем меньше надо выбирать уровень значимости 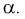
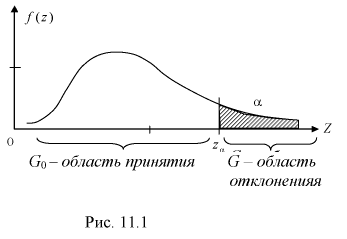
Статистической характеристикой Z гипотезы 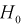
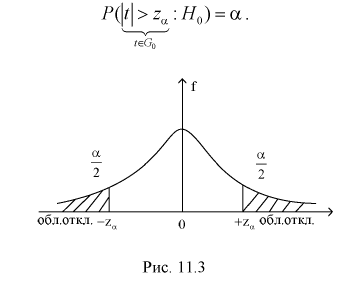
Областью отклонения (критической областью) 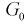
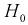
Дополнение области отклонения до всех возможных значений статистической характеристики Z называется областью принятия G.
При попадании статистической характеристики Z в область принятия гипотеза 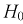
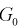
При попадании Z в область принятия гипотеза 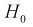
Область отклонения 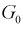
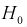
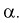
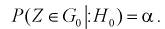
С другой стороны, для того чтобы уменьшить вероятность ошибки второго рода при выбранном 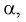
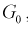
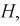
Вероятность 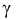
Так как события 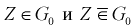
Таким образом, имеем
где 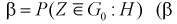
Отметим, что ошибка первого рода существенней, поэтому а мы выбираем, а р — нет (принимаем полученное значение).
Из (11.2) следует, что между 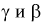
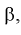
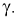
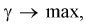
Между 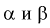
На рис. 11.2 приведены две кривые плотности распределения: одна кривая 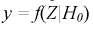
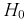
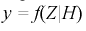
Из рис. 11.2 видно, что при уменьшении 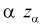
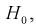
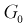
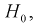
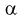
Гипотезы бывают двух видов — параметрические и непараметрические.
Параметрические гипотезы — это гипотезы о проверке параметров законов распределения.
Непараметрические — это гипотезы о виде закона распределения.
Проверка гипотезы равенства математических ожиданий при неизвестной дисперсии (критерий Стьюдента)
Пусть Хи У — независимые нормальные случайные величины.
Введем обозначения:
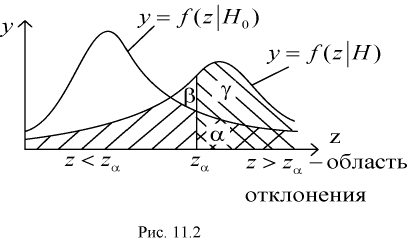
Пусть дисперсии этих случайных величин равны и неизвестны:
где 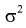
Пусть даны выборки
По выборкам найдем критерий проверки гипотезы 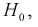
При альтернативной гипотезе
Известно, что случайные величины
имеют распределение 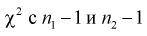
Сумма независимых случайных величин с распределением 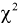
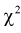
Случайная величина W имеет распределение 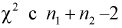
Ранее мы показывали, что несмещенной оценкой математического ожидания является выборочное среднее. Поэтому для проверки гипотезы 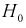
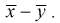
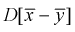
Очевидно, что случайная величина U имеет нормальное распределение, т. к. X и Y нормально распределены. Если проверяемая гипотеза 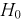
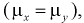
Таким образом, если гипотеза 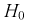
Рассмотрим случайную величину
где 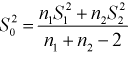
Случайную величину t можно представить в следующем виде через ранее введенные Un W:
Действительно:
т. е. правые части (11.5) и (11.6 или 11.7) совпадают.
Но величина t (11.6) имеет распределение Стьюдента с 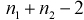
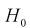
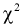
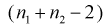
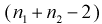
Эту величину t (11.5) примем за статистическую характеристику Z. Проверка гипотезы о равенстве .математических ожиданий состоит в следующем.
По таблицам распределения Стьюдента для заданного уровня значимости 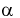
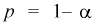
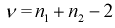
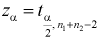
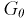
Тогда если фактически найденное по выборкам значение статистической характеристики t (11.5) удовлетворяет условию 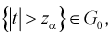
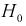
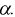
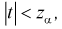
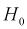
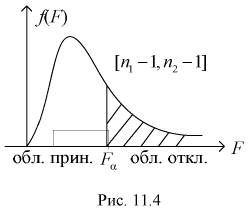
Проверка гипотезы о равенстве дисперсий (критерий Фишера)
Пусть Х и Y — нормальные независимые случайные величины. Обозначим их дисперсии:
По выборкам 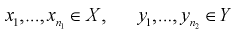
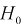
При альтернативной гипотезе 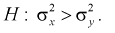
Такая гипотеза выбирается, например, при 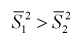
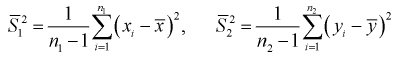
В качестве статистической характеристики возьмем случайную величину
Если гипотеза 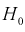
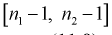
Видим, что величина 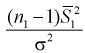
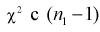
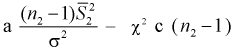
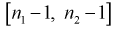
Проверка гипотезы 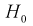
Из таблиц распределения Фишера по выбранному уровню значимости 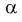
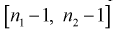
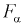
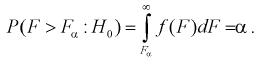
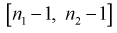
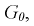
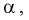
По выборкам, используя (11.8), определяем значение статистической характеристики F. Если фактически вычисленное по формуле (11.8) значение F окажется больше табличного 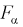
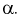
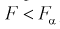
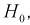
Пример:
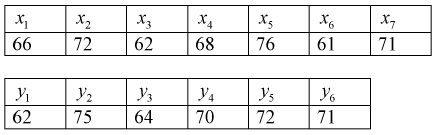
Пусть X — чувствительность телевизоров марки «Горизонт», Y — чувствительность телевизоров марки «Витязь». Проведены выборочные измерения чувствительности телевизоров для 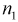
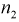
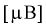
Определить лучшую марку телевизора, если лучшим будет тот, у которого чувствительность в 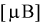
Найдем по результатам измерений средние значения чувствительности, вычисляя
Можно ли сказать, что чувствительность телевизоров марки «Горизонт» лучше? Нет, т. к. выборки, выборочные средние 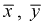
Сначала убедимся в равенстве дисперсий по критерию Фишера — гипотеза
Вычислим несмещенные оценки дисперсий
Используя (11.8), найдем значение статистической характеристики F:
По таблицам распределения Фишера для [6;5] степеней свободы, задавая уровень значимости 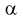
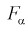
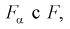
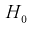
Теперь проверим гипотезу о равенстве математических ожиданий случайных величин X и Y , применяя критерий Стьюдента.
Гипотеза 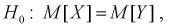
Найдем объединенную выборочную дисперсию:
По формуле (11.5) вычислим статистическую характеристику t :
Задавая уровень значимости 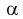
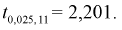
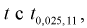
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона. (Критерий согласия 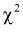
Пусть задана генеральная случайная величинами выборка
Если по выборке построить гистограмму, то по виду гистограммы можно выдвинуть гипотезу о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 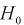
При альтернативной гипотезе
Обычно для построения гистограммы равноинтервальным способом разбивают весь диапазон выборочных значений случайной величины X на 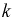
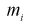
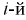
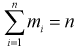
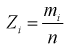
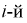
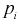
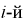
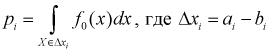
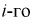
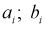
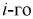
Рассмотрим событие, состоящее в том, что случайная величина X попадет в интервал 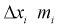
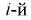
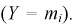
Для введенной ранее случайной величины 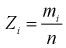
Проведем нормировку случайной величины 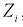
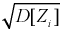
Эта величина распределена по биномиальному закону, т. к. в нее входит случайная величина 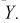
Сумма квадратов нормированных нормальных случайных величин (как было показано ранее) имеет распределение 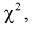
Эта случайная величина имеет закон распределения 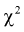
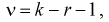
где 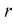
Анализируя правые части формул (11.9) и (11.10), можно отметить, что в критерии согласия 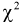
Проверка гипотезы состоит в следующем. Задаем уровень значимости
По таблицам 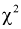
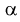
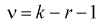
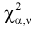
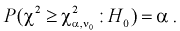
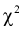
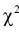
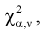
- Если
то нулевая гипотеза
отвергается в пользу альтернативной Н, т. е.
не согласуется с результатами эксперимента.
- Если
, то
, принимается, т. е.
согласуется с экспериментальными данными, закон распределения
подтверждается. При этом вероятность ошибки равна
Критерий Романовского
Рассмотрим неравенство
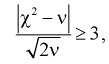
где 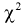
Проверка гипотезы состоит в следующем: если это неравенство выполняется 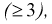
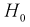
В противном случае гипотеза 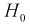
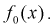
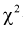
Критерий согласия Колмогорова
В критерии согласия А. Н. Колмогорова проводится сравнение эмпирической и теоретической функций распределения. Укажем этапы проверки гипотез этим критерием.
1. По выборке 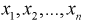
2. По виду графика функции распределения выдвигается гипотеза о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 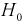
При альтернативной гипотезе
3. По выборке 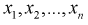
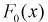
4. На графике эмпирической функции распределения строится график теоретической функции распределения
5. Путем сравнения графиков вычисляется максимальное значение модуля отклонения значений эмпирической функции распределения от теоретической функции распределения
6. Рассчитывают значение 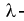
7. Задавая уровень значимости а , определяем квантиль из условия
Отметим, что самостоятельно решать это уравнение не надо, поскольку составлены таблицы квантилей распределения Колмогорова, из которых по заданному уровню значимости 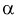
Сравнивая значение 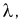
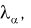
Следует отметить, что критерий Колмогорова применяется тогда, когда полностью известен закон распределения функции распределения F(x) и значения ее параметров. При решении практических задач это не всегда удается выполнить. Для этого прибегают к некоторым дополнительным исследованиям: применяют вероятностные бумаги, строят гистограммы и т. д. Это помогает правильно подобрать теоретический закон распределения для функции распределения F(x). Но в этом случае неизвестны ее параметры. И если их оценивать по этой же выборке, то это может привести к ошибочным выводам в отношении принятой гипотезы. В этом случае следует использовать другие критерии согласия, например 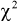
Пример:
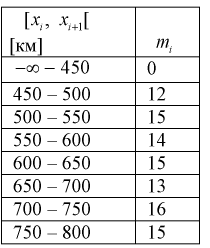
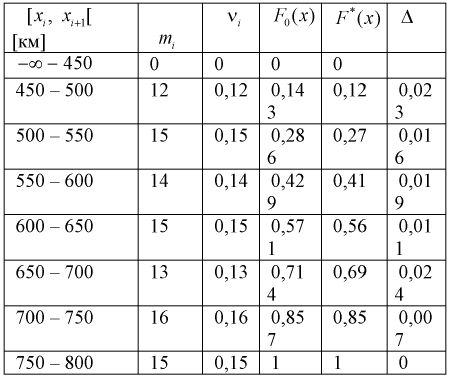
Проведено 100 измерений расстояния радиодальномером до цели. Результаты представлены в виде статистического ряда 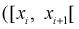
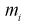
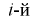
Оценить закон распределения ошибки измерения дальности радиодальномером.
Занесем в таблицу значения относительных частот
Анализ значений относительных частот позволяет выдвинуть гипотезу о равномерном законе распределения. Теоретическая функция распределения для этого закона имеет вид
Принимаем а = 450, b = 800. Полагая 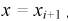
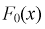
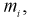
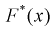
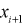
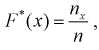
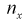
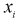
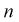
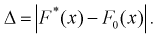
Вычисляем критерий Колмогорова по формуле (11.13), учитывая, что из таблицы 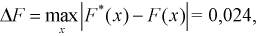
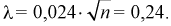
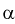
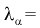
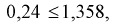
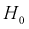
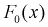
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Дисперсионный анализ
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Статистические оценки
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала


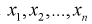
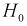 , когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости.
, когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости. 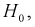 когда она на самом деле не верна — ошибка второго рода, вероятность ошибки —
когда она на самом деле не верна — ошибка второго рода, вероятность ошибки — 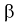 .
.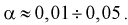
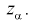
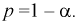
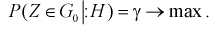
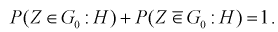

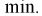

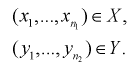
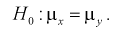
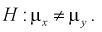
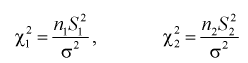
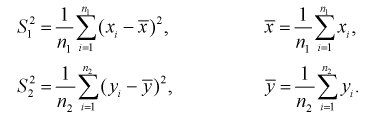
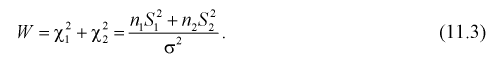
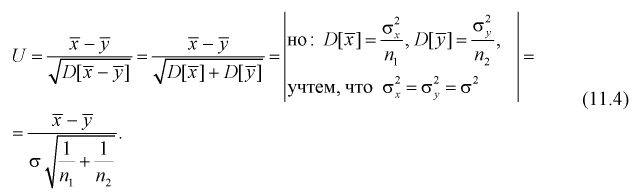
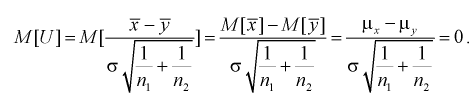
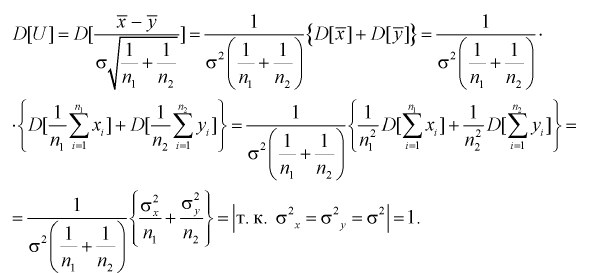
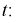


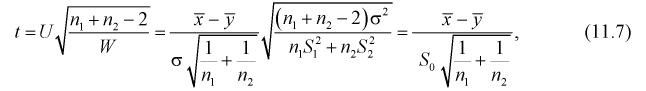
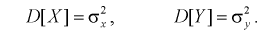
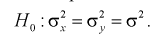

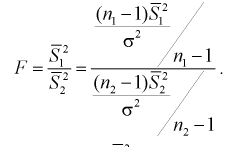
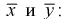
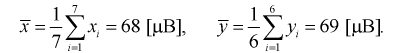
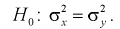
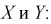
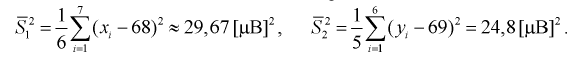
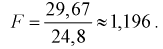
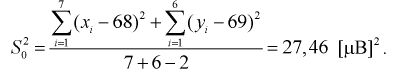
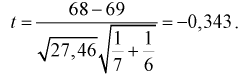
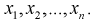
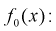
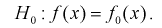
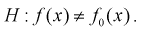
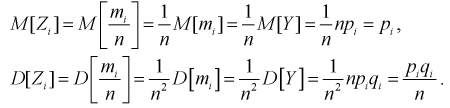
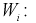

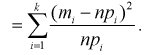

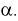
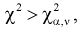 то нулевая гипотеза
то нулевая гипотеза 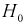 отвергается в пользу альтернативной Н, т. е.
отвергается в пользу альтернативной Н, т. е. 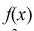 не согласуется с результатами эксперимента.
не согласуется с результатами эксперимента.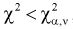 , то
, то 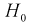 , принимается, т. е.
, принимается, т. е. 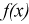 согласуется с экспериментальными данными, закон распределения
согласуется с экспериментальными данными, закон распределения 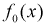 подтверждается. При этом вероятность ошибки равна
подтверждается. При этом вероятность ошибки равна