Мостик уитстона как найти сопротивление

В мире аналоговой электроники мы часто сталкиваемся с различными сигналами, некоторые из них измеряются изменением сопротивления, а некоторые — изменением индуктивности и емкости.

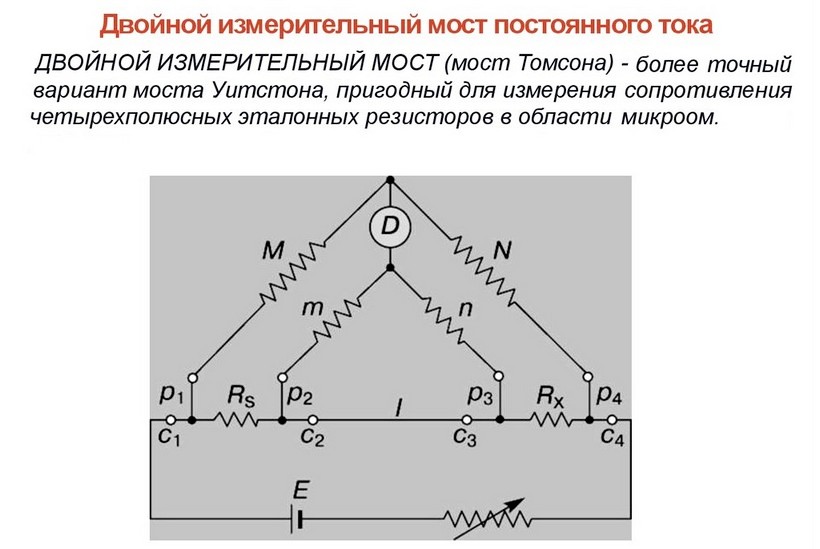
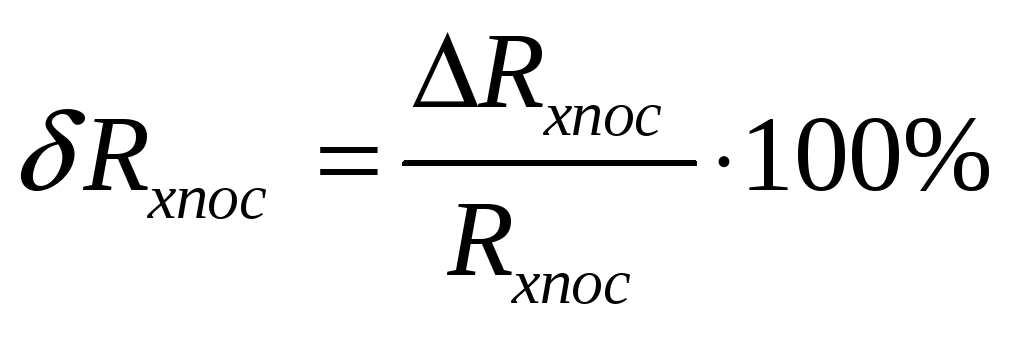Если мы будем рассматривать сопротивление, то большинство промышленных датчиков, таких как датчик температуры, деформации, влажности, смещения, уровня жидкости и т.д., производят изменение значения сопротивления для эквивалентного изменения соответствующей величины. Следовательно, существует потребность в преобразовании сигнала для каждого датчика, основанного на сопротивлении.

Например, самый простой компонент, который сразу может прийти на ум, — это светозависимый резистор или LDR. Как следует из названия, LDR — это компонент, сопротивление которого изменяется в зависимости от количества падающего на него света.

Как правило, измерение сопротивления делится на три типа:

• Измерение низкого сопротивления
• Измерение среднего сопротивления
• Измерение высокого сопротивления

Если измерение сопротивления возможно от нескольких микроом до миллиом, то оно считается измерением низкого сопротивления. Это измерение, фактически, используется в исследовательских целях. Если измерение находится в диапазоне от 1 Ома до нескольких сотен кОм, обычно это измерение среднего сопротивления. К этой категории относится измерение обычных резисторов, потенциометров, термисторов и т.д.

И очень высокое сопротивление считается измерением от нескольких МегаОм до более чем 100 МегаОм. Для нахождения среднего значения сопротивления используются разные методы, но в основном используется мост Уитстона.

Что такое Мост Уитстона?

Мостовые схемы являются одним из самых популярных электрических инструментов, часто используемых в измерительных цепях, схемах преобразователей, схемах переключения, а также в генераторах.

Мост Уитстона — одна из самых распространенных и простых мостовых схем, которую можно использовать для очень точного измерения сопротивления. Но часто мост Уитстона используется с различными датчиками для измерения физических величин, таких как температура, давление, деформация и т.д.

Мост Уитстона используется в устройствах, где датчики должны измерять небольшие изменения сопротивления, и используется для преобразования изменения сопротивления в изменение напряжения преобразователя. Комбинация этого моста с операционным усилителем широко используется в промышленности для различных преобразователей и датчиков.

Например, сопротивление термистора изменяется, когда он подвергается изменению температуры. Точно так же тензорезистор, когда он подвергается давлению, силе или смещению, изменяет свое сопротивление. В зависимости от типа применения, мост Уитстона может работать либо в сбалансированном, либо в несбалансированном состоянии.

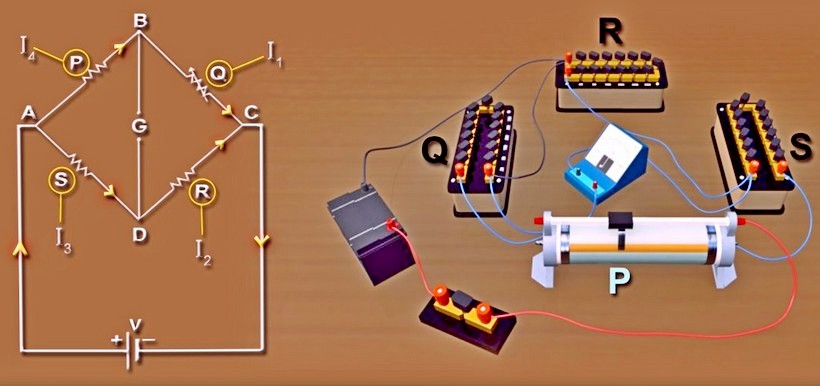
Мост Уитстона состоит из четырех резисторов (R 1 , R 2 , R 3 и R 4 ), которые соединены в форме ромба с источником питания постоянного тока, подключенным через верхнюю и нижнюю точки (C и D в схеме) ромб и выход берутся через два других конца (A и B в цепи).

Этот мост используется для очень точного нахождения неизвестного сопротивления путем сравнения его с известным значением сопротивлений. В этом мосту для нахождения неизвестного сопротивления используется состояние Null (нулевой) или Balanced (сбалансированный).

Чтобы этот мост находился в сбалансированном состоянии, выходное напряжение в точках A и B должно быть равно 0. Из приведенной выше схемы:

Мост находится в сбалансированном состоянии, если:

V_OUT = 0V

Для упрощения анализа вышеприведенной схемы перерисуем ее следующим образом:

Теперь для сбалансированного состояния напряжение на резисторах R1 и R2 одинаково. Если V1 представляет собой напряжение на резисторе R1 , а V2 представляет собой напряжение на резисторе R2 , тогда:

V1 = V2

Точно так же равны и напряжения на резисторах R3 (назовем его V3 ) и R4 (назовем его V4 ):

 V₃ = V₄ 

Отношения напряжений можно записать в виде:

V₁ / V₃ = V₂ / V₄

Из закона Ома получаем:

I₁ R₁ / I₃ R₃ = I₂ R₂ / I₄ R₄ 

Поскольку I1 = I3 и I2 = I4 , получаем:

R₁ / R₃ = R₂ / R₄

Из приведенного выше уравнения, если мы знаем значения трех резисторов, мы можем легко вычислить сопротивление четвертого резистора.

Альтернативный способ расчета резисторов

Из перерисованной схемы, если V _IN является входным напряжением, то напряжение в точке A равно:

V_IN ( R₃ / (R₁ + R₃))

Точно так же напряжение в точке B равно:

V_IN ( R₄ / (R₂ + R₄))

Для сбалансированного моста V_OUT = 0. Но мы знаем, что  V_OUT = VA — V _B 

Итак, в состоянии сбалансированного моста

V_A = V_B

Используя приведенные выше уравнения, мы получаем:

V_IN ( R₃ / (R₁ + R₃)) = V_IN ( R₄ / (R₂ + R₄))

После простых манипуляций с приведенным выше уравнением мы получаем:

R₁ / R₃ = R₂ / R₄

Из приведенного выше уравнения, если R₁ является неизвестным резистором, его значение может быть рассчитано по известным значениям R₂ , R₃ и R₄ . Как правило, неизвестное значение обозначается как R_X , а из трех известных сопротивлений один резистор (в основном R₃ в приведенной выше схеме) обычно представляет собой переменный резистор, называемый R_V .

Найдите неизвестное сопротивление с помощью сбалансированного моста Уитстона

Из приведенной выше схемы предположим, что R₁ является неизвестным резистором. Итак, давайте назовем его R_X . Резисторы R₂ и R₄ имеют фиксированное значение. Это означает, что соотношение R₂ / R₄ также является фиксированным. Теперь, исходя из приведенного выше расчета, для создания сбалансированного состояния, соотношение резисторов должно быть равным, т. е.

R_X / R₃ = R₂ / R₄

Поскольку отношение R₂ / R₄ фиксировано, мы можем легко настроить другой известный резистор (R₃) для достижения вышеуказанного состояния. Отсюда важно, чтобы R₃ был переменным резистором, который мы назовем R_V .

Но как мы обнаруживаем сбалансированное состояние? Здесь можно использовать гальванометр (амперметр старой школы). Поместив гальванометр между точками A и B, мы можем определить состояние равновесия.

Поместив R_X в цепь, отрегулируйте R_V , пока гальванометр не укажет на 0. В этот момент запишите значение R_V . Используя следующую формулу, мы можем вычислить неизвестный резистор R_X .

R_X = R_V (R₂ / R₄)

Несбалансированный мост Уитстона

Если V_OUT в приведенной выше схеме не равно 0 (V_OUT ≠ 0), говорят, что мост Уитстона является несбалансированным мостом Уитстона. Обычно несбалансированный мост Уитстона часто используется для измерения различных физических величин, таких как давление, температура, деформация и т.д.

Чтобы это работало, преобразователь должен быть резистивного типа, т.е. сопротивление преобразователя изменяется соответствующим образом при изменении измеряемой им величины (температура, деформация и т.д.). Вместо неизвестного резистора, в предыдущем примере расчета сопротивления, мы можем подключить преобразователь.

Мост Уитстона для измерения температуры

Давайте теперь посмотрим, как мы можем измерить температуру, используя несбалансированный мост Уитстона. Преобразователь, который мы собираемся здесь использовать, называется термистором, который представляет собой резистор, зависящий от температуры. В зависимости от температурного коэффициента термистора изменения температуры будут либо увеличивать, либо уменьшать сопротивление термистора.

В результате выходное напряжение моста V_OUT станет отличным от нуля значением. Это означает, что выходное напряжение V_OUT пропорционально температуре. Путем калибровки вольтметра мы можем отображать температуру с точки зрения выходного напряжения.

Мост Уитстона для измерения деформации

Одним из наиболее часто используемых применений моста Уитстона является измерение деформации. Тензодатчик — это компонент, электрическое сопротивление которого изменяется пропорционально механическим факторам, таким как давление, сила или деформация.

Обычно диапазон сопротивления тензорезистора составляет от 30 Ом до 3000 Ом. Для данной деформации изменение сопротивления может составлять лишь часть полного диапазона. Поэтому для точного измерения относительных изменений сопротивления используется конфигурация моста Уитстона.

На приведенной ниже схеме показан мост Уитстона, в котором неизвестный резистор заменен тензодатчиком.

Под действием внешней силы изменяется сопротивление тензорезистора и в результате мост становится несбалансированным. Выходное напряжение можно откалибровать для отображения изменений деформации.

Одна из популярных конфигураций тензодатчиков и моста Уитстона — весы. При этом тензодатчики тщательно смонтированы как единое целое, которое представляет собой преобразователь, преобразующий механическую силу в электрический сигнал.

Обычно весы состоят из четырех тензодатчиков, где два тензодатчика расширяются или растягиваются (на растяжение) при воздействии внешней силы, а два тензорезистора сжимаются (на сжатие) при приложении нагрузки.

Если тензорезистор растягивается или сжимается, сопротивление может увеличиваться или уменьшаться. Следовательно, это вызывает разбалансировку моста. Это дает индикацию напряжения на вольтметре, соответствующую изменению напряжения. Если деформация, приложенная к тензодатчику, больше, то разность напряжений на клеммах тензорезистора больше. Если деформация равна нулю, то мост уравновешивается, и счетчик показывает нулевое значение.

Речь идет об измерении сопротивления с использованием моста Уитстона для точного измерения. Из-за дробного измерения сопротивления мосты Уитстона в основном используются в измерениях тензодатчиков и термометров.

Вывод

Из данной статьи вы узнали, что такое схема моста Уитстона, что означает сбалансированный мост, как рассчитать неизвестное сопротивление с помощью моста Уитстона, а также как можно использовать несбалансированный мост Уитстона для измерения различных физических величин, таких как температура и деформация.

С Уважением, МониторБанк

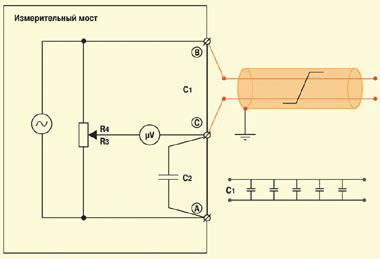
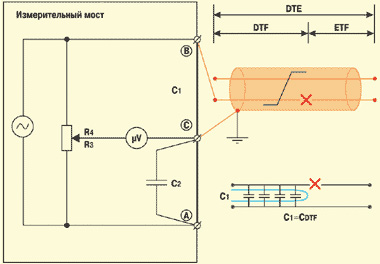
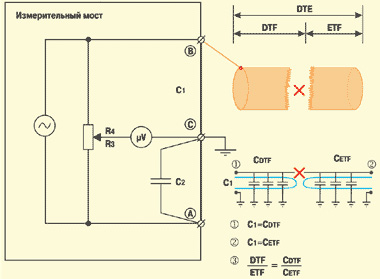
С помощью моста Уитстона при постоянном токе измеряют сопротивление витой пары (шлейфа) (рис. 5), сопротивление изоляции жил пары (рис. 6), сопротивление изоляции между жилами и экраном (рис. 7).

Значения упомянутых параметров используются для диагностики кабельных линий с помощью специальных приборов – измерительных мостов. Локализация же неисправностей требует определения места повреждения на кабельной линии.

При помощи моста постоянного тока несложно вычислить расстояние до места повреждения. Зная сопротивление шлейфа Rшл и погонное сопротивление жил кабеля Rпог, можно воспользоваться формулой: Lпары = Rшл / 2Rпог, и рассчитать длину витой пары.

Погонное сопротивление медных жил определяется табличным способом по их сечению. Оно зависит не только от сечения жил, но и от их температуры. Чтобы избежать ошибки, нужно использовать значение погонного сопротивления для соответствующей температуры (особенно важно это для воздушных кабельных линий, где температура меняется в широких пределах). В простых мостах значения вводятся оператором вручную из таблиц. В более сложных приборах при помощи автоматической или полуавтоматической калибровочной процедуры определяется поправочный коэффициент по измеренному значению температуры (для чего в комплекте прибора присутствует щуп-датчик).

Длина витой пары может быть установлена также мостовым методом при переменном токе (рис. 8). В таком случае измеряемым параметром является емкость витой пары. Разделив емкость витой пары на ее погонную емкость, получим длину витой пары.

Аналогично рассмотренным выше измерениям при постоянном токе, с помощью моста Уитстона при переменном токе определяются емкость витой пары (шлейфа) и емкость каждой из жил пары относительно экрана. Длина жил может быть вычислена по их погонной емкости. Погонная емкость (нФ/км) витой пары зависит от сечения жил, типа скрутки, вида и материала изоляции и определяется табличным способом по типу кабеля.

Резкое увеличение емкости витой пары по сравнению с ее паспортным значением, как правило, свидетельствует о наличии воды в сердечнике кабеля. Для локализации повреждений этого типа применяются другие методы, прежде всего зондирование поврежденной пары с помощью рефлектометра.

Отметим, что, в отличие от сопротивления, погонная емкость слабо зависит от температуры, что существенно упрощает измерения.

Измерения при переменном токе удобно использовать для локализации обрывов жил (рис. 9). В случае экранированного кабеля это лучше всего сделать посредством измерения емкости каждой из жил относительно экрана. Зная погонную емкость жилы Cпог, длину оборванной жилы можно рассчитать по формуле Lпары = Cж-э/Cпог.

При измерении емкости жил оборванной цепи, жилы остальных цепей кабельного пучка соединяют между собой и с надежно заземленным экраном. Если результаты измерений емкости обеих жил одинаковы, то это означает, что и та и другая оборваны в одном месте. Разные значения указывают на наличие обрыва только в одной жиле, причем в той, емкость которой меньше. Расстояние до места обрыва вычисляется по формуле Lпары = Cж-э/Cпог, где Cж-э и Cпог — измеренная и погонная емкость жилы.

Очень важно помнить, что существенное влияние на результат измерений оказывают дефекты экрана кабеля (рис. 10). С помощью рассмотренной выше схемы можно определить и место обрыва экрана кабеля. Для этого экран отключают от заземления и затем с обеих сторон измеряют его емкость относительно земли. Место обрыва вычисляется исходя из отношения результатов этих измерений и длины кабеля (если она неизвестна, необходимо использовать измерения длины шлейфа жил любой пары при постоянном токе). Расстояние до обрыва устанавливается приблизительно — на основании измеренной емкости экрана и его погонной емкости (она оценивается как 0,083 от погонной емкости жилы относительно экрана).

Если кабель не экранирован, то расстояние до места обрыва можно определить, измерив емкость пары жил. Однако применение мостовой схемы Уитстона (Wheatstone) не обеспечивает достаточную точность. Впрочем, и в случае измерений при постоянном токе к схеме Уитстона для локализации неисправности прибегают редко, чаще всего предпочтение отдается мосту Муррея (Murray).

См. также:

• Принцип работы мостовой схемы
• Методики измерений с помощью мостовых приборов
  • Измерения с помощью моста Муррея
  • Измерения с помощью моста Хилборна/Графа
• Полезные советы
• Сравнительная таблица измерительных мостов

Метод
моста Уитстона – один из наиболее точных
методов определения электрического
сопротивления.

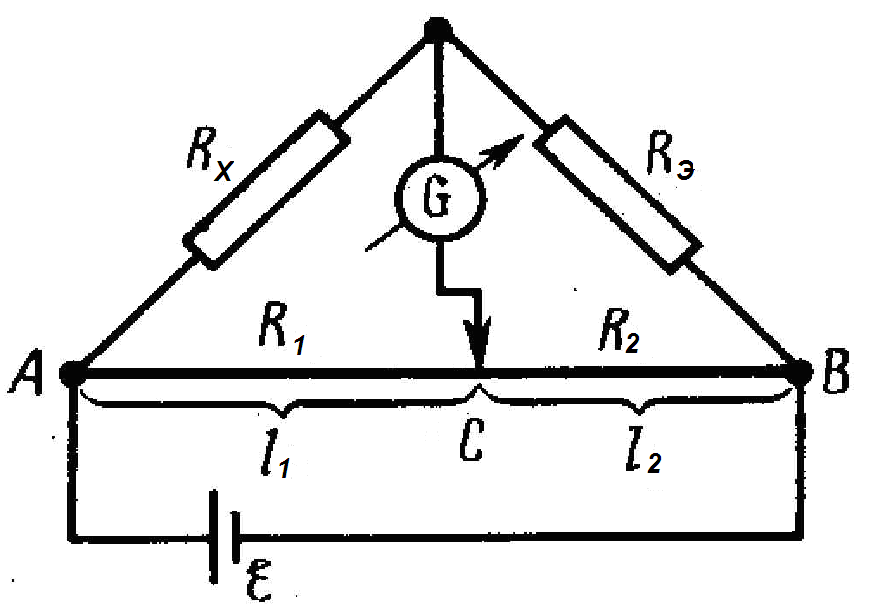
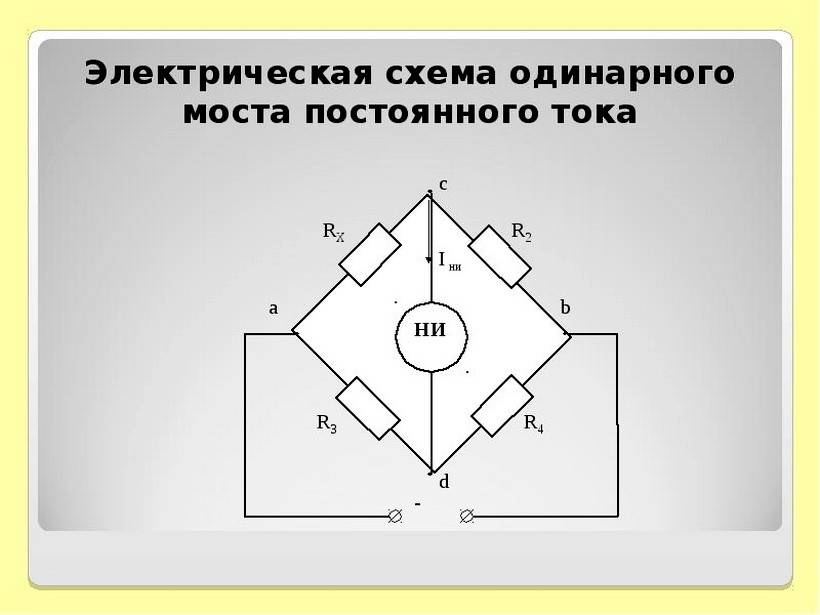
Рис. 3. Схема
моста Уитстона

Сопротивления
образуют
его плечи (рис.3). Между точками А и
В моста включена батарея с э.д.с.

и сопротивлением
,
между точками

и

включен гальванометр с сопротивлением
.
Для узлов А, С и D,
применяя первое правило Кирхгофа,
получим

(3)

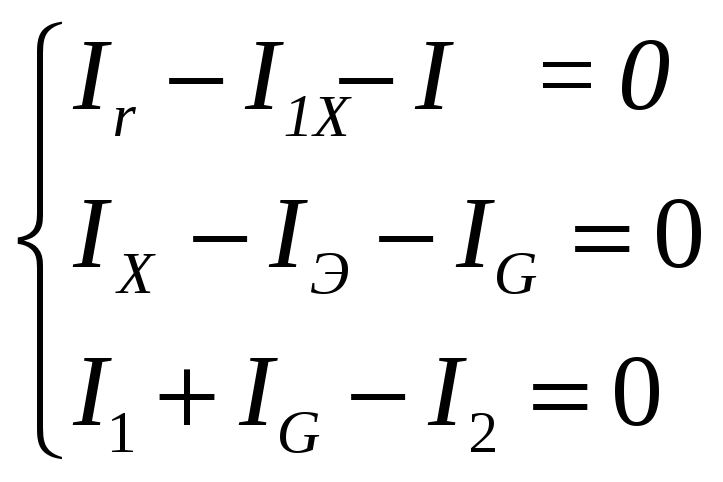
Для контуров
,
и
,
согласно второму правилу Кирхгофа,
можно записать:

(4)

Если известны все сопротивления и
э.д.с., то, решая полученные шесть
уравнений, можно найти неизвестные
токи. Изменяя известные сопротивления

и
,
можно добиться того, чтобы ток через
гальванометр был равен нулю

Тогда из системы (3) следует равенство
для сил токов

,

. (5)

Из системы (4) с учетом (5) получаем

,

.

Откуда

или
. (6)

Таким образом, в случае равновесного
моста

при определении искомого сопротивления

э.д.с. батареи, сопротивления батареи
и гальванометра роли не играют.

На практике обычно используется
реохордный мост Уитстона, где сопротивления

и

представляют собой длинную однородную
проволоку (реохорд) с большим удельным
сопротивлением, так что отношение

можно заменить отношением
.
Тогда, выражение (7) можно записать

. (7)

Длины

и

легко измеряются по шкале, а сопротивления
эталона

всегда известно. Поэтому уравнение (7)
позволяет определить неизвестное
сопротивление
.

Рис. 4. Схема
реохордного моста Уитстона

Так
как электрическое сопротивление реохорда
сравнительно небольшое, то мост Уитстона
описанного типа применяется для измерения
сопротивлений порядка 10³
Ом.

Определим положение
движка реохорда, соответствующее
минимальной погрешности измерения
сопротивления.

Относительная
погрешность измерения сопротивления
мостиком Уитстона, которую легко получить
из формулы (7), равна:

(8)

т.к.
абсолютная погрешность измерения длин
плеча реохорда равна:
,
то

,
(9)

где
l
= l₁
+ l₂
– длина провода реохорда.

Относительная
погрешность будет минимальна тогда,
когда знаменатель второго члена правой
части формулы (9) максимален.

Найдем
условие максимума функции:

Отсюда:

,

Таким
образом, погрешность будет минимальной,
когда при равновесии мостика Уитстона
движок реохорда находится в среднем
положении, т.е. l₁
= l₂.

В
этом случае формула (7) принимает вид:
R_Х
= R_Э.

2. Практическая часть

Задание 1. Определение сопротивления
первого резистора

1. Собрать схему экспериментальной
установки по рисунку 1 или 2, используя
в качестве исследуемого сопротивления
первый резистор с неизвестным
сопротивлением.

2. Начертить таблицу 1 для занесения в
нее результатов измерения и расчетов.

3. Провести измерения сопротивления
первого резистора, меняя эталонные
(известные) сопротивления и измеряя
длины плеч, которые образуются путем
перемещения ползунка реохорда. Результаты
измерений занести в таблицу (измерения
повторяются для каждого эталонного
сопротивления).

4. Длина правого плеча вычисляется по
формуле
,
где
–
длина катушки реохорда.

Таблица
1

Определение
электрического сопротивления первого
резистора

№	Сопротивление эталона Rэ, Ом	Длина левого плеча l1, см	Длина правого плеча l2, см	Сопротивление резистора Rx1, Ом	Абсолют. погрешность сопротивленияRx1, Ом	Относит. погрешность сопротивления Rx1, %
1
2
3
4
5
Средние значения

5.
Вычислить сопротивление первого
резистора по формуле

для каждого измерения.

6.
Вычислить среднее значение сопротивления
первого резистора по формуле
.

7.
Вычислить абсолютную и относительную
погрешности сопротивления первого
резистора по формулам
и

для каждого измерения.

8.
Вычислить среднюю абсолютную и
относительную погрешности сопротивления
первого резистора по формулам
и
,
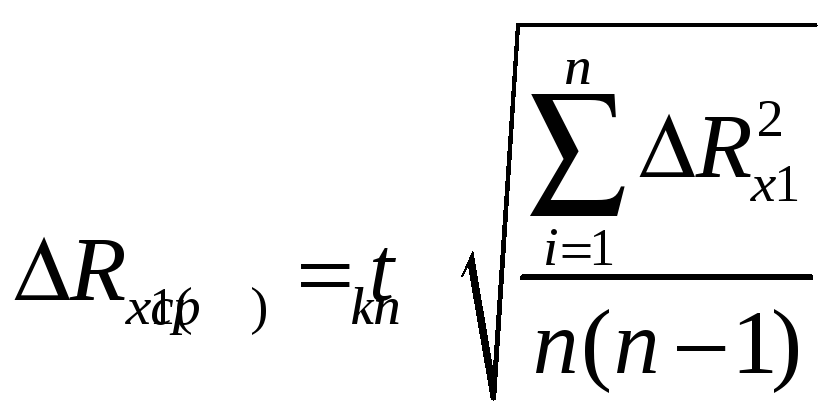
где t_kn —
коэффициент Стьюдента, зависящий от
заданной вероятности k
и числа измерении n.
Для k = 0,95,
принятой в студенческом практикуме,
коэффициент Стьюдента для различного
числа измерения n
указан в таблице ниже.

Количество измерений, n	3	4	5	6	7	8	9	10
Коэффициент Стьюдента, tkn	4,3	3,2	2,6	2,4	2,3	2,0	1,8	1,5

9.
Записать окончательное значение
сопротивления первого резистора в виде
.

Задание 2. Определение сопротивления
второго резистора

10. Заменить в
экспериментальной установке первой
резистор с неизвестным сопротивлением
вторым резистором с неизвестным
сопротивлением.

Таблица
2

Определение
электрического сопротивления второго
резистора

№	Сопротивление эталона Rэ, Ом	Длина левого плеча l 1, см	Длина правого плеча l 2, см	Сопротивление резистора Rx2, Ом	Абсолют. погрешность сопротивленияRx2, Ом	Относит. погрешность сопротивления Rx2, %
1
2
3
4
5
Средние значения

11.
Начертить таблицу 2 для занесения в нее
результатов измерения и расчетов.
Произвести измерение сопротивления
второго резистора и вычислить абсолютные
и относительные погрешности, повторив
пункты 3-9. Результаты измерений и расчетов
занести в таблицу 2.

Задание 3. Определение сопротивления
двух последовательно соединенных
резисторов

12.
Заменить в экспериментальной установке
второй резистор с неизвестным
сопротивлением двумя последовательно
соединенными резисторами с неизвестными
сопротивлениями.

13.
Начертить таблицу 3 для занесения в нее
результатов измерения и расчетов.
Произвести измерение сопротивления
двух последовательно соединенных
резисторов, повторив пункты 3-6. Результаты
измерений занести в таблицу 3.

Таблица 3

Определение
электрического сопротивления
последовательно соединенных резисторов

№	Сопротивление эталона Rэ, Ом	Длина левого плеча l 1, см	Длина правого плеча l 2, см	Сопротив. соедин. резист. , Ом	Абсолют. погрешность сопротивл. Rx пос, Ом	Относит. погрешность сопротивл. Rx пос, %
1
2
3
4
5
Средние значения

14.
Вычислить абсолютную и относительную
погрешности сопротивления двух
последовательно соединенных резисторов
по формулам
и

для каждого измерения, где теоретическое
значение сопротивления двух последовательно
соединенных резисторов определяется
по формуле
.

15. Вычислить среднюю
абсолютную и относительную погрешности
сопротивления двух последовательно
соединенных резисторов согласно пункту
8 и запишите в виде, указанном в пункте
9.

Задание 4. Определение сопротивления
двух параллельно соединенных резисторов

16.
Изменить в экспериментальной установке
последовательное соединение двух
резисторов с неизвестным сопротивлением
на параллельное соединение.

17.
Начертить таблицу 4 для занесения в нее
результатов измерения и расчетов.
Произвести измерение сопротивления и
вычислить абсолютную и относительную
погрешности сопротивления двух
параллельно соединенных резисторов,
повторив пункты 13-15. Результаты измерений
занести в таблицу 4. Теоретическое
значение сопротивления двух параллельно
соединенных резисторов определяется
по формуле
.

Таблица
4

Определение
электрического сопротивления параллельно
соединенных резисторов

№	Сопротивление эталона Rэ, Ом	Длина левого плеча l 1, см	Длина правого плеча l 2, см	Сопротив. соедин. резист. Rx пар , Ом	Абсолют. погрешность сопротивл. Rx пар, Ом	Относит. погрешность сопротивл. .Rx пар, %
1
2
3
4
5
Средние значения

18.
Сформулируйте вывод работы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Измерительный мост – электрическая схема, усовершенствованная английским физиком Чарльзом Уинстоном. Она источник постоянного тока и базовая мостовая схема, которую применяют в конструкциях многих измерительных приборов. Например, в устройствах контроля и измерения температур – термометрах.

Что такое измерительный мост?

Как пример, объясняющий электросхему моста, возьмём терморезистор или термометр. В таких системах механизм ставят в одной ветви схемы. Можно провести аналогию с аптечными весами. Разница только в том, что мост — электрическое устройство.

Рычажные весы и приборы с мостовой схемой действуют компенсационным способом. Величина тока в по Уинстону есть разница между сопротивлениями — чем она выше, тем обширнее протекает электрический ток. При изменении разности меняется и количество электрических зарядов.

Это свойство применяют в различных системах и приборах контроля. Точность замеров достигается за счет изменения сопротивления. Во время измерения электричества, проходящего через измерительный мост постоянного тока, обнаруживаются любые изменения физической величины сопротивления.

Принцип работы моста Уитстона

Мостовая схема Ч. Уинстона состоит из 2-х плеч. В каждом 2 резистора. Соединяет 2 параллельные ветви еще одна. Ее название – мостик. Ток проходит от клеммы с минусом к верхнему пику мостовой схемы.

Разделившись по 2 параллельным ветвям, ток идёт к положительной клемме. Величина сопротивления в каждой ветви непосредственно влияет на количество тока. Равное сопротивление на обеих ветвях говорит о том, что в них течет аналогичное количество тока. В таких условиях мостовой элемент уравновешен.

Если в ветвях неравное сопротивление, ток в электросхеме начинает движение от ветви с высоким уровнем сопротивления к ветви с наименьшим. Так продолжается, пока 2 верхних элемента цепей остаются равны по своей величине. Аналогичное положение резисторы имеют в схемах, которые используют в системах контроля и измерения.

Типы и модификации измерительных мостов

Основная схема измерительного моста – Уинстона. Одинарный мост меряет сопротивление от 1 Ом до 100 Мом. Но есть и модификации, позволяющие измерять разные типы сопротивлений — те, для которых базовая схема не годится.

Разновидности

1. Небольшие сопротивления измеряются посредством прибора Кери Фотера. Можно узнать разницу между противодействиями больших значений.
2. Еще один тип – делитель Кельвина-Варлея. Применяется в приборах лабораторного оборудования. Максимальная измеряющая способность, зафиксированная этим делителем напряжения, достигает 1,0*10-7.
3. Мост Кельвина, который в некоторых странах называют именем Томсона, предназначен для замера неизвестных сопротивлений небольших величин (меньше 1 Ом). По принципу работы похож на одинарный мост Уинстона. Разница лишь в наличии дополнительного сопротивления, снижающего погрешности в измерении, которые появляются в результате падения напряжения в одном из плеч.
4. Еще один тип – мост Максвелла. Измеряет низкодобротную индуктивность неизвестной величины.

Схемы измерительных мостов

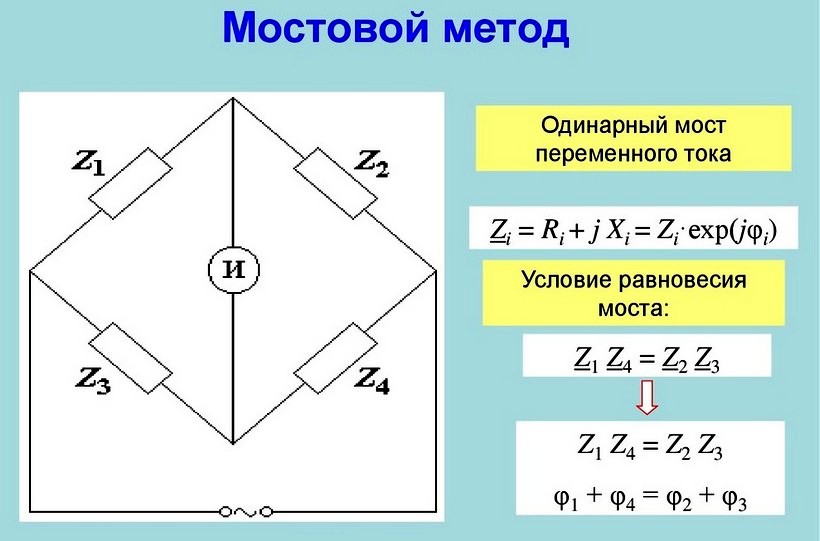
Измерительные мосты переменного тока делят на 2 группы: двойные и одинарные. Одинарные имеют 4 плеча. В них 3 ветви создают цепь с 4 точками подключения.

В диагонали моста есть электромагнитный гальванометр, показывающий равновесие. В другой диагонали моста действует источник постоянного питания. Измерения могут происходить с погрешностями, которые зависят от их диапазона. По мере роста сопротивления чувствительность прибора уменьшается.

Двойной мост называют шестиплечим. Его плечи – измеряемое сопротивление (Rx), резистор (Ro) и 2 пары дополнительных резисторов (Rl, R2, R3, R4).

Двойные измерительные мосты

Небольшие сопротивления измеряются двойными мостами, состоящими из таких компонентов:

• резисторы R (4);
• гальванометр;
• резистор образцовый;
• источник питания;
• амперметр;
• резистор, устанавливающий рабочий ток.

Чтобы узнать условия, при которых возникает равновесие, для замкнутых контуров применяют уравнение Кирхгофа. Соблюдается условие: по гальванометру должен идти нулевой ток.

Где используют измерительный мост Уитстона?

Измерительные элементы применяют в работе с кабельными линиями из металла. Они позволяют нейтрализовать постороннее влияние для более эффективной локализации дефектов. Гарантированы высокоточные результаты в рамках диапазона измеряемых величин.

С помощью мостовой схемы Уитстона можно вычислить сопротивление изменяющегося элемента. Схемы используют в конструкциях электронных весов, электронных термометров и терморезисторов.

Среди промышленных образцов широко известны приборы с ручной калибровкой равновесия:

• ММВ – измеряет сопротивление проводника постоянного напряжения;
• Р333 – схема одинарного моста, с помощью которой выявляется поврежденный участок кабеля.

Заключение

С помощью прибора Уинстона можно мерить индуктивность, содержание газа в воздухе или другом веществе, емкость и иные физические величины. Подробно о данных схемах можно прочитать в учебнике «Измерительные соединения». В книге представлены основные понятия, базовые методики, примеры, иллюстрирующие принцип действия.

Для измерения электрического сопротивления имеется два варианта использования моста Уитстона:

• Определение абсолютного значения сопротивления путем сравнения с известным сопротивлением.
• Определение относительных изменений сопротивления.

Последний вариант используется в отношении тензометрических методов измерения. Он позволяет с большой точностью определить относительные изменения сопротивления тензодатчика в распространённом диапазоне от 10 ^-4 до 10 ^-2 Ом / Ом.

На изображении ниже показаны две разные иллюстрации моста Уитстона: на рисунке а) обычное изображение ромба, в котором используется мост Уитстона; на рисунке b) располагается изображение все той же электрической схемы, но более понятное для новичка.

Четыре ветви мостовой схемы образованы сопротивлениями от R ₁ до R ₄ . Угловые точки 2 и 3 обозначают соединения для напряжения возбуждения моста V _s . Выходное напряжение моста V ₀ , то есть сигнал измерения, доступно в угловых точках 1 и 4.

Если напряжение питания V _s приложено к точкам питания моста 2 и 3, то напряжение питания делится на две половины моста R ₁ , R ₂ и R ₄ , R ₃ как отношение соответствующих сопротивлений моста. , т. е. каждая половина моста образует делитель напряжения.

Мост может быть разбалансирован из-за разницы напряжений и электрических сопротивлений на R ₁ , R ₂ и R ₃ , R ₄ . Это можно рассчитать следующим образом:

если мост уравновешен и

где выходное напряжение моста V ₀ равно нулю.

При заданной деформации сопротивление тензодатчика изменяется на величину ΔR. Это дает нам следующее уравнение:

Для измерения деформации сопротивления R ₁ и R ₂ в мосте Уитстона должны быть одинаковыми.
То же самое относится к R ₃ и R ₄ .

С помощью нескольких упрощений можно вывести следующее уравнение:

На последнем этапе расчета ΔR / R необходимо заменить следующим:

Здесь k — коэффициент k тензодатчика, ε — деформация. Получаем следующее:

Уравнения предполагают, что все сопротивления в мосту изменяются. Обозначения, такие как: четверть моста, полумост, двойная четверть или диагональный мост и полный мост, являются обычными.

Хотя для обозначения таких схем используются вышеупомянутые определения типа: «полумост» или «четверть моста», на самом деле они не совсем корректны. Фактически, цепь, используемая для измерения, всегда является полной и полностью или частично формируется тензометрическими датчиками. Затем они дополняются постоянными резисторами, которые встроены в измерительные приборы.

Весовые терминалы обычно соответствуют очень строгим требованиям к точности. Поэтому, в отличие от экспериментальных измерительных приборов, весовые преобразователи всегда должны иметь полную мостовую схему с активными тензодатчиками на всех четырех плечах.

В случае, если необходимо устранить различные помехи и факторы препятствующие измерению, полномостовые или полумостовые схемы используются для анализа нагрузки. Важным условием является четкое различение напряжений и сил, таких как сжатие или растяжение, а также изгибающие, сдвиговые или скручивающие силы.

В таблице ниже показана зависимость положения тензометрических датчиков, типа используемой мостовой схемы и результирующего коэффициента моста B для нормальных сил, изгибающих моментов, крутящего момента и температуры. В небольших таблицах, приведенных для каждого примера, указан коэффициент моста B для каждого типа влияющей величины. Эти уравнения используются для вычисления эффективного напряжения от выходного сигнала моста V _O / V _S .

	Конфигурация моста	Вычисление	Измерение	Описание	Преимущества и недостатки
1				Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки	Простой четвертьмост Простая четвертьмостовая схема с одним активным тензодатчиком	+ Простая установка — Нормальная деформация и деформация изгиба накладываются друг на друга — Температурные эффекты не компенсируются автоматически
2				Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки	Квартальный мост Две четвертьмостовые схемы, одна активно измеряет деформацию, другая монтируется на пассивном компоненте, изготовленном из того же материала, который не подвергается деформации.	+ Температурные эффекты хорошо компенсируются — Нормальную деформацию и деформацию изгиба нельзя разделить (наложение изгиба)
3				Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки	Полумост Пуассона Два активных тензодатчика, соединенных полумостом, один из которых расположен под углом 90 ° к другому	+ Температурные эффекты хорошо компенсируются, когда материал изотропный
4				Измерение деформации изгибаемой балки	Полумост На противоположных сторонах конструкции установлены два тензодатчика.	+ Температурные эффекты хорошо компенсируются + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект)
5				Измерение деформации на стержне растяжения / сжатия	Диагональный мост На противоположных сторонах конструкции установлены два тензодатчика.	+ Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен)
6				Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки	Полный мост 4 тензодатчика установлены с одной стороны конструкции как полноценный мост.	+ Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) — Нормальную деформацию и деформацию изгиба нельзя разделить (наложение изгиба)
7				Измерение деформации на стержне растяжения / сжатия	Диагональный мост Два активных тензодатчика, два пассивных тензодатчика	+ Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен) + Температурные эффекты хорошо компенсируются
8				Измерение деформации изгибаемой балки	Полный мост Четыре активных тензодатчика соединены как полный мост	+ Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются
9				Измерение деформации на стержне растяжения / сжатия	Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 °	+ Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен) + Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR)
10				Измерение деформации изгибаемой балки	Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 °	+ Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются
11				Измерение деформации изгибаемой балки	Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 °	+ Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются
12				Измерение деформации изгибаемой балки	Полный мост Четыре активных тензодатчика, соединенные как полный мост	+ Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR)
13				Измерение деформации скручивания	Полный мост Установлены четыре тензодатчика, каждый под углом 45 ° к главной оси, как показано.	+ Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются
14				Измерение деформации скручивания при ограниченном пространстве для установки	Полный мост Четыре тензодатчика устанавливаются как полный мост под углом 45 ° и накладываются друг на друга (розетки)	+ Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются
15				Измерение деформации скручивания при ограниченном пространстве для установки	Полный мост Четыре тензодатчика устанавливаются как полный мост под углом 45 ° и накладываются друг на друга (розетки)	+ Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются

Пояснения к символам: