Нагрузка равномерно распределенная как найти

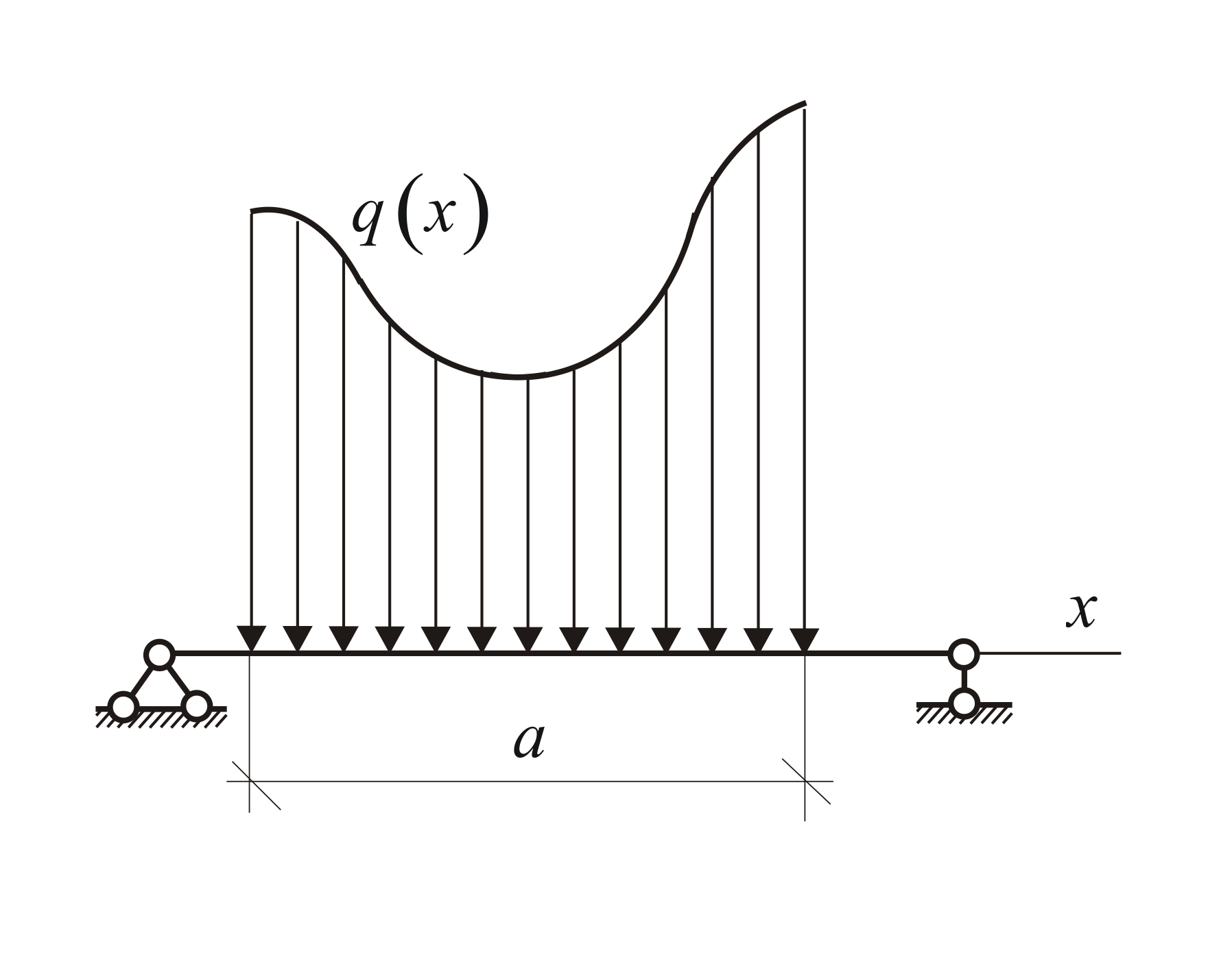
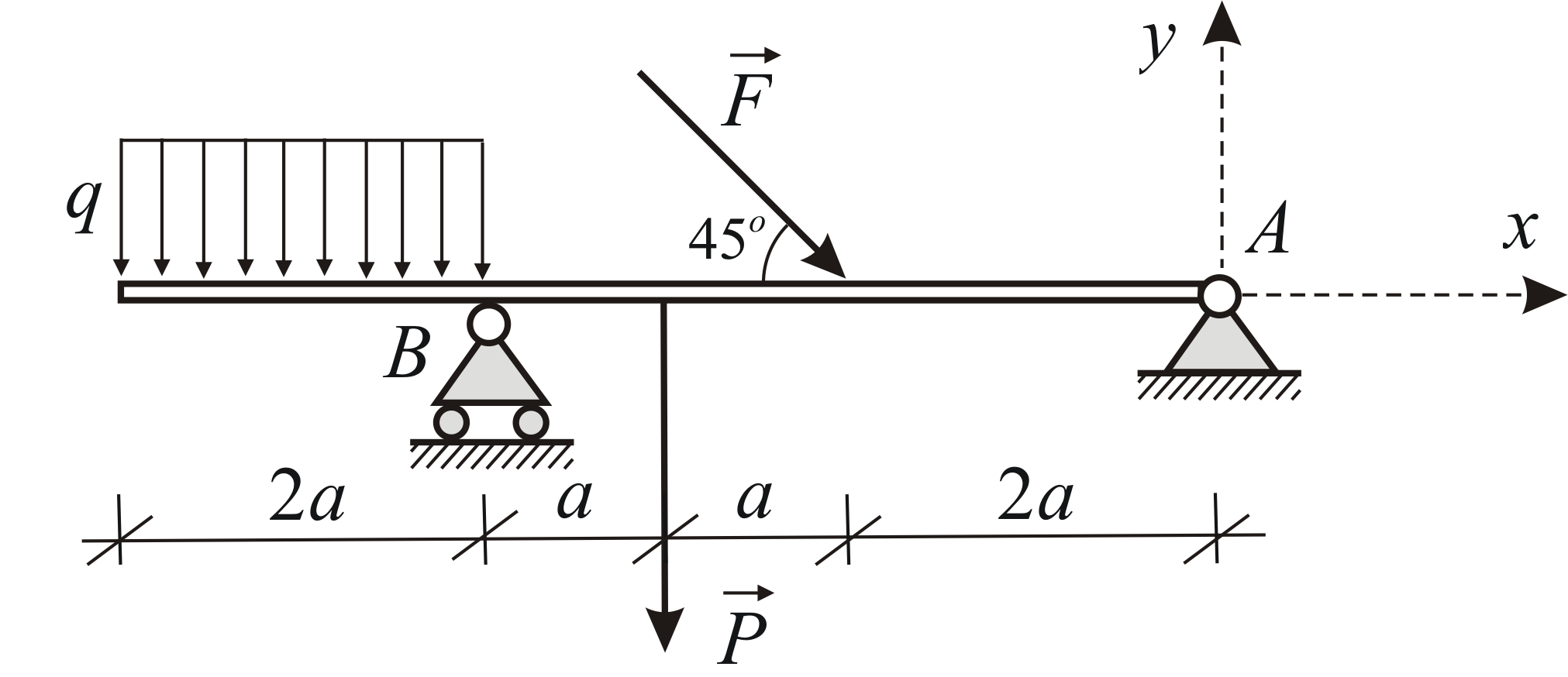
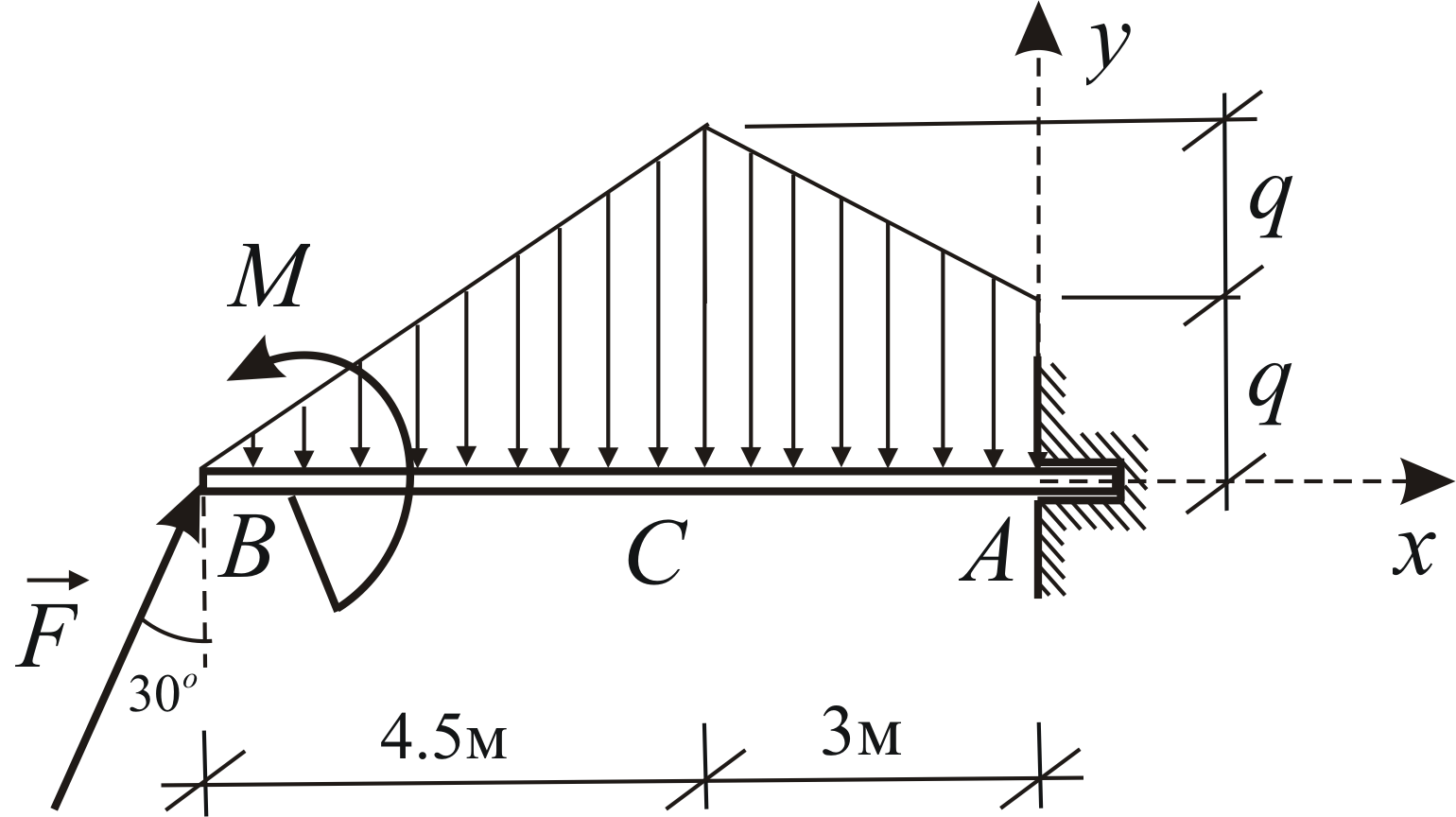
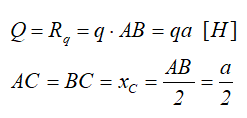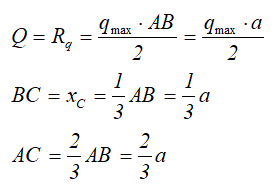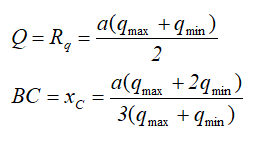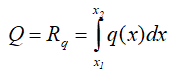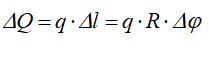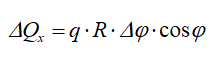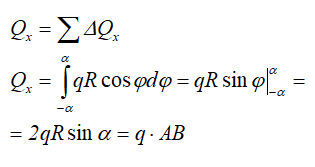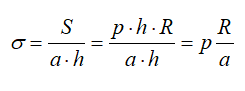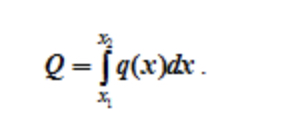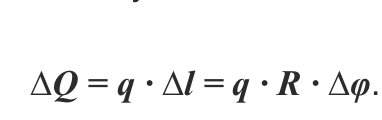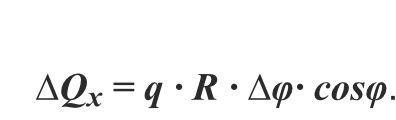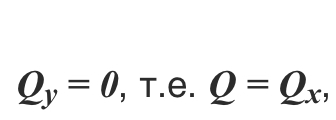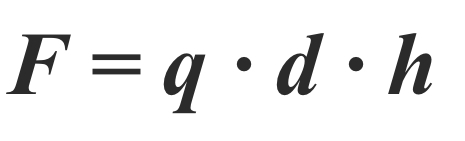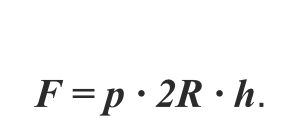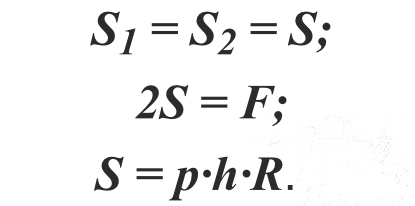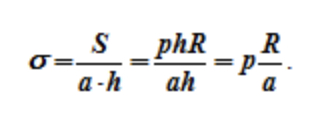Распределенная нагрузка

Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади (поверхности) или объему.

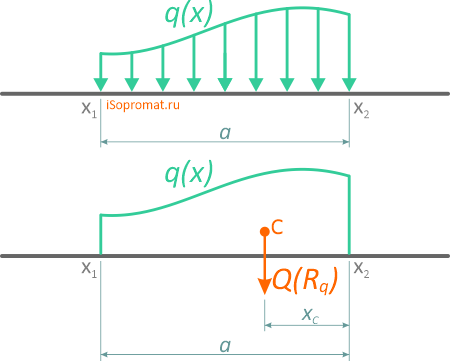
Рассмотрим виды распределенных нагрузок q: линейную, равномерную, треугольную (возрастающую или убывающую), трапециевидную, нелинейную, наклонную (направленную под углом) и замену их результирующей сосредоточенной силой — равнодействующей Q (R_q)

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Это может быть собственный вес элемента конструкции, давление газа или воды, распределенный вес сыпучих материалов, ветровая нагрузка и тому подобное.

Обозначение распределенной нагрузки — q

Размерность:

• линейной нагрузки — Н/м,
• нагрузки распределенной по площади — Н/м²,
• объемной (например при учете собственного веса элементов конструкции) — Н/м³.

или кратные им, например кН/м.

Равнодействующая распределенной нагрузки

При решении некоторых задач технической и теоретической механики, распределенную нагрузку удобно заменять её равнодействующей, обозначаемой Q или R_q, которая для линейного случая распределения, определяется произведением интенсивности нагрузки q на её длину AB.

Равнодействующая распределенной нагрузки действует в точке, расположенной в центре тяжести фигуры, ограниченной профилем её распределения.

Рассмотрим способы замены распределенных нагрузок их равнодействующей.

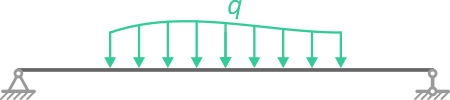
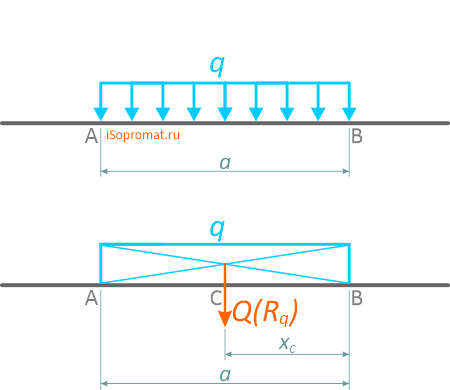
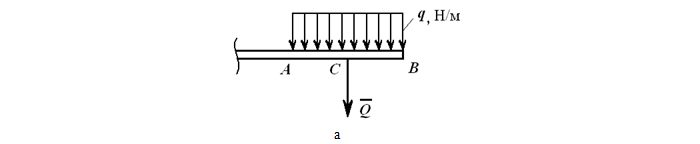
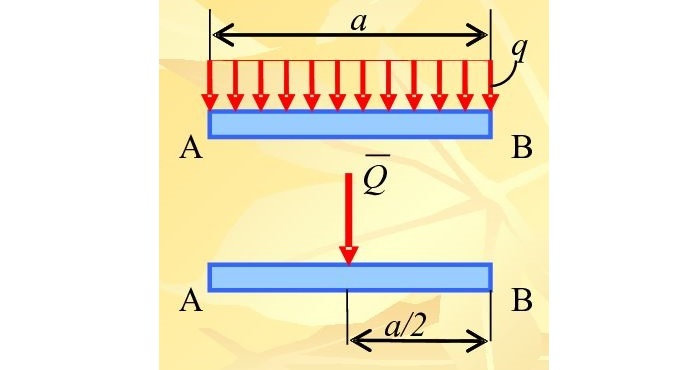
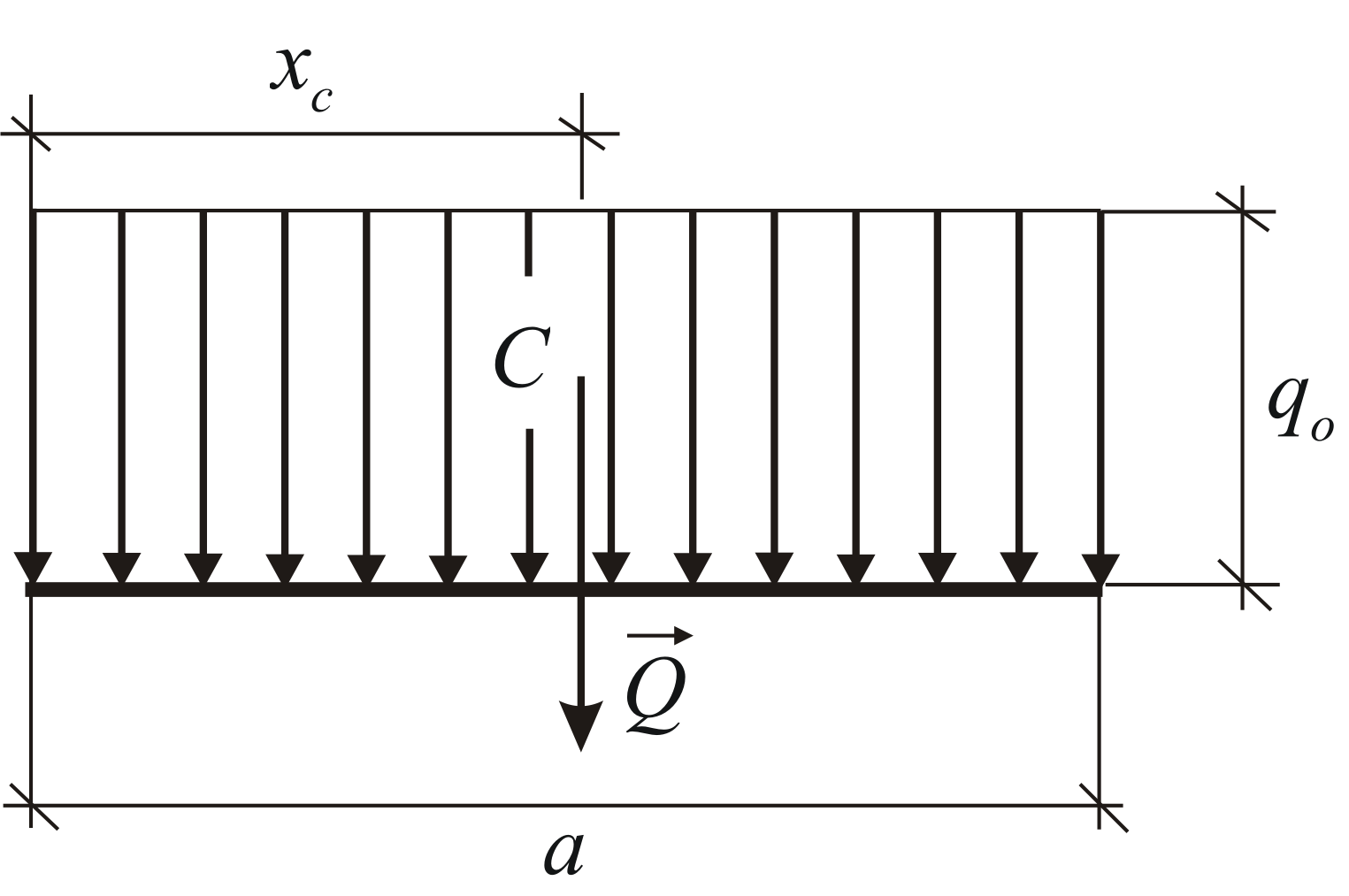
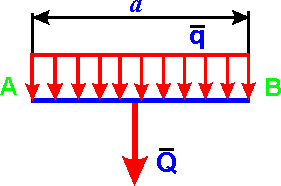
Равномерно распределенная нагрузка

Равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м

может быть заменена сосредоточенной силой Q (R_q)

приложенной в центре (на пересечении диагоналей) прямоугольника, середине отрезка AB.

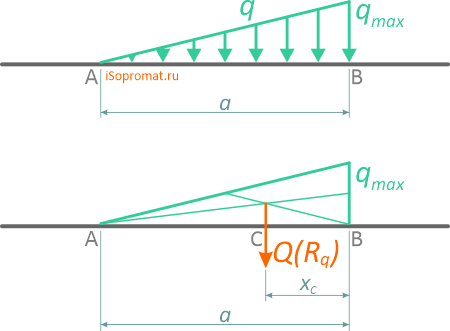
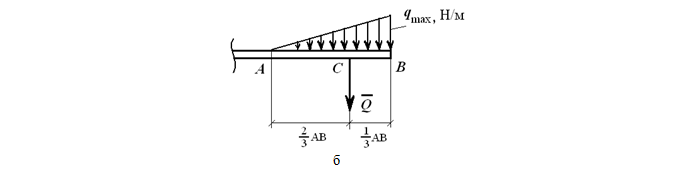
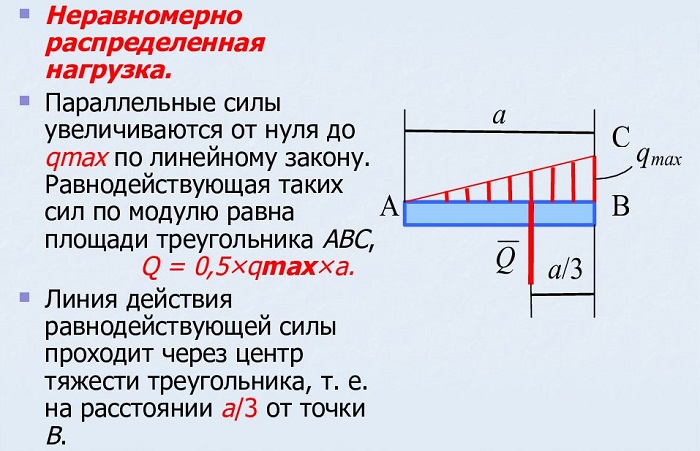
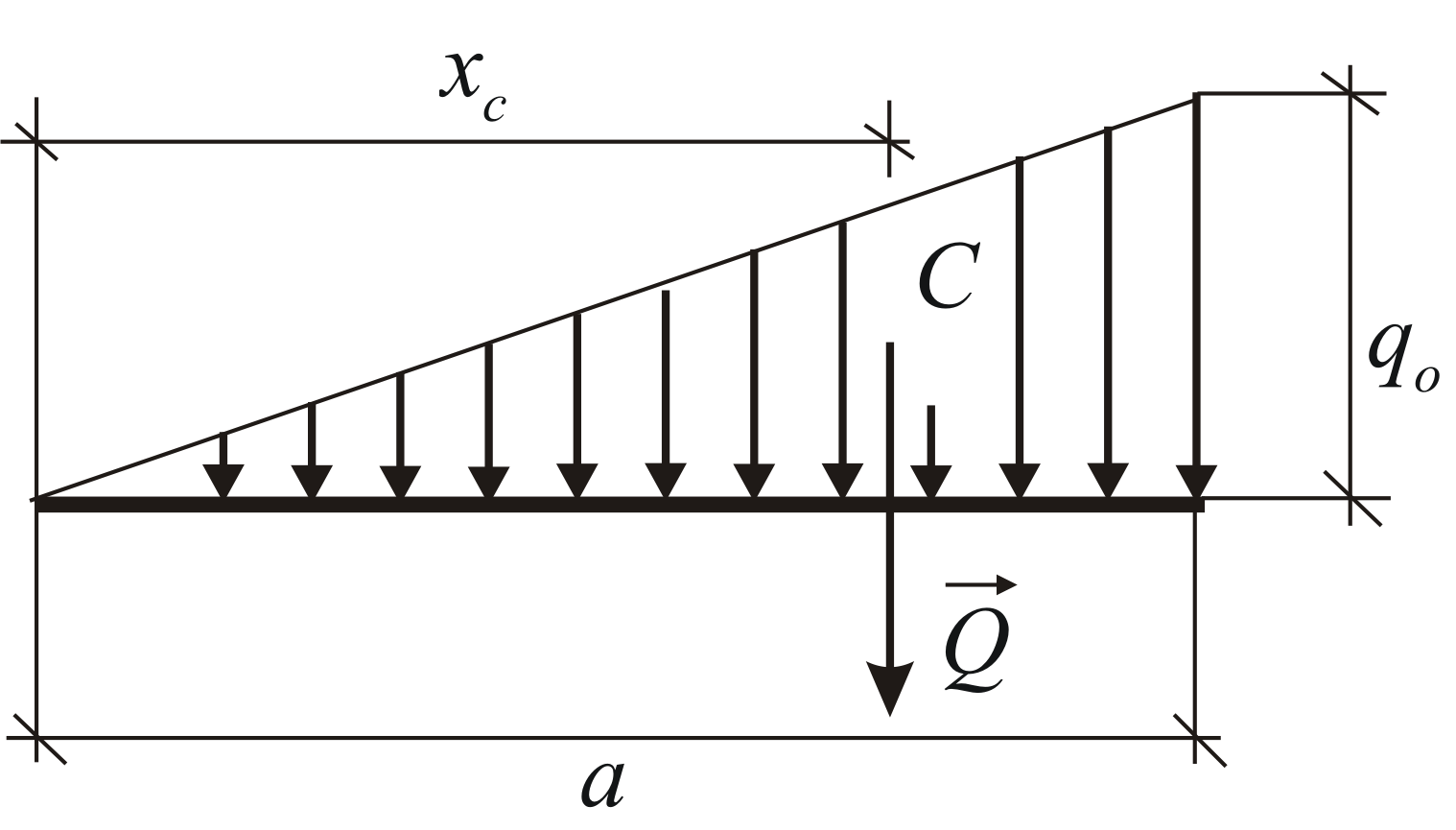
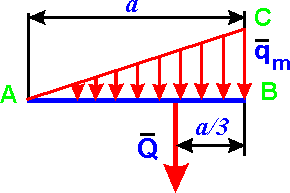
Линейно изменяющаяся (треугольная) нагрузка

Треугольная, линейно изменяющаяся убывающая (возрастающая) нагрузка

может быть заменена равнодействующей силой, приложенной в точке C

Отметим, что центр тяжести треугольника находится на пересечении его медиан, на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин.

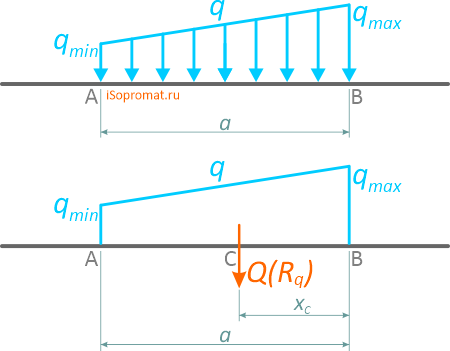
Трапециевидная распределенная нагрузка

Трапециевидная, равномерно убывающая или возрастающая нагрузка характеризуется длиной и двумя значениями интенсивности распределения нагрузки: минимальной q_min и максимальной q_max

Профиль такой нагрузки представляет собой трапецию.
Величина и положение равнодействующей Q в данном случае определяется по выражениям

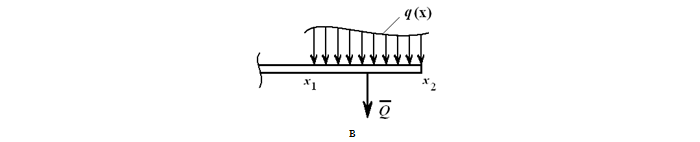
Нелинейная распределенная нагрузка

В произвольном общем случае, интенсивность распределения нагрузки по её длине может описываться одной или несколькими функциями.

Зная функцию q(x), сосредоточенная эквивалентная (равнодействующая) сила рассчитывается по формуле

Эта сила также приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

Для расчета точки приложения равнодействующей нагрузки необходимо вычислить координату положения центра тяжести фигуры, образуемой нагрузкой.

Наклонная распределенная нагрузка

В случаях, когда распределенная нагрузка приложена под определенным углом, величина равнодействующей определяется аналогично ранее описанным способам.

При этом угол наклона самой силы будет равен углу наклона нагрузки q.

Например, линия действия равнодействующей наклонной равномерно распределенной нагрузки будет пересекать ось балки ровно посередине между крайними точками её приложения.

Величина равнодействующей будет равна площади параллелограмма, образованного профилем нагрузки.

Как рассчитывается момент распределенной нагрузки

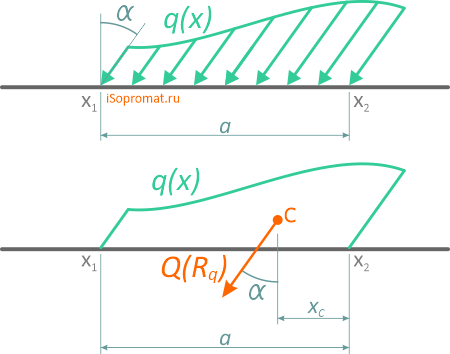
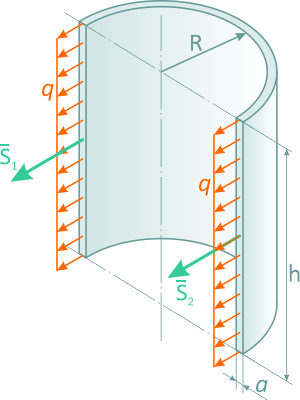
Распределенная нагрузка от давления

Примером распределенной нагрузки от давления может служить расчет усилий, разрывающих стенки баллона со сжатым газом.

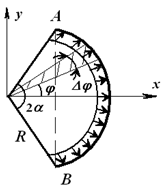
Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м];

где:
R – радиус трубы,
2α – центральный угол,
ось Ox – ось симметрии.

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

Проекция этой силы на ось Ox будет

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

Q_y = 0, т.е. Q = Q_x,

Тогда

где АВ – хорда, стягивающая концы дуги.

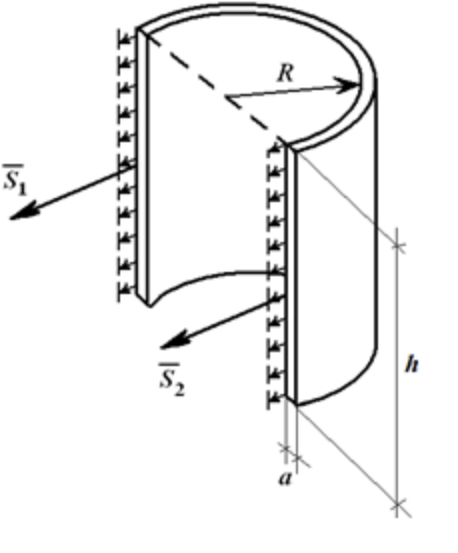
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует равномерно распределенная нагрузка интенсивностью q = p [Н/м²].

Если цилиндр рассечен по диаметру, то равнодействующая этих сил равна

F = q ∙ d ∙ h

где, d – внутренний диаметр, или

F = p ∙ 2R ∙ h.

Тогда, разрывающие баллон по диаметру усилия:

S₁ = S₂ = S;
2S = F;
S = p∙h∙R.

Если принять что a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

Примеры решения задач >
Уравнения равновесия системы сил >

Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.

Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м³] для объемной конструкции, в [H/м²] — для площади, для линейной – в [H/м].

Продемонстрируем это на рисунке:

Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:

Q = q ∗ AB⌈H⌉

здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].

Примечательно, что сила приложена к середине данного отрезка AB.

На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:

Q = q_max ∗ AB/2

где q_max – максимальная интенсивность [Н/м]. 

Q приложена к точке C, где AC равно: AC = 2/3 AB 

Рассматривая функцию q(x), представленную на рисунке:

можно высчитать значение эквивалентной силы по формуле:

Равномерно и неравномерно распределенная нагрузка на балку

Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а. 

Единицы измерения распределённой нагрузки [Н/м].

Её также можно заменить на величину Q, которая приложена в середину AB. 

Составим формулу: Q = q∗a

Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.

При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.

Пример решения задач с распределенной нагрузкой

Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.

Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:

Выделим элемент сектора трубы ∆ϕ.

Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:

Проекция результирующей тяги на ось Оx является:

Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:

AB является хордой, которая стягивает дугу.

В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м²]. 

Разделим цилиндр вдоль его диаметра. 

Исходя из этого, равнодействующая результирующих сил определяется по формуле:

где d – это внутренний диаметр цилиндра, h — его высота. 

Формулу также можно записать следующим образом:

Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:

Изобразим баллон в момент разрыва:

Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:

Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.

Поверхностные и объёмные силы
представляют собой нагрузку, распределённую
по некоторой поверхности или объёму.
Такая нагрузка задаётся интенсивностью

,
которая представляет собой силу,
приходящуюся на единицу некоторого
объёма, или некоторой площади, или
некоторой длины.

Особое место при решении ряда
практически интересных задач занимает
случай плоской распределённой нагрузки,
приложенной по нормали к некоторой
балке. Если вдоль балки направить ось

,
то интенсивность будет функцией
координаты
и измеряется в Н/м. Интенсивность
представляет собой силу, приходящуюся
на единицу длины.

Плоская фигура, ограниченная балкой
и графиком интенсивности нагрузки,
называется эпюрой распределённой
нагрузки (Рис. 1.28). Если по характеру
решаемой задачи можно не учитывать
деформации, т.е. можно считать тело
абсолютно твёрдым, то распределённую
нагрузку можно (и нужно) заменить
равнодействующей.

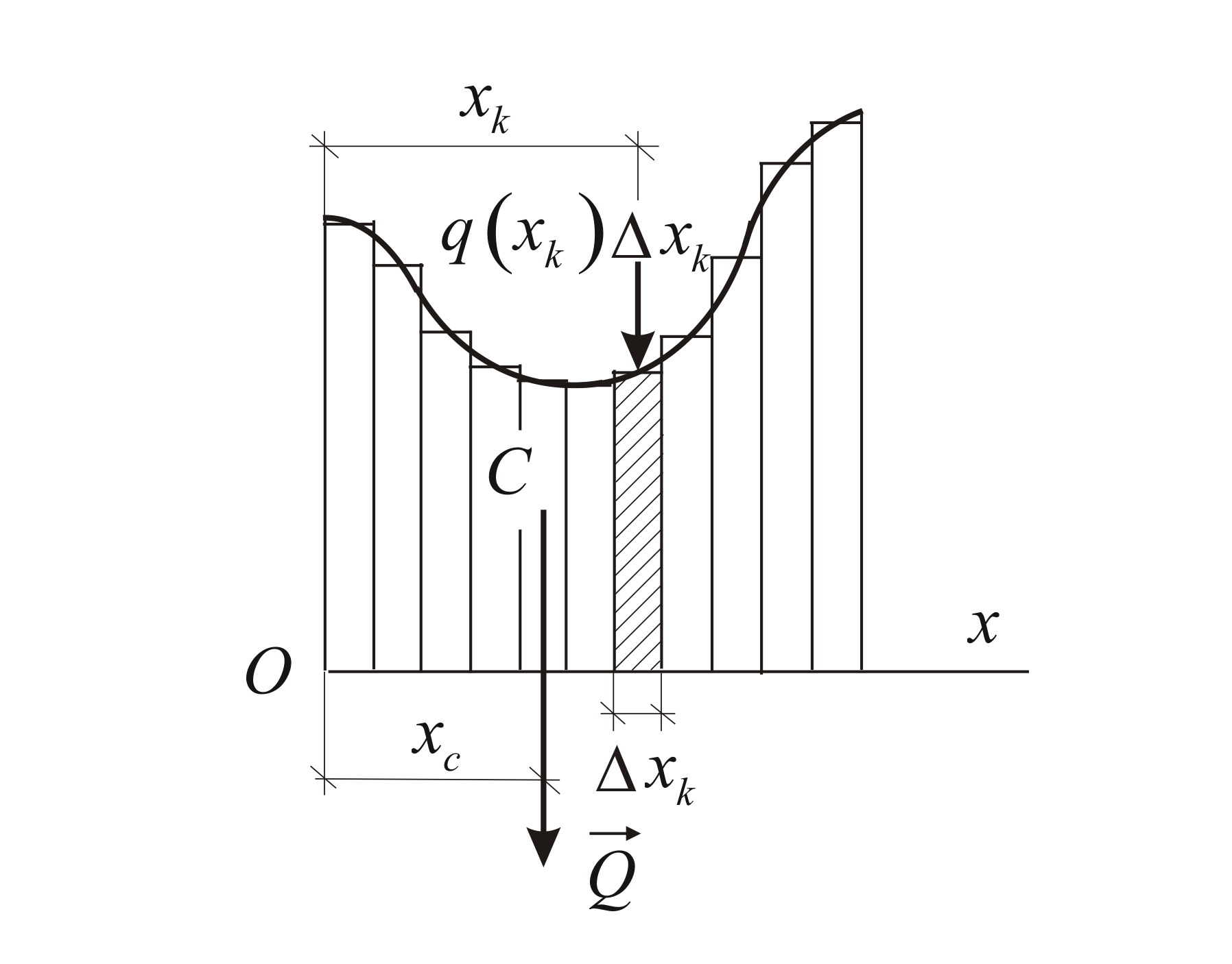
Разобьём балку на
отрезков длиной
,
на каждом из которых будем считать
интенсивность постоянной и равной
,
где
–координата отрезка
.
При этом кривая интенсивности заменяется
ломаной линией, а нагрузка, приходящаяся
на отрезок
,
заменяется сосредоточенной силой
,
приложенной в точке
(Рис. 1.29). Полученная система параллельных
сил имеет равнодействующую, равную
сумме сил, действующих на каждый из
отрезков, приложенную в центре
параллельных сил.

Понятно, что такое представление
тем точнее описывает реальную ситуацию,
чем меньше отрезок
,
т.е. чем больше число отрезков
.
Точный результат получаем, переходя к
пределу при длине отрезка
,
стремящейся к нулю. Предел, получаемый
в результате описанной процедуры,
представляет собой интеграл. Таким
образом, для модуля равнодействующей
получаем:

Для определения координаты точки

приложения равнодействующей используем
теорему Вариньона:

если система сил имеет равнодействующую,
то момент равнодействующей относительно
любого центра (любой оси) равен сумме
моментов всех сил системы относительно
этого центра (этой оси)

Записывая эту теорему для системы сил
в проекциях на ось
и переходя к пределу при длине отрезков,
стремящейся к нулю, получаем:

Очевидно, модуль равнодействующей
численно равен площади эпюры распределённой
нагрузки, а точка её приложения совпадает
с центром тяжести однородной пластины,
имеющей форму эпюры распределённой
нагрузки.

Отметим два часто встречающихся случая.

Равномерно распределённая нагрузка,(Рис. 1.30). Модуль равнодействующей и
координата её точки приложения
определяются по формулам:

В инженерной практике такая нагрузка
встречается довольно часто. Равномерно
распределённой в большинстве случаев
можно считать весовую и ветровую
нагрузку.

Линейно
распределённая нагрузка,(Рис. 1.31). В этом случае:

В
частности, давление воды на вертикальную
стенку прямо пропорционально глубине
.

Пример
1.5

Определить реакции опор
ибалки, находящейся под действием двух
сосредоточенных сил и равномерно
распределённой нагрузки. Дано:

Найдём равнодействующую распределённой
нагрузки. Модуль равнодействующей равен

плечо силы
относительно точкиравноРассмотрим равновесие балки. Силовая
схема представлена на Рис. 1.33.

Условия
равновесия в рассматриваемом случае
имеют вид:

Пример
1.6

Определить реакцию заделки консольной
балки, находящейся под действием
сосредоточенной силы, пары сил и
распределённой нагрузки (Рис. 1.34).

Дано:

Заменим распределённую нагрузку тремя
сосредоточенными силами. Для этого
разобъём эпюру распределённой нагрузки
на два треугольника и прямоугольник.
Находим

Силовая схема представлена на Рис. 1.35.

Вычислим
плечи равнодействующих относительно
оси

Условия
равновесия в рассматриваемом случае
имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что
называется интенсивностью распределённой
нагрузки?

2. Как
вычислить модуль равнодействующей
распределённой нагрузки?

3. Как
вычислить координату точки приложения
равнодействующей распределённой

нагрузки?

4. Чему
равен модуль и какова координата точки
приложения равномерно распределённой
нагрузки?

5. Чему
равен модуль и какова координата точки
приложения линейно распределённой
нагрузки?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из
сборника задач И.В.Мещерского: 4.28;
4.29; 4.30; 4.33; 4.34.

Из
учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА —
теория и практика»: комплекты СР-2; СР-3.

ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 4-5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.2015560.03 Кб15PSY — recommendation.pdf

• #
• #

При расчетах встречается нагрузка, распределенная равномерно или неравномерно по определенному закону.

Интенсивность нагрузки q — это нагрузка, приходящаяся на единицу длины (на 1 метр). Размерность интенсивности распределенной нагрузки [q] = H/м.

Равномерно-распределенная нагрузка — имеет постоянную по длине интенсивность q.

При статических расчетах эту нагрузку можно заменить равнодействующей Q, приложенной посредине, а ее модуль равен

Q = q a.

Неравномерно-распределенная нагрузка имеет переменную интенсивность q.

Равнодействующая Q в этом случае равна площади фигуры, по которой распределена нагрузка, например для треугольной нагрузки

Q = 0,5 q_max a.

Равнодействующая действует в центре тяжести фигуры, т. е. для треугольника — на расстоянии a/3 от основания.

Теоретическая механика



Распределенные нагрузки

Как мы уже знаем, любая сила характеризуется тремя свойствами: модулем (скалярной размерностью), вектором (направлением в пространстве) и точкой приложения. Для того, чтобы иметь полное представление о характере и последствиях воздействия любой силы на тело или элемент конструкции, необходимо знать — какова величина этой силы, куда она направлена и к какой точке приложена.

В действительности сила не может быть приложена к точке, поскольку точка — безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы (приложенные к ничтожно малой площадке тела) называют сосредоточенными.

В реальности часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.
Примером распределенной силы (обычно употребляют выражение «распределенная нагрузка») может послужить выпавший на крышу дома снег. Сила тяжести снежного покрова давит на всю поверхность крыши, нагружая одинаково (или неодинаково) каждую единицу ее площади, а не какую-либо точку.

Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой латинской буквой q.
Интенсивность — это сила, приходящаяся на единицу длины (или площади) нагруженного участка.
Интенсивность в системе единиц СИ выражается в ньютонах на метр (Н/м) или, соответственно, в ньютонах на квадратный метр (для нагрузки, действующей на площадь).

Интенсивность воздействия силы на площадь характеризует такие физические понятия, как давление и напряжение. В плоской системе рассматривается интенсивность действия силы на единицу длины.



Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной (см. рисунок 1).

При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql (см. рисунок).
Равнодействующая равномерно распределенной нагрузки Q прикладывается в середине отрезка АВ.

Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной (рис. 2).
Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину или снег, лежащий на крыше неровным слоем.
Определение точки С приложения равнодействующей неравномерно распределенной нагрузки производится путем геометрических расчетов и построений. Равнодействующая сила Q при таких нагрузках равна площади фигуры, охватываемой эпюрой нагрузки, а точка С приложения равнодействующей расположена в центре тяжести этой фигуры.

Нагрузки, распределенные по поверхности (по площади), характеризуются давлением, т. е. силой, приходящейся на единицу площади. В системе единиц СИ давление измеряется в Паскалях (Па) или ньютонах на квадратный метр (Н/м²).

***

Пример решения задачи с распределенной нагрузкой

Задача: Балка находится в равновесии под действием сосредоточенной силы F = 100 Н и равномерно распределенной нагрузки q = 60 Н/м (см. схему 3).
Необходимо определить реакцию R_В опоры В.

Решение.
Поскольку по условию задачи необходимо определить реакцию опоры В, составим уравнение моментов сил относительно опоры А, учитывая, что равномерно распределенную нагрузку можно заменить сосредоточенной силой:
Q = ql,    где l = (10 — 5) метров — часть балки, к которой приложена распределенная нагрузка.
Точка приложения сосредоточенной силы Q расположена в середине той части балки, к которой приложена распределенная нагрузка; плечо этой силы относительно опоры А будет равно: h = (10 — 5)/2 = 2,5 м.
Cоставляем уравнение моментов сил относительно опоры А из условия, что балка находится в состоянии равновесия (уравнение равновесия).

Учитываем знаки:

• сила R_В создает относительно точки А положительный момент, плечо которого равно 10м;
• сила F создает относительно точки А отрицательный момент, плечо которого равно 5 м;
• распределенная нагрузка q создает (посредством силы Q и плеча h) относительно точки А отрицательный момент.

Получаем уравнение равновесия балки, в котором лишь одна неизвестная величина (R_В):

ΣM = 10R_В — qlh — 5F = 10R_В — q(10-5)(10-5)/2 — 5F = 0, откуда находим искомую реакцию опоры R_В:

R_В = {q(10-5)(10-5)/2 + 5F}/10 = 125 Н

Задача решена.

***

Условия равновесия плоской системы сходящихся сил