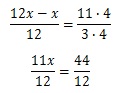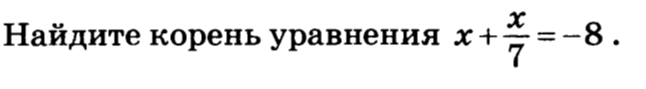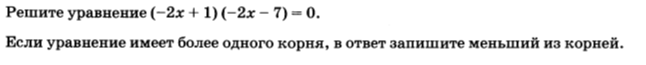Найдите корень уравнения огэ как решать - Исправление недочетов и поиск решений вместе с Examum.ru

а) Для ответа подойдёт только десятичная дробь или целое число. В ответах не может быть обыкновенных дробей, округлённых примерных значений, то есть, если в ответе у тебя получилась обыкновенная дробь, её обязательно надо превратить в десятичную. Если это не получается, ищи ошибку в решении.

б) Десятичные дроби не получатся из несократимых обыкновенных дробей, у которых в знаменателе есть любые простые множители, кроме (2) и (5), т. к. в этом случае добиться того, чтоб в знаменателе было (10), (100), (1000), никак не получится. Если у тебя в ответе такая дробь — ищи ошибку.

в) Отрицательные числа вполне могут быть, знак «минус» будет ставиться в отдельную клеточку.

Источник

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.

Задание 9OM21R

Найти корень уравнения 2 + 3х= – 7х – 5

Имеем линейное уравнение:

2 + 3х= – 7х – 5

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

2 + 3х= – 7х – 5

3х + 7х= – 5 – 2

10х= –7

х=–7:10

х=–0,7

Ответ: –0,7

pазбирался: Даниил Романович | обсудить разбор

Задание OM0906o

Найдите корень уравнения:

Обе части уравнения приводим к единому знаменателю 12:

Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:

11х=44

х=44:11

х=4

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор

Задание OM0905o

Найдите корень уравнения:

режде всего, исключим корень, который не входит в ОДЗ:

x+6≠0 → х≠–6

Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:

Применим правило пропорции. Перемножим между собой крайние ее члены и средние:

1·1=(х+6)·2

Выполним умножение в левой части уравнения и раскроем скобки справа:

1=2х+12

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

2х+12=1

Переносим 12 из левой части в правую:

2х=1–12

2х=–11

Находим корень:

х=–11/2=–5,5

ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5

pазбирался: Даниил Романович | обсудить разбор

Задание OM0904o

Решите уравнение:

7х — 9 = 40

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.

Решение:

7х – 9 = 40

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

7х = 49

х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

х = 49/7, откуда

х = 7

Ответ: 7

pазбирался: Даниил Романович | обсудить разбор

Задание OM0903o

Решите уравнение:

8 x² — 10x + 2 = 0

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

4 x² — 5x + 1 = 0

Далее вычисляем дискриминант:

D = b² — 4ac

D = 5² — 4 •4•1 = 9

Вычисляем корни:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

Ответ: 0,25

pазбирался: Даниил Романович | обсудить разбор

Задание OM0902o

Решите уравнение:

3 x² + 12 x = 0

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

x ( 3 x + 12 ) = 0

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

x = 0

или

3 x + 12 = 0

3 x = -12

x = -4

Так как в ответе просят указать наименьший корень, то это -4.

Ответ: -4

pазбирался: Даниил Романович | обсудить разбор

Задание OM0901o

Найдите корень уравнения:

10 ( x — 9 ) = 7

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x – 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

10x = 7 + 90

10x = 97

Затем делим обе части на 10:

x = 9,7

Ответ: 9,7

pазбирался: Даниил Романович | обсудить разбор

Источник

Джамиля Агишева

При выполнении задания 9 ОГЭ по математике необходимо:

уметь решать линейные и квадратные уравнения, системы уравнений и неравенств.

Пример 1. Решите уравнение .

Решение. Уравнение линейное. Раскрываем скобки, приводим подобные слагаемые, все «иксы» переносим в левую часть равенства, всё без «иксов» – вправо:

Ответ: — 2.

Пример 2. Решите уравнение $frac{5}{4}x^2+7x+9=0$ . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Уравнение является квадратным $a=frac{5}{4}$ , b=7 , c=9 . Вычисляем дискриминант и корни:

$D=b^2-4ac=7^2-4cdot frac{5}{4}cdot 9=49-45=4.$

$x_{1,2}=frac{-bpm sqrt{D}}{2a}=frac{-7pm sqrt{4}}{2 cdot frac{5}{4}}=frac{-7pm 2}{frac{5}{2}}=(-7pm 2)cdot frac{2}{5} Rightarrow left[ begin{array}{c}x_1=left(-7-2right)cdot frac{2}{5}=-9cdot 0,4=-3,6, \x_2=left(-7+2right)cdot frac{2}{5}=-5cdot 0,4=-2. end{array}right.$

Ответ: -3,6-2 .

Пример 3. Решите уравнение . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Решение. В левой части данного уравнения произведение двух множителей-скобок, и это произведение равно нулю. Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю. Значит, получаем два уравнения:

Тогда меньший из корней уравнения равен -0,75.

Ответ: -0,75.

Пример 4. Решите систему уравнений $left{ begin{array}{c}3x+2y=8, \4x- y =7. end{array}right.$

В ответе запишите значение x+y .

Решение. Используем метод подстановки: из второго уравнения можно выразить y и подставить в первое уравнение.

$left{ begin{array}{c}3x+2(4x-7)=8, \y=4x-7. end{array}right. Rightarrow left{ begin{array}{c}3x+8x-14=8, \y=4x-7. end{array}right.Rightarrow$

$Rightarrow left{ begin{array}{c}x=2, \y=4cdot 2-7=1. end{array}right.$

Таким образом, .

Пример 5. На рисунке изображены графики функций y=4-x^2 и y=-2-x . Вычислите ординату точки B.

Решение. Для нахождения координат точек пересечения графиков заданных функций необходимо решить систему уравнений.

$left{ begin{array}{c}y=4-x^2, \y=-2-x. end{array}right. Rightarrow left{ begin{array}{c}-2-x=4-x^2, \y=-2-x. end{array}right.Rightarrow$

$Rightarrow left{ begin{array}{c}x^2-x-6=0, \y=-2-x. end{array}right.$

Найдём корни первого уравнения системы.

$x_{1,2}=frac{1pmsqrt{25}}{2cdot1}=frac{1pm5}{2}Rightarrowleft[ begin{array}{c} x_1=frac{1-5}{2}=-2, \ x_2=frac{1+5}{2}=3. end{array} right.$ ̶ абсцисса точка B.

Тогда ордината точки В:

Ответ: -5.

Пример 6. Найдите наибольшее значение x, удовлетворяющее системе неравенств:

$left{ begin{array}{c}8x+16le 0, \2-2xtextless13. end{array}right.$

Решение. Выразим из каждого неравенства переменную x. Не забываем, что при делении обеих частей неравенства на положительное число знак неравенства не меняется, при делении на отрицательное число ̶ знак неравенства меняется на противоположный.

$left{ begin{array}{c}8x+16le 0, \2-2xtextless13. end{array}right. Rightarrow left{ begin{array}{c}8xle -16, \-2xtextless13-2. end{array}right. Rightarrow left{ begin{array}{c}8xle -16, |:8 \-2xtextless11. |:(-2) end{array}right. Rightarrow$

$Rightarrowleft{ begin{array}{c}xle -2, \xtextgreater-5,5. end{array}right.$

Используем числовую прямую. Решение первого неравенства отметим штриховкой («ёлочкой») с наклоном вправо, второго неравенства ̶ штриховкой с наклоном влево. При этом точка -2 будет «закрашенной», т.к. знак первого неравенства нестрогий, а точка -5,5 будет «выколотой», т.к. знак второго неравенства строгий.

Решением системы неравенств является тот промежуток, на котором пересеклись две «ёлочки», то есть две штриховки. Это промежуток . «Выколотой» точке соответствует круглая скобка, «закрашенной» ̶ квадратная.

Ответим на вопрос задачи. Наибольшее значение x=-2.

Ответ: .

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 9 ОГЭ по математике. Уравнения, неравенства, системы уравнений и неравенств» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Для решения данного номера ученику потребуется знание и умение работать с:

1. Линейными уравнениями. Напомним, что целью преобразований линейного уравнения является получение выражения «неизвестная = число».

2. Квадратными уравнениями. Напомним, что квадратным называется уравнение вида ах2+bx+c=0, корни уравнения находим по формуле

x1,2 =(-b+-(D)1//2) / 2a, где a, b, c –коэффициенты, D=b2-4ac – дискриминант.

Корни квадратного уравнения можно вычислить и по теореме Виета. Кому что нравится, на вкус и на цвет – товарища нет!Рассмотрим характерные примеры.

Решение:

1. Данное уравнение линейное, имеет один корень. Найдем его.

2. Избавимся от 7 в знаменателе. Для этого левую и правую части уравнения умножим на 7. Имеем, 7х+х=-8*7 или 8х=-56

3. х=-7

Ответ: -7.

Решение:

1. Преобразуем данное уравнение к стандартной записи квадратного уравнения, для этого перемножим два многочлена. Имеем

4x²+14x-2x-7=0 или 4x²+12x-7=0

2. Дальше решаем по известным формулам

D=12²-4*4*(-7)=144+112=256 дискриминант больше нуля, имеем 2 корня.

3. x₁=(-12+16)/2*4=4/8=1/2=0,5 x₂₌=(-12-16)/2*4=28/8=3,5

4. Выбираем меньший из корней 0,5.

Ответ: 0,5.

Решение:

1. Данное уравнение не надо преобразовывать, поэтому корни уравнения находим по известным формулам.

2. D=(-15)²-4*4*9=225-144=81

3. x₁ =(-(-15)+9)/2*4=24/8=3 x₂==(-(-15)-9)/2*4=6/8=3/4=0,75

4. Выбираем меньший из корней 0,75.

Ответ: 0,75.

Источник

В задании №9 ОГЭ по математике от ученика требуется решить линейное, квадратное, либо рациональное уравнение. На этом уроке рассмотрим решение линейных и рациональных уравнений.

Для правильного решения линейных и рациональных уравнений необходимо знать:

правила действий с числами и дробями;
свойства степеней;
буквенные выражения (выражения с переменными);
многочлен; сложение, вычитание, умножение многочленов;
формулы сокращённого умножения;
свойства квадратных корней и их применение в вычислениях;
уравнение с одной переменной, корень уравнения;
тождественные преобразования рациональных выражений.

Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то корни уравнения не изменятся!

Примечание. В большинстве заданий с уравнениями есть возможность выполнить проверку. Для этого подставляем найденное значение неизвестного в исходное уравнение. Такая проверка дает нам возможность убедиться в правильности найденного корня.

Пример №1

Найдите корень уравнения $3x+3=5x$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$3x+3=5x$$

$$3x-5x=-3$$

$$-2x=-3$$

$$x=1.5$$

Ответ: $1.5$

Пример №2

Найдите корень уравнения $-1-3x=2x+1$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$-1-3x=2x+1$$

$$-2x-3x=1+1$$

$$-5x=2$$

$$x=-0.4$$

Ответ: $-0.4$.

Пример №3

Найдите корень уравнения $10(x-9)=7$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$10(x-9)=7$$

$$10x-90=7$$

$$10x=7+90$$

$$10x=97$$

$$x=9.7$$

Ответ: $9.7$

Пример №4

Найдите корень уравнения $x+frac{x}{7}=-8$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$x+frac{x}{7}=-8$$

$$7cdot(x+frac{x}{7})=7cdot(-8)$$

$$7x+7cdotfrac{x}{7}=-56$$

$$7x+x=-56$$

$$8x=-56$$

$$x=-7$$

Ответ: $-7$.

Пример №5

Найдите корень уравнения $frac{11}{x+3}=10$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$frac{11}{x+3}=10$$

$$frac{11}{x+3}cdot(x+3)=10cdot(x+3)$$

$$11=10x+30$$

$$-10x=30-11$$

$$-10x=19$$

$$x=-1.9$$

Ответ: $-1.9$.

Пример №6

Найдите корень уравнения $frac{12}{x+5}= -frac{12}{5}$.

Решаем вместе

Скрыть

Показать все решение

Скрыть

$$frac{12}{x+5}= -frac{12}{5}$$

$$frac{12}{x+5}cdot(x+5)= -frac{12}{5}cdot(x+5)$$

$$12= -frac{12cdot(x+5)}{5}$$

$$12= -frac{12x+60}{5}$$

$$12cdot5= -frac{12x+60}{5}cdot5$$

$$60= -12x-60$$

$$12x=-60-60$$

$$12x=-120$$

$$x=-10$$

Ответ: $-10$.

Источник