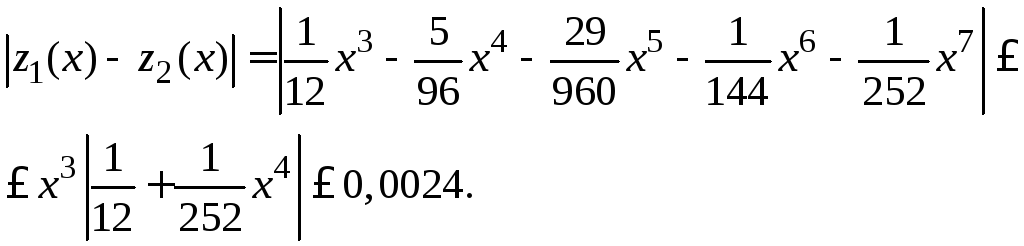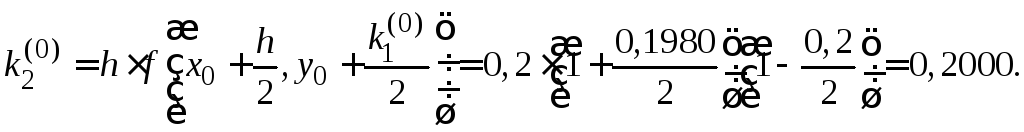Найдите приближение как решать - Исправление недочетов и поиск решений вместе с Examum.ru

Применение производной к приближенным вычислениям

Определение и геометрический смысл дифференциала
Алгоритм приближенных вычислений с помощью дифференциала
Приближение с точностью до квадрата приращения
Полезные формулы приближений для функций вблизи нуля
Примеры

п.1. Определение и геометрический смысл дифференциала

Дифференциал функции (y=f(x)) – это главная, линейная часть приращения функции, равная произведению производной на приращение аргумента: $$ dy=f'(x_0)triangle x $$

Выберем на кривой (y=f(x)) начальную точку (A(x_0,y_0)). Если мы начнем перемещаться к точке (B(x,y)), то приращению аргумента (triangle x=AC) соответствует приращение функции (triangle y=BC). Если считать, что кривая приблизительно совпадает со своей касательной при малых приращениях (triangle x), то (BCapprox MC) и (triangle yapprox dy).

Геометрический смысл дифференциала — замена приращения функции (triangle y) на линейное приращение по касательной (dy: triangle yapprox dy=f'(x_0 )triangle x)
Чем меньше (triangle x), тем ближе дифференциал к полному приращению функции: $$ triangle yrightarrow dy, triangle xrightarrow 0 $$

п.2. Алгоритм приближенных вычислений с помощью дифференциала

На входе: функция (y=f(x)), точка x*, в которой нужно посчитать значение функции
Шаг 1. Определяем ближайшую к x* начальную точку (x_0), для которой значение (y_0=f(x_0)) известно или легко находится.
Шаг 2. Находим выражение для первой производной (f'(x)).
Шаг 3. Находим значение производной в начальной точке (f'(x_0))
Шаг 4. Находим линейное приближение значения функции $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ На выходе: значение y*

Например:
1) Найдем значение корня (sqrt{65})
Функция (y=sqrt{x}, x^*=65)
Начальная точка (x_0=64). Начальное значение функции (y_0=sqrt{64}=8)
Производная: (f'(x)=frac{1}{2sqrt{x}})
Производная в начальной точке: (f'(x_0)=frac{1}{2sqrt{64}}=frac{1}{16})
Подставляем: (y^*=sqrt{65}approx 8+frac{1}{16}(65-64)=8+frac{1}{16}=8,0625)
Оценим относительную ошибку для полученного результата.
Значение, полученное на калькуляторе: (sqrt{65}approx 8,062258). Откуда: $$ partial=frac{|8,062258|}{8,062258}cdot 100text{%}approx 0,003text{%} $$ Таким образом, в данном случае линейное приближение имеет высокую точность, т.к. для (x_0=64) и (x^*=65) кривая (y=sqrt{x}) очень близка к прямой, т.е. своей касательной.

2) Найдем значение корня (sqrt{5})
Пусть начальная точка (x_0=4). Начальное значение функции (y_0=sqrt{4}=2)
Производная в начальной точке: (f'(x_0)=frac{1}{2sqrt{4}}=frac14)
(y^*=sqrt{5}approx 2+frac14 (5-4)=2,25)
Значение, полученное на калькуляторе: (sqrt{5}approx 2,23607) $$ partial=frac{|2,23607-2,25|}{2,23607}cdot 100text{%}approx 0,06text{%} $$ Точность стала хуже. Однако, её можно повысить, если взять (x_0=4,84).

3) Найдем (sqrt{5}) при (x_0=4,84).
(y_0=sqrt{4,84} =2,2)
Производная в начальной точке: (f'(x_0 )=frac{1}{2cdot 2,2}=frac{1}{4,4})
(y^*=sqrt{5}approx 2,2+frac{1}{4,4}(5-4,84)=2,2+frac{0,16}{4,4}=2,2+frac{2}{55}=2,23636…)
Значение (sqrt{5}approx 2,23607) $$ partial=frac{|2,23607-2,23636|}{2,23607}cdot 100text{%}approx 0,01text{%} $$ Точность повысилась.

Вывод: точку (x_0) следует выбирать, исходя из поведения функции (y=f(x)) в окрестности (x^*). Чем ближе (x_0) к (x^*) и чем ближе кривая к касательной, тем точнее будет линейное приближение с помощью дифференциала.

п.3. Приближение с точностью до квадрата приращения

Значение функции в зависимости от приращения (triangle x=x^*-x_0) с точностью до квадратичного слагаемого определяется формулой: $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0)+frac{f»(x_0)}{2}(x^*-x_0)^2 $$

Например:
1) Найдем квадратичное слагаемое для (x^*=65, x_0=64, y=sqrt{x})
Вторая производная: (f»(x)=left(frac{1}{2sqrt{x}}right)’=frac12cdotleft(-frac12right)cdotfrac{1}{xsqrt{x}}=-frac{1}{4xsqrt{x}}) $$ frac{f»(x_0)}{2}(x^*-x_0)^2=-frac{(65-64)^2}{2cdot 4cdot 64cdot 8}=-frac{1}{4096}approx -0,0002 $$ Значит, квадратичное слагаемое дает поправку в 4-м знаке.
Используя полученное выше линейное приближение, получаем: $$ y^*=sqrt{65}approx 8,0625-0,0002=8,0623approx 8,062 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

2) Найдем квадратичное слагаемое для (x^*=5, x_0=4, y=sqrt{x}) $$ frac{f»(x_0)}{2}(x^*-x_0)^2=-frac{(5-4)^2}{2cdot 4cdot 4cdot 2}=-frac{1}{64}approx -0,02 $$ Получаем: $$ y^*=sqrt{5}approx 2,25-0,02=2,23approx 2,2 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 1-го знака после запятой.

3) Найдем квадратичное слагаемое для (x^*=5, x_0=4,84, y=sqrt{x}) $$ frac{f»(x_0)}{2}(x^*-x_0)^2=-frac{(5-4,84)^2}{2cdot 4cdot 4,84cdot 2,2}=-frac{0,0256}{85,184}approx -0,0003 $$ Получаем: $$ y^*=sqrt{5}approx 2,2367-0,0003=2,2364approx 2,236 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

п.4. Полезные формулы приближений для функций вблизи нуля

Рассмотрим свойства приближений некоторых функций при (x_0=0) и (triangle x=xrightarrow 0).
В разложении ограничимся слагаемым (y(0)) и линейным приближением. Только если линейное приближение равно 0, будем учитывать слагаемое квадратичного приближения.
1) (y=sinx)
(y’=cosx, y»=-sinx)
(y(0)=0, y'(0)=1, y»(0)=0)
(sinxapprox 0+1cdot x-frac02cdot x^2approx x)

2) (y=cosx)
(y’=-sinx, y»=-cosx)
(y(0)=1, y'(0)=0, y»(0)=-1)
(cosxapprox 1+0cdot x-frac12cdot x^2=1-frac{x^2}{2})

3) (y=tgx)
(y’=frac{1}{cos^2x}, y»=-frac{2cosxcdot(-sinx)}{cos^4x}=frac{2sinx}{cos^3x})
(y(0)=0, y'(0)=1, y»(0)=0)
(tgxapprox 0+1cdot x-frac02cdot x^2= x)

4) (y=e^x)
(y’=y»=e^x)
(y(0)=y'(0)=y»(0)=1)
(e^xapprox 1+1cdot x+frac12cdot x^2approx 1+x)
Пренебрегаем (frac{x^2}{2}) как очень малым слагаемым.

5) (y=ln(1+x))
(y’=frac{1}{1+x}, y»=-frac{1}{(1+x)^2})
(y(0)=0, y'(0)=1, y»(0)=-1)
(ln(1+x)approx 0+1cdot x-frac12 x^2approx x)

6) (y=sqrt{1+x})
(y’=frac{1}{2sqrt{1+x}}, y»=-frac{1}{4(1+x)^{3/2}})
(y(0)=1, y'(0)=frac12, y»(0)=-frac14)
(sqrt{1+x}approx 1+frac12cdot x-frac18 x^2approx1+frac x2)

7) (y=frac{1}{sqrt{1+x}})
(y’=-frac{1}{2(1+x)^{frac32}}, y»=frac{3}{4(1+x)^{frac52}})
(y(0)=1, y'(0)=-frac12, y»(0)=frac34)
(frac{1}{sqrt{1+x}}approx 1-frac12 x+frac38 x^2approx 1-frac x2)

(y=(1+x)^a, ainmathbb{R})
(y’=a(1+x)^{a-1}, y»=a(a-1)(1+x)^{a-2})
(y(0)=1, y'(0)=a, y»(0)=a(a-1))
((1+x)^aapprox 1+acdot x+frac{a(a-1)}{2}x^2approx 1+ax)

Таблица приближений для функций при (xrightarrow 0)

$$ sinxapprox x $$

$$ e^xapprox 1+x $$

$$ cosxapprox 1-frac{x^2}{2} $$

$$ ln(1+x)approx x $$

$$ tgxapprox x $$

$$ sqrt{1+x}approx 1+frac x2 $$

$$ (1+x)^aapprox 1+ax, ainmathbb{R} $$

$$ frac{1}{sqrt{1+x}}approx 1-frac x2 $$

п.5. Примеры

Пример 1. Найдите линейное приближение значения функции в заданной точке с помощью дифференциала. Ответ представьте с точностью до сотых. $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ a) (sqrt[3]{28})
Функция (y=sqrt[3]{x}, x^*=28, x_0=27)
(f(x_0)=sqrt[3]{27}=3)
Производная: (f'(x)=(sqrt[3]{x})’=frac13 x^{-frac23}=frac{1}{3sqrt[3]{x^2}})
(f'(x_0)=frac{1}{3sqrt[3]{27^2}}=frac{1}{3cdot 9}=frac{1}{27}) $$ y^*=sqrt[3]{28}approx 3+frac{1}{27}(28-27)=3+frac{1}{27}approx 3,037approx 3,04 $$
б) (sin(0,03))
Функция (y=sinx, x^*=0,03, x_0=0)
(f(x_0)=sin0=0)
Производная: (f'(x)=(sinx)’=cosx)
(f'(x_0)=cos0=1) $$ y^*=sin(0,03)approx 0+1cdot(0,03-0)=0,03 $$
в) (sqrt{0,98})
Функция (y=sqrt{x}, x^*=0,98, x_0=1)
(f(x_0)=sqrt[3]{27}=3)
Производная: (f'(x)=(sqrt{x})’=frac{1}{2sqrt{x}})
(f'(x_0)=frac{1}{2sqrt{1}}=frac12) $$ y^*=sqrt{0,98}approx 1+frac12(0,98-1)=1-0,01=0,99 $$
e) (e^{0,01})
Функция (y=e^x, x^*=0,01, x_0=0)
(f(x_0)=e^0=1)
Производная: (f'(x)=(e^x)’=e^x)
(f'(x_0)=e^0=1) $$ y^*=e^{0,01}approx 1+1cdot (0,01-0)=1+0,01=1,01 $$

Пример 2. Найдите приближение значения функции в заданной точке с точностью до квадрата приращения. Ответ представьте с точностью округления последнего слагаемого. $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0)+frac{f»(x_0)}{2}(x^*-x_0)^2 $$ a) (sqrt[4]{80})
Функция (y=sqrt[4]{x}, x^*=80, x_0=81)
(f(x_0)=sqrt[4]{81}=3)
Первая производная: (f'(x)=(sqrt[4]{x})’=frac14 x^{-frac34}=frac{1}{4sqrt[4]{x^3}})
(f'(x_0)=frac{1}{4sqrt[4]{81^3}}=frac{1}{4cdot 27}=frac{1}{108})
Вторая производная: (f»(x)=frac14cdot left(-frac34right)cdotfrac{1}{xsqrt[4]{x^3}}=-frac{3}{16xsqrt[4]{x^3}})
(f»(x_0)=-frac{3}{16cdot 81cdotsqrt[4]{81^3}}=-frac{3}{16cdot 81cdot 27}=-frac{1}{11664}) begin{gather*} y^*=sqrt[4]{80}approx 3+frac{1}{108}(80-81)-frac{1}{11664}cdot frac12(80-81)^2approx 3-0,00926-0,00004=\ =2,99070approx 2,9907 end{gather*}
б) (ln 1,04)
Функция (y=ln x, x^*=1,04, x_0=1)
(f(x_0)=ln 1=0)
Первая производная: (f'(x)=(ln x)’=frac1x)
(f'(x_0)=frac{1}{1}=1)
Вторая производная: (f»(x)=-frac{1}{x^2})
(f»(x_0)=-frac{1}{1^2}=-1) begin{gather*} y^*=ln 1,04approx 0+1cdot (1,04-1)-1frac12(1,04-1)^2=0,04-0,0008=0,0392approx 0,039 end{gather*}
в) (cos0,07)
Функция (y=cosx, x^*=0,07, x_0=0)
(f(x_0)=cos0=1)
Первая производная: (f'(x)=(cosx)’=-sinx)
(f'(x_0)=-sin0=0)
Вторая производная: (f»(x)=(-sinx)’=-cosx)
(f»(x_0)=-cos0=-1) begin{gather*} y^*=cos0,07approx 1+0cdot (0,07-0)-1cdotfrac12(0,07-0)^2=1-0,00245=\ =0,99755approx 0,9976 end{gather*}
г) (tg0,11)
Функция (y=tgx, x^*=0,11, x_0=0)
(f(x_0)=tg0=0)
Первая производная: (f'(x)=(tgx)’=frac{1}{cox^2x})
(f'(x_0)=frac{1}{cos^2x}=1)
Вторая производная: (f»(x)=left(frac{1}{cos^2x}right)’=-frac{2cosxcdot(-sinx)}{cos^4x}=frac{2sinx}{cos^3x})
(f»(x_0)=frac{2sin0}{cos^30}) begin{gather*} y^*=tg0,11approx 0+1cdot (0,11-0)+0cdotfrac12 (0,11-0)^2=0,11 end{gather*}

Источник

Численные методы: решение нелинейных уравнений

Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.

В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.

В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.

Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.

В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.

Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.

Нам нужно найти такое значение при котором такие называются корнями функции

Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.

Метод деления пополам

Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.

Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.

Алгоритм состоит в следующем.

Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .

Поделим отрезок пополам и введем среднюю точку .

Тогда либо , либо .

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.

Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.

Заметьте, описанный алгоритм применим для любой непрерывной функции.

К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.

Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.

Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.

Метод Ньютона: теоретические основы

Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .

Уравнение касательной к функции в точке имеет вид:

В уравнении касательной положим и .

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:

Сходимость метода касательных квадратичная, порядок сходимости равен 2.

Таким образом, сходимость метода касательных Ньютона очень быстрая.

Запомните этот замечательный факт!

Без всяких изменений метод обобщается на комплексный случай.

Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.

Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).

Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).

К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.

Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.

Визуализация метода Ньютона

Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:

1) функция y= f(x) определена и непрерывна при ;

2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x₀, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x₀ сначала удобно выбирать один из концов отрезка.

Рассмотрим метод Ньютона на конкретном примере.

Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.

Уравнение касательной в общем виде имеет представление:

В нашем случае: y-y₀=2x₀·(x-x₀). В качестве точки x₀ выбираем точку B₁(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B₁, и обозначаем точку пересечения касательной и оси Ox точкой x₁. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.

Точка пересечения касательной и оси Ox: x₁ =

Рисунок 2. Результат первой итерации

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₁, получаем точку В₂ =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В₂, и обозначаем точку пересечения касательной и оси Ox точкой x₂.

Точка пересечения касательной и оси Ox: x₂ = .

Рисунок 3. Вторая итерация метода Ньютона

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₂, получаем точку В₃ и так далее.

В3 = ()

Рисунок 4. Третий шаг метода касательных

Первое приближение корня определяется по формуле:

= 1.5.

Второе приближение корня определяется по формуле:

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:

Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|

using namespace std;

float f(double x) //возвращает значение функции f(x) = x^2-2

float df(float x) //возвращает значение производной

float d2f(float x) // значение второй производной

int _tmain(int argc, _TCHAR* argv[])

int exit = 0, i=0;//переменные для выхода и цикла

double x0,xn;// вычисляемые приближения для корня

double a, b, eps;// границы отрезка и необходимая точность

cin>>a>>b; // вводим границы отрезка, на котором будем искать корень

cin>>eps; // вводим нужную точность вычислений

if (a > b) // если пользователь перепутал границы отрезка, меняем их местами

if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня

cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?

xn = x0-f(x0)/df(x0); // считаем первое приближение

cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять

xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона

> while (exit!=1); // пока пользователь не ввел exit = 1

Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.

Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.

Рис. 4. Решение ошибки компиляции проекта

Мы будем искать корни у функции f(x) = x2-2.

Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.

У нас появилось окно приложения:

Рис. 5. Ввод входных данных

Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.

Рис. 6. Ошибка «На этом отрезке корней нет!»

Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».

Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.

Рис. 7. Вычисление корня с необходимой точностью

Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.

Чтобы выйти из приложения, введем «Exit?» => 1.

Метод секущих

Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

/

Итерационный процесс имеет вид:

где .

Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.

Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .

Эта замечательная величина называется золотым сечением:

Убедимся в этом, считая для удобства, что .

Таким образом, с точностью до бесконечно малых более высокого порядка

Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .

После подстановки имеем: и

Для сходимости необходимо, чтобы было положительным, поэтому .

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.

Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.

Такая процедура определения момента окончания итераций называется приемом Гарвика.

Метод парабол

Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .

Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .

В форме Ньютона она имеет вид:

Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.

Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.

Этот метод очень удобен для поиска корней многочленов высокой степени.

Метод простых итераций

Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.

Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).

По теореме Банаха существует и единственна неподвижная точка

Она может быть найдена как предел простой итерационной процедуры

где начальное приближение — произвольная точка промежутка .

Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа

Таким образом, если производная меньше единицы, то является сжатием.

Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.

Рассмотрим уравнение: .

Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .

Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .

Эти итерации сходятся к неподвижной точке для любого начального приближения :

Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.

Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.

т.е. такой итерационный процесс всегда сходится.

Метод Ньютона представляет собой частный случай метода простых итераций.

Здесь нетрудно убедиться, что при существует окрестность корня, в которой .

то если корень кратности , то в его окрестности и, следовательно,.

Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).

Поскольку , то

Таким образом, сходимость метода Ньютона очень быстрая.

Нахождение всех корней уравнения

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.

Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.

Для поиска других корней используется метод удаления корней.

Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.

Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.

Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.

Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.

5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона

Рассмотрим нелинейную систему уравнений

(5.1)

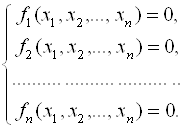
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

(5.2)

Здесь приняты следующие обозначения:

— вектор аргументов, а — вектор – функция.

Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

(5.3)

Где — поправка (погрешность) корня на N – ом шаге.

Подставив выражение (5.3) в (5.2), получим

(5.4)

Предположим, что функция F(X) — непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

, (5.5)

Или в развернутом виде:

(5.6)

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

. (5.7)

Выражение (5.7) в краткой записи можно представить:

(5.8)

Выражение (5.6) представляет собой линейную систему относительно поправок (I = 1, 2, . N) с матрицей W(X), поэтому формула (5.5) может быть записана в следующем виде:

(5.9)

Отсюда, предполагая, что матрица W(X(P)) — неособенная, получим:

(5.10)

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

(5.11)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.

Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

(5.12)

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений

Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W— неособенная, тогда обратная матрица вычисляется

Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение:

Как найти начальное приближение нелинейного уравнения

Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁== 0.268;

X₂== 3.732;

Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

источники:

http://matica.org.ua/metodichki-i-knigi-po-matematike/chislennye-metody-iu-ia-katcman/5-1-priblizhennoe-reshenie-sistem-nelineinykh-uravnenii-metod-niutona

http://nickolay.info/study/methods/01.html

Источник

Рассмотрим задачу
Коши для дифференциального уравнения
первого порядка
с начальным условием.

Метод последовательных
приближений состоит в том, что решение
,
получают как предел последовательности
функций,
которые находятся по рекурсивной формуле

.
(1.4)

Если правая часть
в некотором замкнутом прямоугольнике,
содержащем множество точек,
для которых выполняются условияудовлетворяет условию Липшица по:

то независимо от
выбора начальной функции последовательные
приближения
сходятся на некотором отрезкек точному решению задачи Коши.

Если
непрерывна в области,
то оценка погрешности приближенного
решения
на отрезке
дается неравенством:

,
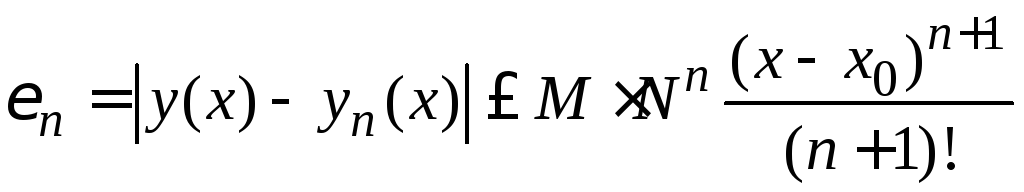
(1.5)

где
,
а число
определяется из условия:

Пример 1.1. Найти
три последовательных приближения
решения уравнения:

с начальным условием
Оценить погрешность третьего приближения
на отрезке.

Решение. Учитывая
начальное условие, заменим уравнение
интегральным

В качестве начального
приближения возьмем
.
Первое приближение находим по формуле
(1.4):

Аналогично получаем
второе и третье приближения:

Оценим погрешность
последнего приближения по формуле
(1.5). Так как функция
,
то она определена и непрерывна во всей
плоскостии в качествеиможно взять любые числа. Возьмем для
определенности.
При таких ограничениях получаем:

Таким образом, на
отрезке [0; 0.4] получаем

и, следовательно:

Замечание: Оценка
погрешности по формуле (1.5) часто
оказывается завышенной. Практически,
применяя метод последовательных
приближений, вычисления продолжают до
такого
при котором значениясовпадают в пределах допустимой
точности.

Пример 1.2.
Дана система

с начальными
условиями
Методом последовательных приближений
найти решение этой системы на отрезке
[0; 0,3] с точностью до.

Решение: Записываем
систему в интегральной форме:

используя
начальные значения, из системы находим
,.
В качестве начальных приближений
выберем:

При выборе начальных
приближений используем первые два члена
разложения функций
в
окрестности точки

Вычислим следующие
приближения
и:

Аналогично получаем:

Оценим разности
ина отрезке [0; 0.3]:

Эти разности
находятся в пределах заданной точности,
причем члены, содержащие
,
малы на отрезке [0; 0,3]. Следовательно, с
заданной точностью можно положить

,
.

1.1.3. Метод Эйлера

Рассмотрим
дифференциальное уравнение
с начальным условием.

Выбрав достаточно
малый шаг
,
построим систему равноотстоящих узлов,
().

Приближенные
значения
по
методу Эйлера вычисляются последовательно
по формулам:

()

При оценке
погрешности обычно используется двойной
пересчет.

Если
– вычисленное значениес шагом,
а– соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:

Пример 1.3. Применяя
метод Эйлера, составить на отрезке [0,1]
таблицу значений решения уравнения:

с начальным условием
,
выбрав шаг.

Решение
дифференциального уравнения приведено
в таблице 1.1.

Таблица 1.1

Приближенное
решение уравнения примера 1.3 методом
Эйлера

№ шага				Точное решение
0	0	1,0000	0,2000	1,0000
1	0,2	1,2000	0,1733	1,1832
2	0,4	1,3733	0,1561	1,3416
3	0,6	1,5294	0,1492	1,4832
4	0,8	1,6786	0,1451	1,6124
5	1,0	1,8237		1,7320

Рассмотрим пример вычисления :

Для остальных
значений
вычисления
проводятся аналогично.

1.1.4. Метод
Эйлера–Коши

Метод Эйлера–Коши
является модификацией метода Эйлера.
Вычисления табличных значений решения
и оценка погрешности проводятся по
следующим формулам.

где
– точное
значение решения в узле,,–
приближенные значения решения в узлес шагом– соответственно.

Таблица 1.2

Приближенное
решение уравнения примера 1.3 методом
Эйлера–Коши

№ шага				Точное решение
0	0	1,0000	0,1867	1,0000
1	0,2	1,1867	0,1617	1,1832
2	0,4	1,3484	0,1454	1,3416
3	0,6	1,4938	0,1341	1,4832
4	0,8	1,6272	0,1263	1,6124
5	1,0	1,7542		1,7320

Рассмотрим
применение метода Эйлера–Коши для
примера 1.3, решенного выше методом
Эйлера.

Покажем пример
вычисления
:

,
.

Остальные значения
проводятся аналогично. Результаты счета
приведены в таблице 1.2.

1.1.5. Метод
Рунге–Кутта четвертого порядка

Рассмотрим метод
Рунге–Кутта четвёртого порядка для
нахождения численного решения уравнения
(1.1) с начальным условием (1.2).

Пусть
является начальным условием (при),
либо получено как результат предыдущего
шага. Для получения следующего значениявначале вычисляются числа:

,
(1.6)

где h– шаг интегрирования.

Затем вычисляют:
.

Новое значение
функции вычисляется по формуле:

.
(1.7)

Метод Рунге–Кутта
четвертого порядка является методом
повышенной точности. На практике для
контроля точности этого метода
используется двойной счет пересчет.

Если
–
вычисленное значениес
шагом,
а–
соответствующее узловое значение,
полученное с шагомh,
то для приближенной оценки погрешности
значенияможно использовать формулу:

Пример 1.4. Решить методом Рунге–Кутта уравнение
на отрезке [0, 1] с шагом h
= 0,2:

Результаты
вычислений оформим в виде таблицы 1.3.

Таблица 1.3

Результаты
приближенного решения примера 1.4 методом
Рунге–Кутта

четвертого порядка


0	0,0	1,0000	0,2000	0,1980	0,2000	0,1916	0,1972
1	0,2	1,1972	0,1916	0,1810	0,4000	0,1653	0,1799
2	0,4	1,3771	0,1653	0,1460	0,6000	0,1218	0,1448
3	0,6	1,5219	0,1217	0,0950	0,8000	0,0646	0,0941
4	0,8	1,6160	0,0646	0,0330	1,0000	0,0000	0,0326
5	1,0	1,6486

Покажем пример
вычисления табличного значения
.

Для вычисления
надо вычислить:

Остальные значения
вычисляются аналогично.

Источник

Содержание:

Приближённые вычисления
Абсолютная и относительная погрешности
Выполнение действий над приближёнными числами
Выполнение действий без точного учёта погрешности

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью приближённой называется модуль разности между точным значением величины и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку а цифры 4 и 6 являются сомнительными, поскольку

В конечной записи приближённого числа сохраняют только верные цифры. Так число можно записать в виде , число в виде Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде:

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись

3. Если

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10³— две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например, будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью (омега) приближённости х величины называется отношением абсолютной погрешности этого приближения к модулю приближённого значения х, то есть

Поскольку абсолютная погрешность обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль:

Число называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле:

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа

Решение: Имеем

Следовательно

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что .

Решение:

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Необходимо уметь устанавливать погрешности результатов вычислений. Их находят с точным и без точного учёта погрешностей исходных данных. Правила нахождения погрешностей результатов действий с точным учётом погрешности приведены в таблице (обозначения — исходные данные; пределы абсолютных погрешностей относительно чисел; пределы относительных погрешностей).

Пример 3. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Пример 4. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

Лекции:

Уравнение сферы
Пределы: примеры решения
Площадь поверхности конуса
Целые рациональные выражения
Числовые ряды. Числовой ряд. Сумма ряда
Свойства логарифмов
Линейные дифференциальные уравнения первого порядка
Скрещивающиеся прямые
Скалярное призведение двух векторов
Теоремы, связанные с понятием производной

Источник

Метод последовательных приближений решения дифференциального уравнения

Пусть требуется найти решение y=y(x) дифференциального уравнения

y'=f(x,y),

(1)

удовлетворяющее начальному условию

$y|_{x=x_0}=y_0.$

(2)

Будем предполагать, что в некотором прямоугольнике $D={|x-x_0|<a,~|y-y_0|<b}$ с центром в точке (x_0,y_0) для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).

Решение задачи (1)-(2) может быть найдено методом последовательных приближений, который состоит в следующем.

Строим последовательность ${y_n(x)}$ функций, определяемых рекуррентными соотношениями

$y_n(x)=y_0+intlimits_{x_0}^{x}f(t,y_{n-1}(t))dt,~ninmathbb{Z}.$

(3)

В качестве нулевого приближения y_0(x) можно взять любую функцию, непрерывную в окрестности точки x=x_0 , в частности $y_0(x)equiv{y_0}$ — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения ${y_n(x)}$ сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале x_0-h<x<x_0+h , где

$h=min!left(a,frac{b}{M}right),~~M=maxlimits_{(x,y)in{D}}|f(x,y)|.$

(4)

Оценка погрешности, получаемой при замене точного решения y(x) n-м приближением y_n(x) , даётся неравенством

$|y(x)-y_n(x)|leqslantfrac{MN^{n-1}}{n!}h^n.$

(5)

где $N=maxlimits_{(x,y)in{D}}left|frac{partial{f}}{partial{y}}right|$ . Применяя метод последовательных приближений, следует остановиться на таком , для которого $|y_{n+1}-y_n|$ не превосходит допустимой погрешности.

Пример 1. Методом последовательных приближений найти решение уравнения $frac{dy}{dx}=y$ , удовлетворяющее начальному условию y(0)=1 .

Решение. Очевидно, что для данного уравнения на всей плоскости xOy выполнены условия теоремы существования и единственности решения задачи Коши. Строим последовательность ${y_n(x)}$ функций, определяемых соотношениями (3), приняв за нулевое приближение y_0(x)equiv1 :

$begin{gathered}y_0(x)equiv1,hfill\y_1(x)=1+intlimits_{0}^{x}y_0(t)dt=1+x,hfill\y_2(x)=1+intlimits_{0}^{x}y_1(t)dt=1+intlimits_{0}^{x}(1+t)dt=1+x+frac{x^2}{2},hfill\y_3(x)=1+intlimits_{0}^{x}y_2(t)dt=1+intlimits_{0}^{x}!left(1+t+frac{t^2}{2}right)!dt=1+x+frac{x^2}{2!}+frac{x^3}{3!},hfill\cdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdotscdots,hfill\y_n(x)=1+intlimits_{0}^{x}y_{n-1}(t)dt=1+frac{x}{1!}+frac{x^2}{2!}+cdots+frac{x^n}{n!}.hfill\end{gathered}$

Ясно, что $y_n(x)to{e^x}$ при ntoinfty . Непосредственной проверкой убеждаемся, что функция y(x)=e^x решает поставленную задачу Коши.

Пример 2. Методом последовательных приближений найти приближенное решение уравнения y'=x^2+y^2 , удовлетворяющее начальному условию $y|_{x=0}=0$ в прямоугольнике -1leqslant xleqslant 1, -1leqslant{y}leqslant1.

Решение. Имеем |f(x,y)|=x^2+y^2leqslant2 , т. е. M=2 . За берем меньшее из чисел $a=1,~frac{b}{M}=frac{1}{2}$ , т. е. $h=frac{1}{2}$ . Последовательные приближения согласно (4) будут сходится в интервале $-frac{1}{2}<x<frac{1}{2}$ . Составляем их

$begin{gathered}y_0(x)=0,hfill\y_1(x)=intlimits_{0}^{x}[t^2+y_0^2(t)],dt=frac{x^3}{3},hfill\y_2(x)=intlimits_{0}^{x}[t^2+y_1^2(t)],dt=intlimits_{0}^{x}!left(t^2+frac{t^6}{9}right)!dt=frac{x^3}{3}+frac{x^7}{63},hfill\y_3(x)=intlimits_{0}^{x}[t^2+y_2^2(t)],dt=intlimits_{0}^{x}!left(t^2+frac{t^6}{9}+frac{2t^{10}}{3cdot63}+frac{t^{14}}{63^2}right)!dt=frac{x^3}{3}+frac{x^7}{63}+frac{2x^{11}}{2,079}+frac{x^{15}}{59,535}.hfill\end{gathered}$

Абсолютная погрешность третьего приближения не превосходит величины

$|y_3(x)-y(x)|leqslantfrac{2}{3!}{left(frac{1}{2}right)!}^32^2=frac{1}{6}$ , здесь $N=maxlimits_{substack{-1leqslant{x}leqslant1\-1leqslant yleqslant1}} left|frac{partial{f}}{partial{y}}right|= maxlimits_{substack{-1leqslant{x}leqslant1\-1leqslant{y}leqslant1}} |2y|=2.$

Замечание. Функция f(x,y) должна удовлетворять всем условиям теоремы существования и единственности решения задачи Коши.

Следующий пример показывает, что одной непрерывности функции f(x,y) недостаточно для сходимости последовательных приближений.

Пусть функция f(x,y) определена следующим образом:

$f(x,y)=left{!begin{gathered}~~~~0,~~~~~~~~text{if}quad{x=0,~-infty<y<+infty};hfill\~~2x,~~~~~~~~text{if}quad0<xleqslant1,~-infty<y<0;hfill\2x-frac{4y}{x},quadtext{if}quad0<xleqslant1,~0leqslant{y}leqslant{x^2};hfill\~-2x,~~~~~~text{if}quad0<xleqslant1,~x^2<y<+infty.hfill\end{gathered}right.$

На множестве 0leqslant{x}leqslant1 , -infty<y<+infty функция f(x,y) непрерывна и ограничена постоянной M=2 . Для начальной точки (x,y)=(0,0) последовательные приближения при имеют вид:

$begin{gathered}y_1(x)=intlimits_{0}^{x}f(x,y_0(x)),dx=x^2,hfill\y_2(x)=intlimits_{0}^{x}f(x,x^2),dx=intlimits_{0}^{x}!left(2x-frac{4x^2}{x}right)!dx=-x^2.hfill\end{gathered}$

и вообще $y_{2n-1}(x)=x^2,~y_{2n}(x)=-x^2,~ninmathbb{N}.$

Поэтому последовательность ${y_n(x)}$ для каждого xne0 не имеет, предела, т. е. последовательные приближения не сходятся. Заметим также, что ни одна из сходящихся подпоследовательностей ${y_{2n-1}(x)}$ и ${y_{2n}(x)}$ не сходится к решению, поскольку

$begin{gathered}y'_{2n-1}(x)=2x ne f(x,x^2)=-2x,hfill\y'_{2n}(x)=-2x ne f(x,-x^2)=2x.hfill\end{gathered}$

Если же последовательные приближения сходятся, то полученное решение может оказаться неединственным, как показывает следующий пример: $y'=y^{1/3}$ .

Возьмем начальное условие y(0)=0 ; тогда $y(x)=intlimits_{0}^{x}y^{1/3}(t),dt.$

Беря в качестве нулевого приближения y_0 функцию y_0(x)equiv0 , будем иметь

y_1(x)equiv0,quad y_2(x)equiv0,quad ldots,quad y_n(x)equiv0,quad ldots,

так что все последовательные приближения равны нулю и поэтому они сходятся к функции, тождественно равной нулю. С другой стороны, функция $y(x)={!left(frac{2x}{3}right)!}^{3/2}$ представляет собой также решение этой задачи, существующее на полупрямой xgeqslant0 .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник