Найдите значение производной функции по графику как - Исправление недочетов и поиск решений вместе с Examum.ru

15 марта 2011

В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:

Значение производной в некоторой точке x₀,
Точки максимума или минимума (точки экстремума),
Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x₀, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

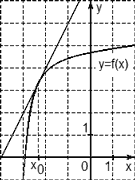
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

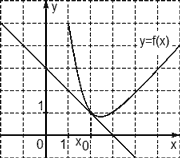
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

Точка x₀ называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
Точка x₀ называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

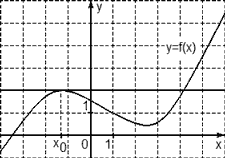
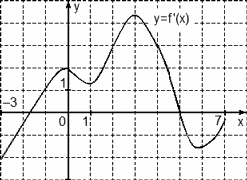
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

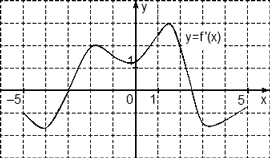
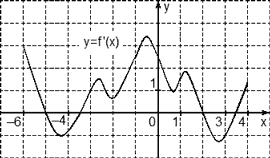
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

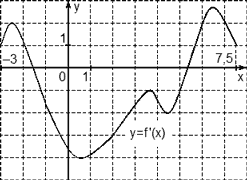
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

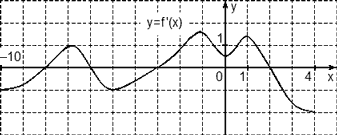
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

Смотрите также:

ЕГЭ 2022, задание 6. Касательная к графику функции
ЕГЭ 2022, задание 6. Касательная к графику функции
Схема Бернулли. Примеры решения задач
Решение задач B6: №362—377
Четырехугольная пирамида: как найти координаты вершин
Нестандартная задача B2: студенты, гонорары и налоги

Источник

Производная функции. Геометрический смысл производной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Определение.

Производная – это скорость изменения функции.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку А с абсциссой x_0 . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси ОХ.

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника AMN:

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

y=kx+b .

Величина k в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси X.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции $y=f{left( x_0 right)}$ . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке A функция $f{left( x_0 right)}$ возрастает. Касательная к графику, проведенная в точке A, образует острый угол alpha с положительным направлением оси X. Значит, в точке A производная положительна.

В точке B наша функция убывает. Касательная в этой точке образует тупой угол beta с положительным направлением оси X. Поскольку тангенс тупого угла отрицателен, в точке B производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках C (точка максимума) и D (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка С — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке С с «плюса» на «минус».

В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

1. Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке E касательная к графику горизонтальна, и производная равна нулю. Однако до точки E функция возрастала — и после точки E продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

2. Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.

Геометрический смысл производной, задачи

Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.

Задача 1. На рисунке изображен график функции y=f(x ). Найдите количество решений уравнения )=0 на отрезке [-2,5; 9,5].

Решение:

Производная функции равна нулю в точках максимума и минимума функции f(x). Таких точек на графике 5.

Ответ: 5.

Задача 2. На рисунке изображен график функции y= ) — производной функции y=f(x ). Сколько точек максимума имеет функция y=f(x ) на отрезке [-1; 5] ? В ответе запишите это число.

Решение:

Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.

В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.

В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке [-1; 5] на графике одна.

Ответ: 1.

Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.

Решение:

Вспомним определение.

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).

Это геометрический смысл производной.

В точке x_0 функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол beta с положительным направлением оси Х. Найдем тангенс острого угла alpha , смежного с углом beta .

$alpha +beta =180{}^circ.$

Ответ: -0,5.

Задача 4. На рисунке изображен график производной функции f(x), определенной на отрезке В какой точке отрезка [1; 5] f(x) принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 1,5.

Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает.

Значит, x=1,5 — точка минимума функции f(x).

Поэтому и свое наименьшее значение функция принимает в точке 1,5.

Ответ: 1,5.

Задача 5. На рисунке изображен график {y=f} — производной функции В какой точке отрезка [1; 5] функция принимает наименьшее значение?

Решение:

На рисунке есть такая точка, и это x = 3.

Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает.

Значит, x=3 — точка минимума функции f(x).

Кстати, вид графика функции f(x) определить нетрудно. Это квадратичная парабола с ветвями вверх.

Ответ: 3.

Задача 6. На рисунке изображен график {y=f} производной непрерывной функции y=f(x). В какой точке отрезка функция y=f(x) принимает наибольшее значение?

Решение:

На отрезке расположена точка x=-2,5, в которой производная равна нулю и меняет знак с «+» на «-».

Это значит, что x=-2,5 — точка максимума функции f(x) на отрезке и наибольшее значение функция f(x) принимает именно в этой точке.

Ответ: — 2,5.

Задача 7. На рисунке изображен график производной функции y=f(x) определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция y=f(x) принимает наименьшее значение?

Решение:

Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс».

Слева от точки 0 производная отрицательна, функция убывает. Справа от этой точки производная положительна, функция возрастает.

Наименьшее значение на отрезке достигается при x = 0.

Ответ: 0.

Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.

Решение:

Производная функции f(x) в точке x_0 равна тангенсу угла наклона касательной, проведенной к графику функции f(x) в этой точке.

y=kx+b — касательная к f(x).

В точке x_0 производная отрицательная, т.к. функция f(x) — убывает в этой точке.

alpha — угол, который образует касательная с положительным направлением оси Х.

Угол alpha — тупой, а смежный с ним угол varphi — острый.

$tgalpha =-tgvarphi =-displaystyle frac{3}{8}=-0,375.$

Ответ: -0,375.

Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:

Найдём значения производных в точках А и В с помощью графика.

где alpha — угол наклона касательной к графику функции в точке с абсциссой x_0.

Для точки А:

Для точки В:

Отношение производных:

Ответ: 0,15.

Условия касания

Пусть прямая y=kx+b касается графика функции y=f(x) в точке x_0. Тогда для точки x_0 выполняются условия касания:

$left{ begin{array}{c}f(x)=kx+b \f$

Первое уравнение показывает, что значения функций y=f(x) и y=kx+b в точке x_0 равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.

Второе условие показывает, что производная функции f(x) в точке x_0 равна угловому коэффициенту касательной, то есть k.

Задача 10. Прямая y=7x+b касается графика функции причем абсцисса точки касания положительна. Найдите b.

Решение:

Запишем условие касания:

$left{ begin{array}{c}f(x)=kx+b \f$

$left{ begin{array}{c}2x^3-x^2+3x-4=7x+b \6x^2-2x+3=7 end{array}right. .$

Начнем со второго уравнения:

$D=b^2-4ac=4+4cdot 6cdot 4=4cdot 25={10}^2;$

$x_{1,2}=displaystyle frac{-bpm sqrt{D}}{2a}=displaystyle frac{2pm 10}{12};$

$x_1=1; x_2=-displaystyle frac{2}{3}.$

Т.к. то x_0=1.

Найдем подставив x_0 в первое уравнение:

отсюда

b=-7.

Ответ: -7.

Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.

Физический смысл производной

Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.

И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».

Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.

Вспомним формулу для равномерного прямолинейного движения: где x — координата.

Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем v_1 = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно едет. Для второго автомобиля v_2 = 40 км/ч, для третьего v_3 = 75 км/ч.

Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.

Скорость тела — это производная от его координаты по времени.

А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени t_0, и проведем в этой точке касательную к графику функции.

Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент t_0.

$v_{x }(t_0) = tg alpha .$

Мы получили, что мгновенная скорость — это производная от координаты по времени.

Это физический смысл производной.

Но не только скорость в физике является производной от другой физической величины, координаты.

Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.

Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются дифференциальными. А само действие взятия производной называется дифференцированием.

Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.

Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Решение:

Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.

Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).

Ответ: 6.

Изучая высшую математику в вузе, вы узнаете еще одно определение производной.

Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.

Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Производная функции. Геометрический смысл производной» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Источник

Download Article

Find the derivative with or without an equation

Download Article

Estimate without an Equation

Finding the Derivative Equation

Finding the Tangent Slope at a Single Point

Tips

Estimate the derivative at a point by drawing a tangent line and calculating its slope. If you have the function, you can find the equation for a derivative by using the formal definition of a derivative. This wikiHow guide will show you how to estimate or find the derivative from a graph and get the equation for the tangent slope at a specific point.

Things You Should Know

To estimate the tangent slope at a point, draw a tangent line at the point. Then, choose two points on the tangent line.
Use the formula slope = (y2 — y1) / (x2 — x1) to find the tangent slope.
To find the derivative, use the equation f’(x) = [f(x + dx) – f(x)] / dx, replacing f(x + dx) and f(x) with your given function.
Simplify the equation and solve for dx→0. Replace dx in the equation with 0. This will give you the final derivative equation.

1
Draw a tangent line. Use a straightedge to draw a tangent line at the point on the graph that you want to estimate the derivative for. The derivative describes how the slope of a curve changes as x, the horizontal value, changes. Drawing a tangent line allows you to estimate the derivative (the tangent slope) at a given point.
- A tangent line is a straight line that touches a curve at a single point.
- The tangent slope is the slope of the tangent line.
- Make sure your curve and tangent line are drawn on a graph with grid lines. This will make it easier to calculate the tangent slope.
- Since this is a hand-drawn method, this calculation will only be an estimate, not the exact derivative at a point.
2
Find the slope of the tangent line. Choose two points that the tangent line passes through. Use the grid to find two simple points, preferably integers. The equation to find the slope with two points is
- slope = (y2 — y1) / (x2 — x1)
- using the points (x1, y1) and (x2, y2)
  - for example, if you have the points (1, 3) and (3, 7),
  - slope = (7 — 3) / (3 — 1)
  - slope = 4 / 2
  - slope = 2

1
Review the formal definition of a derivative. The derivative can be defined as the equation:^[1]
- (df / dx)(x) = [f(x + dx) – f(x)] / dx
- which can be written as f’(x) = [f(x + dx) – f(x)] / dx
- where
  - f(x) is the function f of x (sometimes written as “y”), i.e. how the value of y changes as the value of x changes
  - f’(x) is the derivative of f(x), as indicated by the prime symbol (’)
  - dx is a small change in x that approaches 0
  - f(x + dx) is the value of y at the horizontal value x + dx
2
3
Write the formal definition using the given function. Replace the terms f(x + dx) and f(x) with your given function. For example, if you were given f(x) = x^2, you would write the formal definition as
- f’(x) = [(x + dx)^2 – (x)^2] / dx
4
Simplify the equation. For simple functions, you can simplify the function algebraically. Here’s a step by step example for f’(x) = [(x + dx)^2 – (x)^2] / dx
- Our starting equation:
  - f’(x) = [(x + dx)^2 – (x)^2] / dx
- Writing out the expanded polynomial term:
  - f’(x) = [x^2 + 2xdx + dx^2 – x^2] / dx
- The terms x^2 and – x^2 equal zero, resulting in:
  - f’(x) = [2xdx + dx^2] / dx
- Both terms in the numerator have a dx, which can cancel out with the dx in the denominator, giving the simplified equation:
  - f’(x) = 2x + dx
5
Resolve the equation for dx→0. Replace every instance of dx with a 0. For our example, this would yield the equation:
- f’(x) = 2x + 0
- which simplifies to:
  - f’(x) = 2x
- So, the derivative of f(x) = x^2 is f’(x) = 2x

1

Find the derivative of the curve. Follow the previous method, Finding the Derivative Equation, to get the derivative equation for the given function f(x).
2
Insert the x value of the point. Replace x in the derivative function f’(x). Using our previous example:
- Find the slope of the tangent line at x = 5 for the function f(x) = x^2.
  - f’(x) = 2x
  - f’(5) = 2(5)
  - f’(5) = 10
- The slope of the tangent line at x = 5 is 10.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

References

About This Article

Thanks to all authors for creating a page that has been read 7,598 times.

Did this article help you?

Get all the best how-tos!

You’re all set!

Источник

На этой странице вы узнаете

Где проходит граница между теплом и холодом?
Почему успех фильма не всегда зависит от наличия экшн-сцен?
Чем кофе похож на функцию, ее первообразную и производную?

Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.

Связь графика функции и производной

Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.

Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.

Возьмем график произвольной функции.

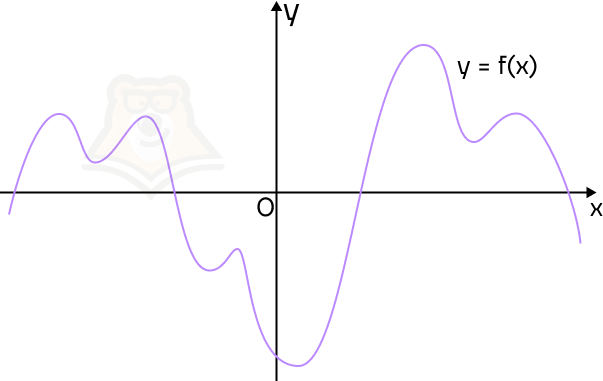
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».

Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.

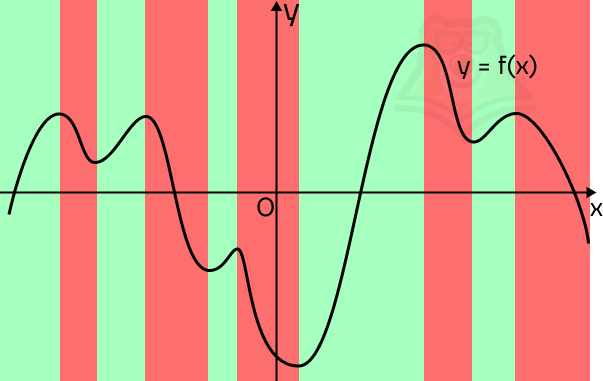
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.

Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.

Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.

Точки экстремума — точки, в которых достигается экстремум.

В точках экстремума производная равна 0.

Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.

Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан

y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.

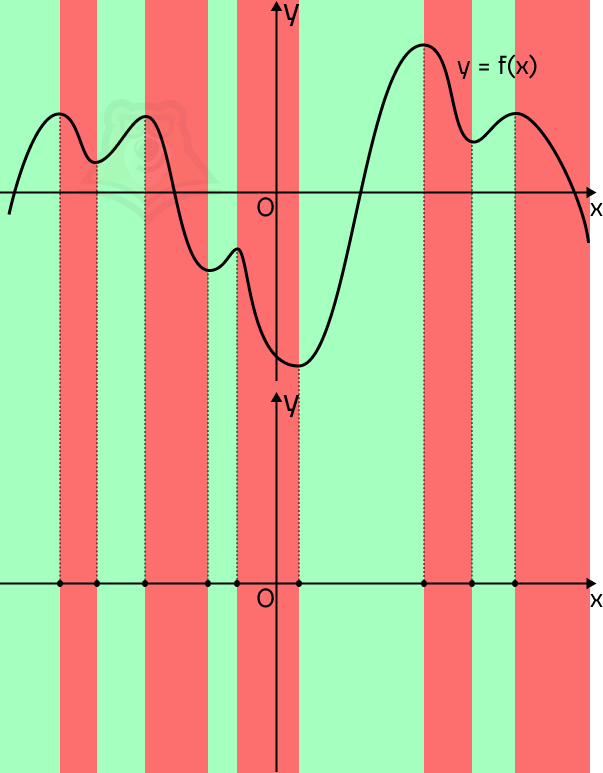
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.

Вспомним, что:

производная положительна на промежутках возрастания функции;
производная отрицательна на промежутках убывания функции.

Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.

Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.

Где проходит граница между теплом и холодом?

Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной.

Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах.

Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.

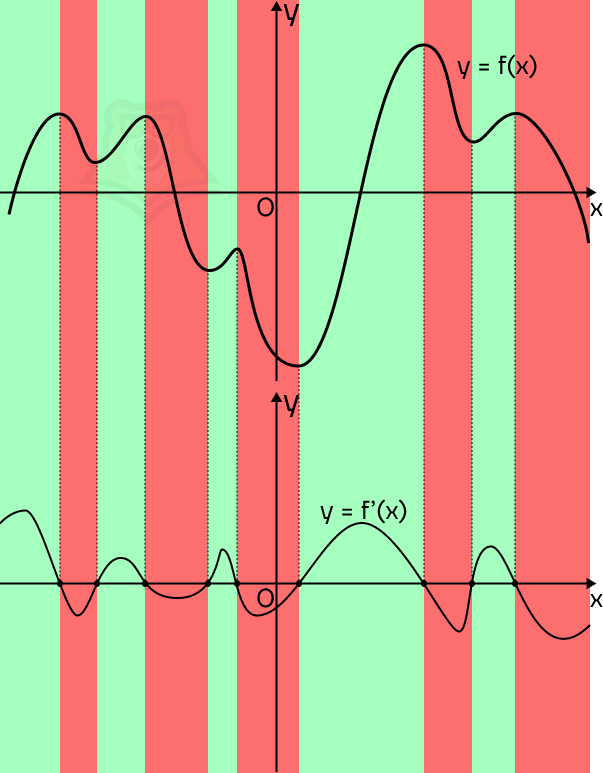
Подведем итоги:

В точках экстремума функции график производной будет проходить через ось х.
На промежутках возрастания функции график производной будет лежать выше оси х.
На промежутках убывания функции график производной будет лежать ниже оси х.

Эти зависимости можно отследить на любых графиках функции и ее производной.

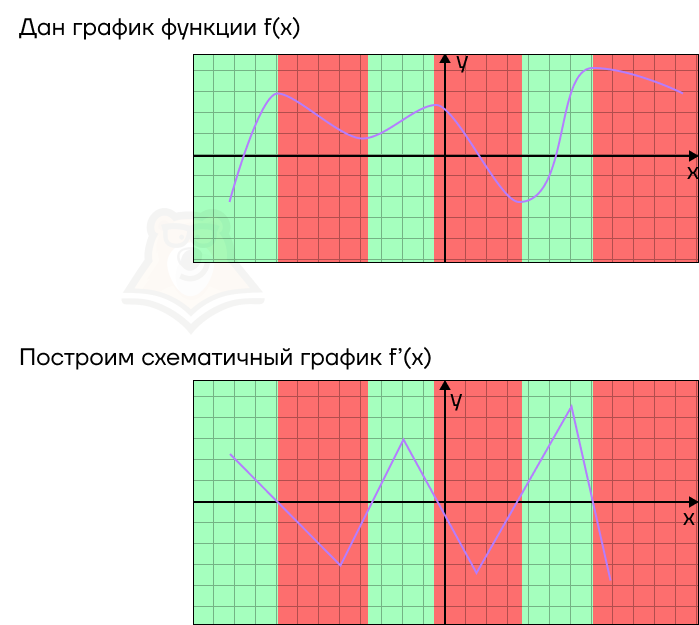
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:

В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.

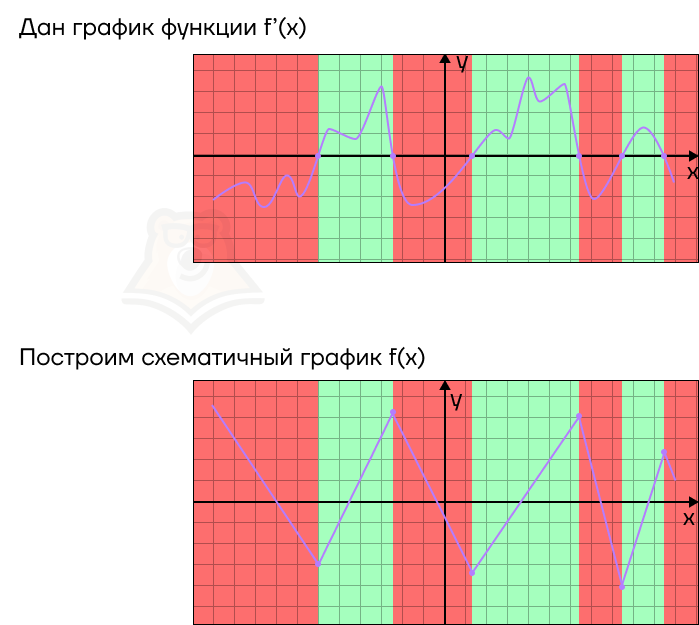
Разберем несколько примеров, где можно применить эти знания.

Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅. В скольких из этих точек производная функции отрицательна?

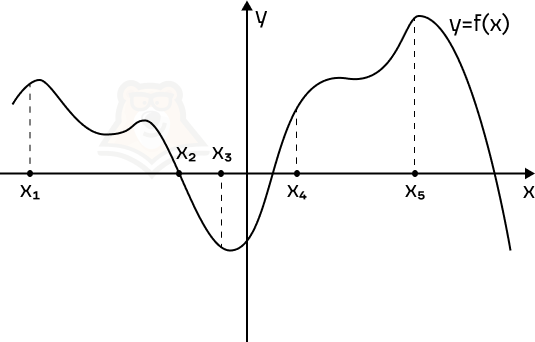
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.

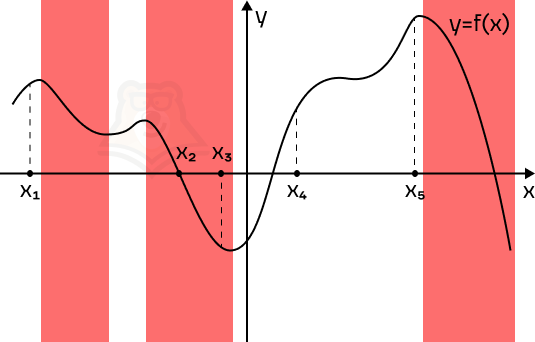
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.

Ответ: 2

Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).

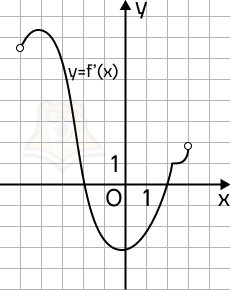
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.

Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.

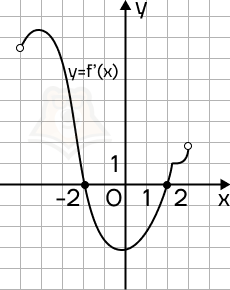
Ответ: -2

Почему успех фильма не всегда зависит от наличия экшн-сцен?

Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Совпадут ли эти графики? Скорее всего, нет.

Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой.

Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются.

Связь графика функции и первообразной

Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?

Вспомним один важный факт: если взять производную от первообразной, то получим функцию.

F'(x) = f(x)

Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.

В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.

	Было	Взяли производную	Стало
Функция и производная	f(x)	f'(x)	f'(x)
Функция и первообразная	F(x)	F'(x)	f(x)

Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.

При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.

Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x₁, x₂, x₃, x₄, x₅, x₆. В скольких из этих точек функция f(x) отрицательна?

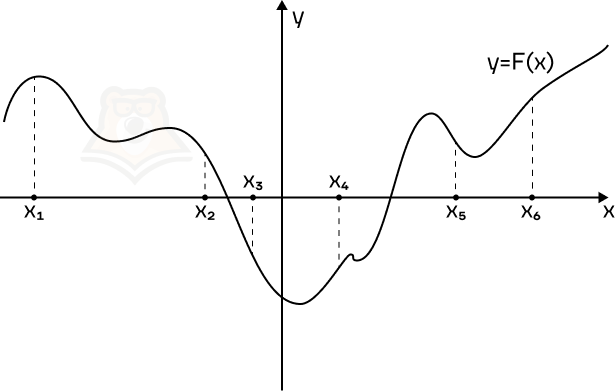
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).

Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.

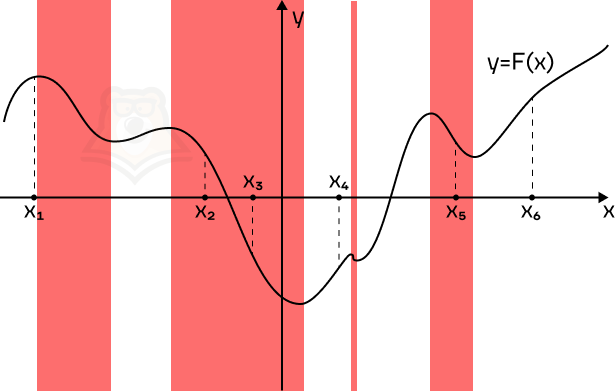
В эти промежутки попадают 3 из 6 точек.

Ответ: 3.

Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].

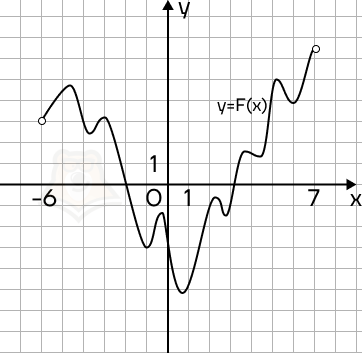
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.

Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.

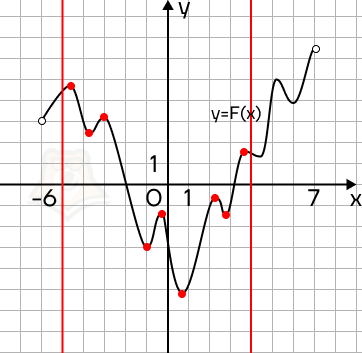
Ответ: 9

Чем кофе похож на функцию, ее первообразную и производную?

Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток.

Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная.

Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной.

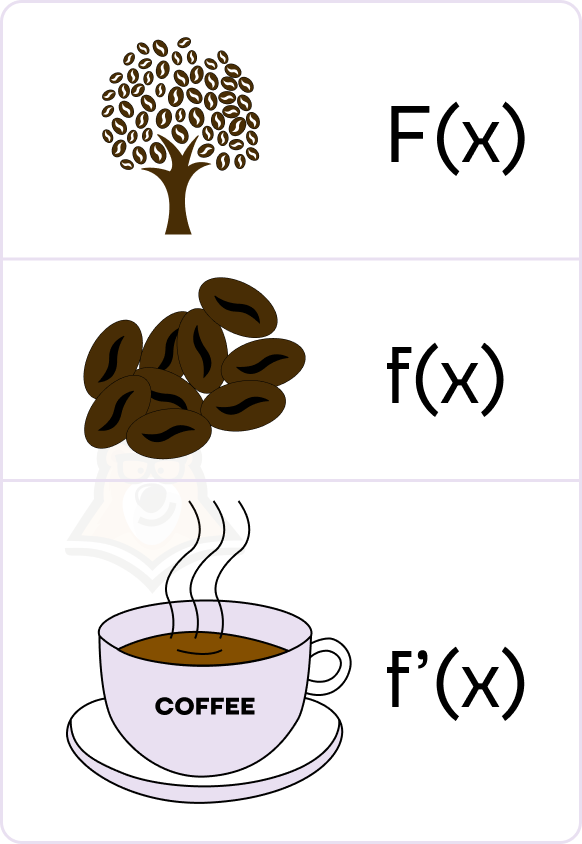
Фактчек

Графики функции, производной и первообразной связаны между собой.
В точках экстремума функции график производной будет проходить через ось х.
На промежутках возрастания функции график производной будет лежать выше оси х.
На промежутках убывания функции график производной будет лежать ниже оси х.
Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.

Проверь себя

Задание 1.
На каких промежутках будет производная функции будет положительна?

На промежутках убывания функции.
На промежутках возрастания функции.
В точках экстремума.
Невозможно определить по графику.

Задание 2.
На каких промежутках производная функции будет отрицательна?

На промежутках возрастания функции.
На промежутках убывания функции.
В точках экстремума.
Невозможно определить по графику.

Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?

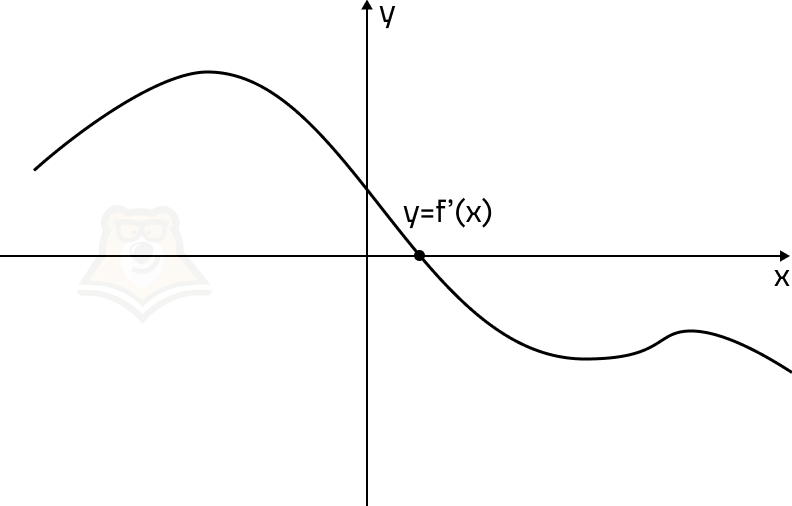
Точка максимума функции.
Точка минимума функции.
Любая произвольная точка на функции.
Невозможно определить по графику.

Задание 4.
Выберите верный вариант:

F(x) = f'(x)
F(x) = f(x)
F'(x) = f'(x)
F'(x) = f(x)

Ответы: 1. — 2 2. — 2 3. — 1 4. — 4

Источник