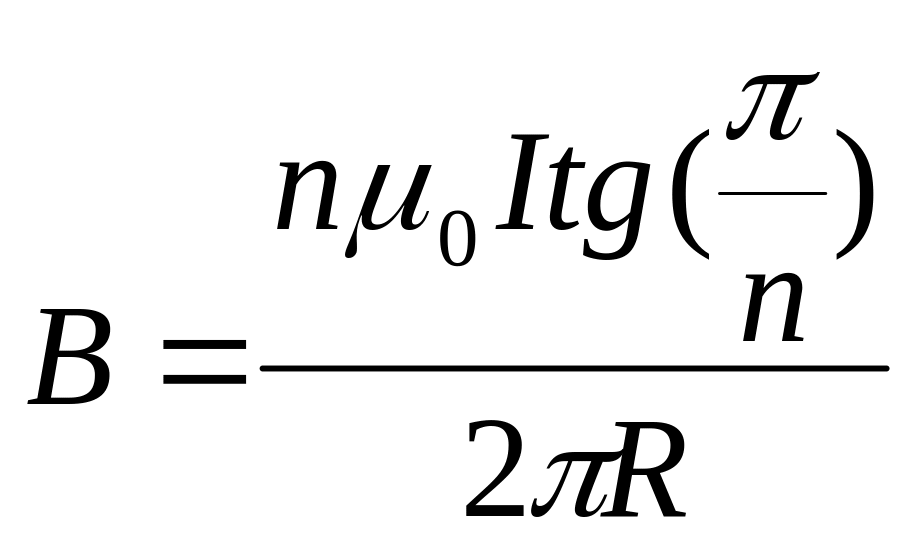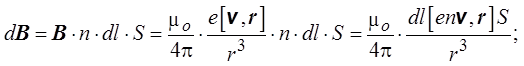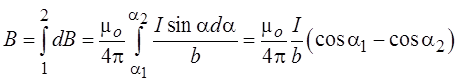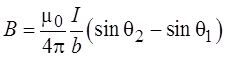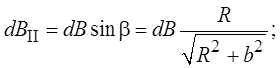2018-05-14
Длинный прямой проводник с током $I$ и П-образный проводник с подвижной перемычкой расположены в одной плоскости, как показано на рис. Перемычку, длина которой $l$ и сопротивление $R$, перемещают вправо с постоянной скоростью $v$. Найти ток, индуцируемый в контуре, как функцию расстояния $r$ между перемычкой и прямым проводником. Сопротивление П-образного проводника и самоиндукция контура пренебрежимо малы.
Решение:
Поле, связанное с проводом в области, направлено в плоскость рисунка, и его величина определяется выражением,
$B = frac{ mu_{0} }{2 pi}$ где $r$ — перпендикулярное расстояние от провода.
Так как $B$ одинаково по длине стержня, таким образом, ЭДС
$mathcal{E}_{ин} = left | — int_{1}^{2} ( vec{v} times vec{B} ) cdot d vec{l} right | = vBl$
и направлено так же как ($vec{v} times vec{B}$)
Итак, ток (индуцированный) в контуре,
$i_{ин} = frac{ mathcal{E}_{ин} }{R} = frac{1}{2} frac{ mu_{0}Ivi }{ pi Rr}$
Найти
суммарный импульс электронов в прямом
проводнике длиной l=1000
м и с током I=70
А.
Решение:
Выражение
для импульса:
P=mv;
v=
;
t=
Тогда
получим:
v=
;
В
итоге получаем,
P=I
l
.
№2.223.
Между двумя плоскими пластинами
конденсатора, отстоящими друг от друга
на расстоянии d,
находится газ. Одна из пластин эмиттирует
ежесекундно
электронов, которые, двигаясь в
электрическом поле, ионизируют молекулы
газа так, что каждый электрон создаёт
на единице длины пути α новых электронов
(и ионов). Найти электронный ток у
противоположной пластины, пренебрегая
ионизацией молекул газа ионами.
Решение:
Рассмотрим
1 электрон, который, эммитировав с
пластины, прошёл путь dx.
За
это время он произведёт αdx
новых электронов, то есть заряд увеличится
в
раз.
И
так до второй пластины. В результате
заряд увеличится в
раз.
Откуда для
электронов :
Ответ:
№2.229
Ток I
течёт по тонкому проводнику, который
имеет вид правильного n-угольника,
вписанного в окружность радиуса R.
Найти магнитную индукцию в центре
данного контура. Исследовать случай
.
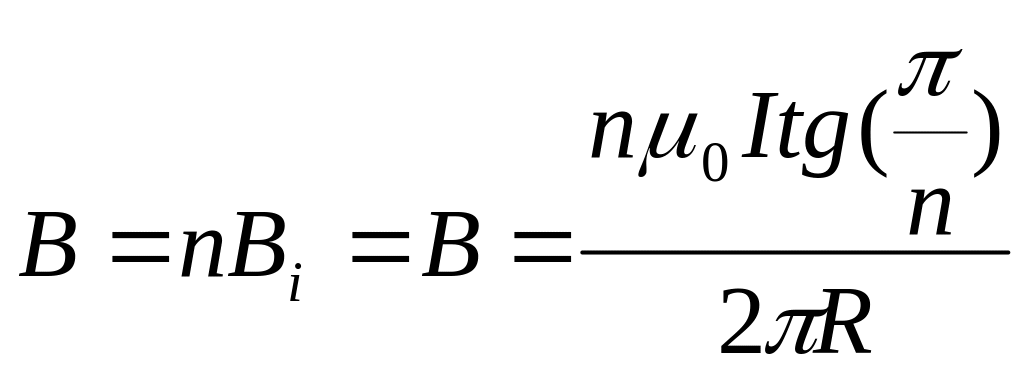
Ответ:
при
Задача 2.230.
Найти
магнитную индукцию в центре контура,
имеющего вид прямоугольника, если его
диагональ d=16
см, угол между диагоналями =30
и ток I=5,0
A.
Решение:
По закону Био-Савара:
B=
L
; отсюда путем геометрических преобразований
получим,что L/r
=16/d
sin
,отсюда
B=
=
=
;
Ответ: B=
.
2
.234
Ток I=11.0A
течёт по длинному прямому проводнику,
сечение которого имеет форму тонкого
полукольца радиуса R=5.0см.
Найти индукцию магнитного поля в точке
O.
Решение:
Разобьём проводник на тонкие нити. По
каждой из них течёт ток
,
и такая нить создаёт в точке О магнитное
поле
2.242 Однородный
ток плотности
течёт внутри неограниченной пластины
толщины 2d параллельно её
поверхности. Пренебрегая влиянием
вещества пластины, найти индукцию
магнитного поля этого тока как функцию
расстояния x от средней
плоскости пластины.
Решение:
copyright
2001 Андрюха, 13РФ.
Для уединённого
проводника с током
.
Элемент тока
создаёт
,

2_243 Условие:
Постоянный то I течёт по
длинному проводу, потом растекается
радиально-симметрично по проводящей
плоскости, перпендикулярной проводу.
Найти индукцию магнитного поля во всех
точках пространства.
Решение:
Построим цилиндр, ось которого лежит
на проводе, нижнее основание лежит в
средней плоскости проводящей плоскости.
Будем рассматривать составляющую
индукции со стороны плоскости. Каждому
элементу тока над нижним основанием
цилиндра найдётся симметричный под
основанием(они компенсируют друг друга).
Следовательно индукция поля в плоскости
основания равна нулю и поток ч/з это
основание также равен нулю. Если
вертикальные составляющие индукции на
другом основании существует, то они
направлены в одну сторону, и тогда
(4-ое уравнение Максвелла)
B=0. На боковой поверхности
индукция также равна нулю.
Получается, что в любой точке
пространства составляющая индукции со
стороны плоскости равна нулю. Остаётся
только составляющая от провода.
Итого в полупространстве, в котором
находится провод B=0I/2r.(r
– расстояние от провода до данной точки)
B=0 в другом полупространстве.
2.246
По прямому
проводу, радиус сечения которого R, течёт
постоянный ток плотности j. Пренебрегая
влиянием вещества провода, найти индукцию
магнитного поля этого тока в точке,
положение которой относительно оси
провода определяется радиусом-вектором
r (перпендикулярен).
Решение:
Рассмотрим
2 случая(r<=R и r>R):
Первый: в
данном случае мы рассматриваем лишь
тот ток, который течет внутри “стержня”
радиуса r, т.к. индукция тока во внешнем
слое будет взаимно уничтожаться. Тогда:
Второй: теперь
мы рассматриваем уже весь провод, а
дальше по аналогии:
Ответ:
№ 2.248.
Найти плотность
тока как функцию расстояния r
от си аксиально-симметричного параллельного
потока электронов, если индукция
магнитного поля внутри потока зависит
от r как
,
где b и
— положительные постоянные.
Р
ЕШЕНИЕ.
Запишем формулу
циркуляции и закон Ампера.
Продифференцируем
правую и левую части уравнения.
ОТВЕТ:
.
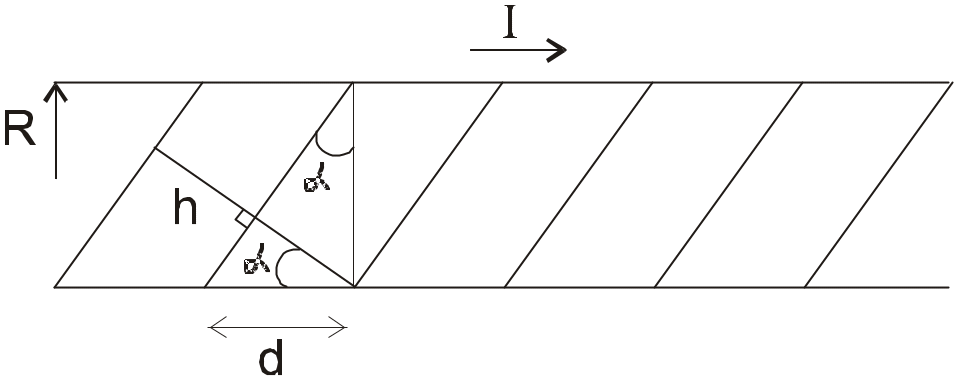
№2.251
У
словие:
Обмоткой длинного соленоида с радиусом
сечения R=2,5
см. служит тонкая лента-проводник ширины
h=5,0
см, намотанная в один слой практически
вплотную. По ленте течет ток I=5,0
А. Найти индукцию магнитного поля внутри
и вне соленоида как функцию расстояния
r
от его оси.
Для
случая r<R:
,
где n
– плотность обмотки
n=1/d;
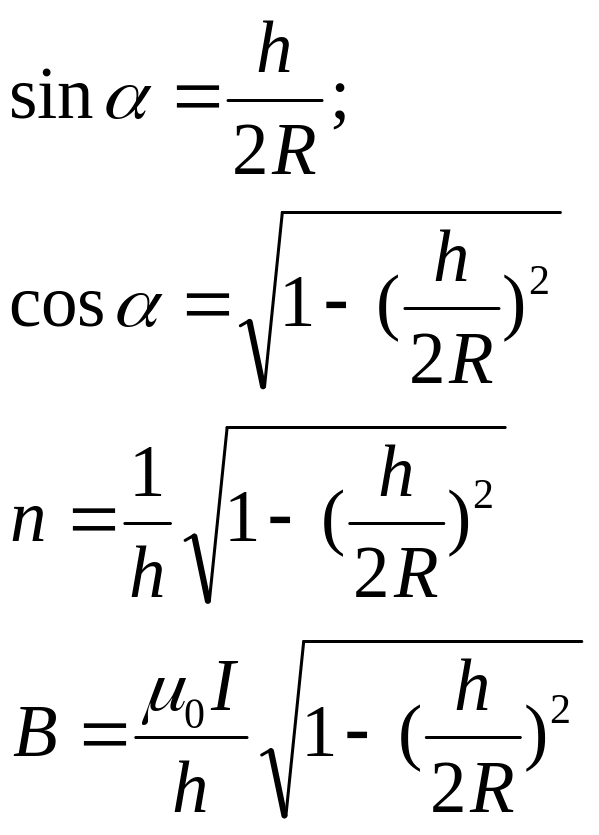
для
случая r>R:
по закону Ампера
№2.253
Условие:
Ток
I=50
А течёт по длинному прямому проводнику
круглого сечения. Пренебрегая влиянием
вещества проводника, найти магнитный
поток через одну из половин осевого
сечения проводника в расчёте на единицу
его длины.
Решение:
— плотность
тока
По
закону Ампера:
(т.к. ldr
= dS)
Ответ:
№-2.256.
Найти магнитный
момент тонкого кругового витка с током
, если радиус витка
100мм
и индукция магнитного поля в его центре
6.0мкТл.
Решение:
По определению
магнитный момент это :
; — где
площадь поверхности, ограниченной
контуром , а
-ток в контуре.
, а
;
;
Ответ:
;
2.260.
Непроводящий тонкий диск радиуса R,
равномерно заряженный с одной стороны
с поверхностной плотностью ,
вращается вокруг своей оси с угловой
скоростью . Найти:
а) индукцию
магнитного поля в центре диска;
б) магнитный
момент диска.
Решение:
Индукция
поля малого движущегося заряда dq:
;
Интегрируем
по поверхности диска
Ответ:
№ 2.264
Два протона
движутся параллельно друг другу с
одинаковой скоростью v=300
км/c.Найти
отношение сил магнитного и электрического
взаимодействия данных протонов.
Решение:
Электрическое
взаимодействие
;
Магнитное
(элемент тока равен ev)
;
Ответ :
.
Задача 2.267
Катушка с
током I=10мА
поместили
в однородное магнитное поле так, что ее
ось совпала с направлением поля. Обмотка
катушки однослойная из медного провода
диаметром d=0,10мм,
радиус витков R=30мм.
При каком значении индукции внешнего
поля обмотка катушки может быть разорвана?
Решение:
Сила ,которую
может выдержать катушка равнва F=S,
где
предел прочности для меди .
С другой стороны
на катушку действует сила Ампера F=BIL,
приравнивая силы получаем:
S=BIL;
d
/4=BIR;
B=d
/4IR;
Ответ:
B=d
/4IR=8кТл.
Вдоль длинного
тонкостенного круглого цилиндра радиуса
R=5,0см
течет ток
I=50A.
Какое давление испытывают стенки
цилиндра?
Решение:
P=F/S;
S=2rH—боковая
поверхность;
На цилиндр дейстует
сила Ампера
F=BIL=BIH;
B=
IL/4r
теперь
подставим все в формулу для давления
P= BIH/2rH=
I
/8
r
.
Ответ:
P=
I
/8
r
.
2.277
Внутри длинного цилиндрического сосуда
радиуса a
параллельно его оси расположен проводящий
стержень радиуса b
с тонкой изоляцией. Расстояние между
осями стержня и сосуда равно l.
Сосуд заполнили электролитом и пустили
вдоль оси ток I,
возвращающийся обратно по стержню.
Найти модуль и направление магнитной
силы, действующей на единицу длины
стержня.
Решение:
П
усть
h-
высота сосуда.
В
силу симметрии
(1)
Определение
Ω2:
—
уравнение
окружности
Т.
к. ρ не может быть меньше нуля, то

т. к. подынтегральная
функция нечетная
Из
(1)
По
3-му закону Ньютона сила стремится
прижать провод к стенке сосуда (на рис.
это сила
).
Ответ:
,
направление силы указано на рис. в
решении задачи (сила
).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Страницы работы
Содержание работы
где v – скорость направленного движения
свободных носителей заряда. Умножив В на количество свободных
носителей заряда в элементе проводника dl, получим индукцию магнитного
поля, созданную этим элементом проводника с током,
поскольку env= j*,
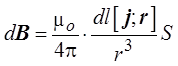
поскольку dl.j
= dl.j
(dl и j совпадают по направлению),
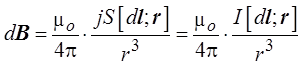
Таким образом, индукция
магнитного поля, созданного элементом dl проводника с током I на
расстоянии r от элемента проводника, определяется выражением
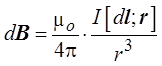
Это выражение и
представляет собой закон Био–Савара–Лапласа.
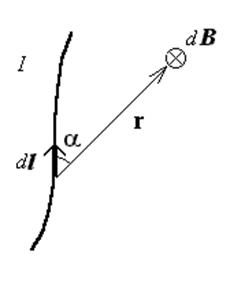
Из закона видно, что вектор
магнитной индукции dB всегда перпендикулярен плоскости, в
ко-торой лежат векторы dl и r. Его направление
определяется по правилу правого винта.
Модуль вектора dB
определяется из выражения
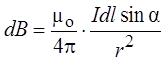
где a – угол между векторами dl
и r.
______________________
* Здесьj – вектор плотности тока.
Необходимо учесть, что
полученное выражение позволяет рассчитать индукцию магнитного поля, созданную
одним бесконечно малым элементом проводника dl с током I.
Для того чтобы найти
магнитную индукцию, созданную всемпроводником, необходимо использовать
принцип суперпозиции, т. е. просуммировать векторы dB, созданные
каждым элементом проводника в интересующей нас точке.
3.4. Расчёт
магнитных полей с помощью закона
Био–Савара–Лапласа
3.4.1. Индукция магнитного поля отрезка
прямолинейного проводника с током
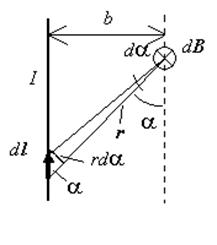
Для
всех бесконечно малых элементов dl отрезка векторы dl
и r лежат в плоскости листа. Поэтому векторы dB,
созданные в выбранной нами точке различными элементами проводника направлены
одинаково – перпендикулярно плоскости листа. Следовательно, сложение векторов dB
можно заменить сложением их модулей dB.
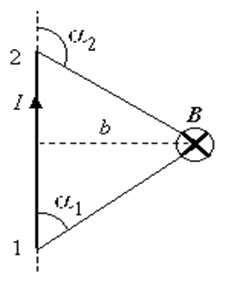
(b – расстояние от проводника до инте-ресующей нас точки), и
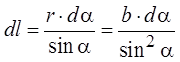
Тогда индукция, созданная
элементом проводника dl, равна
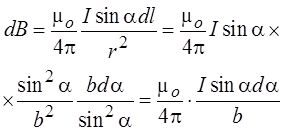
Индукция магнитного поля, созданного
всем проводником, может быть найдена как интеграл от dB в пределах от
a1 до + a2:
Иногда удобнее воспользоваться другим
выражением:
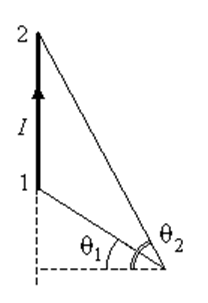
(обратите внимание на рисунок, показывающий углы q1 и q2).
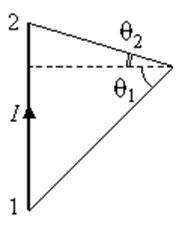
если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля
прямолинейного отрезка записывается следующим образом:
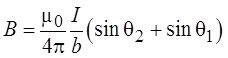
3.4.2. Индукция магнитного поля бесконечно длинного
прямолинейного
проводника с током
Если длина прямого проводника бесконечно
велика, то a1 = 0, а a2 = p.
В этом случае индукция магнитного
поля, созданного проводником, будет равна
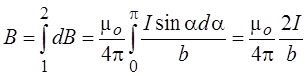
индукция магнитного поля, созданного бесконечно длинным проводником прямо
пропорциональна току в проводнике и обратно пропорциональна расстоянию от
проводника до интересующей нас точки.
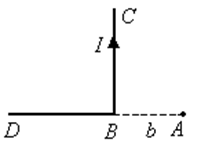
Дополнительно рассмотрим
магнитное поле, созданное бесконечным проводником, который изогнут под прямым
углом.
Ограничимся получением
расчётной формулы для точки А, расположенной на продолжении одной из
половин проводника.
Участок DB в точке А
не создаёт магнитного поля, так как для него a1 и a2 равны 0.
Для участка ВС a1 = 900, a2 =
-1800. Поэтому индукция, созданная этим участком, равна
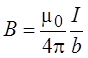
Таким образом, индукция
магнитного поля в точке А равна половине индукции, созданной прямым
бесконечно длинным проводником с таким же током.
3.4.3. Индукция магнитного поля в центре квадрата
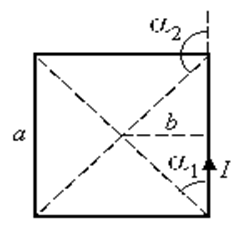
Все стороны
квадрата создают в его центре одинаковое магнитное поле. Поэтому если индукция,
созданная одной стороной, равна В, то магнитная индукция, созданная
всеми сторонами, равна 4В.
В рассматриваемом случае a1 = 450, а a2 =
1350 (см. рисунок).
Индукция магнитного поля,
созданного одной стороной, равна:
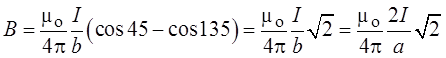
Соответственно индукция магнитного
поля, созданного всеми сторонами, равна
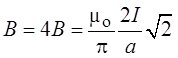
В показанном на рисунке случае
индукция магнитного поля направлена перпендикулярно плоскости квадрата на нас.
3.4.4. Расчёт магнитного поля замкнутого кругового
тока
(витка
с током).
Пусть радиус витка равен R, а
ток в нём – I.
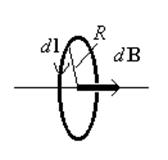
Вначале рассмотрим расчёт поля в
центре витка.
Каждый элемент тока будет создавать
индукцию, направленную вдоль оси витка. Поэтому, как и в предыдущем случае, сложение
dB алгебраическое и
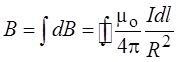
(в каждой точке a = 900)
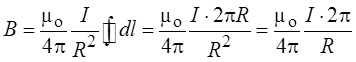
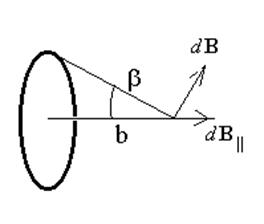
Поле на
оси витка на расстоянии b от центра витка рассчитывается несколько
сложнее. В этом случае векторы dB не параллельны друг
другу.
При суммировании составляющие
векторов dB, перпендикулярные оси, уничтожаются, а параллельные
оси – складываются.
Из рисунка видно, что
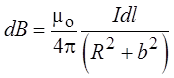
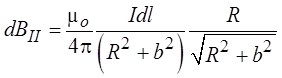
Проинтегрировав это выражение по всему
контуру, получаем
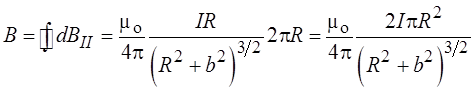
Похожие материалы
- Задачи с раздела общей физики «Динамика вращательного движения твердого тела». Вариант 1
- Задачи с раздела общей физики «Динамика вращательного движения твердого тела». Вариант 10
- Энергия затухающих колебаний. Вынужденные колебания. Волны. Электромагнитные волны (Главы 8-10 учебного пособия по общей физике)
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
, ,
где — магнитная постоянная вакуума, H/A 2 ; — магнитная проницаемость вещества, — алгебраическая сумма токов, охватываемых замкнутым контуром, — намагниченность вещества.
4. Поток вектора через замкнутую поверхность
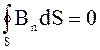
5. Некоторые соотношения для магнетиков:
где — восприимчивость вещества.
6. Граничные условия для векторов и :
где — нормальная составляющая вектора , — тангенциальная составляющая вектора , — углы между векторами и перпендикуляром к поверхности границы раздела в разных средах.
7. Принцип суперпозиции для векторов
где — индукция от полей, созданных различными источниками.
если источники магнитных полей расположены непрерывно.
8. Индукция магнитного поля движущегося заряда
.
9. Индукция магнитного поля элемента тока (закон Био-Савара-Лапласа)
.
10. Индукция магнитного поля прямолинейного проводника с током бесконечной и конечной длины соответственно
, .
11. Индукция магнитного поля в центре и на оси кругового тока соответственно
, .
12. Индукция магнитного поля внутри соленоида и тороида соответственно
где N — общее число витков, — длина. Длина тороида , где — радиус средней линии тороида.
Примеры решения задач
Задача 1.
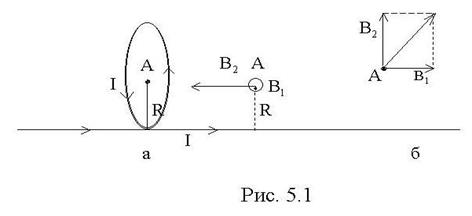
Бесконечно длинный проводник с током 5 А делает петлю, лежащую в перпендикулярной току плоскости. Найти напряженность магнитного поля в центре петли, если её радиус 0,5 м.
Дано:
Направление вектора индукции магнитного поля в обоих случаях определяем по правилу буравчика: от бесконечно длинного тока вектор В 1
направлен к нам, а от кругового тока вектор В 2
направлен справа налево по оси кругового тока
(рис. 5.1а). В 1
и В 2
перпендикулярны друг к другу. Результирующий вектор В
направлен по диагонали параллелограмма, построенного на векторах В 1
и В 2
(рис. 5.1б). Числовое значение В
находим по теореме Пифагора
причём величины и находим по соответствующим формулам:
В вакууме напряжённость Н и индукция В связаны соотношением
Подставляя (3) и (2) в (1), для напряжённости получим формулу
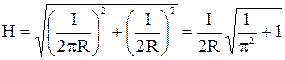
Подставим числовые значения:
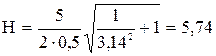
Задача 2.
Ток 5 А течёт по тонкому изогнутому проводнику (рис. 5.2). Радиус изогнутой части проводника R = 12 см, угол . Найти индукцию магнитного поля в точке O.
| Дано: I = 5 A R = 12 см = 0,12 м В — ? |
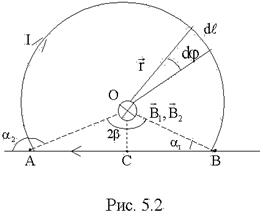 Решение Решение
|
Индукция магнитного поля в точке О является векторной суммой индукций В 1
и В 2
, создаваемых током, протекающим по круговому и прямолинейному участкам проводника. Все элементы тока создают в точке О магнитные поля, векторы индукции которых направлены в одну сторону (перпендикулярно плоскости (рис. 5.2), “от нас”). Поэтому от векторной суммы можно перейти к алгебраической, т.е.
Вычислим индукцию , создаваемую участком кругового тока, используя закон Био-Савара-Лапласа:
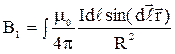
Для всех участков кругового тока угол между и равен , а элемент длины . Угол при интегрировании по участку кругового тока изменяется от 0 до . Вычисление интеграла даёт следующее выражение:
Для вычисления индукции , создаваемой прямолинейным участком тока BCA, можно воспользоваться выражением, определяющим индукцию магнитного поля прямого тока:
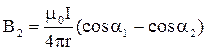
Для данной задачи ;
; (из треугольников AOC и COB) . Подстановка значений даёт
.
Учитывая, что , для величины B окончательно получим
.
Подставим числовые значения:
Задача 3.
Тонкий непроводящий диск радиусом R, равномерно заряженный с поверхностной плотностью , вращается вокруг своей оси с угловой скоростью . Найти: а) индукцию магнитного поля в центре диска; б) магнитный момент диска. (рис. 5.3).
Дано: Решение
Круговой ток создаёт в центре диска магнитное поле с индукцией dB. Используя принцип суперпозиции и учитывая, что все элементарные кольцевые токи dI создают в центре диска магнитные поля одного направления, получим
Магнитный момент тока dI
.
Задача 4.
По круглому однородному прямому проводу радиусом 2 см течёт постоянный ток плотностью j = 10А/м. Найти индукцию магнитного поля в точках, лежащих внутри и вне соленоида на расстояниях 1 и 5 см соответственно. Построить график B(r).
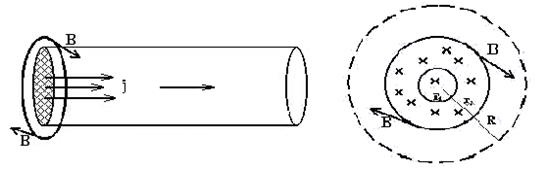
Рассмотрим область точек, лежащих внутри провода . В качестве контура интегрирования выберем окружность радиусом r. Направление обхода и направление вектора j
свяжем правилом буравчика. По теореме о циркуляции вектора В
.
Для точек, лежащих вне провода , решение задачи аналогично предыдущему случаю. Контур интегрирования теперь охватывает площадь сечения проводника, поэтому сила тока
По теореме о циркуляции вектора В
,
Произведём расчёт формул (1) и (2) .
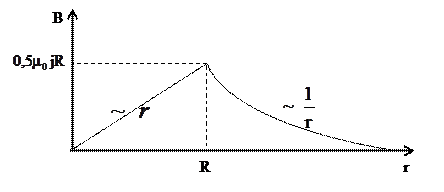
Задача 5.
Постоянный ток 10 А течёт по прямому проводнику круглого сечения длиной 50 см (рис. 5.6). Найти поток вектора магнитной индукции через одну из половин осевого сечения.
Дано: Решение
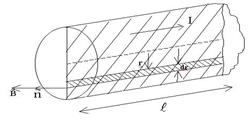
Поток вектора индукции определяется интегралом
,
где — проекция вектора на нормаль к площадке. В нашем случае , т.к. вектор совпадает по направлению с вектором . Из решения предыдущей задачи для точек, лежащих внутри проводника, индукция зависит от расстояния.
Выделим в сечении полоску шириной dr и длиной , находящуюся на расстоянии r от оси провода. В пределах площадки dS величину индукции можно считать постоянной, тогда элементарный поток вектора магнитной индукции через неё
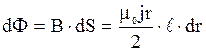
Полный поток магнитной индукции
.
Учитывая, что , получим
Подставим числовые значения:
нВб.
.
.
Полный поток вектора через поверхность S рамки равен алгебраической сумме элементарных потоков :
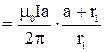
Подставим числовые значения:
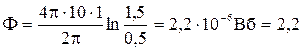
По длинному прямому цилиндрическому проводу радиуса R
течет ток с постоянной плотностью j
. Определить индукцию магнитного поля как функцию расстояния r
от оси провода и построить график этой зависимости.
Решение
где I=pR 2 j
– полный ток в проводнике. Отсюда следует
r
r>R
По оси длинного тонкостенного проводящего цилиндра радиуса R
натянут провод. По цилиндру и проводу течет постоянный ток силы I
, направление тока в проводе и цилиндре противоположны. Определить индукцию магнитного поля в зависимости от расстояния r
от провода и построить график этой зависимости.
Решение
Индукция магнитного поля обладает в этой задаче осевой симметрией и вследствие однородности вдоль проводника от координаты вдоль проводника не зависит. Силовые линии поля – концентрические окружности с общим центром на оси проводника. Вектор индукции направлен по касательным к этим окружностям. Эти окружности следует выбрать в качестве замкнутых контуров для применения теоремы о циркуляции:
0
0
, B(r)=0
r>R,
Тороидальная однослойная катушка содержит N
витков плотно намотанного провода, по которому течет ток I
.
Внутренний радиус тора R 1
,
внешний — R 2
. Определить индукцию магнитного поля внутри и вне тора на расстоянии r
от его оси.
Решение
Тор представляет собой поверхнсть вращения окружности радиуса R
= (R 2 — R 1
)/2 вокруг оси, расположенной вне окружности. Полагая провод тонким по сравнению с радиусом тора, можно считать, что линии тока лежат в меридианальных плоскостях, т.е. в плоскостях, проходящих через ось вращения. При этом предположении при повороте тора с намотанным на него проводом с током вокруг оси он совмещается сам с собою. То же относится и к силовым линиям индукции магнитного поля тока. Поэтому силовые линии поля представляют собой концентрические окружности с центрами на оси вращения. Циркуляция вектора индукции магнитного поля вдоль каждой такой окружности радиуса r
равна 2prB(r)
Полный ток, пронизывающий площадь, ограниченную этой окружностью, равен NI
, если окружностьпроходит внутри тора, и равен нулю, если она проходит вне тора.
Таким образом, индукция поля отлична от нуля только внутри тора, т.е при R 1 R 2
и составляет
. Величина n=NI/2pr
представляет собой число витков, приходящееся на единицу длины обмотки. Величина i=nI
представляет собой линейную плотность тока.
Соленоид представляет собой полый цилиндр радиуса R
и длины L
, на поверхность которого плотно намотан в один слой тонкий провод. Отношение числа витков провода в обмотке соленоида к его длине составляет n
. Определить индукцию магнитного поля внутри и вне соленоида, если по его обмотке течет ток I
. Провести оценки для следующих величин: R=1 см, L=50 см, n=15 витков/см, I=1 А
.
Решение
Соленоид можно представить себе как предельный случай тора очень большого радиуса вращения, но фиксированного радиуса цилиндра R
при увеличении числа витков обмотки, но фиксированном отношении n
числа витков к длине окружности вращения. Индукция магнитного поля внутри соленоида составляет B=
m 0 nI
, вне соленоида B
=0.
Давление магнитного поля p=B 2 /2m 0
. Сила давления, действующая на боковую поверхность соленоида, площадь которой S=2pRL
составит
F=pS=m 0 (nI) 2 S/2=pm 0 (nI) 2 RL
Численные оценки:
B=1.256 10 -6 15 1=1.88 10 -5 Тл p=1.41 10 -4 Н/м 2 F=4.44 10 -6 Н
Магнитное поле проводника с током.
При прохождении тока по прямолинейному проводнику вокруг него возникает магнитное поле (рис. 38). Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.
Направление магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику. Направление магнитных силовых линий можно определить по правилу буравчика. Его формулируют следующим образом. Если поступательное движение буравчика 1 (рис. 39, а) совместить с направлением тока 2 в проводнике 3, то вращение его рукоятки укажет направление силовых линий 4 магнитного поля вокруг проводника.
Рис. 39. Определение направления магнитного поля по правилу буравчика
Например, если ток проходит по проводнику в направлении от нас за плоскость листа книги (рис. 39, б), то магнитное поле, возникающее вокруг этого проводника, направлено по часовой стрелке. Если ток по проводнику проходит по направлению от плоскости листа книги к нам, то магнитное поле вокруг проводника направлено против часовой стрелки. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле. При изменении направления тока магнитное поле также изменяет свое направление.
По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля и его напряженность уменьшаются. Напряженность магнитного поля в пространстве, окружающем проводник,
H = I/(2πr)
где r — расстояние от рассматриваемой точки до оси проводника.
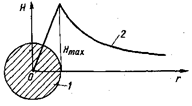
Максимальная напряженность H MAX
имеет место на внешней поверхности проводника 1 (рис. 40). Внутри проводника также возникает магнитное поле, но напряженность его
Рис. 40. Кривая распределения напряженности магнитного поля Н вокруг и внутри проводника с током
линейно уменьшается по направлению от внешней поверхности к оси (кривая 2). Магнитная индукция поля вокруг и внутри проводника изменяется таким же образом, как и напряженность.
Магнитное поле катушки с током.
Способы усиления магнитных полей.
Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют обмоткой, или катушкой.
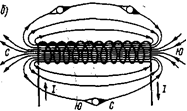
При проводнике, согнутом в виде витка (рис. 41, а), магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются (рис. 41,б) и их силовые линии соединяются в общий магнитный поток. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается. Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле.
Рис. 41. Магнитные поля, созданные витком с током (а) и катушкой (б)
Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки. Магнитное поле катушки, обтекаемой током, имеет такую же форму, как и поле прямолинейного постоянного магнита (см. рис. 35, а): силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка, обтекаемая током, представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такое устройство называется электромагнитом.
Электромагниты, нашли чрезвычайно широкое применение в технике. Они создают магнитное поле, необходимое для работы электрических машин, а также электродинамические усилия, требуемыедля работы различных электроизмерительных приборов и электрических аппаратов.
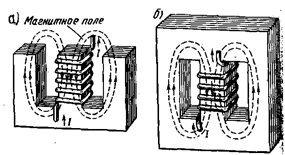
Электромагниты могут иметь разомкнутый или замкнутый магнитопровод (рис. 42).
Рис. 42. Электромагниты с разомкнутым (а) и замкнутым (б) магнитопроводом
Полярность конца катушки электромагнита можно определить, как и полярность постоянного магнита, при помощи магнитной стрелки. К северному полюсу она поворачивается южным концом. Для определения направления магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика. Если совместить направление вращения рукоятки с направлением тока в витке или катушке, то поступательное движение буравчика укажет направление магнитного поля.
Полярность электромагнита можно определить и с помощью правой руки. Для этого руку надо положить ладонью на катушку (рис. 43) и совместить четыре пальца с направлением в ней тока, при этом отогнутый большой палец покажет направление магнитного поля
Рис. 43. Определение полярности электромагнита с помощью правой руки
|
0 / 0 / 0 Регистрация: 24.11.2012 Сообщений: 111 |
|
|
1 |
|
|
19.01.2014, 16:01. Показов 2315. Ответов 7
Задача звучит так:
0 |
|
4179 / 2822 / 709 Регистрация: 16.09.2012 Сообщений: 11,484 |
|
|
19.01.2014, 17:33 |
2 |
|
Начинать всегда надо с рисунка.
0 |
|
0 / 0 / 0 Регистрация: 24.11.2012 Сообщений: 111 |
|
|
19.01.2014, 17:41 [ТС] |
3 |
|
вот рисунок и это не я ниже постом, просто еще один человек заинтересовался этой задачей, зачем мне создавать второй акк?)
0 |
|
4179 / 2822 / 709 Регистрация: 16.09.2012 Сообщений: 11,484 |
|
|
19.01.2014, 18:00 |
4 |
|
Ты,считаешь, что внёс ясность?
0 |
|
0 / 0 / 0 Регистрация: 24.11.2012 Сообщений: 111 |
|
|
19.01.2014, 18:22 [ТС] |
5 |
|
точно в задаче не написано, но будем считать что а b и с — радиусы, и пусть будут в мм, все равно нужно только общее решение пожалуйста, не надо злится
0 |
|
4179 / 2822 / 709 Регистрация: 16.09.2012 Сообщений: 11,484 |
|
|
19.01.2014, 21:02 |
6 |
|
LATEX]B={mu }_{0}*mu *H
1 |
|
0 / 0 / 0 Регистрация: 24.11.2012 Сообщений: 111 |
|
|
19.01.2014, 21:19 [ТС] |
7 |
|
просто скобочку забыли [
0 |
|
OldFedor |
|
19.01.2014, 21:33
|
|
Не по теме:
0 |