Найти комплексные корни это как - Исправление недочетов и поиск решений вместе с Examum.ru

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней z₀, z₁, z₂, … z_n_-1, которые можно вычислить с помощью формулы:

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z₀ и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.

Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:

Отмеряем транспортиром 45° и ставим на чертеже точку z₀.

Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z₁.

По этому же алгоритму ставим точку z₂.

Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.

Квадратное уравнение с комплексными корнями

Всем известно из школы квадратное уравнение:

поиск дискриминанта и решение вопроса: имеет ли квадратное уравнение корни или корень или нет. Как следует из основной теоремы алгебры, любое уравнение — ой степени имеет ровно корней с учетом кратности этих корней. Таким образом, любое квадратное уравнение с действительными или комплексными коэффициентами имеет ровно два корня. При этом кратные корни в комплексном анализе считаются ровно столько раз, какая у них кратность.

Утверждение. Пусть коэффициенты многочлена — ой степени

– действительные и его комплексный корень, тогда тоже является корнем этого многочлена.

Доказательство. Перейдем к комплексному сопряжению в равенстве : , так как . Поскольку коэффициенты многочлена действительны, то: .

Получили , следовательно, — также корень многочлена .

Если коэффициенты квадратного трехчлена действительны, а дискриминант отрицательный, то пару сопряженных корней можно найти через дискриминант.

При этом в формуле

нужно учесть что .

Решить квадратное уравнение с действительными коэффициентами: .

Решаем по «половинной» формуле: .

Если квадратный трехчлен имеет хотя бы один не действительный коэффициент, то корни не будут комплексно сопряженными.

Рассмотрим уравнение с комплексными коэффициентами:

Решаем через дискриминант. .

Таким образом, — корни нашего уравнения.

Пример 3

Решить квадратное уравнение:

Опять используем школьную формулу решения. Находим дискриминант:

Чтобы извлечь корень из дискриминанта обратимся к формуле извлечения корня ой степени из комплексного числа. Если , то корни ой степени из имеют вид:

В нашем случае .

Так что корни такие:

Теперь запишем корни исходного квадратного уравнения: .

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.

При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.

При $k=1$ получаем

[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]

При $k=2$ получаем

[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

Регистрация прошла успешно!

На email мы отправили пароль для доступа ко всем сервисам

Не пропусти промокод на скидку в ближайших письмах

источники:

http://khab.work5.ru/spravochnik/matematika/kvadratnoe-uravnenie-s-kompleksnymi-kornyami

http://spravochnick.ru/matematika/kompleksnye_chisla_i_mnogochleny/kvadratnoe_uravnenie_s_kompleksnymi_kornyami/

Источник

Извлечение корня из комплексного числа

30 ноября 2021

Третий урок по комплексным числам. В этом уроке вы узнаете:

Определение комплексного корня;
Основная формула — как извлекать корни;
Геометрическая интерпретация;
Почему корней всегда ровно n;
Краткие выводы — если лень читать урок.:)

Начнём с ключевого определения.

1. Определение комплексного корня

Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb{N}$, $n gt 1$, называется такое комплексное число $omega $, что

[{{omega }^{n}}=z]

т.е. $n$-я степень числа $omega $ равна $z$.

Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:

[omega =sqrt[n]{z}]

Пример. Вычислить $sqrt[3]{-1}$ на множестве комплексных чисел.

Очевидно, привычная нам единица является таким корнем, потому что ${{left( -1 right)}^{3}}=-1$. Но есть ещё два корня:

[begin{align} {{left( frac{1}{2}+icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos frac{pi }{3}+icdot sin frac{pi }{3} right) right)}^{3}}= \ & =1cdot left( cos pi +isin pi right)=-1 \ {{left( frac{1}{2}-icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos left( -frac{pi }{3} right)+icdot sin left( -frac{pi }{3} right) right) right)}^{3}}= \ & =1cdot left( cos left( -pi right)+isin left( -pi right) right)=-1 end{align}]

Итого три корня. Как и предполагалось.

Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$

Все эти корни считаются по следующей формуле.

2. Формула корней

Теорема. Пусть комплексное число записано в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Тогда все корни степени $n$ из этого числа можно найти по формуле:

[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0,1,2,…,n-1 right} \ end{align}]

По сути, эта теорема является обратной к формуле Муавра:

[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos nvarphi +isin n varphi right)]

Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:

Перевести комплексное число в тригонометрическую форму;
Записать общую формулу корня степени $n$;
Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
Получим $n$ комплексных корней. Вместе они и будут ответом.

В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.

Пример. Вычислить $sqrt[3]{-8i}$.

Представим число $-8i$ в тригонометрической форме:

[begin{align} -8i &=0+left( -8 right)cdot i= \ & =8cdot left( 0+left( -1 right)cdot i right)= \ & =8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right) end{align}]

Запишем формулу корней в общем виде:

[begin{align} sqrt[3]{-8i} & =sqrt[3]{8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right)}= \ & =sqrt[3]{8}cdot left( cos frac{-frac{pi }{2}+2pi k}{3}+isin frac{-frac{pi }{2}+2pi k}{3} right)= \ & =2cdot left( cos left( -frac{pi }{6}+frac{2pi k}{3} right)+isin left( -frac{pi }{6}+frac{2pi k}{3} right) right) \ end{align}]

Подставим $k=0$:

[sqrt[3]{-8i}=2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right)=sqrt{3}-i]

Подставим $k=1$:

[sqrt[3]{-8i}=2cdot left( cos frac{pi }{2}+isin frac{pi }{2} right)=2i]

И, наконец, $k=2$:

[sqrt[3]{-8i}=2cdot left( cos frac{7pi }{6}+isin frac{7pi }{6} right)=-sqrt{3}-i]

В ответе нужно указать все три числа: $2i$; $sqrt{3}-i$; $-sqrt{3}-i$.

Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left{ 0,1,…,n-1 right}$, то корни начнут повторяться, и ничего нового мы не получим.

3. Геометрическая интерпретация

Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n]{left| z right|}$. Более того: эти точки образуют правильный $n$-угольник.

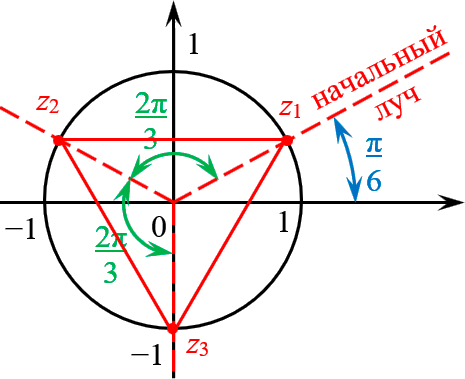
Отметить на комплексной плоскости все числа вида $sqrt[3]{i}$.

Представим число $z=i$ в тригонометрической форме:

[begin{align} z & =1cdot left( 0+icdot 1 right)= \ & =1cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) end{align}]

Формула комплексных корней:

[sqrt[3]{z}=1cdot left( cos left( frac{pi }{6}+frac{2pi k}{3} right)+isin left( frac{pi }{6}+frac{2pi k}{3} right) right)]

Это три точки ${{z}_{1}}$, ${{z}_{2}}$ и ${{z}_{3}}$ на окружности радиуса $R=1$:

Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол ${pi }/{6};$.

Рассмотрим более сложный пример:

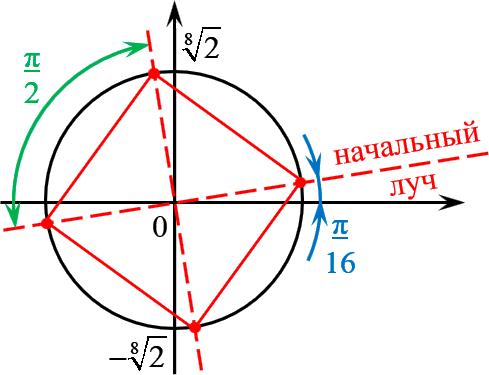
Отметить на комплексной плоскости все числа вида $sqrt[4]{1+i}$.

Сразу запишем формулу корней с выделением начального луча:

[sqrt[4]{z}=sqrt[8]{2}cdot left( cos left( frac{pi }{16}+frac{pi k}{2} right)+isin left( frac{pi }{16}+frac{pi k}{2} right) right)]

Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8]{2}$, начальный луч ${pi }/{16};$:

И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча ${pi }/{16};$.

Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:

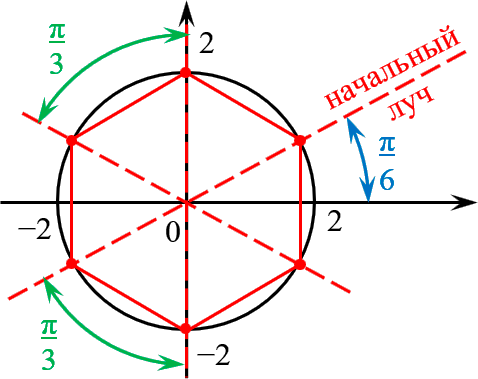
Отметить на комплексной плоскости все числа вида $sqrt[6]{-64}$.

Формула корней с выделением начального луча:

[sqrt[6]{z}=2cdot left( cos left( frac{pi }{6}+frac{pi k}{3} right)+isin left( frac{pi }{6}+frac{pi k}{3} right) right)]

Получили правильный шестиугольник со стороной 2 и начальным лучом ${pi }/{6};$.

Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:

Перевести число в тригонометрическую форму;
Найти модуль корня: $sqrt[n]{left| z right|}$ — это будет радиусом окружности;
Построить начальный луч с отклонением $varphi ={arg left( z right)}/{n};$;
Построить все остальные лучи с шагом ${2pi }/{n};$;
Получим точки пересечения лучей с окружностью — это и есть искомые корни.

Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде ${pi }/{6};$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)

4. Почему корней всегда ровно n

С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.

Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:

[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]

Последовательно подставим в эту формулу указанные значения параметра $k$:

[begin{align} {{omega }_{0}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right) \ {{omega }_{1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi }{n}+isin frac{varphi +2pi }{n} right) \ & … \ {{omega }_{n-1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi cdot left( n-1 right)}{n}+isin frac{varphi +2pi cdot left( n-1 right)}{n} right) \ end{align}]

Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:

[begin{align} {{omega }_{n}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi n}{n}+isin frac{varphi +2pi n}{n} right)= \ & =sqrt[n]{left| z right|}cdot left( cos left( frac{varphi }{n}+2pi right)+isin left( frac{varphi }{n}+2pi right) right)= \ & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right)={{omega }_{0}} \ end{align}]

Поскольку синус и косинус — периодические функции с периодом $2pi $, ${{omega }_{n}}={{omega }_{0}}$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.

5. Выводы

Ключевые факты из урока.

Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что ${{omega }^{n}}=z$.

Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n]{z}$.

Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.

Алгоритм нахождения корней состоит из двух шагов.

Шаг 1. Представить исходное число в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Шаг 2. Воспользоваться формулой Муавра для вычисления корней:

[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]

Все полученные корни лежат на окружности радиуса $sqrt[n]{left| z right|}$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол ${varphi }/{n};$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.

Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».

Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)

Смотрите также:

Тригонометрическая форма комплексного числа
Системы линейных уравнений: основные понятия
Радианная мера угла
Как представить обычную дробь в виде десятичной
Задача B2 на проценты: железнодорожные билеты
Логарифмические уравнения в задаче C1

Источник

Математическая продлёнка. Квадратные уравнения во всей красе

Время на прочтение
9 мин

Количество просмотров 12K

Продолжаю потихоньку публиковать свои наработки к занятиям математического кружка. На этот раз речь пойдёт о до боли знакомых квадратных уравнениях и их свойствах, о которых нет времени поговорить в школе.

Геометрия квадратных уравнений

В восьмом классе мы встречаемся с квадратными уравнениями, выводим или заучиваем формулу для их решения, запоминаем страшное слово «дискримитант», в общем, становимся суровыми математиками! Либо окончательно понимаем, что «математика не моё» и наивно называем себя «гуманитариями».

Положа руку на сердце, признаю, что умение решать квадратные уравнения пригодится не всем нам во взрослой жизни. Чаще всего, мы оставляем это знание на полке со школьными тетрадками и учебниками.

Но вот какое важное универсальное знание даёт знакомство с ними: уравнение может не иметь решений, либо одно из решений может не иметь смысла, как, например, отрицательное время в какой-нибудь физической задаче.

Это важный жизненный опыт, который помогает осознавать и познавать границы возможного, применимого, разрешимого.

Квадратные уравнения могут научить ещё кое-чему, а именно, видеть алгебру, отыскивать геометрический смысл алгебраических результатов.

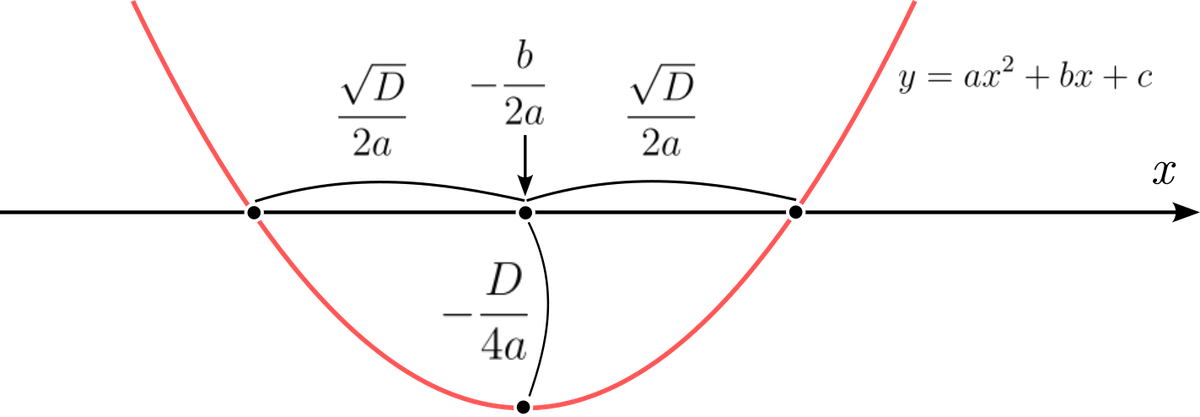
Давайте вспомним, как выглядит общий вид решения квадратного уравнения:

$begin{eqnarray}&ax^2+bx+c=0\ &x_{1,2} = frac{-bpmsqrt{b^2-4ac}}{2a} = A pm Bend{eqnarray}$

Что означает эта формула? Что два решения расположены по разные стороны некоторого числа и отстоят от него на расстоянии . Какой же смысл у этих чисел?

Мы знаем, что график квадратного уравнения — это парабола. Кривая, которая имеет осевую симметрию относительно своего минимума. Эта симметрия присутствует и в решении. Число — это положение оси симметрии, то есть, минимума, а — половина ширины отрезка, который парабола отсекает на оси. Если отсекает, конечно.

Давайте подставим в уравнение положение минимума:

$y = aleft(frac{-b}{2a}right)^2+bleft(frac{-b}{2a}right)+c = frac{4ac-b^2}{4a}$

Смотрите-ка, в числителе сам собой образовался дискриминант! Теперь нам легко понять его смысл — вертикальное положение минимума параболы.

Геометрический смысл частей решения квадратного уравнения с дискриминантом D.

Пусть, для определённости, коэффициент будет положительным, а значит, ветви параболы будут идти наверх. Если дискриминант отрицателен, то парабола расположена над осью и не пересекает её. В этом случае решений не будет. Если дискриминант положителен, минимум находится под осью и парабола неизбежно пересечёт эту ось в двух точках.

Наконец, давайте посмотрим, как в само квадратное уравнение входят числа и из которых состоят его решения. Это легко увидеть с помощью теоремы Виета:

$begin{eqnarray}&a&x^2+bx+c=a(x-A-B)(x-A+B)=a(x^2+2Ax+A^2-B^2)\ &downarrow&\ &b&=2aA,quad c = a(A^2-B^2)end{eqnarray}$

На такой разбор может не хватить времени на школьном уроке, но он полезен для того, чтобы уравнения и их решения стали несколько более говорящими.

Пространство квадратных уравнений

Задачки в учебниках придумывают люди. И они хотят, чтобы задачи в них не просто решались, а ещё и красиво решались. Чтобы чудесным образом извлекались квадратные корни, чтобы дроби сокращались как надо.

Предположим, вам для проведения экзамена нужно сочинить десятка три задачек на решение квадратных уравнений. Вы выписываете наугад тридцать уравнений с целыми коэффициентами. Какую долю из них составят те что, не имеют вещественных решений? А сколько из них будут иметь целочисленные корни? Понятно, что во всех этих вопросах речь идет об ожидаемых величинах и долях.

Доля нерешаемых уравнений

Мы знаем, что квадратное уравнение решается, если его дискриминант оказывается неотрицательным. А какая доля пространства троек будет удовлетворять этому условию?

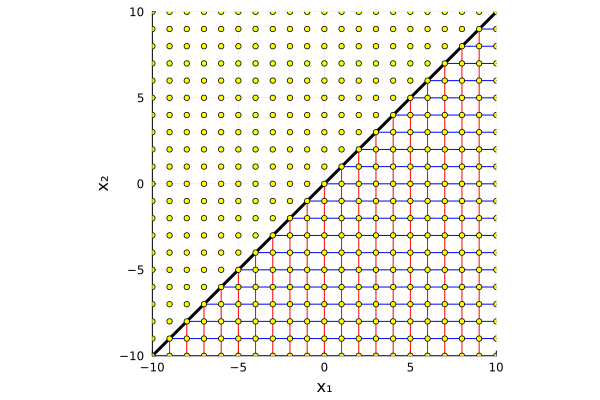
На этот вопрос проще ответить не в целых числах, а в действительных, сформулировав вопрос геометрически: какой фигурой в пространстве ограничивается объём нерешаемых уравнений?

Мы знаем уравнение границы этой фигуры: . Давайте преобразуем координаты так, чтобы стало очевидным, с чем мы имеем дело. Для этого сделаем преобразование координат:

$(a, c) to left(frac{1}{2}(x-y), frac{1}{2}(x+y)right)$

и получим:

Мы видим уравнение окружностей в координатах с радиусами . Значит, все нерешаемые уравнения попадают внутрь некоторого кругового конуса. Обратное преобразование к координатам превратит этот круговой конус в эллиптический и повернёт его, как показано на рисунке:

Часть конуса, ограничивающего область уравнений, не имеющих вещественных корней.

Нам повезло! Конус, даже эллиптический, на всех масштабах выглядит одинаково, а это значит, что можно вычислить долю его объёма в объёме всего пространства параметров. Не буду здесь вдаваться в подробности расчёта, приведу конечный результат: доля нерешаемых уравнений составляет .

Получается, что если наугад выбрать три числа и составить с их помощью квадратное уравнение, то вероятность того, что оно будет иметь вещественные решения составит чуть менее двух третей. Конечно, эта вероятность будет зависеть от конкретного способа выбора коэффициентов, но в случае их равномерного распределения результат можно ожидать таким.

Конечно, если стоит задача составить список заведомо решаемых уравнений, то наугад их сочинять не придётся. Достаточно сгенерировать нужное количество пар решений и с помощью теоремы Виета сформировать соответствующие им уравнения:

Целочисленные решения

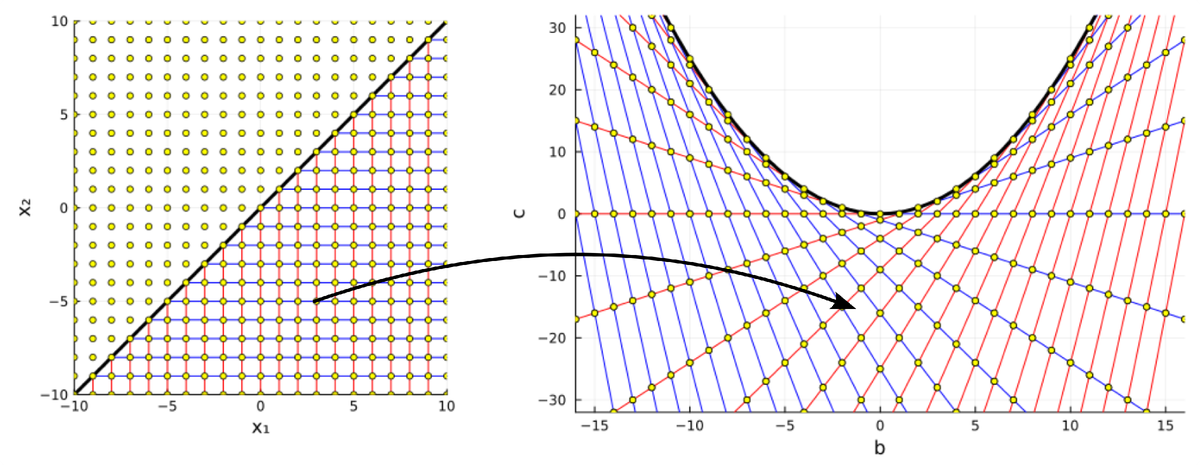
И теперь можно перейти ко второму вопросу: как выглядит в пространстве целочисленных коэффициентов квадратных уравнений подмножество «хороших» уравнений? Хорошими будем считать квадратные уравнения с целочисленными коэффициентами, у которых и дискриминант является полным квадратом, и дроби сокращаются так, что решения тоже получаются целочисленными.

Для наглядности, эту задачу будем решать для приведённых квадратных уравнений, то есть, таких, у которых .

В поиске ответа нам опять поможет теорема Виета. Она определяет преобразование координат, отображающее пространство решений в пространство коэффициентов:

Назовём это преобразование именем Виета. Все пары целочисленных решений образуют равномерную решётку в пространстве всех действительных решений.

На этой решётке выделяется линия , которая соответствует нулевому дискриминанту и кратным корням. Эта линия является осью симметрии всего пространства решений. Действительно, одному уравнению соответствует две пары решений и , которые расположены симметрично относительно линии кратных корней. Так что достаточно рассмотреть как отображается в пространство коэффициентов только подпространство уникальных решений, например, нижняя полуплоскость.

Горизонтальные и вертикальные прямые линии, соответствующие уравнениям и (красные и синие линии на диаграммах) преобразование Виета снова превращает в прямые:

Отображение решётки целочисленных решений в пространстве коэффициентов. Каждая точка здесь — пара коэффициентов (b, c).

Какая красивая картинка! Линия кратных решений окаймляет «мёртвую область», в которой оказываются коэффициенты уравнений, не имеющих вещественных решений. К ней по касательной подходят линии, вдоль которых располагаются пары решений с одинаковым первым или одинаковым вторым элементом.

Линии, касательные параболе образуют прямолинейную, но непрямоугольную сетку. У неё есть интересное свойство: расстояния между всеми точками пересечений любой отдельно взятой касательной со всеми другими всегда одинаково. Нам оно потребуется, но мы позволим себе принять это эмпирическое наблюдение за факт без доказательства.

В отличие от доли нерешаемых уравнений, доля тех, что имеют целочисленные решения, будет сильно зависеть от диапазона, в котором выбираются коэффициенты. По мере его увеличения, число вариантов будет расти квадратично, как площадь в пространстве коэффициентов. В то же время, коэффициенты, дающие целочисленные решения будут располагаться на касательных к линии кратных корней, и их число будет расти линейно с увеличением диапазона, из-за того, что на касательных они располагаются на равном удалении друг от друга. Так что можно ожидать, что доля целочисленных решений будет падать пропорционально , если и . Численный эксперимент показывает, что на очень больших сказывается отличие от обратной пропорциональности, но это уже такие тонкости, в которых возиться большого смысла нет.

Это значит, что уравнения с небольшими по модулю целыми коэффициентами с большей вероятностью будут иметь целочисленные корни, чем уравнения с большими коэффициентами.

И последнее замечание. В плоскости область нерешаемых уравнений ограничена параболой, тогда как в пространстве эта область представляет собой конус. В этом нет противоречия, плоскость сечёт конус параллельно образующей конуса, а такое коническое сечение является параболой.

Истинный облик квадратных уравнений

А куда деваются корни квадратного уравнения, когда оно не имеет действительных решений и откуда берутся комплексные корни? Как выглядят квадратные уравнения «на самом деле»? Сегодня мы увидим скрытый от вещественного мира облик привычных со школы квадратных уравнений.

Грамотные маткружковцы знают про существование комплексных корней квадратного уравнения, и даже знают, как правильно ставить ударение в слове «комплéксный». А как и откуда эти комплексные корни появляются по мере исчезновении вещественных? Где они располагаются и какой имеют геометрический смысл, применительно к параболе ?

Для того, чтобы порассуждать об этом, надо выйти за пределы вещественной числовой оси и увидеть уравнение таким, каким оно предстаёт в своём мире: в чудесном поле комплексных чисел, в которых любые алгебраические уравнения имеют решения.

Подставим в уравнение вместо переменной x комплексное число в форме :

Теперь раскроем все скобки и приведём подобные слагаемые относительно , не забывая, что

Равенство будет верным, если одновременно и вещественная и мнимая части левой половины равенства обратятся в ноль. Таким образом, мы свели одно уравнение в комплексных числах к системе вещественных уравнений на и :

$left{begin{align}&a(u^2-v^2)+bu+c=0\&(2au+b)v=0end{align}right.$

Второе уравнение при этом распадается на два: либо , либо .

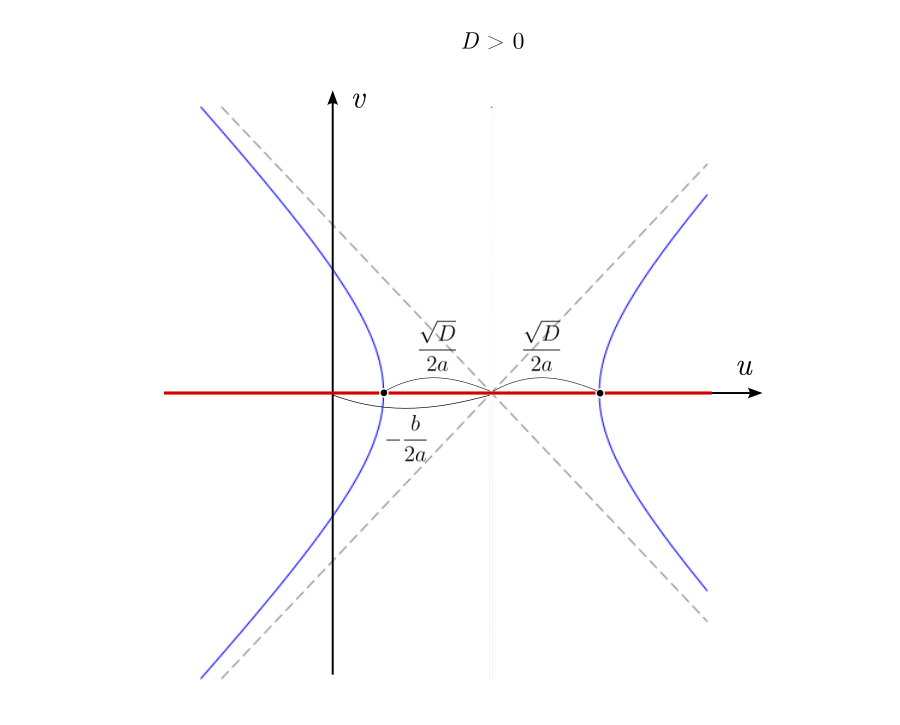
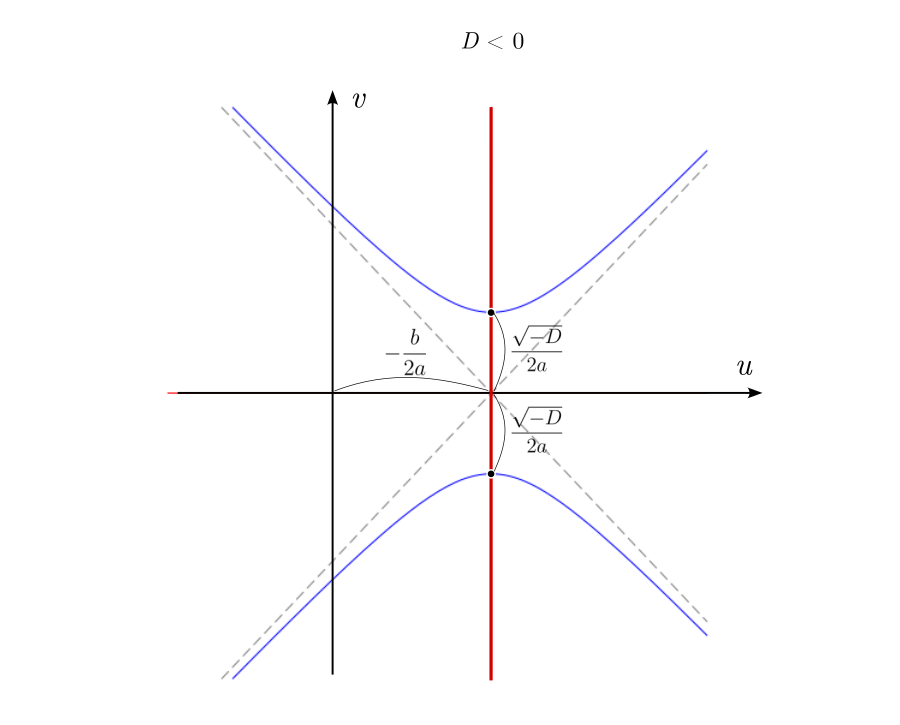
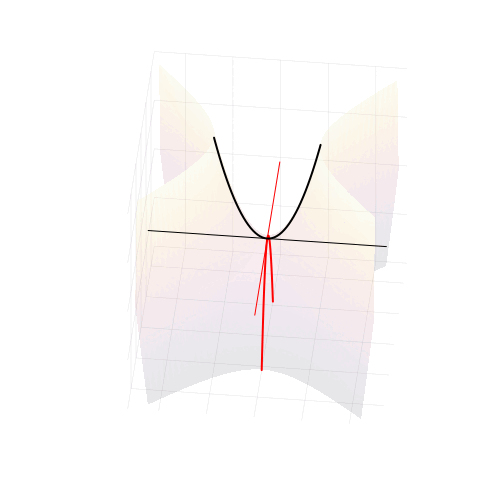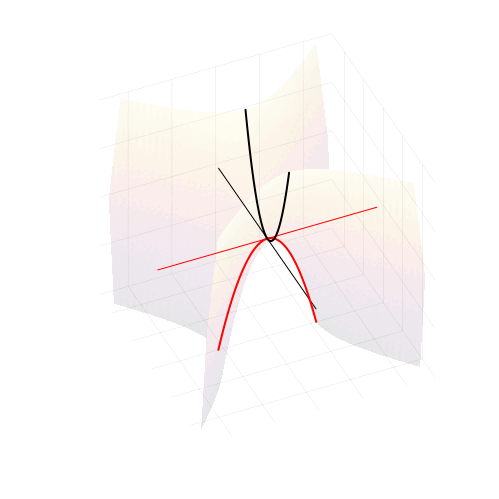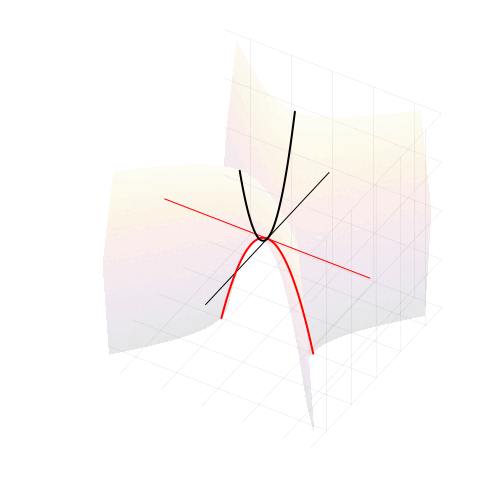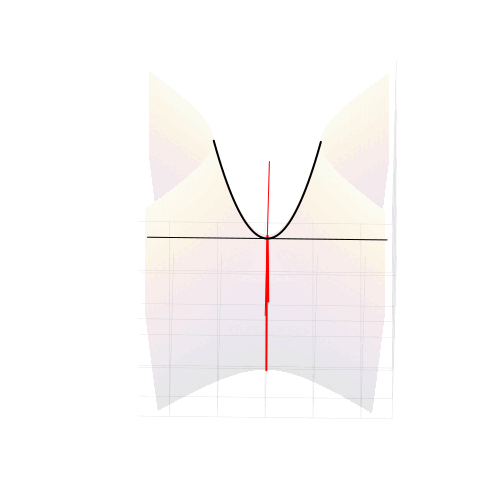
Можно изобразить геометрические места точек, удовлетворяющих всем трём уравнениям в плоскости и увидеть, что происходит с корнями. Первое уравнение описывает гиперболы с асимптотами, пересекающимися в точке и симметрично расходящимися под наклоном . Ветви гиперболы могут проходить двумя разными способами, в зависимости от знака дискриминанта, либо пересекая ось абсцисс, либо нет. А второе и третье уравнения — это прямые линии, горизонтальная и вертикальная, соответственно.

Вещественные корни

При положительном дискриминанте гиперболы пересекают вещественную ось, и точки пересечения соответствуют двум вещественным числам. Симметрия гипербол в точности согласуется с симметрией параболы, о которой мы говорили в самом начале.

Комплексные корни

Когда дискриминант отрицателен, ветви гиперболы проходят выше и ниже вещественной оси и пересекают вертикальную линию в двух точках. Это и есть два комплексных корня с вещественной частью равной , и мнимой частью, отличающейся от нуля на величину

Нулевому дискриминанту соответствует вырожденная гипербола, совпадающая с асимптотами. Корень при этом кратный, и равен

Кратные корни

Но откуда же взялись гиперболы? Квадратное уравнение — это же про параболы?

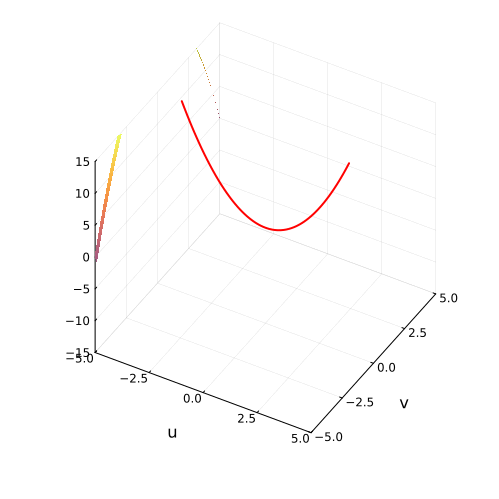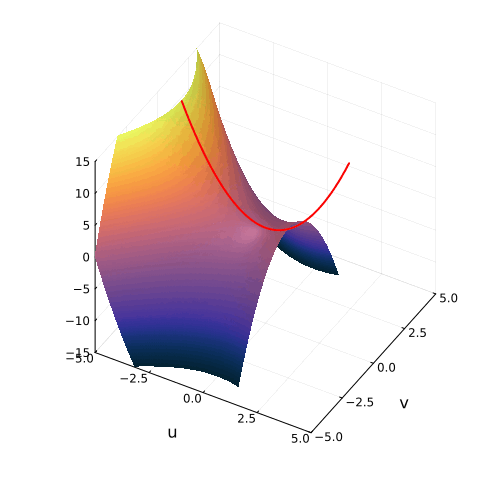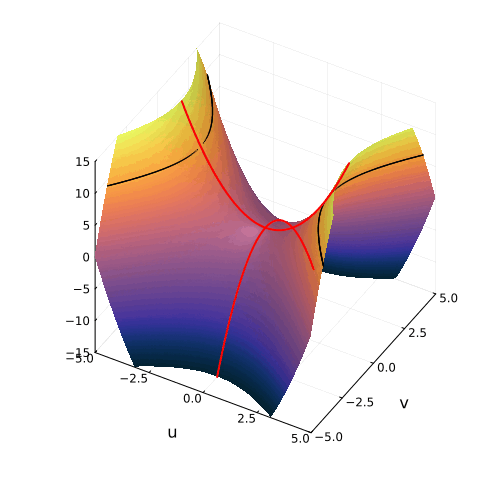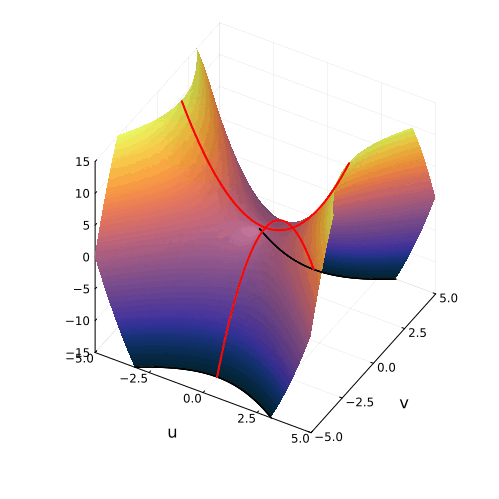
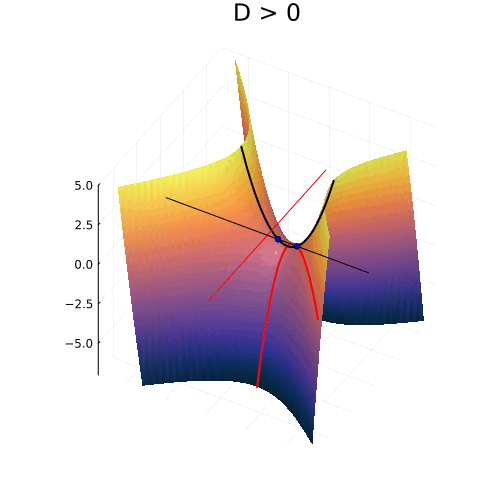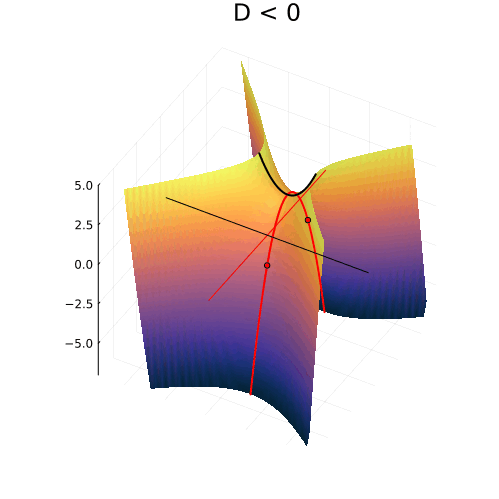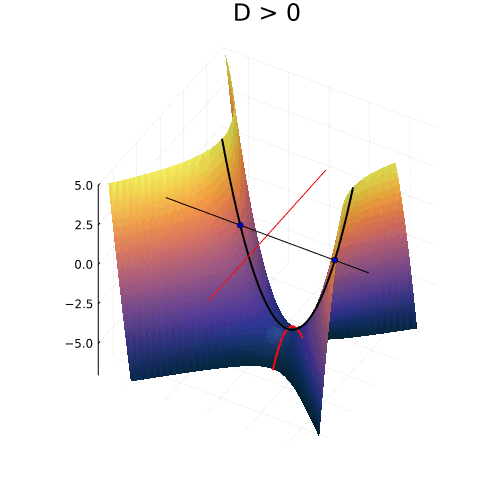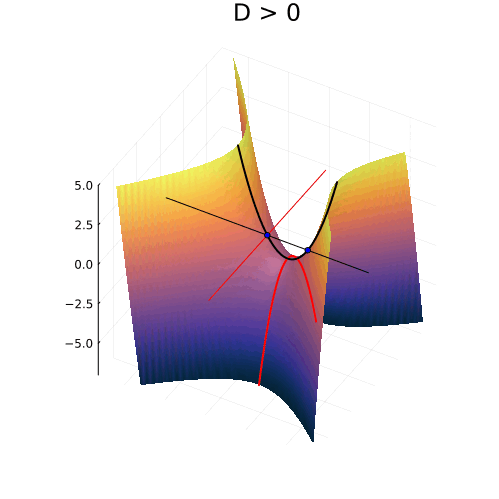
Истинное лицо квадратного уравнения

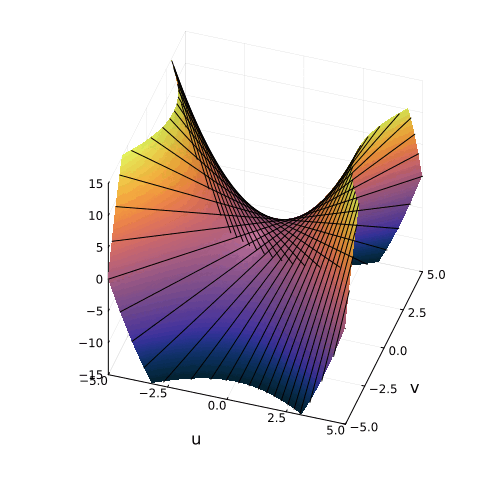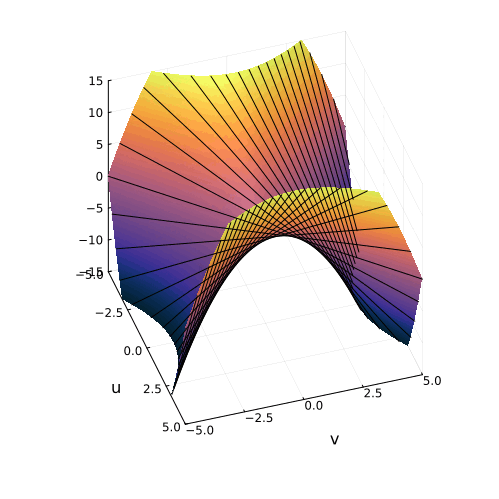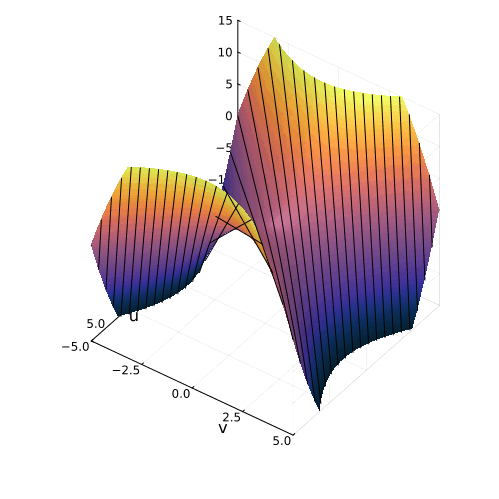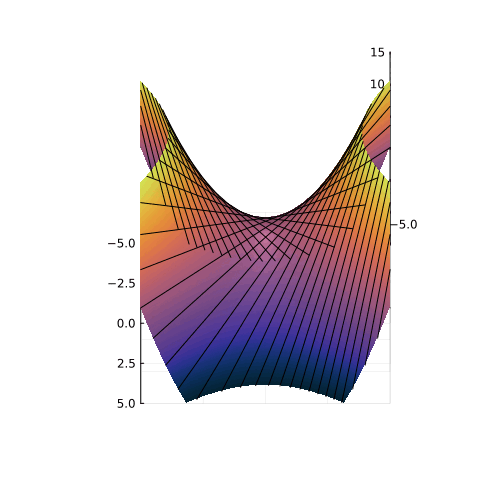
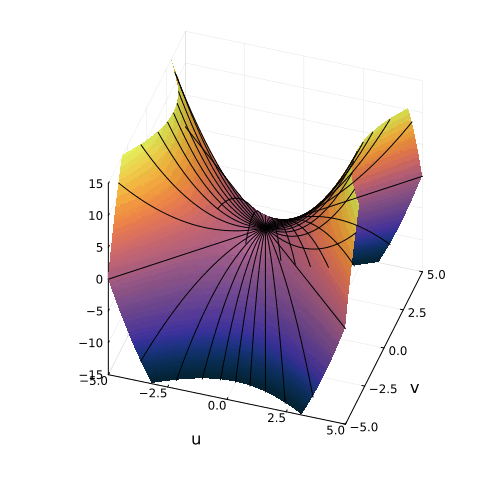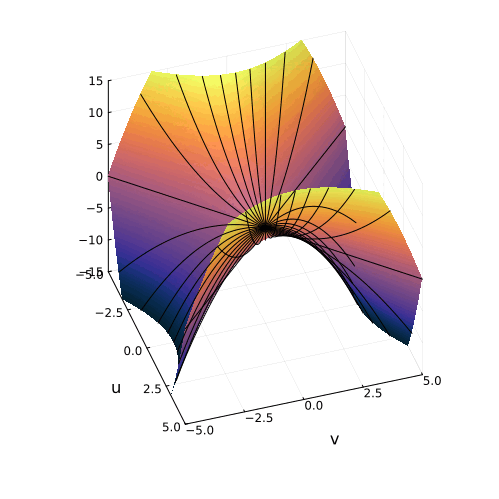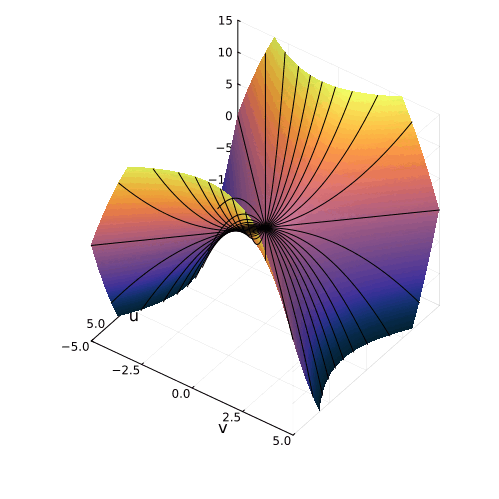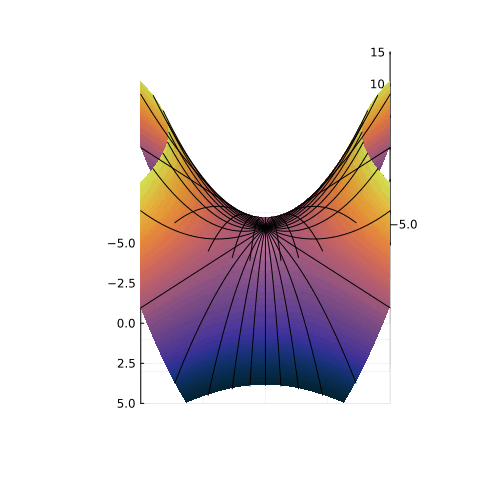
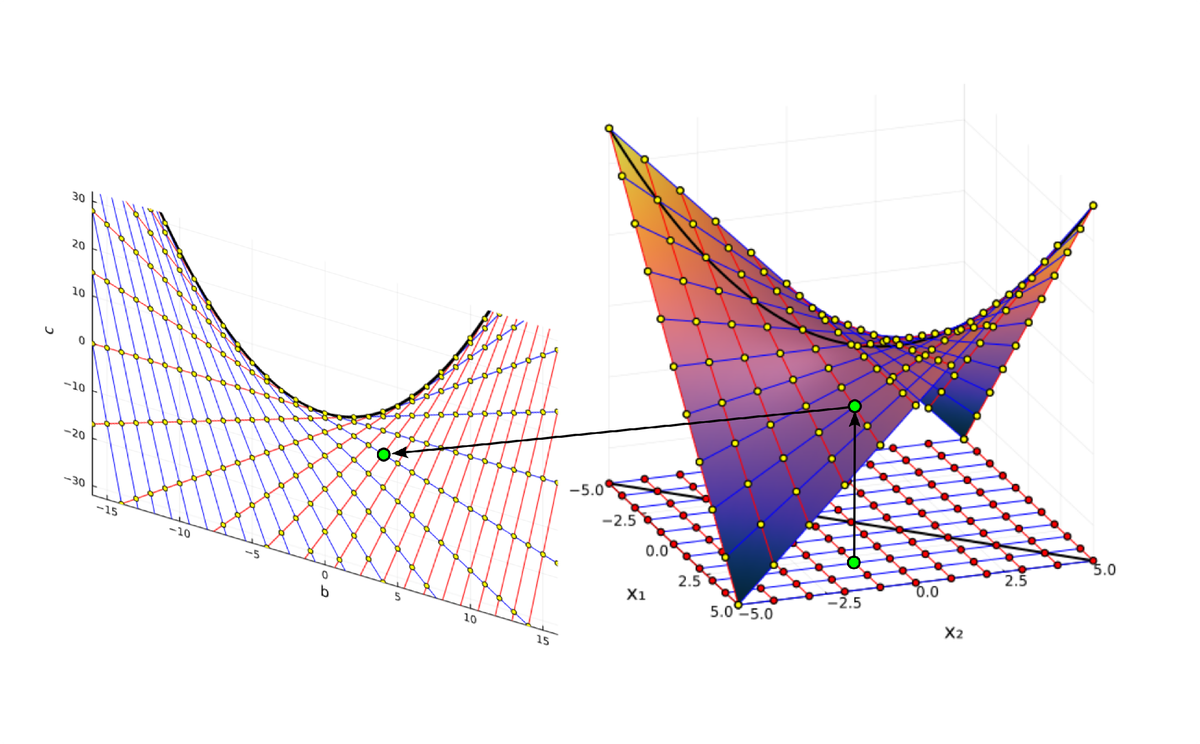
На самом деле, вещественная часть уравнения в комплексных числах описывает гиперболический параболоид. Вот как он выглядит:

Построение гиперболического параболоида, как поверхности, образованной движением параболы, или семейством гипербол.

Гиперболический параболоид может быть образован движением прямой.

Все вертикальные сечения гиперболического параболоида являются параболами.

Эта поверхность замечательна во многих отношениях. Её можно построить с помощью движения прямой или параболы, либо представить, как поверхность, порождённую многообразием парабол, проходящих через одну точку, которая называется седловой, или многообразием гипербол, лежащих в параллельных плоскостях. Наконец, именно такую форму имеют картофельные чипсы известной марки. Прекрасный иллюстрированный рассказ об этом можно найти здесь.

Линии пересечения параболоида с плоскостью это и есть знакомые нам гиперболы — горизонтальные сечения гиперболического параболоида. Теперь на корни квадратного уравнения мы можем взглянуть, увидев их во всей полноте. Плоскости и , пересекая параболический гиперболоид в вертикально, образуют две параболы, касающиеся друг друга в седловой точке и расположенные во взаимно перпендикулярных плоскостях. Эти две параболы представляют собой многообразия всех корней квадратного уравнения.

Многообразия вещественных (черные) и комплексных (красные) корней квадратного уравнения в пространстве (u, v, Re(ax² + bx + c))

Положение седловой точки гиперболического параболоида это знакомое нам число Посмотрите, что происходит с поверхностью, при изменении знака дискриминанта. Если мы станем изменять коэффициенты квадратного уравнения, то параболоид станет перемещаться в пространстве пересечение многообразий корней уравнения с плоскостью рождает пару чисел, либо вещественных, либо комплексных

Положение корней уравнения ax²+bx+c = 0 при меняющемся значении коэффициента с в комплексной плоскости, показанной чёрной (вещественной) и красной (мнимой) осями.

Теперь мы с уверенностью можем сказать, что видим, куда деваются вещественные корни уравнения и откуда берутся комплексные!

Параболоид в пространстве квадратных уравнений

Очертания гиперболического параболоида можно разглядеть и в сетке, образованной линиями равных решений в пространстве коэффициентов квадратных уравнений, которую мы построили в предыдущей части. И это, конечно же, не случайно. Мы рассмотрели преобразование Виета, которое строит найти отображение из пространства решений в пространство коэффициентов:

Где же здесь прячется параболоид? Уравнение гиперболического параболоида имеет два канонических вида:

которые переходят друг в друга при линейном преобразовании координат Это преобразование поворачивает и двое уменьшает все фигуры, не меняя их формы. Отсюда следует, что в сердце преобразования между вещественными корнями уравнения и коэффициентами тоже лежит гиперболический параболоид. Вот как выглядит это преобразование геометрически:

Преобразование Виета, как композиция проекций из плоскости корней на параболоид, и из параболоида на плоскость коэффициентов. При этом области, лежащие выше и ниже линии кратных корней отображаются в одну и ту же область коэффициентов, лежащую ниже линии кратных корней.

Здесь чёрная линия соответствует кратным корням, а на параболоид проецируется решётка целочисленный корней.

Вертикальная ось на этом графике соответствует свободному коэффициенту в уравнении. Коэффициент при линейном члене , это сумма корней, так что плоскость представляет собой вертикальную плоскость, параллельную линии кратных корней. Проекцию параболоида на эту плоскость мы и видим, как преобразование Виета.

Параболоид в преобразовании Виета и параболоид, образуемый вещественной частью квадратного уравнения в комплексных числах, это разные фигуры, не связанные друг с другом. Но квадратные уравнения настолько пронизаны параболами, что не удивительно встретить параболоиды в разных частях их теории.

Можно бы завершить рассказ сакраментальной фразой: «Теперь мы знаем о квадратных уравнениях всё». Но, конечно же, главное, это разобраться а зачем нам вообще знать что-то про квадратные уравнения?

Приглашаю вас в свой Дзен-канал Онлайн-кружок математики, в котором различные занимательно-математические материалы появляются в облегчённом варианте, но зато регулярно.

Источник

Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты
$a$,
$b$ и
$c$ — в общем случае являются комплексными.
Его решение находим с помощью дискриминанта

$$D=b^{2}-4 a c$$

тогда

$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}$$

В общем случае и дискриминант, и корни уравнения являются
комплексными числами.

Пример

Задание. Составить квадратное уравнение, которое имеет корни
$z_{1}=1-i$ и
$z_{2}=4-5i$. Решить его.

Решение. Известно, что если
$z_1$, $z_2$ — корни квадратного уравнения
$z^2+bz+c=0$, то указанное уравнение можно записать в виде
$(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что
искомое уравнение можно записать следующим образом:

$$(z-(1-i))(z-(4-5 i))=0$$

Раскрываем скобки и выполняем операции над комплексными числами:

$$z^{2}-(4-5 i) z-(1-i) z+(1-i)(4-5 i)=0$$
$$z^{2}+z(-4+5 i-1+i)+4-5 i-4 i+5 i^{2}=0$$

$z^{2}+(-5+6 i) z-(1+9 i)=0$ — искомое квадратное уравнение.

Решим полученное уравнение. Найдем дискриминант:

$$D=(-5+6 i)^{2}-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$
$$=-7-24 i$$

Так как при извлечении корня из комплексного числа в
результате получится комплексное число, то корень из
дискриминанта будем искать в виде $sqrt{D}=a+b i$. То есть

$$sqrt{-7-24 i}=a+b i Rightarrow-7-24 i=(a+b i)^{2} Rightarrow$$
$$Rightarrow-7-24 i=a^{2}+2 a b i-b^{2}$$

Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно,
получим систему для нахождения неизвестных значений $a$ и
$b$:

$$left{begin{array}{l}a^{2}-b^{2}=-7 \ 2 a b=-24end{array}right.$$

решив которую, имеем, что $a_1=3$,
$b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из
полученных пар, например, первую, получаем, что
$sqrt{D}=3-4 i$, а тогда

$$z_{1}=frac{-(-5+6 i)+(3-4 i)}{2 cdot 1}=4-5 i$$
$$z_{2}=frac{-(-5+6 i)-(3-4 i)}{2 cdot 1}=1-i$$

Ответ. $z^{2}+(-5+6 i) z-(1+9 i)=0$

Читать дальше: элементарные функции комплексного аргумента.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Алгебра и начала математического анализа, 11 класс

Урок №41. Извлечение корня из комплексного числа.

Перечень вопросов, рассматриваемых в теме

1) понятие корня из комплексного числа;

2) алгоритмы извлечения корня из комплексного числа;

3) пример извлечения корня из комплексного числа в тригонометрической форме.

Глоссарий по теме

Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через .

Теорема. Уравнение zⁿ=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.

Все n корней z_k лежат на оркужности радиусом с центом в начале кооринат; они делят окружность на n дуг величиной каждая и являются вершинами вписанного в нее правильного n-угольника.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Теорема. Уравнение zⁿ=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.

Доказательство. Пусть ω=|ω|∙(cosφ+isinφ), число z будем искать в виде

z=|z|∙(cosα+isinα).

Преобразуем уравнение zⁿ=ω, используя формулу Муавра:

|z|n(cosnζ+isinnζ)=|ω|∙(cosθ+isinθ).

Отсюда вытекают равенства:

|z|ⁿ=|ω|, nζ= θ+2πk, k- целое,

Из которых для модуля искомого корня получается определенное значение , тогда как его аргумент , k- целое, может принимать различные значения при разных k. При этом значениям k= 0, 1, 2, …, n-1 соответствуют различные значения корня, а при k= n значение корня совпадает с его значением при k=0. При k=n+1 получим значение корня, что и при k=1, и т.д.

Таким образом, число различных значений корня равно n- это

, где k=0, 1, 2,…, n-1 что и требовалось доказать.

Пример 1. Найдите все корни n-ой степени из действительного числа x>0.

Решение. Если х- положительное действительное число, то |x|=x, θ=arg x=0. Формула корней в этом случае дает ответ:

, где k=0, 1, 2,…, n-1.

При k=0 получим – это арифметический корень. При четном n=2m имеется еще один дейсвтиельный корень., получающийся при k=m. (ζ= arg z_m=π):

Корни n-ой степени из 1 часто обозначают через ε_k,k= 0, 1, 2, …, n-1. Согласно предыдущему примеру:

Пример 2. Вычислите корни третьей степени из комплексного числа 2+2i.

Решение: Найдем тригонометрическую форму данного числа:

По формуле корней из комплексного числа имеем:

, где k пробегает значения 0, 1, 2. Запишем полученные корни:

Используя формулы для косинуса и синуса разности углов, получаем:

Ответ: ; -1+i; .

Немного иначе извлекаются корни из комплексных чисел, аргумент которых не приводится к виду , где m, n – целые числа.

Пример 3. Найдите

Решение. Пусть ω=3+4i. Положим φ=arg ω.

, тогда ω=5(cosφ+isinφ), где , .

Следовательно, , где k=0, 1.

Запишем подробнее:

Найдем и , используя формулу двойного угла:

, откуда , ; тогда , Угол φ лежит в первой четверти, а следовательно, и угол тоже, поэтому Тогда

Ответ:

Пример 4. Выполнить операцию извлечения корня z³ для заданных комплексных чисел в алгебраической форме представления: .

Решение: Тригонометрическая форма записи некоторого комплексного числа имеет вид z=r(cosφ+i⋅sinφ). По условию . Вычислим модуль исходного комплексного числа: