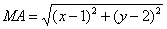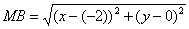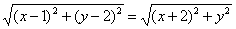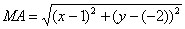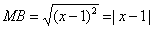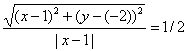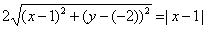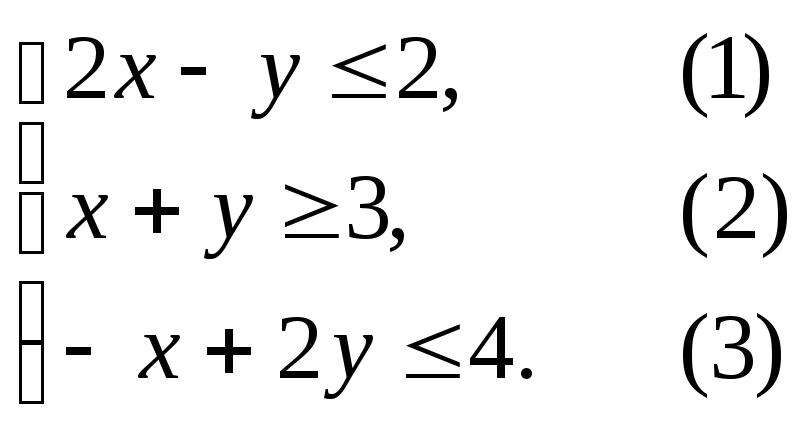Построение множеств точек на плоскости
Пример 15. Построим множество точек (x,y)(x, y), удовлетворяющих уравнению x2+xy=0x^2 + xy = 0.
Преобразуем уравнение: x(x+y)=0x(x + y) = 0. Таким образом, заданное уравнение равносильно совокупности двух уравнений x=0x = 0 или x+y=0x + y = 0 (y=−x)(y = − x). Поэтому искомым множеством точек будет объединение этих двух прямых.
Построим множество точек (x,y)(x, y) таких, что
x2+4x+4+4y2=0x^2 + 4x + 4 + 4y^2 = 0.
Преобразуем уравнение с помощью выделения полного квадрата: (x+2)2+4y2=0(x + 2)2 + 4y^2 = 0. Поскольку точные квадраты неотрицательны, то такому уравнению может удовлетворять лишь одна точка (–2,0)(–2, 0).
Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.
Построим множество точек (x,y)(x, y) таких, что |x−y−1|+x2+2xy+y2=0|x − y − 1| + x^2 + 2xy + y^2 = 0. Преобразуем уравнение: |x−y−1|=−(x+y)2|x − y − 1| = −(x + y)^2. Так как модуль равен неотрицательному числу, то
x−y−1=0,−(x+y)2=0; x−y=1,x+y=0,left{begin{array}{l}x-y-1=0,\-{(x+y)^2}=0;end{array}right.;;left{begin{array}{l}x-y=1,\x+y=0,end{array}right.
т. е. уравнению снова будет удовлетворять единственная точка (0,5;–0,5)(0,5; – 0,5) (см. рис. 39).
Множеством точек может быть область на плоскости. Рассмотрим пример.
Построим множество точек (x,y)(x, y) таких, что
(x−3)(y+2)=3−x−y−2sqrt{(x − 3)(y + 2)} = sqrt{3 − x} sqrt{−y − 2}.
Равенство (x−3)(y+2)=3−x−y−2sqrt{(x − 3)(y + 2)} = sqrt{3 − x} sqrt{−y − 2} будет верно для всяких xx и yy, удовлетворяющих ОДЗ. Поэтому искомым множество точек будет ОДЗ, т. е. часть плоскости, ограниченная двумя прямыми y=−2y = −2 и x=3x = 3 (рис. 40).
Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.
Построим множество точек, удовлетворяющих |y|=|x||y| = |x|.
По определению модуля получаем: y=±xy = ±x. Поэтому множество точек – объединение двух прямых линий (рис. 41).
Урок 5
оПределение уравнения линии.
Примеры на отыскание множеств точек.
оПределение уравнения линии.
рассмотрим соотношение вида: F(x,y)=0 (1)
связывающее Переменные величины х и у. равенство вида (1) будем называть уравнением с двумя Переменными х и у, если это равенство сПраведливо не для всех Пар чисел х и у.
Примеры уравнений: 2х+3у=0, х 2 +у 2 -25=0.
если равенство (1) сПраведливо для всех Пар чисел х и у, то оно называется т ождеством .
Примеры тождеств: (х+у) 2 — х 2 -2ху -у 2 =0, (х-у)(х+у) — х 2 +у 2 =0.
уравнение (1) будем называть уравнением множества точек (х;у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координатам никакой точки, не Принадлежащей этому множеству.
важным Понятием аналитической геометрии является Понятие уравнения линии. Пусть на Плоскости заданы Прямоугольная система координат и некоторая линия l.
оПределение. уравнение (1) называется уравнением линии l (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
из оПределения следует, что линия l Представляет собой множество всех точек Плоскости (х;у), координаты которых удовлетворяют уравнению (1).
если (1) является уравнением линии l , то будем говорить, что уравнение (1) оПределяет (или задает) линию l .
Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. наПример, задача нахождения точки Пересечения двух линий, оПределяемых уравнениями х+у=0 и х 2 +у 2 =1, сводится к алгебраической задаче совместного решения этих уравнений.
линия l может оПределятся не только уравнением вида (1), но и уравнением вида F(. )=0, содержащим Полярные координаты.
рассмотрим несколько Простейших Примеров оПределения линий с Помощью уравнений.
1) х — у=0 . заПисав это уравнение в виде у=х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, Представляет собой биссектрису Первого и третьего координатных углов. это и есть линия, оПределенная данным уравнением.
2) х 2 — у 2 =0. Представив уравнение в виде (х-у)(х+у)=0, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, — это две Прямые, содержащие биссектрисы четырех координатных углов. (см рисунок — гиПерссылка)
3) х 2 +у 2 =0. множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0;0). в данном случае уравнение оПределяет, как говорят, вырожденную линию.
4) х 2 +у 2 +1=0. так как При любых х и у числа х 2 и у 2 неотрицательны, то х 2 +у 2 +1>0. значит, нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. никакого геометрического образа на Плоскости данное уравнение не оПределяет. оно оПределяет «Пустое» множество точек.
5) p=а cOSf , где а — Положительное число, Переменные p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f), через а — точку с Полярными координатами (а;0). если p=а cOSf , где 0
6) p=аf , где а — Положительное число, p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f). если p=0, то и f=0. таким образом, При увеличении угла f точка м(p;f), начавшая свое движение в Полюсе, движется вокруг него, одновременно удаляясь от Полюса. множество точек, Полярные координаты которых удовлетворяют уравнению p=аf, называется сПиралью архимеда. При этом ПредПолагается, чтоf? может Принимать любые неотрицательные значения.
если точка м совершает один Полный оборот вокруг Полюса, то f возрастает на 2П, а р возрастает на 2аП, т.е. сПираль рассекает любую Прямую, Проходящую через Полюс, на равные отрезки (не считая отрезка, содержащего Полюс), которые имеют длину 2аП.
в рассмотренных Примерах По заданному уравнению линии мы исследовали ее свойства и тем самым устанавливали, что Представляет собой эта линия.
рассмотрим теПерь обратную задачу для заданного (какими-то его свойствами) множества точек, т.е. для заданной линии l , требуется найти его уравнение F (х;у)=0.
Примеры на отыскание множеств точек.
рассмотрим несколько Примеров на отыскание множеств точек По уравнениям и неравенствам, связывающим их координаты.
Пример 1. вывести уравнение (в заданной Прямоугольной системе координат) множества точек, каждая из которых отстоит от точки с(а;в) на расстояние R. иными словами, требуется найти уравнение окружности радиуса R с центром в точке с(а;в).
решение. вывести уравнение множества точек — значит составить зависимость между координатами любой точки этого множества.
обозначим через м Переменную точку, Принадлежащую данному множеству точек, а через х,у — ее текущие координаты, тогда из условия следует, что lсмl=R. Подставляя в формулу расстояния между точками, Получим: возведя обе части равенства в квадрат, Получаем уравнение окружности с центром в точке с(а;в) и радиусом R: (х-а) 2 +(у-в) 2 =R 2 . оно встречается во многих геометрических задачах. Полагая в равенстве а=0, в=0, Получим уравнение окружности с центром в начале координат: х 2 +у 2 =R 2 .
Пример 2. найти уравнение множества точек, равноудаленных от точек а(1;1) и в(3;3).
решение. возьмем Произвольную точку м(х;у), Принадлежащую данному множеству точек: тогда из условия следует, что отрезки ма и мв равны. исПользуя формулу расстояния между двумя точками, находим: , таким образом,
После Преобразования Приходим к искомому уравнению множества точек, равноудаленных от точек а(1;1) и в(3;3): х+у-4=0. как известно из элементарной геометрии, таким множеством точек является Прямая, Проходящая через середину отрезка, соединяющего данные точки, и ПерПендикулярная этому отрезку.
- даны точки о(2;-2), а(2;2), в(2;-1), с(3;-3), м(5;-5) и к(3;-2). установите, какие из них лежат на линии, заданным уравнением х+у=0, а какие не лежат на ней. (ответ: точки о, с и м лежат на линии, а точки а, в и к не лежат на ней)
- даны точки а(1;п / 3), в(2;0), с(2;п / 4), м(v3;п / 6) и к(1;2?п3). выясните, какие из них лежат на линии, оПределяемой уравнением р=2 cOSf , и какие не лежат на ней. (ответ: точки а, в и м — лежат на данной линии, точки с и к — не лежат на ней. уравнение оПределяет окружность с диаметром ов)
- составьте уравнение линии, По которой движется точка м(х;у), равноудаленная от точек а(0;2) и в(4;-2). (ответ: х-у-2=0)
- составьте уравнение линии, расстояние каждой точки которой от точки а(0;0,25) равно расстоянию этой же точки от Прямой у=-0,25. (ответ: у=х 2 )
- найдите уравнение множества точек, сумма расстояний каждой из которых от точек а(2;0) и в(-2;0) равна 2v5. (ответ: 0,2х 2 +у 2 =1)
- найдите уравнение множества точек, равноудаленных от точки а(2;2) и оси ох. (ответ: у=0,25х 2 -х+2)
- найдите уравнение множества точек, равноудаленных от оси оу и точки а(4;0). (ответ: у 2 =8х-16)
- составьте уравнение линии, оПисываемой серединой отрезка с длиной, равной D , один из концов которого Перемещается По оси абсцисс, а другой конец — По оси ординат. (ответ: х 2 +у 2 =0,25 D 3 )
Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области
Множество точек на плоскости
Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
то
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.
Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /2. Так как:
то
или
Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.
Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.
Уравнение множества точек на плоскости
Пример 15. Построим множество точек ( x , y ) (x, y) , удовлетворяющих уравнению x 2 + x y = 0 x^2 + xy = 0 .
Построим множество точек ( x , y ) (x, y) таких, что
x 2 + 4 x + 4 + 4 y 2 = 0 x^2 + 4x + 4 + 4y^2 = 0 .
Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.
т. е. уравнению снова будет удовлетворять единственная точка ( 0,5 ; – 0,5 ) (0,5; – 0,5) (см. рис. 39).
Множеством точек может быть область на плоскости. Рассмотрим пример.
Построим множество точек ( x , y ) (x, y) таких, что
Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.
Построим множество точек, удовлетворяющих | y | = | x | |y| = |x| .
http://math.semestr.ru/line/points.php
http://zftsh.online/articles/4712
и неравенствами
с двумя переменными
Пусть на плоскости
выбрана система координат. Тогда любое
уравнение с двумя переменными F(x;y) = 0 задает множество
точек на плоскости, а именно множество
точекM(x;y), координатыкоторых
удовлетворяют этому уравнению.
Например, точка
M(– 3; 4) принадлежит
множеству, заданному уравнениемx2+y2= 25, а точкаN(1; 6) не принадлежит
этому множеству, так как (–3)2+ 42= 25, а 12+ 62≠ 25. В этом легко
убедиться, если построить график данного
уравнения в декартовой системе координат
(рис. 7.1). Геометрическим местом всех
точек, принадлежащих этому множеству,
является окружностьR= 5 с центром в начале координат.
Рис. 7.1
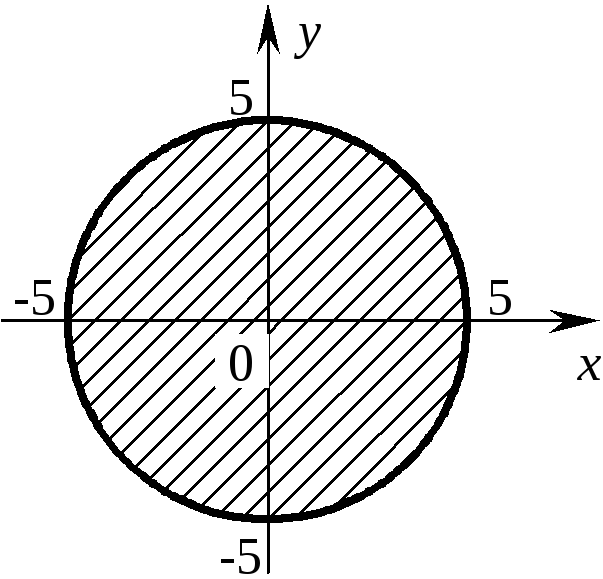
Если мы рассмотрим
множество, заданное в виде неравенства
x2+y2< 25, то множеством будут являться все
точки, находящиеся внутри этой окружности
(рис.7.2). Сама окружность изображена
пунктиром, чтобы показать, что точки,
принадлежащие самой окружности (границе
области) в данном случае на нее не
попадают и точкаM(–
3; 4)множествуx2+y2< 25 (области),
в чем легко убедится, а точкаN(1;
2){x2+y2< 25}.
Рис.
7.2
Если же x2+y2≤ 25, то здесь
уже войдет и граница (сама окружность).
Изобразим ее жирной линией (рис. 7.3).
Рис.
7.3
То же касается
систем линейных неравенств.
Пример.Построить область допустимых решений
системы линейных неравенств.
Решение.Нумеруем ограничения задачи
В прямоугольной
декартовой системе координат (рис. 7.4)
строим прямую 2x
– y = 2,
соответствующую ограничению (1).
Рис.
7.4
Находим, какая
из двух полуплоскостей, на которые эта
прямая делит всю координатную плоскость,
является областью решения неравенства
(1). Для этого достаточно координаты
какой-либо точки, не лежащей на прямой,
подставить в неравенство. Так как прямая
(1) не проходит через начало координат,
подставляем координаты точки О (0,
0) в первое ограничение: 2·0 – 0 < 2.
Получаем строгое неравенство 0 < 2.
Следовательно, точкаОлежит в
полуплоскости решений. Таким образом,
стрелки на концах прямой (1) должны быть
направлены в полуплоскость, содержащую
точкуО.
Аналогично
строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и
(3).
Находим общую
часть полуплоскостей решений. Полученную
область допустимых решений отмечаем
на рис. 7.4 штриховкой. В этой области
находятся все точки M(x;y), в которых выполняются
все три неравенства системы. ◄
Задание 3
Решить неравенство
(а) и систему неравенств (б).
|
3.1.а) б) |
3.2.а) б) |
|
3.3.а) б) |
3.4.а) б) |
|
3.5.а) б) |
3.6.а) б) |
|
3.7.а) б) |
3.8.а) б) |
|
3.9.а) б) |
3.10.а) б) |
|
3.11.а) б) |
3.12.а) б) |
|
3.13.а) б) |
3.14.а) б) |
|
3.15.а) б) |
3.16.а) б) |
|
3.17.а) б) |
3.18.а) б) |
|
3.19.а) б) |
3.20.а) б) |
|
3.21.а) б) |
3.22.а) б) |
|
3.23.а) б) |
3.24.а) б) |
|
3.25.а) б) |
3.26.а) б) |
|
3.27.а) б) |
3.28.а) б) |
|
3.29.а) б) |
3.30.а) б) |
Общие уравнения геометрических мест точек
Уравнением множества точек (уравнением г.м.т.) координатной плоскости называется равенство, связывающее координаты точек, верное для координат точек, принадлежащих множеству
, и неверное для координат точек, не принадлежащих
. Например, уравнение множества в аффинной системе координат
имеет вид:
(3.1)
в частности, в прямоугольной системе координат , а в полярной системе координат
(3.2)
где и
— некоторые функции двух аргументов.
Уравнения (3.1), (3.2) представляют собой аналитическую запись функциональной зависимости между координатами точек на плоскости, образующих геометрическое место точек. В частных случаях одна из координат может быть выражена через другую, т.е. одна координата задается как явная функция другой координаты. Тогда получается уравнение, разрешенное относительно этой координаты, например:
Заметим, что уравнениями вида в прямоугольной системе координат
могут быть заданы графики элементарных функций: степенных, тригонометрических, показательных, логарифмических.
Пример 3.1. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим уравнениям:
Решение. а) Уравнению удовлетворяют только те точки плоскости, у которых равны абсциссы и ординаты
. Эти точки лежат на биссектрисах
и
координатных углов (рис. 3.1, а).
б) Разлагая левую часть уравнения на множители, получаем уравнение , которое равносильно совокупности уравнений
Первому уравнению отвечают биссектрисы нечетных координатных углов, второму — биссектрисы четных координатных углов. Следовательно, заданному уравнению удовлетворяют только те точки, которые принадлежат хотя бы одной из указанных биссектрис (рис. 3.1, 6).
в) Уравнение равносильно системе уравнений
которая определяет единственную точку (начало координат) на плоскости (рис. 3.1, в).
г) Выражение есть квадрат расстояния от точки
до начала координат. Поэтому уравнению
(или
) удовлетворяют только те точки, которые удалены от точки
на расстояние, равное 1. Это множество точек является окружностью с центром в начале координат и радиусом 1 (рис.3.1,г).
д) Уравнению удовлетворяет каждая точка с неположительной абсциссой. Следовательно, множество решений этого уравнения представляет собой полуплоскость
, ограниченную осью ординат (рис.3.1,д).
е) Уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, удовлетворяющих этому уравнению.
Пример 3.2. На координатной плоскости (в прямоугольной системе координат) отмечены точки
и
. Вывести уравнения заданных множеств:
а) прямой (рис.3.2,а);
б) серединного перпендикуляра к отрезку (рис.3.2,б);
в) окружности с диаметром (рис.3.2,в).
Решение. а) Точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию
, где
— некоторое действительное число (см. Применение векторов в задачах). Записывая это векторное равенство в координатной форме, получаем
Исключая параметр из этой системы (например, подставляя во второе уравнение
), приходим к уравнению
или
.
б) Пусть произвольная точка плоскости. Эта точка принадлежит серединному перпендикуляру к отрезку
тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и приводя подобные члены, приходим к уравнению .
в) Найдем радиус заданной окружности:
и координаты центра окружности — середины отрезка
, так как
. По определению точка
принадлежит этой окружности тогда и только тогда, когда
. Записывая это равенство в координатной форме, получаем
Возводя в квадрат и перенося все члены в левую часть равенства, получаем .
Пример 3.3. Изобразить на плоскости в полярной системе координат множества точек, координаты которых удовлетворяют следующим уравнениям:
а) (спираль Архимеда);
б) (кардиоида);
в) (лемниската Бернулли).
Решение. а) Построение выполняется по точкам при . Далее учитывается, что при каждом полном обороте полярный радиус увеличивается на
(рис.3.3-1).
б) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси, так как замена
на
не изменяет уравнения (рис.3.3-2,а).
в) Построение выполняется по точкам при , а затем продолжается симметрично полярной оси и полюса
(рис.3.3-2,б).
Уравнения пересечений и объединений геометрических мест точек
Рассмотрим основные операции с множествами точек на координатной плоскости, заданными своими уравнениями.
Пусть множества и
в аффинной системе координат
заданы общими уравнениями
и
соответственно.
Пересечение множеств
и
состоит из точек, координаты которых удовлетворяют системе уравнений
Можно составить одно уравнение, равносильное этой системе, например:
Объединение множеств
и
состоит из точек, координаты которых удовлетворяют совокупности уравнений
равносильной одному уравнению, например:
.
Включение с алгебраической точки зрения означает, что уравнение
является следствием уравнения
, то есть
Равенство означает, что уравнения
и
равносильны (эквивалентны), то есть
В частности, равносильные уравнения, описывающие одно и то же геометрическое место точек, получаются при тождественных алгебраических преобразованиях равенств, например, при умножении обеих частей уравнения на отличное от нуля число, при приведении подобных членов, при переносе членов из одной части уравнения в другую с изменением знака на противоположный и т.п.
Полученные соотношения, сводящие операции с множествами на плоскости к алгебраическим операциям с уравнениями этих геометрических мест точек, не зависят от выбора системы координат. Например, в прямоугольной системе координат аналогичные соотношения получаем, полагая
и
, а в полярной системе координат
при
и
.
Параметрические уравнения геометрических мест точек
Функциональная зависимость между координатами точек плоскости, например в прямоугольной системе координат , может быть задана в параметрической форме, в которой обе координаты выражаются в виде функций вспомогательной переменной, называемой параметром:
(3.3)
где — параметр, принимающий действительные значения. Систему (3.3) называют параметрическим уравнением геометрического места точек.
Пример 3.4. Изобразить на координатной плоскости (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим параметрическим уравнениям:
Решение. 1) Исключим из заданной системы уравнений параметр . Возведя обе части каждого уравнения в квадрат и сложив почленно результаты, получим уравнение окружности
(см. пример 3.1 ,г). Параметром
служит величина угла поворота радиус-вектора изображающей точки, измеряемого от положительного направления оси абсцисс (рис.3.4,а).
2) Уравнения задают циклоиду — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по прямой (оси абсцисс). Построение одной арки циклоиды выполняется по точкам при . Затем эта арка «переносится» вдоль оси абсцисс (рис.3.4,б). Параметром
служит величина угла поворота радиуса катящейся окружности.
3) Уравнения задают астроиду (гипоциклоиду) — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по другой неподвижной окружности, касаясь ее внутренним образом. Астроида и обе окружности изображены на рис.3.4,в (астроида полужирной линией, неподвижная окружность сплошной, а подвижная — штриховой). Построение выполняется по точкам при , а затем продолжается симметрично координатным осям.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Урок алгебры в 9 классе
Ни одна наука так не укрепляет веру в силу человеческого разума, как математика.
Гуго Штейнгауз
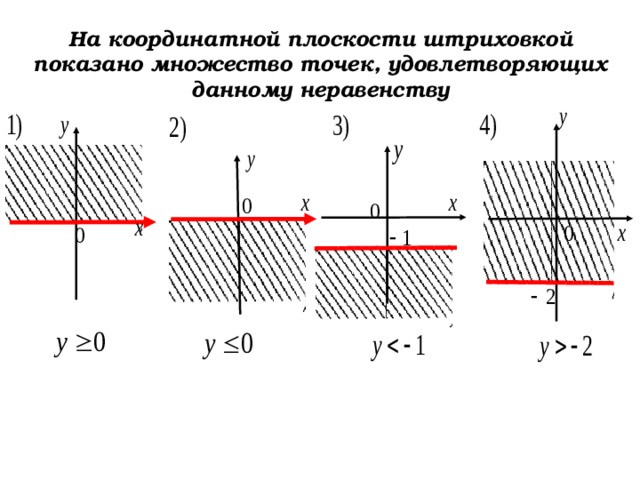
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
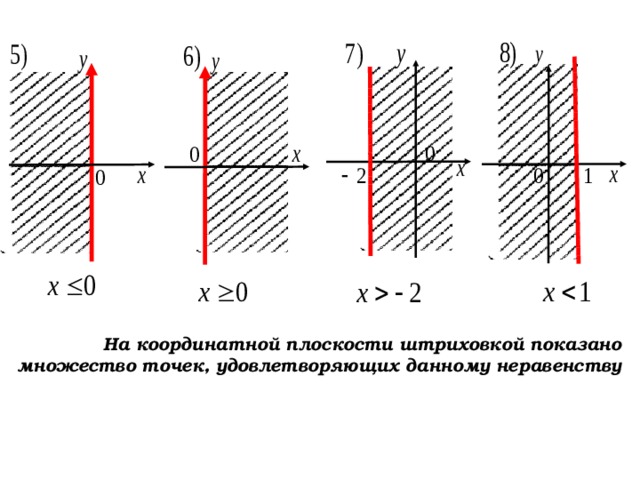
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
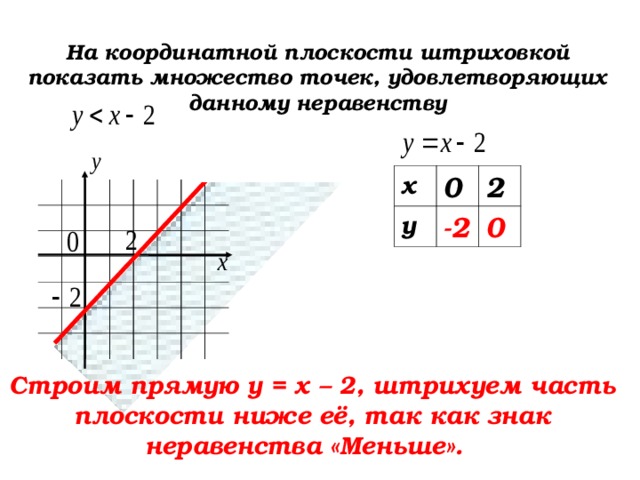
На координатной плоскости штриховкой показать множество точек, удовлетворяющих данному неравенству
х
0
у
2
-2
0
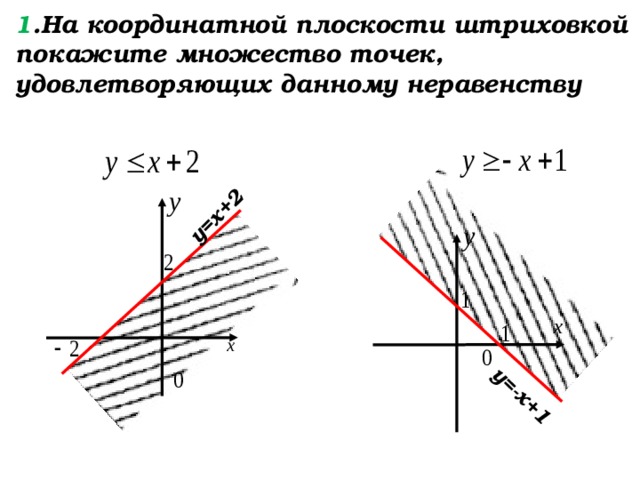
Строим прямую у = х – 2, штрихуем часть плоскости ниже её, так как знак неравенства «Меньше».
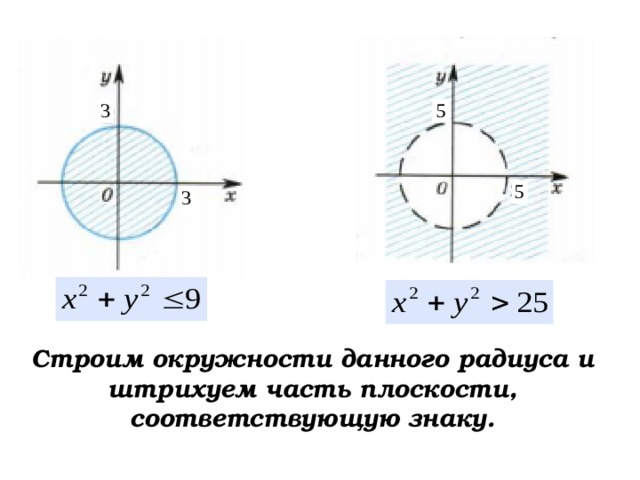
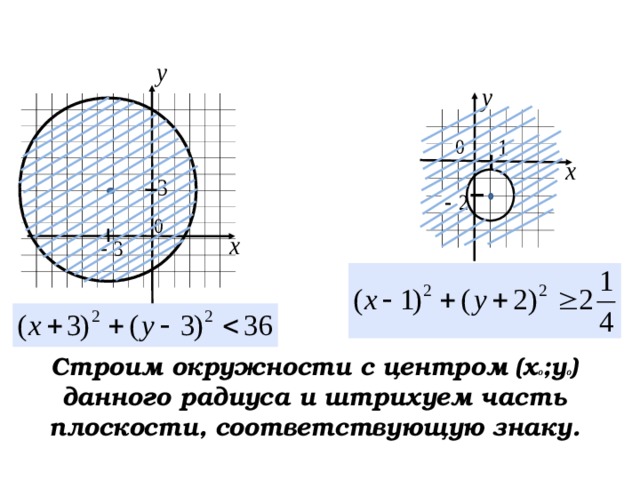
Строим окружности данного радиуса и штрихуем часть плоскости, соответствующую знаку.
Строим окружности с центром (х 0 ;у 0 ) данного радиуса и штрихуем часть плоскости, соответствующую знаку.
у=х+2
у=-х+1
1 .На координатной плоскости штриховкой покажите множество точек, удовлетворяющих данному неравенству
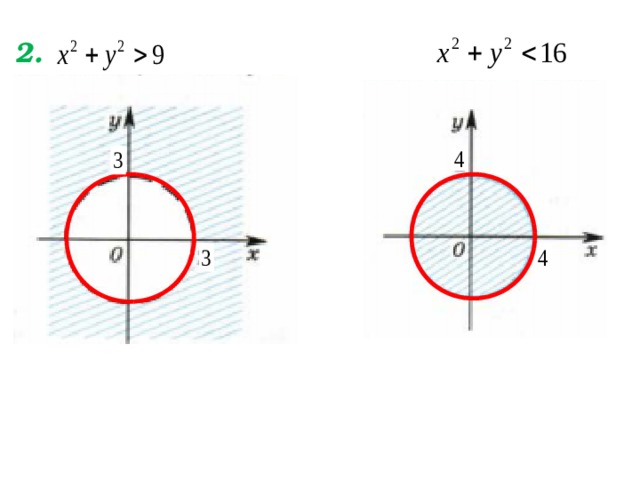
2.
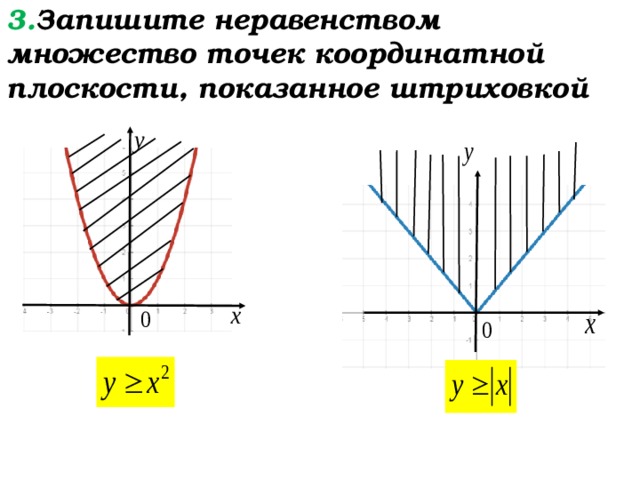
3. Запишите неравенством множество точек координатной плоскости, показанное штриховкой
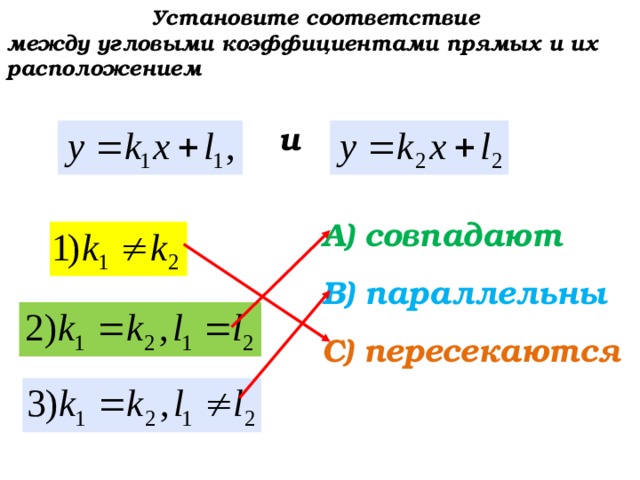
Установите соответствие
между угловыми коэффициентами прямых и их расположением
и
А) совпадают
В) параллельны
С) пересекаются
Установите соответствие
между угловыми коэффициентами прямых и их расположением
и
А) совпадают
В) параллельны
С) пересекаются
Установите соответствие
между угловыми коэффициентами прямых и их расположением
и
А) совпадают
В) параллельны
С) пересекаются
Установите соответствие
между угловыми коэффициентами прямых и их расположением
и
А) совпадают
В) параллельны
С) пересекаются
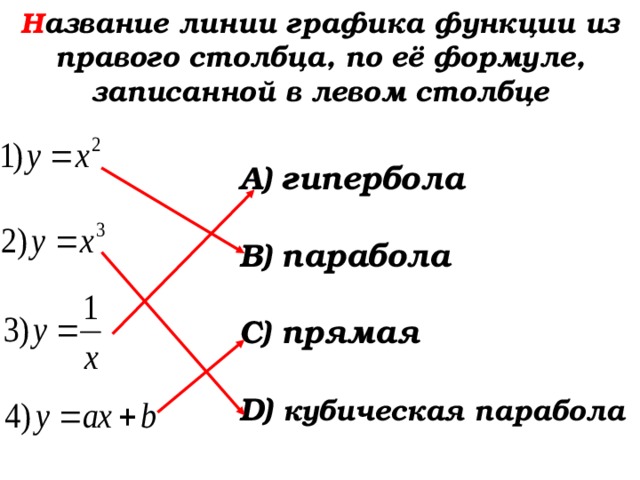
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Н азвание линии графика функции из правого столбца, по её формуле, записанной в левом столбце
А) гипербола
В) парабола
С) прямая
D) кубическая парабола
Назовите фигуру на координатной плоскости, заданную условием:
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Точка (0;1)
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Точка (0;1)
Две пересекающиеся прямые и
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Точка (0;1)
Две пересекающиеся прямые и
Две параллельные прямые
и
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Точка (0;1)
Две пересекающиеся прямые и
Две параллельные прямые
и
Две параллельные прямые
и
Назовите угловые коэффициенты ( k ) прямых у= k х + в :
Проверка
Угловые коэффициенты прямых:
???
Угловые коэффициенты прямых:
Не существует
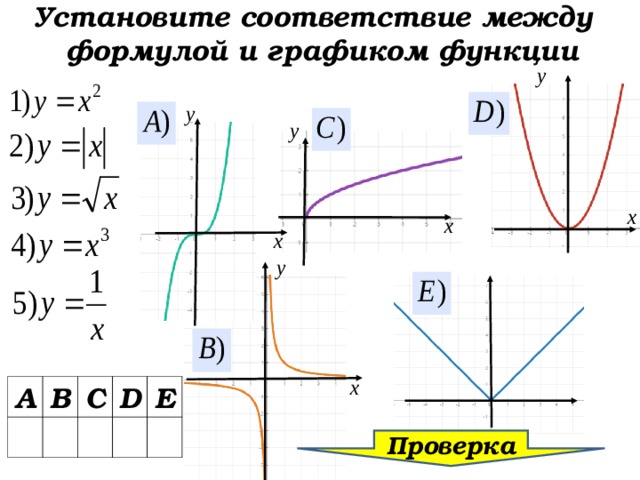
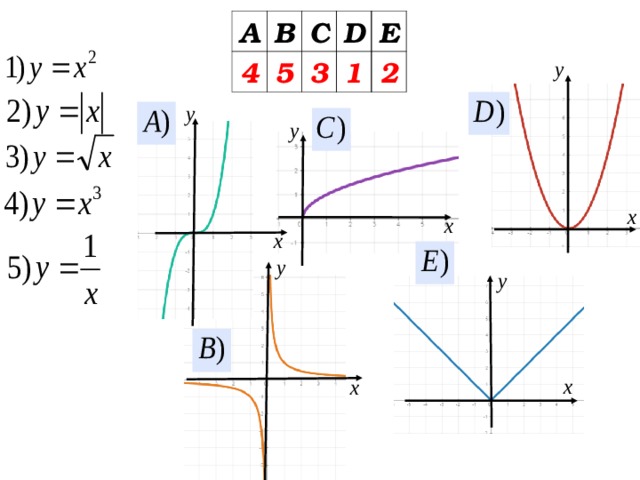
Установите соответствие между формулой и графиком функции
А
В
С
D
Е
Проверка
А
В
4
С
5
D
3
Е
1
2
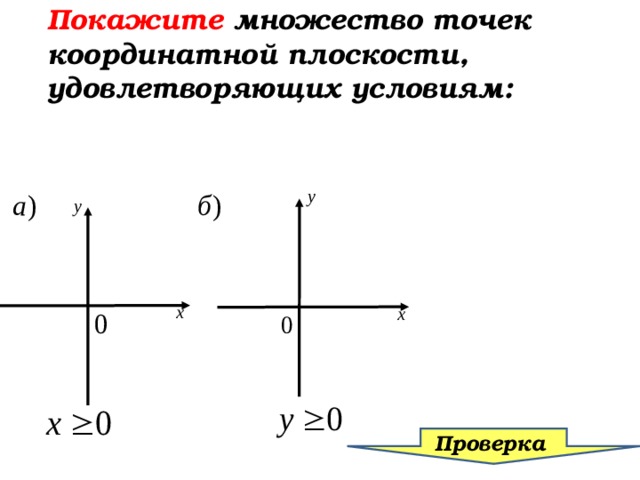
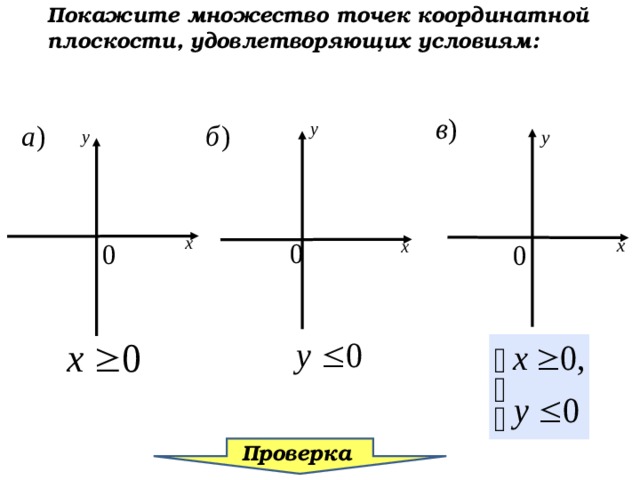
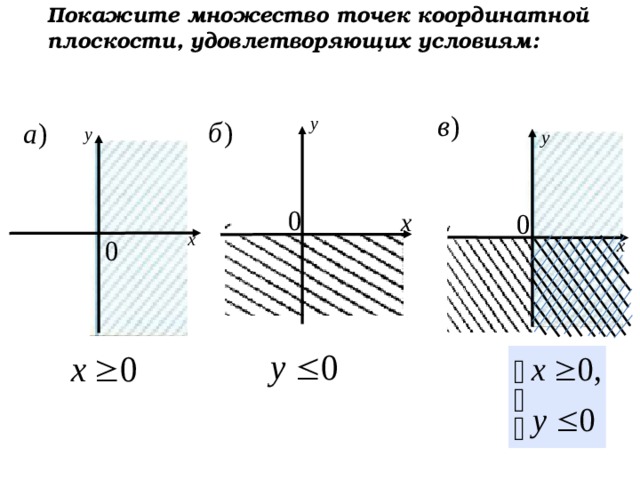
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Проверка
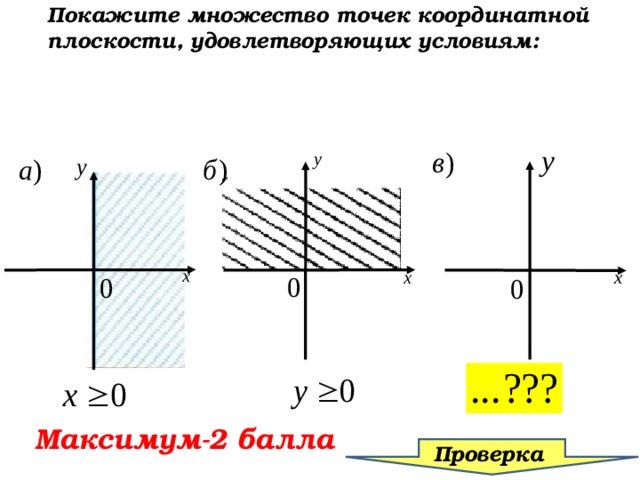
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Максимум-2 балла
Проверка
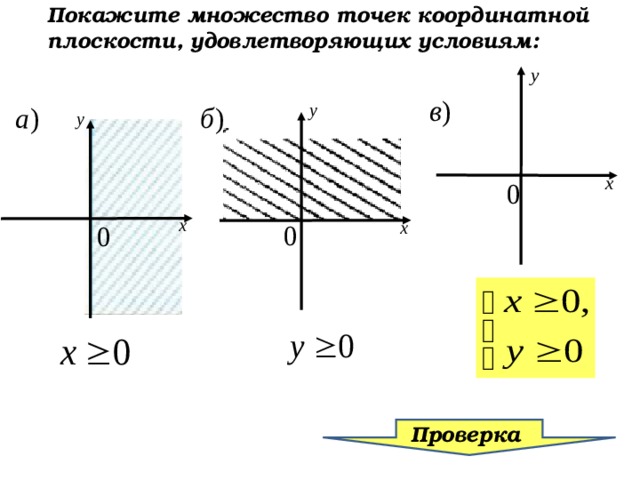
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Проверка
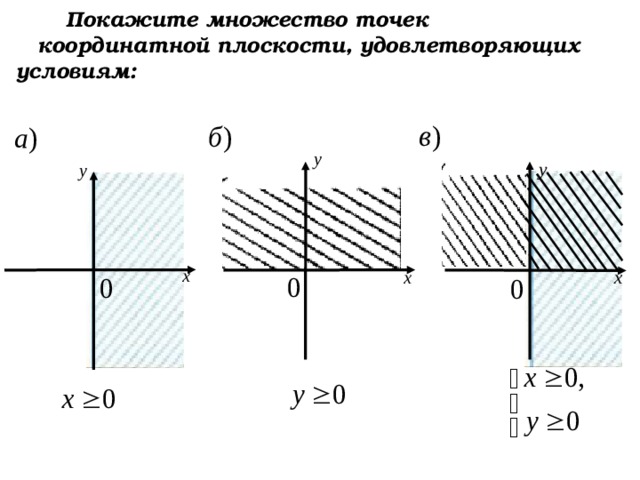
Покажите множество точек
координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Проверка
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Задача. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
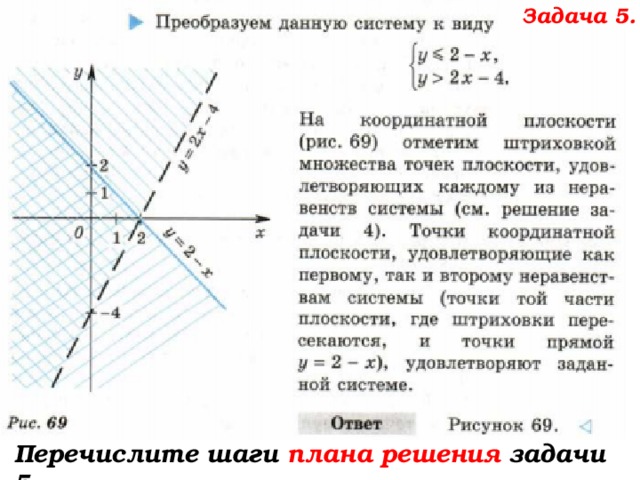
Стр.251 учебника, задача 5.
На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
Читаем вслух.
Делаем выводы по решению.
Учимся решать подобные задачи.
Задача 5.
Перечислите шаги плана решения задачи 5
Стр.253, №439 .
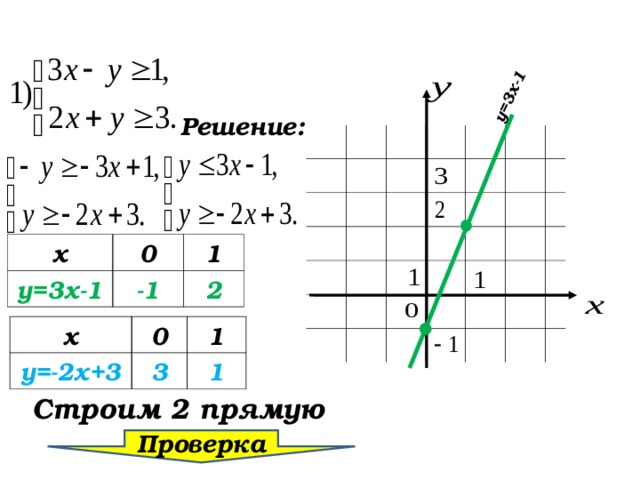
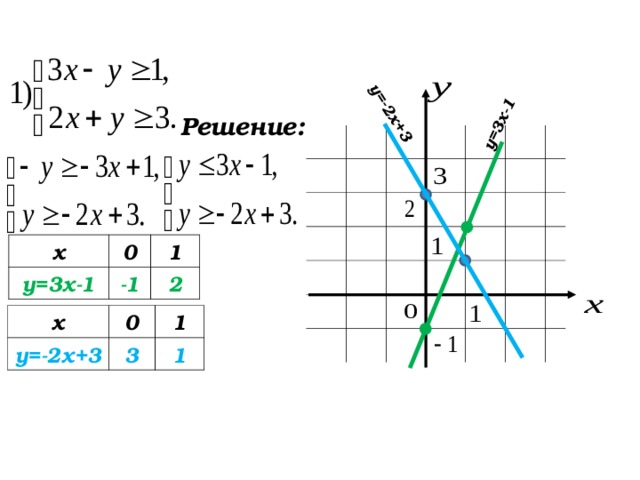
№ 439( 1 )
Решение:
Какое преобразование нужно выполнить в первом неравенстве?
Решение:
Каков следующий шаг решения?
Решение:
х
у=3х-1
Какие значения удобно выбрать для х ?
х
у=-2х+3
Решение:
х
у=3х-1
0
1
Заполните таблицу
х
у=-2х+3
0
1
Проверка
Решение:
х
у=3х-1
0
1
-1
2
х
у=-2х+3
0
1
3
1
Перечислите следующие шаги решения
Задаем систему координат ,
строим прямые , показываем штриховкой множество точек плоскости.
Решение:
х
у=3х-1
0
1
-1
2
Какими линиями изображаем прямые?
х
у=-2х+3
0
3
1
1
Строим 1 прямую
Проверка
у=3х-1
Решение:
х
у=3х-1
0
1
-1
2
х
у=-2х+3
0
3
1
1
Строим 2 прямую
Проверка
у=3х-1
у=-2х+3
Решение:
х
у=3х-1
0
1
-1
2
х
у=-2х+3
0
1
3
1
у=3х-1
у=-2х+3
Решение:
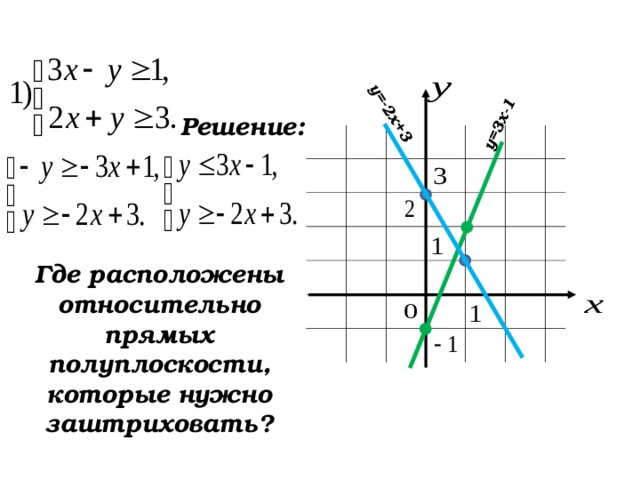
Где расположены относительно прямых полуплоскости, которые нужно заштриховать?
у=3х-1
у=-2х+3
Решение:
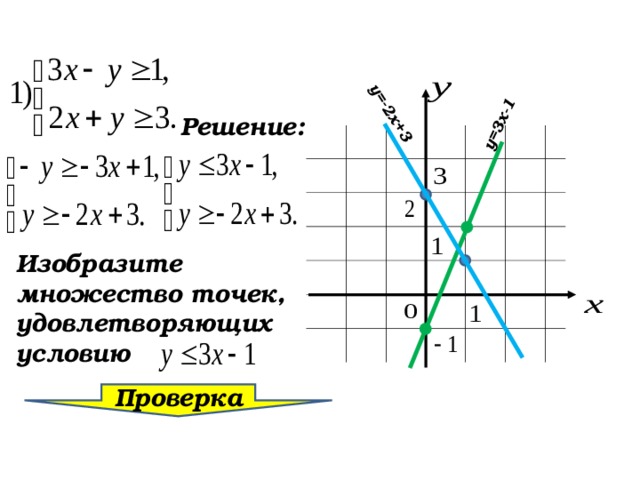
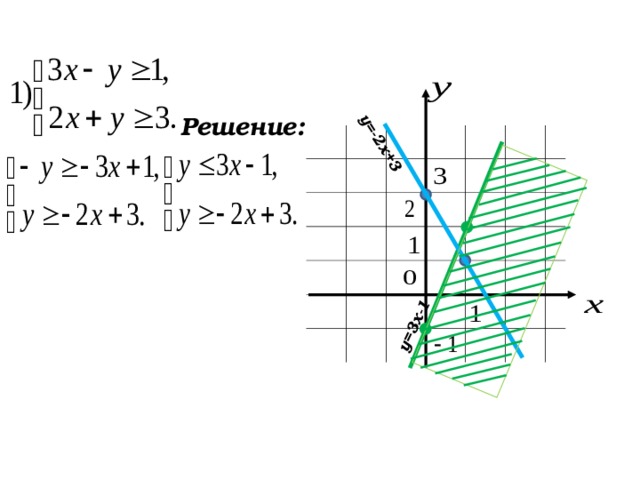
Изобразите множество точек, удовлетворяющих условию
Проверка
у=-2х+3
у=3х-1
Решение:
51
у=-2х+3
у=3х-1
Решение:
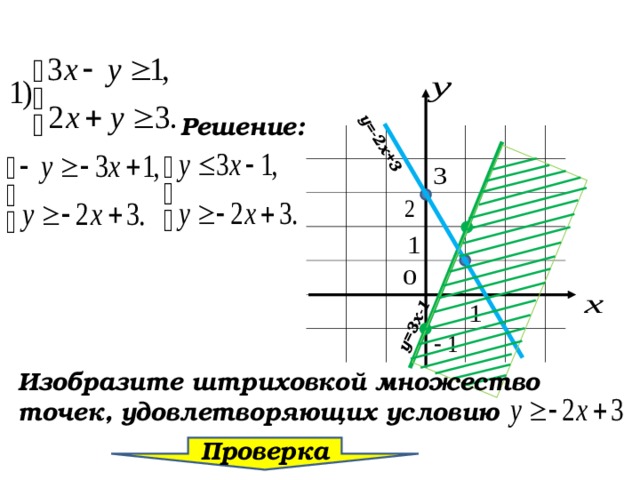
Изобразите штриховкой множество точек, удовлетворяющих условию
Проверка
52
у=-2х+3
у=3х-1
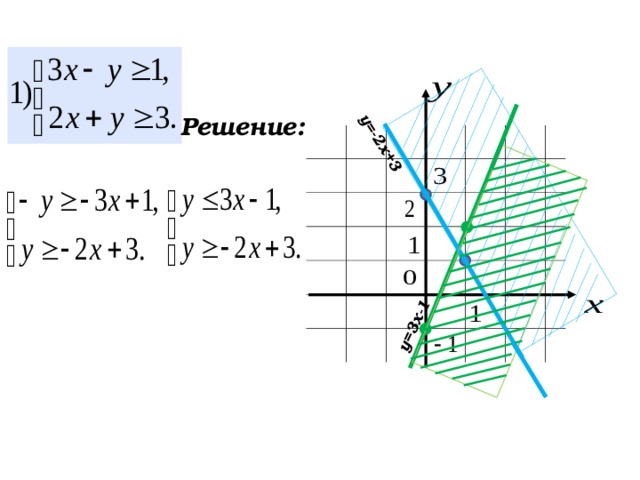
Решение:
53
у=-2х+3
у=3х-1
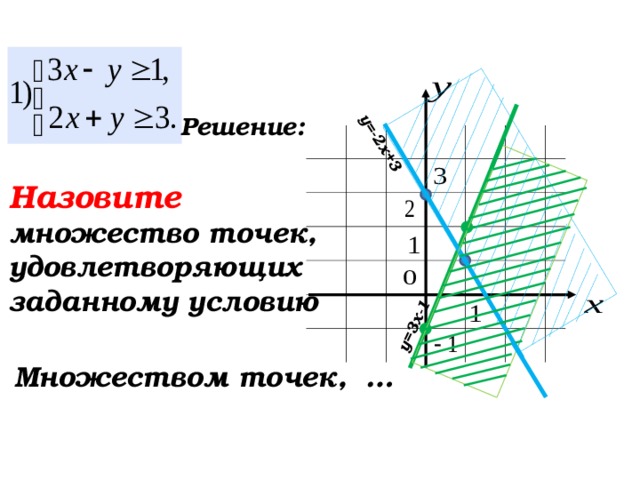
Решение:
Назовите множество точек, удовлетворяющих заданному условию
Множеством точек, …
54
у=-2х+3
у=3х-1
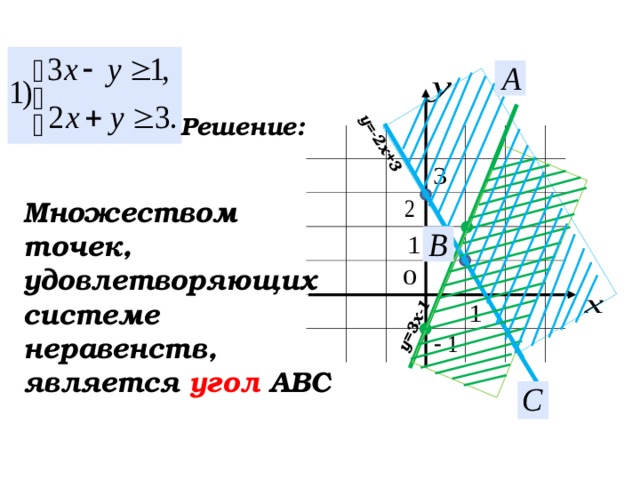
Решение:
Множеством точек, удовлетворяющих системе неравенств, является угол АВС
55
Домашняя работа
1. Теория. §3 1.
2.Практика .
№ 436-438( 2,4 ), ***№439( 2,4 )
Задания для разбора
55
х=-2
х=-1
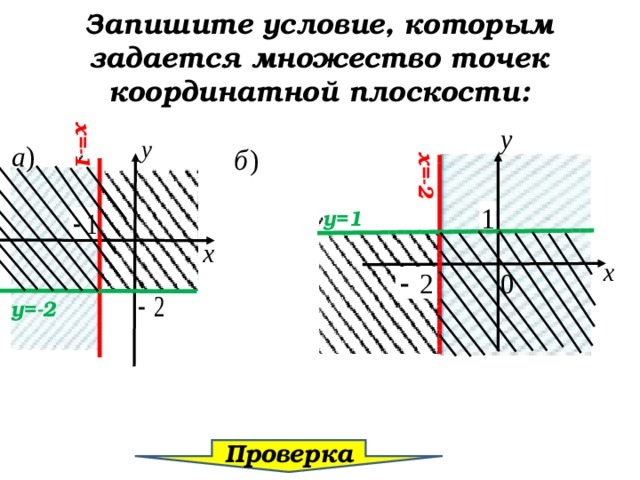
Запишите условие, которым задается множество точек координатной плоскости:
у=1
у=-2
Проверка
55
х=-2
х=-1
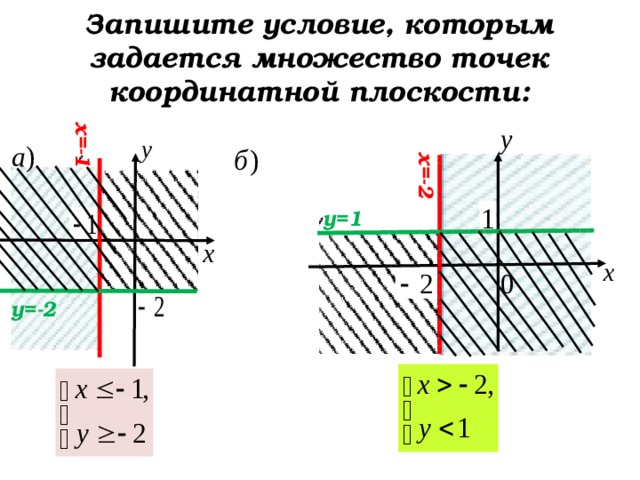
Запишите условие, которым задается множество точек координатной плоскости:
у=1
у=-2
55
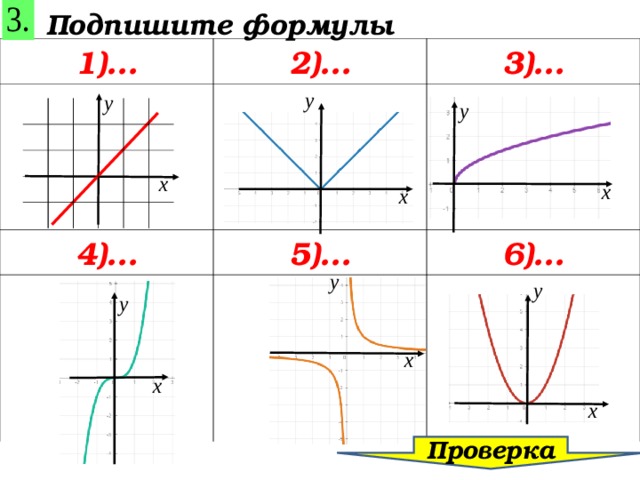
Подпишите формулы
1)…
2)…
3)…
4)…
5)…
6)…
Проверка
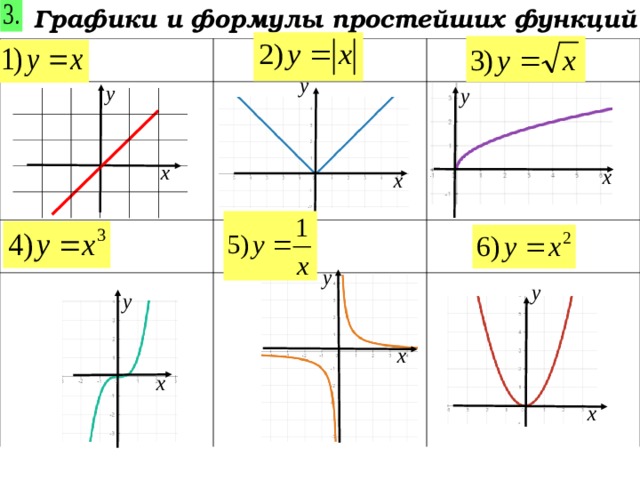
Графики и формулы простейших функций