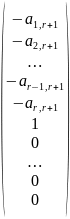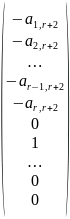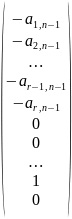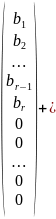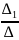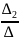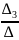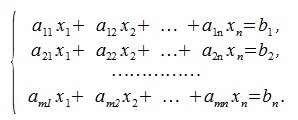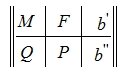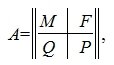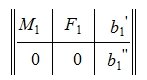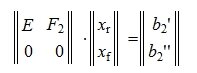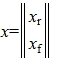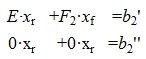Найти общее решение системы уравнений это как

Структура общего решения системы уравнений

Однородная система линейных уравнений

или

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений:

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

---

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

Получим решений

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений.

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

---

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

---

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

---

Замечания 5.3

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

, где — столбец произвольных постоянных.

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

---

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

1) если , то ;

2) если , то .

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

и общее решение системы

Несмотря на различия, обе формулы задают одно и то же множество решений.

---

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

, где — решение однородной системы.

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

---

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

Замечания 5.4

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

где — частное решение неоднородной системы, а — столбец произвольных постоянных.

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

---

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

которое совпадает с ранее полученным.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1. Системы линейных уравнений: определение, общее решение, частное решение. Метод Крамера.

Системой m линейных
уравнений с n неизвестными
x₁,x₂,…x_n  называется
система S вида

S=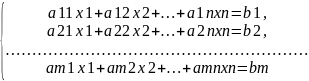

,                                                                        

Где
a_ij
— коэффициенты при неизвестных, b_j
— свободные члены (a_ij,
b_j
— заданные числа).

Решением
системы S называется
упорядоченный набор действительных
чисел a₁,a₂,…a_n,
при подстановке которых в каждое
уравнение системы вместо x₁,x₂,…x_n 
соответственно будут получены верные
числовые равенства.

Система S называется
совместной (несовместной), если она
имеет хотя бы одно решение (не имеет
решений).

Совместная
система S линейных
алгебраических уравнений называется
определённой (неопределённой), если она
имеет единственное решение (множество
решений).

ФУНДАМЕНТАЛЬНАЯ
СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ

Множество решений однородной
линейной системы относительно n неизвестных
является линейным
подпространством пространства Rn. Размерность этого
подпространства равна n − r,
где r − ранг матрицы
системы A.

Любой базис пространства
решений однородной системы линейных
уравнений называется фундаментальной
системой решений однородной
системы.

Иначе говоря, любая
упорядоченная совокупность n − r линейно
независимых решений
однородной линейной системы
образует фундаментальную
систему решений однородной
системы.

СТРУКТУРА
ОБЩЕГО РЕШЕНИЯ ОДНОРОДНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ

Любая однородная система
линейных алгебраических уравнений,
ранг матрицы которой равен r,
с помощью элементарных
преобразований может
быть приведена к каноническому
виду:

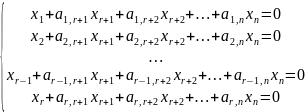
Общее решение однородной
линейной системы, записанной в каноническом
виде, очевидно, определяется формулами:

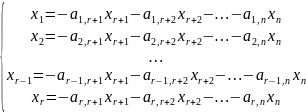
Свободные переменные x_r+1 , x_r+2 ,
…, x_m−1, x_m могут
принимать произвольные значения.

Вычисленные по этим
формулам n − r линейно
независимых решений образуют фундаментальную
систему решений:

E₁=
,
E₂=
,
E_n-r-1=
,
E_n-r=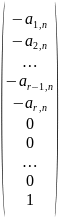

Тогда общее решение системы
можно записать в вектороной форме в
виде:

X=C₁E₁+C₂E₂+…+C_n-r-1E_n-r-1+C_n-rE_n-r,

X=C₁
+C₂
+…+C_n-r-1
+C_n-r

Здесь С₁, С₂,
…, С_n−r−1, С_n−r —
произвольные константы.

СТРУКТУРА
ОБЩЕГО РЕШЕНИЯ НЕОДНОРОДНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ

Общее
решение неоднородной системы линейных
уравнений равно сумме общего
решения приведенной однородной системы
и любого частного
решения неоднородной системы.

Поскольку общее решение
линейной системы, записанной в каноническом
виде, определяется формулами:

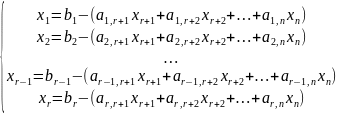
то общее решение неоднородной
системы можно записать в векторной
форме в виде:

X=

C₁
+C₂
+…+C_n-r-1
+C_n-r

Здесь С₁, С₂,
…, С_n−r−1, С_n−r —
произвольные константы, r —
ранг матрицы системы.

Метод
Крамера (правило Крамера) —
способ решения квадратных систем
линейных алгебраических уравнений с
ненулевым определителем основной
матрицы (причём
для таких уравнений решение существует
и единственно).

Система
линейных уравнений:

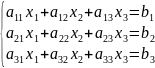
1. В
   данной системе составим определитель
   и вычислим.

=

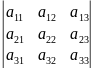
1. Составить
   и вычислить следующие определители:

₁=
,
₂=
,
₃=

3.
Воспользоваться формулами Крамера.x₁=
,
x₂=
,
x₃=
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Система линейных уравнений. Общее решение

Система линейных уравнений (СЛУ) может быть записана в виде

(1)

где m, n натуральные числа, a_ij (i=1,2, …m, j=1,2,…n) называются коэффициентами, b_i (i=1,2,…m) называются свободными членами, x_i (i=1,2,…n) называются неизвестными.

Систему линейных уравнений (1) можно записать в виде

где A матрица порядка m×n , x — вектор порядка n (x∈Rⁿ), b — вектор порядка m (b∈R^m).

Решением системы (2) называется выбор такого вектора x’, что выполнено равенство

Ax’≡b.

Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.

Если СЛУ не имеет решения, то СЛУ называется несовместным.

Если СЛУ имеет единственное решение, то СЛУ называется определенным.

Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.

 Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.

Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.

Нахождение общего решения системы линейных уравнений

Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.

Пусть A m×n — матрица rankA=r. В общем случае можем предположить что r<n, r<m. Тогда r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Запишем систему (2) в блочном виде:

(3)

где M — r×r — матрица, Q -m-r×r — матрица, F — n-r×r — матрица, P — m-r×n-r — матрица, .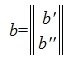

Применяя метод исключения Гаусса для системы (3), получим:

(4)

где M₁ верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

(5)

где E — единичная матрица порядка r×r.

Запишем (5) в виде системы линейных уравнений:

(6)

где

Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:

(7)

Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b₂»≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора x_r:

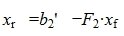(8)

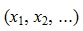
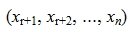
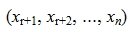
Таким образом первые r координаты вектора x выражены через остальные координаты . — свободные координаты, т.е. могут принимать любые значения.

Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).

Рассмотрим множество всех векторов х, удовлетворяющих условию

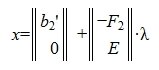(9)

где λ — произвольный вектор-столбец длины n-r.

Подставляя (9) в (6) получим:

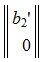
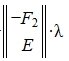
Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор является частным решением неоднородной системы линейных уравнений Ax=b, а является общим решением однородной системы линейных уравнений Ax=0;

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы

Обозначим через R(A) пространство столбцов матрицы A, т.е.

R(A)={z: z=Ax, ∀x∈Rⁿ}.

1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A^-1, и следовательно единственное решение СЛУ (2) примет вид:

x’=A⁻¹b.

(10)

Действительно, подставляя (3) в (2) имеем:

Ax’=AA⁻¹b=Eb=b,

где E − единичная матрица.

2. Пусть A m×n − матрица, rank(A)=r.

Вычислим следующий вектор:

x’=A⁺b.

(11)

где A⁺ — псевдообратная к A матрица.

Подставляя (11) в (2), имеем:

AA⁺b=b.

(12)

Из равенства (12) следует, что для того, чтобы система линейных уравнений (2) имела решение, должно выполняться условие

b∈R(A).

Если СЛУ совместна, т.е. если AA⁺b=b, то x’=A⁺b является решением СЛУ (2).

Общее решение системы линейных уравнений является суммой частного решения неоднородной системы линейных уравнений и множества всех решений соответствующей однородной системы линейных уравнений.

Общее решение системы линейных уравнений (2) имеет следующий вид:

x=x*+(E−A+A)z, ∀z∈Rn.

(13)

где x^* — один из решений неоднородной системы (2) (например (4)), (E−A⁺A) образует ядро (нуль пространство) матрицы A.

Сделаем скелетное разложение матрицы (E−A⁺A):

E−A⁺A=Q·S

где Q n×n−r — матрица rank(Q)=n−r, S n−r×n-матрица rank(S)=n−r.

Тогда (13) можно записать в следующем виде:

x=x*+Q·k,   ∀k∈R^n-r.

где k=Sz.

Итак, процедура нахождения общего решения системы линейных уравнений с помощью псевдообратной матрицы можно представить в следующем виде:

1. Вычисляем псевдообратную матрицу A⁺.
2. Вычисляем частное решение неоднородной системы линейных уравнений (2): x*=A⁺b.
3. Проверяем совместность системы. Для этого вычисляем AA⁺b. Если AA⁺b≠b, то система несовместна. В противном случае продолжаем процедуру.
4. Высисляем E−A⁺A.
5. Делаем скелетное разложение E−A⁺A=Q·S.
6. Строим решение

x=x*+Q·k,   ∀k∈R^n-r.

Решение системы линейных уравнений онлайн

Онлайн калькулятор позволяет найти обшее решение системы линейных уравнений с подробными объяснениями.

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

В теме «Теорема Кронекера-Капелли» было указано, что если ранг расширеной матрицы системы $widetilde{A}$ и ранг матрицы системы $A$ равны между собой, то заданная система линейных алгебраических уравнений (СЛАУ) совместна, т.е. имеет решение. Вопрос о количестве этих решений разрешим с помощью следствия из теоремы Кронекера. Согласно ему, если $rang A=rangwidetilde{A} = n$ ($n$ – количество неизвестных), то СЛАУ имеет единственное решение. Если же $rang A=rangwidetilde{A} < n$, то количество решений заданной СЛАУ бесконечно.

Особый интерес представляет именно случай $rang A=rangwidetilde{A} < n$, которым и займёмся в этой теме. Так как $rang A=rangwidetilde{A}$, то обозначим эти ранги просто буквой $r$, т.е. $rang A=rangwidetilde{A}=r$. Итак, $r < n$ и система неопределена, т.е. имеет бесконечное количество решений.

Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.

Если коэффициенты при $r$ переменных совместной СЛАУ образуют базисный минор матрицы системы $A$, то эти $r$ переменных называют базисными или основными. Остальные $n-r$ переменных именуют свободными или неосновными.

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Решение СЛАУ, в котором все свободные переменные равны нулю, называется базисным.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.

Пример №1

Решить СЛАУ $
left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=9\
& -x_1+2x_2+x_3+x_4=-11;\
& x_1-2x_2+2x_3+3x_4=5.
end{aligned} right.$. Если система является неопределённой, указать базисное решение.

Решение

Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 9 \
-1 & 2 & 1 & 1 & -11 \
1 & -2 & 2 & 3 & 5 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
-1 & 2 & 1 & 1 & -11 \
3 & -6 & 9 & 13 & 9
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1 end{array} rightarrow

left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 3 & 4 & -6
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-r_2end{array} rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Примечание. показатьскрыть

Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:

$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6
end{array}right)
$$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 3 & -6 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 1 & -2 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \

rightarrow left(begin{array} {cc|ccc}
1 & 0 & 9 & 2 & -1/3\
0 & 1 & -2 & 0 & -4/3
end{array}right).
$$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:

$$
left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$

Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:

$$
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.
$$

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left{begin{aligned}
& x_1=frac{2}{3};\
& x_2=-4;\
& x_3=-frac{10}{3};\
& x_4=1.
end{aligned}right.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac{1}{3}x_4$ и $x_3=-2-frac{4}{3}x_4$ в левую часть первого уравнения, получим:

$$
3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-2-frac{4}{3}x_4right)+13x_4=9.
$$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Ответ: Общее решение: $left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$, базисное решение: $
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.$.

Пример №2

Решить СЛАУ

$$left{begin{aligned}
& x_1-2x_2+4x_3+2x_5=0;\
& 4x_1-11x_2+21x_3-2x_4+3x_5=-1; \
& -3x_1+5x_2-13x_3-4x_4+x_5=-2.
end{aligned}right.$$

Если система является неопределённой, указать базисное решение.

Решение

Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.

$$
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
4 & -11 & 21 & -2 & 3 & -1\
-3 & 5 & -13 & -4 & 1 & -2
end{array} right)
begin{array} {l} phantom{0} \r_2-4r_1\r_3+3r_1end{array} rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -3 & 5 & -2 & -5 & -1\
0 & -1 & -1 & -4 & 7 & -2
end{array} right) rightarrow \

rightarrow left|begin{aligned}
& text{поменяем местами вторую и третью}\
& text{строки, чтобы диагональным элементом}\
& text{второй строки стало число (-1).}
end{aligned}right|rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & -3 & 5 & -2 & -5 & -1
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-3r_1end{array} rightarrow \

rightarrow left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & 0 & 8 & 10 & -26 & 5
end{array} right).
$$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde{A} = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

$$
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 8 & 5 & -10 & 26
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\1/8cdot{r_3}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1-4r_3 \r_2+r_3\ phantom{0}end{array} rightarrow \

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & -1 & 0 & -11/8 & 11/4 & -15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l} phantom{0} \ -1cdot{r_2}\ phantom{0}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow\

rightarrowleft( begin{array} {ccc|ccc}
1 & 0 & 0 & 1/4 & -1/2 & -15/2\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
$$

Из последней матрицы имеем общее решение заданной СЛАУ: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$. Базисное решение получим, если приравняем свободные переменные к нулю, т.е. $x_4=0$, $x_5=0$:

$$
left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.
$$

Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.$.

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.