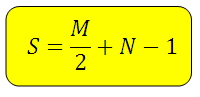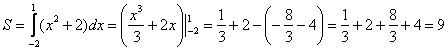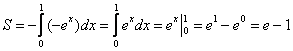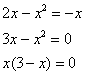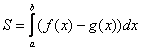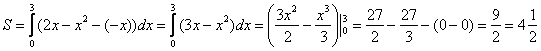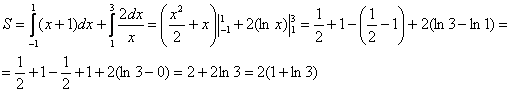Найти площадь по шаблону как

Математика, 4 класс

Урок №14. Измерение площади фигуры с помощью палетки

Перечень вопросов, рассматриваемых в теме:

Площадь геометрической фигуры.

Вычисление площади фигур произвольной формы, используя палетку.

Глоссарий по теме:

Площадь — свойство фигур занимать место на плоскости.

Длина — свойство предмета “быть протяжённым в пространстве”

Палетка — прозрачная пластинка, разделенная на единицы площади.

Основная и дополнительная литература по теме урока:

1. Математика: 4 класс: учебник в 2 ч. Ч.1/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение, 2016. – с. 36-38
2. Всероссийские проверочные работе. Математика. Рабочая тетрадь 4 класс в 2 ч. Ч 1/ под.ред. Н.А. Сопруновой – М.; Просвещение, 2016. – с. 50 -68

Теоретический материал для самостоятельного изучения

Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.

Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см²

А теперь попробуйте вычислить площадь данной фигуры:

-?

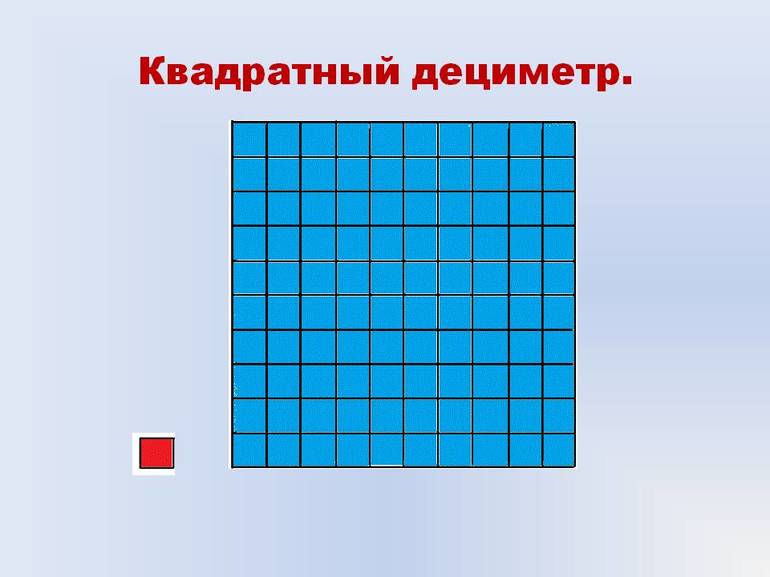
Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка — лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:

1) На данную фигуру наложить палетку. Не сдвигать!

2)Сосчитать, сколько целых клеток- квадратных единиц — содержится в фигуре.

Целых 34 клетки.

3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

Неполных 8 клеток.

4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.

8 : 2 = 4

5) Сложить числа, полученные в пунктах 2 и 4.

6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.

S = 34 + (8 : 2) = 38 см²

Ответ: S = 38 см²

Задания тренировочного модуля:

1. Определите, какая фигура имеет большую площадь, а какая — меньшую, и решите ребус соответствия.

Правильный ответ: Прямоугольник – большую, круг – меньшую.

Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Правильный ответ:

Площадь 7 см²

Периметр 12 см

Методы изготовления

Для математических вычислений площади сложных фигур правильно использовать заводской набор. В инструкции от производителя школьник может найти следующую информацию: для чего нужна палетка по математике, из каких материалов она изготовлена, как нужно её использовать. Внешне модель выглядит, как прозрачная пластина либо плёнка с разлиновкой в клетку.

С учётом параметров фигуры, площадь которой необходимо найти, образец разделяется на квадратные миллиметры, сантиметры, дециметры. Некоторые фирмы производят подобные инструменты с магнитной основой. Выбор зависит от предпочтений ребёнка и условий задачи.

Но можно сделать палетку по математике и своими руками.

Для этого потребуются следующие материалы:

• лист в клеточку;
• карандаш;
• скотч;
• линейка.

Если предстоит работа с маленькими величинами, рекомендуется воспользоваться миллиметровой бумагой. Внешне самодельная палетка схожа на заводскую — расчерчена на клетки гибкого листа, предназначенного для нахождения площадей неправильных и правильных фигур, а также выполнения иных упражнений.

Самостоятельный шаблон будет стоить дешевле, чем заводской.

Кроме перечисленных материалов, потребуется прозрачная плотная полиэтиленовая обложка для дневника или тетради. Нужно измерить ее и расчертить ручкой на квадраты со сторонами 1 см. Данный шаблон будет иметь размеры 10х10 см. Если для изготовления применяется миллиметровка, рекомендуется обклеить её сверху скотчем, повторно расчертив клетки. Таким способом продлевается срок эксплуатации инструмента и дополнительно он защищается от влаги.

Чтобы сделать палетку площадью в 100 кв. см, потребуется придерживаться следующего алгоритма:

• На листе в клетку отображается схема инструмента.
• На палетку накладывается обложка.
• Правильно обводятся клеточки. Чтобы инструмент выглядел аккуратно, используется линейка.
• Вырезается готовый шаблон.

Рекомендации по использованию

Процесс измерения площади с помощью палетки простой, если она изготовлена правильно. Инструмент нужно приблизить к фигуре, наложив его сверху, и произвести расчет целых и неполных квадратов. Сложнее пользоваться палеткой, если все точки плоскости не поместились в неё.

В таком случае рекомендуется придерживаться следующего метода:

• Разделить фигуру на части.
• Произвести подсчёт каждой части отдельно.
• Найти суммарный результат.

Рекомендуется подсчитывать отдельно, сколько целых квадратов вмещается в фигуру и сколько неполных. Площадь фигуры вычисляется по специальной формуле: S = количество целых квадратов (количество неполных/2). На уроках математики в начальной школе рекомендуется использовать палетку в виде прозрачного листка, на который нанесена сетка с квадратами (стороны по 1 см). Это объясняется тем, что в младших классах ученики работают с фигурами небольших размеров.

В современных учебниках по математике описаны подробные шаги по изготовлению и применению палетки. Рекомендуется использовать лист из тетради в клеточку. Из него вырезается самостоятельно школьником квадрат со сторонами 10х10 и ячейками в 1 см. Такой инструмент значительно упрощает работу, связанную с вычислением площадей фигур с неровными краями.

Очертания полученного шаблона обводятся чёрным маркером. Им же осуществляется дополнительная разметка составных квадратиков. Предполагается, что подобный метод значительно упростит и ускорит вычисления. Школьнику будет легко и просто посчитать количество полных и неполных квадратов. Полученная палетка оборачивается с двух сторон скотчем либо самоклеющейся обложкой.

За счёт использования маркера отсутствует необходимость в повторной обводке прозрачного шаблона.

Чтобы школьнику было удобно понять, как получается математическое значение, палетку нужно наложить на неровно очерченную поверхность и подсчитать количества полных и неполных квадратов. В современных учебниках по математике первого понятие обозначается буквой P, а второе — N. Общий вид формулы: S=PxN/2.

Другой вариант записи: S=N+M/2, где

• N — целые квадраты.
• M — неполные квадраты.

Необходимо учесть, что полученный результат считается приблизительным, так как площадь и размер неполных квадратиков разная.

Примеры вычислений

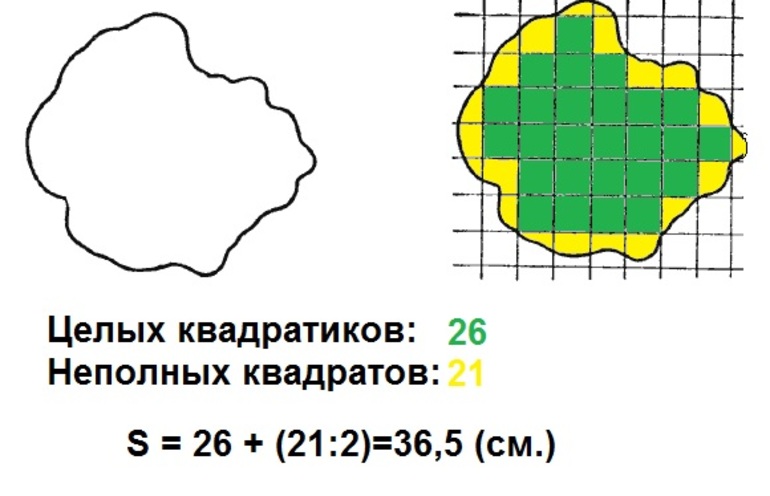
В математике встречаются фигуры с неправильными границами, к примеру, овал. Для вычисления его площади понадобится палетка. Её нужно наложить сверху, подсчитав квадраты внутри границ овала. Предварительно подсчитывается количество целых клеток. Их вышло 34.

Кусочков насчитывается 8. Так как 8 — чётное число, поэтому два неполных квадрата можно засчитать за один целый. Если восемь разделить на два, получится четыре. Если к 34 добавить 4, получится 38. Площадь овала будет примерно равна 38 квадратиков или 38 квадратных сантиметров.

Задача: на тетрадь разлились чернила, появилось пятно. Чтобы выяснить, сколько клеток запачкалось, используется палетка. Так как пятно не имеет чёткой формы, поэтому накладывается сверху шаблон. При подсчёте выходит 17 целых клеток и 24 неполных.

Последнее число делится на два. К результату добавляется 17. Получается около 29 квадратных сантиметров. Другого алгоритма рекомендуется придерживаться, если количество клеток нечётное, к примеру, 30 либо 25. В таком случае на два нужно разделить ближайшую чётную цифру, но больше данного значения на единицу.

Моря и земельные участки

Палетка часто используется учениками на уроках географии. Чтобы найти площадь моря или озера, рекомендуется найти географический атлас либо карту с максимально возможным масштабом. Математический инструмент прикладывается к объекту. Выполняются следующие шаги:

• Считаются целые квадраты.
• Затем — неполные.
• Последний результат делится на два.
• Полученное число суммируется с количеством целых квадратиков.
• Записывается ответ.

Можно воспользоваться схемой и для расчёта площади страны, земельного участка, города. Чтобы выяснить примерную площадь местности, потребуется миллиметровая бумага. На ней с помощью карандаша приблизительно рисуется контур участка. Масштаб можно подобрать самостоятельно.

Современные педагоги и психологи считают, что с помощью палетки у детей формируется умение добывать информацию из текста. Дополнительно ученики начальной школы учатся формулировать и аргументировать свои мысли. За счёт шаблона развиваются вычислительные навыки при подсчёте площади разных геометрических фигур.

Плюсы развития операции логического мышления:

• анализ;
• синтез;
• обобщение;
• аналогия.

Используя палетку, ребёнок учится анализировать свою деятельность. Одновременно развиваются действия самоконтроля, взаимоконтроля, прививается аккуратность, точность при построении разных фигур. Палетка помогает ученикам научиться записывать правильно площадь, переводить одни единицы в другие, решать математические и географические задачи.

С её помощью дети учатся работать с геометрическими фигурами, соблюдая порядок выполняемых действий в числовых выражениях со скобками либо без них.

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри  треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно  это делать и таким образом. 

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см.  Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ«.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.



Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
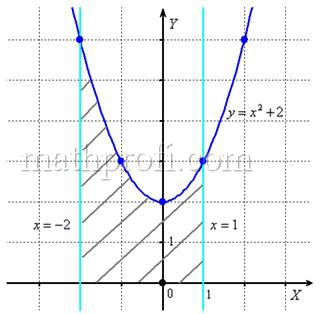
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая  определяет ось , прямые  параллельны оси  и парабола  симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке   график функции  расположен над осью , поэтому искомая площадь:

Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

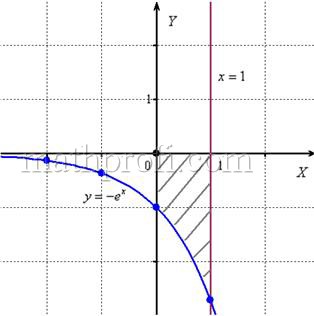
Пример 11
Вычислить площадь фигуры, ограниченной линиями  и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
Вычислить площадь фигуры, ограниченной линиями ,  и координатными осями.

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
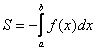
В данном случае:

Ответ:  – ну что же, очень и очень похоже на правду.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы  и прямой , поскольку здесь будут находиться пределы интегрирования.  Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:

таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

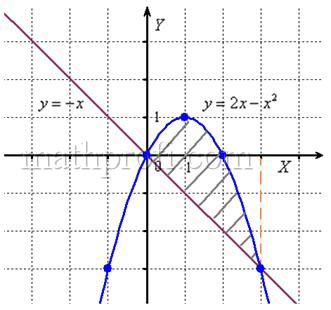
С прямой  всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
 – именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

А теперь рабочая формула: если на отрезке  некоторая непрерывная функция  больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из  нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 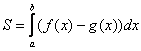. Поскольку ось  задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу  либо

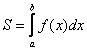
А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

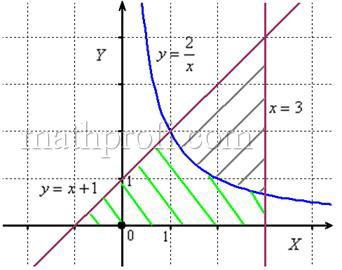
Пример 15
Вычислить площадь фигуры, ограниченной линиями

Решение: выполним бесхитростный чертёж,

хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую  можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке  над осью  расположен график прямой ;
2) на отрезке  над осью  расположен график гиперболы .

Совершенно понятно, что площади можно (и нужно) сложить:

Ответ:

И познавательный пример для самостоятельного решения:

Пример 16
Вычислить площадь фигуры, ограниченной линиями , ,  и координатными осями.

Итак, систематизируем важные моменты этой задачи:

На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс  зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.

Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.

Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой  и прямой , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:

и находим его корни:
 – нижний предел интегрирования,  – верхний предел.

Во-вторых, не всегда понятен «внешний вид» линии, и функция  (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html

После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.

Составляем определённый интеграл или несколько интегралов по формуле 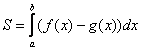, все основные вариации мы разобрали выше.

Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.

Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!

1.9. Объём тела вращения

1.7. Геометрический смысл определённого интеграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин