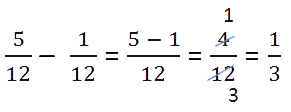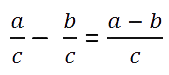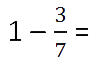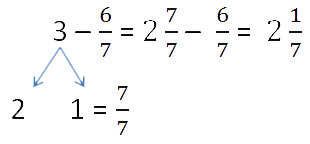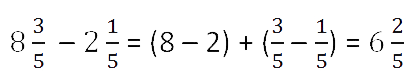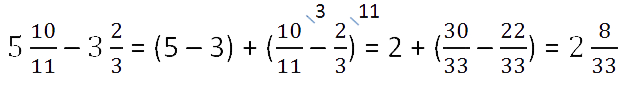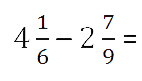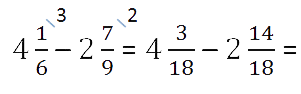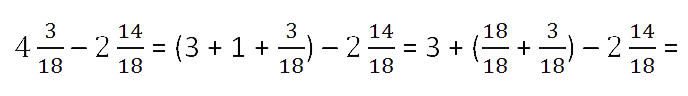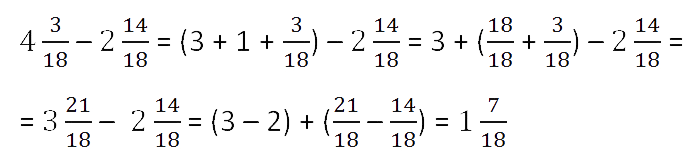Найти разность чисел дробей как это

При вычитании дробей, как и при сложении, могут встретиться несколько случаев.

Вычитание дробей с одинаковыми знаменателями

При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают
числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.

Пример.

В буквенном виде правило вычитания дробей с одинаковыми знаменателями
записывают так:

Вычитание правильной дроби из единицы

Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде
неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.

Пример.

Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную
дробь

и вычитают по правилу вычитания дробей с одинаковыми знаменателями.

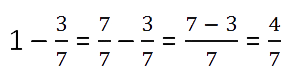
Вычитание правильной дроби из целого числа

Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число
в виде смешанного числа.

Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби,
знаменатель которой равен знаменателю вычитаемой дроби.

Пример.

В примере единицу мы заменили неправильной дробью

и вместо 3 записали смешанное
число и от дробной части отняли дробь.

Вычитание смешанных чисел

При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части
вычитают дробную часть.

При подобных расчётах могут встретиться разные случаи.

Первый случай вычитания смешанных чисел

У дробных частей одинаковые знаменатели и числитель дробной части
уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого
(что вычитаем).

Пример.

Второй случай вычитания смешанных чисел

У дробных частей разные знаменатели.

В этом случае вначале нужно

привести к общему знаменателю
дробные части, а затем
выполнить вычитание целой части из целой, а дробной из дробной.

Пример.

Третий случай вычитания смешанных чисел

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример.

Так как у дробных частей разные знаменатели, то как и
во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.

3 < 14

Поэтому, вспомнив
вычитание правильной дроби из целого числа, займём единицу из целой части и представим
эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.

Сложим полученную неправильную дробь

и дробную часть
уменьшаемого и получим:

Все рассмотренные случаи можно описать с помощью правил вычитания
смешанных чисел.

• Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
• Если дробная часть уменьшаемого меньше дробной части
  вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу
  превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
• Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
• Вычитаем из целой части целую, а из дробной — дробную.
• Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.

---

Ваши комментарии

Оставить комментарий:

---

Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:

где a — числитель, b — знаменатель.

Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/3), неправильной — если числитель больше знаменателя (например, 5/2).

Вычитание обыкновенных дробей

Вычитание дробей — это арифметическое действие, в результате которого получается новое число, содержащее разность заданных чисел.

Разберем на конкретных примерах: как находить разность дробей с одинаковыми и разными знаменателями, как из натурального числа вычесть дробь и наоборот, познакомимся с вычитанием смешанных дробей.

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть дроби с одинаковыми знаменателями нужно из числителя первой дроби вычесть числитель второй, а знаменатели оставить без изменения. В общем виде это будет выглядеть следующим образом:

Пример 1:

7 8

—

2 8

Решение:

7 8

—

2 8

=

7 — 2 8

=

5 8

Таким образом, чтобы вычесть дроби с одинаковыми знаменателями нужно найти разность их числителей, а знаменатель оставить без изменения.

Как вычитать дроби с разными знаменателями

В общем виде, вычитание дробей с разными знаменателями, выглядит следующим образом:

a b

—

c d

=

a ∙ m1 — c ∙ m2 e

где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).

Пример 3:

5 3

—

2 7

Решение:

5 3

—

2 7

=

5 ∙ 7 21

—

2 ∙ 3 21

=

35 21

—

6 21

=

35 — 6 21

=

29 21

=

1

8 21

Подробнее про нахождение НОЗ — смотрите тут.

Как из целого числа вычесть дробь?

Вычитание обыкновенной дроби из целого числа, сводится к представлению целого числа в виде дроби, в которой знаменатель будет единицей, а числитель самим числом, к примеру:

Дальнейшее вычисление происходит по стандартному алгоритму.

Как из обыкновенной дроби вычесть целое число?

Порядок действий, при вычитании целого числа из дробного, аналогичен, т.е. представляем целое число в виде дроби со знаменателем — 1 и находим разность, согласно представленным выше алгоритмам вычитания.

Как вычитать смешанные дроби?

Вычитание смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:

Пример 4:

3

2 4

—

3 5

Решение:

3

2 4

—

3 5

=

3 ∙ 4 + 2 4

—

3 5

=

14 4

—

3 5

=

14 ∙ 5 20

—

3 ∙ 4 20

=

70 20

—

12 20

=

70 — 12 20

=

58 20

=

29 10

=

2

9 10

Правила вычитания дробей

Резюмируя вышесказанное, выведем общий алгоритм вычитания дробей:

• Если дробь смешанная — приводим её к неправильному виду;
• Если дроби имеют одинаковые знаменатели — из числителя первой дроби вычитаем числитель второй;
• Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, находим разность числителей;
• При необходимости сокращаем и приводим к неправильному виду.

Смотрите также:

• Смотрите также
• Калькуляторы
• Последние примеры

Калькулятор вычитания дробей

Оцените материал:

Загрузка…

Содержание:

• Вычитание дробей с одинаковыми знаменателями
• Вычитание дробей с разными знаменателями
• Вычитание смешанных дробей

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть дроби с одинаковыми знаменателями, нужно от
числителя первой дроби отнять числитель второй, а
знаменатель оставить без изменений.

Вычитание дробей с разными знаменателями

Чтобы вычислить дроби с разными знаменателями, нужно вначале привести их к наименьшему
общему знаменателю, а затем отнимать их как дроби с одинаковым знаменателем.

Вычитание смешанных дробей

Чтобы вычесть одно смешанное число из другого смешанного числа, надо, если это возможно, от целого отнять целое, а от дроби отнять дробь.

В случае, когда дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом: берут одну единицу
(целое) из целого числа уменьшаемого, записывают его как неправильную дробь, числитель и знаменатель которой равны между
собой и равны знаменателю дробной части, и прибавляют к дробной части, далее отнимают две смешанные дроби, как описано выше.

Аналогичным образом поступают, когда надо вычесть из целого числа дробное.

Замечание. Производить операции со
смешанными числами можно и иначе: записать смешанное число в виде
неправильной дроби и уже работать далее как с
обыкновенными дробями.

Читать следующую тему: умножение дробей.

Математика

5 класс

Урок № 59

Вычитание дробей

Перечень рассматриваемых вопросов:

– вычитание дробей с одинаковыми знаменателями;

– вычитание дробей с разными знаменателями;

– проверка вычитания сложением.

Тезаурус

Разность двух дробей – это дробь, которая в сумме с вычитаемым даёт уменьшаемое.

Разность двух дробей с общим знаменателем – это дробь с тем же знаменателем, числитель которой равен разности числителей уменьшаемого и вычитаемого.

Обязательная литература:

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС. / С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 272.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты. 5 кл. / П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009, стр.142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. / И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Вспомним, что такое разность дробей. Разностью двух дробей называют дробь, которая в сумме с вычитаемым даёт уменьшаемое.

Будем пока рассматривать случаи, когда уменьшаемое больше вычитаемого.

Разность двух дробей с общим знаменателем есть дробь с тем же знаменателем, числитель которой равен разности числителей уменьшаемого и вычитаемого.

Какую часть корзинки осталось набрать?

Давайте подумаем, как построить ход решения и какими арифметическими действиями его сопроводить?

Так как Таня ходила за ягодами два раза, то найти, сколько всего ягод она набрала, нам поможет арифметическое действие – сложение:

Вопрос в задаче – какую часть корзинки осталось набрать?

Значит, нам нужно из объёма всей корзинки, вычесть ту часть, которую Таня уже набрала.

Сделаем проверку:

Сумма разности и вычитаемого действительно равна уменьшаемому.

Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему знаменателю, а затем применить правило вычитания дробей с общим знаменателем.

Например, найдём разность семи восьмых и трёх пятых. Знаменатели дробей взаимно простые числа, поэтому общий знаменатель равен их произведению, т. е. сорока.

Не забываем умножить дополнительные множители и на числители. В итоге получаем дробь одиннадцать сороковых.

Решим задачу. Две сестры помогли маме помыть посуду.

Младшая – ?

Найдём разность всей вымытой посуды и той части, которую вымыла старшая дочь.

Итак, чтобы найти разность двух дробей, нужно определить равные или разные у них знаменатели, а затем использовать то правило вычитания дробей, которое подходит в конкретном случае.

Вычитание обыкновенных дробей

Разбор решения заданий тренировочного модуля

№1. На ветке сидели воробьи. Когда четверть воробьёв улетела, их осталось 9. Сколько воробьёв было на ветке?

По рисунку видно, что в трёх равных оставшихся частях 9 воробьёв, значит в одной части:

1. 9 : 3 = 3 – воробья в одной части.

Одна часть воробьёв улетела, значит, улетело 3.

Тогда:

1. 3 + 9 = 12 – воробьёв было всего на ветке.

Или можно ответить на вопрос так: в одной части 3 воробья, а всего таких частей 4, значит:

1. 3 ∙ 4 = 12 – воробьёв было всего на ветке.

Ответ: 12 воробьёв сидело на ветке.

№2. Выберите выражения, в которых в результате вычитания получается единица.

Решение: найдём результаты каждого выражения.

Мы видим, что только в двух выражениях в результате получилась единица. Это и есть верные ответы.

В данной публикации мы рассмотрим, каким образом можно найти разность обыкновенных (простых) дробей с разными или одинаковыми знаменателями, и как выполняется вычитание смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Вычитание дробей

С одинаковыми знаменателями

При вычитании дробей с одинаковыми знаменателями, из числителя первой дроби отнимается числитель второй дроби. Знаменатель при этом остается тем же.

 
Примечание: Следует проверить новую дробь, полученную путем вычитания. Возможно, ее можно сократить.

С разными знаменателями

Чтобы вычесть одну дробь из другой, знаменатель которой отличаются от первой, нам нужно:

1. Привести данные дроби к наименьшему общему знаменателю.
2. Затем выполнить вычитание – как для дробей с одинаковыми знаменателями.

Разность смешанных дробей

Чтобы найти разность смешанных дробей, сперва отдельно вычитаем их целые части, затем – отдельно дробные. Полученные результаты складываем.

 
Примечание: Если дробные части имеют разные знаменатели, сперва их приводим к наименьшему общему знаменателю, затем – вычитаем.

Примеры задач

Задание 1

 
Решение

У данных дробей один и тот же знаменатель, следовательно:

 
Задание 2

 
Решение

Сперва приводим дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 140. Значит, дополнительный множитель для первой дроби – 20, для второй – 7.

 
Теперь у нас дроби с одинаковыми знаменателями, и мы можем вычесть из первой вторую:

 
Задание 3

 
Решение

Так как дробные части имеют одинаковые знаменатели, мы сразу можем выполнить вычитание: