Найти скорость точки как функцию времени

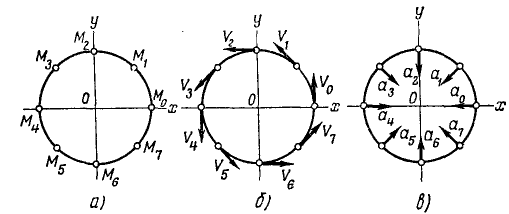
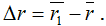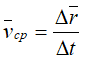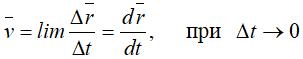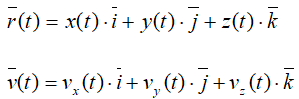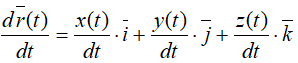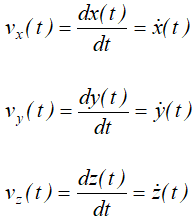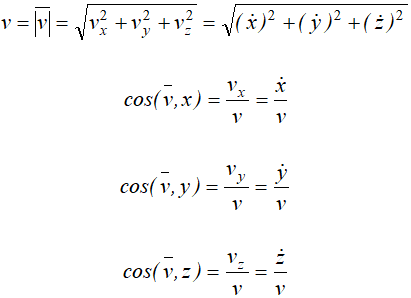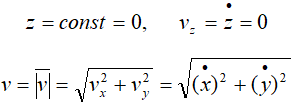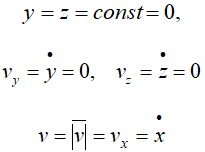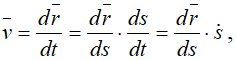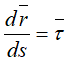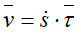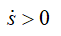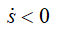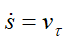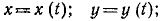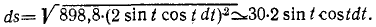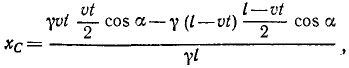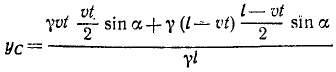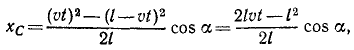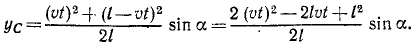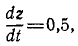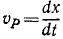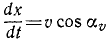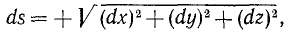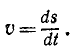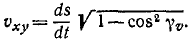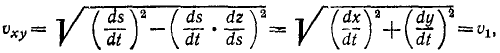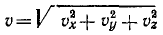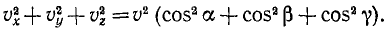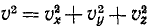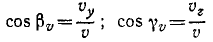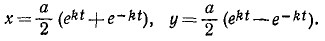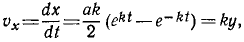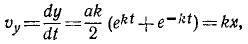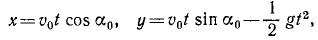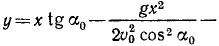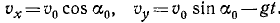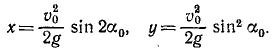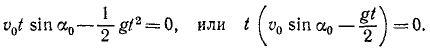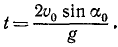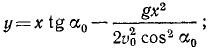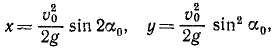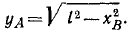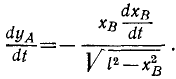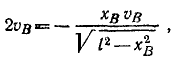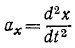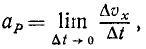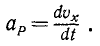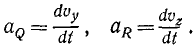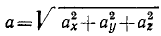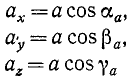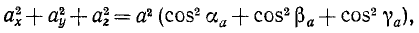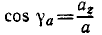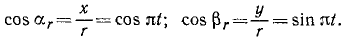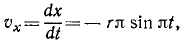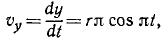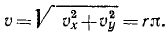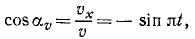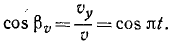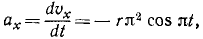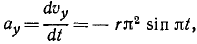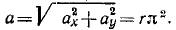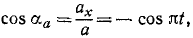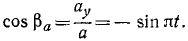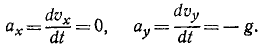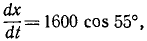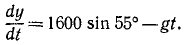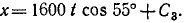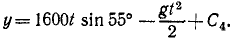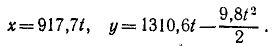Содержание:

1. Определение скорости
2. Определение ускорения
3. Пример с решением №1.
4. Пример с решением №2.
5. Определение траектории, скорости и ускорения точки при векторном способе задания движения
6. Определение траектории, скорости и ускорения точки при координатном способе задания движения
7. Пример с решением №3.
8. Пример с решением №4.
9. Пример с решением №4.
10. Определение скорости и ускорения точки при естественном способе задания движения

Определение скорости

Вспомним основную формулу кинематики для определения скорости

Здесь — вектор перемещения точки, — время перемещения (рис. 86). Обозначим перемещение вдоль траектории за этот же промежуток времени и представим правую часть этого равенства в виде произведения двух пределов:

Первый из этих пределов равен производной и может быть вычислен, поскольку закон движения по траектории при естественном способе описания движения задается. Далее, простые рассуждения показывают, что второй предел равен по модулю единице (как предел отношения длины хорды к длине дуги) и направлен по касательной в сторону возрастания Следовательно, он определяет орт касательной для которого попутно получаем формулу

Таким образом, при естественном способе задания движения скорость точки определяется формулой

Формулу можно рассматривать как результат разложения вектора на составляющие по естественному координатному базису. Величина равна проекции скорости на направление касательной, а проекции скорости на главную нормаль и бинормаль равны нулю. В общем случае где — модуль скорости. Если точка движется в положительном направлении, то и можно записать

Определение ускорения

Будем исходить из общей формулы для ускорения

Пусть, для определенности, точка движется в положительную сторону отсчета дуг; тогда вектор скорости выражается формулой

где — модуль скорости, — орт касательной. В общем случае криволинейного движения переменны оба сомножителя в этой формуле; последний — вследствие изменения направления касательной. Поэтому орт имеет производную по времени, которая выражается формулой

где и — соответственно орт главной нормали и радиус кривизны траектории в рассматриваемом положении движущейся точки.*

Возможно вам будут полезны данные страницы:

Дифференцируя по времени выражение для скорости, получим

Формула выражает ускорение точки в виде суммы составляющих по осям естественной системы координат. Из нее следует, что ускорение имеет на эти оси проекции

Первая из них есть проекция ускорения на касательную и называется касательным ускорением. Вектор касательного ускорения

направлен в сторону скорости, если движение ускоренное и против скорости, если движение замедленное

Проекция ускорения на главную нормаль называется нормальным ускорением. Модуль и вектор нормального ускорения выражаются формулами

Так как величина положительна, нормальное ускорение всегда направлено в сторону орта то есть по главной нормали в сторону вогнутости траектории.

Проекция ускорения на бинормаль (аь) равна нулю, что означает, что вектор ускорения лежит в соприкасающейся плоскости. Таким образом, ускорение при естественном способе задания движения точки определяется как сумма касательного и нормального ускорений:

Это правило дополнительно проиллюстрировано на рис. 87, где случай а) соответствует ускоренному движению точки, а случай б) — замедленному движению. Модуль ускорения в обоих случаях определяется по теореме Пифагора:

Если точка движется прямолинейно, то нормальное ускорение не и ускорение состоит только из касательного:

При равномерном криволинейном движении наоборот, отсутствует касательное ускорение и полное ускорение точки равно ее нормальному ускорению:

Пример с решением №1.

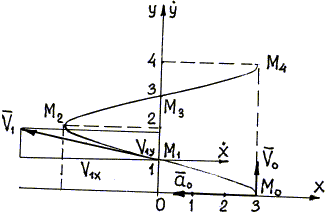
Точка движется по окружности радиуса согласно закону Вычислить и построить скорость и ускорение точки в момент когда она пройдет половину окружности.

В момент дуговая координата точки равна половине длины окружности: откуда находим

Определяем скорость точки в момент ив расчетный момент

Определяем касательное ускорение

Видно, что оно не изменяется с течением времени — точка движется равноускоренно. Это же значение касательное ускорение имеет и в расчетный момент:

Определяем нормальное ускорение

Определяем полное ускорение в момент

На рис. 88 показаны положения точки в текущий и расчетный моменты времени, а также векторы скорости и ускорений точки в момент

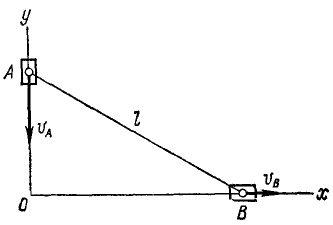
В заключение заметим, что от одногоспособа задания движения можно перейти к другим способам. Например, при определении скорости в случае координатного способа описания движения был предварительно сделан переход к векторному способу в виде

• Чтобы перейти от координатного способа к естественному, прежде всего требуется найти уравнение траектории. Как было показано выше, это делается исключением из уравнений движения времени Закон движения по траектории можно получить на основе равенств

и

определяющих скорость точки при естественном и координатном способах задания движения. Приравняв правые части равенств, разрешая полученное соотношение относительно и интегрируя, находим

Это выражение определяет закон движения по траектории в общем

виде.

Если отсчет дуговой координаты вести от начального положения точки в сторону движения, то радикал положителен, и закон движения примет вид

Различают векторный, координатный и естественный (натуральный) способы задания движения.

Векторный способ задания движения состоит в следующем.

Пусть — движущаяся точка, — тело отсчета (рис. 72). Выберем в теле произвольную точку — точку отсчета, построим вектор Этот вектор, начало которого совпадает с точкой отсчета , а конец — с точкой называется радиусом-вектором точки При движении точки радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени

Если эта функция известна, то для каждого момента времени может быть построен вектор и тем самым найдено положение движущейся точки в этот момент.

Функция (1) называется векторным законом (векторным уравнением) движения точки

При координатном способе задания движения с телом отсчета связывается какая-либо, например декартова прямоугольная, система координат (рис. 73). Движение точки будет задано, если ее координаты будут известны как функции времени

Зависимости (2), выражающие текущие координаты движущейся точки в виде функций времени, называются уравнениями движения точки в декартовых координатах.

Если точка движется, оставаясь все время в одной плоскости, то оси можно расположить в той же плоскости и ограничиться двумя уравнениями движения

При движении в плоскости часто удобно пользоваться полярной системой координат, задавая положение точки ее полярным углом и полярным радиусом (рис. 74). В этом случае уравнения движения точки имеют вид

Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. Естественный способ задания движения состоит в задании траектории точки и закона движения по траектории.

Пусть траектория точки суть заданная кривая, — положение точки на ней (рис. 75). Будем рассматривать траекторию как криволинейную координатную ось, для чего выберем на ней начало отсчета дуг (точку ) и направление отсчета дуг (на рис. 75 направление отсчета дуг выбрано вправо от точки ). Длина дуги взятая со знаком плюс или минус в зависимости от положения точки относительно начала отсчета дуг вполне определяет положение точки в пространстве и называется дуговой координатой точки. Движение точки будет задано, если ее дуговая координата будет выражена в виде функции времени

Зависимость (4) называется законом движения точки по траектории или, что то же самое, законом движения точки в естественной форме.

Пример с решением №2.

Написать уравнения движения точки, движущейся равномерно по окружности радиуса и делающей оборотов за одну минуту.

Начнем с естественного способа описания движения. Изображаем траекторию- окружность радиуса с центром в точке (рис. 76). Начало отсчета дуг совместим с положением точки в момент начала наблюдения, то есть при за положительное направление отсчета выберем направление в сторону движения точки.

Пусть — положение движущейся точки в текущий момент времени Для центрального угла который будем отсчитывать в сторону движения точки, согласно условию, можем написать

Здесь измеряется в радианах, — в секундах.

Длина дуги радиус окружности и центральный угол связаны геометрическим соотношением

Подставляя сюда найденное значение получаем

Это и есть естественной форме.

Для описания движения в координатной форме прежде всего следует выбрать подходящую систему координат, например, изображенную на рис. 77. Далее строят координатные отрезки и определяют соответствующие переменные расстояния. В нашем случае будем иметь:

Подставляя сюда угол как функцию времени, получаем уравнения движения в координатной форме

Пусть — координатные орты. Тогда для радиуса-вектора точки будем иметь:

Полученное равенство, выражающее радиус-вектор точки как функцию времени, служит векторным уравнением ее движения.

Определение траектории, скорости и ускорения точки при векторном способе задания движения

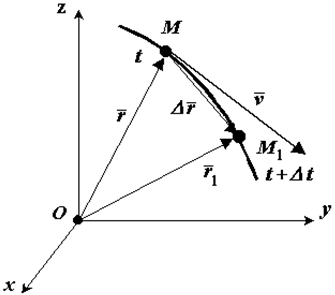
Пусть движение точки задано векторным способом, то есть задан радиус-вектор точки как функция времени

Линия, описываемая концом переменного вектора, начало которого находится в заданной неподвижной точке, называется годографом этого вектора. Отсюда и из определения траектории следует правило: траектория точки есть годограф ее радиуса-вектора.

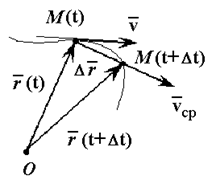
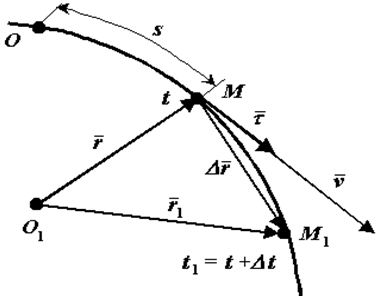
Пусть в некоторый момент точка занимает положение и имеет радиус-вектор а в момент — положение и радиус-вектор (рис. 78).

Вектор соединяющий последовательные положения точки в указанные моменты, называется вектором перемещения точки за время Вектор перемещения следующим образом выражается через значения вектор-функции (5):

Если вектор перемещения поделить на величину промежутка получим вектор средней скорости точки за время

Будем теперь уменьшать промежуток устремляя его к нулю. Предел, к которому стремится вектор средней скорости при неограниченном уменьшении промежутка называется скоростью точки в момент или просто скоростью точки В соответствии со сказанным для скорости получаем:

Итак, вектор скорости точки равен производной по времени от ее радиуса-вектора:

Поскольку секущая в пределе (при ) переходит в касательную приходим к выводу, что вектор скорости направлен по касательной к траектории в сторону движения точки.

В общем случае скорость точки также переменна, и можно интересоваться быстротой изменения скорости. Скорость изменения скорости называется ускорением точки.

Для определения ускорения выберем какую-либо неподвижную точку и будем откладывать из нее вектор скорости в различные моменты времени. Линия, которую опишет конец вектора скорости, представляет собой годограф Годограф и скорости (рис. 79). Изменение вектора скорости выражается в том, что геометрическая точка движется по годографу скорости, а скорость этого движения служит, по определению, ускорением точки

Применив для переменного вектора все те рассуждения, которые были использованы выше для переменного вектора для ускорения получаем:

или, при обозначении производной по времени точкой:

Формулы (6) — (8) являются наиболее общими формулами кинематики для определения скорости и ускорения.

Определение траектории, скорости и ускорения точки при координатном способе задания движения

Пусть движение точки задано уравнениями движения в декартовых координатах:

Для каждого момента времени по этим уравнениям можно определить координаты точки в этот момент и указать ее положение в пространстве. Придавая всевозможные значения, получим множество положений движущейся точки в пространстве — ее траекторию. Следовательно, уравнения движения одновременно являются уравнениями траектории точки в параметрической форме, причем параметром служит время . Чтобы получить уравнение траектории в виде зависимости между координатами точки, достаточно из уравнений движения исключить время.

Пример с решением №3.

Движение точки задано уравнениями ( — в сантиметрах, — в секундах). Найти уравнение траектории точки в координатной форме.

Для определения уравнения траектории из уравнений движения исключаем время Для этого из первого уравнения выражаем

и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:

Опуская промежуточные выражения, получаем уравнение траектории

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке Траекторией служит кусок этой параболы, заключенный между точками с координатами и (рис. 80).

Пример с решением №4.

Определить уравнение траектории, если точка движется согласно уравнениям (— в сантиметрах, — в секундах):

Для исключения времени из уравнений движения выразим из этих уравнений и

Возводя эти равенства в квадрат и почленно складывая, получаем уравнение траектории в координатной форме:

Это уравнение эллипса с центром в точке и с полуосями (рис. 81). Траекторией служит вся кривая эллипса.

Займемся теперь определением скорости и ускорения.

Зная уравнения движения точки, можно выразить в функции времени радиус-вектор точки (рис. 82):

Теперь находим скорость, дифференцируя радиус-вектор по времени:

При дифференцировании учитывается, что оси неподвижны, поэтому координатные орты являются постоянными векторами, и их производные равны нулю.

Полученная формула определяет скорость точки в виде разложения

по координатному базису Так как коэффициенты при ортах равны проекциям скорости на соответствующие координатные оси, отсюда следуют формулы

По известным проекциям находим модуль и направляющие косинусы скорости:

Аналогичным образом определяется и ускорение. Дифференцируя выражение для вектора скорости, получаем:

Откуда для проекций ускорения следуют формулы

Проекции ускорения можно выразить также через проекции скорости:

Модуль и направляющие косинусы ускорения выражаются равенствами

Пример с решением №4.

Точка движется в плоскости ху согласно уравнениям

где — заданы в сантиметрах, время — в секундах, а величины — заданные постоянные. Найти скорость и ускорение точки в момент, когда она впервые после начала движения пересекает ось

Скорость и ускорение находим, вычисляя их проекции на координатные оси. Сначала это сделаем для произвольного момента

Когда точка находится на оси , выполняется равенство Подставляя это значение во второе уравнение движения и решая полученное уравнение относительно находим

Момент соответствует началу движения, а первое после начала движения пересечение оси происходит при Подставляя это значение в предыдущие формулы, найдем

Таким образом, в расчетный момент времени скорость ускорение имеют модули

и направляющие косинусы

На рис. 83 показана геометрическая картина движения. Траекторией точки служит окружность радиуса с центром в точке Подставляя в уравнения движения находим, что в начальный момент точка находится в положении Придавая времени малое положительное значение и определяя знаки координат получаем из чего следует, что точка движется из положения против хода часовой стрелки. В расчетный момент она находится в начале координат, имея скорость и ускорение

Определение скорости и ускорения точки при естественном способе задания движения

Естественные координатные оси и их орты

Пусть заданы траектория точки, начало и направление отсчета дуг. Выберем на траектории произвольным образом точку и проведем касательную . Плоскость, проходящая через точку перпендикулярно к касательной называется нормальной плоскостью траектории в точке (рис. 84).

Придадим дуговой координате приращение и отметим точку с координатой Пусть — касательная к траектории в точке В общем случае траектория точки — пространственная кривая, поэтому касательные и суть скрещивающиеся прямые.

Проведем прямую параллельную касательной Прямые и образуют плоскость Предельное положение плоскости когда точка ‘ неограниченно приближается к точке называется соприкасающейся плоскостью траектории в точке Соприкасающаяся плоскость представляет собой ту из бесконечного множества плоскостей, проходящих через касательную которая наиболее тесно примыкает к траектории в окрестности точки В случае плоской траектории соприкасающаяся плоскость совпадает с плоскостью траектории.

Нормальная и соприкасающаяся плоскости взаимно перпендикулярны. Проведем через точку третью плоскость, перпендикулярную к обеим указанным плоскостям — так называемую спрямляющую плоскость. В итоге получаем прямой трехгранный угол с вершиной в точке называемый естественным трехгранником траектории в этой точке. Ребрами естественного трехгранника являются касательная главная нормаль — линия пересечения нормальной и соприкасающейся плоскостей и бинормаль (вторая нормаль) — линия пересечения нормальной и спрямляющей плоскостей (рис. 85).

Касательная, главная нормаль и бинормаль взаимно перпендикулярны и после установления на них направлений образуют естественную систему координатных осей. Положительное направление касательной выбирается в сторону возрастания дуговой координаты и задается ортом касательной Положительное направление главной нормали задается ортом который направляют от точки в сторону вогнутости траектории. Орт бинормали выбирают согласно правилу чем обеспечивается правосторонность естественного координатного базиса (см. рис. 85).

    В
задачах данного раздела определяются
координаты, скорость, ускорение точки
в любой назначенный момент времени при
различных способах задания движения.
Из всех способов задания движения точки
наибольшее распространение получили
координатный и естественный способы.

    Рассмотрим
вначале координатный способ задания
движения точки. Положение в пространстве
движущейся точки определяется тремя
координатами в декартовой системе
координат. Эти координаты задаются как
функции времени:

                      
(1.1)

    Зависимости
(1.1) называются уравнениями движения
точки в декартовых координатах.

    Если
движение точки происходит в плоскости
ху, то задаются только два уравнения
движения:

x
= x(t);              
y = y (t).

    При
прямолинейном движении точки достаточно
задать одно уравнение движения:

x
= x(t),

если
принять, что ось х совпадает с прямой,
по которой движется точка.

    Скорость
точки представляет собой вектор,
характеризующий быстроту и направление
движения точки в данный момент времени.

    При
задании движения точки уравнениями
(1.1) проекции скорости на оси декартовых
координат равны:

    Модуль
скорости

                               
.
                                         
(1.2)

    Направление
скорости определяется направляющими
косинусами:

.

    Если
движение точки задается в плоскости
ху, то

.

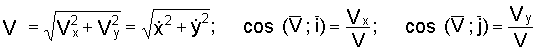
    При
прямолинейном движении по оси х:

.

    Характеристикой
быстроты изменения скорости является
ускорение
а.
Ускорение точки равно производной от
вектора скорости по времени:

.

    При
задании движения точки уравнениями
(1.1) проекции ускорения на координатные
оси равны:

    Модуль
ускорения:

                      
.
                                         
(1.3)

    Направление
ускорения определяется направляющими
косинусами

;
;.

    Если
движение точки задается в плоскости
ху, то
;

;
;.

    При
прямолинейном движении по оси х

;
.

    Далее
рассмотрим естественный способ задания
движения точки.

    Считается,
что движение точки задано естественным
способом, если указаны ее траектория и
закон изменения криволинейной координаты
s = s(t). Уравнение s = s(t) называется
законом движения точки по траектории.
При этом на траектории указывается
начало отсчета, а также положительное
направление отсчета координаты s в виде
стрелки
.

    Модуль
скорости точки определяется по формуле

                              
.
                                                                 
(1.4)

    Вектор
скорости
V направлен по касательной к траектории
в сторону стрелки
,
если,
и в противоположную сторону, если.

    Ускорение
точки определяется как векторная сумма
касательного и нормального ускорений
точки:

 а
=
а
+
а_n
.

    Модуль
касательного ускорения определяется
по формуле

                             
.
                                                   
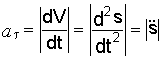
(1.5)

    Вектор
касательного ускорения
а
направлен
по касательной к траектории в сторону
стрелки
,
если,
и в противоположную, если.

    Модуль
нормального ускорения определяется по
формуле

                                         
,
                                                            
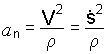
(1.6)

где

– радиус кривизны траектории в данной
точке.

    Вектор
нормального ускорения
а_n
всегда направлен по главной нормали в
сторону центра кривизны траектории.

    Модуль
полного ускорения

                                           
.
                                                          
(1.7)

    Если
движение точки задано координатным
способом, то можно определить параметры
движения, характерные для естественного
способа задания движения.

    Так
можно, например, по уравнениям движения
точки (1.1) найти уравнение ее траектории
в форме зависимости между координатами.
Для этого надо из уравнений движения
исключить время t. Затем можно найти
закон движения точки по траектории s =
s(t), используя формулу (1.4). Из этой формулы
следует, что ds = V dt; с учетом формулы
(1.2) имеем
и

                                       
.
                                                
(1.8)

    В
законе движения (1.8) за начало отсчета
координаты s принимается начальное
положение точки, когда t = 0. Знак “плюс”
или “минус” перед интегралом ставится
в зависимости от выбора положительного
направления отсчета координаты s: если
движение точки начинается в сторону
стрелки
,
то следует брать знак “плюс”, в противном
случае – знак “минус”.

    Рассмотрим
вначале методику решения задач, в которых
движение точки задано координатным
способом. Уравнения (1.1) определяются
либо из геометрических условий, либо в
результате интегрирования дифференциальных
уравнений движения точки. Интегрирование
дифференциальных уравнений движения
точки рассматривается в разделе “Динамика
точки”, который не входит в данное
пособие. Получение уравнений (1.1) с
использованием геометрии движения
рассмотрим на примере исследования
движения точки обода колеса.

Задача
1.1 (3)

Задача
1.2 (1)

Задача
1.3 (2)

Задача
1.4 (4)

Задача
1.5 (4)

Задача
1.6 (5)

Задача
1.7 (6)

Задача
1.8 (7)

Задача
1.1 (3)

    Найти
уравнения движения точки М обода колеса
радиуса R вагона, который движется по
прямолинейному участку пути со скоростью
V. Колесо катится без скольжения. Точка
М в начальный момент движения соприкасалась
с рельсом, т.е. занимала положение М₀
(рис. 1.1).

Рис.
1.1

    Решение

    Изобразим
на расчетной схеме (рис. 1.1) оси координат
х и у, начало координат поместим в
начальное положение точки М₀.

    Рассмотрим
два положения колеса: в начальный момент
t = 0 и в текущий момент времени t.

    Отметим
положение точки М на ободе колеса и
положение центра С колеса в момент t,
координаты точки: x_м
= М₀В,
у_м
= МВ.

    Расстояние
от центра колеса до рельса остается
постоянным и равным R; это значит, что
центр C колеса движется по прямой,
параллельной оси х. За время t центр
колеса переместится на расстояние C₀C
= Vt (закон равномерного движения точки
C), одновременно колесо повернется на
угол 
.

    Чтобы
получить уравнения движения точки М,
надо координаты этой точки представить
как функции времени.

    Из
расчетной схемы (рис. 1.1) видно, что

х_м
= C₀C
– ЕС, у_м
= ВЕ – МЕ;

или

х_м
= Vt – ЕС, у_м
= R – МЕ.

    Из
треугольника МЕС имеем;

МЕ
= Rsin (90
– 
) = Rcos
,

ЕC
= Rcos (90
– 
) = Rsin
,

Тогда
х_м
= Vt – Rsin
, (a)

у_м
= R – Rcos
.

    Найдем
зависимость угла 
от времени t: так как колесо катится без
скольжения, то длина дуги АМ окружности
обода колеса (рис.1.1) равна длине отрезка
М₀А.

    При
этом

М₀А
= С₀С
= Vt ,

но
длина дуги АМ равна также произведению
радиуса R на центральный угол 
; поэтому Vt = R
, отсюда
.

    Теперь
уравнения (а) будут иметь вид

;
                
.

    Полученные
уравнения представляют собой уравнения
движения точки М. В аналитической
геометрии показано, что это параметрические
уравнения циклоиды (параметром в данном
случае является время t). Таким образом,
траектория точки обода колеса, движущегося
по прямолинейному участку пути без
проскальзывания, является циклоидой.
Длина одной ветви циклоиды L (рис. 1.1)
равна 2
R, высота – H = 2R.

Задача
1.2 (1)

    Даны
уравнения движения точки:

      
;       
(х,
у – м; t – с).                          
(б)

1. Определить
   уравнение траектории и построить ее.

2. Определить
   начальное положение точки на траектории.

3. Указать
   моменты времени, когда точка пересекает
   оси координат.

4. Найти
   закон движения точки по траектории s =
   s(t), принимая за начало отсчета расстояний
   начальное положение точки.

5. Построить
   график движения точки.

    Решение

    1.
Для получения уравнения траектории
вида F(x, y) = 0 исключим из уравнений
движения (б) время t: из первого уравнения
системы (б) найдем

,

подставляя
это выражение во второе уравнение той
же системы, получим уравнение траектории

y
= x + 5.

Рис. 1.2

Это – уравнение прямой линии. Для построения прямой представим ее уравнение в отрезках , где а– отрезок, отсекаемый прямой на оси х, b – отрезок, отсекаемый прямой на оси у. В данном случаеа= -5 м, b = 5 м. Откладываем на оси х отрезока= -5 м, по оси у – отрезок b = 5 м. Через полученные точки проводим прямую (рис. 1.2).

    2.
Для определения положения точки в
начальный момент времени необходимо
подставить значение t = 0 в уравнения
движения (б)

м;

м.

Точка
при t = 0 занимает положение М₀
(-1;4).

    3.
В момент пересечения точкой оси у
координата х равна нулю, а первое
уравнение системы (б) примет вид:

.

Отсюда

где
n = 0, 1, 2 …

    В
момент пересечения точкой оси х координата
у равна нулю, а второе уравнение системы
(б) примет вид:

или
.

Но
косинус не может быть больше 1.
Следовательно, точка не пересекает ось
х (см. об этом также п. 4 решения задачи).

    4.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
начальное положение точки М₀.
Подставляя в уравнения (б) значения t >
0, видим, что с выходом из начального
положения М₀
координаты точки х и у увеличиваются.
Это направление движения точки примем
за положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.2), а в формуле (1.8) оставим знак
“плюс”:

.

    Учитывая,
что

получим

или

                                         
.
                                                      
(в)

    Из
закона (в) следует, что координата s не
может быть отрицательной, т.е. точка
движется по полупрямой М₀М
(рис.1.2) и ось х не пересекает (см. по этому
поводу п. 3 решения задачи).

    5.
График движения точки – это графическое
представление зависимости расстояния
s от времени t. Для построения такого
графика по оси абсцисс откладывают
последовательные значения времени t, а
по оси ординат – соответствующие им
значения расстояния s. Построенные точки
соединяют плавной линией. График
зависимости (в) можно построить быстрее,
если воспользоваться известным графиком
косинуса. Для этого вначале построим
график функции
(штриховая
линия на рис. 1.3), затем этот график
сместим вдоль оси s на величинум.

Рис.
1.3.

Задача
1.3 (2)

    Даны
уравнения движения точки:

          
;       
(х,
у – см; t – с ).                            
(г)

1. Определить
   уравнение траектории и построить ее.

2. Определить
   начальное положение точки на ее
   траектории.

3. Найти
   закон движения точки по траектории s =
   s(t), принимая за начало отсчета расстояний
   начальное положение точки.

4. Определить
   время T прохождения точкой полной
   окружности.

    Решение

Рис. 1.4

1. Чтобы найти уравнение траектории точки необходимо из уравнений движения (г) исключить время t. Для этого уравнения движения (г) разрешим относительно ии возведем полученные результаты в квадрат ; ,

    сложим
эти уравнения и после преобразования
получим

.

    Это
уравнение окружности радиуса R = 5 см,
центр окружности расположен в точке
С (-2,5; 5) (рис. 1.4).

    2.
Для определения начального положения
точки подставим значение времени t = 0 в
уравнения (г)

х₀
= 5 соs0 – 2,5 = 2,5 см; у₀
= 5 sin0 – 5 = 5 см;

    Точка
при t = 0 занимает положение М₀
(2,5; 5).

    3.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
точку M₀.
Из системы уравнений (г) видно, что с
увеличением времени t от нуля x уменьшается,
а y увеличивается.

    Такое
возможно, если после выхода из начального
положения точка будет двигаться по
окружности против часовой стрелки. Это
направление движения точки примем за
положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.4), а в формуле (1.8) перед интегралом
оставим знак “плюс”:

,
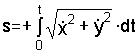
где
;.

    Отсюда

                                              
;
.
                                          
(д)

    4.
Определим время Т прохождения точкой
полной окружности.
Т – время, по
истечении которого s в формуле (д) станет
равным длине окружности 2
R:

                                       
.

    Отсюда
с.

Задача
1.4 (4)

    Даны
уравнения движения точки:

                              
;
               
y = t (x, y – м; t – с ).                                
(е)

1. Определить
   уравнение траектории точки.

2. Определить
   скорость и ускорение точки при t = 0 и t
   = 1 с.

3. Построить
   траекторию и указать полученные векторы
   скорости и ускорения на чертеже.

    Решение

    1.
Уравнение траектории получается
подстановкой в первое уравнение системы
(е) величины t = y, полученной из второго
уравнения этой системы:

                                                  
.
                                                            
(ж)

    2.
Модуль скорости точки определяется по
формуле
,
где–
проекции вектора скорости на координатные
оси. Для заданного движения (е) имеем

,
                            
м/c.

    При
t = 0                  
,м/c.

    Модуль
скорости V₀
= 1 м/c.

    При
t = 1 с,          
м/c,м/c.

    Модуль
скорости V₁
= 4,82 м/с.

    Модуль
ускорения точки определяется по формуле
,
где,–
проекции вектора ускорения на координатные
оси. Для заданного движения (е) имеем

                               
,
                          
.

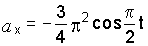
    При
t = 0             
м/с²
,
               
.

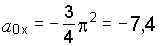
    Модуль
ускорения a₀
= 7,4 м/с².

    При
t = 1 с                  
,.

    Модуль
ускорения a₁
= 0.

    3.
Траектория точки (ж) представляет собой
косинусоиду.

Рис.1.5

Для построения траектории найдем по уравнению (ж) пять точек, задавшись пятью значениями у: у = 0, 1, 2, 3, 4, М0(3; 0), М1(0; 1), М2(-3; 2), М3(0; 3), М4(3; 4). По этим точкам построена траектория на рис. 1.5.   Определим положение точки в моменты времени t = 0 и t = 1 с, учитывая (е). При t = 0 x0 = 3 м, y0 = 0, точка занимает положение М0(3; 0).

  При
t = 1 с x₁
= 0, y₁ =
1 м, точка занимает положение М₁(0;
1). Для этих положений точки построим
векторы скорости и ускорения. От точки
M₀
отложим проекции скорости V_0x = 0
и V_0y = 1
м/с (см. п.2); направление вектора 
V₀
показано на рис. 1.5. Вектор скорости 
V₁
построим следующим образом: через точку
M₁
проведем оси
и,
осьпараллельна
оси x, а осьсовпадает
с осью y. Вдоль этих осей от точки M₁
отложим отрезки, равные проекциям V_1x
и V_1y
(с
учетом их знаков); затем построим
прямоугольник, диагональ которого есть
вектор 
V₁.
Модуль вектора ускорения
a₀
равен модулю проекции a_0x
(см. п. 2), 
a₀
направлен от точки M₀
в сторону, противоположную положительному
направлению оси x (cкорости 
V₀,

V₁
должны совпадать с касательными к
траектории соответственно в точках M₀
и M₁.
Вектор
a₀
должен быть направлен от точки M₀
внутрь кривой).

Задача
1.5 (4)

    Даны
уравнения движения точки:

                       
;
         
(х,
у – м; t – с ).                     
(з)

1. Определить
   уравнение траектории точки.

2. Определить
   скорость и ускорение точки при t = 1 с.

3. Построить
   траекторию и указать полученные векторы
   скорости и ускорения на чертеже.

    Решение

    1.
Для того чтобы получить уравнение
траектории, необходимо из уравнений
движения (з) исключить время. Запишем
эти уравнения в виде

,
.

    Возведем
оба уравнения в квадрат, вычтем второе
из первого и получим уравнение траектории:

                                                  
x²
– y²
= 4².
                                                              
(и)

    Это
уравнение равнобочной гиперболы, полуось
которой b = 4 м.

    2.
Определим проекции скорости

    В
заданный момент времени t = 1с, V_1x
= 4,68 м/с, V_1у
=
6,16 м/с
модуль скорости
м/с.

    Определим
проекции ускорения

м/с²,
           
м/с²
.

    В
момент времени t = 1с, а_1x
= 6,16 м/с²,
а_1у
=
4,68 м/с²
модуль
ускорения
м/с².

    3.
Построим траекторию точки по уравнению
(и). Действительной осью гиперболы
является ось х (рис. 1.6). На траектории
найдем точку М₁,
соответствующую моменту времени t = 1 с.
Координаты этой точки: x₁ = 2(e +
e^-1)
= 6,16 м; y₁ = 2(e –
e^-1)
= 4,68 м; M₁
(6,16; 4,68).

Рис.
1.6

Вектор
скорости построим следующим образом:
через точку М₁
проведем оси
и,
параллельные соответствующим осям x и
y; вдоль этих осей от точки М₁
отложим отрезки, равные проекциям V_1x
и V_1y
(с учетом их знаков). Диагональ
прямоугольника, построенного на этих
отрезках, есть вектор
V₁.
Вектор ускорения
a₁
строим подобным образом: от точки М₁
вдоль оси
отложим
отрезок, равный проекцииa_1x,
а вдоль оси
отложим
отрезокa_1y.
Затем на этих отрезках строим прямоугольник,
диагональ которого есть вектор
a₁.
Вектор скорости
V₁
должен быть направлен по касательной
к траектории в точке M₁,
а вектор ускорения
a₁
должен быть направлен от точки M₁
внутрь кривой.    
Задача 1.6 (5)

Рис. 1.7

Даны уравнения движения точки М шатуна АВ кривошипно-ползунного механизма (рис. 1.7): (х, у – м; t – с ).         (к) Определить уравнение траектории точки. Определить скорость и ускорение точки в момент, когда она пересечет прямую y = 20 см.

    Решение

1.
Чтобы определить уравнение траектории,
следует исключить время из уравнений
движения (к). Учитывая, что

,

получим
.

Траектория
представляет собой эллипс с полуосями
20 см и 40 см.

    2.
Определим время Т, когда точка пересечет
прямую у = 20 см, первое уравнение системы
(к) в этот момент примет вид:
20 = 40 sin2
t, отсюда следует
с.

    Найдем
величины скорости и ускорения по
значениям их проекций в момент времени
с:

см/с;
               
см/с.

    Модуль
скорости
см/с.

    Проекции
ускорения

см/с²;

см/с².

    Модуль
ускорения

см/с².

Задача
1.7 (6)

    Дан
закон движения точки по окружности
радиуса R = 5 м:

                 
(s
– см; t –с ).                                             
(л)

1. Определить
   скорость и ускорение точки при t = 0 и t₁
   = 10 с.

2. Определить
   моменты остановки точки.

3. Определить
   путь, пройденный точкой за 10 с.

    Решение

Рис. 1.8

1. На траектории отметим точку O – начало отсчета координаты s и укажем положительное направление отсчета этой координаты стрелкой (рис. 1.8). Отметим положение точки в моменты времени t = 0 и t1= 10 с. При t = 0 s0= -15 см; при t1= 10 с s1= 355 см. Положение точек M0и M1указано на рис. 1.8. Проведем из точек M0и M1естественные оси координат0, n0;1, n1.

Определим
проекцию скорости на касательную
,
учитывая (л),

                                          
.
(м)

При
t = 0,                 
V
_o
= 162 см/с             
и t₁
= 10 c                
V
₁
= 12 см/с.

    Теперь
отложим найденные проекции скорости
из точек M₀
и M₁
по соответствующим касательным: V
_o
– по касательной 
_o,
V
₁
– по касательной 
₁.
Векторы 
V_o
и 
V₁
совпадают со своими проекциями V
_o
и V₁.

Определим
проекции ускорения на естественные оси
координат, учитывая (л),

см/с²;
см/с².

    Ускорение
точки
.

При
t = 0                       
см/с²;
                   
см/с²;

см/с².

При
t₁
= 10 с             
см/с²;
                     
см/с²;

см/с².

    Отложим
из точек M₀
и M₁
по естественным осям проекции а_o,
а_no,
а
₁,
а_n1.
Векторы
a₀,
a₁
изображаются диагоналями прямоугольников,
построенных на проекциях ускорений.

    2.
Чтобы найти моменты остановки, необходимо
найти время t*, когда скорость точки
равна нулю. Из уравнения (м) получим

3(t*)²
– 45t* + 162 = 0.

    Решив
это уравнение, будем иметь t₁*
= 6 с, t₂*
= 9 с.

    3.
Поскольку за 10 с точка сделала две
остановки (см. п. 2), пройденный ею путь
за 10 с можно найти как сумму пути,
пройденного точкой от начального
положения до первой остановки, пути,
пройденного точкой от первой до второй
остановки, и пути, пройденного точкой
от второй остановки до момента времени
t₁
= 10 с, т.е.

,

где
s₀
= -15 см;

см;

см;

см.

Путь,
пройденный точкой за 10 с, равен

 см.

Задача
1.8 (7)

    По
заданным уравнениям движения точки:

       
;
               
(х,
у – м; t – с)                         
(н)

найти
ее касательное и нормальное ускорение,
а также радиус кривизны траектории для
заданного момента времени t₁
= 0,5 
с.

    Решение

    Заданные
уравнения движения точки (н) позволяют
найти проекции скорости точки, м/с,

;

.

    Модуль
скорости, м/с,

                                    
.
                                  
(о)

    В
момент времени t₁
= 0,5 
с V₁
= 2 м/с.

    Проекции
ускорения точки, м/с²:

.

    Модуль
полного ускорения, м/с²

                                   
.
                                      
(п)

    В
момент времени t₁
= 0,5 
                        
с_а
= 2 м/с².

    Зная
выражение скорости, как функции времени
t (о), определим модуль касательного
ускорения точки, м/с²,
по формуле (1.5)

                                          
.
                                       
(р)

    В
момент
см/с².

    По
полному ускорению (п) и касательному
ускорению (р) найдем модуль нормального
ускорения точки для
с,
учитывая формулу (1.7)

м/с².

    Нормальное
ускорение а_n1
и радиус кривизны траектории 
₁
связаны зависимостью (1.6), из которой
следует, что при
с

м.

15 мая 2014

Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.

На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.

Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.

Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:

[v={S}’={x}’left( t right)]

Точно так же мы можем посчитать и ускорение:

[a={v}’={{S}’}’={{x}’}’left( t right)]

Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.

Давайте посмотрим, как это работает при решении реальных задач.

Пример № 1

Материальная точка движется по закону:

[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.

Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.

[v={S}’={x}’left( 2 right)]

Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.

Давайте решать. В первую очередь, посчитаем производную:

[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

Нам требуется найти производную в точке 2. Давайте подставим:

[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]

[=-16+32-12+5=9]

Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.

Пример № 2

Материальная точка движется по закону:

[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]

[{x}’left( t right)={{t}^{2}}-8t+19]

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

[{{t}^{2}}-8t+19=3]

[{{t}^{2}}-8t+16=0]

[{{left( t-4 right)}^{2}}=0]

[t-4=0]

[t=4]

Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.

Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.

Смотрите также:

1. Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
2. ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
3. Схема Бернулли. Примеры решения задач
4. Комбинаторика в задаче B6: средний тест
5. Как решать задачи про летающие камни?
6. B4: счетчики на электричество

Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.

Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.

Вектор скорости направлен по касательной к траектории точки в сторону движения.

Рассмотрим перемещение точки за малый промежуток времени Δt:

тогда

средняя скорость точки за промежуток времени Dt.

Наш видеоурок по теме:

Другие видео

Скорость точки в данный момент времени

Скорость точки при векторном способе задания движения

Положение движущейся точки М относительно системы отсчета в момент времени t₁ определяется радиус-вектором r.

Рис. 1

В другой момент времени t₁=t+Δt точка займет положение М₁ с радиус-вектором r₁.

За время Δt радиус-вектор движущейся точки изменится на

Средней скоростью v_ср называется отношение изменения радиус-вектора Δr к изменению времени Δt.

Скорость точки равна первой производной по времени от ее радиус-вектора.

Скорость точки при координатном способе задания движения

Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим

После дифференцирования

Отсюда следует

Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.

Модуль скорости и направляющие косинусы равны:

Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда

Скорость точки при естественном способе задания движения

Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).

Рис. 2

Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O₁

— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.

При ds>0 направления векторов τ и dr совпадают.

Если точка движется в сторону убывающих расстояний, то ds<0 и направления векторов τ и dr противоположны.

При

вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;

при

он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.

— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.

Естественное задание движения точки полностью определяет скорость по величине и направлению.

Примеры решения задач >
Ускорение точки >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Содержание:

Координатный способ определения движения точки:

При координатном способе определения движения точки должны быть даны уравнения движения, т. е. заданы координаты точки как функции времени:

Задание движения точки в прямоугольных координатах

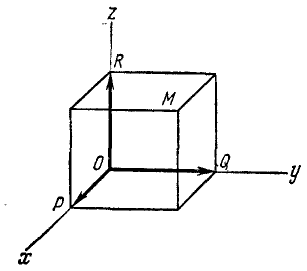
Как известно из курса аналитической геометрии, положение точки M в пространстве может быть определено положением ее проекций P, Q и R на три взаимно перпендикулярные оси (рис. 84), называемые осями координат.

Рис. 84

Положение точки P на оси Ox вполне определяют абсциссой х. Совершенно так же положение точек Q и R определяют ординатой у и аппликатой z.

Если точка M движется относительно осей xOyz, то проекции Р, Q и R перемещаются по осям и координаты точки M изменяются.

Для определения движения точки M нужно знать ее координаты для каждого мгновения, выразить их в функциях времени.

x = x(t),    (58′)
y = y(t),    (58″)
z = z(t), (58″‘)

Эти функции непрерывны, так как точка не может из одного положения перейти в другое, минуя промежуточные. Они должны быть однозначны, так как точка занимает в пространстве в каждое мгновение только одно положение.

Соотношения (58) называют кинематическими уравнениями движения точки в прямоугольных координатах, а способ определения движения точки посредством соотношений (58) называют координатным способом определения движения точки. Это название неточно, потому что, кроме прямолинейных прямоугольных координат, существует множество других координатных систем.

Если траектория точки лежит в одной плоскости, то движение точки определяют двумя уравнениями в системе координат xОy: x=x(t), y=y(t).

Следовательно, при координатном способе задания движения точки в пространстве нужно задать ее три координаты, а на плоскости—две координаты как функции времени. Если точка движется прямолинейно, то, приняв прямую, по которой она движется, за ось абсцисс, мы определим движение точки одним уравнением

x = x(t).

Если движение точки задано в координатной форме, то для определения ее траектории надо из уравнений движения исключить время

Уравнение траектории

Можно определить траекторию точки, если в уравнениях движения (58) давать аргументу t различные значения и, вычислив соответствующие значения функций, отмечать положения точки по ее координатам. Следовательно. кинематические уравнения движения точки (58) можно
рассматривать как уравнения ее траектории в параметрической форме, а время — как независимый переменный параметр.

Однако более удобно получить уравнение траектории, исключив время из уравнений (58). В самом деле, траекторией называют геометрическое место всех положений движущейся точки, но в геометрии нет понятия времени, а поэтому для получения уравнения траектории нужно из кинематических уравнений движения (58) исключить время t. Если точка движется в плоскости, то, исключив время из уравнений (58′) и (58″), мы получим соотношение, связывающее х и у:

f(x, у) = 0.    (59)

Это уравнение плоской кривой—траектории точки. Если же движение задано тремя уравнениями (58), то, исключив время, получим два уравнения между тремя координатами:
    (59^/)

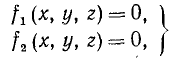
выражающие, как известно из аналитической геометрии, кривую (траекторию) в пространстве. Точнее говоря, уравнения (59) или (59′) выражают кривую, которая полностью или в некоторой своей части является геометрическим местом всех положений движущейся точки.

Иногда бывает нужно выразить в естественной форме движение точки, заданное в прямоугольных координатах уравнениями (58), и, кроме уравнения траектории, дать также уравнение (51) движения точки по траектории. Чтобы его получить, надо продифференцировать уравнения (58) и полученные дифференциалы координат точки подставить в известную из курса высшей математики формулу, выражающую абсолютную величину элемента дуги:

    (60)

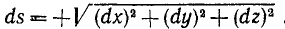
Проинтегрировав (60), мы получим уравнение (51), выражающее длину дуги s как функцию времени, или, что то же, закон движения точки по траектории.

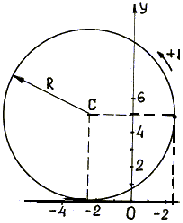
Задача №1

По заданным уравнениям движения точки в координатной форме найти уравнение траектории и уравнение движения по траектории:

1)    х = 5 cos 2t,       y = 3+5sin 2t;
2)    x=21,2 sin² t,    у = 21,2 cos 2t.

В обоих примерах за единицу длины принят сантиметр, за единицу времени — секунда.

Решение. Чтобы определить уравнение траектории по уравнениям движения, перенесем во втором из заданных уравнений 3 влево, возведем оба уравнения в квадрат и, сложив, получим

x² + (y-3)² = 25.

Это уравнение окружности с центром в точке: x = 0, y = +3.

Чтобы получить закон движения, продифференцируем заданные уравнения: dx=—10 sin 2t dt, dy = 10 cos 2t dt.

Возводя в квадрат, складывая, извлекая квадратный корень и интегрируя, находим закон движения по траектории:
s=10t + C, где C = s₀.

2) Исключим время из уравнений движения во втором примере:

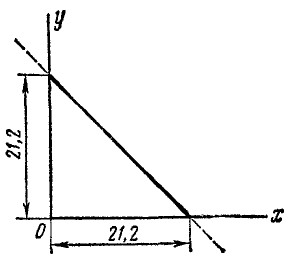
x+y = 21,2.

Это уравнение первого порядка относительно х и у, следовательно, траектория-прямая линия. Прямая отсекает на положительных направлениях осей координат отрезки по 21,2 см. Однако не вся прямая служит траекторией точки: из заданных уравнений видно, что х и у должны быть всегда положительны и не могут быть больше 21,2 см каждый, поэтому траекторией точки является лишь отрезок прямой x+y = 21,2, лежащей в первом квадранте (рис. 85).

Рис. 85

На этом примере мы видим, что траекторией точки иногда является лишь часть линии, выражаемой уравнением траектории.

Продифференцируем уравнения движения:

dx = 21,2 ∙ 2 sin t cos t dt,
dy = 21,2 ∙ 2 sin t cos t dt.

Теперь no формуле (60) нетрудно найти элемент дуги траектории:

ля получения уравнения (51) движения точки по траектории остается лишь проинтегрировать найденное выражение. Интегрируем и подставляем начальные условия (при t= 0, s₀ = 0):

Ответ. Уравнения траекторий x²+(y-3)²= 25 и x+y=21,2; уравнения движения по траектории s=10t+s₀ и s = 30 sin ²t.

Задача №2

Движение точки задано уравнениями:
х = x’ cos φ (t)—y’ sin φ (t),
y = x’ sin φ (t) + y’ cos φ (t),

где х’ и у’ — некоторые постоянные величины, a φ(t)— любая функция времени. Определить траекторию точки.

Решение. Возведем каждое из уравнений в квадрат, а затем сложим их:

x² + y² = χ^‘2 + y^‘2.

По условию, х’ и у’ — постоянные. Обозначая сумму их квадратов через r², получим

x² + y² = r².

Ответ. Окружность с центром в начале координат радиуса .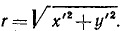

Задача №3

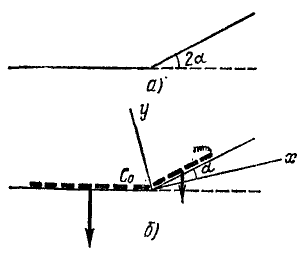
Поезд длиной l м сначала идет по горизонтальному пути (рис. 86, а), а потом поднимается в гору под углом 2α к горизонту. Считая поезд однородной лентой, найти траекторию его центра тяжести.

Рис. 86

Решение. Для решения задачи нужно определить координаты центра тяжести поезда, найти уравнения движения центра тяжести и исключить из них время.

Направим оси координат по внутренней и внешней равиоделяшнм угла 2α (рис. 86, б). Траектория центра тяжести поезда не зависит от скорости поезда. Для простоты подсчетов предположим, что он идет равномерно со скоростью υ м/сек и в начальное мгновение t=0 подошел к горе.

Тогда за время t сек на гору поднимется υt м состава поезда и останется на горизонтальном пути l — υt м. Будем считать, что единица длины поезда весит γ. 

Применяя формулы (48), найдем координаты центра тяжести поезда:

Координаты центра тяжести представлены здесь как функции времени, следовательно, полученные соотношения являются уравнениями движения центра тяжести поезда. Определяя t (или υt) из первого уравнения и подставляя во второе, найдем уравнение траектории:

Ответ. Парабола.

Задача №4

Мостовой кран движется вдоль цеха согласно уравнению х = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5t (х и у—в м, t — в сек). Цепь укорачивается со скоростью t>=0,5. Определить траекторию центра тяжести груза (в начальном положении центр тяжести груза находился в горизонтальной плоскости хОу, ось Oz направлена вертикально вверх).

Решение. В условии задачи даны лишь два уравнения движения и вертикальная скорость груза:

откуда dz = 0,5dt, и легко получаем третье уравнение:

z = 0,5t

Определив t из первого уравнения, подставим во второе и в третье:

y= 1,5x, z = 0,5x

Координаты груза должны удовлетворять одновременно обоим уравнениям, т. е. траектория лежит одновременно в обеих плоскостях и является линией их пересечения.
Ответ. Прямая.

Алгебраическая величина скорости проекции точки на координатную ось равна первой производной от текущей координаты по времени:

Алгебраическая величина скорости проекции точки на ось

Пусть движение точки M определяется тремя уравнениями:
x =x(t),    (58′)
y = y(t),   (58″)
z = z(t).    (58″‘)

По мере движения точки M в пространстве ее проекции P, Q и R движутся по своим прямолинейным траекториям, т. е. по осям координат, и их движения вполне соответствуют движению точки М.

Так, координата (абсцисса) точки P всегда равна абсциссе точки М, а координаты точек QnR всегда равны ординате и аппликате точки М. Следовательно, при движении точки M в пространстве согласно уравнениям (58) точка P движется по оси Ox согласно уравнению (58′), а точки Q и R— соответственно по осям Oy и Oz согласно уравнениям (58″) и (58″‘).

Таким образом, движение точки M в пространстве можно разложить на три прямолинейных движения ее проекций P, Q и R.

Определим скорость υ_p точки P при движении этой точки по ее прямолинейной траектории Ох, иными словами, определим скорость проекции точки M на ось Ох.

Алгебраическая величина скорости выражается по формуле (53), причем дифференциалом расстояния точки P является дифференциал абсциссы х, а поэтому

    (61)

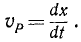
Следовательно, алгебраическая величина скорости проекции P точки M на координатную ось равна первой производной от текущей координаты х по времени t. Она положительна, если точка P движется в положительном направлении оси Ох, и отрицательна, если точка P движется в отрицательном направлении.
Аналогично получаем алгебраические скорости проекций Q и R на ось Oy и на ось Oz:

    (61″)

     (61″‘)   

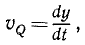
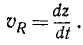
Чтобы получить векторы скоростей проекций, надо умножить величины (61) на единичные векторы:
     (61)   

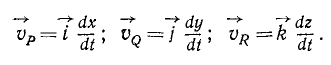
Алгебраическая величина скорости проекции точки на ось равна проекции скорости той же точки на туже ось:

Скорость проекции и проекция скорости

Пусть точка М за бесконечно малый отрезок времени dt передвинулась по своей траектории на элемент дуги ds, абсолютную величину которого выразим формулой (60):

где dx, dy и dz — проекции элемента дуги на оси координат, или, Что то же, элементарные приращения координат точки М.

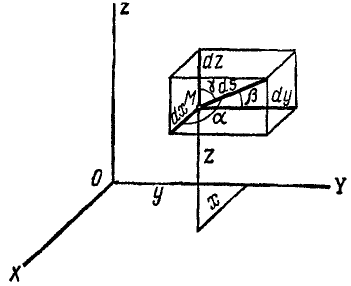
На рис. 87 эти элементы условно изображены конечными отрезками. Как видно из чертежа, косинусы углов, составляемых элементарным перемещением (а следовательно, и скоростью точки), с осями х, у и z соответственно равны

     (62)   

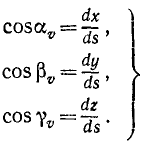
Величина скорости точки M может быть определена по (53):

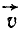
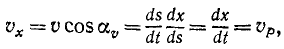
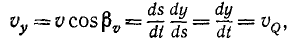
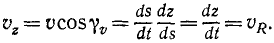
Чтобы определить проекцию скорости на какую-либо ось, надо умножить абсолютную величину скорости на косинус угла между  направлением скорости и направлением этой оси. Таким образом, для проекций скорости точки M на оси координат имеем:

   (63′)

   (63″)

    (63″‘)

Рис. 87

Равенства (63) словами нужно читать так: проекция скорости точки на ось равна алгебраической скорости проекции точки на ту же ось.

Задача №5

Доказать, что проекция скорости точки M (х, у, z) иа плоскость хОу равняется скорости , с которой движется по плоскости проекция M₁ (х, у, О) точки M на ту же плоскость.

Решение. Скорость 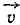точки M составляет с осью Oz угол γ_υ, следовательно, угол, составляемый ею с плоскостью хОу, равен 90° — yυ п косинус этого угла равен sinγ_υ. Поэтому модуль проекции скорости точки M на плоскость хОу

Подводя 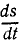под радикал и выражая cosγ_υ, по формуле (62), мы убедимся, что проекция скорости на плоскость равна по величине скорости проекции:

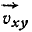
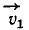
Направления векторов и тоже совпадают, так как направляющие косинусы их одинаковы. Теорема доказана.

Модуль скорости точки равен квадратному корню из суммы квадратов проекций скорости на оси координат:

Модуль скорости. Возведем в квадрат каждое из равенств:
   (63)

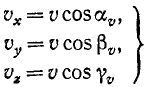
и сложим их:

Сумма квадратов направляющих косинусов равна единице и

или

   (64)

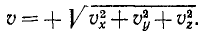
Перед радикалом взят положительный знак, так как величина скорости (ее модуль) всегда положительна. В этом ее существенное отличие от алгебраической величины скорости (53), характеризующей скорость точки при движении по заданной траектории и имеющей знак « + » или «—» в зависимости от направления движения. Величину (64) иногда называют полной скоростью.

Направление скорости можно определить по направляющим косинусам скорости:
 

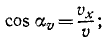
Направляющие косинусы скорости

Равенство (64) позволяет определить модуль скорости точки, движение которой задано уравнениями (58). Направление скорости определяется по косинусам углов, составляемых положительными направлениями осей координат с направлением скорости. Значения этих косинусов, называемых направляющими косинусами скорости, мы получим из уравнений (63):

   (62′)

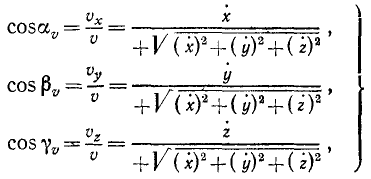
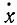
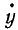
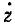
где , и — производные от х, у и z по t.

Если точка движется в плоскости хОу, то γ_υ = 90^o, cosγ_υ = 0 и cos α_υ = sin β_υ.

Задача №6

Уравнения движения суть

 

Определить траекторию и скорость.

Решение. Из уравнений движения следует, что х и у всегда больше нуля.
Для определения уравнения траектории возведем каждое из уравнений движения в квадрат и составим разность

x² — у² = a²

Для определения скорости найдем сначала ее проекции:

а затем уже и полную скорость.

Ответ. Траектория — ветвь гиперболы x² — у² = a² — расположена в области положительных значений х; скорость .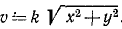

Задача №7

Движение точки задано уравнениями

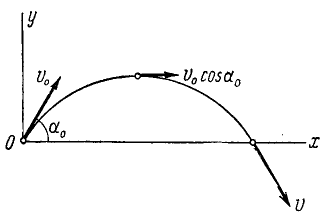
причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, υ₀, g и 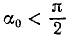—величины постоянные. Найти траекторию точки, координаты наивысшего ее положения, проекции скорости на координатные оси в тот момент, когда точка находится на оси Ох.

Решение. Уравнения описывают движение тела, брошенного со скоростью υ₀ под углом α₀ к горизонту (к оси Ох).
Чтобы найти уравнение траектории, определим время из первого уравнения и подставим найденное значение во второе; получим

уравнение параболы, проходящей через начало координат (рис. 88).

Рис. 88

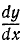
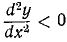
Чтобы определить координаты наивысшего положения, мы можем применить известные из дифференциального исчисления правила нахождения максимума функции, т. е. взять производную , приравняв ее нулю, определить значение х и, подставив его в уравнение траектории, определить соответствующее значение у, убедившись при этом, что вторая производная . Однако мы найдем координаты наивысшего положения точки другим методом, для чего, продифференцировав по времени уравнения движения точки, найдем проекции ее скорости:

Первое из этих уравнений показывает, что проекция скорости на горизонтальную ось постоянна и равна проекции начальной скорости.

Исследование второго уравнения убеждает, что проекция скорости на вертикальную ось в начальное мгновение положительна и равна υ₀ sin α₀; затем, по мере увеличения t, проекция υ_y уменьшается, оставаясь положительной до мгновения 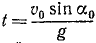, когда υ_y обращается в нуль, после чего υ_y становится отрицательной, возрастая по абсолютной величине с течением времени t.

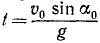
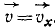
Таким образом, точка движется вправо, сначала поднимаясь, затем опускаясь. Мгновение , при котором точка кончила подниматься, но еще не начала опускаться, соответствует максимальному подъему точки. В это мгновение скорость горизонтальна и . Подставляя найденное значение t в уравнения движения, найдем координаты наивысшей точки траектории:

Определим проекции скорости в мгновение, когда точка находится на оси Ох. В это мгновение ордината точки равна нулю. Приравняем пулю второе из уравнений движения:

Точка находится на оси Ox два раза: при t=0 при 

Первое значение t соответствует началу движения, второе —падению точки на ось Ох. Второе значение равно времени всего полета, и оно вдвое больше полученного нами ранее времени наивысшего подъема: время падения равно времени подъема.

Подставляя значение t=0 в уравнения, определяющие проекции скорости, найдем проекции скорости в начальное мгновение:

υ_x = + υ₀ cos α₀, υ_y = + υ₀ sin α₀.

Подставляя второе из найденных значений t, найдем скорости в момент падения:

υ_x = + υ₀ cos α₀, υ_y = — υ₀ sin α₀.

Ответ: 1) Парабола 

2) 

3) υ_x = υ₀ cos α₀, υ_y = 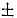υ₀ sin α₀.

причем верхний знак соответствует началу движения, а нижний—концу.

Задача №8

По осям координат (рис. 89) скользят две муфты A и B, соединенные стержнем AB длиной l. Скорость В равна υ_B.

При каком положении муфт скорость муфты А вдвое больше υ_B?

Рис. 89

Решение. Координата точки А связана с координатой точки В соотношением

Считая х и у функциями времени и продифференцировав это равенство по времени, найдем зависимость между скоростями обеих точек:

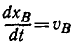
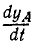
Но и по условию надо, чтобы величина  была равна 2υ_B, т. е.

откуда после алгебраических преобразований получаем ответ.

Ответ: 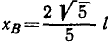 (см. задачи № 57 и 89, где даны другие решения).

Проекция ускорения точки на координатную ось равна первой производной по времени от проекции скорости на ту же ось или второй производной от текущей координаты по времени:

Ускорение проекции и проекция ускорения

Ускорение характеризует изменение скорости точки в данное мгновение. Оно выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка времени к нулю.

Для того чтобы определить ускорение точки M при ее движении в пространстве, рассмотрим сначала движение по оси Ox точки Р, являющейся проекцией точки M на эту ось.

Пусть в некоторое мгновение t алгебраическая величина скорости точки P была υ_х, а в мгновение t_l = t + Δt стала υ_x+∆υ_x. Тогда ускорение точки P по величине и по знаку выразится пределом

Если знаки υ_x и a_p одинаковы, то движение точки P ускоренное, а если различны, то замедленное.

Аналогично выразятся ускорения проекций Q и R точки M на другие координатные оси:

Проекции υ_x, υ_y и υ_z сами являются производными по времени от координат точки, поэтому ускорения проекций можно выразить вторыми производными по времени от координат точки. Эти равенства характеризуют не только величины, но и знаки ускорений проекций. Иными словами, они выражают изменение алгебраических скоростей проекций P, Q и R в мгновение t.

Только что доказанная теорема о равенстве алгебраической скорости проекции точки на ось и проекции скорости той же точки на ту же ось справедлива для любого момента времени. Следовательно, эта теорема относится не только к скорости, но и к ее изменению в любое мгновение, т. е. к ускорению. Это значит, что написанные выше равенства выражают также проекции a_x, а_у и а_z ускорения а точки M на оси координат O_x, O_y и O_z:

   (65)

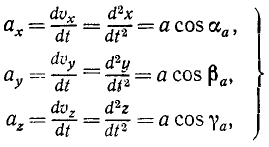
где cosα_a, cosβ_a и cosγ_a—направляющие косинусы ускорения.

Можно рассматривать эти величины (65) как векторы, направленные по осям координат:

   (65′)

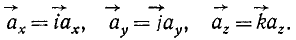
Модуль ускорения точки равен квадратному корню из суммы квадратов проекций ускорения на оси координат:

Величина ускорения при координатном способе задания движения точки

Возведем в квадрат каждое из равенств:

и затем сложим их:

откуда 

   (66)

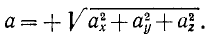
Перед радикалом взят знак плюс, так как модуль вектора—величина положительная. Ускорение точки в отличие от проекций ускорения на оси координат или на другие направления обычно называют полным ускорением. Поэтому равенство (66) можно прочитать так: величина полного ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат.

Направление ускорения можно определить по направляющим косинусам ускорения:
, 

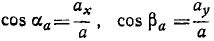
Направляющие косинусы ускорения

Направление ускорения определяют по косинусам углов, составляемых положительными направлениями осей координат с вектором ускорения. Формулы направляющих косинусов получаем из уравнений (65):
   (67′)

   (67»)

   (67»’)

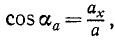
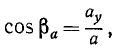
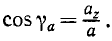
Для определения направления ускорения в каждом конкретном случае надо сначала найти ускорение проекций по (65), для чего необходимо дважды продифференцировать уравнения движения (58), затем найти величину ускорения по (66), а потом определить направляющие косинусы ускорения по (67).

Направление ускорения обычно не совпадает с направлением скорости, и направляющие косинусы (67) ускорения только при прямолинейном ускоренном движении точки постоянно равны направляющим косинусам (62) скорости.

Если точка движется в плоскости хОу, то γ_a = 90^o, cosγ_a = 0, cosα₀ = sin βa.

Задача №9

Точка M движется в системе координат хОу согласно уравнениям х= r cos πt, y=r sinπt, где х и у—в см, a t — в сек. Найти уравнение траектории точки М, ее скорость, направляющие косинусы скорости, ускорение, направляющие косинусы ускорения. Для значений времени t=0; 0,25; 0,5; 0,75, …. 2 сек дать чертежи положений точки M, вектора скорости и вектора ускорения.

Решение. Из уравнения движения видно, что координаты точки M являются проекциями на соответствующие оси радиуса-вектора r, составляющего с осью абсцисс угол πt:

Для определения траектории точки исключаем время из уравнений движения. Получаем уравнение окружности

x² + y² = r²

Найдем теперь проекции скорости на оси координат, для чего продифференцируем по времени уравнения движения:

откуда по (64) получаем модуль скорости

Величина скорости точки M постоянна.

Направляющие косинусы скорости определим по формуле (62′):

Эти соотношения показывают, что направление скорости непрерывно меняется и что скорость перпендикулярна радиусу-вектору, проведенному из центра О в точку М.

Ускорение точки M найдем по его проекциям, для чего продифференцируем выражения, полученные для проекций скорости:

откуда по (66) получаем величину ускорения

Ускорение характеризует быстроту изменения вектора скорости не только по величине, но и по направлению, поэтому, несмотря на постоянство модуля скорости точки М, ускорение этой точки не равно нулю. Как видно из полученного

Рис. 90

равенства, величина полного ускорения постоянна. Направление ускорения определим по направляющим косинусам согласно (67):

Направление ускорения точки M противоположно направлению радиуса-вектора.
Положения точки M в различные мгновения показаны на рис. 90, а, векторы скорости — на рис. 90,6 и векторы ускорения — на рис. 90, в.

Ответ. Точка M движется по окружности радиуса r против часовой стрелки с постоянной по величине скоростью υ = rπ и с постоянным по величине ускорением a = rπ².

Задача №10

Снаряд выбрасывается из орудия с начальной скоростью υ=1600 м/сек под утлом α₀ = 55^o к горизонту. Определить теоретическую дальность и высоту обстрела, учитывая, что ускорение свободно падающих тел g = 9,81 м/сек².

Решение. Сначала составим уравнения движения снаряда в координатной форме, направив оси, как показано на чертеже (см. рис. 88), для этого определим проекции ускорения:

Разделив переменные, интегрируем:
υ_х= С₁, υ_y = — gt + С2

Подставляя вместо переменных величин их начальные значения, увидим, что C₁ и C₂ равны проекциям начальной скорости:

1600 cos 55^o = C_1, 1600 sin 55^o = — gt + C_2.

Подставим их в уравнения, полученные для проекций скорости:

Разделяя переменные и интегрируя, найдем

При t = 0 координаты снаряда были: х =0, у = 0. Подставляя эти данные, найдем, что C₃ = O и C₄ = O. Значения cos 55° и sin 55° найдем в тригонометрических таблицах. Уравнения движения снаряда примут вид:

Далее поступим, как при решении задачи № 42: приравняв вертикальную скорость нулю, найдем время подъема снаряда (t= 133,7 сек); подставляя это значение t в уравнение движения по оси Оу, найдем теоретическую высоту обстрела (h = 87 636 м); удваивая время /, найдем время полета снаряда (t = 267,4 сек); подставляя это значение- в уравнение движения по оси Ох, найдем теоретическую дальность обстрела (l = 245 393 м).
Ответ. l = 245 км; h = 87,5κм.