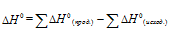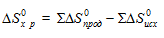Расчет температуры, при которой наступает равновесие системы. Определение направления реакции
Температура наступления равновесия системы
Задача 10.
Термохимическое уравнение реакции: СО(г) + 2H2(г) = CH3OH(ж) + 128 кДж.
Вычислите, при какой температуре наступает равновесие в этой системе?
Решение:
Так как при реакции выделяется тепло, то это экзотермическая реакция. При экзотермических реакциях энтальпия системы уменьшается и ∆H < 0 (Н2 < H1). Тепловые эффекты выражаются через ∆H.
В основе термохимических расчетов лежит закон Гесса (1840 г.): тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.
В термохимических расчетах применяют чаще следствие из закона Гесса: тепловой эффект реакции (∆Hх.р.) равен сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов.
Энтропия S, так же как энтальпия Н, является свойством вещества, пропорциональным его количеству. Энтропия является функцией состояния, т.е. ее изменение (∆S) зависит только от начального (S1) и конечного (S2) состояния и не зависит от пути процесса:
∆Sх.р. = ∆S0прод. – ∆S0исх.
Так как энтропия растет с повышением температуры, то можно считать, что мера беспорядка (– Т∆S). При Р = const и Т = const общую движущую силу процесса, которую обозначают ∆G, можно найти из соотношения:
∆G = (Н2 – H1) – (TS2 – TS1); ∆G = ∆H – T∆S.
Химическое равновесие — состояние системы, в котором скорость прямой реакции (V1) равна скорости обратной реакции (V2). При химическом равновесии концентрации веществ остаются неизменными. Химическое равновесие имеет динамический характер: прямая и обратная реакции при равновесии не прекращаются.
В состояния равновесия:
∆G = 0 и ∆H = T∆S.
Находим ∆S. для данной системы:
S0(СО) = 197,55·10-3 кДж/моль·К;
S0(Н2) = 130,52·10-3 кДж/моль·К;
S0(СН3ОН) = 126,78·10-3 кДж/моль·К;
∆Sх.р. = 126,78·10-3-(197,55·10-3) + (2·130,52·10-3) = -331,81·10-3.
Из условия равновесия :
∆H = T∆S находим Т = ∆H/∆S.
Т = (-128 кДж/моль)/(-331,81·10-3 кДж/моль·К) = 385,7 K.
Ответ: при 385,7 K наступит равновесие в системе.
Определение направления протекания реакции
Задача 11.
Определить направление протекания реакции:
СН4(г) + СО2(г) ⇔ 2СО(г) + 2Н2(г) при стандартных условиях. Вычислить ∆G0298
Решение:
В основе термохимических расчетов лежит закон Гесса (1840 г.): тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.
В термохимических расчетах применяют чаще следствие из закона Гесса: тепловой эффект реакции (∆Hх.р.) равен сумме энтальпий образования ∆Hобр продуктов реакции за вычетом суммы энтальпий образования исходных веществ с учетом стехиометрических коэффициентов:
∆Нх.р. = [2∆Н(СО(г)] + [2∆Н(Н2(г)] — [∆Н(СН4(г)]+ [∆Н(СО2(г)]
т.к. ∆Н для простых веществ равна 0, то выражение принимает вид:
∆Нх.р. = [2∆Н(СО(г)] — [∆Н(СН4(г)]- [∆Н(СО2(г)]
∆Нх.р. = 2(-110,53)-(-74,85)-(-393,51) = 247,3 кДж/моль.
Энтропия — функция состояния, т.е. ее изменение (∆S) зависит только от начального (S1) и конечного (S2)состояния и не зависит от пути процесса:
∆Sх.р. = [2∆S(СО(г)] + [2∆S(Н2(г)] — [∆S(СН4(г)] + [∆S(СО2(г)] =
= 2(197,55) + 2(130,52) — 186,27 — 213,66 = 256,26·10-3 кДж/моль·К.
∆G, можно найти из соотношения:
∆G = ∆H – T∆S.
Необходимо рассчитать возможность самопроизвольного протекания реакции при стандартных условиях (Т = 298 K), получим:
∆G = 247,3 — (298·256,26·10-3) = +170,9 кДж.
Ответ: ∆G = +170,9 кДж. Так как ∆G > 0, следовательно, при стандартных условиях невозможно протекание прямой реакции. Реакция может протекать в обратном направлении.
Направление самопроизвольных процессов
Самопроизвольно
могут протекать реакции, сопровождающиеся
не только выделением, но и поглощением
теплоты.
Реакция, идущая
при данной температуре с выделением
теплоты, при другой температуре идет в
обратном направлении, т.е. с поглощением
теплоты. Здесь проявляется диалектический
закон единства и борьбы противоположностей.
С одной стороны, система стремится к
упорядочению (агрегации), уменьшению
Н, с другой стороны, система стремится
к беспорядку (дезагрегации). Первая
тенденция растет с понижением температуры,
вторая растет с повышением температуры.
Тенденцию к беспорядку характеризует
величина, которую называют энтропией.
Энтропия (S),
так же как и внутренняя энергия (U),
энтальпия (H),
объем(V)
и др., является свойством вещества,
пропорциональным его количеству. S,
U,
H,
V
обладают аддитивными свойствами, т.е.
при соприкосновении систем суммируются.
Энтропия
отражает движение частиц вещества и
является мерой неупорядоченности
системы. Она
возрастает с увеличением движения
частиц: при нагревании, испарении,
плавлении, расширении газа, при ослаблении
или разрыве связей между атомами и т.п.
Процессы, связанные с упорядоченностью
системы: конденсация, кристаллизация,
сжатие, упрочнение связей, полимеризация
и т. п. – ведут к уменьшению энтропии.
Энтропия является функцией состояния,
т.е. ее изменение (S)
зависит только от начального (S1)
и конечного
(S2)
состояния и не зависит от пути процесса
S
= S2
– S1.
Если
S2
>
S1
,
то
S
> 0.
Если
S2
<
S1
, то
S
< 0.
Так как энтропия
растет с повышением температуры, то
можно считать, что мера беспорядка
TS
. Энтропия
выражается в Дж/мольград.
Таким образом, движущая сила процесса
складывается из двух сил: стремление к
упорядочению (Н)
и стремление к беспорядку (TS).
При p =
const
и Т =
const общую
движущую силу процесса, которую обозначают
G
, можно найти из соотношения
G =
(Н2
–
Н1)
– (TS2
–
TS1)
= H
–
TS;
G =
H
–
TS.
Величина
G называется
изобарно- изотермическим потенциалом
или энергией Гиббса. Итак, мерой
химического сродства является убыль G
потенциала
или G
, которая зависит от природы вещества,
его количества и от температуры. Энергия
Гиббса является функцией состояния,
поэтому
G
x.р.=
G
–
G
.
Самопроизвольно
протекающие процессы идут в сторону
уменьшения любого потенциала и, в
частности, в сторону уменьшения G.,
Если G
< 0, процесс
принципиально осуществим, если G
> 0 – процесс
самопроизвольно проходить не может.
Чем меньше G
, тем сильнее
стремление к протеканию данного процесса
и тем дальше он от состояния равновесия,
при котором G
= 0 и H
=
TS
.
Из соотношения G
= H
–
TS
видно, что самопроизвольно могут
протекать и процессы, для которых H
> 0 (эндотермические). Это возможно,
когда S
> 0, но | TS
| > |H
|, и тогда G
< 0. С другой стороны, экзотермические
реакции (H
< 0) самопроизвольно не протекают, если
при S
< 0
окажется, что G
> 0.
Таблица 2
Стандартные изобарные потенциалы образования
G0298
некоторых
веществ
|
Вещество |
Состояние |
G0298, кДж/моль |
Вещество |
Состояние |
G0298, кДж/моль |
|
ВаCO3 |
к |
–1138,8 |
FeO |
к |
–244,3 |
|
СаCO3 |
к |
–1128,37 |
H2O |
ж |
–237,19 |
|
Fe3О4 |
к |
–1014,2 |
H2O |
г |
–228,59 |
|
ВеCO3 |
к |
–944,75 |
CO |
г |
–137,27 |
|
СаO |
к |
–604,2 |
CH4 |
г |
–50,79 |
|
ВeO |
к |
–581,61 |
NO2 |
г |
+51,84 |
|
ВаO |
к |
–528,4 |
NO |
г |
+86,69 |
|
CO2 |
г |
–394,38 |
C2H2 |
г |
+209,20 |
Пример 1.
Что имеет большую энтропию: 1 моль
кристаллического вещества или 1 моль
его паров при той же температуре?
Решение.
Энтропия есть мера неупорядоченного
состояния вещества. В кристалле частицы
(атомы, ионы) имеют упорядоченное
расположение и могут находиться лишь
в некоторых точках пространства, а для
газа таких ограничений нет. 1 моль
газа имеет гораздо больший объем, чем
1 моль
кристалла, и возможность хаотичного
движения молекул газа больше. А так как
энтропию можно рассматривать как
количественную меру хаотичности
атомно-молекулярной структуры вещества,
то энтропия моля паров вещества больше
энтропии моля его кристаллов при
одинаковой температуре.
Пример 2.
Прямая или обратная реакция будет
протекай при стандартных условиях в
системе
СН4(г)
+
СО2(г)
⇄
2СО(г)
+2Н2(г);
Решение.
Для ответа на вопрос следует вычислить
G0298
прямой
реакции. Значения G0298
соответствующих
веществ даны в табл. 2. Зная, что G
есть функция состояния и что G
для простых веществ, находящихся в
агрегатных состояниях, устойчивых при
стандартных условиях, равны нулю, находим
G0298
процесса:
G0298
= 2(–137,27) +
2 (0) – (–50.79 – 394,38) = +170,63 кДж.
То, что G0298
> 0, указывает
на невозможность самопроизвольного
протекания прямой реакции при Т
= 298 К
и равенстве давлений взятых газов 101,3
кПа.
Таблица 3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
…
Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).
Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.
Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.
При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.
Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:
ΔG= Gкон – Gисх
При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:
ΔG = ΔH– TΔS
Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).
Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:
- Если ΔG отрицательно (ΔG<0), то реакция протекает самопроизвольно в прямом направлении.
- Если ΔG равно нулю (ΔG=0), то реакция находится в равновесном состоянии.
- Если ΔG положительно (ΔG>0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.
Энтальпийный и энтропийный факторы и направление процесса
Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:
ΔG= ΔH – TΔS
Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.
Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.
А при при ΔS<0, член – TΔS напротив уменьшает возможность реакции протекать самопроизвольно.
Если ΔH и – TΔS имеют противоположные знаки, то от их величины зависит будет ли ΔG отрицательным или положительным. В таком случае, необходимо учитывать температурный фактор. Т.о. при высоких температурах роль энропийного фактора становится значительным.
Далее приведена таблица, наглядно показывающая влияние температуры на самопроизвольное протекание реакции.
|
ΔH |
ΔS | ΔG |
Протекание реакции |
| ˂0 | >0 | Всегда ˂0 | Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна |
| >0 | ˂0 | Всегда >0 | Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна |
| ˂0 | ˂0 | При низких температурах ˂0, при высоких температурах >0 | Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах |
| >0 | >0 | При низких температурах >0, при высоких температурах ˂0 | Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной |
Изменение энергии Гиббса. Для удобства принято сравнивать значения ΔG при стандартных условиях – концентрации равны 1 моль/л, парциальное давление газообразных веществ равно 101,3 кПа, температура 298,15 К. Тогда свободную энергию обозначают через ΔG0, на основе значений которой можно вычислить изменение энергии Гиббса химической реакции:
ΔG0р-ции = Σ ΔG0прод — Σ ΔG0исх
Величина ΔG0р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю.
Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением:
A = U – TS
Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением:
ΔA= ΔU – TΔS
ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния.
Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается.
Таким образом, при ΔA<0 процесс идет самопроизвольно в прямом направлении,
при ΔA>0 – в обратном направлении,
а при ΔA=0 система находится в состоянии равновесия.
Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия:
ΔG0Т = ΔH0Т – TΔS0Т = —RTlnK,
Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура.
Если K>>1, т.е. реакция идет в прямом направлении, то ΔG0˂˂0.
Если K<<1, т.е. реакция идет в обратном направлении, то ΔG0>>0
Если K=1, то ΔG0=0
В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG0 можно связать с ЭДС гальванического элемента следующим соотношением:
ΔG0=-nFE0, где
nF – количество прошедшего электричества
E0 – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии.
При самопроизвольном протекании процесса, его ΔG<0, а ЭДС>0.
Порог реакционной способности веществ для большинства реакций имеет значение ΔG0≈41 кДж/моль.
То есть, если ΔG0<-41 кДж/моль, то процесс осуществим,
если ΔG0>+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях.