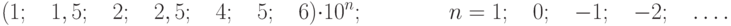Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: 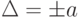
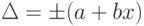
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, «Класс точности М», а на приборе – буквой «М». Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле 

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 
Рис.
3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
Рис.
3.2.
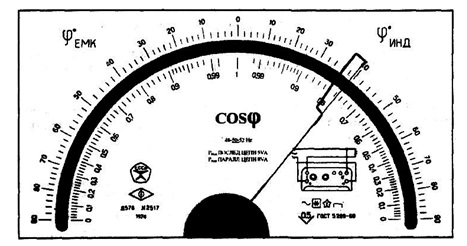
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой 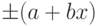
![delta=Delta/x=pm[c+d(|x_{k}/x|-1)]](https://intuit.ru/sites/default/files/tex_cache/3898a996678dab895193a1773d11ffc8.png) |
( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: 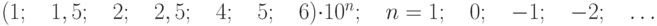
Рис.
3.3.
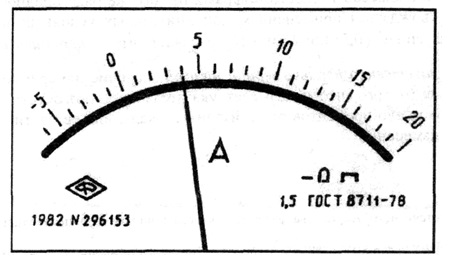
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле 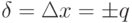
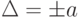
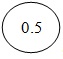
Рис.
3.4.
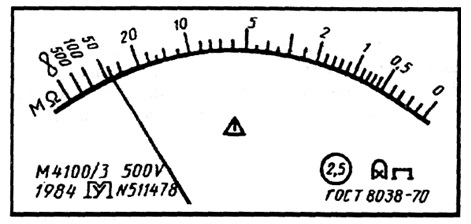
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?
Нормирование погрешностей средств измерения
Точность
средств измерения определяется предельно
допустимыми погрешностями, которые
могут иметь место при его использовании.
Нормированием
погрешностей средств измерений
называют
процедуру назначения допустимых границ
основной и дополнительных погрешностей,
а также выбор формы указания этих границ
в нормативно-технической документации.
Пределы
допускаемой основной и дополнительных
погрешностей определяются разработчиками
для каждого типа средств измерений на
стадии его проектирования и подготовки
производства. В зависимости от назначения
средства измерений и характера изменения
погрешности в пределах диапазона
измерений для средств измерений
различного типа нормируется предельно
допустимое значение: либо основной
абсолютной погрешности, либо основной
приведенной погрешности, либо основной
относительной погрешности.
Для
каждого типа средств измерений характер
изменения погрешности в пределах
диапазона измерений зависит от принципа
действия этого средства измерений и
может быть самым разнообразным. Однако,
как показала практика, среди этого
многообразия часто удается выделить
три типовых случая, предопределяющих
выбор формы представления пределов
допускаемой погрешности.
Типовые
варианты отклонения реальных передаточных
характеристик средств измерений от
номинальной характеристики (т.е.
зависимости показаний средства измерения
x
от действительного значения xд,
поданного на его вход) и соответствующие
им графики изменения предельных значений
абсолютной и относительной погрешностей
в зависимости от измеряемой величины
приведены на рис. 1.
Если
реальная передаточная характеристика
средства измерений смещена по отношению
к номинальной (1-й график на рис. 1, а),
то предельное значение абсолютной
погрешности средства измерения
(1-й
график на рис. 1, б)
не зависит от измеряемой величины.
Предельное
значение основной абсолютной погрешности
средства измерений, не изменяющееся от
значения измеряемой величины, называют
аддитивной
погрешностью.
Если
угол наклона реальной передаточной
характеристики средства измерений
отличается от номинального (2-й график
на рис. 1, а),
то предельное значение абсолютной
погрешности будет линейно зависеть от
измеряемой величины (2-й график на рис.
1, б).
Предельное
значение основной абсолютной погрешности
средства измерений, линейно изменяющееся
от значения измеряемой величины, называют
мультипликативной
погрешностью.
Если
реальная передаточная характеристика
средства измерений смещена по отношению
к номинальной и угол ее наклона отличается
от номинального (3-й график на рис. 1, а),
то в этом случае имеет место как
аддитивная, так и мультипликативная
составляющая предельного значения
основной абсолютной погрешности.
Аддитивная
погрешность определяется, например,
неточной установкой нулевого значения
перед началом измерений, уходом нуля в
процессе измерений, наличием термоэдс
в контактных соединениях и т.д.
а
б
в
Рис.
1. Иллюстрации
к выбору формы представления пределов
допус-
каемой
основной погрешности:
а
– типовые варианты отклонения реальных
передаточных характеристик средств
измерений от номинальной характеристики;
б
– пределы допускаемой абсолют-
ной погрешности; в
–
пределы допускаемой относительной
погрешности
Мультипликативная
погрешность определяется, например,
изменением коэффициентов усиления или
ослабления входных сигналов (например,
при изменении температуры окружающей
среды или вследствие старения элементов),
изменением значений, воспроизводимых
мерами, встроенными в измерительные
приборы, изменением жесткости пружин,
создающих противодействующий момент
в электромеханических приборах, и т.д.
Ширина
полосы неопределенности значений
абсолютной (рис. 1, б)
и относительной (рис. 1, в)
погрешностей характеризует разброс и
изменение в процессе эксплуатации
индивидуальных характеристик средств
измерений определенного типа.
А.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с преобладающей аддитивной
погрешностью.
Для
средств измерений с преобладающей
аддитивной погрешностью (1-е графики на
рис. 1) одним числом (∆max=
±а)
удобно нормировать предельно допустимое
значение основной абсолютной погрешности.
В этом случае фактическая абсолютная
погрешность измерения ∆ может иметь
различные значения в различных точках
шкалы, но не должна превышать предельно
допустимой величины (∆ ≤ ±а).
В многопредельных измерительных приборах
с преобладающей аддитивной погрешностью
для каждого предела измерений пришлось
бы указывать свое значение предельно
допустимой абсолютной погрешности. К
сожалению, как видно из 1-го графика на
рис. 1, в,
нормировать одним числом предел
допускаемой относительной погрешности
в различных точках шкалы не представляется
возможным. По этой причине для средств
измерений с преобладающей аддитивной
погрешностью часто нормируют одним
числом значение так называемой основной
приведенной
относительной
погрешности:
,
где
xN
– нормирующее значение.
Таким
способом, например, нормируются
погрешности большинства электромеханических
и электронных приборов со стрелочными
индикаторами. В качестве нормирующего
значения xN
обычно используется предел измерений
(xN
= xmax),
удвоенное значение предела измерений
(если нулевая отметка находится в
середине шкалы) или длина шкалы (для
приборов с неравномерной шкалой). Если
xN
= xmax,
то значение приведенной погрешности γ
равно пределу допускаемой относительной
погрешности средства измерений в точке,
соответствующей пределу измерений. По
заданному значению предела допускаемой
основной приведенной погрешности легко
определить предел допускаемой основной
абсолютной погрешности для каждого
предела измерений многопредельного
прибора:
.
После
этого для любой отметки шкалы x
может быть произведена оценка предельно
допустимой основной относительной
погрешности:
.
Б.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с преобладающей мультипликативной
погрешностью.
Как
видно из рис. 1 (2-й график), для средств
измерений с преобладающей мультипликативной
погрешностью одним числом удобно
нормировать предел допускаемой основной
относительной погрешности (рис. 1, в)
δmax
= ± b.
В этом случае фактическая относительная
погрешность измерений на различных
участках шкалы может иметь различные
значения, но не должна превышать предельно
допустимой величины (δ ≤ ± b).
По заданному значению предельно
допустимой относительной погрешности
δmax
для любой точки шкалы может быть
произведена оценка предельно допустимой
абсолютной погрешности:
.
К
числу средств измерений с преобладающей
мультипликативной погрешностью относится
большинство многозначных мер, счетчики
электрической энергии, счетчики воды,
расходомеры и др. Следует отметить, что
для реальных средств измерений с
преобладающей мультипликативной
погрешностью не удается полностью
устранить аддитивную погрешность. По
этой причине в технической документации
всегда указывается наименьшее значение
измеряемой величины, для которого предел
допускаемой основной относительной
погрешности еще не превышает заданного
значения δmax.
Ниже этого наименьшего значения
измеряемой величины погрешность
измерений не нормируется и считается
неопределенной.
В.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с соизмеримыми аддитивной и
мультипликативной погрешностями.
Если
аддитивная и мультипликативная
составляющие погрешности средства
измерений соизмеримы (3-й график на рис.
1), то задание предельно допустимой
погрешности одним числом не представляется
возможным, поскольку предельные значения
абсолютных погрешностей будут определяться
выражением
.
В
этом случае нормируется либо предел
допускаемой абсолютной основной
погрешности (указываются предельно
допустимые значения a
и b),
либо (чаще всего) предел допускаемой
относительной основной погрешности. В
последнем случае выражение для оценки
численных значений предельно допустимых
относительных погрешностей в различных
точках шкалы приобретает следующий
вид:
,
где
xmax
– предел измерений; x
– измеренное значение; с
– предел допускаемой относительной
погрешности в конце диапазона измерения
данного прибора; d
– аддитивная относительная погрешность
прибора.
Рассмотренным
выше способом (указанием численных
значений с
и d)
нормируются, в частности, предельно
допустимые значения относительной
основной погрешности цифровых
измерительных приборов. В этом случае
предел основной относительной погрешности
каждого экземпляра средств измерений
определенного типа не должен превышать
установленных для этого типа средств
измерений значений предельно допустимой
погрешности:
.
При этом значение
абсолютной основной погрешности не
должно превышать величины
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные погрешности средств измерения нормируются путем задания пределов допускаемой основной погрешности, при которой средство измерения (СИ) по техническим требованиям может быть допущено к применению.
Для того чтобы оценить погрешность, которую внесет данное СИ в конечный результат, пользуются предельными значениями погрешности для данного типа СИ.
Предел допускаемой основной абсолютной погрешности D может быть представлен одним из трех способов:
— постоянным для любых значений X числом, характеризующим аддитивную погрешность,
D = ± а; (6.1)
— в виде двухчленной формулы, включающей аддитивную и мультипликативную погрешности,
D = ± (а + bх); (6.2)
— в виде уравнения
D=f(х) (6.3)
При сложной зависимости (6.3) допускается представлять погрешность в виде графика и таблицы.
Пределы допускаемой относительной погрешности для случая (6.1) в процентах выражают формулой
(6.4)
для случая (6.2) – формулой

где Хк – предел измерений;
— имеет смысл приведенной погрешности в конце диапазона измерений (при Х=Хк);
— имеет смысл приведенной погрешности в начале диапазона измерений (при Х = 0), причем c > d.
Предел допускаемой приведенной погрешности в процентах выражается формулой
(6.5)
где р – отвлеченное положительное число.
Согласно ГОСТ 8.401-80 для указания нормированных пределов допускаемых погрешностей значения р, q, с, d выражаются в процентах и выбираются из ряда чисел: (1;1,5;2;2,5;3;4;5 и 6) ´10n , где n=+1;0;-1;-2;-3 и т.д.
В настоящее время в эксплуатации большое число средств измерений, метрологические характеристики которых нормируются на основе классов точности.
Класс точности – обобщенная характеристика средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значение которых устанавливают в соответствующих стандартах.
Класс точности позволяет судить о том, в каких пределах находится погрешность средст измерений одного типа, но не характеризует точности измерений, выполняемых такими средствами, так как погрешность зависит и от метода измерений, и от условий измерений и т.д.
С использованием чисел указанного выше ряда чисел разработаны следующие условные обозначения классов точности СИ, наносимые на них.
1. Класс точности указывают просто одним из чисел приведенного выше предпочтительного ряда р (например, 1,5). Это используют для СИ, у которых предел допускаемой приведенной погрешности постоянен (присутствует только аддитивная погрешность), как в (6.1), Xn в (6.5) выражена в единицах измеряемой величины. Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой или степенной (с показателем степени не более двух) шкалой.
2. Класс точности указывает числом из приведенного выше ряда, под которым ставится треугольная скобка, например, . Такое обозначение применяют для приборов с резко неравномерной шкалой, для которых Хn выражают в единицах длины шкалы (мм, см, условных делениях). В этом случае при измерении, кроме значения измеряемой величины, обязательно должен быть записан отсчет X в единицах длины шкалы и предел Хn в этих же единицах, иначе нельзя будет вычислить погрешность результата. Таким способом обозначают класс точности омметров.
3. Число, обозначающее класс точности, обводят кружком например, . Такое обозначение применяют для СИ, у которых предел допускаемой относительной погрешности постоянен во всем диапазоне измерений (имеется только мультипликативная погрешность, (a в (6.2) равна нулю) и его определяют по (6.4). Таким способом нормируют погрешности измерительных мостов, магазинов, масштабных преобразователей. При этом обычно указывают границы рабочего диапазона, для которых справедлив данный класс точности.
4. Класс точности обозначается двумя числами, записываемыми через косую черту, т. е. в виде условной дроби c/d, например, 0,02 / 0,01. Такое обозначение применяют для СИ, у которых погрешность нормирована по двухчленной формуле (6.2). Таким способом указывают классы точности цифровых вольтметров, высокоточных потенциометров постоянного тока и других высокоточных приборов.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Бывает три видов погрешности:
Абсолютная
Относительная
Приведенная
Погрешности средств измерения
Школьные средства измерения имеют вполне нормированные основные погрешности. Включенные в новый «Перечень оборудования», эти средства делятся на стрелочные приборы (амперметры, вольтметры, динамометры и др.), цифровые приборы (мультиметры демонстрационные и лабораторные, счетчик-секундомер и др.), многопредельные меры (линейка, мерная лента, мерный цилиндр), наборы мер (набор грузов по механике и набор гирь, набор резисторов).Несколько особняком в этой номенклатуре оказываются весы для фронтальных работ и практикума. Весы с точки зрения принципа действия можно отнести к нуль-индикаторам, в которых измерение сводится к прямому сравниванию массы взвешиваемого тела с массой гирь. Особенность погрешностей многопредельных мер состоит в том, что они линейно нарастают вдоль шкалы. Именно поэтому либо указано значение погрешностей номинальных значений (т.е. всей длины), либо значение на 100 мм шкалы. Обратим внимание на то, что погрешности деревянных инструментов меньше, чем пластмассовых. Все инструменты, маркированные знаком «ГОСТ», имеют погрешности меньшие, чем погрешности инструментов, не имеющих этих знаков.
В чем метрологический смысл погрешности меры? Она показывает интервал, внутри которого с вероятностью, близкой к 100% находится неизвестное истинное значение меры. Например, каждый груз из набора грузов имеет номинальное значение массы 100 г, погрешность меры ± 2 г. Следовательно, истинное значение груза находится в интервале (100 – 2) г < m < (100 + 2) г.
Если номинальное значение сопротивления резистора равно 4,0 Ом, а погрешность 0,12 Ом, следовательно, истинное значение сопротивления содержится в интервале (4,00 – 0,12) Ом Ј R Ј (4,00 + 0,12) Ом.
Погрешности стрелочных электроизмерительных приборов чаще всего задаются специальной величиной, которая называется классом точности и обозначается символом g. Класс точности g показывает значение допускаемой погрешности в процентах от предела измерения (или суммы пределов для приборов, нуль которых находится внутри шкалы). Например, если класс точности амперметра равен g = 2,5, то основная погрешность равна
Если миллиамперметр имеет ноль посередине шкалы, его основная погрешность равна
В чем смысл основной погрешности стрелочных приборов? Она показывает интервал, внутри которого с вероятностью равной 100% находится истинное значение измеряемой величины, если стрелка прибора совпадает со штрихом шкалы. Например, пусть стрелка амперметра совпадает со штрихом 1,6 А. Следовательно, истинное значение силы тока находится в интервале
(1,60 – 0,05) А Ј I Ј (1,60 + 0,05) А.
Основная погрешность весов складывается из погрешности гирь и чувствительности. Например, если на весах находится взвешиваемое тело и две гири номинальными значениями 100 г и 50 г, то погрешность весов складывается из погрешностей гирь (40 + 30) мг.
Погрешность мультиметра указана двумя числами. Например, для диапазона 700 В записано: «± 1,2% ± 3». Эта запись означает, что погрешность мультиметра в диапазоне от 200 В до 700 В равна сумме единицы младшего разряда считываемого показания U. Пусть считываемое показание равно U = 237 В. Следовательно, погрешность измерения равна
Истинное значение напряжения находится в интервале (237 – 6) В < U < (237 + 6) В.
Отметим, что погрешности измерений определяются, главным образом, погрешностями средств измерений, но они не тождественны им.
В общем случае погрешность средства измерений(меры измерительного преобразователя, измерительного прибора) — это отклонение его реальной функции преобразования от номинальной.
Отклонения реальной характеристики от номинальной, отсчитанные вдоль оси Х или оси У, т. е. разности вида y = Ур— Унилиx = Хр— Хн, естьабсолютные погрешности преобразования, выраженные в единицах величин Х или У (рис. 1).
Мерой точности абсолютная погрешность быть не может, т. к., например, Х = 0.5 мм при измерении высоты пенного слоя пульпы, равной Х = 200 мм, достаточно мала, а при измерении толщины листа стали, при Х = 1 мм, эта погрешность очень велика.
Абсолютная погрешность измерительного прибора XП— это разность между показанием прибора ХПи истинным (действительным) ХДзначением измеряемой величины:
XП= ХП– ХД.
Рис. 1. К пояснению понятия абсолютной погрешности
При этом за действительное значение физической величины при оценке погрешности рабочего средства измерений принимают показания образцового средства измерений, при оценке погрешности образцового средства — показания, полученные с помощью эталонного средства измерений.
Абсолютная погрешность измерительного преобразователя по входу— это разность между значением величины на входе преобразователя ХВи истинным (действительным) значением этой величины на входе ХВД. При этом значение величины на входе ХВопределяется по истинному (действительному) значению величины на выходе преобразователя с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
ХВ=Х*ВД – ХВД,
где ХВ— погрешность измерительного преобразователя по входу;
Х*ВД — истинное (действительное) значение величины на выходе, найденное по градировочной характеристике преобразователя;
ХВД— истинное (действительное) значение преобразуемой величины на входе.
Абсолютная погрешность измерительного преобразователя по выходу— это разность между истинным (действительным) значением величины преобразователя на выходеDХВЫХ.Д и значением величины на выходе Х*ВЫХ.Д, определяемым по истинному (действительному) значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю. Таким образом,
DХВЫХ.П = ХВЫХ.Д — Х*ВЫХ.Д ,
где DХВЫХ.П— погрешность измерительного преобразователя по выходу;
ХВЫХ.Д — действительное значение преобразуемой величины на выходе преобразователя;
Х*ВЫХ.Д — действительное значение преобразуемой величины на выходе, определяемое по действительному значению ее на входе с помощью градуировочной характеристики.
Абсолютная погрешность— это разность между номинальным значением меры ХН и истинным (действительным) ХД воспроизводимой ею величины, т. е.
ХМ= ХН– ХД,
где ХМ— абсолютная погрешность мepы;
ХН— номинальное значение мepы;
ХД— действительное значение воспроизводимой мерой величины.
Пример. Погрешность меры длины (линейки) с номинальным значением 100 мм и действительным значением 100,0006 мм равна 0,6 мкм; погрешность меры сопротивления с номинальным значением 1 Ом и действительным значением 1,0001 Ом равна 0,0001 Ом.
Относительная погрешность меры или измерительного прибора(П) — это отношение абсолютной погрешности меры или измерительного прибора к истинному (действительному) значению воспроизводимой или измеряемой величины.
Относительная погрешность меры или измерительного прибора, в процентах, может быть выражена как:
.
Относительная погрешность измерительного преобразователя по входу (выходу) — это отношение абсолютной погрешности измерительного преобразователя по входу (выходу) к истинному (действительному) значению величины на входе (выходе), определяемому по истинному значению величины на входе (выходе) с помощью номинальной характеристики, приписанной преобразователю.
Итак, относительная погрешность средства измерений, выражаемая в процентах или в относительных единицах, не остается постоянной вследствие изменения величин Х или Y по шкале измерительного устройства.
С учетом того, что относительная погрешность средства измерений не остается постоянной, то вводится понятие приведенной погрешности, в общем виде определяемой:
,
где - приведенная погрешность средства измерений;
XN- нормирующее значение измеряемой величины.
Приведенная погрешность измерительного прибора— это отношение абсолютной погрешности измерительного прибораХПк нормирующему значению.Нормирующее значение XN- это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений**, или длине шкалы***.
Приведенную погрешность обычно выражают в процентах:
.
Приведенная погрешность позволяет сравнивать по точности приборы, имеющие разные пределы точности.
Пример. Определить абсолютную, относительную и приведенную погрешности амперметра с диапазоном измерения 0 -15 А при показании его ХП= 12 А и действительном значении измеряемой силы тока ХД= 12,6 А. За нормирующее значение примем верхний предел измерения Xv = 15 А.
Абсолютная погрешность амперметра
ХП= ХП– ХД= 12 — 12,6 = -0,6 А.
Относительная погрешность амперметра
Приведенная погрешность
При характеристике погрешностей средств измерений часто пользуются понятием предела допускаемой погрешности измерений.
Предел допускаемой погрешности средства измерений— это наибольшая, без учета знака, погрешность средства измерений, при котором оно может быть признано и допущено к применению. Определение применимо к основной и дополнительной погрешности средств измерений.
Пример. Одинаков ли предел допускаемой относительной погрешности измерения во всех точках шкалы автоматического потенциометра?
Для всех точек шкалы одинаков предел допускаемой абсолютной погрешности, определяемой классом точности средства измерений и диапазоном измерений, а предел допускаемой относительной погрешности измерения зависит от конкретной отметки шкалы, т. е. чем меньше показания прибора по шкале, тем больше относительная погрешность. Вследствие этого верхний предел показаний прибора нужно выбирать таким образом, чтобы значение измеряемой величины находилось в конце шкалы.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности— это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений, К этим погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений
Методическая погрешность— это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Основная и дополнительная погрешности.Деление это чисто условно. Погрешность средств измерений, определяемую для работающих в нормальных условиях, называютосновной погрешностью. Нормальными условиями принято считать условия, когда температура окружающего воздуха t = (20 ± 5) 0C, относительная влажность W = 30 – 80 %, атмосферное давление Р = 630 — 795 мм рт. ст., напряжение питающей сети (U = (220 ± 4,4) В, частота питающей сети f = (50 ± 0,5) Гц. Такие условия выдерживаются в лабораторных условиях при градуировке средств измерений.
В реальных условиях производства эти параметры отличаются от лабораторных. Средства измерения помимо чувствительности к измеряемой величине обладают и некоторой чувствительностью к изменяющимся величинам окружающей среды, что приводит к искажению результатов измерения. Погрешность, появляющуюся у средств измерений, работающих в реальных производственных условиях, называют дополнительной погрешностью. Так же, как основная, дополнительная погрешность нормируется путем указания коэффициентов влияния изменения отдельных влияющих величин на изменение показаний в виде
α = , α =· Uпит.
Систематические и прогрессирующие погрешности средств измерений вызываются: первые — погрешностью градуировки шкалы или ее небольшим сдвигом, вторые — старением элементов средства измерения. Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Аддитивные и мультипликативные погрешности. Аддитивная погрешность не зависит от чувствительности прибора и является постоянной для всех значений входной (измеряемой) величины в пределах диапазона измерений (рис.2).
Если реальная характеристика 1 средства измерения смещена относительно номинальной 2 (см. рис. 2) так, что при всех значениях преобразуемой величины Х выходная величина У оказывается больше (или меньше) на одну и ту же величину Δ, то такая погрешность называется аддитивной погрешностью нуля.
Рис. 2. К пояснению понятия аддитивной погрешности средства измерения
К аддитивным погрешностям средств измерений можно отнести погрешности, вызванные трением в опорах электроизмерительных приборов, погрешность дискретности (квантования) в цифровых приборах. Аддитивная погрешность может носить систематический характер. В этом случае она может быть скорректирована смещением шкалы или нулевого положения указателя.
В случае же, если аддитивная погрешность является случайной, то она не может быть скорректирована, и реальная характеристика средства измерения, смещаясь произвольным образом, но, оставаясь параллельной самой себе, образует полосу погрешностей, ширина которой остается постоянной для любых значений измеряемой величины Х (см. рис. 4.2, б).
Мультипликативная погрешность– это погрешность чувствительности средства измерения. Она может иметь систематическую и случайную составляющие.
Сущность мультипликативной погрешности заключается в том, что если абсолютная погрешность возникает от некоторого независимого от Х изменения чувствительности преобразователя (изменение коэффициента деления делителя, добавочного сопротивления вольтметра и т. д.), то реальная характеристика 1 преобразователя отклоняется от номинальной 2 так, как это показано на рис. 4.3, а, или образует полосу погрешностей (рис. 4.3, б), если это отклонение является случайным.
Рис. 4.3. К пояснению понятия мультипликативной погрешности измерений
Список использованной литературы:
http://fiz.1september.ru/2001/16/no16_01.htm
https://studfiles.net/preview/6269920/page:2/
СКАЧАТЬ .pdf
О.А. Цыбульский
АО «ПромСервис», г. Димитровград, Ульяновская обл., Российская Федерация,
e-mail:
multimer@list.ru
Приведены формулы для нормирования предельной относительной погрешности прибора. С использованием критерия совокупного показателя точности и диапазона прибора показано преимущество нормирования по расширенной формуле, содержащей три составляющих предельной погрешности: аддитивную, мультипликативную и гиперболическую. Такое нормирование учитывает гиперболическую нелинейность характеристики преобразования, свойственную приборам с параметрическими преобразователями и многим приборам с широким диапазоном измерения, имеющим дробно-линейное (проективное уравнение измерения. Для приборов с широким диапазоном измерения предложено применять расширенную формулу нормирования предельной относительной погрешности измерения.
Ключевые слова: измерение, широкий диапазон, нормирование, полоса предельной погрешности, критерий, плотность вероятности, дробно-линейное (проективное) уравнение измерения, гиперболическая составляющая.
Formulas are given for normalizing the limiting relative error of the device. Using the criterion of the aggregate indicator of accuracy and range of the device, the advantage of standardization is shown by an extended formula containing three components of the marginal error: additive, multiplicative and hyperbolic. Such rationing takes into account the hyperbolic non-linearity of the conversion characteristic inherent in devices with parametric converters and many devices with a wide measuring range having a linear-fractional (projective) measurement equation. For instruments with a wide measuring range, it is proposed to use the extended formula for normalizing the limiting relative measurement error.
Точность прибора в диапазоне измерений нормируют полосой предельной погрешности. При нормировании широкодиапазонных приборов диапазон измерения разделяют на поддиапазоны. В каждом поддиапазоне предельная погрешность задана либо значением мультипликативной составляющей, либо двухчленной формулой, включающей аддитивную и мультипликативную составляющие погрешности. В руководствах по эксплуатации представлены большие таблицы, нормирующие относительные погрешности в каждом поддиапазоне и для каждой модификации прибора. Значения погрешностей и границы поддиапазонов могут задаваться достаточно произвольно. Это осложняет анализ и сравнение результатов измерений прибороводного типа.
С повышением точности измерения и расширением динамического диапазона приборов требуется учитывать нелинейную составляющую полосы погрешности. В [1] отмечено, что «наиболее общим видом формулы текущей относительной погрешности является трехчленная формула».
Формулы для нормирования предельной относительной погрешности прибора.
В настоящий момент для нормирования предельной относительной погрешности прибора в широком диапазоне измерения применяется формула, содержащая две (аддитивную и мультипликативную) составляющие предельной погрешности:
где X, Xн – текущее значение измеряемой величины и нижняя граница диапазона измерений соответственно;
δа=Δа/Xн – составляющая аддитивной погрешности измерения Δа;
δм – мультипликативная составляющая.
Существует целый класс измерительных преобразователей, относящихся к параметрическим преобразователям (например, измерительные мосты), предельная относительная погрешность которых описывается формулой с тремя составляющими – аддитивной, мультипликативной и гиперболической [1]. Это связано с тем,что согласно теореме вариации для измерительных цепей характеристика преобразования параметрических преобразователей, к которым относится большинство датчиков, имеет дробно-линейную функцию преобразования. Дробно-линейная функция описывает равностороннюю гиперболу. Даже после линеаризации характеристики параметрического преобразования (например, при введении обратной связи) остаточная нелинейность сохраняется. Остаточная гиперболическая нелинейность включается в суммарную погрешность в качестве погрешности нелинейности характеристики преобразования. Гиперболическая нелинейность характеристики преобразования имеет одну особенность, важную для измерительных приборов. Осуществляемое дробно-линейной функцией преобразование относится к проективным, образующим группу, т. е. «каждую конечную последовательность преобразований можно заменить одним преобразованием этой же группы» [2].
Структурная схема широкодиапазонного измерительного прибора, как правило, состоит из последовательной цепочки линейных преобразователей. Существование в этой цепочке хотя бы одного преобразователя с дробно-линейной характеристикой делает результирующую характеристику также дробно-линейной.
Соответственно, формула нормирования предельной погрешности этого преобразования должна включать нелинейную гиперболическую составляющую.
В работе [3] на примерах преобразователей расхода и калибратора-вольтметра показано, что не только при параметрических преобразованиях, но и в ряде других широкодиапазонных приборов предельную относительную погрешность измерений можно нормировать во всем диапазоне измерений формулой с тремя составляющими погрешности: аддитивной, мультипликативной и гиперболической:
где Xв –верхняя границы диапазона измерений;
δг=Δг/Xв–составляющая погрешности нелинейности (гиперболической) Δг при X=Xв.
Формула (2) содержит в виде частных случаев двухчленное (1) и одночленное представление предельной погрешности, т.е. позволяет осуществлять нормирование всеми применяемыми в настоящее время способами. Одновременнов формуле (2) учтена специфика параметрических и широкодиапазонных приборов, для которых становится существенной погрешность нелинейности. Третья – гиперболическая составляющая предельной относительной погрешности, в отличие от аддитивной и мультипликативной составляющих, нормирует гиперболическую нелинейность функции преобразования прибора.
В работе [3] показано, что для приборов с широким диапазоном измерения формулу нормирования предельной относительной погрешности (2) можно представить в удобном виде:
где δXн, δXв–предельные относительные погрешности соответственно в нижней и верхней границах диапазона измерений.
Применение формул (2), (3) позволяет во многих случаях нормировать предельную погрешность прибора во всём диапазоне измерений без поддиапазонов. Для примера сравним табличное нормирование расходомера Прамер-550-D в диапазоне измерений 1–1000 м3/час с нормированием по формуле (2). В таблице приведены значения нормируемых параметров Xн, δXн, Xв, δXв расходомера, где строки 1–3 соответствуют табличному нормированию в поддиапазонах, строка 4–нормированию по трёхчленной формуле (2) во всём диапазоне.
Формула нормирования предельной относительной погрешности расходомера Прамер-550-D (в диапазоне 1–1000м3/час) имеет вид
В диапазоне измерения расхода 0,1–100 м3/час получены составляющие полосы предельной относительной погрешности:
δа=4,86%; δм=0,57 %; δг=0,43 %, т.е. в формуле нормирования (4) в явном виде указаны значения основных метрологических параметров прибора:
диапазон измерения и составляющие полосы предельной относительной погрешности. Формула (4) получена аппроксимацией полосы погрешности, заданной табличным способом, по трём точкам:Xн=0,1; δXн=5 %; X=1; δX=1 %; Xв=100; δXв=1 %.
Рис. Нормирование предельной относительной погрешности расходомера Прамер-550-D табличным способом и по формуле (2)
Критерий эффективности совокупного показателя точности и диапазона прибора. На рисунке изображены полосы предельной относительной погрешности, заданные табличным способом и по
формуле (2). Нормирование по формуле (2) позволяет более адекватно задать значение предельной относительной погрешности в любой точке диапазона измерения. Для оценки преимущества нормирования с помощью формулы (2) используем критерий Nэфф совокупного показателя точности и диапазона прибора [1]. Для аддитивно-мультипликативной полосы предельной относительной погрешности (1) этот критерий определим как
где D=Xв/Xн – динамический (относительный) диапазон измерений.
Физический смысл критерия Nэфф– количество эффективных (реальных) квантов (делений), на которые данный прибор может разделить диапазон измерений с заданной полосой предельной погрешности, т. е. сколько непересекающихся интервалов предельной абсолютной погрешности последовательно уложатся в диапазон измерений. Это ресурс, которым обладает прибор для проведения измерения, и чем больше Nэфф, тем точнее прибор. Выражение (5) показывает взаимосвязь параметров измерительного преобразования.
При разделении диапазона измерения прибора на поддиапазоны количество эффективных квантов всего диапазона измерений равно сумме эффективных квантов всех поддиапазонов. В случае
D выражение (5) можно представить в удобном для анализа виде
где δXв≈δм, δXн=δа+δм – соответственно, предельные относительные погрешности на верхней и нижней границах диапазона измерений.
Поскольку критерий (6) был предложен для полосы предельной погрешности с двухчленной формулой нормирования, то для расчёта числа эффективных квантов шкалы прибора, предельная погрешность которого нормируется по формуле (2) с тремя составляющими погрешности, в работе [4] получено расширенное выражение критерия:
где δXн≈δа+δм, δXв≈δг+δм–относительные погрешности соответственно на нижней и верхней границах диапазона измерений при условии
D = Xв/Xн 1.
По критерию (7) можно определить более эффективный способ нормирования. Например, при нормировании относительной предельной погрешности расходомера Прамер-550-D табличным способом (см. таблицу) число эффективных квантов Nэфф=267, при нормировании по формуле (2) Nэфф=366. Следовательно, точность при нормировании табличным способом меньше в 366/267=1,371 раз или на 37,1%. Таким образом, применение монотонной функции (2) вследствие большего количества составляющих позволяет более адекватно (без потерь точности и разделения на поддиапазоны) нормировать полосу предельной погрешности, чем табличный метод.
Дробно-линейное уравнение измерения прибора. Полоса предельной относительной погрешности (2) в логарифмическом масштабе имеет U-образный вид (см. рисунок). Увеличение погрешности в верхней части диапазона U-образной полосы предельной относительной погрешности определяется нелинейной (гиперболической) составляющей погрешности. При описании
характеристики преобразования прибора с помощью линейной функции гиперболическую составляющую погрешности по возможности корректируют. Однако если вместо линейного уравнения измерения применять дробно-линейное (проективное) уравнение [4,5], то гиперболическая составляющая будет учтена и её не надо будет корректировать.
В общем случае дробно-линейное (проективное) уравнение измерения имеет вид
где a0, b0, b1 – постоянные масштабные коэффициенты;
Х, Хоп – измеряемая и опорная величины;
К – выходной код аналого-цифрового преобразователя (АЦП).
Для перехода от линейного к дробно-линейному уравнению необходимо, чтобы измерительный прибор осуществлял сравнение измеряемого сигнала не с фиксированным опорным сигналом,
формируемым мерой, а с линейной комбинацией опорного и измеряемого сигналов [5]. В этом случае характеристика преобразования вместо линейной функции станет равносторонней гиперболой, а полоса предельной относительной погрешности прибора описываться формулой (2).
Способ преобразования шкалы измерений с целью задания требуемой полосы предельной погрешности с помощью дробно-линейного (проективного) преобразования линейной шкалы измерения
предложен в [5,6]. Способ позволяет более рационально распределить эффективные кванты по шкале измеряемой величины АЦП с линейной шкалой квантования. Увеличение относительной погрешности квантования в нижней части линейной измерительной шкалы является существенным фактором, ограничивающим диапазон измерения.
Применение дробно-линейного (проективного) преобразования позволяет с помощью преобразования линейной измерительной шкалы получить «квазилогарифмическую» шкалу, существенно расширяющую диапазон измерения. При этом полоса предельной погрешности соответствует трёхчлену (2).
Если оставить уравнение измерений линейным, то в зависимости от алгоритма аппроксимации градуировочной кривой, например, минимизации по диапазону абсолютной или относительной погрешности аппроксимации, можно получить полосу погрешности, описываемую одно-, двух- или трёхчленной формулой нормирования. Посчитав количество эффективных квантов, можно убедиться,что наибольшее значение критерия, а значит, и наибольшую точность обеспечивает трёхчленная формула нормирования.
Подтверждение целесообразности применения трёхчленной формулы. Существуют (помимо критерия эффективности) факторы, подтверждающие целесообразность нормирования по трёхчленной
формуле. Количество эффективных квантов ограничено, и это только ресурс, заложенный в прибор. Ресурс надо эффективно применить: распределить кванты по шкале измерений, чтобы оптимизировать информационные, финансовые потери (далее – потери) вследствие погрешности измерений. Для этого требуется дополнительная информация об измеряемой величине: о частоте появления различных значений измеряемой величины, а также о законе изменения плотности вероятности измеряемой величины. Потери при измерении определяются не только погрешностью измерения δХi, но и частотой появления значения Хi. Если вероятность появления значения Хi близка к нулю, то потери из-за большой погрешности измерения малы и ими можно пренебречь (за исключением особых случаев, когда важно само экстремальное значение). Но если вероятность появления значения Хi максимальна, то погрешность измерения должна быть минимальна.
Влияние плотности вероятности измеряемой величины на закон изменения предельной погрешности по диапазону измерения подробно исследовано П.В. Новицким в информационной теории измерений [1]. В результате он сделал вывод, что при измерениях в широком диапазоне необходимо применять закон априорного логарифмически-равномерного распределения измеряемой величины:
Согласно выражению (9) оптимальной с информационной точки зрения является шкала с постоянной относительной погрешностью.
Впервые этот закон сформулирован в работе К. Шеннона [7]: в результате общего анализа больших множеств (в общем случае) наиболее характерным законом изменения плотности распределения для больших множеств является логарифмически-равномерный закон распределения.
Гипотезу К. Шеннона о логарифмически-равномерном законе априорного распределения плотности вероятностей экспериментально проверил П. В. Новицкий и подтвердил, что в центральной части широкого диапазона измерений закон можно трактовать, как логарифмически-равномерный. При этом на краях диапазона измерений наблюдалось снижение плотности P(lnX), т. е. закон распределения приближался к логарифмически-нормальному. Именно такой характер распределения с физической точки зрения Шеннон считал наиболее вероятным. Тем не менее, в дальнейшем для упрощения анализа было принято простое логарифмически-равномерное распределение, соответствующее применению шкалы измерения с постоянной относительной погрешностью.Но априори понятно, что предельная относительная погрешность должна возрастать на концах диапазона измерения. Полоса погрешности, нормируемая трёхчленной формулой для предельной относительной погрешности, этой закономерности соответствует.
В настоящее время во многих приборах (например, расходомерах) предельная относительная погрешность так и нормируется постоянной относительной погрешностью. Однако если погрешность на краях диапазона будет выше, чем в центральной части, то количество эффективных квантов станет больше. Вблизи нижней границы диапазона приборов это утверждение выполняется, а вблизи верхней границы, как правило, нет. Конечно, можно игнорировать эту закономерность и нормировать предельную относительную погрешность во всём диапазоне постоянным значением. Это целесообразно для измерительной шкалы с бесконечным количеством эффективных квантов. Но в реальном приборе количество эффективных квантов ограничено, и требование уменьшения погрешности противоречит требованию расширения диапазона измерения. Ресурса прибора не хватает для обеспечения наивысшей точности в наибольшем диапазоне.
Современные приборы обеспечивают большие динамические диапазоны измерений. Например, при выборе расходомера максимальный расход задают ориентировочно в 3–10 раз больше
ожидаемого среднесуточного расхода [8,9]. Учитывают не только возможное превышение максимального расхода над среднесуточным в 2–5 раз, но и увеличение верхней границы дополнительно в 1,5-2 раза с учётом запаса расхода «на вырост». Естественно, вероятность появления больших расходов меньше вероятности среднесуточного расхода. Таким образом, верхняя половина диапазона измерения имеет в среднем малую вероятность использования, а значит в ней допустима погрешность большая по сравнению с погрешностью при среднем расходе. Однако в действительности, все выпускаемые расходомеры имеют наивысшую точность и, соответственно, наибольшие затраты эффективных квантов именно вблизи верхней границы диапазона.
Если предельная относительная погрешность прибора с увеличением верхней границы измерения имеет тенденцию к росту, то ее целесообразно нормировать по формуле (2) с гиперболической
составляющей, поскольку она обеспечивает требуемую форму полосы погрешности. Чтобы формула нормирования (2) задавала наивысшую точность измерения в точке, соответствующей расчётному среднему значению, необходимо соблюдение равенства
Например, при нормировании расходомера Прамер-550-D (см.рисунок) минимальная погрешность измерения согласно (10) соответствует точке .
Ещё один фактор в пользу применения трёхчленной формулы нормирования связан с использованием именно гиперболической составляющей. Как отмечено выше, U-образный вид полосы предельной относительной погрешности достаточно распространён в измерительных приборах:во всех параметрических измерительных преобразователях [1], а также во многих широкодиапазонных приборах [3]. В работах [4,5] показано, что если полоса предельной относительной погрешности измерительного аналого-цифрового преобразования описывается функцией вида (2), то характеристика этого преобразования дробно-линейная функция. Преобразование, описываемое дробно-линейной функцией, изучается в рамках проективной (наиболее фундаментальной) геометрии. Применению в технических дисциплинах геометрических моделей посвящено много работ, например [10–14].
В работе [15] рассмотрена закономерность проявления проективных свойств в характеристике преобразования измерительных приборов при большом динамическом диапазоне преобразования.
Показано, что с увеличением динамического диапазона и изменением полосы предельной относительной погрешности от чисто аддитивной до U-образной изменяется уравнение измерения от линейного к дробно-линейному. Аналогичная закономерность характерна, например, для изобразительного искусства и фотографии при проецировании отображаемого объекта на плоскость картины или фотоплёнки. Согласно теории перспективы с увеличением размера объекта в глубину пространства закономерности евклидовой геометрии при изображении объекта меняются на закономерности проективной геометрии. В алгебраической записи это соответствует переходу от линейного уравнения к дробно-линейному. Это же происходит и с уравнением линейного измерения (аналого-цифрового преобразования) при переходе от узкого к широкому динамическому диапазону измерения. При измерениях также осуществляется проецирование объекта измерения на измерительную шкалу.
В работе [16] показано, что линейное аналого-цифровое преобразование является частным случаем такого дробно-линейного преобразования. Выполнено сравнение характеристик линейного и
дробно-линейного (проективного), построенного на той же линейной элементной базе, аналого-цифровых преобразований. Показано, что дробно-линейное аналого-цифровое преобразование эффективнее линейного и решает задачи оптимизации погрешности квантования, расширения диапазона измерений, снижения разрядности преобразователя. При этом все выражения, критерии, инварианты, справедливые для линейного преобразования, являются частным случаем соответствующих выражений, критериев и инвариантов дробно-линейного преобразования. Это же относится и к формуле нормирования предельной погрешности измерений. Таким образом, формула (2) нормирует полосу предельной погрешности приборов с дробно-линейным (проективным) уравнением измерения и, в частном случае –без гиперболической составляющей, нормирует полосу предельной погрешности приборов с линейным уравнением измерения.
Заключение. Расширенная формула представления предельной относительной погрешности (2) позволяет более качественно (без потерь точности) нормировать полосу предельной погрешности в широком диапазоне измерений. Формула (2) в общем случае соответствует полосе предельной погрешности дробно-линейного (проективного) уравнения измерения. В то время, как формула представления предельной относительной погрешности (1) в общем случае соответствует полосе предельной погрешности линейного уравнения измерения. Линейное уравнение измерения является частным случаем дробно-линейного (проективного) уравнения измерения. Таким образом, чтобы учесть нелинейность характеристики преобразования в полосе погрешности линейного измерительного прибора целесообразно при нормировании предельной относительной погрешности применять расширенную формулу нормирования (2) с тремя составляющими погрешности и использовать дробно-линейное уравнение измерения (8).
Список литературы:
1. Новицкий П.В. Основы информационной теории измерительных устройств. Л.:Энергия, 1968. 248с.
2. Ефимов Н. В. Высшая геометрия. Москва: Физматлит, 2004.
3. Цыбульский О.А. Погрешность широкодиапазонных измерений//Законодательная и прикладная метрология. 2010.№ 4. С.5–10.
4. Цыбульский О. А. Критерий для обобщенной оценки широкодиапазонного прибора по точности и диапазону измерений // Измерительная техника. 2014. № 5. С. 5–7.
5.Цыбульский О.А. Дробно-линейное уравнение измерений //Измерительная техника. 2017. №5. С. 25–30.
6. Пат. №2618903 РФ / Цыбульский О.А. //Изобретения. Полезные модели. 2017. Бюл.№ 14.
7. Шеннон К. Работы по теории информации и кибернетике. М.:Иностранная литература,1963.
8. Николадзе Г.И., Сомов М. А. Водоснабжение. М. Стройиздат,1995.
9. Ионин А. А. Газоснабжение. М.:изд. Лань, 2012.
10. Мазин В.Д. Обобщенная геометрическая модель измерительного преобразования//Междунар. науч.-практ.конф. «175 лет ВНИИМ им. Д.И. Менделеева и национальной системе обеспечения единства измерений», Санкт-Петербург, 14–15 июня 2017. СПб.: Издательство: Издательско-полиграфическая ассоциация высших учебных заведений 2017. С. 253.
11. Мазин В.Д. Векторное выражение единицы физической величины//Измерительная техника 2019. № 3. С. 26–29. DOI:
10.32446/0368-1025it.2019-3-26-29
12. Penin A. Analysis of electrical circuits with variable load regime parameters: projective geometry method. 2nd edition. Cham, Springer International Publishing Switzerland, 2016. 417p. DOI https://doi.org/10.1007/978-3-319-28451-4
13. Пенин А .А. Инварианты параметров источников неизменной мощности// Электричество.2018.№ 12.С. 52–63.
14. Пенин А. А., Сидоренко А. Проективная геометрия в электронике, технике и живой природе//Россия и Германия. 2014. Т. 2. № 6. С. 44–49.
15. Цыбульский О.А. Проективные свойства широкодиапазонных измерений // Измерительная техника. 2013. № 1. С. 27–29.
16. Цыбульский О.А. Сравнение характеристик линейного и дробно-линейного (проективного) аналого- цифровых преобразований.// Международный форум «Микроэлектроника-2017». 3-я международная научная конференция «Электронная компонентная база и электронные модули» Сборник докладов. Республика Крым г. Алушта, 02-07 октября 2017 г.// НАНОИНДУСТРИЯ. Спецвыпуск 2018 (82) ТЕХНОСФЕРА, С.344-350
Refe rences
1. Novitskii P. V. Osnovy informacionnoj teorii izmeritel’nyh ustrojstv [Fundamentals of information theory of measuring devices]. Leningrad, Energiy Publ., 1968, 248 p. [In Russ.].
2. Efimov N. V. Higher geometry. Moscow: Fizmatlit, 2004. [In Russ.].
3. Tsybul’skii O.A. Pogreshnost’ shirokodiapazonnykh izmereniI// Zakonodatel’naya i prikladnaya metrologiYA. 2010.№ 4. S.5–10. [In Russ.].
4. Tcybulskii O. A. Measurement Techniques, 2014, vol. 57, no. 5, рр. 479–483. DOI: 10,1007 / s11018-014-0484-2
5. Tsybul’skiy O.A. Measurement Techniques, 2017, vol. 60, no. 5, рр. 443–450. DOI 10.1007/s11018-017-1215-2
6. Pat. No. 2618903 of the Russian Federation / Tcybulskii O. A.//Inventions. 2017. Bull. №14 [In Russ.].
7. Shennon K. Raboty po teorii informatsii i kibernetike.M.:Inostrannaya literatura,1963. [In Russ.].
8. Nikoladze G.I., Somov M. A. Vodosnabzheniye. M. Stroyizdat, 1995.[In Russ.].
9. Ionin A. A. Gazosnabzheniye. M.:izd. Lan’, 2012 [In Russ.].
10. Mazin V.D. Obobshchennaya geometricheskaya model’izmeritel’nogo preobrazovaniya//Mezhdunar. nauch.-prakt.konf. «175 let VNIIM im. D.I. Mendeleyeva i natsional’noy sisteme obespecheniya yedinstva izmereniy», Sankt-Peterburg, 14–15 iyunya 2017. SPb.: Izdatel’stvo: Izdatel’sko-poligraficheskaya assotsiatsiya vysshikh uchebnykh zavedeniy 2017. S. 253. [In Russ.].
11. Mazin V.D. Vektornoye vyrazheniye yedinitsy fizicheskoy velichiny//Izmeritel’naya tekhnika 2019. № 3. S. 26–29. DOI: 10.32446/0368-1025it.2019-3-26-29
12. Penin A. Analysis of electrical circuits with variable load regime parameters: projective geometry method. 2nd edition. Cham, Springer International Publishing Switzerland, 2016. 417 p.
13. Penin A .A. Invarianty parametrov istochnikov neizmennoy moshchnosti// Elektrichestvo.2018.№ 12.S. 52–63. [In Russ.].
14. Penin A. A., Sidorenko A. Proyektivnaya geometriya v elektronike, tekhnike i zhivoy prirode//Rossiya i Germaniya. 2014. T. 2. № 6. S. 44–49. [In Russ.].
15. Tcybulskii O. A. Measurement Techniques, 2013, vol. 56, no. 1, pp 37–40. DOI https://doi.org/10.1007/s11018-013-0155-8
16. Tsybul’skii O.A. Sravneniye kharakteristik lineynogo i drobnolineynogo (proyektivnogo) analogo- tsifrovykh preobrazovaniy.//Mezhdunarodnyy forum «Mikroelektronika-2017». 3-ya Mezhdunarodnaya nauchnaya konferentsiya «Elektronnaya komponentnaya baza i elektronnyye moduli» Sbornik dokladov. Respublika Krym g. Alushta, 02-07 oktyabrya 2017 g.// NANOINDUSTRIYA. petsvypusk 2018 (82) TEKHNOSFERA, S.344-350 [In Russ.].