Онлайн калькулятор предназначен для определения нулей функции они же точки пересечения графика функции с осями координат.
Например: Функция (x-2)(x-3) имеет нули в точках x=2; x=3; y=6.
: x^a
модуль x: abs(x)
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]
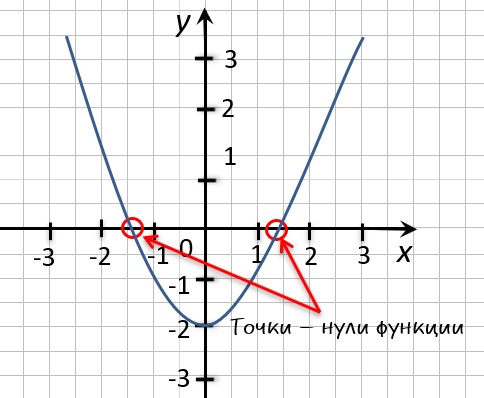
Одной из задач, возникающих при исследовании функции, является нахождение её нулей — т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции
:
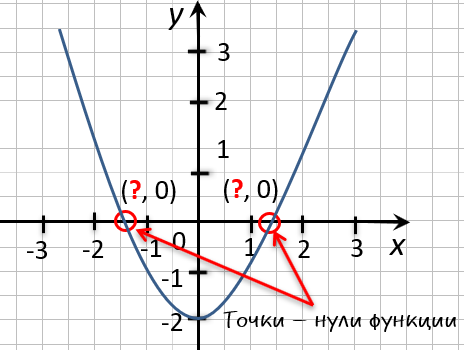
Нулями функции
являются точки
в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти
нули функции
необходимо и достаточно
решить уравнение:
Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках
.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.
Нули функции онлайн
Одной из задач, возникающих при исследовании функции, является нахождение её нулей — т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции :
Нулями функции являются точки в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти нули функции необходимо и достаточно решить уравнение:
Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках .
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.
Рациональные уравнения онлайн калькулятор
Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.
Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.
Добро пожаловать на сайт Pocket Teacher
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
начать
Рациональные уравнения
В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.
Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.
Действия с рациональными числами обладают свойствами действий с целыми числами.
К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.
Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.
Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».
Делить на ноль в рациональных уравнениях, как и в обычных нельзя.
Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.
Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.
Бесплатный онлайн калькулятор
Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Как найти нули функции по уравнению с дробью?
Алгебра | 5 — 9 классы
Как найти нули функции по уравнению с дробью?
У = дробь в числителе х ^ 2 — 6х + 5 ; в знаменателе х — 5 Объясните пожалуйста!
Ответ : решение представлено на фотоОбъяснение :
Знаменатель несократимой дроби больше ее числителя на 5?
Знаменатель несократимой дроби больше ее числителя на 5.
Если числители дроби увеличить на 2, а ее знаменатель уменьшить на 2 то полученая дробь будет больше на 18 / 35 больше данной дроби.
Найти данную дробь.
Прочитайте задачу «Знаменатель обыкновенной дроби на 5 больше её числителя?
Прочитайте задачу «Знаменатель обыкновенной дроби на 5 больше её числителя.
Если из числителя вычесть 1, а из знаменателя вычесть 3, то дробь увеличится на 1 / 18.
Чему равен числитель этой дроби?
«. Пусть x — числитель данной дроби, какое уравнение позволяет найти x?
Как приравнять к нулю?
Как приравнять к нулю?
Дробь : в числителе 2х3 — 2 в знаменателе х2 и всё это равно нулю.
Числитель обыкновенной дроби на 7 меньше его знаменателя?
Числитель обыкновенной дроби на 7 меньше его знаменателя.
Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).
Найти данную дробь
Задача решается через «пусть» и уравнение!
Числитель обыкновенной дроби на 7 меньше его знаменателя?
Числитель обыкновенной дроби на 7 меньше его знаменателя.
Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).
Найти данную дробь
помогите решить пожалуйста!
Задача решается через «пусть» и уравнение.
Найти область определения функции y = дробь числитель 4 + х знаменатель х — 5?
Найти область определения функции y = дробь числитель 4 + х знаменатель х — 5.
Числитель некоторой обыкновенной дроби на 11 больше знаменателя?
Числитель некоторой обыкновенной дроби на 11 больше знаменателя.
Если к числителю дроби прибавить 5, а к знаменателю 12, то получится дробь, втрое меньше исходной.
Найти эту дробь.
Сумма числителя и знаменателя некоторой дроби равна 13?
Сумма числителя и знаменателя некоторой дроби равна 13.
Найти эту дробь, если числитель меньше знаменателя на 3.
Числитель обыкновенной дроби на 7 меньше его знаменателя?
Числитель обыкновенной дроби на 7 меньше его знаменателя.
Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4 , то дробь уменьшится на 1 / 6 (одну шестую).
Найти данную дробь.
Задача решается через «пусть» и уравнение))
Числитель дроби на 12 меньше знаменателя ?
Числитель дроби на 12 меньше знаменателя .
Если к числителю добавить 29, а из знаменателя вычесть 7, то получится дробь обратная данной .
Найти эту дробь.
На странице вопроса Как найти нули функции по уравнению с дробью? из категории Алгебра вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.
x + 2≠0 x≠ — 2 Значит, вертикальная асимптота : х = — 2 горизонтальная асимптота : у = 1 Поэтому, область определения функции : (∞ ; — 2)∪( — 2 ; + ∞) множество значений функции : ( — ∞ ; 1)∪(1 ; + ∞).
5х — 10 — 30х = 2х — 6 — 10 + 6 = 2х — 5х + 30х 27х = — 4 х = — 4 / 27 48 + 6х — 10х = — 9 10х — 6х = 9 + 48 4х = 57 х = 57 / 4 = 14, 25 5 + 15х — 5х = — 1 10х = — 6 х = — 0, 6 — 24 — 36х — х = 5 36х + х = — 24 — 5 37х = — 29 х = — 29 / 37 — 63 — 7х ..
Исследование функции прилагаю.
F(x) = 10ˣ * 1 / ln10 + 4 / (x² — 5x — 7) нужно найти f'(x) и x₀ = 2 f'(x) = 10ˣ * ln10 * 1 / ln10 — 4(2x — 5) / (x² — 5x — 7)² = 10ˣ — 4(2x — 5) / (x² — 5x — 7)² f'(2) = 10² — 4 * ( — 1) / 169 = 100 + 4 / 169.
Решение в приложении.
F(x) = 3x² — 5x + 2 f(0. 5) = 3 / 2² — 5 / 2 + 2 = 0. 25 f( — 1) = 3 * ( — 1²) + 5 * 1 + 2 = 10.
Разделили уравнение на 2 x² — x — 2 = 0Найдем дискриминант квадратного уравнения : D = ( — 1)2 — 4·1·( — 2) = 1 + 8 = 9a1 = (1 — √9) / 2·1 = — 1 a2 = (1 + √9) / 2·1 = 2 Там где у² = — 1 / 2 надо написать, у²≥ 0, не имеет решения.
12 + x = 72 x = 72 — 12 x = 60 ________ Проверка 12 + 60 = 72.
http://www.pocketteacher.ru/calculator-rationalnih-uravneniy-ru
http://algebra.my-dict.ru/q/2083898_kak-najti-nuli-funkcii-po-uravneniu/
Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
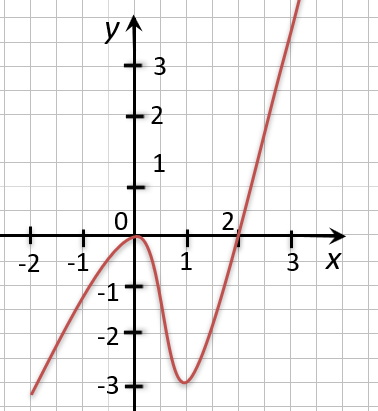
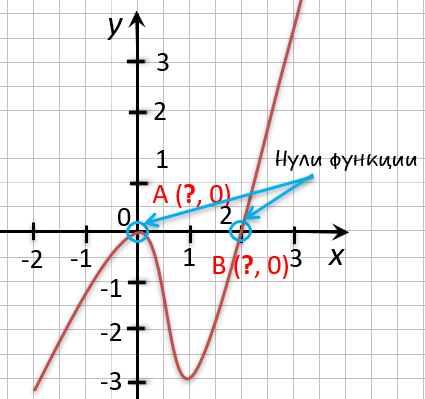
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
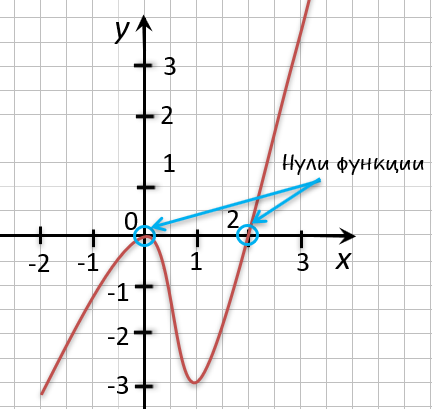
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
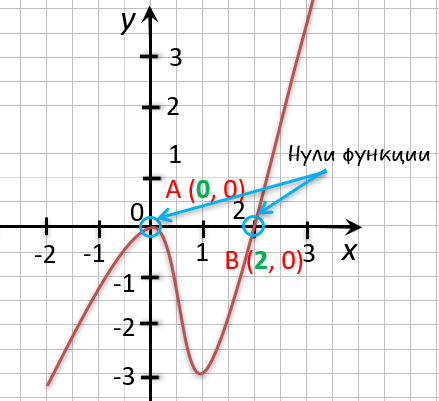
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
- Каноническая.
- Квадратичная.
- Общая.
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).
Рисунок 2. Директриса и фокус.
Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:
- Абсцисса вершины параболы: xa = -b / 2a.
- Координата «игрек» по оси ординат: yb = — D / 2a.
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.
Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Видео
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2+11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
- Если вершина не задана, то нужно найти ее любым из методов.
- Определить точки пересечения с осями декартовой системы координат.
- Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
- Выполнить построение, соединив точки.
Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.
Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.


 : x^a
: x^a : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]