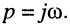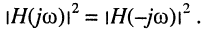Понятие полюсов и нулей в передаточных функциях
Добавлено 24 декабря 2019 в 23:34
Данная статья объясняет, что такое полюсы и нули, и обсуждает, как полюсы и нули передаточной функции связаны с поведением схем аналоговых фильтров относительно амплитуды и фазы.
В предыдущей статье я представил два стандартных способа представления передаточной функции в s-области для RC фильтра нижних частот первого порядка. Давайте кратко рассмотрим некоторые важные концепции.
- Передаточная функция математически выражает поведение фильтра в частотной области при передаче сигнала от входа к выходу.
- Мы можем написать передаточную функцию относительно переменной s, которая представляет собой комплексную частоту, и мы можем заменить s на jω, когда нам нужно вычислить амплитуду и сдвиг фазы на конкретной частоте.
- Нормированная форма передаточной функции похожа на шаблон, который помогает нам быстро определять определяющие характеристики фильтра.
- Математическое манипулирование нормированной передаточной функцией первого порядка позволяет нам продемонстрировать, что частота среза фильтра – это частота, на которой амплитуда уменьшается на 3 дБ, а фаза сдвигается на –45°.
Полюсы и нули
Предположим, что у нас есть передаточная функция, в которой переменная s появляется как в числителе, так и в знаменателе. В этой ситуации, по крайней мере, одно значение s приведет к тому, что числитель будет равен нулю, и, по крайней мере, одно значение s приведет к тому, что знаменатель будет равен нулю. Значение, при котором числитель равен нулю, является нулем передаточной функции, а значение, которое приводит к нулю в знаменателе, является полюсом передаточной функции.
Давайте рассмотрим следующий пример:
[T(s)=frac{Ks}{s+omega _{0}}]
В этой системе мы имеем ноль при s = 0 и полюс при s = –ω0.
Полюсы и нули являются определяющими характеристиками фильтра. Если вы знаете расположение полюсов и нулей, то у вас много информации о том, как система будет реагировать на сигналы с разными входными частотами.
Влияние полюсов и нулей
Диаграмма Боде (логарифмическая амплитудно-частотная характеристика, АЧХ) обеспечивает простую визуализацию взаимосвязи между полюсом или нулем и поведением системы при передаче сигнала от входа к выходу.
Частота полюса соответствует угловой частоте, при которой наклон кривой АЧХ уменьшается на 20 дБ/декада, а ноль соответствует угловой частоте, при которой наклон увеличивается на 20 дБ/декада. В следующем примере амплитудно-частотная характеристика представляет собой аппроксимацию амплитудного отклика системы, которая имеет полюс при 102 радиана в секунду (рад/с) и ноль при 104 рад/с.
Влияние на фазу
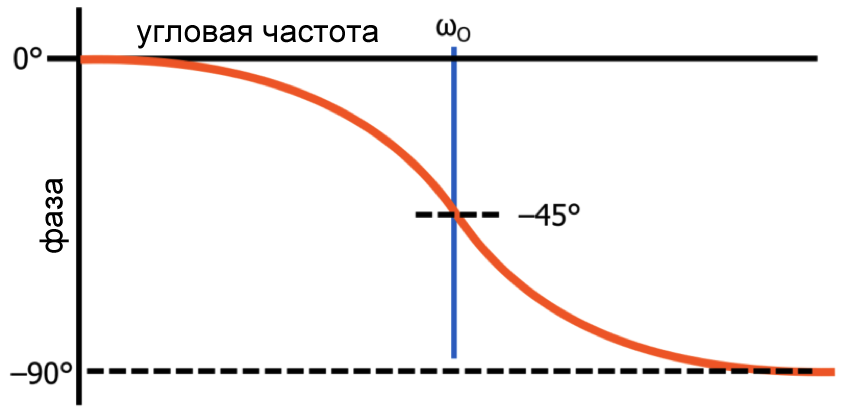
В предыдущей статье мы видели, что математическим источником фазо-частотной характеристики фильтра нижних частот является функция арктангенса. Если мы используем функцию арктангенса (точнее, функцию отрицательного арктангенса), чтобы сгенерировать график зависимости фазы (в градусах) от частоты в логарифмическом масштабе, мы получим следующий график:
Аппроксимация логарифмической фазо-частотной характеристики для сдвига фазы, генерируемого полюсом, представляет собой прямую линию, представляющую сдвиг фазы -90°. Эта линия центрируется на частоте полюса и имеет наклон –45 градусов на декаду, что означает, что наклонная линия начинается за одну декаду до частоты полюса и заканчивается через одну декаду после частоты полюса. Влияние нуля будет таким же, за исключением того, что линия имеет положительный наклон, поэтому итоговый сдвиг фазы составляет +90°.
В следующем примере представлена система, которая имеет полюс при 102 рад/с и ноль при 105 рад/с.
Скрытый ноль
Если вы читали предыдущую статью, вы знаете, что передаточная функция фильтра нижних частот может быть записана следующим образом:
[T(s)=frac{a_0}{s+omega_0}]
У этой системы есть ноль? Если мы применим определение, данное ранее в этой статье, мы сделаем вывод, что его нет – переменная s не появляется в числителе, и поэтому никакое значение s не приведет к тому, что числитель станет равным нулю.
Однако оказывается, что у нее на самом деле есть ноль, и чтобы понять почему, нам нужно рассмотреть более обобщенное определение полюсов и нулей передаточной функции: ноль (z от «zero») возникает при значении s, которое заставляет передаточную функцию уменьшаться до нуля, а полюс (p от «pole») возникает при значении s, которое заставляет передаточную функцию стремиться к бесконечности:
[lim_{srightarrow z}T(s)=0]
[lim_{srightarrow p}T(s)=∞]
Имеет ли фильтр нижних частот первого порядка значение s, которое приводит к T(s) → 0? Да, это так, а именно, s = ∞. Таким образом, система фильтра нижних частот первого порядка имеет полюс в точке ω0 и ноль в точке ω = ∞.
Я попытаюсь дать физическую интерпретацию нуля при ω = ∞: это указывает на то, что фильтр не может «всегда» продолжать увеличивать ослабление (где «всегда» относится к частоте, а не ко времени). Если вам удастся создать входной сигнал, частота которого продолжает увеличиваться до тех пор, пока она не «достигнет» бесконечности рад/с, то ноль при s = ∞ заставит фильтр прекратить увеличивать ослабление, т.е. наклон амплитудно-частотной характеристики увеличится с –20 дБ/декада до 0 дБ/декада.
Заключение
Мы изучили основные теоретические и практические аспекты полюсов и нулей передаточной функции и увидели, что можем создать прямую связь между частотами полюса и нуля фильтра и его амплитудно-частотной и фазо-частотной характеристиками. В следующей статье мы рассмотрим передаточную функцию фильтра верхних частот первого порядка.
Теги
АЧХ (амплитудно-частотная характеристика)Передаточная функцияФильтрФНЧ (фильтр нижних частот)ФЧХ (фазо-частотная характеристика)Частота среза
-
Определение нулей и полюсов передаточных функций замкнутой системы по каналам управления и возмущения
Для получения корневых показателей
качества системы управления необходимо
рассчитать корни полиномов числителя
и знаменателя передаточной функции
замкнутой системы для случаев, когда
запаздывание в канале регулирования
объектаравно нулю.
Передаточную функцию замкнутой системы
в общем виде можно представить в виде
отношения передаточных функций
разомкнутой системы:
Передаточную функцию разомкнутой
системы представим в виде произведения
передаточных функций объекта и
ПИрегулятора:
где
С учетом отсутствия запаздывания по
каналу регулирования, подставим выражение
полученное в формулу передаточной
функции замкнутой системы и получим
передаточную функцию замкнутой системы
в виде отношения полиномов числителя
и знаменателя:
Полюса передаточной функции найдем,
приравняв характеристический полином
к нулю:
Вычисляя это характеристическое
уравнение на компьютере, получим
решение:
Нахождение нулей передаточной функции
сводиться к нахождению нулей полинома
числителя, приравняв полином к нулю:
решив это уравнение, получим нуль
передаточной функции замкнутой
системы:
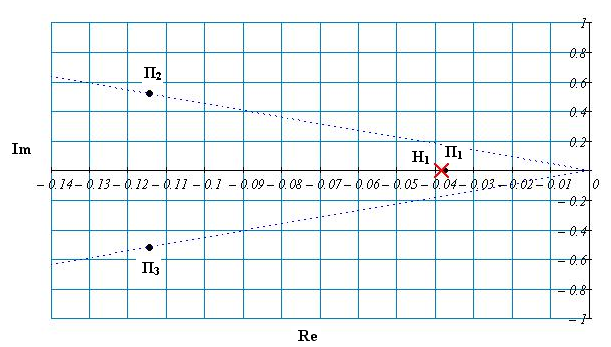
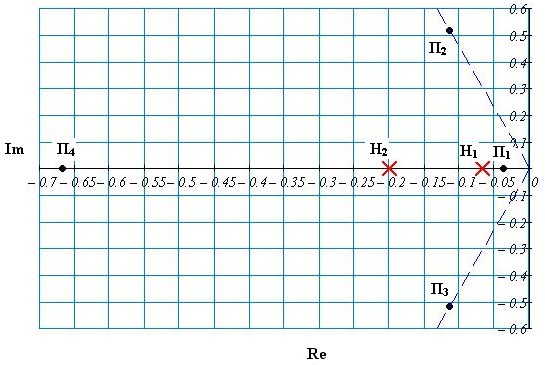
Рис. 59 Нули и полюса передаточной функции
замкнутой
системы по каналу регулирования
Близко расположенные полюс П1и
нуль Н1 взаимно компенсируют друг
друга. Доминирующими полюсами являются
П2и П3. Уменьшение амплитуды
колебательной составляющей, создаваемое
комплексными полюсами П2и П3зависит от модуля вещественной
составляющей этих полюсов. Время
регулирования переходной характеристики
зависит от абсолютного значения
вещественной части доминирующих полюсов.
Для нахождения нулей и полюсов передаточной
функции замкнутой системы по первому
каналу возмущенияв выражении
передаточной функции замкнутой системы
приравняем числитель и знаменатель к
нулю. Полюса передаточной функции
найдем, приравняв характеристический
полином к нулю:
Вычисляя это характеристическое
уравнение на компьютере, получим
решение:
Нахождение нулей передаточной функции
сводиться к нахождению нулей полинома
числителя, приравненного к нулю:
Рис.60 Нули и полюса передаточной функции
замкнутой системы по первому каналу
возмущения
Доминирующими полюсами являются
П1,П2,П3. Уменьшение
амплитуды колебательной составляющей,
создаваемое комплексными полюсами П2и П3зависит от модуля вещественной
составляющей этих полюсов. Время
регулирования переходной характеристики
зависит от абсолютного значения
вещественной части доминирующих полюсов,
наибольшее значение из доминирующих
полюсов оказывает П1. Полюс П4не оказывает существенного влияния
из-за удаленности от мнимой оси. Ноль
Н1оказывает влияние на время
регулирования переходной характеристики.
Ноль Н2не оказывает существенного
влияния из-за удаленности от мнимой
оси.
Для нахождения нулей и полюсов передаточной
функции замкнутой системы по второму
каналу возмущенияв выражении
передаточной функции замкнутой системы
приравняем числитель и знаменатель к
нулю. Полюса передаточной функции
найдем, приравняв характеристический
полином к нулю:
Вычисляя это характеристическое
уравнение, получим решение:
Нахождение нулей передаточной функции
сводиться к нахождению нулей полинома
числителя, приравненного к нулю:
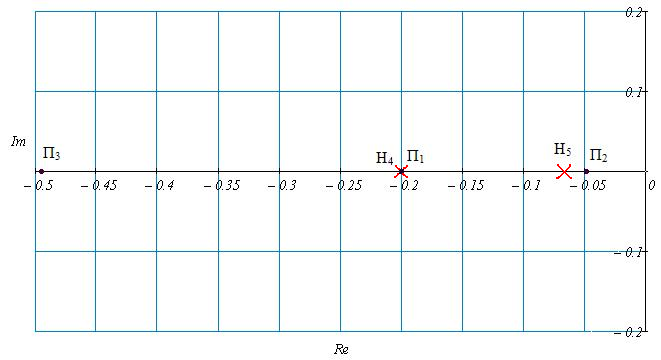
Рис.61 Нули и полюса передаточной функции
замкнутой
системы по второму каналу возмущения
Доминирующим полюсом являются П2.
Уменьшение амплитуды колебательной
составляющей, создаваемое полюсами П2и П3зависит от модуля вещественной
составляющей этих полюсов. Время
регулирования переходной характеристики
зависит от абсолютного значения
вещественной части доминирующих полюсов.
Полюс П1и ноль Н4взаимно
компенсируют друг друга. Время
регулирования переходной характеристики
также зависит от Н5. Полюс П3 не
оказывает существенного влияния из-за
удаленности от мнимой оси.
Для нахождения нулей и полюсов передаточной
функции замкнутой системы по третьему
каналу возмущенияв выражении
передаточной функции замкнутой системы
приравняем числитель и знаменатель к
нулю. Полюса передаточной функции
найдем, приравняв характеристический
полином к нулю:
Вычисляя это характеристическое
уравнение на компьютере, получим
решение:
Нахождение нулей передаточной функции
сводиться к нахождению нулей полинома
числителя, приравненного к нулю.:
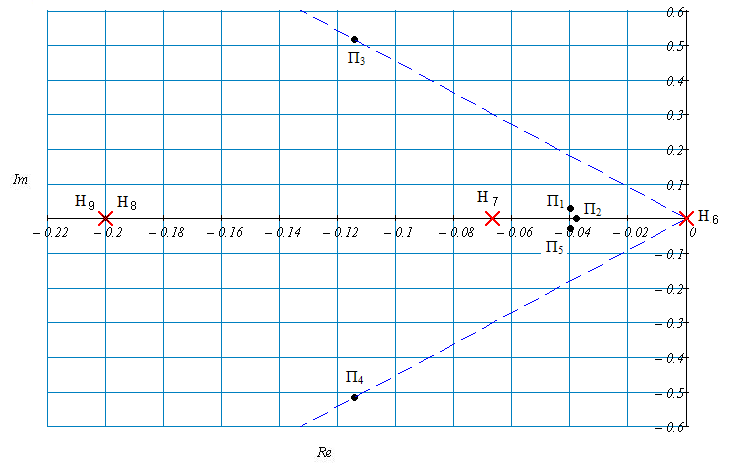
Рис.62 Нули и полюса передаточной функции
замкнутой системы
по третьему каналу возмущения
Доминирующими полюсами являются П1П2, П5. Уменьшение амплитуды
колебательной составляющей, создаваемое
комплексными полюсами П1и П5зависит от модуля вещественной
составляющей этих полюсов. Время
регулирования переходной характеристики
зависит от абсолютного значения
вещественной части доминирующих полюсов,
наибольшее значение из доминирующих
полюсов оказывает П2. Полюса П3,
П4оказывают малое влияние из-за
удаленности от мнимой оси.
Время регулирования переходной
характеристики также зависит от ноля
Н6, который оказывает сильное
влияние. Время регулирования переходной
характеристики также зависит от нулей
Н7, Н8, Н9.Ноль Н6оказывает существенное влияние. Нули
Н7, Н8, Н9не оказывает
существенного влияния из-за удаленности
от мнимой оси.
Лекция № 6
Свойства передаточной функции.
Поскольку передаточная функция получается в результате решения алгебраических уравнений для операторной схемы, то она представляет из себя дробно-рациональную функцию:
Поскольку 


Если m < n – то в ∞ числителя 0.
Коэффициенты числителя и знаменателя состоят из элементов схемы R, L, C и параметров управляемых источников, т.е. являются действительными числами. Отсюда вывод: нули и полюса либо действительные числа, либо, если они комплексные, то они комплексно сопряжённые. Поскольку полюса являются корнями характеристического уравнения, то корни знаменателя, если действительные, то отрицательные; если комплексные, то имеют отрицательную действительную часть. Из этого следует, что все коэффициенты знаменателя имеют один и тот же знак.
Приведём 
Рекомендуемые материалы
Представление передаточной функции с помощью нулей и полюсов более информативно. И обычно пользуются этим представлением.
Иногда говорят, что полюса лежат в левой плоскости (к ней относится и мнимая ось)


Х – полюса
Нули могут быть как в левой, так и в правой полуплоскости Если нули находятся только в левой полуплоскости, то такая цепь называется минимально-фазовой.
Если хотя бы один из нулей находится в правой полуплоскости, то такая цепь называется неминимально-фазовой.
Получение частотных характеристик по расположению нулей и полюсов на комплексной плоскости.



Для того, чтобы получить значения АЧХ и ФЧХ для заданной частоты, нужно из всех нулей и полюсов провести вектора в эту частоту, найти 


|
|
|
|
|
|
|
|
0 |
0 |
2 |
3,2 |
3,2 |
0 |
|
2 |
2 |
2,8 |
1,4 |
5,1 |
1,6 |
|
3 |
3 |
3,6 |
1 |
6,1 |
3,5 |
|
4 |
4 |
4,5 |
1,4 |
7 |
3,8 |
|
∞ |
∞ |
∞ |
∞ |
∞ |
2 |

|
|
|
|
|
|
|
|
0 |
90° |
0 |
-70° |
70° |
90° |
|
2 |
90 |
45 |
-45 |
78 |
102 |
|
3 |
90 |
55 |
0 |
80 |
65 |
|
4 |
90 |
62 |
45 |
81 |
26 |
|
∞ |
90 |
90 |
90 |
90 |
0 |
Задача (может быть при защите к.р.)

Чем ближе полюс к оси, тем больше добротность. Вводят понятие полюсная добротность:

Пусть мы имеем следующее расположение нулей и полюсов:


— частотная характеристика для магнитофона.
Связь между АЧХ и ФЧХ.
Для минимально-фазовой цепи существует связь между АЧХ и ФЧХ, для неминимально-фазовой не существует.
Каждая 


Можно добавить нули и полюса, но и слагаемые в фазовой характеристике тоже прибавляются. Т.е. нельзя изменить АЧХ без изменения ФЧХ.

Добавим дополнительный ноль и полюс:


Ещё посмотрите лекцию «2 Двигательные нарушения» по этой теме.

Есть цепи, которые имеют только нули и полюса симметричные относительно мнимой оси:

Например, задано
Получение: 
Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
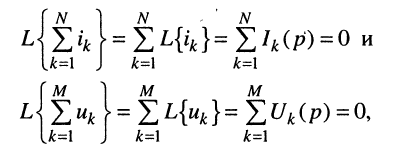
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 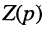
Для элемента активного сопротивления
откуда
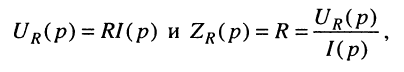
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
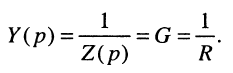
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
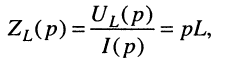
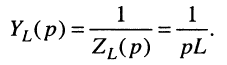
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
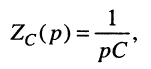
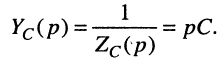
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 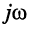
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 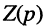
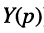
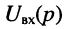
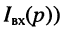
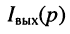
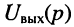
(соответственно 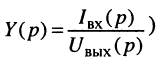
Пример 17.1.
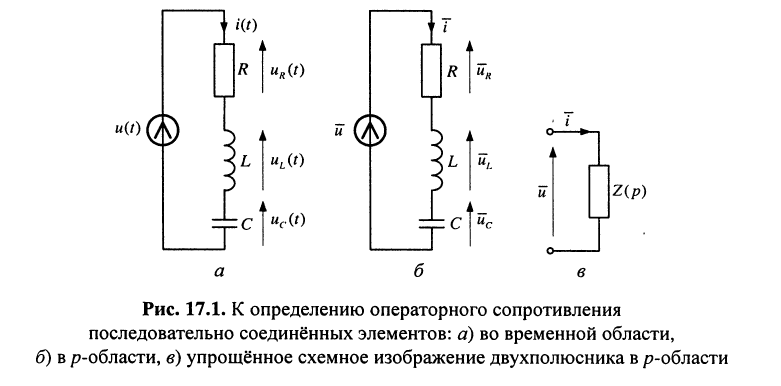
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 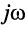
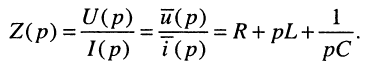
Пример 17.2.
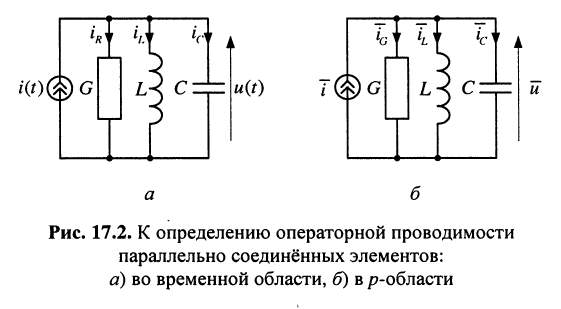
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 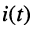
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
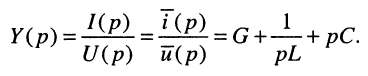
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 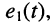
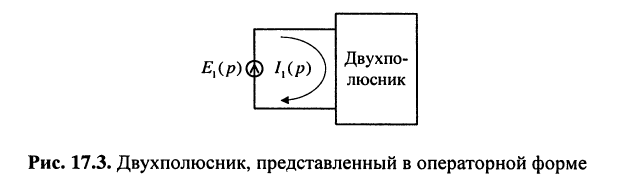
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
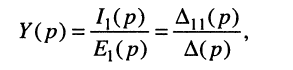
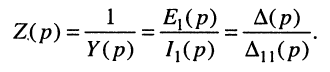
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
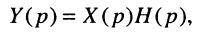
откуда получаем соотношения вход/выход в операторной форме
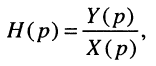
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
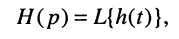
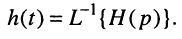
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда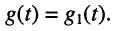
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
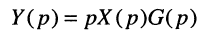
и
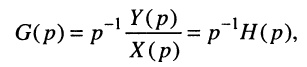
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 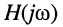
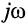
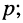
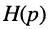
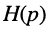
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
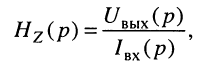
операторную передаточную проводимость
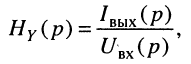
передаточную функцию по току
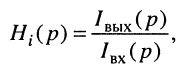
передаточную функцию по напряжению
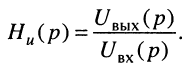
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
поэтому
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
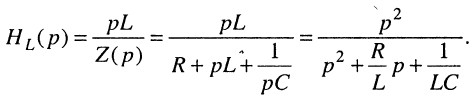
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
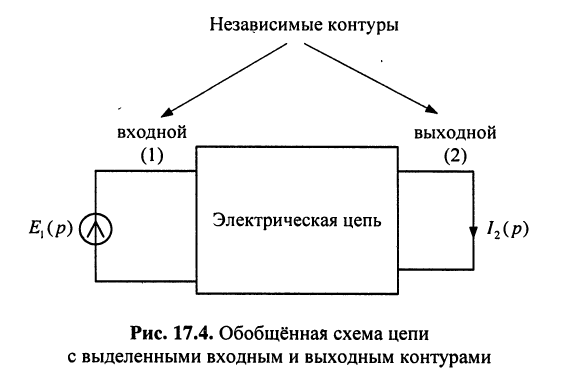
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
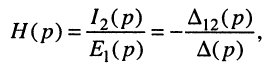
где 
a 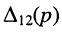
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
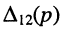
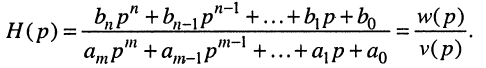
Полиномы числителя 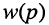
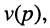
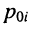
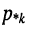
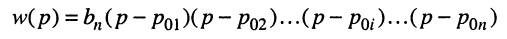
и
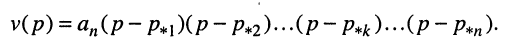
Отсюда передаточная функция (17.24) приобретает вид:
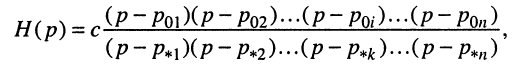
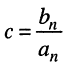
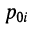
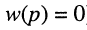
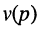
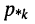
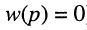
Названия корней уравнения 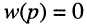
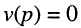
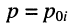
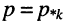
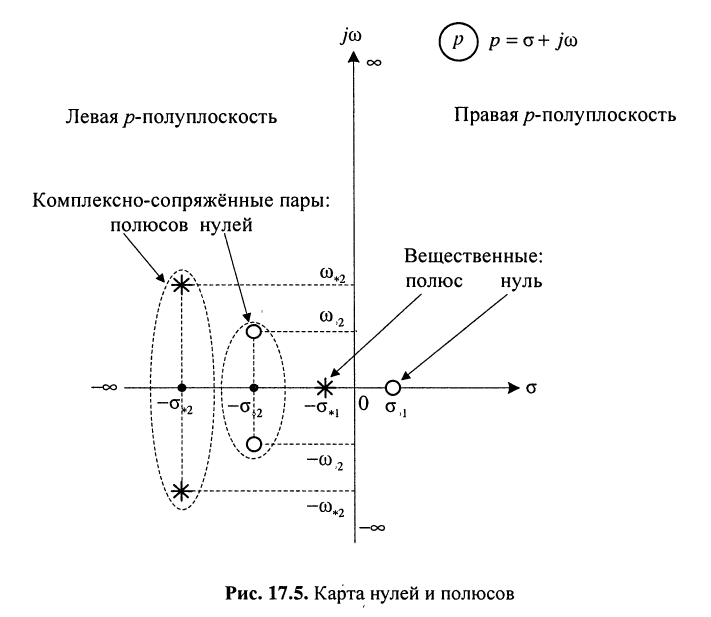
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
и 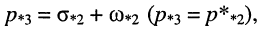
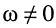
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
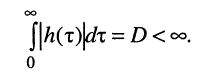
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
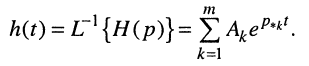
Подставим в интеграл (17.28) правую сумму (17.29)
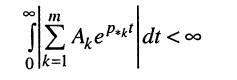
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
которое проинтегрируем:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
Здесь, во-первых,
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 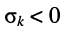
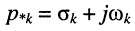
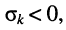
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 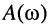
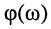
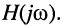
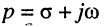
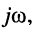
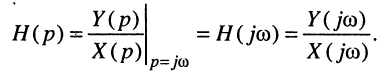
Отсюда имеем:
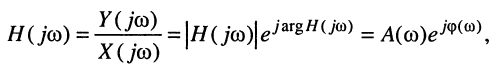
где
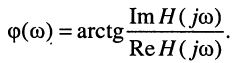
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
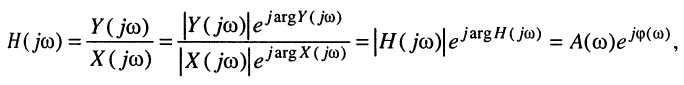
где
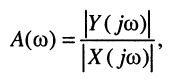
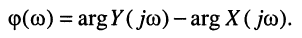
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
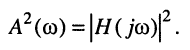
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
- По передаточной функции можно изобразить схему цепи
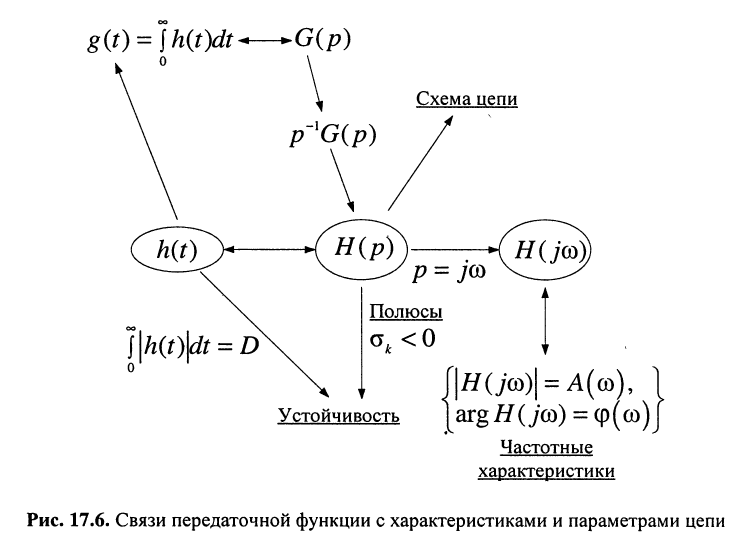
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей



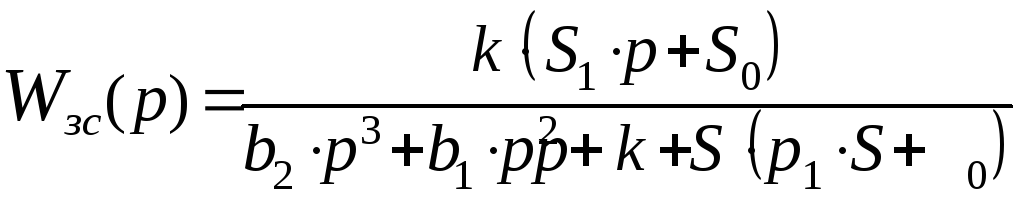

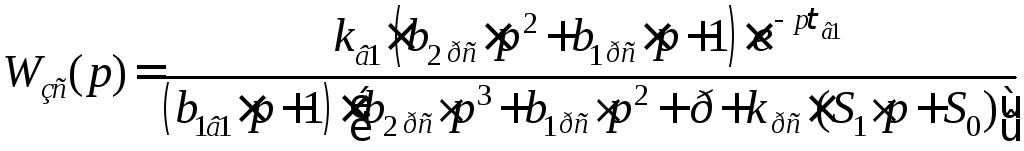
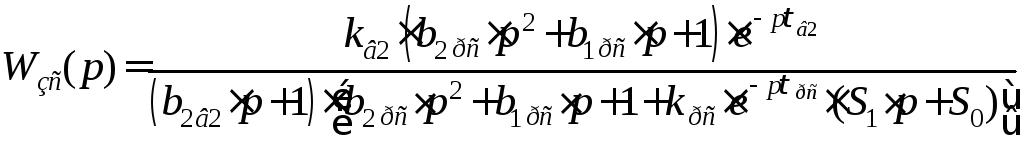
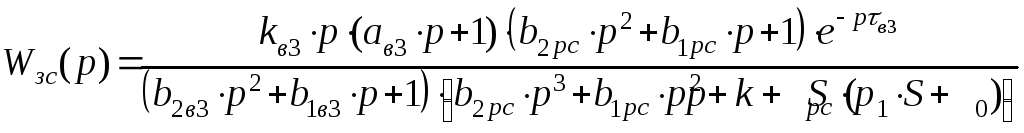












































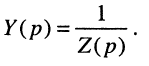
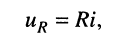
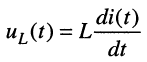
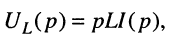
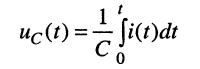
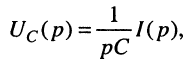
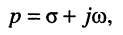
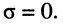
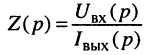
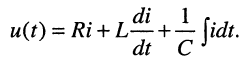
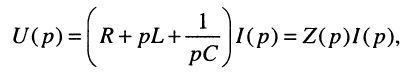
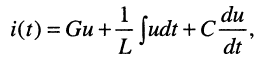
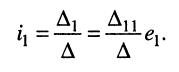
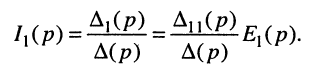
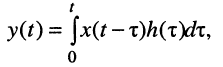
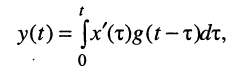
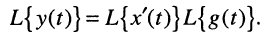
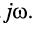
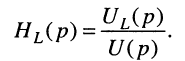
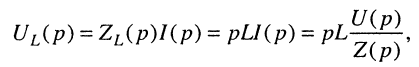
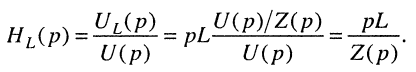
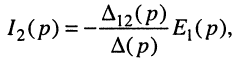
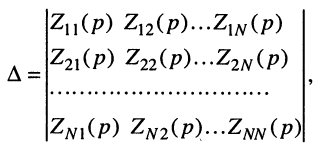
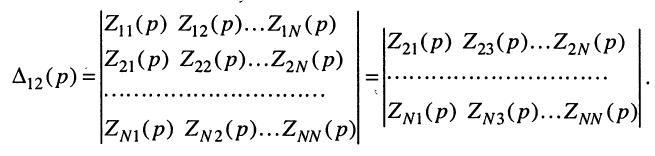
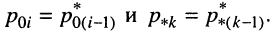
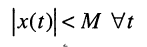
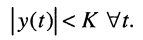
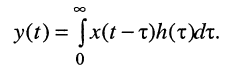
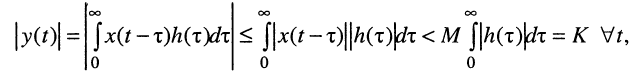
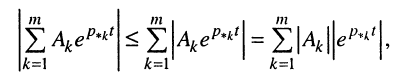
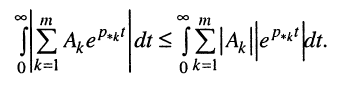
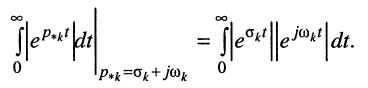
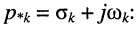
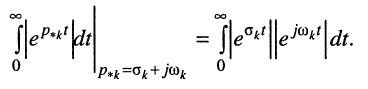
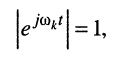
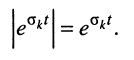
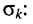
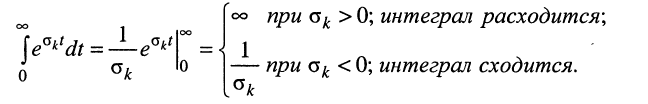
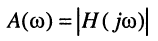
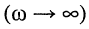 должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.