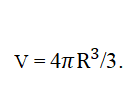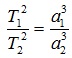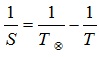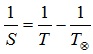Объем спутника как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Элементы астрофизики. Солнечная система, звёзды, галактики

В. З. Шапиро

Задание 24 ЕГЭ по физике – это основы астрофизики. Здесь необходимо выбрать несколько утверждений из пяти предложенных.

Для этого необходимо изучить диаграмму Герцшпрунга – Рессела: величины, отложенные по осям, и закономерности, которые отражены на диаграмме. Кроме того, надо обратить внимание на различия в средней плотности звёзд главной последовательности (порядка плотности воды), белых карликов и гигантов.

На рисунке представлена диаграмма Герцшпрунга – Рессела

Выберите все верные утверждения о звёздах.

1)	Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, а значит, она относится к сверхгигантам.
2)	Плотность белых карликов существенно больше средней плотности гигантов.
3)	«Жизненный цикл» звезды спектрального класса K главной последовательности более длительный, чем звезды спектрального класса В главной последовательности.
4)	Температура поверхности звёзд спектрального класса G выше температуры поверхности звёзд спектрального класса А.
5)	Звезда Антарес имеет температуру поверхности 3300 К и относится к звёздам спектрального класса А.

Ответ: ___________________________.

Необходимая теория:

По горизонтальной оси диаграммы Герцшпрунга-Рессела отложены спектральные классы в порядке понижения температур звезд, начиная со спектрального класса О (очень горячие звезды) слева и заканчивая спектральным классом М (относительно холодные звезды) справа.

По вертикальной оси отложены светимости или абсолютные звездные величины. Каждая звезда имеет какую-то определенную абсолютную величину и относится к какому-то определенному спектральному классу, а потому может быть представлена точкой в определенном месте диаграммы. В среднем, чем горячее звезда, тем она ярче. Поэтому, чем левее находился на диаграмме спектральный класс исследуемой звезды (и значит, чем больше ее температура), тем выше оказывалась она по шкале абсолютных величин. В результате большинство звезд, нанесенных на диаграмму, расположилось по диагонали от верхнею левого угла к нижнему правому. Они образуют так называемую главную последовательность. По современной оценке, более 90% всех доступных нашему наблюдению звезд попадают на главную последовательность. Диаграмма Герцшпрунга-Рессела даёт возможность найти абсолютную величину нужной звезды по её спектральному классу (особенно точно это работает для спектральных классов O—F), оценить её примерный возраст и представить ближайшее будущее и прошлое наблюдаемого объекта.

Проверим каждое из предложенных утверждений.

1. На главной последовательности располагаются звезды, радиусы которых сравнимы или немного превышают радиус Солнца. Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, поэтому, согласно диаграмме, она относится к сверхгигантам. Утверждение верное.

2. Массы белых карликов сравнимы с массой Солнца, а массы гигантов только в десятки раз превышают солнечную массу. По диаграмме видно, что белые карлики имеют диаметр порядка 0,01 солнечного, а гиганты — 10 солнечных. В соответствии с формулой плотности $rho=frac{m}{V},$ это утверждение верное.

3. Звезда спектрального класса K главной последовательности имеет сравнимую с солнечной светимость 10^0 , а светимость звезды спектрального класса В главной последовательности в тысячи раз превышает солнечную. Значит, звезда спектрального класса K медленнее тратит свою внутреннюю энергию и имеет более длительный «жизненный цикл». Утверждение верное.

4. В соответствии с диаграммой спектральному класс G соответствует температура около 5500 К, а спектральному классу А – температура 9000 К. Поэтому это утверждение неверное.

5. Точно также, как и в предыдущем утверждении, по диаграмме можно определить спектральный класс для соответствующей температуры. Указанной температуре 3300 К соответствует спектральный класс М. Поэтому это утверждение неверное.
Ответ: 1, 2, 3.

Секрет решения. Данное задание надо выполнять в строгом соответствии с прилагаемой диаграммой Герцшпрунга-Рессела. Но иногда встречаются задачи, в которых сама диаграмма не представлена. Запомнить последовательность спектральных классов можно по фразе «Один бритый англичанин финики жевал, как морковь». Первой букве каждого слова соответствует наименование спектрального класса в порядке понижения температуры.

«Один(О) бритый (В) англичанин (А) финики(F) жевал(G) как(K) морковь(M)».

Есть и еще одна «запоминалка»:

O, Be A Fine Girl, Kiss Me!

Рассмотрите таблицу, содержащую характеристики некоторых спутников планет Солнечной системы.

Название спутника	Радиус спутника, км	Радиус орбиты, тыс. км	Вторая космическая скорость, м/с	Планета
Луна	1737	384,4	2400	Земля
Фобос	~12	9,38	11	Марс
Ио	1821	421,6	2560	Юпитер
Европа	1561	670,9	2025	Юпитер
Каллисто	2410	1883	2445	Юпитер
Титан	2575	1221,8	2640	Сатурн
Оберон	761	583,5	725	Уран
Тритон	1354	354,8	1438	Нептун

Выберите все верные утверждения, которые соответствуют характеристикам спутников.

1)	Объём Оберона примерно в 2 раза меньше объёма Европы.
2)	Первая космическая скорость для искусственного спутника Луны составляет примерно 1,7 км/с.
3)	Чем больше радиус орбиты спутника, тем больше масса планеты, вокруг которой он вращается.
4)	Объём Луны больше объёма Европы.
5)	Ускорение свободного падения на Фобосе составляет примерно 11 м/с².

Ответ: ___________________________.

Необходимая теория. Сила тяготения

Проверим каждое из предложенных утверждений.

1. Объем спутника можно рассчитать, используя формулу объема шара.
$V = frac{4}{3} pi R^3.$ Подставляя данные из таблицы, проведем расчет.

Такой подробный расчет можно было заменить следующими рассуждениями.

Так как радиусы спутников отличаются в 2 раза , то объем Европы будет больше объема Оберона приблизительно в 8 раз.
Утверждение неверное.

2. Первая и вторая космические скорости связаны соотношением:
$nu_2 = nu_1 cdot sqrt{2}$ Отсюда первая космическая скорость равна:
$nu_1 = frac{nu_2}{sqrt{2}}.$ Проведем расчет.

Утверждение верное.

3. Юпитер, у которого самая большая масса из предложенных в таблице планет, имеет спутник Ио, находящийся на орбите радиусом 421,6 тыс. км, а у Урана спутник Оберон имеет орбиту 583,5 тыс. км. Масса Урана значительно меньше массы Юпитера, поэтому это утверждение неверное.

4. Для сравнения объемов Луны и Европы проведение расчетов не требуется. Достаточно увидеть, что радиус Луны больше радиуса Европы, поэтому объем Луны также будет больше. Утверждение верное.

5. Ускорение свободного падения можно рассчитать по формуле:
$g=frac{v_1^2}{R},$ где v_1 – первая космическая скорость, R – радиус спутника. Первую космическую скорость выразим через вторую $nu_1 = frac{nu_2}{sqrt{2}}$ Проведем расчет
Утверждение неверное.
Ответ: 2, 4.

Секрет решения. Для решения подобных задач требуются прочные знания по темам «Закон всемирного тяготения», «Ускорение свободного падения», «Первая и вторая космические скорости». Кроме формул, надо уметь проводить «громоздкие» расчеты на калькуляторе и не забывать про перевод единиц измерения в систему СИ.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 24 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

В прошлых статьях мы уже начали рассматривать задание №24 из ЕГЭ по физике. В этот раз рассмотрим задание по теме «Спутники планет».

Выберите все утверждения, которые соответствуют характеристикам спутников планет.

1) Ускорение свободного падения на Титане равно 26, 40 м/с²

2) Объем Ио в 3 раза больше объема Оберона

3) Первая космическая скорость для искусственного спутника Каллисто составляет 1, 7 км/с

4) Объем Титана больше объема Луны

5) Ио находится дальше от поверхности Юпитера, чем Европа

Для выбора верных утверждений необходимо анализировать данные о спутниках планет, представленные в таблице.

Решение

1) Из таблицы данных о спутниках нам известна вторая космическая скорость и радиус спутника, следовательно, можно найти ускорение свободного падения на спутнике по формуле второй космической скорости:

. Отсюда, . g = = 1,35 м/с²

Ответ: утверждение 1 неверно

2) Спутники планет представляют собой почти шары, поэтому их объём примерно равен объёму шара. Формула для определения объема шара

Для сравнения объемов спутников достаточно сравнить их радиусы:

Ответ: утверждение 2 неверно

3) из таблицы находим информацию о том, что вторая космическая скорость для спутника Каллисто равна 2445 м/с.Существует формула связи между первой и второй космической скростью, которая поможет рассчитать первую космическую скорость:

Ответ: утверждение 3 верно

4) Для сравнения объемов космических объектов достсаточно сравнить радиусы спутников, так как в формуле для определения объема спутника надо знать радиус спутника. В данном случае сравнивая радиусы Титана и Луны, значения которых представлены в таблице, видим что радиус Титана больше радиуса Луны: .Следовательно, объем Титана больше объема Луны.

Ответ: утверждение 4 верно

5) Для сравнения удаленности спутников от планеты необходимо знать расстояние от спутника до планеты. Данная информация представлена в таблице как радиус орбиты. Следовательно, сравним радиус орбиты Ио и Европы: 421,6 км 670,9 км.

Ответ: утверждение 5 неверно

Правильный ответ: 34

В следующей статье мы рассмотрим содержание следующего типа 24 задания по теме «Звёзды: разнообразие звёздных характеристик и их закономерности. Источники энергии звёзд».

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник

Мы редко задумываемся о том, как сильно наша жизнь зависит от спутников. А ведь без них многие давно вошедшие в повседневный обиход вещи, начиная от долгосрочных прогнозов погоды и заканчивая навигаторами, были бы невозможны. Спутники также навсегда изменили картину современной войны. Они позволяют заглянуть за линию фронта и отследить перемещения вражеской техники, обеспечивают доступ к Интернету в зоне боевых действий, а также дают возможность задокументировать следы военных преступлений.

Источник: Geospatial World

Но при всей важности спутников среднестатистический обыватель зачастую слабо разбирается даже в базовых вещах, связанных с ними. Поэтому мы подготовили материал, посвященный ответам на самые часто задаваемые вопросы о спутниках.

Что такое спутник?

Спутником называют искусственный объект, запущенный в космос с достаточной скоростью, чтобы он мог оставаться на постоянной орбите вокруг небесного тела. В случае с Землей эта скорость (также называемая первой космической) составляет примерно 7,8 км/с.

Копия «Спутника-1» — первого в истории космического аппарата, вышедшего на околоземную орбиту в 1957 году. Источник: NSSDC

Сколько действующих спутников находится в космосе?

По последним оценкам, на начало 2022 года в космосе находилось порядка пяти тысяч действующих космических аппаратов. Примерно половина из них — это спутники Starlink и OneWeb, предназначенные для предоставления услуг глобального интернета.

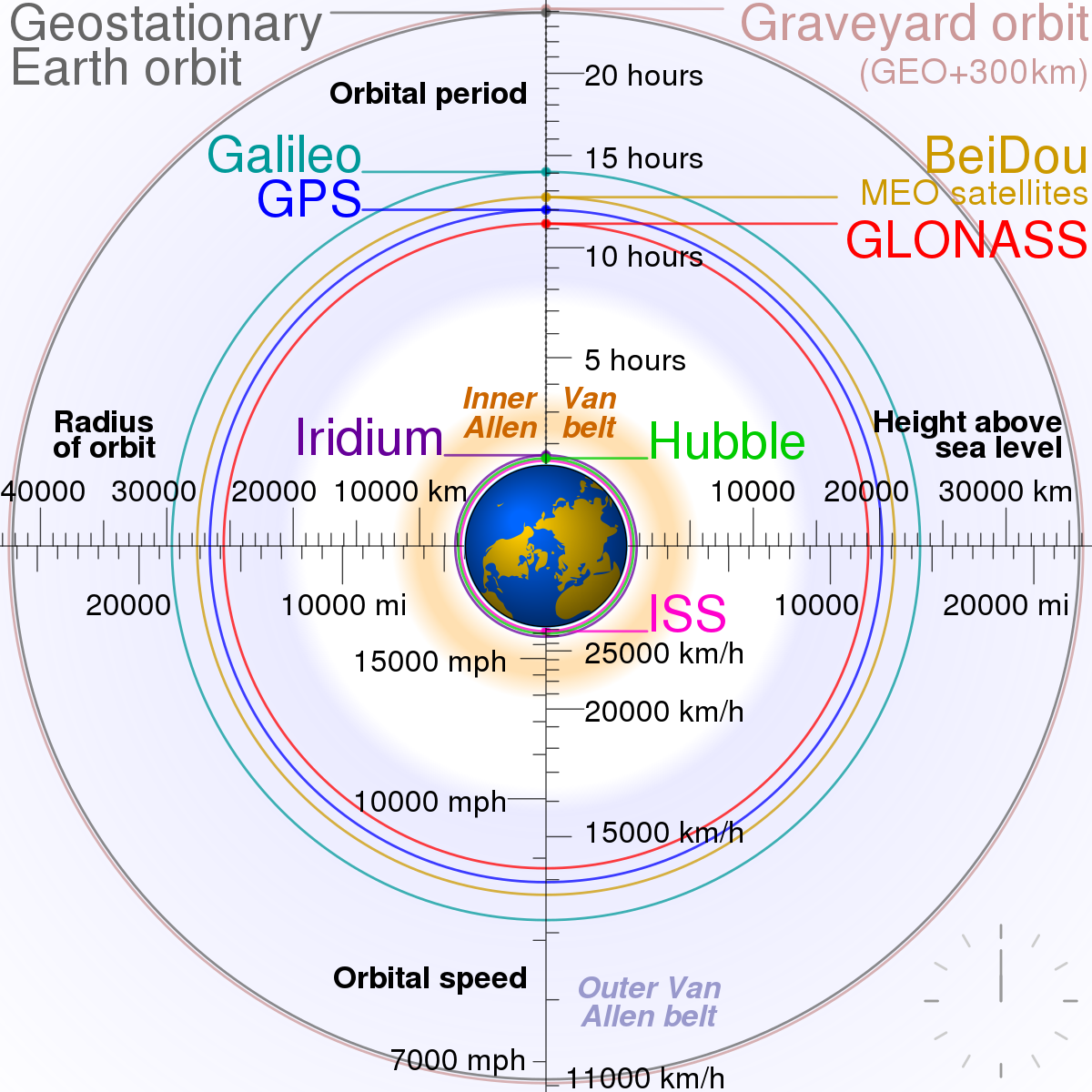
Спутники Starlink в представлении художника. Источник: SpaceX

На каких высотах летают спутники?

В зависимости от предназначения, спутники могут находиться на орбитах высотой от нескольких сотен км до сотен тысяч км. Нижняя граница высоты полета спутников определяется земной атмосферой. Чем она ближе к поверхности Земли, тем сильнее будет тормозить аппарат.

Шаттл Endeavour на фоне «среза» земной атмосферы. Источник: NASA

На практике, находящиеся на высоте 200 км аппараты без постоянных коррекций курса сойдут с орбиты всего за несколько дней. Средняя продолжительность существования объектов на 400-километровой орбите (на такой высоте летает МКС) составляет примерно один год. Спутники, находящиеся на орбитах, высота которых превышает 800 км, практически не подвергаются воздействию земной атмосферы и потому смогут оставаться в космосе в течение многих тысяч лет.

Каковы размеры спутников?

Размеры спутников определяются грузоподъемностью ракет-носителей и габаритами их грузового отсека. На сегодняшний день масса наиболее тяжелых коммерческих аппаратов на околоземной орбите составляет порядка 7—8 тонн (без учета МКС и китайской орбитальной станции). Как правило, это коммуникационные спутники и космические телескопы. По некоторым данным, масса последних модификаций американских спутников оптической разведки KH-11 может достигать 17—19 тонн.

Envisat — один из крупнейших в истории спутников, чья масса превышала 8 тонн. Источник: ESA

В то же время на каждый подобный «гигант» приходится куда большее количество меньших по размерам аппаратов. Например, спутники системы Starlink (наиболее массовые серийные космические аппараты в истории) имеют массу 260—300 кг в зависимости от модификации.

Фемтоспутник Sprite. Источник: NASA

Но это далеко не предел. Последние достижения в области миниатюризации и электроники позволили серьезно уменьшить габариты спутников, сделав возможным создание работоспособных аппаратов размером с печатную плату. В качестве примера можно привести фемтоспутники Sprite. Их масса составляет 4 грамма при диаметре 3,5 см и стоимости менее 100 долларов.

Почему у спутников разные орбиты?

Орбита спутника определяется его функциональным предназначением. Например, аппараты, предназначенные для съемки земной поверхности, располагаются на низких орбитах, что позволяет добиться наиболее высокого разрешения снимков. Для спутников систем глобального позиционирования обычно выбираются орбиты высотой порядка 19—21 тыс. км. Коммуникационные спутники и аппараты, предназначенные для мониторинга погоды, как правило, размещают на геостационарных орбитах. Более подробно о существующих видах околоземных орбит вы можете прочитать здесь.

Различные виды орбит. Источник: Wikipedia.org

Почему геостационарная орбита так важна?

Геостационарной называют круговую орбиту над земным экватором, пролегающую на высоте примерно 35 тыс. км. Расположенный на ней спутник обращается вокруг Земли со скоростью, равной ее скорости вращения вокруг своей оси. То есть с точки зрения наземного наблюдателя он всегда находится в одной и той же точке неба, что позволяет направить на него фиксированную антенну наземной станции. Благодаря этому геостационарная орбита идеальна для размещения аппаратов, предназначенных для ретрансляции телевизионных и радиосигналов, мониторинга погоды, а также солнечной активности.

Находящийся на геостационарной орбите спутник Intelsat-901 (фото сделано космическим буксиром MEV-1). Источник: Northrop Grumman

В то же время, в отличие от большинства других орбит, «ресурс» геостационарной орбиты ограничен. Спутники, использующие сходные или близкие частотные диапазоны, должны находиться на значительном удалении друг от друга, иначе их сигналы могут наложиться. Согласно международным нормам, каждое государство на Земле имеет собственный участок геостационарной орбиты. При этом оно может как самостоятельно использовать его, так и продать или сдать в аренду. Многие страны так и поступают, используя его в качестве источника пополнения бюджета.

Как спутники получают энергию?

Ранние спутники оснащались химическими аккумуляторами. Но вскоре инженеры перешли на использование солнечных батарей. Сейчас практически все космические аппараты оснащены ими. Также стоить сказать, что в прошлом некоторые советские разведывательные аппараты оборудовались ядерными реакторами, но позже эта практика была прекращена.

Одна из панелей солнечных батарей МКС. Источник: NASA

Что происходит с прекратившими работу спутниками?

Они становятся космическим мусором, создающим потенциальную опасность для других космических аппаратов. Это не так страшно в случае со спутниками на низких орбитах, ибо со временем они сгорят в атмосфере. Однако если речь идет об аппаратах на высоких орбитах, все значительно усложняется.

Космический мусор в представлении художника. Источник: Intelligent Living

В случае с геостационарной орбитой существующие правила предписывают спутниковым операторам по завершению срока эксплуатации уводить старые аппараты на более высокую орбиту (она называется орбитой захоронения), где они не будут создавать угрозу для своих соседей.

С каким разрешением могут снимать спутники?

Разрешение спутниковых снимков зависит от множества факторов, начиная от высоты орбиты и заканчивая возможностями камеры. В настоящее время наибольшее разрешение, обеспечиваемое коммерческими спутниками, составляет порядка 25—30 см. Но этот предел связан не с техническими, а с законодательными ограничениями. Например, в США установлен запрет на публикацию спутниковых снимков с разрешением больше 25 см.

Фотография места взрыва иранской ракеты, сделанная американским спутником-шпионом. Источник: Donald Trump

Что касается военных аппаратов, то максимально возможное разрешение их камер является тайной. Но, по некоторым оценкам, американские разведывательные спутники серии KH-11 могут делать снимки с разрешением как минимум 10 см.

Как долго может работать спутник?

Все зависит от его орбиты, предназначения и количества топлива на борту. Но в целом современные спутники отличаются высоким уровнем надежности. Зачастую их эксплуатацию приходится прекратить не из-за отказов оборудования, а по причине исчерпания запасов топлива, необходимого для удержания рабочей орбиты. Именно поэтому многие компании сейчас работают над созданием специализированных космических заправщиков, способных продлить срок службы старых аппаратов.

Космический буксир MEV-1, предназначенный для продления срока службы старых спутников. Источник: Northrop Grumman

Можно ли сбить спутник?

Да, его можно сбить с помощью противоспутниковой ракеты. За последние годы четыре страны (россия, США, Китай и Индия) провели испытания такого оружия, закончившиеся поражением цели на орбите.

Пуск ракеты SM-3, способной поражать цели на орбите. Источник: U.S. Navy

Для уничтожения спутников могут использоваться и иные методы. Например, в СССР существовала программа «Истребитель спутников», в рамках которой в космос выводились аппараты-«камикадзе». В случае получения соответствующего приказа они должны были вплотную сблизиться с вражеским спутником и взорваться, поразив его осколками.

Только самые интересные новости и факты в нашем Telegram-канале!
Присоединяйтесь: https://t.me/ustmagazine

Источник

Авторы: Пурышева И.С., Важеевская Н.Е., Чаругин В.М.

Издательство: Дрофа

Тип: Учебник

Источник

Тема: Законы Кеплера. Определение масс небесных тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

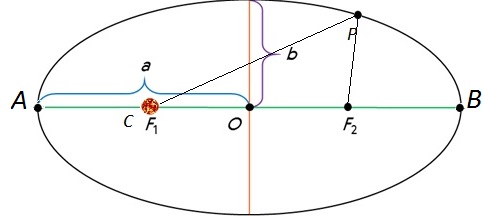
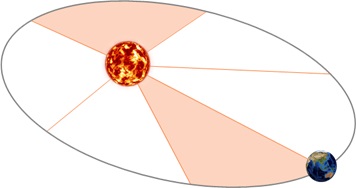
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

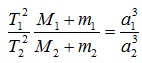
где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ — соответственно массы их спутников.

Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

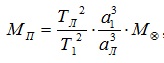
где Т_л и α_л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

б) для внутренней планеты:

Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Источник