Область изменения функции по графику как найти

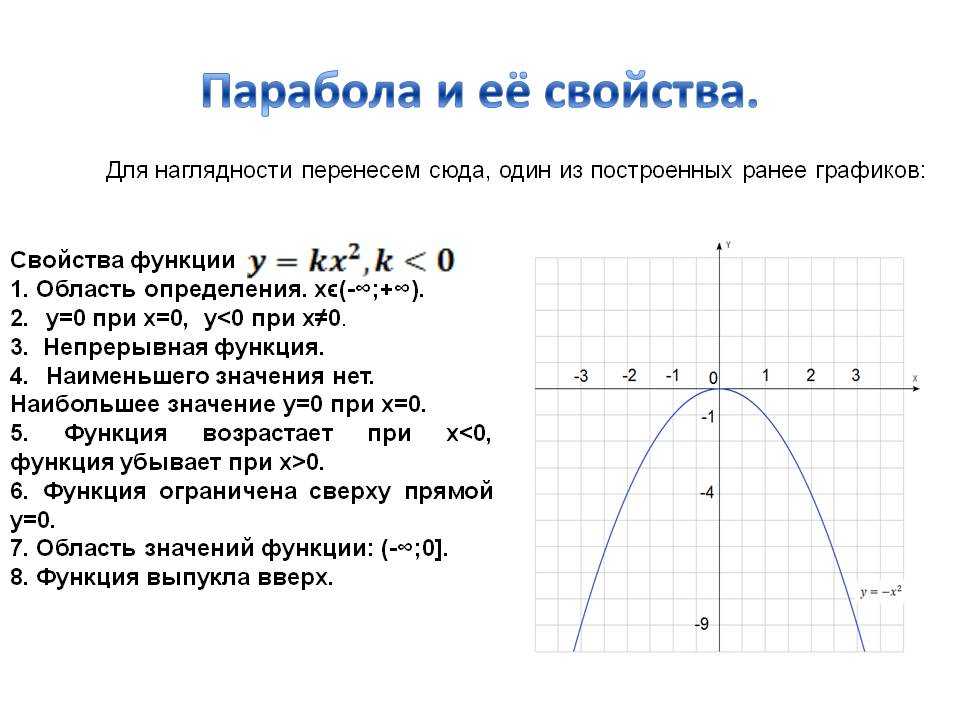
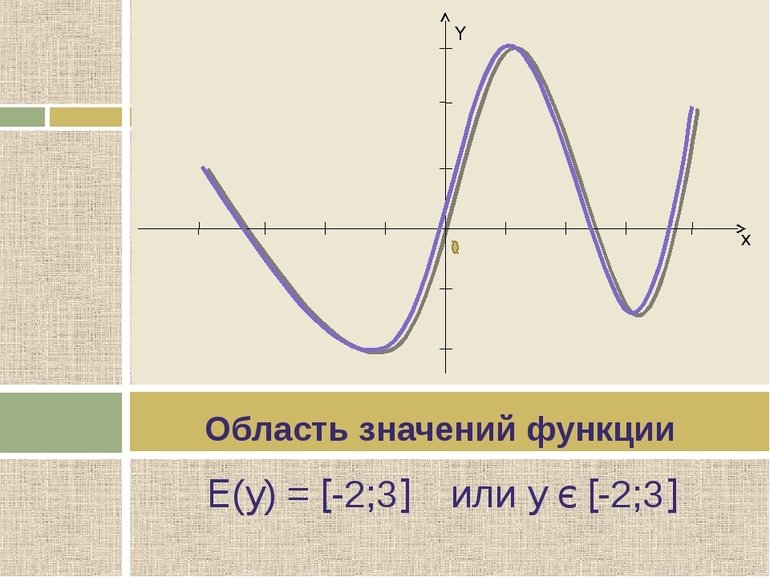
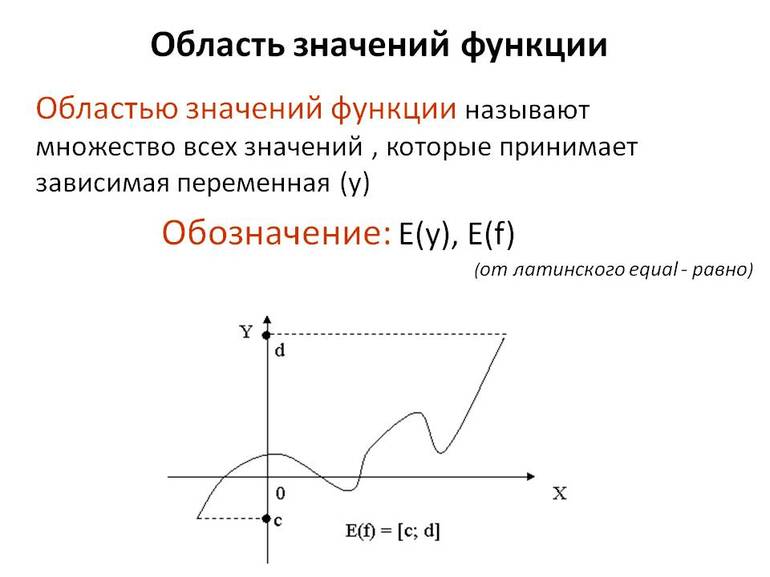
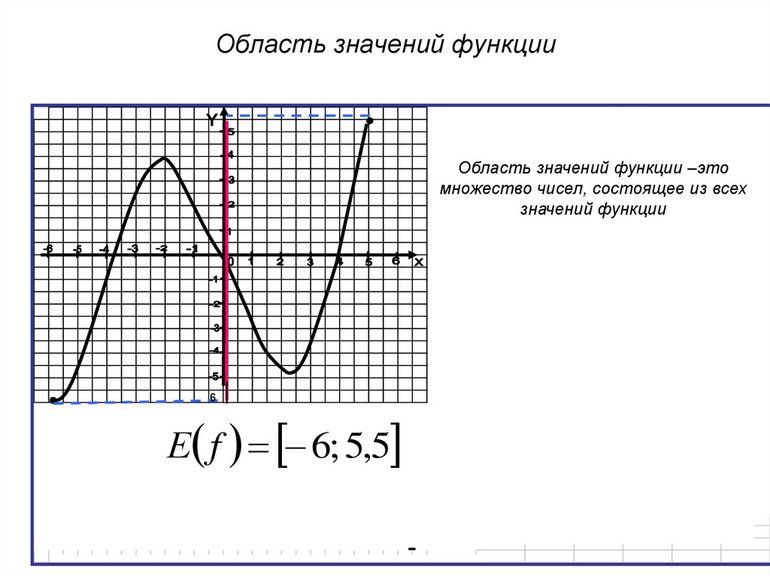
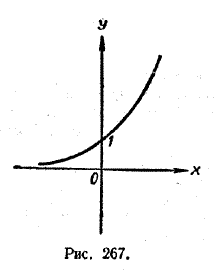Презентация — Область определения и область изменения функции

Слайд 1

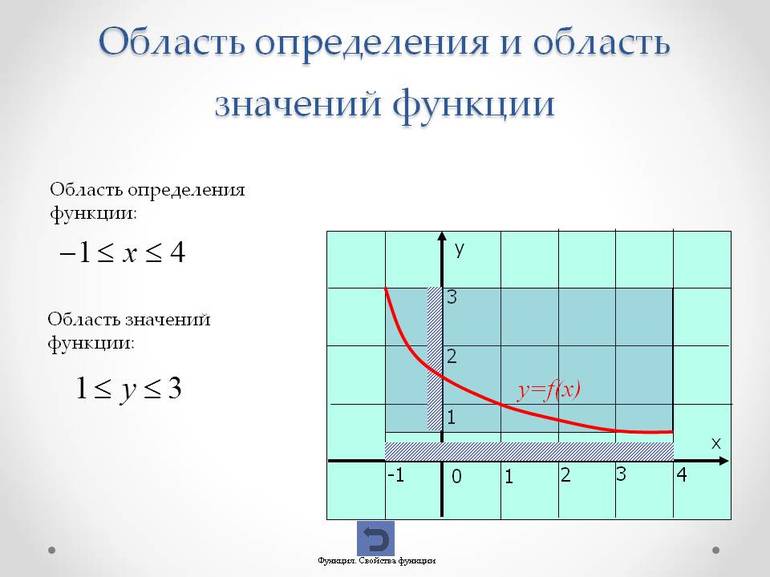
Область определения и область изменения функции. Ограниченность функции.

Слайд 2

Укажите область определения функции
06.09.2016
2

Слайд 3

Устно:
Даны элементарные функции:

Задайте сложную функцию:

Слайд 4

Устно:
Вычислите значение сложной функции:

Слайд 5

Область определения функции
Область определения функции обозначают Х или D(f).
Иногда , задавая функцию аналитически не указывают явно ее область определения.
В таких случаях рассматривают функцию на ее полной области определения.
06.09.2016
5

Слайд 6

Область определения функции
Полной областью определения функции, заданной аналитически называют множество всех действительных значений независимой переменной х, для каждого из которых функция принимает действительные значения.
Полную область определения называют областью существования функции.
06.09.2016
6

Слайд 7

Примеры:
Найдите область определения функции:

Слайд 8

Примеры:
Найдите область определения функции:
, т.к. -1≤sinx≥1,то

Слайд 9

Область изменения(область значений) функции
Область изменения функции f(x) называют множество всех чисел f(x) , соответствующих каждому х из области определения функции.
Область изменения функции f(x) обозначают У или Е(f).
06.09.2016
9

Слайд 10

Примеры:
Найдите область изменения функции:

Слайд 11

Примеры:
Найдите область определения функции:

Слайд 12

Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют ограниченной снизу на множестве Х, если существует число А, такое, что А≤f(x) для любого х из множества Х
06.09.2016
12

Слайд 13

Ограниченность функции Примеры:
Функция у= х2 , определенная на множестве R, ограниченa снизу, т. к. х2 ≥0, для любого действительного числа.

06.09.2016
13

Слайд 14

Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют ограниченной сверху на множестве Х, если существует число В, такое, что f(x)≤В для любого х из множества Х
06.09.2016
14

Слайд 15

Ограниченность функции Примеры:
Функция у=- х2 , определенная на множестве R, ограниченa сверху, т.к. -х2 ≤0, для любого действительного числа.

06.09.2016
15

Слайд 16

Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют ограниченной на множестве Х, если существует число М, такое, что │f(x)│≤М для любого х из множества Х
06.09.2016
16

Слайд 17

Ограниченность функции Примеры:
Функция у=sinx, определенная на множестве R, ограниченa на всей области существования, т.к. │sinx│≤1, для любого действительного числа.

06.09.2016
17

Слайд 18

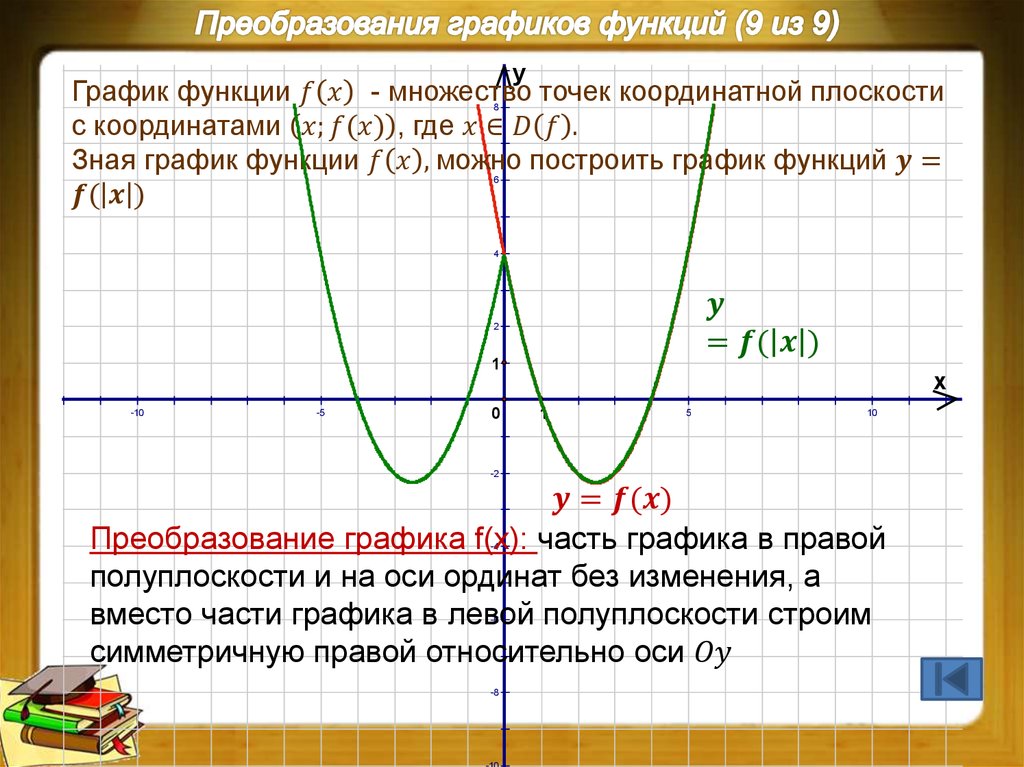
Наименьшее и наибольшее значение функции
Про функцию у= f(x) говорят,что она принимает на множестве Х, наименьшее значение в точке х0, если

Про функцию у= f(x) говорят,что она принимает на множестве Х, наибольшее значение в точке х0, если

06. 09.2016
18

Слайд 19

Примеры:
Функция у= х2 , определенная на множестве R, принимает наименьшее значение у=0 при х=0. наибольшего значения нет, не ограничена сверху.

06.09.2016
19

Слайд 20

Примеры:
Функция у= 2х , определенная на множестве R, не принимает наименьшего значения, ограничена снизу числом 0.

06.09.2016
20

Слайд 21

Примеры:
Функция у= log2x , определенная на множестве R+, не принимает ни наименьшего ни наибольшего значения.
06.09.2016
21

Слайд 22

Упражнения:
Стр. 7
№1.8(г-е)
№1.9(г-е)
№1.10(а-г)
№1.14(а-в)

Слайд 23

Домашнее задание:
Стр. 7
№1.8(а-в)
№1.10(д-з)
№1.12(в)
№1.14(г-е)

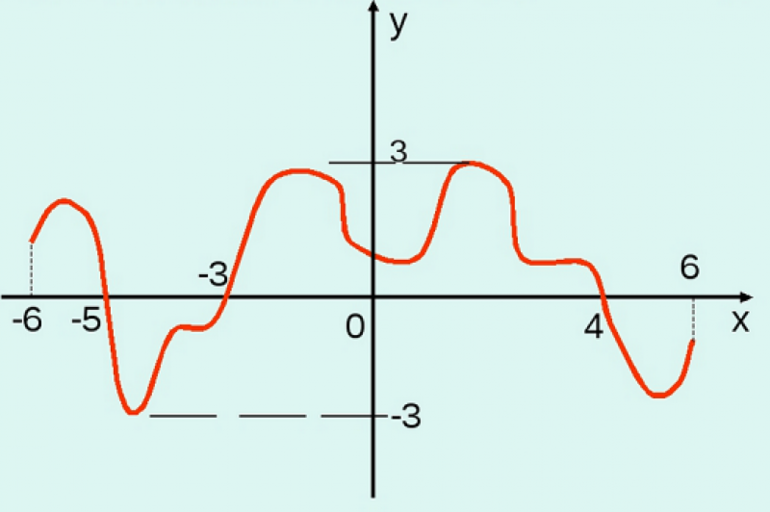
Урок 10. Нахождение области определения и области значения функции с помощью графика

Если функция задана
графически, то для нахождения области определения её график надо спроектировать
на ось  Ох. А если график функции спроектировать на ось  Оу, получим
область изменения (значения) функции.

Нахождение области значений
функции по её графику.

Постройте график
функции. Во многих случаях проще найти область значений функции, построив её
график.

Областью значений
многих квадратичных функций является

(–∞, 0]  или  [0, ∞),

так как вершина
параболы, направленной вправо или влево, лежит на оси  Х. В этом случае область значений включает все
положительные значения  у,
если парабола возрастает, или все отрицательные значения 

у, если парабола убывает.

Вершины графиков
некоторых функций лежат выше или ниже оси 
Х. в этом случае область значений определяется
координатой  у  вершины параболы.

ПРИМЕР:

Если координата 
у  вершины параболы равна  –4,
а парабола возрастает, то область значений равна

[–4, ∞).

Построив график
функции, вы увидите на нём точку, в которой функция имеет минимальное значение.
Если наглядного минимума нет, он не существует, а график функции уходит в
бесконечность.

Построив график
функции, вы увидите на нём точку, в которой функция имеет максимальное
значение. Если наглядного максимума нет, он не существует, а график функции
уходит в бесконечность.

Самый простой
способ построить график функции – это воспользоваться графическим калькулятором
или специальным программным обеспечением. Если нет графического калькулятора,
постройте приблизительный график, подставив в функцию несколько значений  х  и, вычислив
соответствующие значения  у,
нанесите найденные точки на координатную плоскость, чтобы получить общее
представление о форме графика.

ПРИМЕР:

Найдите область определения и область значения
функции по графику.

РЕШЕНИЕ:

Из графика видно, что функция стремится в
бесконечность и  вправо и влево вдоль
оси  х,

не пересекая её (на графике белая точка), а также пересекает ось  у  в точке 
у = 9 (на графике тёмная
точка),  значит область определения будет

(–∞, –∞).

Область
значения очевидна:

(0, 9].

Ноль
не входит в область значений, а девять входит.

Что такое область действия переменных в Javascript

Каждый язык программирования в современном мире имеет концепцию переменных. Переменные используются для хранения значений (число, строка, логическое значение), которые могут измениться в любой момент времени. Но вы когда-нибудь замечали, что у этих переменных всегда есть область видимости, и вы не можете использовать их вне этой области? В этом руководстве вы изучите область действия переменных в JavaScript.

Понимание переменных в JavaScript

Переменные в JavaScript работают иначе, чем в других языках. Здесь вам не нужно указывать тип используемой переменной. В отличие от других языков программирования, у вас нет разных типов данных для разных типов значений.

• Вы можете использовать ключевое слово var, const и let для объявления переменной, и JavaScript автоматически определит тип этой переменной в соответствии с переданным значением.

Итак, это было краткое введение в переменные в JavaScript. В следующем разделе вы ознакомитесь с областью действия переменных в JavaScript.

Какова область действия переменных в Javascript?

Область действия переменных относится к доступности конкретной переменной в программе.

Например, предположим, что у вас есть две разные функции. Сначала вы объявляете переменную в функции 1. Затем вы переходите к следующей функции, то есть к функции 2. Возможно ли, если вы попытаетесь получить доступ к переменной, созданной в функции 1, из функции 2? Это относится к области действия переменной в JavaScript.

 Переменные JavaScript имеют разные области видимости, а именно:

• Глобальный охват
• Локальная область
• Блочный прицел
• Область действия

Подробно ознакомьтесь с различными прицелами.

Что такое глобальная область видимости?

• Говорят, что любая переменная, объявленная вне функции, имеет глобальную область видимости.
• Проще говоря, переменная, к которой можно получить доступ в любом месте программы, называется переменной с глобальной областью действия. Глобальные переменные можно определить с помощью любого из трех ключевых слов: let, const и var.

Что такое локальная область?

• Говорят, что любая переменная, объявленная внутри функции, имеет локальную область видимости. Вы можете получить доступ к локальной переменной внутри функции.
  Если вы попытаетесь получить доступ к любой переменной, определенной внутри функции, извне или из другой функции, она выдаст ошибку.

• Поскольку вы не можете получить доступ к локальной переменной извне функции, вы можете иметь переменную с тем же именем и в другой функции.

Что такое область блока?

• До введения ES6 (ECMAScript 6) в 2015 году в JavaScript было только два типа областей видимости: глобальная область действия и локальная область действия.
• С введением ключевых слов let и const в JavaScript был добавлен новый тип Scope. Вы не можете получить доступ к переменным, объявленным внутри определенного блока (представленного {}), из-за пределов блока.

• Область блока не работает с ключевым словом var. Для этого вы можете использовать ключевые слова let или const.

Что такое область действия функции?

• При создании каждой новой функции создается новая область видимости в JavaScript. Вы не можете получить доступ к переменным, определенным внутри функции, извне функции или из другой функции. Var, let и const работают одинаково при использовании внутри функции.

Строгий режим JavaScript для определения области действия переменной 

В JavaScript, если вы забудете объявить переменную с ключевым словом: var, let и const, JavaScript автоматически примет ее как глобальную переменную, и вы сможете получить к ней доступ в любом месте программы.

Чтобы избежать таких ошибок и путаницы, строгий режим был введен в JavaScript с ES5 (ECMAScript 5) в 2009 году.

• Строгий режим вызовет ошибку, если вы попытаетесь использовать тот же синтаксис после включения «строгого режима» в вашу программу. Это поможет вам писать более чистый и безопасный код.

• Точно так же, как и переменные, строгий режим может использоваться как глобально, так и локально. Если вы напишете «use strict» в начале программы, она будет использоваться глобально. В противном случае вы также можете использовать строгий режим локально внутри функции.

• Все современные браузеры поддерживают строгий режим, кроме Internet Explorer 9 и его предыдущих версий.

Жизнь переменной в JavaScript

Срок жизни переменной в JavaScript зависит от области видимости этой переменной. Он начинается, когда он объявляет переменную.

• Локальная переменная существует до тех пор, пока не выполняется функция. В момент завершения функции локальная переменная удаляется.
• Глобальная переменная существует до тех пор, пока пользователь не закроет программу или пока не будет закрыт веб-браузер. Однако, если пользователь меняет окно, не закрывая программу, глобальная переменная остается там.

На этом вы достигли конца этого руководства «Область действия переменных в JavaScript».

Изучите основы JavaScript, jQuery, Ajax и многое другое с помощью сертификационного учебного курса по JavaScript. Ознакомьтесь с предварительным просмотром курса!

Заключение 

В этом руководстве вы изучили область действия переменных в JavaScript. Объем зависит от двух аспектов:

• Где объявлена ​​переменная
• Как объявлена ​​переменная

Вы также узнали о необходимости и использовании «строгого режима» в JavaScript. После этого вы также поняли, как долго переменная будет присутствовать для вас во время программирования. Вы также столкнулись с реализацией кода и должны понимать область видимости переменной, представленную в JavaScript.

Вы заинтересованы в расширении своих знаний о JavaScript или ищете онлайн-обучение программированию на JavaScript?

Если ответ положительный на один или оба вышеуказанных вопроса, вам следует изучить сертификационный курс по JavaScript, предлагаемый Simplilearn. Эта прикладная учебная программа разработана, чтобы помочь вам понять концепции JavaScript от основ до продвинутого уровня.

На этом примечании, если у вас есть какие-либо сомнения, связанные с этим руководством по области видимости переменных в JavaScript, не стесняйтесь размещать их в виде комментариев в конце этой страницы; мы ответим на них в ближайшее время!

Объем функций

Объем функций

Все
Сообщения в блоге
Страницы

• О
  
• Книга (2-е изд.)
  
• Книга
  
• Блог
• Программы
• Контакт

 защита external_func():
    определение внутренней_функции():
        а = 9
        print('внутри inner_func, a равно {:d} (id={:d})'.format(a, id(a)))
        print('внутри inner_func, b равно {:d} (id={:d})'. format(b, id(b)))
        print('внутри inner_func, len is {:d} (id={:d})'.format(len,id(len)))
    длина = 2
    print('внутри external_func, a is {:d} (id={:d})'.format(a, id(a)))
    print('внутри external_func, b равно {:d} (id={:d})'.format(b, id(b)))
    print('внутри external_func, len is {:d} (id={:d})'.format(len,id(len)))
    внутренняя_функция()
а, б = 6, 7
внешняя_функция()
print('в глобальной области видимости a равно {:d} (id={:d})'.format(a, id(a)))
print('в глобальной области видимости b равно {:d} (id={:d})'.format(b, id(b)))
print('в глобальной области len is', len, '(id={:d})'.format(id(len)))
 

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Например, нужно найти область значений квадратичной функции y = 3x ² — 2x — 1. Следует записать уравнение 3x ² — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b ² — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

1. (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
2. [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
3. (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
4. [-1;1]: y = sin (x) и y = cos (x).
5. [0;Pi]: y = arccos (x) и arcsin (x).
6. [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

1. В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
2. Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
3. При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

1. Отдельное нахождение значений элементов сложной функции.
2. Оценочный.
3. Учет непрерывности и монотонности.
4. Взятие производной.
5. Использование max и min функции.

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

1. Выполнить необходимые преобразования — упростить выражение.
2. Разбить выражение на элементы.
3. Выполнить поиск E (f) для каждого элемента.
4. Произвести замену.
5. Анализ.
6. Результат решения.

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

1. Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
2. Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
3. Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
4. Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
5. Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
6. Результат решения — искомый интервал: E (f) = (-2;+бесконечность).

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

1. Доказать непрерывность.
2. Составить неравенство или неравенства для нескольких функций.
3. Узнать оценку.
4. Записать интервал.

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

1. Функция вида y = cos (x) является непрерывной.
2. Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
3. Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
4. Интервал: E (y) = [-6;6].

Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.

Учет непрерывности и монотонности

Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:

1. Упростить выражение.
2. Выполнить замену при необходимости.
3. Найти вершину графика.
4. Определить промежуток.
5. Вычислить максимальное и минимальное значения.
6. Записать E (f).

Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:

1. Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
2. Замена t = cos (x): y = 2 * t ² + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
3. Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
4. Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] — MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
5. Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].

Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = — 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

1. Найти производную.
2. Анализ.
3. Указать MAX (f) и MIN (f).
4. Запись интервала в формате (MIN (f);MAX (f)).

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

1. Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x ² )^0.5].
2. Функция возрастает на интервале (-1;1).
3. Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
4. Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

1. Производная: y’ = [sin (x)]’ = cos (x).
2. Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
3. Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
4. E (sin (x)) = [-1;1].

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Для исследования
различных явлений полезно знать, как
изменение одних величин влияет на другие
величины.

Понятие функции
связано с установлением зависимости
(связи) между двумя (несколькими)
переменными величинами при их совместном
изменении, или установлением зависимости
между элементами двух (нескольких)
множеств.

Определение.

Пусть даны две
переменные х
и y
с областями изменения Х
и Y.
Переменная y
называется функцией
от х,
если по некоторому правилу или закону
каждому значению
ставится в соответствие одно определенное
значение.

Для указания этого
факта, что y
есть функция от х,
пишут:
,,и т.п.

Можно также сказать,
что функция f
отображает
множество Х
на множество Y.
Это обозначается так
(рис.1.1).

Рис. 1.1

Переменная х
называется независимой
переменной
или аргументом.

Переменная y
называется зависимой
переменной
или функцией.

Относительно самих
величин х
и y
говорят, что они находятся в функциональной
зависимости.

1.3. Область определения и изменения функции

Определение.

Совокупность всех
значений независимой переменной х,
для которых функция y
определена, называется областью
определения
или областью
существования
этой функции.

Определение.

Множество Х
называется областью
определения
функции и обозначается
.

Обычно областью
определения функции являются:

• отрезок (сегмент
  или замкнутый промежуток)

;

• интервал (открытый
  промежуток)

;

• полуоткрытые
  интервалы (полуоткрытые отрезки)

;

;

• бесконечные
  интервалы (промежутки)

; ;

; ;

,

где
,и.

Например, для
функций:

1)
;

2)
.

Область определения
функции может состоять из одного или
нескольких промежутков и из отдельных
точек.

Определение.

Множество значений
Y
называется областью
изменения
или областью значений функции, и
обозначается
.

Область изменения
функции (множество ее значений)
определяется законом соответствия.

Например, для
функций

1)
;;

2)
;.

Определение.

Функция
называетсячисловой
функцией, если ее область определения
и множество значенийсодержатся в множестве действительных
чиселR.

В дальнейшем будем
изучать лишь числовые функции. Частное
значение функции
призаписывается так:.

Например, если
,
то,,и т.п.

1.4. Последовательность

Определение.

Функция, определенная
на множестве натуральных чисел
,
называетсяпоследовательностью.

Значения функции
т.е. элементы множестваназываются членами последовательности,
а– общим членом последовательности.

Последовательность
обычно обозначают через
или.

Например,
;.

1.5. График функции

Для наглядного
представления функции строят ее график.

Определение.

Графиком функции
называется множество всех точек плоскости,
для каждой из которыхх
является значением аргумента,
а y
– соответствующим значением функции.

Например, графиком
функции
является верхняя полуокружность радиусас центром в(рис. 1.2).

Рис. 1.2

1.6. Способы задания функции

Задать функцию –
это значит указать правило, позволяющее
по данному значению независимой
переменной находить соответствующее
значение функции.

Существует три
основных способа задания функции:
аналитический, табличный и графический.

Аналитический
способ
состоит в том, что зависимость между
переменными величинами задается в виде
формулы (аналитического выражения),
указывающей, какие и в каком порядке
действия надо выполнить, чтобы получить
значение функции, соответствующее
данному значению аргумента.

Например,
;;,
где.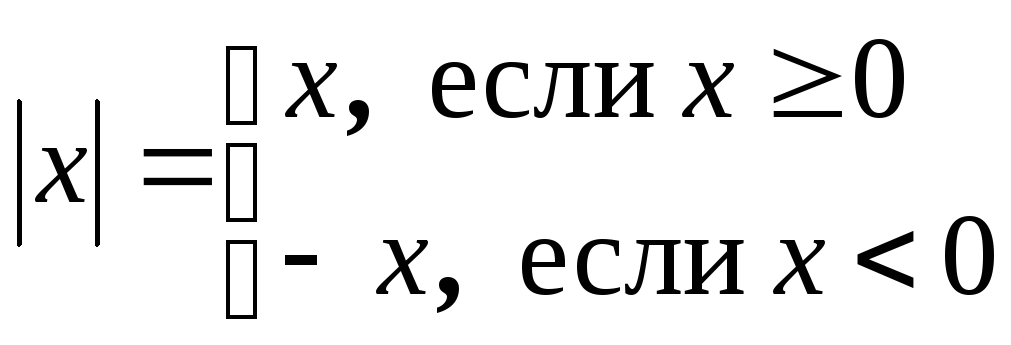

Аналитический
способ является наиболее совершенным,
т.к. к нему могут быть применены методы
математического анализа, позволяющие
полностью исследовать функцию.

Табличный способпредусматривает задание таблицы, в
которой различным значениям аргументапоставлены соответствующие значения
функции:

Такие таблицы
составляются, например, по данным
эксперимента; для облегчения вычислений
с часто встречающимися функциями
(таблицы логарифмов, таблицы
тригонометрических функций и т.д.).

Графический
способзадания функции состоит в том,
что в данной системе координат задается
некоторая кривая. Преимуществом
графического задания является его
наглядность, недостатком – его неточность.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ФУНКЦИИ И ПРЕДЕЛЫ    IX

§ 203. Область определения и область изменения функции

Каким бы способом ни была задана функция y = f (x), рассматривая ее, мы всегда имеем дело с двумя множествами: множеством значений, которые может принимать аргумент х, и множеством значений, которые может принимать функция у. Например, для функции у = 2^х (рис. 267) множеством всех значений, которые может принимать аргумент х, является совокупность всех действительных чисел, а множеством всех значений, которые может принимать функция у,—совокупность всех положительных чисел.

Совокупность всех тех значений, которые принимает аргумент х функции y = f (x), называется областью определения этой функции. Совокупность всех тех значений, которые принимает сама функция у, называется областью изменения этой функции.

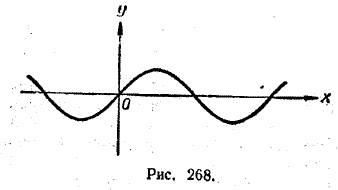
Например, областью определения функции у = sin x (рис. 268) является совокупность всех действительных чисел, а областью изменения — совокупность всех чисел, заключенных между — 1 и 1, включая эти два числа.

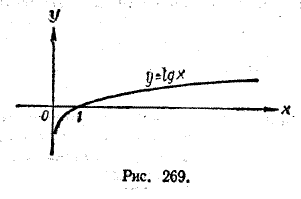
Для функции у = lg x (рис. 269) областью определения является совокупность всех положительных чисел, а областью изменения — совокупность всех действительных чисел и т. д.

Ранее мы изучали числовые последовательности. Члены любой числовой последовательности можно рассматривать как    возможные значения некоторой функции, определенной для натуральных значений аргумента. Например, члены последовательности

1, ¹/₂ , ¹/₃ , ¹/₄ , … ,¹/_n , ….

являются значениями функции у = ¹/_n, а   члены  последовательности

1, —1, 1, —1,.

—  значениями функции у = (— 1)ⁿ⁺¹. Каждую из этих функций мы рассматриваем как функцию, определенную только для натуральных значений аргумента п. Вот почему иногда говорят, что числовая последовательность есть функция натурального аргумента.

Рассмотрим несколько более сложных примеров на нахождение области определения функции.

Пример 1. Найти область определения функции

Эта функция определена для всех значений х, кроме тех, при которых знаменатель дроби x²  + 2x — 3 обращается в нуль. Решая уравнение x²  + 2x — 3 = 0, находим: x₁ = 1,  x₂ = —3. Полому облжтыо определении данной функции является совокупность всех действительных чисел, кроме 1 и —3.

Пример  2.   Найти область определения функции

Корни квадратные определены только для неотрицательных чисел. Поэтому область определения данной функции можно рассматривать как совокупность всех значений х, удовлетворяющих неравенству

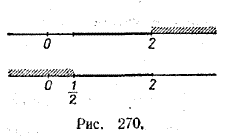
Прежде всего выясним, при каких значениях аргумента х числитель и знаменатель этой дроби положительны и при каких отрицательны. Решая неравенство 2х — 4 > 0, получаем х > 2. Таким образом, при х >2 числитель положителен;   при х < 2 он, очевидно, отрицателен. Это отмечено на рисунке 270. Заштрихованная часть верхней числовой прямой соответствует той области, в которой он положителен, а незаштрихованная — той области, в которой он отрицателен.

Аналогично исследуется   знаменатель  3 — 6х.   Имеем:

3 — 6х > 0;
3 > 6х;
6x < 3;
x <  ¹/₂  

Заштрихованная часть второй  числовой  прямой  на рисунке   270 соответствует области,   в  которой  знаменатель  3 — 6х  положителен, а незаштрихованная — области, в которой он отрицателен. Из   рисунка   270   видно,   что  оба   выражения   (числитель   и знаменатель) имеют одинаковые знаки только при ¹/₂ < х < 2. Поэтому в этой области дробь    положительна.   При х = 2 она обращается в 0. Следовательно, областью определения данной функции является совокупность действительных чисел, удовлетворяющих неравенству

¹/₂ < х < 2.

Пример  3.   Найти область определения функции

Десятичные логарифмы определены только для положительных чисел. Поэтому область определения данной функции можно рассматривать как совокупность всех значении х, удовлетворяющих неравенству

Выполнив вычитание в левой части этого неравенства, получим:

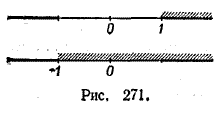
Числитель  этой  дроби   положителен   при  х > 1   и  отрицателен при х < 1, а знаменатель положителен при х > — 1 и отрицателен при х < — 1 (рис. 271).

Поэтому дробь положительна при х < — 1 и при х > 1. Все эти значения х можно записать в виде одного неравенства  | х | > 1.

Пример 4.  Найти область определения функции

Во-первых, tg х не определен для х = ^π/₂ + nπ.     Во-вторых,  данная дробь не определена для тех значений х, при которых знаменатель обращается в нуль. Эти значения находятся из уравнения sin х — cos х = 0. Это однородное тригонометрическое уравнение. Деля обе его части на cos x (докажите, что это деление возможно!), получим:

tg x = 1,

откуда

х = ^π/₄ + kπ.

Итак, областью определения данной функции является совокупность всех действительных чисел, кроме  ^π/₂ + nπ   и  ^π/₄ + kπ ,  где п и k — произвольные целые числа.

Теперь мы рассмотрим несколько примеров на нахождение области изменения функции.

Пример 5. Как известно, линейная функция у = ах + b при а =/= 0 принимает любые действительные значения. Поэтому областью изменения этой функции является совокупность всех действительных чисел.

Пример 6.  Найти область изменения функции

у = x² — 4х + 7.

Преобразуем квадратный трехчлен  x² — 4х + 7,  выделив из него полный квадрат:

у = x² — 4х + 4 + 3 = (х — 2)² + 3.

Выражение (х — 2)² принимает, очевидно, все неотрицательные значения. Поэтому областью изменения данной функции является совокупность всех чисел, больших или равных 3. Эту область можно задать с помощью неравенства у > 3.

Пример 7.  Найти область изменения функции

у = sin х + cos x.

Представив данную функцию в виде

y = √2 sin ( x + ^π/₄ )

(вспомните,  как это делается!),  нетрудно понять, что область её изменения определяется неравенством

— √2  <  у <  √2    или   | у | < √2,

ОТВЕТЫ