Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
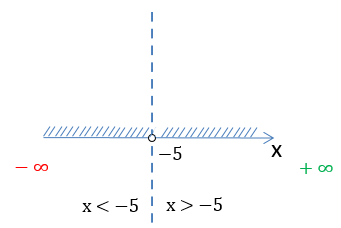
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
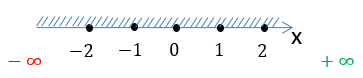
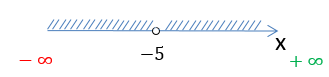
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
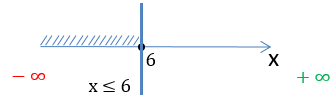
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
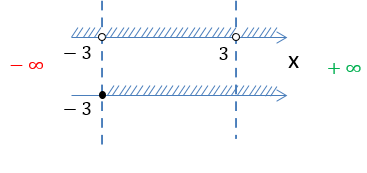
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
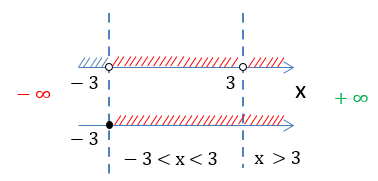
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
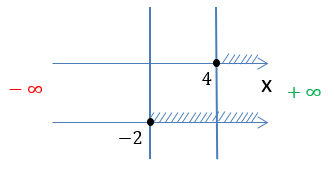
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
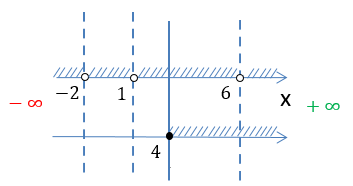
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Загрузить PDF
Загрузить PDF
Область определения функции — это множество чисел, на котором задается функция. Другими словами, это те значения х, которые можно подставить в данное уравнение. Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
-
1
Запомните, что такое область определения. Область определения — это множество значений х, при подставлении которых в уравнение мы получаем область значений у.
-
2
Научитесь находить область определения различных функций. Тип функции определяет метод нахождения области определения. Вот основные моменты, которые вы должны знать о каждом типе функции, о которых пойдет речь в следующем разделе:
- Полиномиальная функция без корней или переменных в знаменателе. Для этого типа функции областью определения являются все действительные числа.
- Дробная функция с переменной в знаменателе. Чтобы найти область определения данного типа функции, знаменатель приравняйте к нулю и исключите найденные значения х.
- Функция с переменной внутри корня. Чтобы найти область определения данного типа функции, задайте подкоренное выражение больше или равно 0 и найдите значения х.
- Функция с натуральным логарифмом (ln). Задайте выражение под логарифмом > 0 и решите.
- График. Нарисуйте график для нахождения х.
- Множество. Это будет список координат х и у. Область определения — список координат х.
-
3
Правильно обозначайте область определения. Легко научиться правильному обозначению области определения, но важно, чтобы вы правильно записывали ответ и получали высокую оценку. Вот несколько вещей, которые вы должны знать о написании области определения:
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
- Например, [-1; 5). Это означает область определения от -1 до 5.
-
Используйте квадратные скобки [ и ] , чтобы указать, что значение принадлежит области определения.
- Таким образом, в примере [-1; 5) область включает -1.
-
Используйте круглые скобки ( и ) , чтобы указать, что значение не принадлежит области определения.
- Таким образом, в примере [-1; 5) 5 не принадлежит области. Область включает только значения, бесконечно близкие к 5, то есть 4,999(9).
-
Используйте знак U для объединения областей, разделенных промежутком.
- Например, [-1; 5 ) U (5; 10]. Это означает, что область проходит от -1 до 10 включительно, но не включает 5. Это может быть у функции, где в знаменателе стоит «х — 5».
- Вы можете использовать несколько U по мере необходимости, если область имеет несколько разрывов/промежутков.
-
Используйте знаки «плюс бесконечность» и «минус бесконечность», чтобы выразить, что область бесконечна в любом направлении.
- Со знаком бесконечности всегда используйте ( ), а не [ ].
Реклама
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
-
1
Запишите пример. Например, вам дана следующая функция:
- f(x) = 2x/(x2 — 4)
-
2
Для дробных функций с переменной в знаменателе надо приравнять знаменатель к нулю. При нахождении области определения дробной функции необходимо исключить все значения х, при которых знаменатель равен нулю, потому что нельзя делить на ноль. Запишите знаменатель как уравнение и приравняйте его к 0. Вот как это делается:
- f(x) = 2x/(x2 — 4)
- x2 — 4 = 0
- (x — 2 )(x + 2) = 0
- x ≠ 2; — 2
-
3
Запишите область определения:
- х = все действительные числа, кроме 2 и -2
Реклама
-
1
Запишите пример. Дана функция y =√(x-7)
-
2
Задайте подкоренное выражение больше или равным 0. Вы не можете извлечь квадратный корень из отрицательного числа, хотя вы можете извлечь квадратный корень 0. Таким образом, задайте подкоренное выражение больше или равным 0. Заметим, что это относится не только к квадратным корням, но и ко всем корням с четной степенью. Тем не менее, это не относится к корням с нечетной степенью, так как отрицательное число может стоять под корнем нечетной степени.
- х — 7 ≧ 0
-
3
Выделите переменную. Для этого перенесите 7 в правую часть неравенства:
- x ≧ 7
-
4
Запишите область определения. Вот она:
- D = [7; +∞)
-
5
Найдите область определения функции с корнем, когда есть несколько решений. Дано: y = 1/√( ̅x2 -4). Приравняв знаменатель к нулю и решив это уравнение, вы получите х ≠ (2; -2). Вот как вы действуете далее:
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0. И это так:
- (-3)2 — 4 = 5
- Теперь проверьте область между -2 и +2. Подставьте, например, 0.
- 02 — 4 = -4, так что числа между -2 и 2 не подходят.
- Теперь попробуйте числа больше 2, например 3.
- 32 — 4 = 5, так что числа больше 2 подходят.
- Запишите область определения. Вот как записывается эта область:
- D = (-∞; -2) U (2; +∞)
Реклама
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0. И это так:
-
1
Запишите пример. Допустим, дана функция:
- f(x) = ln(x —
- f(x) = ln(x —
-
2
Задайте выражение под логарифмом больше нуля. Натуральный логарифм должен быть положительным числом, поэтому задаем выражение внутри скобок больше нуля.
- x — 8 > 0
-
3
Решите. Для этого обособьте переменную х, прибавив к обеим частям неравенства 8.
- x — 8 + 8 > 0 + 8
- x > 8
-
4
Запишите область определения. Область определения этой функции есть любое число больше 8. Вот так:
- D = (8; +∞)
Реклама
-
1
Посмотрите на график.
-
2
Проверьте значения х, которые отображены на графике. Это может быть легче сказать, чем сделать, но вот несколько советов:
- Линия. Если на графике вы видите линию, которая уходит в бесконечность, то все значения х верны, и область определения включает все действительные числа.
- Обычная парабола. Если вы видите параболу, которая смотрит вверх или вниз, то область определения — все действительные числа, потому что подходят все числа на оси х.
- Лежачая парабола. Теперь, если у вас есть парабола с вершиной в точке (4; 0), которая простирается бесконечно вправо, то область определения D = [4; +∞)
-
3
Запишите область определения. Запишите область определения в зависимости от типа графика, с которым вы работаете. Если вы не уверены в типе графика и знаете функцию, описывающую его, для проверки подставьте координаты х в функцию.
Реклама
-
1
Запишите множество. Множество — это набор координат х и у. Например, вы работаете со следующими координатами: {(1; 3), (2; 4), (5; 7)}
-
2
Запишите координаты х. Это 1; 2; 5.
-
3
Область определения: D = {1; 2; 5}
-
4
Убедитесь, что множество является функцией. Для этого необходимо, чтобы каждый раз, когда вы подставляете значение х, вы получали одно и то же значение y. Например, подставляя х = 3, вы должны получить у = 6, и так далее. Приведенное в примере множество не является функцией, потому что дано два разных значения у: {(1; 4), (3; 5), (1; 5)}.
Реклама
Об этой статье
Эту страницу просматривали 854 199 раз.
Была ли эта статья полезной?
Область определения дроби
Когда дробь существует?
Дробь существует тогда, когда знаменатель не равен нулю.
Чтобы найти область определения дроби, нужно:
- весь знаменатель приравнять к нулю.
- найти значения, при которых знаменатель обращается в нуль.
Областью определения дроби будут все числа, кроме найденных значений, обращающих знаменатель в нуль.
Пример 1
Найти область определения дроби:
Приравняем знаменатель дроби к нулю:
Решим уравнение. Произведение равно нулю, если один из множителей равен нулю:
Решим каждое из линейных уравнений:
Итак, при x = -4 или x = 3 дробь будет равна нулю, следовательно, область определения этой дроби: все числа, кроме – 4 и 3.
Пример 2
Найти область определения дроби:
Приравняет знаменатель к нулю:
Произведение равно нулю, если один из множителей равен нулю:
Решим полученные линейные уравнения:
Итак, при x = 4 или x = -4 дробь будет равна нулю, следовательно, область определения этой дроби: все числа, кроме – 4 и 4.
Как найти область определения функции
Что такое область определения функции?
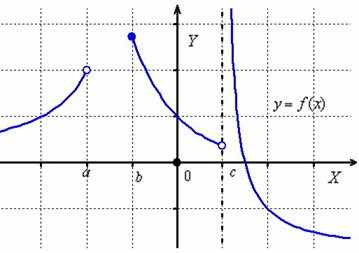
Начнём с краткого определения. Область определения функции y=f(x) — это множество значений X, для которых существуют значения Y.
Войдём в тему более основательно. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Можно понимать область определения функции и как проекцию графика функции на ось Ox.
Что требуется, чтобы уверенно находить область определения функции? Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно. При изучении темы области определения функции поможет материал Свойства и графики элементарных функций. А поскольку областью определения функции служат различные множества, а также их объединения и пересечения, то пригодится и материал Множества и операции над множествами.
Итак, чтобы находить области определения распространённых функций, порешаем уравнения и неравенства с одной переменной.
После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно.
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы. Приступаем к практике.
Общий принцип на самых простых примерах
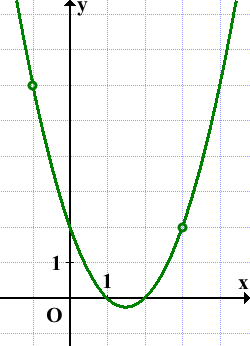
Пример 1. На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю
и решая это уравнение:
получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.
Пример 2. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Так как подкоренное выражение должно быть неотрицательным, нужно решить неравенство
Если перенести какое-либо слагаемое в другую часть неравенства с противоположным знаком, то мы получим равносильное неравенство с тем же знаком неравенства. Переносим минус 5 и получаем неравенство
Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Область определения корня n-й степени
В случае, функции корня n-й степени, то есть когда функция задана формулой и n — натуральное число:
если n — чётное число, то областью определения функции является множество всех неотрицательных действительных чисел, то есть [0; + ∞[ ;
если n — нечётное число, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ .
Пример 3. Найти область определения функции .
Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно. Поэтому решаем неравенство
.
Это квадратное неравенство
,
По формуле находим дискриминант:
.
По формуле находим корни квадратного трёхчлена:
.
Найденные точки разбивают числовую прямую на три промежутка:
и .
При этом знак квадратного трёхчлена (больше или меньше нуля) совпадает со знаком коэффициента a во всех точках промежутков
и
и противоположен знаку коэффициента a во всех точках промежутка .
В нашем случае имеем отрицательный коэффициент a=-1 , поэтому квадратный трёхчлен неотрицателен во всех точках промежутка .
Следовательно, область определения данной функции — [- 1; 1] .
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Область определения степенной функции
Область определения степенной функции находится в зависимости от вида степени в выражении.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество [0; + ∞[ , то есть нуль входит в область определения;
если — отрицательное, то областью определения функции является множество (0; + ∞[ , то есть нуль не входит в область определения.
Пример 4. Найти область определения функции .
Решение. Выражение функции можно представить так:
Квадратный трёхчлен в скобках в знаменателе должен быть строго больше нуля (ещё и потому, что дробный показатель степени данной степенной функции — отрицательный). Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля:
.
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[ .
Пример 5. Найти область определения функции .
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[ .
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ ;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[ , то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 6. Найти область определения функции .
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[ .
Область определения показательной и логарифмической функции
Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[ . Подробнее о графике такой функции.
Область определения логарифмической функции
Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[ . Подробнее о графике такой функции.
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 7. Найти область определения функции .
Пример 8. Найти область определения функции .
Область определения тригонометрических функций
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 9. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Пользуясь тригонометической таблицей (или поворачивая воображаемый циркуль по окружности), видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного ( 2kπ ) или нечётного целого числа ( (2k+1)π ).
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1] .
Область определения функции y = arccos(x) — так же множество [-1; 1] .
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 10. Найти область определения функции .
Решение. Решим неравенство:
Решение получили, основываясь на свойстве неравенств: если все части верного неравенства умножить на одно и то же положительное число, то получится также верное неравество. В данном случае умножали на 4.
Таким образом, получаем область определения данной функции — отрезок [- 4; 4] .
Пример 11. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение получили, основываясь на свойстве неравенств: если обе части верного неравенства умножить на одно и то же отрицательное число изменить знак неравенства на противоположный, то получится верное неравенство. В данном случае умножали на минус 2.
Аналогично и решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1] .
Область определения дроби
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x , при которых знаменатель дроби обращается в нуль.
Пример 12. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби:
находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[ , то есть все числа, кроме минус 2.
Пример 13. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[ , то есть все числа, кроме минус единицы и единицы.
Пример 14. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — ]- ∞; — 2[ ∪ ]- 2 ; 2[ ∪ ]2 ;+ ∞[ , то есть все числа, кроме -2 и 2.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[ .
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 16. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[ .
Пример 17. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2] .
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 18. Найти область определения функции .
Пример 19. Найти область определения функции .
Область определения постоянной
Постоянная (константа) определена при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[ .
Пример 20. Найти область определения функции y = 2 .
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
Область определения линейной функции
Если функция задана формулой вида y = kx + b , то область определения функции — множество R действительных чисел.
График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
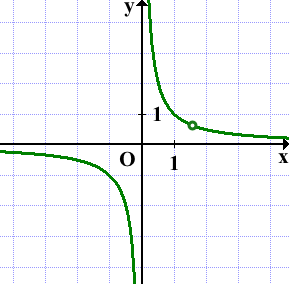
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
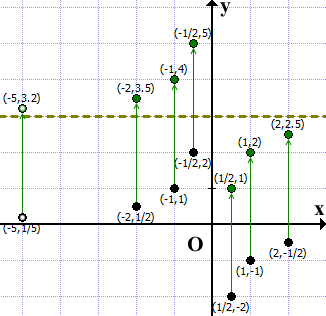
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
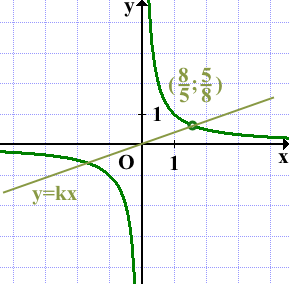
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
в формулу y=kx и находим k:
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
Сокращаем дробь на x+5:
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.
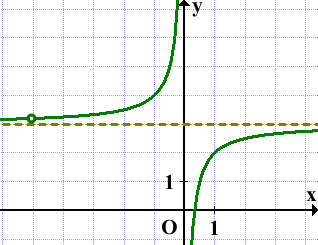
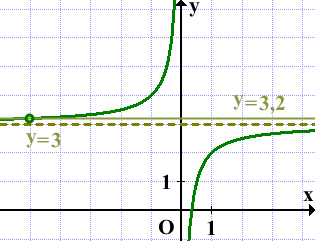
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Найдём область определения функции.
и сократим её на (x+1):
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1
имеет одно решение.
Приравниваем правые части равенств:
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
Ищем область определения функции.
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
Находим координаты выколотых точек
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
http://function-x.ru/function_definition_area.html
Область определения функции, в которой есть дробь
Стр 1 из 12Следующая ⇒
Как исследовать функцию и построить её график?
1) Область определения, непрерывность, четность/нечётность, периодичность функции.
2) Асимптоты графика функции.
3) Нули функции, интервалы знакопостоянства.
4) Возрастание, убывание и экстремумы функции.
5) Выпуклость, вогнутость и перегибы графика.
6) Дополнительные точки и график по результатам исследования.
Как найти область определения функции?
Примеры решений
Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:
Область определения данной функции представляет собой объединение промежутков:
(для тех, кто позабыл: – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».
Грубо говоря, где область определения – там есть график функции. А вот полуинтервал и точка «цэ» не входят в область определения, поэтому графика там нет.
Область определения функции, в которой есть дробь
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения:
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
Найти область определения функции
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:
Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.
Ответ: область определения:
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru
Область определения функции, в которой есть дробь
Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции. Самый широкий набор значений, как правило — это все действительные числа. От -∞ до+∞. Перебирать все возможные числа мы не будем, да…) В математике поступают по-другому. Работаем в два этапа.
На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.
На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.
Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет.
Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю:
До 9-го класса включительно:
1. Деление. Нельзя делить на ноль.
2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.
В выпускных классах и ВУЗах:
3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0.
4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения:
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание
, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
.
Пример 3
Найти область определения функции
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:
Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.
Ответ: область определения:
Определение.
Областью значений функции y = f(x) называется множество всех значений функции, которые она принимает при переборе всех x из области определения .
Пример.
Определите множество значений функции на интервале (-2; 2).
Решение.
Найдем точки экстремума функции, попадающие на промежуток (-2; 2):
Точка x = 0 является точкой максимума, так как производная меняет знак с плюса на минус при переходе через нее, а график функции от возрастания переходит к убыванию.
есть соответствующий максимум функции.
Выясним поведение функции при x стремящемся к -2 справа и при xстремящемся к 2 слева, то есть, найдем односторонние пределы:
Что мы получили: при изменении аргумента от -2 к нулю значения функции возрастают от минус бесконечности до минус одной четвертой (максимума функции при x = 0), при изменении аргумента от нуля к 2 значения функции убывают к минус бесконечности. Таким образом, множество значений функции на интервале (-2; 2) есть .
Как найти область значения функции y=3x(квадрат)-6x +1
1 способ.
Найдем x0. x0=-b/(2a)=-(-6)/(2*3)=1
Найдем значение y при x=1.
y=3*1^2-6*1+1=3-6+1=-2.
Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
2 способ.
Найдем производную функции. y’=6x-6. Приравним производную функции к нулю.
6x-6=0. Найдем точки экстремума. 6x=6, x=1. Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то x=1- это точка минимума. Найдем значение функции наданной точке. y=3*1^2-6*1+1=3-6+1=-2. Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
P.S. Если вы ещё не прошли производную, воспользуйтесь первым способом.
studopedya.ru
как найти область определения функции??
найти все х-удовлетворяющие данному условию
смотря какой, если есть квадратный корень, то под ним больше или =0 и т. д
При решении многих задач приходится искать область определения функции. Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.
И так, область определения функции – это множество всех тех значений переменной х, при каких функция f(x) имеет смысл. То есть значения переменной х, при которых функция от этой переменной существует, а могут быть и такие, при каких она не существует, нам нужны, только те, при которых – существует.
Рассмотрим конкретные варианты, в каких случаях функция может существовать не при всех значениях переменной:
Во-первых, когда есть дробь, в этом случае знаменатель дроби, недолжен быть равным нулю, потому, что такая дробь не может существовать. То есть, если ваша функция — дробь и в знаменателе есть переменная (потому, что если там только число, то оно никогда не станет нулём) то вам надо всё то выражение, что в знаменателе прировнять к нулю. И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения.
Во-вторых, когда есть корень чётной степени, думаю, вы знаете, что в поле вещественных чисел, корень чётной степени может быть только с положительного числа. То есть если в вас есть функция с корнем чётной степени, то что бы найти те числа, которые не будут попадать в область определения, вам надо решить неравенство, где выражение, что под корнем будет меньше нуля.
В-третьих, когда есть логарифм. Здесь понятно, что область определения логарифма все числа, которые больше ноля. То есть что бы найти те значения переменной, которые надо исключить с области определения, вам надо составить и решить неравенство, где выражение, которое будет под логарифмом должно быть меньше нуля.
В-четвёртых, не надо забыть о таких обратных тригонометрических функциях, как арксинус и арккосинус, которые определены, только на промежутке [-1;1]. Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают.
И в-пятых, в одном примере может быть несколько этих случаев. Надо разбирать всё, до мельчайших подробностей. Например, в знаменателе дроби, может быть корень из арксинуса, поэтому вам надо отобрать, только те значения переменной, при которых существует арксинус, при чём значение этого арксинуса должно не должно быть равное нулю (так как оно в знаменателе) и также не должно быть отрицательным (так как есть корень) .
touch.otvet.mail.ru
Область определения функции
| Область визначення функції — це множина всіх значень незалежної змінної, при яких функція має зміст.
Для функцій, заданих формулою, область визначення знаходять виходячи з наступних принципів:. |
Область определения функции — это множество всех значений переменной х, при которых функция имеет смысл.
Для функций, заданных формулой, область определения находится исходя из следующих принципов: |
Область визначення функції — це множина допустимих значень аргументу функції. Вона позначається як D(y), якщо треба вказати область визначення функції y = f(x).
Якщо задані: числова множина та правило, що дозволяє поставити у відповідність кожному елементу з множини певне число, то говорять, що задана функція з областю визначення . Визначення області значень функції є необхідною умовою визначення функції. Значення змінних, при яких значення функції має зміст, називають допустимими значеннями аргументу. Множину всіх допустимих значень аргументу називають областю допустимих значень аргументу функції . |
Область определения функции — это множество допустимых значений аргумента функции. Она обозначается как D(y), когда нужно указать область определения функции y = f(x).
Если заданы: числовое множество и правило, которое позволяет сопоставить в соответствие каждому элементу из множества определенное число, говорят, что задана функция с областью определения. Определение области значений функции является необходимым условием определения функции. Значения переменных, при которых значение функции имеет смысла, называют допустимыми значениями аргумента. Множество всех допустимых значений аргумента называют областью допустимых значений аргумента функции. |
profmeter.com.ua
График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
В знаменателе вынесем за скобки общий множитель x:
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
x(5x-8)≠0,
x≠0, x≠8/5.
Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
(8/5; 5/8)
в формулу y=kx и находим k:
Ответ : 25/64.
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
x(x+5)≠0
x≠0; x≠-5;
D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).
Сокращаем дробь на x+5:
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
параллельным переносом на 3 единицы вверх вдоль оси Oy.
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
Ответ: 3; 3,2.
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции.
-1-x≠0
x≠-1.
D(y):x∈(-∞;-1)∪(-1;∞).
Преобразуем дробь:
и сократим её на (x+1):
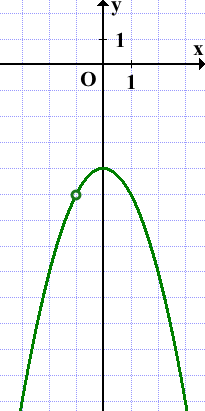
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):
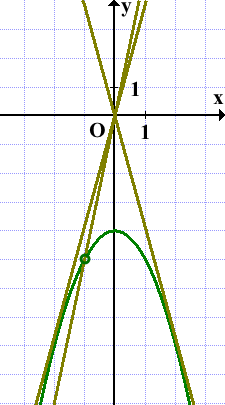
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:
Значения k в данном случае удобнее искать аналитически, а не с помощью графика.
Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система
имеет одно решение.
Приравниваем правые части равенств:
-x²-4=kx
x²+kx+4=0.
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
D=b²-4ac=k²-4·1·4=k²-16.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
(-1)²+k·(-1)+4=0
k=5.
Ответ: -4; 4; 5.
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
1)x²-4x+3=0
x1=1; x2=3
x²-4x+3=(x-1)(x-3).
2)x²-x-2=0
x1=-1; x2=2
x²-x-2=(x+1)(x-2).
3)x²-2x-3=0
x1=-1; x2=3
x²-2x-3=(x+1)(x-3).
Ищем область определения функции.
(x+1)(x-3)≠0
x≠-1, x≠3.
D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
x=1; x=2.
При x=0 y=0²-3·0+2=2.
Находим координаты выколотых точек
При x=-1 y=(-1)²-3·(-1)+2=6,
при x=3 y=3²-3·3+2=2.
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
Ответ: -0,25; 2; 6.

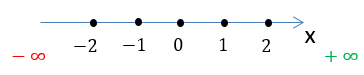
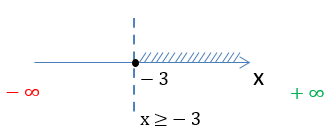
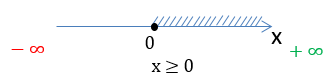













































![Rendered by QuickLaTeX.com [ frac{x}{y}left| {frac{{ - 2}}{{ - frac{1}{2}}}} right.left| {frac{{ - 1}}{{ - 1}}} right.left| {frac{{ - frac{1}{2}}}{{ - 2}}} right.left| {frac{{frac{1}{2}}}{2}} right.left| {frac{1}{1}} right.left| {frac{{frac{8}{5}}}{{frac{5}{8}}}} right.left| {frac{2}{{frac{1}{2}}}} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-6b01205fceeb7f3128d1e7f3e964e8c5_l3.png)
![Rendered by QuickLaTeX.com [ frac{x}{y}left| {frac{{ - 5}}{{frac{1}{5}}}} right.left| {frac{{ - 2}}{{frac{1}{2}}}} right.left| {frac{{ - 1}}{1}} right.left| {frac{{ - frac{1}{2}}}{2}} right.left| {frac{{frac{1}{2}}}{{ - 2}}} right.left| {frac{1}{{ - 1}}} right.left| {frac{2}{{ - frac{1}{2}}}} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-f0cd4ba35e486534ca4ff13d0cb17fe5_l3.png)
![Rendered by QuickLaTeX.com [ left{ begin{array}{l} y = - x^2 - 4, \ x ne - 1, \ y = kx \ end{array} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-908c51743e7d36c9c27e60f6fea674ff_l3.png)