Образующая полученного тела вращения как найти - Исправление недочетов и поиск решений вместе с Examum.ru

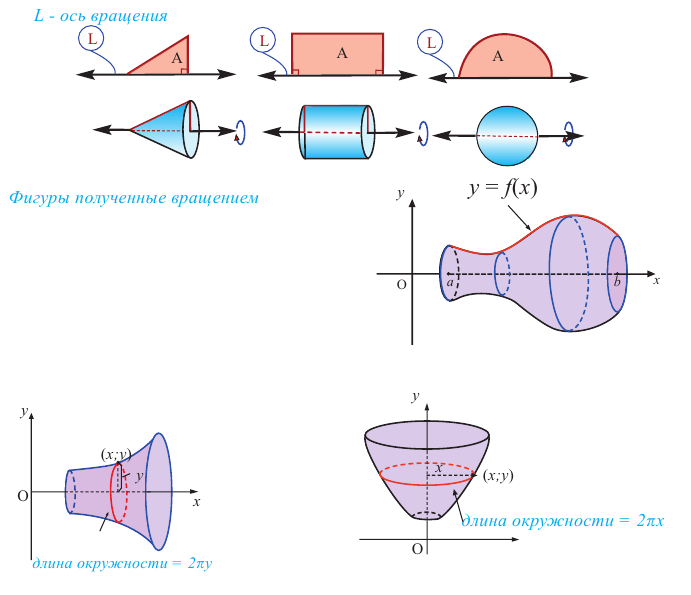
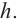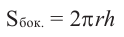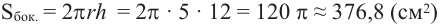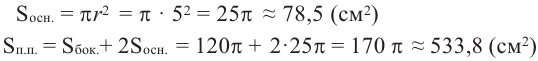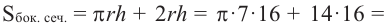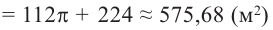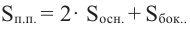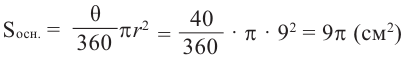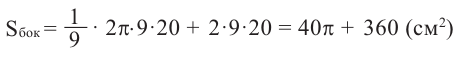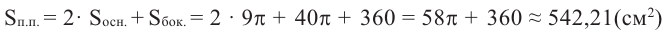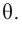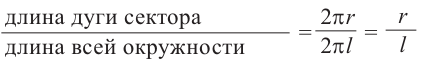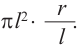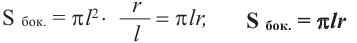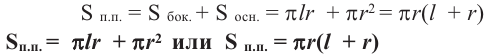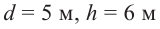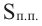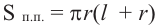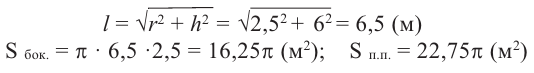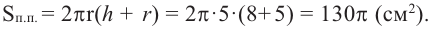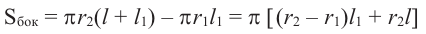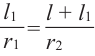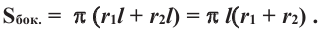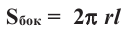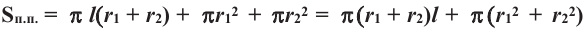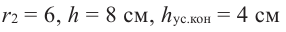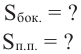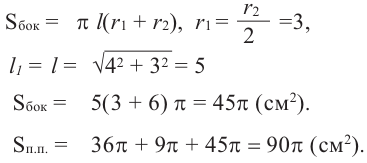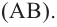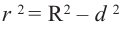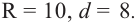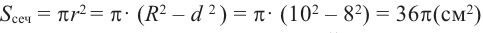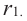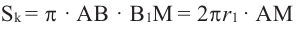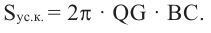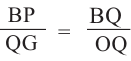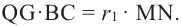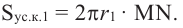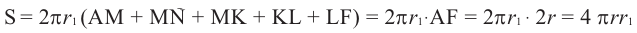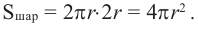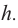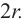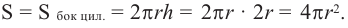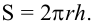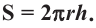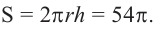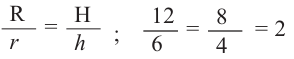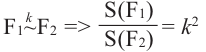Телом вращения называют пространственную фигуру, полученную в результате вращения некоторой плоской фигуры вокруг оси. Среди всех тел вращения выделяют цилиндр, конус и шар.

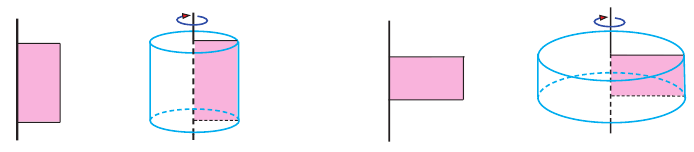
Цилиндром называют фигуру, полученную в результате вращения прямоугольника вокруг одной из его сторон (оси цилиндра).

Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.

Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.

На рисунке 9.66 прямая – ось вращения; – высота, – образующая цилиндра, полученного вращением прямоугольника вокруг стороны . Основание цилиндра – круг радиуса . Прямоугольник – осевое сечение цилиндра.

Объем цилиндра высоты находят по формуле:

$LaTeX formula: V=S_{o.}cdot h$ . (9.15)

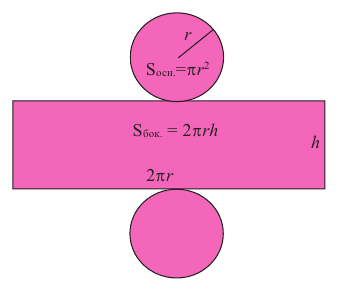
Площадь основания цилиндра ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r ^2$ . (9.16)

Площадь поверхности цилиндра находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.17)

Площадь боковой поверхности цилиндра находят по формуле:

$LaTeX formula: S_{delta .}=2pi r l$ , (9.18)

где – радиус основания, – высота, – образующая цилиндра.

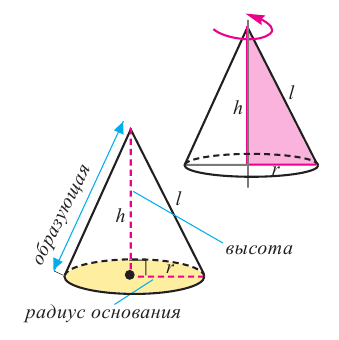
Конусом называют фигуру, полученную в результате вращения прямоугольного треугольника вокруг одного из катетов (оси конуса).

Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.

Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.

На рисунке 9.67 прямая – ось вращения; – высота конуса, – образующая конуса, – осевое сечение конуса, полученного вращением прямоугольного треугольника вокруг катета .

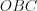
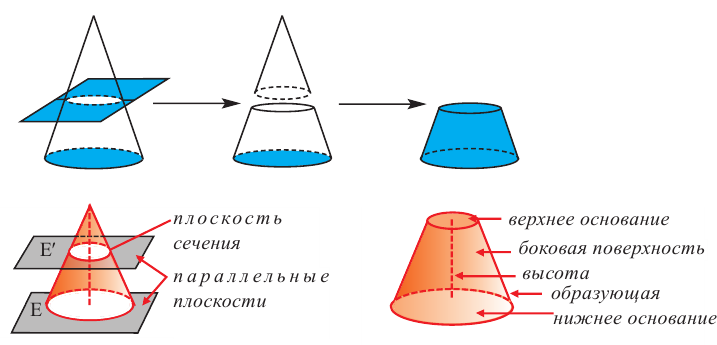
Усеченным конусом называют часть конуса, ограниченную его основанием и сечением, параллельным плоскости основания.

На рисунке 9.68 изображен усеченный конус.

Объем конуса высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.}cdot h$ . (9.19)

Площадь основания конуса ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r^2$ . (9.20)

Площадь поверхности конуса находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.21)

Площадь боковой поверхности конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi r l$ , (9.22)

где – радиус основания, – образующая конуса.

Объем усеченного конуса находят по формуле:

$LaTeX formula: V=frac{1}{3}pi h(r^2_1+r^2_2+r_1r_2)$ , (9.23)

где и – радиусы оснований, – высота.

Площадь боковой поверхности усеченного конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi (r_1+r_2)l$ , (9.24)

где и – радиусы оснований, – высота, – образующая усеченного конуса.

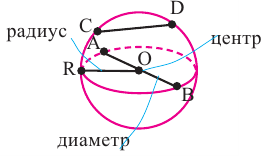
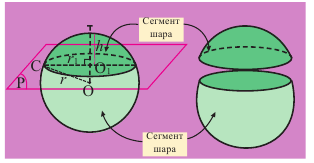
Сферой называют фигуру, полученную в результате вращения полуокружности вокруг ее диаметра (рис. 9.69).

Шаром называют фигуру, полученную вращением полукруга вокруг его диаметра.

Сечение сферы плоскостью – окружность.

Сечение шара плоскостью – круг.

Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке и радиусом ).

Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (на рисунке 9.69 плоскость ). Эту точку называют точкой касания сферы и плоскости (на рисунке 9.69 точка ).

Касательная плоскость перпендикулярна радиусу сферы в точке касания.

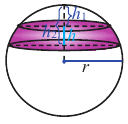
Площадь сферы радиуса находят по формуле:

$LaTeX formula: S_{cphi .}=4pi R^2$ . (9.25)

Объем шара радиуса находят по формуле:

$LaTeX formula: V_{wapa}=frac{4}{3}pi R^3$ . (9.26)

Выпуклый многоугольник вписан в сферу, если все его вершины лежат на поверхности сферы, и описан около сферы, если все его стороны касаются поверхности сферы.

Сферическим (шаровым) сегментом называют часть сферы (шара), отсекаемую плоскостью.

Высотой шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70 ).

Шаровым сектором называют тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов.

Высотой шарового сектора называют высоту части его сферической поверхности.

На рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса .

Объем шарового сегмента находят по формуле:

$LaTeX formula: V_{c.}=pi h^2(R-frac{1}{3}h)$ . (9.27)

Площадь сферической поверхности находят по формуле:

$LaTeX formula: S_{n.}=2pi Rh$ , (9.28)

где – радиус шара; – высота сегмента.

Объем шарового сектора находят по формуле:

$LaTeX formula: V_{cekappa .}=frac{2}{3}pi R^2h$ , (9.29)

где – радиус шара; – высота сегмента.

Пример 1. Осевое сечение цилиндра – квадрат со стороной . Найдите объем и площадь поверхности цилиндра.

Решение. Так как осевое сечение квадрат (рис. 9.71), то , $LaTeX formula: r=frac{a}{2}$ .

По формулам 9.15 и 9.16 найдем объем цилиндра: $LaTeX formula: V=pi cdot frac{a^2}{4}cdot a=frac{pi a^3}{4}$ .

По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра: $LaTeX formula: S_{n.}=frac{2pi a^2}{4}+frac{2pi a^2}{2}=frac{3pi a^2}{2}$ .

Ответ: ; .

Пример 2. Площадь боковой поверхности цилиндра равна , а объем его равен . Найдите высоту этого цилиндра.

Решение. Площадь боковой поверхности и объем цилиндра найдем по формулам 9.18 и 9.15 , где – радиус основания, – высота цилиндра.

Тогда согласно условию задачи запишем: $LaTeX formula: begin{cases} 2pi Rh=119, \ pi R^2h=7pi. end{cases}$

Разделим первое уравнение системы на второе и получим: $LaTeX formula: frac{2pi Rh}{pi R^2h}=frac{119}{7pi }$ , $LaTeX formula: frac{2}{R}=frac{17}{pi }$ , $LaTeX formula: R=frac{2pi }{17}$ .

Найдем из первого уравнения системы: $LaTeX formula: h=frac{119}{2pi R}=frac{119cdot 17}{2pi cdot 2pi }=frac{2023}{4pi ^2}$ .

Ответ: $LaTeX formula: frac{2023}{4pi ^2}$ .

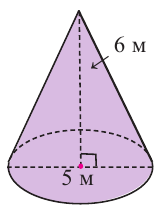
Пример 3. Найдите объем и площадь поверхности конуса, осевым сечением которого является правильный треугольник со стороной см (рис. 9.72).

Решение. Так как см, а см, то из теоремы Пифагора: $LaTeX formula: h=sqrt{l^2-r^2}$ , (см).

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 3cdot 3=3pi$ ( $LaTeX formula: _{CM}\^3$ ).

По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса: $LaTeX formula: S_{n.}=3pi +6pi =9pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 4. Радиус основания конуса равен , а угол при вершине в развертке его боковой поверхности равен $LaTeX formula: 90^{circ}$ . Определите объем конуса.

Решение. Рассмотрим конус радиуса и развертку его боковой поверхности – круговой сектор радиуса (рис. 9.73).

Найдем длину окружности в основании конуса: $LaTeX formula: C_{okappa p.}=2pi r=2sqrt{15}pi$ .

Найдем длину дуги в развертке боковой поверхности конуса: $LaTeX formula: C_{g.}=frac{2pi l}{360^{circ}}cdot 90^{circ}=frac{pi l}{2}$ .

Так как $LaTeX formula: C_{okappa p.}=C_{g.}$ , то $LaTeX formula: 2pi r=frac{pi l}{2}$ и .

Из теоремы Пифагора: , .

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 15cdot 15=75pi$ .

Ответ: .

Пример 5. Осевое сечение конуса – равнобокая трапеция с основаниями и . Образующая конуса равна . Найдите площадь боковой поверхности и объем конуса.

Решение. Имеем усеченный конус (рис. 9.74), радиусы оснований которого соответственно равны и . Зная образующую конуса , найдем его высоту: $LaTeX formula: h=sqrt{l^2-(r_1-r_2)^2}$ , .

По формуле 9.24 найдем площадь боковой поверхности конуса: $LaTeX formula: S_{delta .}=20sqrt{7}pi$ .

По формуле 9.23 найдем объем конуса:

$LaTeX formula: V=frac{1}{3}pi 2sqrt{7}(64+4+16)=56sqrt{7}pi$ .

Ответ: ; .

Пример 6. Периметр правильного шестиугольника, все вершины которого лежат на поверхности шара, равен . Объем шара равен . Найдите расстояние от центра шара до плоскости шестиугольника.

Решение. Найдем сторону правильного шестиугольника, зная его периметр: . Так как радиус окружности, описанной около правильного шестиугольника, равен его стороне, то на рисунке 9.75 .

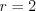
Объем шара находят по формуле 9.26 .

Так как , то $LaTeX formula: 36pi =frac{4}{3}pi R^3$ , $LaTeX formula: 9=frac{1}{3}R^3$ , , .

Из теоремы Пифагора: $LaTeX formula: d=sqrt{R^2-r^2}$ , .

Ответ: .

Пример 7. Сторона квадрата, описанного около шара, равна . Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен (рис. 9.76).

Решение. 1. Найдем диагональ квадрата, зная его сторону: , . Поскольку сечение шара плоскостью – круг, а квадрат описан около этого круга, то радиус сечения равен: $LaTeX formula: r=frac{d}{2}$ , .

2. Из теоремы Пифагора: $LaTeX formula: l=sqrt{R^2-r^2}$ , .

3. Найдем высоту сферической поверхности:

, .

4. По формуле 9.28 найдем площадь сферической поверхности:

$LaTeX formula: S_{n.}=2pi Rh$ , $LaTeX formula: S_{n.}=10pi (5-sqrt{17})$ .

Ответ: .

Пример 8. Равнобедренная трапеция с основаниями см и см и острым углом $LaTeX formula: 60^{circ}$ вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.

Решение. Рассмотрим равнобедренную трапецию с основаниями см и см (рис. 9.77). Вращая трапецию вокруг основания , получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов: $LaTeX formula: S_{n.}=S_{delta .}+2S_{delta .kappa .}$ . В трапеции из вершин и проведем высоты и . Тогда $LaTeX formula: BN=CM=R_{v.}=R_{kappa .}=h_{mp.}$ .

Рассмотрим прямоугольный треугольник : $LaTeX formula: angle BAN=60^{circ}$ , $LaTeX formula: AN=frac{1}{2}(AD-NM)=frac{1}{2}cdot 1=frac{1}{2}$ (см),

тогда (см) и $LaTeX formula: BN=sqrt{1^2-left ( frac{1}{2} right )^2}=frac{sqrt{3}}{2}$ (см).

Согласно формуле $LaTeX formula: S_{delta .v.}=2pi R_{v.}l_{v.}$ получим: $LaTeX formula: S_{delta .v.}=2pi cdot frac{sqrt{3}}{2}cdot 13=13sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Согласно формуле $LaTeX formula: S_{delta .kappa .}=pi R_{kappa .}l_{kappa .}$ получим: $LaTeX formula: S_{delta .kappa .}=pi frac{sqrt{3}}{2}cdot 1=frac{sqrt{3}pi }{2}$ ( $LaTeX formula: _{CM}\^2$ ).

Найдем площадь поверхности тела вращения: $LaTeX formula: S_{n.}=13sqrt{3}pi +2cdot frac{sqrt{3}pi }{2}=14sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^2$ .

1. В цилиндре умейте определять: радиус основания, высоту, образующую, осевое сечение.

2. В конусе умейте определять: радиус основания, высоту, образующую, осевое сечение.

3. Различайте шар и сферу (поверхность шара). Умейте определять: 1) центр, радиус и диаметр сферы; 2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.

Источник

Содержание:

Великий греческий ученый Архимед был очень взволнован, когда он обнаружил, что отношение площади поверхности шара и описанного около него цилиндра и отношение их объемов равно 2:3. Великий математик, физик, инженер, Архимед, среди всех своих работ самой значимой считал именно эту. Он завещал на своей могильной плите выгравировать доказательство данной теоремы. Из истории известно, что долгое время его родной город Сиракузы, располагающийся на Сицилии, противостоял римлянам именно благодаря оружию, которое изобрел Архимед. Поэтому при взятии города римский военачальники приказал сохранить ученому жизнь. Но римский воин, который не знал Архимеда в лицо, убил его. Великий философ и писатель Цицерон потратил много времени, чтобы отыскать могилу Архимеда (по историческим сведениям он нашел ее через 137 лет). Это дело Цицерона стало идеей для работ многих художников.

Определение фигур вращения

Гончарное ремесло позволяет создавать керамическую посуду из глины. Форму глиняной лепешке придают вращением вокруг оси. Затем полученную форму обжигают. Это ремесло живо и по сей день. В различных районах Азербайджана есть ремесленники, которые изготавливают керамическую посуду. Исследуйте принцип работы по которому кусок глины приобретает какую-либо форму.

Плоские фигуры (плоская часть ограниченная кривой), совершая один полный оборот вокруг определенной оси, образуют пространственные фигуры. Эта ось называется осью вращении.

Цилиндр, конус и сфера являются простыми пространственными фигурами, полученными при вращении.

Например, при вращении прямоугольного треугольника вокруг одного из катетов получается конус, при вращении прямоугольника вокруг стороны образуется цилиндр, а при вращении полукруга вокруг диаметра — шар.

Цилиндр

Наглядно образование фигур вращения можно увидеть на примере вращающихся стеклянных дверей, которые мы часто видим в общественных зданиях, отелях и больницах. Прямоугольный слой двери, прикрепленный к неподвижной стойке, при вращении очерчивает цилиндр.

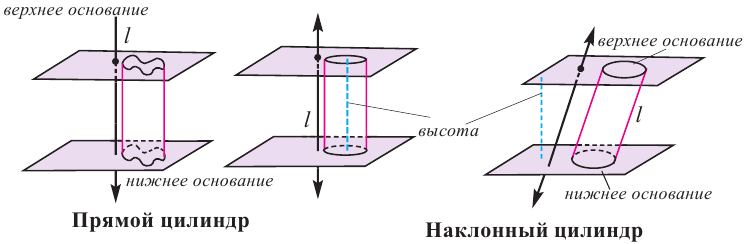
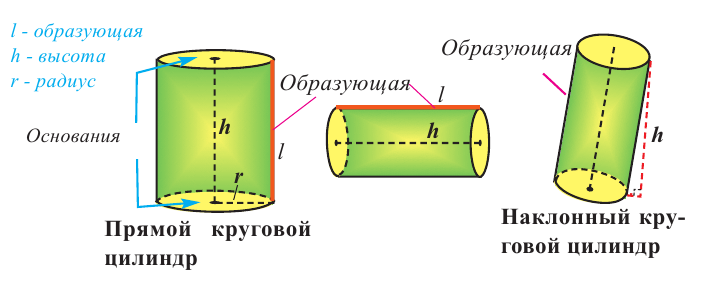
Цилиндром называется пространственная фигура, образованная двумя параллельными и конгруэнтными плоскими фигурами, которые совпадают при параллельном переносе, и отрезками, соединяющими соответствующие точки данных фигур. Плоские фигуры называются основаниями цилиндра, отрезки, соединяющие соответствующие точки основания называются образующими цилиндра. Если образующая перпендикулярна основанию, то цилиндр называется прямым, иначе — наклонным. Расстояние между основаниями называется высотой цилиндра.

На рисунках ниже изображены прямые и наклонные цилиндрические фигуры.

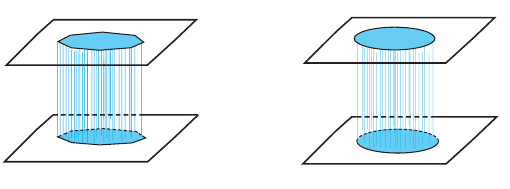
Сравнивая рисунки, изображенные ниже, можно сделать вывод, что призму можно рассматривать как частный случай цилиндра.

Прямой цилиндр, в основании которого лежит круг, называют прямым круговым цилиндром.

Далее, говоря о цилиндре, мы будем иметь в виду прямой круговой цилиндр. В любом другом случае будут отмечены его особенности.

Прямой круговой цилиндр также можно рассматривать как фигуру, полученную вращением прямоугольника вокруг одной из его сторон. Высота прямого кругового цилиндра равна его образующей. Радиусом цилиндра называется радиус круга в основании.

Вращая прямоугольник вокруг любой стороны, можно получить цилиндр, высота которого равна стороне прямоугольника.

Прямая, проходящая через центры оснований прямого кругового цилиндра называется осью цилиндра.

Площадь поверхности цилиндра

Площадь боковой и полной поверхностей цилиндра.

Изобразите на листе бумаги рисунки разверток цилиндров различных размеров, вырежьте и склейте цилиндры.

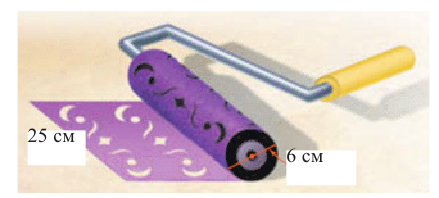
Мустафа красит стену цилиндрической кистью. Чтобы подсчитать время, потраченное на покраску, он захотел узнать, какую площадь покрывает кисть при одном полном обороте? Какие советы вы могли бы дать мальчику?

Так как кисть имеет цилиндрическую форму, то за один полный оборот кисть покрывает площадь в форме прямоугольника, равную боковой поверхности цилиндра.

Полная поверхность цилиндра находится но формуле схожей с формулой полной поверхности призмы. Полная поверхность цилиндра состоит из боковой поверхности и двух конгруэнтных кругов.

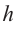
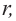
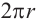
Боковую поверхность цилиндра с высотой и радиусом можно рассматривать как свернутый вокруг окружности прямоугольник со сторонами и

Боковая поверхность цилиндра равна произведению длины окружности основания и высоты.

Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований

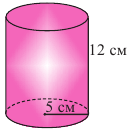
Пример №1

Найдите площадь полной поверхности цилиндра выстой 12 см и радиусом 5 см.

Решение:

Пример №2

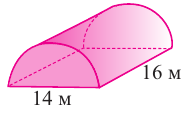
По данным рисунка, найдите площадь боковой поверхности прямого цилиндра, основанием которой являются полукруг.

Решение:

Пример №3

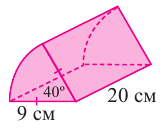
По данным на рисунке найдите площадь полной поверхности прямого цилиндра, основанием которой является круговой сектор с углом 40°.

Решение: известно, что

По формуле площади сектора:

Боковая поверхность фигуры равна 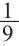части боковой поверхности цилиндра с радиусом 9 см и высотой 20 см плюс площадь двух конгруэнтных прямоугольников размерами

Таким образом,

Конус

Конусом называется пространственная фигура, образованная всеми отрезками, соединяющими какую-либо плоскую фигуру с точкой, не принадлежащей данной плоскости. Плоскую фигуру называют основанием конуса, а точку —вершиной конуса.

Перпендикуляр, проведенный из вершины конуса на плоскость его основания, называется высотой конуса. Конус, в основании которого лежит круг, называется круговым конусом. Если ортогональная проекция вершины конуса лежит в центре основания, то конус называется прямым круговым конусом. Отрезок, соединяющий вершину конуса с любой точкой окружности основания кругового конуса, называется образующей конуса. В дальнейшем, говоря о конусе, будем иметь ввиду прямой круговой конус.

Конус можно рассматривать как фигуру, образованную вращением прямоугольного треугольника вокруг одного из катетов.

Прямая, выходящая из вершины конуса и проходящая через центр основания, называется осью конуса, радиус основания называется радиусом конуса. Для образующей, высоты и радиуса конуса справедливо отношение 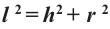(по теореме Пифагора)

Сооружение конуса

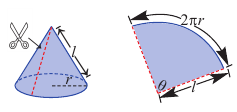
Известно, что при сворачивании прямоугольника можно получить цилиндр. Скручивая круговой сектор можно соорудить конус.

Радиус сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания.

Боковая поверхность конуса, полная поверхность конуса

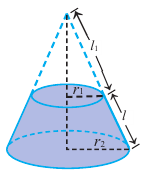
Поверхность конуса состоит из боковой поверхности и круга в основании. На рисунке показаны радиус основания 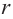и образующая

Боковая поверхность конуса — круговой сектор с радиусом 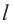и соответствующим центральным углом

Значит, площадь сектора и есть площадь боковой поверхности.

Значит, сектор составляет 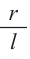часть окружности.

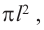
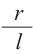
* Зная, что площадь круга тогда часть площади круга будет

Значит,

Боковая поверхность конуса равна произведению половины длины окружности основания и образующей.

* Площадь полной поверхности конуса

Пример №4

По рисунку найдите площадь боковой и полной поверхностей конуса.

Решение: Дано:

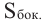
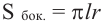
Найти: и

Чтобы найти образующую 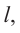применим теорему Пифагора

Сечения цилиндра и конуса плоскостью

Сечения поверхности конуса плоскостью (теория конических сечений) считались одной из вершин античной геометрии. Исследования Аполлония (3-й в.до н.э.) показали, что сечением плоскостью конуса, с бесконечной образующей (лучом) является: эллине (плоскость пересекает все образующие), парабола (плоскость сечения параллельна одной из образующих) или ветвь гиперболы (плоскость сечения параллельна двум образующим).

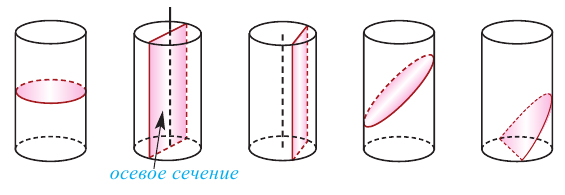
Сечения цилиндра плоскостью

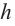
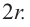
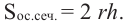
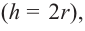
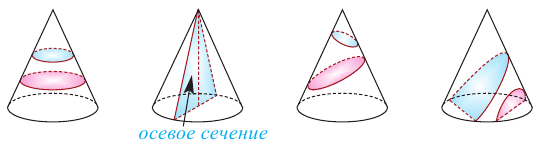
Сечением цилиндра плоскостью, параллельной основанию, является круг. Сечение цилиндра плоскостью, проходящей через ось симметрии, называется осевым сечением. Осевое сечение цилиндра является прямоугольником со сторонами и Значит, Цилиндр, осевое сечение которого является квадратом называется равносторонним цилиндром.

Сечения конуса плоскостью

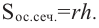
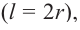
Сечением конуса плоскостью, параллельной основанию, является круг. Сечение конуса, проходящее через ось конуса называется осевым сечением конуса. Это сечение является равнобедренным треугольником, боковые стороны которого являются образующими, а основание равно диаметру конуса: Если осевое сечение конуса является правильным треугольником то конус называется равносторонним конусом.

Пример №5

Сечением цилиндра плоскостью, проведенного параллельно оси цилиндра на расстоянии 3 см от оси, является квадрат, площадь которого равна 64 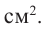Найдите площадь полной поверхности цилиндра.

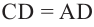
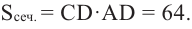
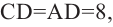
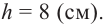
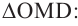
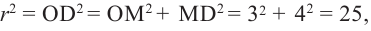
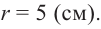
Решение: сначала найдем радиус и высоту цилиндра. По условию и Отсюда значит Из отсюда Таким образом,

Усеченный конус и площадь поверхности

Усеченный конус

Если параллельно основанию прямого кругового конуса провести плоскость, то получим маленький конус и усеченный конус.

Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.

Боковая поверхность усеченного конуса равна разности боковых поверхностей большого конуса и маленького конуса, отсеченного плоскостью, параллельной основанию, от большого конуса. Используя обозначения на рисунке, можно записать:

Из подобия треугольников запишем следующее отношение

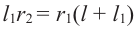
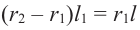
Тогда, подставив или в формулу для нахождения боковой поверхности, получим:

В данной формуле введем обозначение 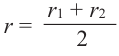среднего радиуса

усеченного конуса. Тогда

Полная поверхность усеченного конуса равна сумме боковой поверхности и площадей нижнего и верхнего оснований.

Пример №6

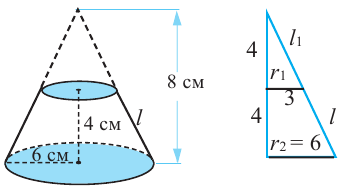
Конус высотой 8 см и радиусом 6 см рассечен плоскостью, параллельной основанию. Высота полученного усеченного конуса равна 4 см. Найдите площади боковой и полной поверхностей усеченного конуса

Решение: дано:

Найти:

Площадь поверхности шара и его частей

Шаром называется множество всех точек пространства находящихся от данной точки на расстоянии, не больше данного. Данная точка называется центром шара, данное расстояние радиусом 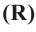шара.

Множество всех точек, расположенных на расстоянии 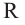от центра шара, образует поверхность шара. Поверхность шара называется сферой. Прямая, соединяющая любые две точки на поверхности шара, называется хордой Хорда, проходящая через центр шара называется диаметром шара

Шар получается, при вращении полукруга вокруг диаметра.

Любое сечение шара плоскостью является кругом. Центр этого круга является основанием перпендикуляра, проведенного к плоскости и проходящего через центр шара. Если — радиус шара, — расстояние между плоскостью и центром, а — радиус сечения, то получим:

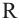
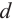
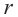
Пример №7

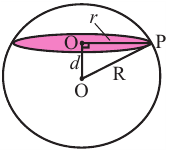
Шар радиуса 10 см пересечена плоскостью на расстояние

8 см от центра. Вычислите площадь сечения.

Решение: По условию

Тогда

Сечение шара плоскостью, проходящей через центр шара, называется

большим кругом. Центр, радиус и диаметр большого круга равны

центру, радиусу и диаметру шара.

Также для шара известны следующие части:

Площадь поверхности шара

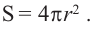
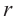
Площадь поверхности шара находится по формуле Здесь радиус шара.

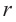
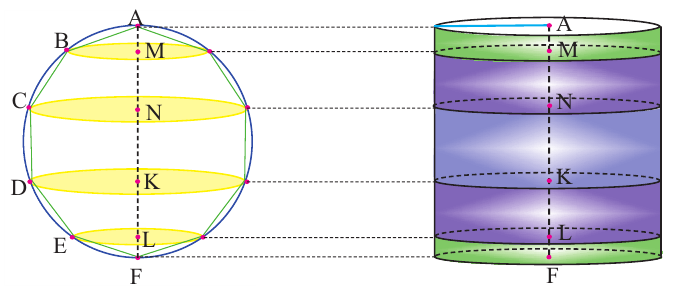
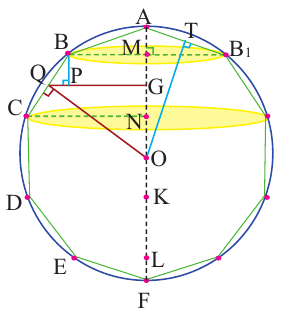
В окружность радиусом впишем правильный многоугольник. Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур — конуса,усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника.

Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через

— площадь боковой поверхности конуса с образующей Так как то Умножим на 2 обе части равенства

Учитывая, что получим Значит,

— площадь боковой поверхности усеченного конуса.

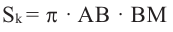
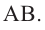
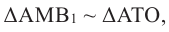
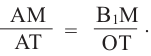
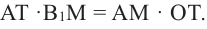
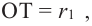
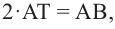
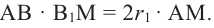
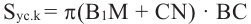
Зная, что 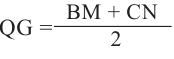получим, что

Так как 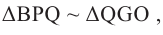то

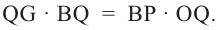
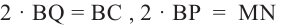
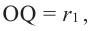
Умножим на 2 обе части равенства Учитывая,что

и получим

Значит,

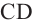
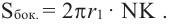
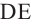
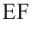
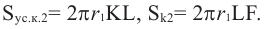
Понятно, что площадь боковой поверхности цилиндра с образующей равна Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей и конуса с образующей можно найти но формулам Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :

При бесконечном увеличении количества сторон многоугольника значение

стремится к радиусу, а площадь поверхности полученного тела к площади

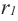
поверхности шара, т. е.

Площадь поверхности шара

Доказательство Архимеда:

Пусть, в правильный многоугольник вписан круг, как показано на рисунке.

При вращении получается шар и покрывающее шар тело

Это тело состоит из двух усеченных конусов и цилиндра.

При увеличении количества сторон до бесконечности, тело будет стремится принять форму шара.

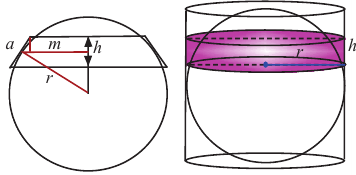
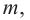
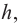
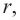
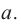
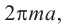
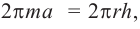
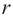
Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен а высота радиус шара сторона многоугольника, описанного вокруг большего круга равна Площадь боковой поверхности усеченного конуса будет а также т. е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен и высота

Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания 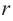и высотой

Т. е.,

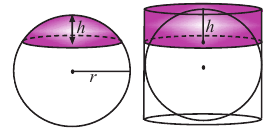
Площадь сегмента шара

Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента.

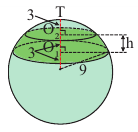
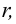
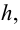
Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса площадь сферической поверхности сегмента высотой вычисляется по формуле

Площадь шарового пояса

Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом. Расстояние между параллельными плоскостями называется высотой шарового пояса.

Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.

Площадь поверхности шарового пояса высотой 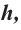отсекаемого от шара радиуса вычисляется по формуле

Пример №8

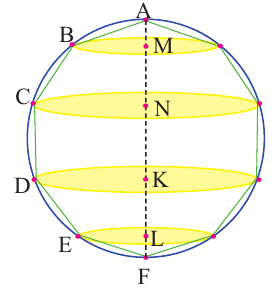
Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара 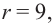найдите площадь поверхности шарового пояса.

Решение: если 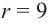и то площадь поверхности шарового пояса будет

Площади поверхностей подобных фигур

Отношение соответствующих линейных размеров подобных пространственных фигур постоянно и равно коэффициенту подобия.

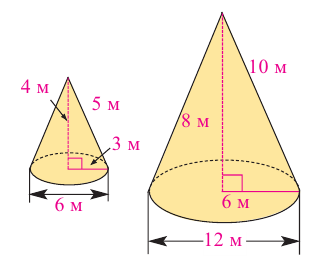
Например, чтобы проверить подобны ли конусы на рисунке, найдем отношение соответствующих размеров. Если эти конусы подобны, то отношение радиусов должно быть равно отношению высот.

Значит эти конусы подобны и коэффициент подобия равен 2. Это говорит о том, что если все линейные размеры маленького конуса пропорционально увеличить в два раза, то получим конус, конгруэнтный большому конусу. Или наоборот, пропорционально уменьшив размеры большого конуса в два раза, получим конус, конгруэнтный маленькому. Если пропорционально увеличить или уменьшить размеры какой-либо фигуры, то можно получить подобные фигуры.

Отношение площадей подобных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия

Объем фигур вращения
Длина дуги кривой
Геометрические фигуры и их свойства
Основные фигуры геометрии и их расположение в пространстве
Вписанные и описанные многоугольники
Площадь прямоугольника
Объем пространственных фигур
Объёмы поверхностей геометрических тел

Источник

Тела и поверхности вращения. Шар. Цилиндр. Конус

Тела и поверхности вращения.

Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.

Подробная теория с наглядными иллюстрациями и основные формулы.

Читай эту статью, здесь все это есть.

Всего за 15 минут ты полностью во всём разберешься!

Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.

Вот самый простой пример: цилиндр.

Берем прямоугольник и начинаем вращать его вокруг одной из сторон.

Смотри.

Было–вращаем–стало:

А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.

Например, так:

Вращаем:

Что получится? Бублик. А по-научному – ТОР.

Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.

Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.

Шар

Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.

Было–вращаем–стало:

Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)

Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.

Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:

«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.

Ну, в общем, шар он и есть шар.

Названия, которые ты должен знать:

Незнакомое тебе, наверное, только одно.

Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.

А вообще:

Любое сечение шара – круг.
Граница шара называется сфера. (Так же, как граница круга – окружность.)

Площадь поверхности сферы

( {{S}_{поверхности }}=4pi {{R}^{2}})

( R) – радиус

Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.

Объем шара

( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})

( R) – радиус

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.

Если ты знаком с производной, то можешь заметить это:

( {{V’}_{шара}}={{S}_{поверхности}})

И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!

Цилиндр

Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.

Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:

Основания у цилиндра – это круги

Еще у цилиндра есть так называемая развертка.

Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.

Что получится? Представь себе, прямоугольник.

Развертка цилиндра – прямоугольник.

Площадь боковой поверхности цилиндра

( {{S}_{бок.}}=2pi RH)

( R) – радиус

( H) – высота, она же образующая.

Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).

Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра.

Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому

( {{S}_{бок.}}=2pi RH)

Площадь полной поверхности цилиндра

Прибавляем теперь площадь двух кругов – оснований и получаем:

( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})

Можно вынести (хотя и не обязательно) ( 2pi R):

( {{S}_{полн .}}=2pi Rleft( H+R right))

Но эту формулу неудобно запоминать!

Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что

( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})

Объем цилиндра

( V=pi {{R}^{2}}H)

( R) – радиус основания ( H) – высота

Это точно как у призмы и параллелепипеда!

( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) — это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) — это площадь круга.

Конус

Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.

Было–вращаем–стало:

И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».

Названия, относящиеся к конусу:

Что тут нужно твердо помнить?

Основание корпуса – круг
Все образующие конуса – равны.

Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.

У конуса тоже есть развертка.

Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?

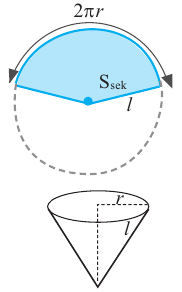
Представь себе сектор круга. Пусть длина образующей равна ( l).

Развертка конуса – сектор круга радиуса ( l)

Площадь поверхности конуса

Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.

По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.

И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.

Но если все же даны только образующая и радиус основания, как быть?

Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).

С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому

( alpha cdot l=2pi R)

Подставляем

( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)

Итак,

( {{S}_{бок.}}=pi Rl), где

( R) — радиус окружности основания,

( l) — длина образующей

Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:

( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})

Можно вынести ( pi R):

( {{S}_{полн. }}=pi Rleft( l+R right))

Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.

Объём конуса

( V=frac{1}{3}pi {{R}^{2}}H)

( R) – радиус основания (

H) – высота

Это так же, как у пирамиды

( V=frac{1}{3}{{S}_{осн.}}cdot H), только

( {{S}_{осн. }}) — это не площадь многоугольника, а площадь круга.

А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.

А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.

Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео:

Как нарисовать шестиугольную пирамиду.
Как подписать вершины пирамиды чтобы потом легче было решать задачу.
Как исправить рисунок, если грани пирамиды сливаются.
Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
Нахождение площади основания и объема пирамиды.
Самое главное, на что нужно обратить внимание.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

На этой странице вы узнаете

Как вода в кружке иллюстрирует сечение цилиндра?
Как лист бумаги превратить в цилиндр?

Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон.

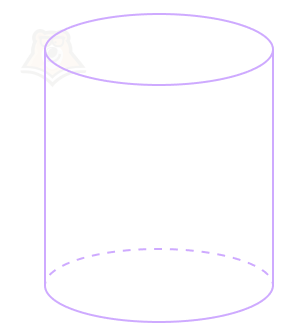
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения».

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру. Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра.

Также, как у Земли есть ось вращения, она есть и у цилиндра.

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра.

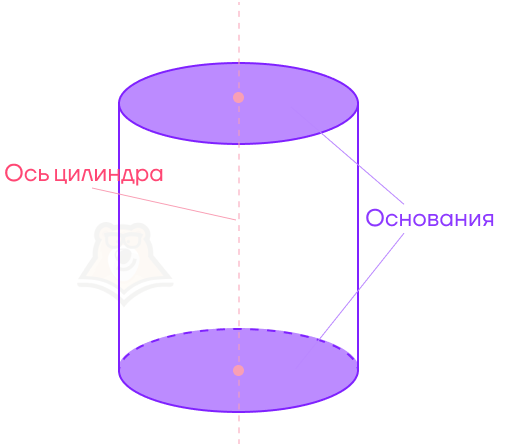
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра.

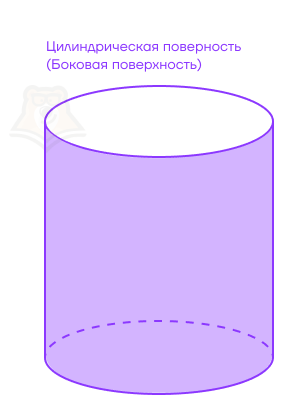
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований.

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих.

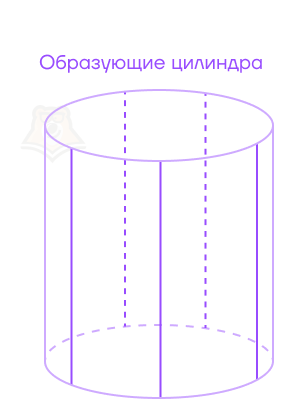
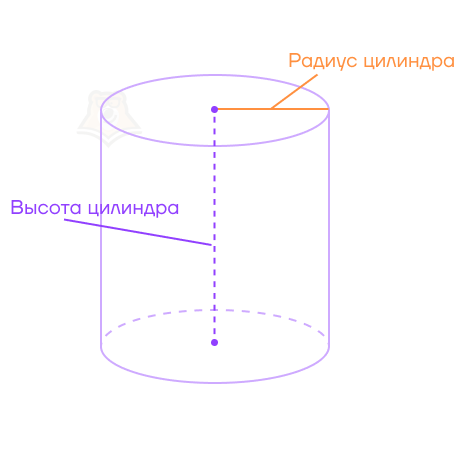
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра.

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки.

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами».

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания.

Свойства цилиндра

Рассмотрим, какими свойствами обладает цилиндр.

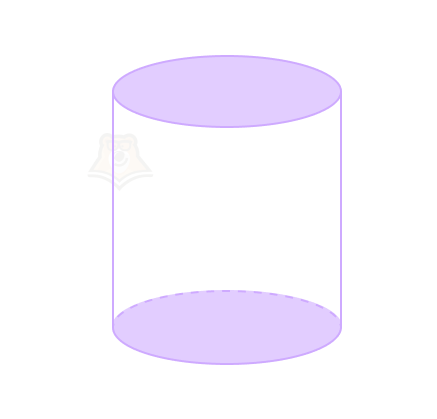
Свойство 1. Основания цилиндра равны и параллельны.

Это всегда два равных круга, лежащих в параллельных плоскостях.

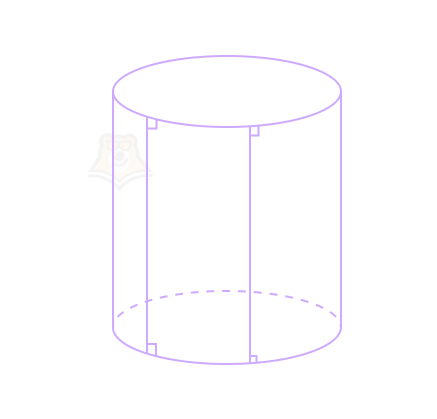
Свойство 2. Образующие цилиндра равны и параллельны.

Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве».

А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.

Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра.

Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником.

Подробности про сечения фигур можно найти в статье «Сечения».

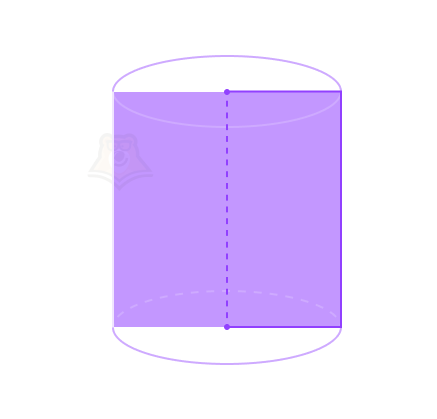
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником.

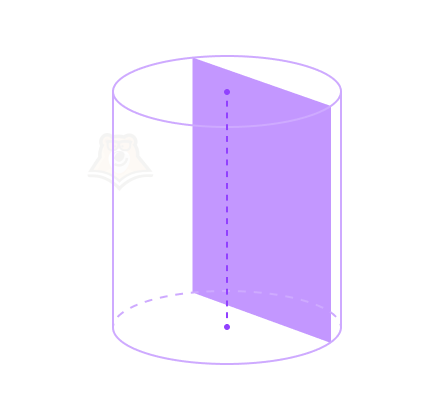
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра.

Как вода в кружке иллюстрирует сечение цилиндра?

Если налить в кружку воду, то ее поверхность примет круглую форму. При этом совершенно без разницы, сколько воды наливать: поверхность останется кругом.

Поскольку поверхность воды параллельна дну кружки, то есть основаниям цилиндра, то она является перпендикулярным сечением цилиндра.

Этим опытом можно подтвердить свойство 5.

Заметим, что все вышеописанные свойства относятся к прямому цилиндру.

Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям.

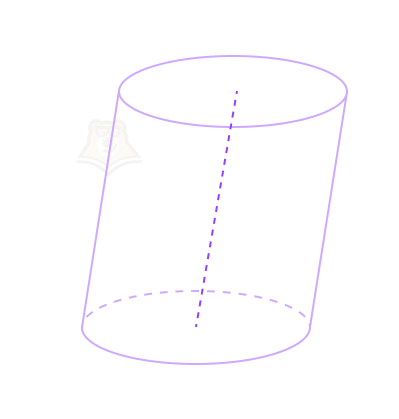
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник.

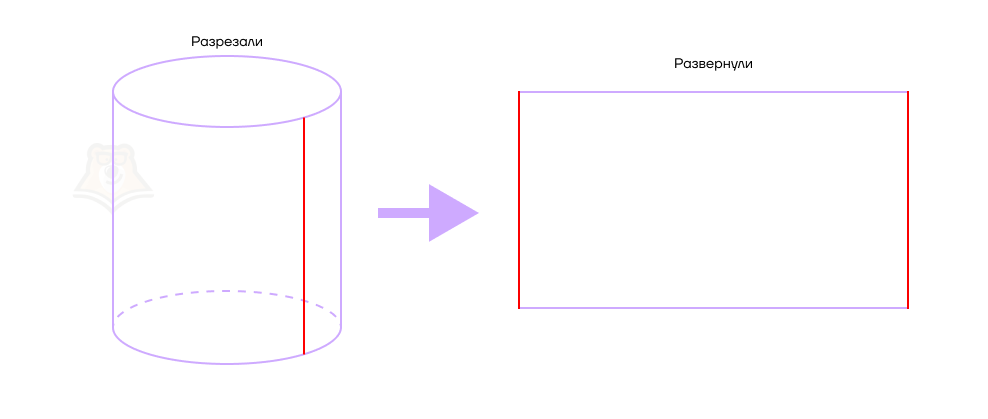
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму.

Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания.

Как лист бумаги превратить в цилиндр?

Поскольку развертка боковой поверхности цилиндра — это прямоугольник, то любой лист бумаги можно превратить в цилиндр. Для этого достаточно скрутить его в трубочку. При этом чем тоньше будет трубочка, тем меньше будет радиус цилиндра.

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти его площадь. Нам нужно умножить его длину на высоту. Так мы получаем площадь боковой поверхности цилиндра.

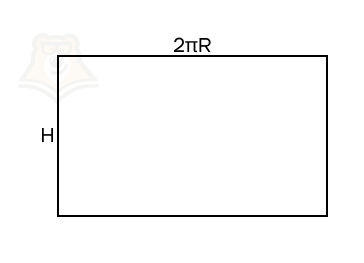
(S_{бок.} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а Н — образующая (или высота) цилиндра. Подробнее про площадь прямоугольника и длину окружности (а также про площадь круга) можно прочесть в статьях «Параллелограмм» и «Окружность и круг».

Мы нашли площадь боковой поверхности. Как же теперь найти площадь полной поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Следовательно, мы получаем следующую формулу.

(S = S_{бок.} + 2S_{осн.} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили сделать чашку очень вкусного чая, но чтобы правильно его заварить нам нужно знать точный объем воды. Для этого вычислим объем цилиндра. Воспользуемся следующей формулой:

(V = S_{осн.}H = pi R^2H)

В этой формуле R — радиус цилиндра, Н — высота.

Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду.

Пример 1. В цилиндрическом сосуде налито 1650 см³ жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см³.

Решение.

Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х.

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = V_ж + V_д.

Шаг 3. С помощью объема жидкости выразим площадь основания сосуда:

V_ж = S_осн.H
1650 = S_осн.x
(S_{осн} = frac{1650}{x})

Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь:

(V = S_{осн.}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

V_д = V — V_ж
V_д = 1980 — 1650 =330

Ответ: 330 см³

Фактчек

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. Цилиндр может быть прямым и наклонным. В наклонном цилиндре ось не перпендикулярна основаниям цилиндра.
Цилиндр состоит из двух оснований и цилиндрической поверхности (боковой поверхности цилиндра). Основания имеют форму кругов, равны между собой и лежат в параллельных плоскостях. Развертка боковой поверхности имеет форму прямоугольника.
Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра.
Осевое сечение цилиндра проходит через его ось и является прямоугольником. Любое сечение, параллельное осевому, также будет являться прямоугольником. Перпендикулярное сечение проходит перпендикулярно оси цилиндра и параллельно его основаниям. Перпендикулярное сечение имеет форму круга.

Проверь себя

Задание 1.
Что такое образующая цилиндра?

Ось вращения, с помощью которой получен цилиндр.
Диаметр оснований цилиндра.
Любой перпендикуляр, проведенный от одного основания к другому.
Отрезок, соединяющий точки окружности основания.

Задание 2.
Площадь боковой поверхности цилиндра равняется 44. Его радиус равен 8. Найдите высоту цилиндра.

2,75
5,5
(2,75 pi)
2

Задание 3.
Площадь основания цилиндра равна 16. Его высота равна 4. Найдите площадь полной поверхности цилиндра.

64
(64 pi)
32
(32 pi)

Задание 4.
Объем цилиндра равен 28, а его высота равняется 7. Найдите диаметр основания.

Ответы: 1. – 4 2. – 1 3. – 2 4. – 1

Источник

Телами
вращения называют тела,
ограниченные либо поверхностью вращения,
либо поверхностью вращения и плоскостью
(рисунок 134). Под поверхностью вращения
понимают поверхность, полученную от
вращения какой-либо линии (ABCDE),
плоской или пространственной,
называемой образующей, вокруг неподвижной
прямой (i) — оси
вращения.

Рисунок
134

Любая
точка образующей поверхности вращения
описывает окружность, расположенную в
плоскости, перпендикулярной к оси
вращения – параллель,
следовательно, плоскость, перпендикулярная
к оси вращения, всегда пересекается с
поверхностью вращения по окружности.
Наибольшая параллель
— экватор. Наименьшая
параллель — горло
(горловина).

Плоскости,
проходящие через ось вращения, называют
меридиональными плоскостями.

На
комплексном чертеже изображение тел
вращения выполняется посредством
изображения ребер оснований и линий
очерков поверхности.

Линии
пересечения меридиональных плоскостей
с поверхностью называют меридианами.

Меридиональная
плоскость, параллельная плоскости
проекций, называется главной
меридиональной плоскостью.
Линия ее пересечения с поверхностью —
главный меридиан.

Прямой
круговой цилиндр.Прямым круговым
цилиндром (рисунок 135) называют тело,
ограниченное цилиндрической поверхностью
вращения и двумя кругами — основаниями
цилиндра, расположенными в плоскостях,
перпендикулярных к оси цилиндра.Цилиндрической поверхностью вращенияназывается поверхность, полученная при
вращении прямолинейной образующейAA₁вокруг параллельной ей неподвижной
прямой —i(ось вращения). Размерами,
характеризующими прямой круговой
цилиндр, являются его диаметрDци высотаl(расстояние между
основаниями цилиндра).

а
б в

Рисунок
135

Прямой
круговой цилиндр можно также рассматривать
как тело, полученное при вращении
какого-либо прямоугольника ABCD
вокруг одной из его сторон, например,
ВС (рисунок 136).
Сторона ВС
является осью вращения, а сторона AD
— образующей цилиндра. Две другие
стороны обозначат основания цилиндра.

Рисунок
136

Прямоугольника
АВ и CD
при вращении образуют круги — основания
цилиндра.

Построение
проекций цилиндра.

Построение
горизонтальной и фронтальной проекций
цилиндра начинают с изображения основания
цилиндра, т. е. двух проекций окружности
(см. рисунок 135, б). Так как окружность
расположена на плоскости Н,
то она проецируется на эту плоскость
без искажения. Фронтальная проекция
окружности представляет собой отрезок
горизонтальной прямой линии, равный
диаметру окружности основания.

После
построения основания на фронтальной
проекции проводят две очерковые
образующие (крайние
образующие) и на них
откладывают высоту цилиндра. Проводят
отрезок горизонтальной прямой, который
является фронтальной проекцией верхнего
основания цилиндра (рисунок 135, в).

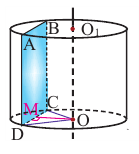
Определение
недостающих проекций точек А и В,
расположенных на поверхности цилиндра,
по заданным фронтальным проекциям
в данном случае затруднений не вызывает,
так как вся горизонтальная проекция
боковой поверхности цилиндра представляет
собой окружность (рисунок 137, а).
Следовательно, горизонтальные проекции
точек А и В
можно найти, проводя из данных точек
A» и B»
вертикальные линии связи до их пересечения
с окружностью в искомых точках A’
и B’.

Профильные
проекции точек А
и В строят также
при помощи вертикальных и горизонтальных
линий связи.

Изометрическую
проекцию цилиндра
вычерчивают, как показано на рисунок
137, б.

В
изометрии точки А
и В строят по их
координатам. Например, для построения
точки В от начала
координат О по
оси x откладывают
координату ∆x,
а затем через ее конец проводят прямую,
параллельную оси у,
до пересечения с контуром основания в
точке 2. Из этой
точки параллельно оси z
проводят прямую, на которой откладывают
координату Z_B,
точки В.

а
б

Рисунок
137

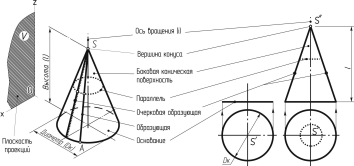
Прямой
круговой конус.Прямым круговым
конусом (рисунок 138) называют тело,
ограниченное конической поверхностью
вращения и кругом, расположенным в
плоскости, перпендикулярной к оси
конуса.Коническая поверхностьполучается при вращении прямолинейной
образующейSA(рисунок 138, а),
проходящей через неподвижную точкуSна оси вращенияiи составляющей
с этой осью некоторый постоянный угол.
ТочкаSназываетсявершиной
конуса, а коническая поверхность —
боковой поверхностью конуса. Размер
прямого кругового конуса характеризуют
диаметр его основанияD_Kи высотаН.

а) б) в)

Рисунок
138

Прямой
круговой конус можно также рассматривать
как тело, полученное при вращении
прямоугольного треугольника SAB
вокруг его катета SB
(рисунок 139). При таком вращении гипотенуза
описывает коническую поверхность, а
катет АВ — круг,
т. е. основание конуса.

Рисунок
139

Построение
проекций конуса.

Последовательность
построения двух проекций конуса показана
на рисунке 167, б и в. Сначала строят две
проекции основания. Горизонтальная
проекция основания — окружность.
Фронтальной проекцией будет отрезок
горизонтальной прямой, равный диаметру
этой окружности (рисунок 138, б). На
фронтальной проекции из середины
основания восставляют перпендикуляр,
и на нем откладывают высоту конуса
(рисунок 138, в). Полученную фронтальную
проекцию вершины конуса соединяют
прямыми с концами фронтальной проекции
основания и получают фронтальную
проекцию конуса.

Построение
точек на поверхности конуса

Если
на поверхности конуса задана одна
проекция точки А
(например, фронтальная проекция на
рисунке 140), то две другие проекции этой
точки определяют с помощью вспомогательных
линий — образующей, расположенной на
поверхности конуса и проведенной через
точку А, или
окружности, расположенной в плоскости,
параллельной основанию конуса.

а
б в

Рисунок
140

В
первом случае (рисунок 140, а) через точку
A проводят
фронтальную проекцию 1»S»
вспомогательной образующей. Пользуясь
вертикальной линией связи, проведенной
из точки 1,
расположенной на фронтальной проекции
окружности основания, находят
горизонтальную проекцию 1′
этой образующей, на которой при помощи
линии связи, проходящей через A’,
находят искомую точку A.

Во
втором случае (рисунок 140, б) вспомогательной
линией, проходящей через точку А,
будет окружность, расположенная на
конической поверхности и параллельная
плоскости Н —
параллель. Фронтальная проекция этой
окружности изображается в виде отрезка
1»1» горизонтальной
прямой, величина которого равна диаметру
вспомогательной окружности. Искомая
горизонтальная проекция A’
точки А находится
на пересечении линии связи, опущенной
из точки A’, с
горизонтальной проекцией вспомогательной
окружности.

Если
заданная фронтальная проекция 1»
точки 1 расположена
на контурной (очерковой) образующей, то
горизонтальная проекция точки находится
без вспомогательных линий.

В
изометрической проекции
точку А, находящуюся
на поверхности конуса, строят по трем
координатам (см. рисунок 140, в): X,
Y
и Z_А.
Эти координаты последовательно
откладывают по направлениям, параллельным
изометрическим осям. В рассматриваемом
примере от точки О
по оси х отложена
координата X;
из конца ее параллельно оси у проведена
прямая, на которой отложена координата
Y;
из конца отрезка, параллельно оси z
проведена прямая, на которой отложена
координата Z_А.
В результате построений получим искомую
точку А.

Шар.Шаром (рисунок 141) называют тело, полученное
при вращении полукругаABC(образующая) вокруг его диаметраАС
(ось вращения), а поверхность, которую
при этом описывает дугаABC,
называется шаровой или сферической.
Шар относится к телам, ограниченным
только поверхностью вращения.

Рисунок
141

Шаровая
(сферическая) поверхность является
геометрическим местом точек, равноудаленных
от одной точки О,
называемой центром шара.
Если шар рассечь горизонтальными
плоскостями, то в сечении получатся
окружности – параллели.
Наибольшая из параллелей имеет диаметр
равный диаметру шара. Такая окружность
называется экватором.
Окружности же, получаемые в результате
сечений шара плоскостями, проходящими
через его ось вращения, называются
меридианами.

Построение
проекций шара и точек на его поверхности

Проекции
шара приведены на рисунке 142, а.
Горизонтальная и фронтальная проекции
— окружности радиуса, равного радиусу
сферы.

а
б

Рисунок
142

Если
точка А расположена
на сферической поверхности, то
вспомогательная линия 1» 2»,
проведенная через эту точку параллельно
оси Ох (параллель),
проецируется на горизонтальную плоскость
проекций окружностью. На горизонтальной
проекции вспомогательной окружности
находят с помощью линии связи искомую
горизонтальную проекцию A’
точки А.

Величина
диаметра вспомогательной окружности
равна фронтальной проекции 1»2».

Аксонометрическое
изображение сферы
(шара) выполняется
в виде окружности (рисунок 142 б), радиус
которой геометрически определяется
как расстояние от центра сферы до
проекции экватора (эллипса) вдоль большей
ее оси (перпендикулярной Oz).

В
аксонометрической
проекции точку А,
находящуюся на поверхности шара, строят
по трем координатам: X_А,
Y_А
и Z_А.
Эти координаты последовательно
откладывают по направлениям, параллельным
изометрическим осям. В рассматриваемом
примере от точки О
по оси х отложена
координата X_А;
из конца ее параллельно оси у проведена
прямая, на которой отложена координата
Y_А;
из конца отрезка, параллельно оси z
проведена прямая, на которой отложена
координата Z_А.
В результате построений получим искомую
точку А.

Тор– тело (рисунок 143), образованное вращением
окружности или ее дуги вокруг оси,
расположенной в одной с ней плоскости
но не проходящей через центр окружности
или ее дуги.

а
б

Рисунок
143

Если
ось вращения не пересекает образующую
окружность, то тор называют кольцом
(открытый тор) (рисунок 143, а). Если же ось
вращения пересекает образующую
окружность, то получается торовая
поверхность бочкообразном формы
(закрытый тор или пересекающийся тор)
(рисунок 143, б). В последнем случае
образующей торовой поверхности является
дуга ABC окружности.

Наибольшую
из окружностей, которые описывают точки
образующей торовой поверхности, называют
экватором, а наименьшую
— горлом, или
горловиной.

Построение
проекций тора

Круговое
кольцо (или открытый тор) имеет
горизонтальную проекцию в виде двух
концентрических окружностей, разность
радиусов которых равна толщине кольца
или диаметру образующей окружности
(рисунок 145). Фронтальная проекция
ограничивается справа и слева дугами
полуокружностей диаметра образующей
окружности.

На
рисунке 144, а и б приведены два вида
закрытого тора. В первом случае образующая
дуга окружности радиуса R
отстоит от оси вращения на расстоянии
меньше радиуса R,
а во втором случае — больше. В обоих
случаях фронтальные проекции тора
представляют собой действительный вид
двух образующих дуг окружности радиуса
R, расположенных
симметрично по отношению к фронтальной
проекции оси вращения. Профильными
проекциями тора будут окружности.

а
б

Рисунок
144

Построение
точек на поверхности тора

В
случае, когда точка А
лежит на поверхности кругового кольца
и дана одна ее проекция, для нахождения
второй проекции этой точки применяется
вспомогательная окружность, проходящая
через данную точку А
и расположенная на поверхности кольца
в плоскости, перпендикулярной оси кольца
(рисунок 145).

Если
задана фронтальная проекция A»
точки А, лежащей
на поверхности кольца, то для нахождения
ее второй проекции (в данном случае —
горизонтальной) через A»
проводят фронтальную проекцию
вспомогательной окружности — отрезок
горизонтальной прямой линии 2»2».
Затем строят горизонтальную проекцию
2’2′ этой окружности
и на ней, применяя линию связи, находят
точку A’.

Если
задана горизонтальная проекция B’
точки B,
расположенной на поверхности этого
кольца, то для нахождения фронтальной
проекции этой точки через 1′
проводят горизонтальную проекцию
вспомогательной окружности радиуса
R₁.
Затем через левую и правую точки 1′
и 1′
этой окружности проводят вертикальные
линии связи до пересечения с фронтальными
проекциями очерковой образующей
окружности радиуса R
и получают точки 1»
и 1». Эти точки
соединяют горизонтальной прямой, которая
представляет собой фронтальную проекцию
вспомогательной окружности (она будет
видима). Проводя вертикальную линию
связи из точки B’
до пересечения с прямой 1»1»
получаем искомую точку B».

Такие
же приемы построения применимы и для
точек, находящихся на поверхности тора.

Рисунок
145

Построение
аксонометрического изображения
тора можно разделит на три этапа (рисунок
146). Сначала строится в виде эллипса
проекция радиальной осевой линии
(траектория движения центра образующей
окружности). Затем определяем радиус
сферы, касающейся тора по образующей
(окружности). Для этого строим в виде
меньшего эллипса проекцию фронтальной
очерковой образующей тора. Радиус сферы
определим как длину отрезка О₁F
от центра эллипса до точки на этом
эллипсе, лежащей на большой оси эллипса
(перпендикулярной Oy).
Далее строим большое количество
окружностей радиусом R_сферы
с центрами на проекции радиальной осевой
тора О_1

… О_n
(чем больше, тем точнее контур будущего
тора). В завершение проводим линию
контура тора как линию, касающуюся
каждой окружности сферы.

а
б

Рисунок
146

В
аксонометрической проекции
точку А, находящуюся
на поверхности тора, строят по трем
координатам: X_А,
Y_А
и Z_А.
Эти координаты последовательно
откладывают по направлениям, параллельным
изометрическим осям.

Источник