Данные задания направлены на изучение информации, представленной в графическом виде, после изучения которой, учащийся должен произвести определенные расчеты.
Выполнять необходимые записи при выполнении задания можно прямо в контрольно-измерительном материале. В бланк записываются только ответы.
Блок заданий 15МО1 (первый вариант)
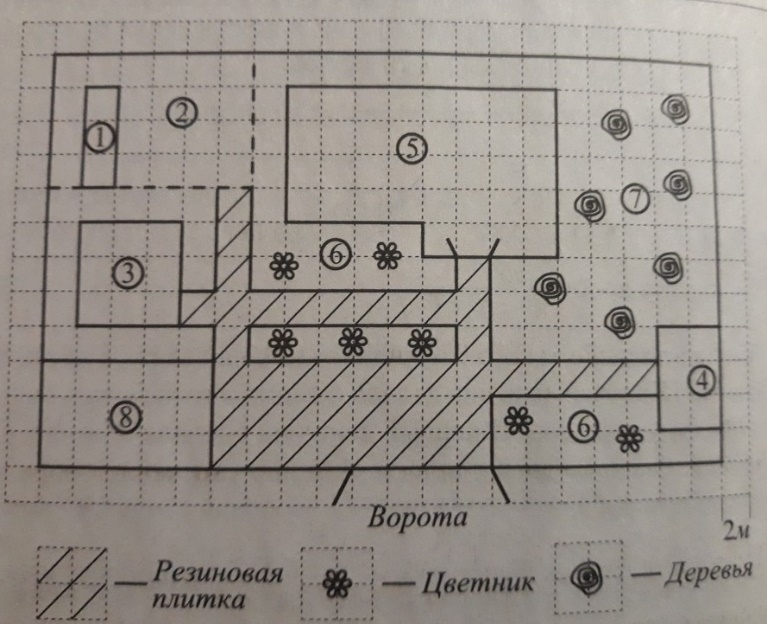
Графическая информация (план-схема) и описание к ней.
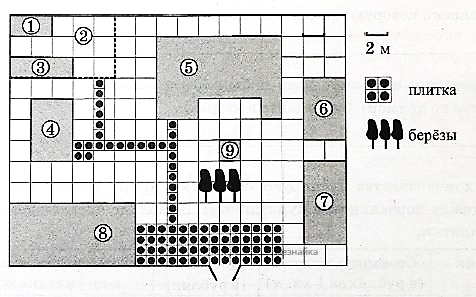
На плане изображен загородный дачный участок садоводства «Товарищество», Улица Виноградная, 45. (Сторона каждой клетки на плане равна 2м) Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота. При въезде на участок слева от ворот находится гараж, а справа – баня, отмеченная цифрой 4.
Площадь, занятая гаражом, равна 60 кв.м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеются квадратный бассейн, расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Справа от жилого дома имеются посадки фруктовых деревьев: яблоневых, вишневых, абрикосовых, грушевых.
Перед жилым домом и рядом с баней разбиты клумбы с цветами. Перед домом растут розы, а рядом с баней – гладиолусы. Перед гаражом имеется площадка, вымощенная резиновой плиткой размером 2м˟2м. Все дорожки внутри участка имеют ширину 2м и вымощены такой же плиткой.
К домохозяйству подведены электричество и вода. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
| Объекты | Жилой дом | Бассейн | Гараж | Теплица |
| Цифры |
Для того, чтобы правильно определить номера объектов, необходимо при чтении информации выделять (почеркивать) их как в тексте, так и сразу же подписывать в план-схеме. Ниже показана часть текста, в которой подчеркнуты основные моменты.
При въезде на участок слева от ворот находится гараж, а справа – баня, отмеченная цифрой 4.
Площадь, занятая гаражом, равна 60 кв.м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеются квадратный бассейн, расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Справа от жилого дома имеются посадки фруктовых деревьев: яблоневых, вишневых, абрикосовых, грушевых. Перед жилым домом и рядом с баней разбиты клумбы с цветами. Перед домом растут розы, а рядом с баней – гладиолусы.
Все эти объекты подписываем на схеме. Таким образом, получаем:
- Теплица
- Огород
- Бассейн
- Баня
- Дом
- Клумба с гладиолусами
- Деревья
- Гараж
Теперь расставляем номера необходимых объектов в таблицу:
| Объекты | Жилой дом | Бассейн | Гараж | Теплица |
| Цифры | 5 | 3 | 8 | 1 |
В бланк записываем ответ: 5381
Задание №2
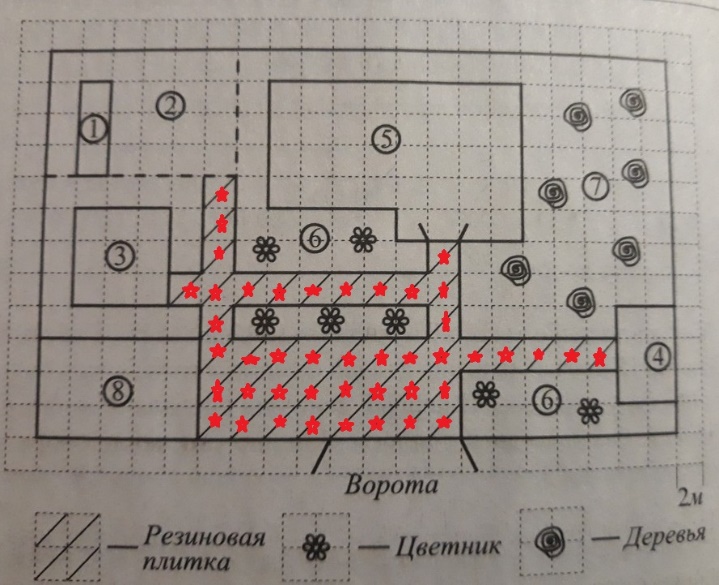
Резиновая плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?
Решение: для того, чтобы узнать, какое количество упаковок нужно купить, надо посчитать количество резиновых плиток на схеме. Под схемой показано, как она обозначена. Это количество небольшое, поэтому просто считаем клеточки на схеме. Отметим их красной звездочкой.
В данном случае их 44. Зная, что в 1 упаковке их 4 штуки, разделим 44 на 4 и получим 11 упаковок. Значит, наш ответ 11. Записываем его в бланк.
Задание №3
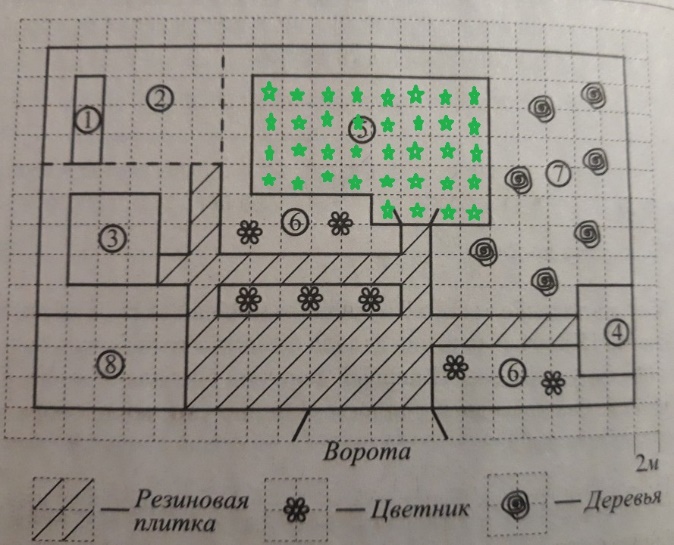
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Решение: дом – это объект под номером 5. Для нахождения площади нам необходимо знать сторону каждой клетки на плане. Это указано в первом абзаце текста. Подчеркнем это место.
На плане изображен загородный дачный участок садоводства «Товарищество», Улица Виноградная, 45. (Сторона каждой клетки на плане равна 2м)
Если сторона одной клетки 2 метра, то ее площадь 2*2=4 квадратных метра. Считаем количество клеток в доме и умножаем его на 4.
Количество клеток равно 36 (отмечены зелеными звездочками). Умножаем 36 на 4, получаем 144. Значит 144 квадратных метра – площадь дома. Записываем ответ 144 в бланк.
Задание №4
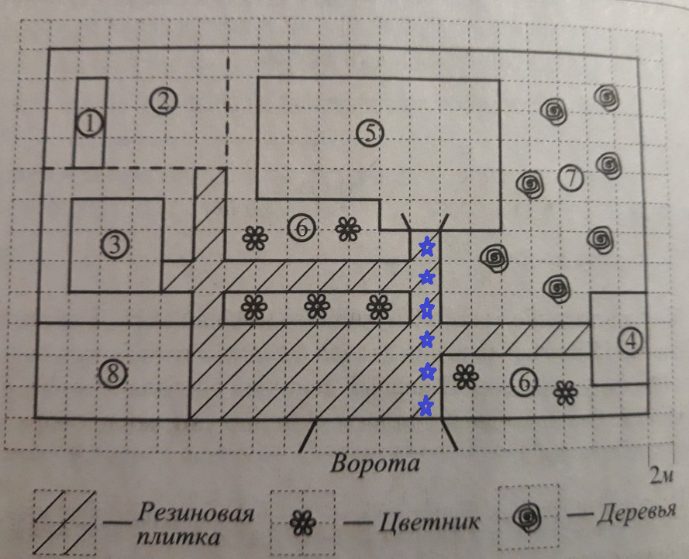
Найдите наименьшее расстояние (в метрах) от жилого дома до входных ворот.
Решение: наименьшее расстояние – это всегда прямо от одного объекта до другого. Считаем количество клеток от объекта 5 до ворот, их 6 (выделены синими звездами).
Помним, что сторона клетки по условию – 2 метра, значит, 6 умножаем на 2 и получаем 12 метров. В бланк записываем число 12.
Задание №5
Хозяин планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: газовое или электрическое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимость даны в таблице.
| Нагреватель (котел) | Прочее оборудование и монтаж | Средний расход газа/средняя потребляемая мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 25 тыс. руб | 20 000 руб. | 1,4 куб. м/ч | 4,5 руб./куб.м |
| Электр. отопление | 22 тыс. руб | 16 520 руб. | 5,5 кВт | 3,6 руб./(кВт.ч) |
Обдумав оба варианта, хозяин решал установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Решение: для решения этого задания необходимы данные только из таблицы. Рассматриваем сначала стоимость каждого оборудования в отдельности:
25 000 + 20 000 = 45 000 рублей – стоит оборудование для газового отопления
22 000 + 16520 = 38 520 рублей – стоит оборудование для электрического отопления
Теперь находим разницу в стоимости, так как в вопросе конкретно указано, что это надо найти: компенсирует разность в стоимости установки газового и электрического отопления.
45000 – 38520 = 6480 рублей разница в стоимости установки
Дальше высчитываем стоимость потребления газа и электричества по указанным в таблице данным:
1,4 умножаем на 4,5 и получаем 6,3 рубля — стоимость потребления газа в час
5,5 умножаем на 3,6 и получаем 19,8 рублей – стоимость потребления электроэнергии в час
Теперь также находим разницу в стоимости между ними, то есть сколько сэкономит хозяин при установке газового оборудования: 19.8 – 6,3= 13,5 рублей.
Чтобы ответить на главный вопрос задания — Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Нужно разницу в стоимости установки разделить на разницу в стоимости потребления:
6480:13,5=480 часов.
Записываем в ответ число 480.
Блок заданий 15МО2 (второй вариант)
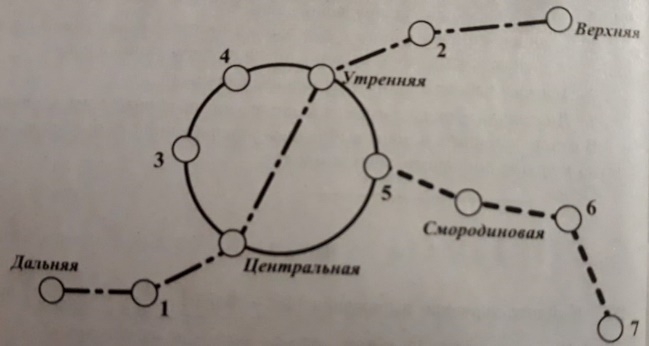
На рисунке изображена схема метро в городе N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Веселая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная. Всего в метрополитене города N есть три станции, от которых тоннель ведет только в одну сторону – это станции Дальняя, Верхняя и Звездная. Максим живет недалеко от станции Надежда.
Задание №1
Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры |
Решение: для того, чтобы правильно определить номера станций, необходимо при чтении информации выделять (подчеркивать) их как в тексте, так и сразу же подписывать на рисунке. Ниже показана часть текста, в которой подчеркнуты основные моменты, а также расстановка станций, которая выполняется сразу по ходу чтения текста.
Станция Ветреная расположена между станциями Центральная и Дальняя (значит, это номер 1). Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя (сразу видно, что двигаться надо от Центральной к Утренней, значит, Быстрая будет под номером 5), Птичья и Веселая (соответственно 4 и 3, так как двигаемся по кольцу). Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная (видим эту ветку справа нижнюю, соответственно Хоккейная – номер 6, а Звездная – 7). Максим живет недалеко от станции Надежда (она под номером 2, так как осталась одна не указанная).
Теперь расставляем номера необходимых объектов в таблицу:
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры | 6 | 2 | 4 | 1 |
В бланк записываем ответ: 6241
Задание №2
Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяженностью 8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 500 метров. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Решение: для того, чтобы узнать, сколько дней был закрыт проезд, нужно узнать, сколько рабочих дней они прокладывали рельсы. По условию длина участка 8 км, переводим ее в метры, так как в 1 день меняли по 500 метров. Получаем 8000 метров. Теперь делим 8000 метров на 500 метров, получаем 16 рабочих дней трудилась бригада. Нам надо узнать, сколько дней всего был закрыт проезд, так как в выходные работ не было, а проезд был закрыт. По условию работы начались с понедельника, значит бригада работала 3 полных недели и 1 понедельник на четвертой неделе (16 дней делим на 5 рабочих в неделю, получается 3 недели и 1 остается – понедельник). После каждой недели у нас два дня выходных: 2 после первой, 2 после второй, 2 после третьей. Таким образом, 6 выходных был закрыт проезд. Значит, 16 рабочих и 6 выходных, это 22 полных дня был закрыт проезд.
Записываем ответ 22 в бланк.
Задание №3
Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в квадратных километрах), если длина кольцевой ветки равна 32 км. В ответе укажите S*.
Решение: так как известна длина кольцевой ветки, то это значит, что мы имеем длину окружности (по условию – кольцевая ветка – это окружность). Длина окружности вычисляется по формуле 2πR. Значит, 2πR=32. Делим обе части на 2, получаем πR=16. Находим радиус, для этого надо 16 разделить на число π. То есть R=16/π. Формула площади круга S=πR2. Подставляем в нее вместо радиуса 16/π. Получаем, что S=π(16/π) 2. Возводим в квадрат, получаем S=π(256/π2). Теперь сокращаем числитель и знаменательна число π. Получается, что S=256/π . Поскольку в задании есть указание, что в ответ надо записать S* , то умножая эти величины в нашей формуле S=256/π, получаем, что S*= 256. Записываем ответ 256 в бланк.
Задание №4
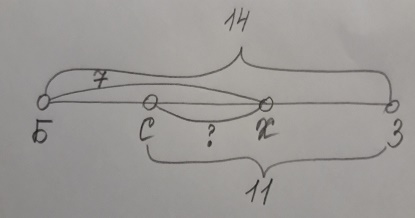
Найдите расстояние (по железной дороге) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 14 км, расстояние от Звездной до Смородиновой 11 км, а от Быстрой до Хоккейной – 7 км. Все расстояния даны по железной дороге.
Решение: итак, Радужная ветка – это станции Быстрая, Смородиновая, Хоккейная и Звездная. Можно для удобства сделать чертеж и обозначить на нем станции первыми буквами их названий и расставить длины. Получится вот такой рисунок, по которому можно легко определить расстояние от Смородиновой (С) до Хоккейной (Х).
Для этого из длины отрезка СЗ=11 нужно вычесть длину отрезка БХ=7, получим длину СХ=4. В бланк записываем число 4.
Задание №5
Школьник Максим в среднем за месяц совершает 45 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Максим уедет из города к бабушке в деревню и неиспользованные карточки обнулятся. Во сколько рублей обойдется самый дешевый вариант?
| Количество поездок | Стоимость одной поездки(в рублях) | Дополнительные условия |
| 1 | 40 | Школьникам скидка 20% |
| 10 | 37 | Школьникам скидка 10% |
| 30 | 35 | Школьникам скидка 10% |
| 50 | 32 | Нет |
| Безлимит | — | Любое число поездок в течение месяца за 2000 рублей |
Решение: для решения этого задания необходимы данные только из таблицы. Итак, нужно совершить 45 поездок за наименьшую стоимость. Значит, два последних варианта не подходят, так как 50 поездок – это много, деньги на карте обнулятся, а по Безлимиту в среднем приблизительно выйдет одна поездка 44 рубля (2000 : 45 поездок), скидки здесь не предусмотрены. Следовательно, будем составлять наборы из первых трех вариантов, а затем выбирать самый дешевый.
Для удобства надо посчитать каждый из трех вариантов, как карточку для школьника, т.е. с указанной скидкой. Затем посчитать стоимость каждой карточки полностью. Вспомним, чтобы найти количество процентов от данного числа, надо число разделить на 100 и умножить на количество процентов. Запишем это решение в таблице.
| Количество поездок | Стоимость одной поездки(в рублях) | Стоимость одной поездки для школьника(в рублях) | Стоимость 1 карточки для школьника(в рублях) |
| 1 | 40 | 40-40:100*20=32 | 1*32=32 |
| 10 | 37 | 37-37:100*10=33,3 | 10*33,3=333 |
| 30 | 35 | 35-35:100*10=31,5 | 30*35=945 |
- Допустим, что можно купить из первого варианта 45 карточек по 32 руб. Тогда получим, что 32*45=1440 руб.
- Допустим, что можно купить на 45 поездок: одну третью (на 30 поездок), 1 вторую (на 10 поездок) и пять первых (на пять поездок). Рассчитаем стоимость.
Одна третья карточка на 30 поездок – это 945 рублей.
Одна вторая карточка на 10 поездок – это 333 рубля.
Пять первых карточек: 32*5=160 рублей.
Теперь складываем стоимость всех карточек. 945+333+160=1438 рублей. Это уже меньше, чем в решении 1.
- Допустим, что можно купить 1 третью карточку (на 30 поездок) и 15 первых, так как это тоже 45 поездок. Одна третья карточка на 30 поездок – это 945 рублей. 15 первых будут стоить 15*32=480 рублей. Складываем стоимости 945 и 480, получаем 1425 рублей.
- Допустим, что можно еще купить 4 вторых (на 40 поездок) и 5 первых карточек. Тогда 4*333=1332 руб; 5*32=160 руб. Вместе это составит 1332+160=1492 рубля.
Записываем в ответ число 1425, так как это самый дешевый вариант из всех.
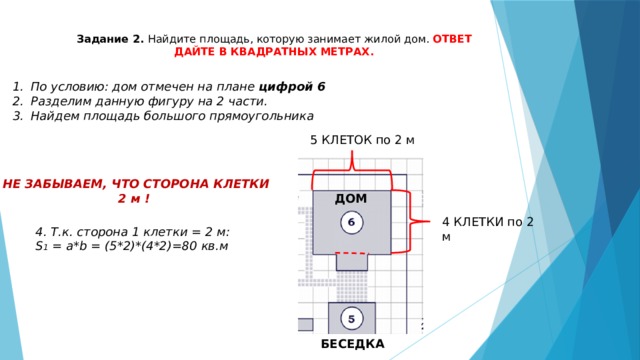
Задание 2. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
1. ВОЗВРАЩАЕМСЯ К УСЛОВИЮ:
Задание 2. Найдите площадь, которую занимает жилой дом. ОТВЕТ ДАЙТЕ В КВАДРАТНЫХ МЕТРАХ.
- По условию: дом отмечен на плане цифрой 6
- Разделим данную фигуру на 2 части.
- Найдем площадь большого прямоугольника
5 КЛЕТОК по 2 м
НЕ ЗАБЫВАЕМ, ЧТО СТОРОНА КЛЕТКИ 2 м !
ДОМ
4 КЛЕТКИ по 2 м
4. Т.к. сторона 1 клетки = 2 м:
S 1 = a*b = (5*2)*(4*2)=80 кв.м
БЕСЕДКА
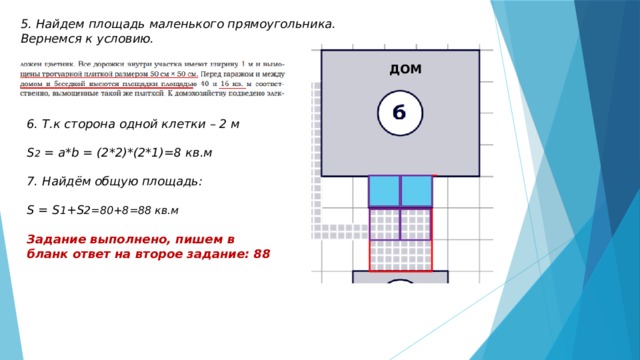
5. Найдем площадь маленького прямоугольника. Вернемся к условию.
ДОМ
6. Т.к сторона одной клетки – 2 м
S 2 = a*b = (2*2)*(2*1)=8 кв.м
7. Найдём общую площадь:
S = S 1 +S 2=80+8=88 кв.м
Задание выполнено, пишем в бланк ответ на второе задание: 88
ПОПРОБУЙТЕ САМОСТОЯТЕЛЬНО
ВЫПОЛНИТЬ АНАЛОГИЧНОЕ ЗАДАНИЕ
Задание 2. Найдите площадь, которую занимает цветник. Ответ дайте в квадратных метрах.
Для начала распишем, под какой цифрой какие здания зашифрованы.
В условии указано, что гараж обозначен цифрой 7, а огород — 2. На территории огорода есть теплица 1.
Справа находится баня, она обозначена цифрой 6.
В глубине территории находится дом. У него самая большая площадь. Он зашифрован под цифрой 3.
Сарай — 4.
Яблоневые посадки обозначены 5.
Получается правильный ответ на первый вопрос — 3461.
Площадь жилого дома можно определить несколькими способами.
Сторона одной клетки равна 2 метра.
Ширина дома 5 клеток или 2*5=10 метров.
Длина — 3*2=6 метров.
Габариты пристройки — 1х2 или 2х4 метра.
Получается площадь жилого дома
10*6+2*4=68 квадратных метров.
Чтобы поставить газовый нагнетатель, необходимо
24000 + 18280 = 42280 рублей.
Час обогрева будет стоять
1,2*5,6 = 6,72 руб/ч.
Чтобы поставить электронагреватель, необходимо
20000 + 15000 = 35000 рублей.
За час электронагреватель потребляет
5,6*3,8 = 21,28 руб/ч.
Разница в стоимости монтажа
42280-35000 = 7280 рублей.
Разница в потреблении ресурсов
21,28 — 6,72 = 14,56.
Посчитаем экономию
7280/14,56 = 500 часов.
Задание № 26353
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Показать ответ
Комментарий:
Одна клеточка на плане занимает 2х2=4м2
Дом занимает 4х6-3=21 клеточку
Его площадь: 21х4=84м2
Ответ: 84
Улучши свой результат с курсами ЕГЭ/ОГЭ/ВПР на egevpare.ru
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Предложи свой вариант решения в комментариях 👇🏻
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Прочитайте внимательно текст и выполните задание.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | сарай | баня | теплица |
|---|---|---|---|---|
| Цифры |
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
2
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
3
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
4
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котел) |
Прочее оборудование и монтаж |
Сред. расход газа / сред. потребл. мощность |
Стоимость газа / электро-энергии |
|
|---|---|---|---|---|
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
Исходя из рисунка и условия задачи, под цифрой 1 зашифрован гараж (слева от входа на участок).
Под цифрой 2 зашифрована баня.
Внутри дома находятся: кухня, гостиная, спальня, детская комната, подсобные помещения.
В центре дома находится гостиная — 3.
Подсобные помещение — 7.
Кухня зашифрована под цифрой 4.
В ответе на первое задание необходимо указать последовательность цифр: 3214.
___________________________
Площадь дома.
Из условия известно, что сторона каждой клетки на плане равна 1 метру. Посчитаем количество клеток, которые укладываются в ширине и длине дома. Перемножим их.
Площадь дома равна = 8 * 15 = 120 м2.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
Жилой дом — номер 3 — находится по правую руку, если зайти на участок через ворота.
Гараж — номер 7 — слева от ворот, а за ним сарай под цифрой 6.
Баня — номер 5 — к ней ведет вымощенная плиткой дорожка.
Теплица — номер 1 — расположена на территории огорода, который идет под номером 2.
Ответ: 3571.
2. Тротуарная плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Каждый квадратик на дорожке имеет размер 1х1 м и равен одной плитке. Чтобы посчитать количество плиток, большого ума не надо — их 68.
В каждой упаковке лежит 4 плитки, значит 68 : 4 = 17 упаковок потребовалось для выкладки дорожек и площадки.
Ответ: 17.
3. Найдите площадь дома. Ответ дайте в квадратных метрах.
Дом можно условна разделить на 2 прямоугольника.
Измерим стороны большого: длины сторон имеют длину 4 и 5 клеточек, но не забываем, то одна клеточка — это 2 метра. Значит, стороны большого прямоугольника равна 8 м и 10 м, а его площадь равна 8 · 10 = 80 м2.
Теперь измерим стороны маленького прямоугольника: 1 клетка и 2 клетки соответствуют 2 м и 4 м. Площадь этого прямоугольника равна 2 · 4 = 8 м2.
Найдем площадь всего дома.
80 + 8 = 88 м2.
Ответ: 88.
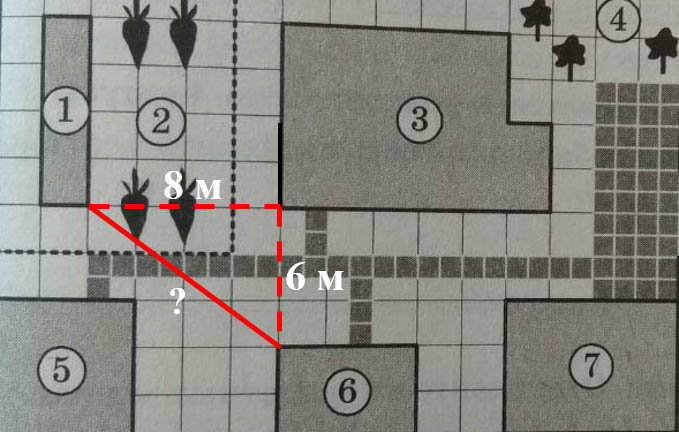
4. Найдите расстояние от сарая до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Кратчайшим расстоянием между теплицей и сараем будет красный сплошной отрезок. Достроим его до прямоугольного треугольника.
По теореме Пифагора найдем это расстояние. Для этого складывает квадраты катетов и извлекаем из результата корень.
s2 = 82 + 62 = 64 + 36 = 100;
s = 10.
Ответ: 10.
5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице. Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости установки газового и электрического оборудования?
Чтобы установить газовое отопление нужно потратить 21 000 + 15 536 = 36 536 рублей.
Для установки электрического отопления надо потратить 18 000 + 14 000 = 32 000 рублей.
Разница между стоимостью установки равна 36 536 — 32 000 = 4 536 рублей.
Ориентируясь на средний расход, посчитаем, сколько стоит час обогрева газом и электричеством.
Газ: 4,8 · 1,5 = 7,2 руб./ч
Электричество: 4,2 · 4,8 = 20,16 руб./ч
Посчитаем, за сколько рублей в час хозяин сэкономит, установив газовое оборудование: 20,16 — 7,2 = 12,96 руб./ч.
Осталось посчитать через сколько часов ЭКОНОМИЯ компенсирует РАЗНОСТЬ, т.е. 4 536 : 12,96 = 350 часов.
Ответ: 350.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.