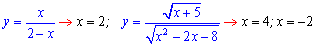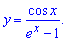Содержание:
- Критические точки и экстремумы функции
- Теорема Ферма (Необходимое условие существовании экстремумов)
- Достаточное условие существования экстремума
- Задача пример №117
- Задача пример №118
- Задача пример №119
- Задача пример №120
- Задача пример №121
Критические точки и экстремумы функции
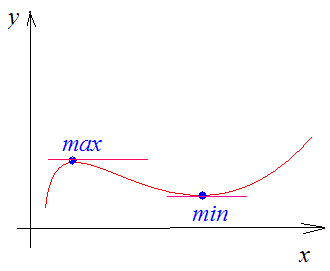
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 
равных 
угловой коэффициент касательной к графику равен 0. Т.e. 
. Эти точки являются критическими точками функции.
2. В точках 
функция не имеет производной. Эти тоже критические точки функции.
3. Для рассматриваемой нами функции критические точки 
делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки 
— критические точки, которые не изменяют возрастание и убывание (или наоборот).
По графику видно, что в точках внутреннего экстремума 
производная функции равна нулю, а в точке 
производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 
производная функции 
равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 
непрерывна на промежутке 
и 
. Если 
является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
1 ) 
слева от точки положительна, а справа — отрицательна, то точка является точкой максимума.
2) слева от отрицательна, а справа — положительна, то точка является точкой минимума
3) с каждой стороны от точки имеет одинаковые знаки, то точка не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 
на отрезке 
записываются как 
и 
.
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Задача пример №117
Для функции 
определите максимумы и минимумы и схематично изобразите график.
Решение:
Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции: 
2. Критические точки функции: 
3. Точки 
и 
разбивают область определения функции на три промежутка.
Проверим знак 
на интервалах, выбрав пробные точки:
для интервала 
для интервала 
для интервала 
Интервал 
Пробные точки 
Знак 
Возрастание и убывание 
При 
имеем 
. (-1;3) — максимум
При 
имеем 
(1;-1) — минимум
4. Используя полученные для функции 
данные и найдя координаты нескольких дополнительных точек, построим график функции.
Задача пример №118
Найдите наибольшее и наименьшее значение функции 
на отрезке [-1;2].
Решение:
Сначала найдем критические точки. Так как 
, то критические точки можно найти из уравнения 
. Критическая точка 
не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке 
и на концах отрезка.
Из этих значений наименьшее — 4, наибольшее 12. Таким образом: 
Задача пример №119
Найдите экстремумы функции 
.
Решение:
1. Производная функции: 
2. Критические точки: 
, 
3. Интервалы, на которые критические точки делят область определения функции: 
Проверим знак 
на интервалах, выбрав пробные точки.
Для промежутка 
возьмем 
Для промежутка (0; 1,5) возьмем 
Для промежутка 
возьмем 
Интервал 
Пробные точки 
Знак 
Возрастание-убывание 
Используя полученную для функции 
информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами 
и 
касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
• Функция 
на промежутке 
возрастает.
• Точка 
критическая точка функции , но не является экстремумом.
• Функция на промежутке [0; 1,5] возрастает.
• Функция на промежутке 
убывает.
• 
Задача пример №120
Найдите экстремумы функции 
Решение:
1. Производная 
2. Критические точки: для этого надо решить уравнение 
или найти точки, в которых производная не существует. В точке 
функция не имеет конечной производной. Однако точка 
принадлежит области определения. Значит, точка 
является критической точкой функции.
3. Промежутки, на которые критическая точка делит область определения функции: 
и 
Определим знак 
, выбрав пробные точки для каждого промежутка:
Для 
возьмем 
Для 
возьмем 
Интервал 
Пробные точки 
Знак 
Возрастание-убывание 
• Функция на промежутке 
убывает.
• Функция на промежутке 
возрастает.
• 
Задача пример №121
По графику функции производной схематично изобразите график самой функции.
Решение:
Производная в точке равна нулю, а при 
отрицательна, значит, на интервале 
функция убывающая. При 
производная положительна, а это говорит о том, что функция на промежутке 
возрастает. Точкой перехода от возрастания к убыванию функции является точка 
. Соответствующий график представлен на рисунке.
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Экстремумы функции двух переменных. Производная по направлению
- Доказательство неравенств
- Системы уравнений
- Максимальные и минимальные значения функции
- Действия с корнями
- Отрицательное биномиальное распределение
- Длина дуги кривой
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма
Критические точки – это точки в которых производная функции равна нулю или не существует. Если производная равна 0 то функция в этой точке принимает локальный минимум или максимум. На графике в таких точках функция имеет горизонтальную асимптоту, то есть касательная параллельна оси Ох.
Такие точки называют стационарными. Если видите на графике непрерывной функции «горб» или «яму» помните, что максимум или минимум достигается в критической точке. Рассмотрим для примера следующее задание.
Пример 1. Найти критические точки функции y=2x^3-3x^2+5 .
Решение. Алгоритм нахождения критических точек следующий:
Итак функция имеет две критические точки.
Далее, если нужно провести исследование функции то определяем знак производной слева и справа от критической точки. Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция принимает локальный минимум. Если с «+» на «-» должны локальный максимум.
Второй тип критических точек это нули знаменателя дробных и иррациональных функций
Функции с логарифмами и тригонометрические, которые не определены в этих точках
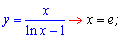
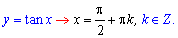
Третий тип критических точек имеют кусочно-непрерывные функции и модули.
Например любая модуль-функция имеет минимум или максимум в точке излома.
Например модуль y = | x -5 | в точке x = 5 имеет минимум (критическую точку).
Производная в ней не существует, а справа и слева принимает значение 1 и -1 соответственно.
Попробуйте определить критические точки функций
1) 
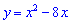
2) 
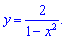
3) 
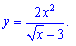
4) 
5) 
Если в ответе у Вы получите значение
1) x=4;
2) x=-1;x=1;
3) x=9;
4) x=Pi*k;
5) x=1.
то Вы уже знаете как найти критические точки и сможете справиться с простой контрольной или тестами.
Как определить критические точки
Критические точки являются одним из важнейших аспектов исследования функции с помощью производной и имеют широкую область применения. Они используются в дифференциальном и вариационном исчислениях, играют большую роль в физике и механике.
Инструкция
Понятие критической точки функции тесно связано с понятием ее производной в этой точке. А именно, точка называется критической, если производная функции в ней не существует или равна нулю. Критические точки являются внутренними точками области определения функцию.
Чтобы определить критические точки данной функции, необходимо выполнить несколько действий: найти область определения функции, вычислить ее производную, найти область определения производной функции, найти точки обращения производной в ноль, доказать принадлежность найденных точек области определения исходной функции.
Пример 1Определите критические точки функции y = (x — 3)²·(x-2).
РешениеНайдите область определения функции, в данном случае ограничений нет: x ∈ (-∞; +∞);Вычислите производную y’. По правилам дифференцирования произведения двух функций имеется: y’ = ((x — 3)²)’·(x — 2) + (x — 3)²·(x — 2)’ = 2·(x — 3)·(x — 2) + (x — 3)²·1. После раскрытия скобок получается квадратное уравнение: y’ = 3·x² – 16·x + 21.
Найдите область определения производной функции: x ∈ (-∞; +∞).Решите уравнение 3·x² – 16·x + 21 = 0 для того, чтобы найти, при каких x производная обращается в ноль: 3·x² – 16·x + 21 = 0.
D = 256 – 252 = 4×1 = (16 + 2)/6 = 3; x2 = (16 — 2)/6 = 7/3.Итак, производная обращается в ноль при значениях x, равных 3 и 7/3.
Определите, принадлежат ли найденные точки области определения исходной функции. Поскольку x (-∞; +∞), то обе эти точки являются критическими.
Пример 2Определите критические точки функции y = x² – 2/x.
РешениеОбласть определения функции: x ∈ (-∞; 0) ∪ (0; +∞), поскольку x стоит в знаменателе.Вычислите производную y’ = 2·x + 2/x².
Область определения производной функции та же, что у исходной: x ∈ (-∞; 0) ∪ (0; +∞).Решите уравнение 2·x + 2/x² = 0:2·x = -2/x² → x = -1.
Итак, производная обращается в ноль при x = -1. Выполнено необходимое, но недостаточное условие критичности. Поскольку x=-1 попадает в интервал (-∞; 0) ∪ (0; +∞), то эта точка являются критической.
Источники:
- Критический объем реализации , штПорог
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Что такое экстремум функции и каково необходимое условие экстремума?
Экстремумом функции называется максимум и минимум функции.
Необходимое условие максимума и минимума (экстремума) функции следующее: если функция f(x) имеет экстремум в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.
Это условие необходимое, но не достаточное. Производная в точке х = а может обращаться в нуль, в бесконечность или не существовать без того, чтобы функция имела экстремум в этой точке.
Каково достаточное условие экстремума функции (максимума или минимума)?
Первое условие:
Если в достаточной близости от точки х = а производная f?(x) положительна слева от а и отрицательна справа от а, то в самой точке х = а функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна.
Если в достаточной близости от точки х = а производная f?(x) отрицательна слева от а и положительна справа от а, то в самой точке х = а функция f(x) имеет минимум при условии, что функция f(x) здесь непрерывна.
Вместо этого можно воспользоваться вторым достаточным условием экстремума функции:
Пусть в точке х = а первая производная f?(x) обращается в нуль; если при этом вторая производная f??(а) отрицательна, то функция f(x) имеет в точке x = a максимум, если положительна – то минимум.
О случае f??(а) = 0 можно прочитать в Справочнике по высшей математике М.Я. Выгодского.
Что такое критическая точка функции и как её найти?
Это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f?(x) и, приравняв её к нулю, решить уравнение f?(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной: нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.
Для примера найдём экстремум параболы.
Функция y(x) = 3x2 + 2x – 50.
Производная функции: y?(x) = 6x + 2
Решаем уравнение: y?(x) = 0
6х + 2 = 0, 6х = -2, х=-2/6 = -1/3
В данном случае критическая точка – это х0=-1/3. Именно при этом значении аргумента функция имеет экстремум. Чтобы его найти, подставляем в выражение для функции вместо «х» найдённое число:
y0 = 3*(-1/3)2 + 2*(-1/3) – 50 = 3*1/9 – 2/3 – 50 = 1/3 – 2/3 – 50 = -1/3 – 50 = -50,333.
Как определить максимум и минимум функции, т.е. её наибольшее и наименьшее значения?
Если знак производной при переходе через критическую точку х0 меняется с «плюса» на «минус», то х0 есть точка максимума; если же знак производной меняется с минуса на плюс, то х0 есть точка минимума; если знак не меняется, то в точке х0 ни максимума, ни минимума нет.
Для рассмотренного примера:
Берём произвольное значение аргумента слева от критической точки: х = -1
При х = -1 значение производной будет у?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (т.е. знак – «минус»).
Теперь берём произвольное значение аргумента справа от критической точки: х = 1
При х = 1 значение производной будет у(1) = 6*1 + 2 = 6 + 2 = 8 (т.е. знак – «плюс»).
Как видим, производная при переходе через критическую точку поменяла знак с минуса на плюс. Значит, при критическом значении х0 мы имеем точку минимума.
Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала. Те критические точки, которые находятся за пределом интервала, нужно исключить из рассмотрения. Если внутри интервала находится только одна критическая точка – в ней будет либо максимум, либо минимум. В этом случае для определения наибольшего и наименьшего значений функции учитываем также значения функции на концах интервала.
Например, найдём наибольшее и наименьшее значения функции
y(x) = 3sin(x) — 0,5х
на интервалах:
а) [-9; 9]
б) [-6; -3]
Итак, производная функции —
y?(x) = 3cos(x) — 0,5
Решаем уравнение 3cos(x) — 0,5 = 0
3cos(x) = 0,5
cos(x) = 0,5/3 = 0,16667
х = ±arccos(0,16667) + 2πk.
Находим критические точки на интервале [-9; 9]:
х = arccos(0,16667) — 2π*2 = -11,163 (не входит в интервал)
х = —arccos(0,16667) — 2π*1 = -7,687
х = arccos(0,16667) — 2π*1 = -4,88
х = —arccos(0,16667) + 2π*0 = -1,403
х = arccos(0,16667) + 2π*0 = 1,403
х = —arccos(0,16667) + 2π*1 = 4,88
х = arccos(0,16667) + 2π*1 = 7,687
х = —arccos(0,16667) + 2π*2 = 11,163 (не входит в интервал)
Находим значения функции при критических значениях аргумента:
y(-7,687) = 3cos(-7,687) — 0,5 = 0,885
y(-4,88) = 3cos(-4,88) — 0,5 = 5,398
y(-1,403) = 3cos(-1,403) — 0,5 = -2,256
y(1,403) = 3cos(1,403) — 0,5 = 2,256
y(4,88) = 3cos(4,88) — 0,5 = -5,398
y(7,687) = 3cos(7,687) — 0,5 = -0,885
Видно, что на интервале [-9; 9] наибольшее значение функция имеет при x = -4,88:
x = -4,88, у = 5,398,
а наименьшее – при х = 4,88:
x = 4,88, у = -5,398.
На интервале [-6; -3] мы имеем только одну критическую точку: х = -4,88. Значение функции при х = -4,88 равно у = 5,398.
Находим значение функции на концах интервала:
y(-6) = 3cos(-6) — 0,5 = 3,838
y(-3) = 3cos(-3) — 0,5 = 1,077
На интервале [-6; -3] имеем наибольшее значение функции
у = 5,398 при x = -4,88
наименьшее значение —
у = 1,077 при x = -3
Как найти точки перегиба графика функции и определить стороны выпуклости и вогнутости?
Чтобы найти все точки перегиба линии y = f(x), надо найти вторую производную, приравнять её к нулю (решить уравнение) и испытать все те значения х, для которых вторая производная равна нулю, бесконечна или не существует. Если при переходе через одно из этих значений вторая производная меняет знак, то график функции имеет в этой точке перегиб. Если же не меняет, то перегиба нет.
Корни уравнения f ? (x) = 0, а также возможные точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом их интервалов определяется знаком второй производной. Если вторая производная в точке на исследуемом интервале положительна, то линия y = f(x) обращена здесь вогнутостью кверху, а если отрицательна – то книзу.
Как найти экстремумы функции двух переменных?
Чтобы найти экстремумы функции f(x,y), дифференцируемой в области её задания, нужно:
1) найти критические точки, а для этого — решить систему уравнений
fх? (x,y) = 0, fу? (x,y) = 0
2) для каждой критической точки Р0(a;b) исследовать, остается ли неизменным знак разности
f(x,y) – f(a,b)
для всех точек (х;у), достаточно близких к Р0. Если разность сохраняет положительный знак, то в точке Р0 имеем минимум, если отрицательный – то максимум. Если разность не сохраняет знака, то в точке Р0 экстремума нет.
Аналогично определяют экстремумы функции при большем числе аргументов.
Источники:
- Выгодский М.Я. Справочник по высшей математике
- Черненко В.Д. Высшая математика в примерах и задачах. В 3-х томах. Том 1.
найти экстремумы функции
f(x)=x2x−1
.
Производная этой функции —
f′(x)=xx−2(x−1)2
, значит, критические точки функции — это (x=0) и (x=2). Точка (x=1) не принадлежит области определения функции.
Они делят реальную числовую прямую на четыре интервала:
−∞;0∪0;1∪1;2∪2;+∞
. Знак первого интервала положительный (например,
f′
((-1)=0.75)). Второго — отрицательный, третьего — отрицательный, четвёртого — положительный.
|
−∞;0 |
0;1 |
1;2 |
2;+∞ |
|
(+) |
(-) |
(-) |
(+) |
Значит, производная меняет знак только в точках (x=0) и (x=2).
В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).
В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).