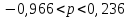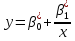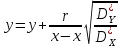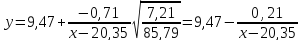Доверительный интервал для математического ожидания нормальной случайной
величины при неизвестной дисперсии
Пусть
, причем
и
неизвестны. Необходимо построить доверительный интервал,
накрывающий с надежностью
истинное значение параметра
.
Для этого из генеральной
совокупности СВ
извлекается
выборка объема
:
.
1) В качестве точечной
оценки математического ожидания
используется
выборочное среднее
, а в
качестве оценки дисперсии
–
исправленная выборочная дисперсия
которой соответствует стандартное отклонение
.
2) Для нахождения
доверительного интервала строится статистика
имеющая в этом случае распределение Стьюдента с
числом степеней свободы
независимо
от значений параметров
и
.
3) Задается требуемый
уровень значимости
.
4) Применяется следующая
формула расчета вероятности:
где
–
критическая точка распределения Стьюдента, которая находится по таблице критических точек распределения Стьюдента (односторонняя критическая область).
Тогда:
Это означает, что
интервал:
накрывает неизвестный
параметр
с
надежностью
Доверительный интервал для математического ожидания
нормальной случайной величины при известной дисперсии
Пусть количественный
признак
генеральной
совокупности имеет нормальное распределение
с
заданной дисперсией
и
неизвестным математическим ожиданием
. Построим
доверительный интервал для
.
1) Пусть для оценки
извлечена
выборка
объема
. Тогда
2) Составим случайную
величину:
Нетрудно показать, что случайная величина
имеет стандартизированное нормальное распределение, то есть:
3) Зададим уровень
значимости
.
4) Применяя формулу нахождения
вероятности отклонения нормальной величины от математического ожидания, имеем:
Это означает, что
доверительный интервал
накрывает неизвестный
параметр
с надежностью
. Точность оценки определяется величиной:
Число
определяется
по таблице значений функции Лапласа из равенства
Окончательно получаем:
Доверительный интервал для
дисперсии нормальной случайной величины при неизвестном математическом ожидании
Пусть
, причем
и
–
неизвестны. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется
исправленная выборочная дисперсия
:
которой соответствует стандартное отклонение
.
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
4) Тогда, используя таблицу критических точек хи-квадрат распределения, нетрудно указать критические
точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
дисперсии нормальной случайной величины при известном математическом ожидании
Пусть
, причем
–
известна, а
–
неизвестна. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется выборочная дисперсия:
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
4) Тогда, используя таблицу критических точек хи-квадрат распределения,
нетрудно указать критические точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
среднего квадратического отклонения
Извлекая квадратный корень:
Положив:
Получим следующий
доверительный интервал для среднего квадратического
отклонения:
Для отыскания
по заданным
и
пользуются специальными таблицами.
Для проверки на нормальность заданного распределения случайной величины можно использовать
правило трех сигм.
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.
Построить
доверительные интервалы для среднего и дисперсии с надежностью
Указание:
воспользоваться таблицами Стьюдента и хи-квадрат.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычисление средней и дисперсии
Вычислим среднее и
исправленную дисперсию
:
Нахождение доверительных интервалов для средней и дисперсии
Найдем доверительный интервал для оценки
неизвестного среднего. Он считается по формуле:
По таблице критических точек t-критерия Стьюдента, для уровня значимости
(односторонняя критическая область):
Искомый
доверительный интервал для среднего:
Найдем доверительный интервал для оценки дисперсии.
Он считается по формуле:
Для уровня значимости
и
получаем по таблице значений хи-квадрат:
Искомый доверительный интервал для дисперсии:
Ответ
Кроме этой задачи на другой странице сайта есть
пример расчета доверительного интервала математического ожидания и среднего квадратического отклонения для интервального вариационного ряда
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Для помощи во время экзамена/зачета в онлайн режиме необходимо договариваться заранее.
Преподаватель который помогает студентам и школьникам в учёбе.
Доверительный интервал для дисперсии — определение и вычисление с примерами решения
Доверительный интервал для дисперсии:
Пусть случайная величина X имеет нормальный закон распределения
В этих условиях, согласно теореме Фишера, величина 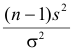
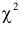
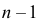
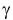
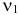
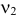
Тогда
Величины 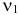
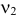
где 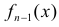
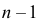
Решения этих уравнений находят с помощью таблиц (см. прил., табл. П4).
Для 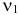
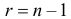
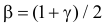
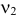
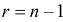
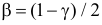
Если 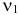
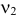
или
Это и есть доверительный интервал для дисперсии, соответствующий уровню надежности 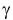
Пример:
Даны результаты наблюдений случайной величины, имеющей нормальный закон распределения с неизвестными параметрами: 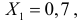
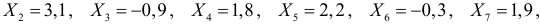
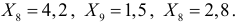
Решение. Оценим сначала математическое ожидание:
По формуле (3.1.3) оценим дисперсию
Обратимся к таблице распределения «хи-квадрат» (см. прил., табл. П4).
Для величины 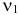
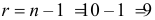
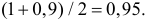
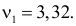
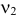
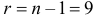
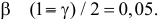
В итоге с вероятностью 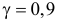
Для среднего квадратического отклонения имеем с той же надежностью 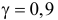
Ответ.
- Проверка статистических гипотез
- Регрессионный анализ
- Корреляционный анализ
- Статистические решающие функции
- Точечные оценки, свойства оценок
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
Доверительный интервал для дисперсии
Найдем
доверительный интервал для дисперсии
при условии, что среднее значение
величины неизвестно, а доверительная
вероятность равна 1 – α.
Для
расчета доверительного интервала
применим формулу:


выборочная дисперсия
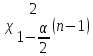
распределения
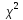
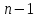
-
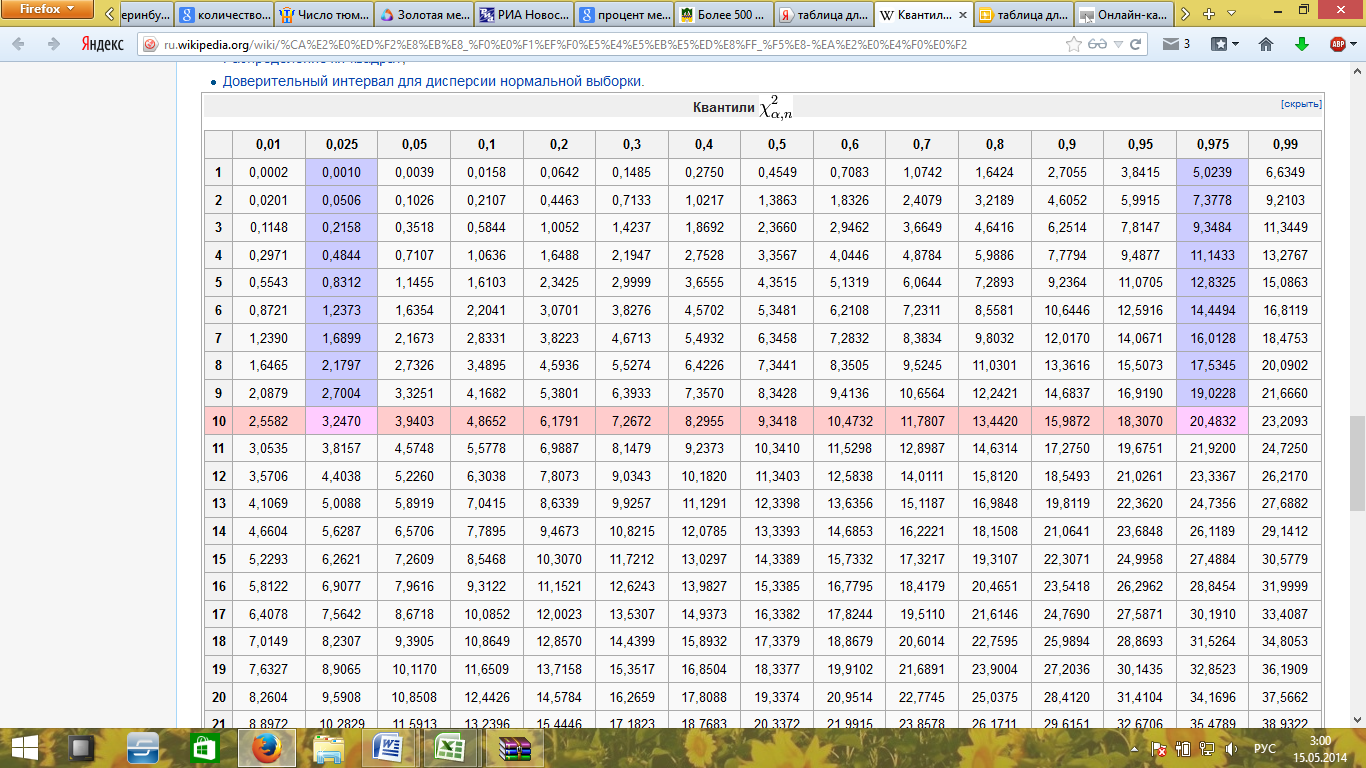
Определим
квантиль распределения
,
для этого воспользуемся специальной
таблицей:
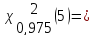
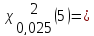
-
Подставим
найденные значения в формулу из пункта
1):
Для
Х:
Для
У:
Доверительный интервал для корреляции
Найдем
доверительный интервал для корреляции
при условии, что выборка получена из
генеральной совокупности, r
– выборочный коэффициент корреляции.
Для
расчета доверительного интервала
применим формулу:
-
Рассчитаем
:
-
возьмем
из таблицы квантилей нормального
распределения:
-
Подставим
все в формулы:
-
Найдем
с помощью таблицы гиперболических
тангенсов:
-
Проверка гипотез
Таким
образом было установлено, что между
заработной платой преподавателей
средних школ и количеством
выпускников-медалистов существует
связь. Искомая
корреляция равна -0.7132. Это
высокая степень взаимосвязи – значения
коэффициента корреляции находится в
пределах от 0,7 до 0,99. Нам удалось выявить
зависимость, но результаты оказались
крайне неожиданными. Чем выше средняя
заработная плата по субъекту РФ, тем
меньше медалистов в этом субъекте.
Почему получились такие результаты,
нам остается только гадать. Да и не было
нашей целью объяснять почему именно
так. Мы должны были, ради личного интереса,
посмотреть есть ли связь.
-
Регрессия
Любая
нелинейная регрессия, в которой уравнение
регрессии для изменений в одной переменной
(у) как функции t изменений в другой (х)
является квадратичным, кубическим или
уравнение более высокого порядка. Хотя
математически всегда возможно получить
уравнение регрессии, которое будет
соответствовать каждой «загогулине»
кривой, большинство этих пертурбаций
возникает в результате ошибок в
составлении выборки или измерении, и
такое «совершенное» соответствие
ничего не дает. Не всегда легко определить,
соответствует ли криволинейная регрессия
набору данных, хотя существуют
статистические тесты для определения
того, значительно ли увеличивает каждая
более высокая степень уравнения степ
совпадения этого набора данных.
Теперь,
будем считать, что выборочная криволинейная
регрессия определяется уравнением:
Коэффициенты
называются выборочными коэффициентами
регрессии.
Из
ранее изученных пунктов, нам известны
следующие параметры:
х
= 20,35
у
= 9,47
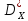
85,79

7,21

-0.71
Теперь
мы можем подставить все значения в
уравнение:
В
итоге имеем:
Вывод
Итак,
в ходе исследований и расчетов,
проделанных в данной работе, мы увидели,
что есть обратная зависимость между
заработной платой преподавателей
средней школы и количеством выпускников
–медалистов. Я не берусь объяснять
причины данного факта, их крайне много
и они довольно субъективны. Мы выяснили,
что такая зависимость довольно сильная.
Соседние файлы в папке МДЗ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Для начала напомним следующее определение:
Пусть нам дано исправленное среднее квадратическое отклонение $S$. Оценим неизвестное генеральное среднее квадратическое отклонение, то есть найдем доверительный интервал, который покрывает величину $sigma $.
Для этого нам необходимо, чтобы выполнялось равенство
неравенство
Отметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
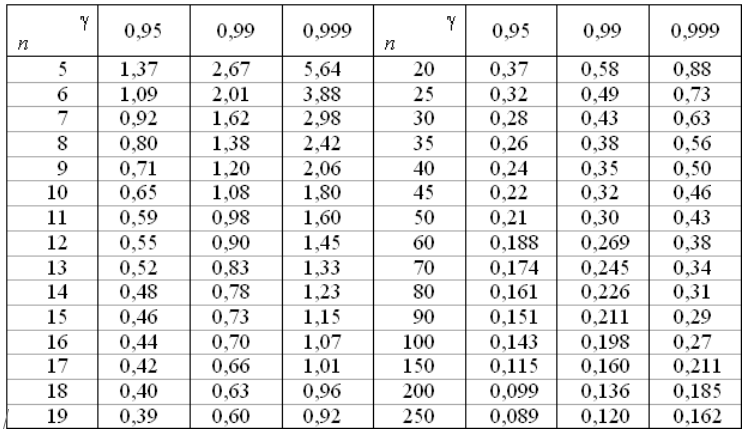
Величина $q$ имеет табличные значения:
Рисунок 1. Таблица значений величины $q$.
Доверительный интеграл для оценки дисперсии
С понятием среднего квадратического отклонения тесно связано понятие дисперсии.
Пусть нам дано исправленная дисперсия. Оценим неизвестное генеральную дисперсию, то есть найдем доверительный интервал, который покрывает величину $D$.
Так как среднее квадратическое отклонение равно квадратному корню от дисперсии, то исправленная дисперсия равна квадрату исправленного среднего квадратического отклонения $S^2.$
Таким образом, получим, что доверительный интервал имеет вид:
Отметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
Пример задач на нахождение доверительного интервала
Пример 1
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,4$. Пусть объем выборки $n=60$, а надежности равна $gamma =0,95$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=60$ и $gamma =0,95$, то получим, что $q=0,188$.
Видим, что $q
[left(Sleft(1-qright),Sleft(1+qright)right)] [left(0,4cdot 0,812;0,4cdot 1,188right)=(0,3248;0,4752)]
Ответ: $(0,3248;0,4752)$.
«Доверительные интервалы для оценки среднего квадратического отклонения» 👇
Пример 2
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,9$. Пусть объем выборки $n=10$, а надежности равна $gamma =0,999$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=10$ и $gamma =0,999$, то получим, что $q=1,8$.
Видим, что $q
[left(0;Sleft(1+qright)right)] [left(0;0,9cdot 2,8right)=(0;;2,52)]
Ответ: $(0;2,52)$.
Пример 3
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,3$. Пусть объем выборки $n=30$, а надежности равна $gamma =0,99$. Найти доверительный интервал для дисперсии данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=30$ и $gamma =0,99$, то получим, что $q=0,43$.
Видим, что $q
[left(S^2left(1-qright),S^2left(1+qright)right)] [left(0,09cdot 0,57;0,09cdot 1,43right)=(0,0513;0,1287)]
Ответ: $(0,0513;0,1287)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Построим доверительный интервал для оценки дисперсии случайной величины, распределенной по нормальному закону, в
MS
EXCEL
.
Построение
доверительного интервала
для оценки
среднего
приведено в статье
Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
. Процедура построения
доверительного интервала
для оценки
дисперсии
имеет много общего с процедурой для оценки
среднего
, поэтому в этой статье она изложена менее подробно, чем в указанной статье.
Формулировка задачи.
Предположим, что из
генеральной совокупности
имеющей
нормальное распределение
с неизвестным
средним значением
μ и неизвестной
дисперсией
σ
2
взята
выборка
размера n. Необходимо на основании этой
выборки
оценить
дисперсию распределения
и построить
доверительный интервал
.
Примечание
: Построение
доверительного интервала для оценки среднего
относительно нечувствительно к отклонению
генеральной совокупности
от
нормального закона
. А вот при построении
доверительного интервала для оценки
дисперсии
требование
нормальности
является строгим.
СОВЕТ
: Для построения
Доверительного интервала
нам потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
доверительный интервал для оценки среднего
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
нормальное распределение
и
распределение ХИ-квадрат
.
В качестве
точечной оценкой дисперсии распределения,
из которого взята
выборка
, используют
Дисперсию выборки
s
2
.
Также, перед
процедурой проверки гипотезы
, исследователь устанавливает требуемый
уровень значимости
– это допустимая для данной задачи
ошибка первого рода
, т.е. вероятность отклонить
нулевую гипотезу
, когда она верна (
уровень значимости
обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01)
В статье про
ХИ2-распределение
показано, что
выборочное распределение статистики
y=(n-1)
s
2
/σ
2
, имеет
ХИ2-распределение
с n-1 степенью свободы.
Воспользуемся этим свойством и построим
двухсторонний доверительный интервал
для оценки
дисперсии
:
где χ
2
α/2,n-1
–
верхний α/2-квантиль
распределения ХИ-квадрат с
n
-1 степенью свободы (
такое значение случайной величины
χ
2
n-1
,
что
P
(
χ
2
n-1
>=
χ
2
α/2,n-1
)=α/2)
. Чтобы найти этот
квантиль
в MS EXCEL используйте формулу
=ХИ2.ОБР.ПХ(α; n-1)
.
χ
2
1-α/2,n-1
– верхний 1-α/2-квантиль
, который равен
нижнему α/2-
квантилю.
Чтобы найти этот
квантиль
в MS EXCEL используйте формулу
=ХИ2.ОБР(α; n-1)
.
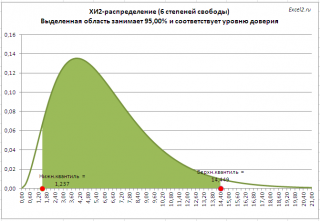
Примечание
: В
файле примера на листе Квантили
показан расчет
квантилей
для
распределения ХИ2
. На рисунке выделена область соответствующая уровню доверия 95%, которая ограничена верхним и нижним
квантилем
. Обратите внимание, что в отличие от
нормального
и
t-распределения
распределение
ХИ2
несимметрично, поэтому для двустороннего
доверительного интервала
потребуется вычислить два
квантиля
, значения которых будут отличаться.
Примечание
:
Доверительный интервал
для
стандартного отклонения
может быть получен путем извлечения квадратного корня из вышеуказанного выражения.
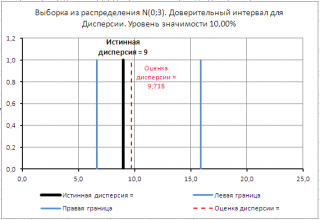
В
файле примера на листе 2х сторонний
создана форма для расчета и построения двухстороннего
доверительного интервала
.
Для построения
односторонних доверительных интервалов
используйте нижеследующие выражения:
Задача
В следующей задаче найдем
верхний односторонний доверительный интервал
для
дисперсии
.
Автоматический аппарат заполняет емкости с растворителем. Предполагается, что объемы налитой жидкости в емкостях распределены по
нормальному закону
. Если разброс значений объемов будет слишком велик, то значительная часть емкостей будет существенно переполнена или не заполнена. Для оценки
дисперсии
в качестве выборки взято 20 наполненных жидкостью емкостей. На основе выборки была вычислена
дисперсия выборки
s
2
, которая составила 0,0153 (литров
2
). Принято решение оценить верхний уровень
дисперсии
с
уровнем доверия
95%.
Для решения задачи воспользуемся выражением
Сначала найдем
верхний (1-α)-квантиль
(или равный ему
нижний α-квантиль
)
ХИ2-распределения
с n-1
степенью свободы
при у
ровне значимости
α равном 1-0,95=0,05. Это можно сделать в MS EXCEL по формулам:
=ХИ2.ОБР.ПХ(1-0,05; 20-1)
или
=ХИ2.ОБР(0,05; 20-1)
В результате получим
верхний доверительный интервал для дисперсии:
σ
2
<=0,0287
Или тоже, но словами и для
стандартного отклонения:
«Значения
выборки
показывают, что с вероятностью 95%,
стандартное отклонение
процесса наполнения емкости растворителем меньше или равно 0,17 литров».
Ход решения приведен в
файле примера на листе 1 сторонний
.
СОВЕТ
: О построении других
доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.


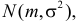
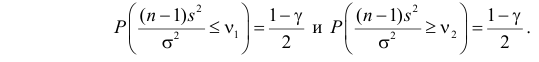
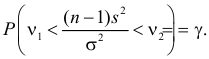
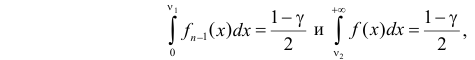
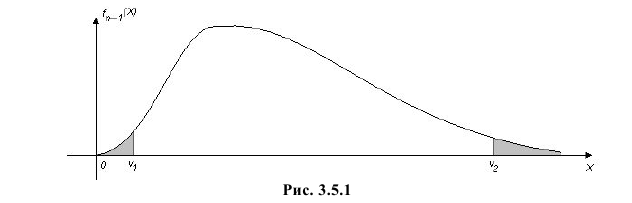
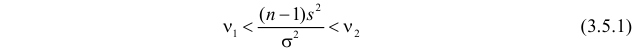
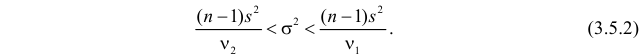
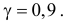
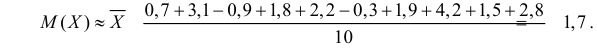
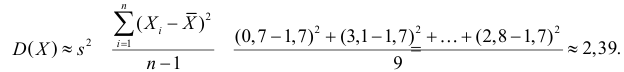
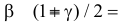
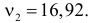
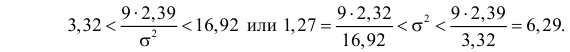
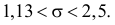

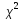 ,
,

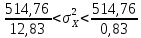
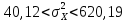
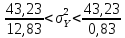
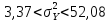
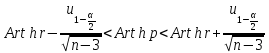
 :
: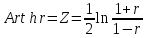
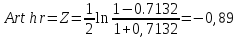
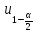 возьмем
возьмем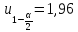
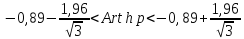
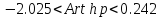
 с помощью таблицы гиперболических
с помощью таблицы гиперболических