Памятка «Площадь и периметр квадрата и прямоугольника»
Скачать:
Предварительный просмотр:
|
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
Предварительный просмотр:
|
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
Предварительный просмотр:
|
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
Площадь прямоугольника S=a*b где S – площадь, а – длина, b – ширина Отсюда: а = S : b b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2 Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4 |
По теме: методические разработки, презентации и конспекты
Задачи «Периметр квадрата и прямоугольника»
Данный материал позволяет учащимся закрепить и твёрдо усвоить тему «Периметр квадрата и прямоугольника». Тренажёр можно использовать для проведения проверочных работ по данной те…
- Мне нравится
Только факты
сайт о самом интересном вокруг нас
- Главная
- Интересные факты
- Полезные советы
- Документы
Главная » Образцы документов » Начальная школа
Памятка «Формулы площади, периметра для прямоугольника и квадрата»
02.12.2021
2247
242
Памятка в помощь ученикам начальной школы для вычисления площади и периметра для прямоугольника и квадрата. Лист с формулами и чертежами нужно распечатать и дать ребёнку.
Скачать документ
Похожие статьи:

Карточки по математике «Площадь. Единицы площади» для 3 класса
Всего 14 карточек по этой теме. Они позволят проверить полученные знания на вычисление площадей прямоугольника, используя разные единицы площади.

Итоговый тест по математике, 3 класс
Итоговый тест по математике проводится в 3 классе в конце учебного года с целью проверки знаний.

Карточки по математике «Таблица умножения и деления на 9» для 3 класса
Карточки с разными примерами на знание таблицы умножения на 9.

Карточки по математике «Таблица умножения и деления на 8» для 3 класса
Восемь карточек на проверку знания таблицы умножения и деление на число 8.

Карточки по математике «Таблица умножения и деления на 7» для 3 класса
Карточки с примерами на умножение и деление чисел на 7 для учеников 3 класса позволят проверить как ученики знают таблицу умножения.

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a — сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d — диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r — радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R — радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P — периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Конфигурация
Название фигуры
Формула
Правило
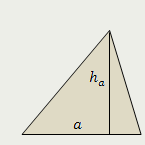
Треугольник
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне
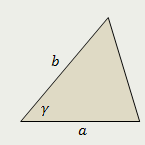
Треугольник
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
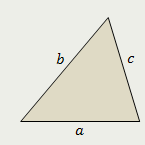
Треугольник
Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон
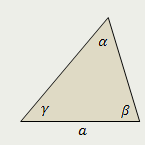
Треугольник
Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла
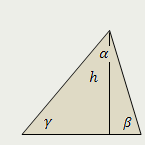
Треугольник
Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов
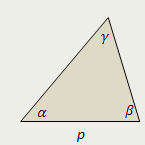
Треугольник
Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника
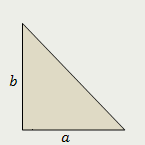
Прямоугольный треугольник
Площадь прямоугольного треугольника равна половине произведения его катетов
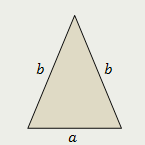
Равнобедренный треугольник
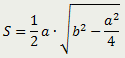
Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания
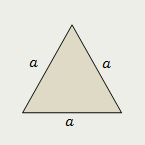
Равносторонний треугольник
Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх
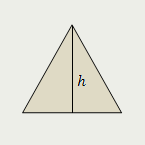
Равносторонний треугольник
Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх
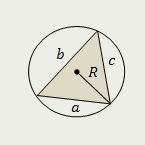
Треугольник
Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности
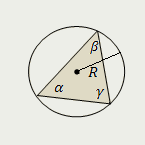
Треугольник
Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов
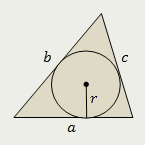
Треугольник
Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник)
Треугольник
Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника
Прямоугольник
Площадь прямоугольника равна произведению двух соседних его сторон
Квадрат
Площадь квадрата равна квадрату его стороны
Квадрат
Площадь квадрата равна половине квадрата его диагонали
Параллелограмм
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне
Параллелограмм
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними
Ромб
Площадь ромба равна произведению квадрата его стороны на синус одного из его углов
Ромб (дельтоид)
Площадь ромба (как и дельтоида) равна половине произведения его диагоналей
Трапеция
Площадь трапеции равна произведению полусуммы её оснований на высоту
Трапеция
Площадь трапеции равна произведению её средней линии на высоту
Выпуклый четырёхугольник
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними
Вписанный четырёхугольник
Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон
Круг
Площадь круга равна произведению числа «пи» на квадрат радиуса
Круг
Площадь круга равна четверти произведения числа «пи» на квадрат диаметра
Круговой сектор
формулы для случаев градусной и радианной мер центральных углов
Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору
Круговое кольцо
Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов
Круговое кольцо
Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров
Круговое кольцо
Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины
Загрузить PDF
Загрузить PDF
Вычислить площадь квадрата очень просто, если вам известна длина стороны, периметр или длина диагонали. Вот, как это можно сделать.
-
1
Запишите длину стороны. Предположим, у вас есть квадрат с длиной стороны 3 см. Запишите это значение.
-
2
Возведите длину стороны в квадрат. Это все, что от вас требуется. Если длина сторон квадрата равна 3 см, то для вычисления площади квадрата нужно просто возвести ее в квадрат: 3 см x 3 см = 9 см2.
-
3
Не забудьте записать ответ в квадратных единицах.
- Возвести сторону в квадрат — это то же самое, что умножить высоту на ширину, так как у квадрата высота и ширина равны.
Реклама
-
1
Измерьте или найдите в условиях длину диагонали квадрата.
-
2
Запомните, как рассчитывается площадь квадрата на основании длины диагонали. Длину диагонали нужно возвести в квадрат и затем разделить на 2: S = (диагональ^2)/2.
-
3
Возведите в квадрат длину диагонали. Предположим, у вас есть квадрат с диагональю 5 см. Возведите ее в квадрат: 5 см x 5 см = 25 см2.
-
4
Теперь разделите результат на 2. 25 см2/2 = 12,5 см2. Площадь нашего квадрата составляет 12,5 см2.
Реклама
-
1
Умножьте периметр на 1/4, чтобы узнать длину стороны. Это то же самое, что разделить его на 4. Поскольку у квадрата четыре стороны равной длины, длину стороны можно узнать, просто разделив периметр на 4. Предположим, вам дан квадрат с периметром 20 см. Умножьте 20 на 1/4: 20 см x 1/4 = 5 см. Теперь мы знаем, что длина стороны составляет 5 см.
-
2
Возведите длину стороны в квадрат. Теперь, когда мы знаем, что длина стороны равна пяти сантиметрам, ее можно возвести в квадрат и получить площадь: (5 см)2 = 25 см2.
Реклама
Об этой статье
Эту страницу просматривали 217 124 раза.

















