Параллельные прямые пересечены секущей как найти углы - Исправление недочетов и поиск решений вместе с Examum.ru

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы при параллельных прямых и секущей

Пусть прямая пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна $180^{circ}$ .

Углы 3 и 5 (а также 1 и 7, 2 и 8, 4 и 6) — накрест лежащие.

Накрест лежащие углы равны.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна $180^{circ}$ , то есть

$angle 1+angle 6=180^{circ}$ ,

$angle 4+angle 7=180^{circ}$ .

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и называются соответственными.

Соответственные углы равны, то есть

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач по геометрии, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть две параллельных прямые и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это – один из шагов, из которых и состоит решение.

В этой статье – полезные теоремы и примеры решения задач ЕГЭ и ОГЭ по теме «Углы при параллельных прямых и секущей».

Этот материал можно использовать для проектов по геометрии, в работе на уроке и самостоятельно.

Теорема 1.

Углы с соответственно параллельными сторонами равны, если они оба острые или тупые.

Доказательство:

Дано два острых угла: и Известно, что их стороны параллельны: и

Докажем, что

Пусть

Тогда как соответственные углы при параллельных прямых CA и NF и секущей CB.

как соответственные углы при параллельных прямых CB и NM и секущей NF.

Отсюда следует, что что и требовалось доказать.

Аналогично и для тупых углов.

Теорема 2.

Углы с соответственно параллельными сторонами в сумме составляют $180{}^circ ,$ если один из них острый, а другой тупой.

Доказательство:

Дано: – острый, а – тупой. Известно, что их стороны параллельны: и

Докажем, что сумма углов и равна $180{}^circ .$

Пусть Продолжим луч NM за точку N и получим прямую MK.

Получили два острых угла, и с параллельными сторонами. Согласно теореме 1, они равны, т. е.

$angle MNF+angle FNK=180{}^circ$ как смежные. Значит, $angle MNF+angle ACB=180{}^circ.$

Теорема доказана.

Теорема 3.

Если накрест лежащие углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей AB накрест лежащие углы равны:

Докажем, что Если углы 1 и 2 прямые, то прямые и перпендикулярны к прямой AB и, следовательно, параллельны.

Рассмотрим случай, когда углы 1 и 2 не прямые.

Из середины О отрезка АВ проведем перпендикуляр OH к прямой

На прямой от точки В отложим отрезок ${BH}_1$ равный отрезку AH

по двум сторонам и углу между ними, поэтому и Из равенства следует, что точка H_1 лежит на продолжении луча OH, т. е. точки H, O и H_1 лежат на одной прямой, а из равенства следует, что угол 6 – прямой (так как угол 5 – прямой). Итак, прямые и перпендикулярны к прямой HH_1, поэтому они параллельны. Теорема доказана.

Теорема 4.

Если соответственные углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей соответственные углы равны, например

Так как углы 2 и 3 – вертикальные, то Из этих двух равенств следует, что . Но углы 1 и 3 – накрест лежащие, поэтому прямые и параллельны. Теорема доказана.

Теорема 5.

Если сумма односторонних углов равна 180 градусов, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей сумма односторонних углов равна $180{}^circ ,$ например $angle 1+angle 4=180{}^circ.$

Так как углы 3 и 4 – смежные, то Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые и параллельны. Теорема доказана

И самое главное. Подборка примеров заданий ОГЭ и ЕГЭ по темам: углы при параллельных прямых и секущей, внешние накрест лежащие и внутренние накрест лежащие углы, односторонние углы.

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задача 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.

Решение:

Стороны BC и AD параллелограмма параллельны, АК – секущая. Углы и равны как накрест лежащие.

– равнобедренный треугольник.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

AB=BK=5.

$P_{ABCD}=left(AB+BCright)cdot 2;$

$P_{ABCD}=left(5+19right)cdot 2=48.$

Ответ: 48.

Задача 2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.

Найдите AB, если AF=24, BF=10.

Решение:

Основания трапеции АD и ВС параллельны, поэтому углы BAD и АВС – односторонние при параллельных прямых АD и ВС и секущей АВ. Сумма односторонних углов равна

Сумма углов, прилежащих к боковой стороне трапеции, равна $180{}^circ .$

Мы получили, что

AF — биссектриса угла А,

BF — биссектриса угла В, поэтому

$angle FAB=frac{1}{2}angle BAD;; angle ABF=frac{1}{2}angle ABC,$ тогда

Из треугольника AFB получим, что $AFB=90{}^circ .$

Мы доказали теорему:

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AFB – прямоугольный.

По теореме Пифагора, ${AB}^2={AF}^2+{BF}^2Rightarrow AB=sqrt{{24}^2+{10}^2}=sqrt{676}=26.$

Ответ: 26.

Задача 3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.

Решение:

Пусть М – середина АВ, N – середина ВС. Тогда MN – средняя линия треугольника АВС,

Значит, как односторонние углы при параллельных прямых и и секущей АВ.

по двум углам.

Отсюда $displaystyle frac{AB}{BM}=displaystyle frac{AC}{MN}Rightarrow BM=displaystyle frac{ABcdot MN}{AC}$ ;

$BM=displaystyle frac{28cdot 12}{16}=21.$

Ответ: 21.

Задача 4. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108 ${}^circ.$ Найдите угол B этой трапеции. Ответ дайте в градусах.

Решение:

ABCD – трапеция, – основания, AB – секущая.

Значит, angle A и angle B – внутренние односторонне углы.

Отсюда $angle B=180{}^circ -108{}^circ =72{}^circ.$

Ответ: 72.

Задача 5. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Сумма углов, прилежащих к боковой стороне параллелограмма, равна $180{}^circ .$

Это значит, что $angle BAD +angle ABC = 180{}^circ.$

AК — биссектриса угла А,

BК — биссектриса угла В, поэтому

$angle KAB=frac{1}{2}angle BAD; ; angle ABK=frac{1}{2}angle ABC,$ тогда

$angle KAB+angle ABK= 90{}^circ .$

Из треугольника AKB получим, что $angle ABK= 90{}^circ .$

Мы доказали теорему:

Биссектрисы углов параллелограмма, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AKB – прямоугольный.

Расстояние от точки K до стороны AB – это длина перпендикуляра, проведенного из точки на прямую АВ, т.е. KH=4.

по гипотенузе и острому углу

Аналогично, по гипотенузе и острому углу

Получили:

Тогда $S_{ABCD}=ADcdot MN$ ; $S_{ABCD}=8cdot 7=56.$

Ответ: 56.

Задача 6. На плоскости даны четыре прямые. Известно, что $angle 1=120{}^circ ,$ $angle 2=60{}^circ ,$ $angle 3=55{}^circ .$ Найдите Ответ дайте в градусах.

Решение:

angle 1 и angle 2 – это внутренние односторонние углы,

$angle 1+angle 2=120{}^circ +60{}^circ =180{}^circ.$

Отсюда следует, что прямые параллельны, т.е.

Рассмотрим углы при параллельных прямых и секущей d.

angle 3 и angle 4 – это односторонние углы, а значит, они равны: $angle 3=angle 4=55{}^circ.$

Ответ: 55.

Задача 7. Прямые m и n параллельны. Найдите если $angle 1=22{}^circ ,$ $angle 2=72{}^circ .$ Ответ дайте в градусах.

Решение:

$mparallel nRightarrow angle 1=angle 4=22{}^circ$ как односторонние углы.

Сумма углов треугольника равна $180{}^circ .$

Для треугольника на рисунке:

$angle 2+angle 3+angle 4=180{}^circ Rightarrow angle 3=180{}^circ -72{}^circ -22{}^circ =86{}^circ .$

Ответ: 86.

Задача 8. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30 ${}^circ$ и 45 ${}^circ.$ Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение:
$angle A=angle BAC+angle CAD=30{}^circ +45{}^circ =75{}^circ ,$

angle A и angle B – это внутренние односторонние углы при параллельных прямых.

и секущей АВ, их сумма равна $180{}^circ .$

Тогда $angle B=180{}^circ -angle A=180{}^circ -75{}^circ =105{}^circ .$

Это и есть наибольший угол параллелограмма.

Ответ: 105.

Задача 9. Найдите величину тупого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15 ${}^circ.$ Ответ дайте в градусах.

Решение:

AK – биссектриса угла А параллелограмма ABCD, $angle A=30{}^circ.$

angle A и angle B – внутренние односторонние углы при параллельных прямых.

и секущей АВ. Их сумма равна $180{}^circ ,$ значит, $angle B=180{}^circ -30{}^circ =150{}^circ.$

Ответ: 150.

Задача 10. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=169{}^circ .$ Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение: тогда – равнобедренный, в нем OC= CD. Значит, $angle COD=angle CDO=displaystyle frac{180{}^circ -169{}^circ }{2}=5,5{}^circ .$

Ответ: 5,5.

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Задача 1, ЕГЭ. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Пусть BM – биссектриса тупого угла B. По условию, отрезки MD и AB равны 3x и 4x соответственно.

Рассмотрим углы CBM и BMA. Поскольку AD и BC параллельны, BM – секущая, углы CBM и BMA являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник ABM – равнобедренный, следовательно, AB = AM = 4x.

Периметр параллелограмма – это сумма всех его сторон, то есть

7x+7x+4x+4x=88.

Отсюда x=4, 7x=28.

Ответ: 28.

Задача 2, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на рисунок. По условию, $alpha -beta =50{}^circ ,$ то есть $alpha =beta +50{}^circ .$

Углы alpha и beta – односторонние при параллельных прямых и секущей, следовательно,

$alpha +beta =180{}^circ ,$ по свойству односторонних углов.

Итак, $2beta +50{}^circ =180{}^circ.$

$beta =65{}^circ ,$ тогда $alpha =115{}^circ .$

Ответ: 115.

Задача 3, ЕГЭ. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение:

angle B и angle C – внутренние односторонние углы и при параллельных прямых

и и секущей BC; их сумма равна $180{}^circ .$

BE – биссектриса угла В, значит как накрест лежащие углы при и секущей BE. Тогда – равнобедренный,

Аналогично, CE – биссектриса угла С, значит как накрест лежащие углы при и секущей CE. Тогда – равнобедренный и

Значит

Ответ : 10.

Задача 4, ЕГЭ. В ромбе ABCD угол ABC равен 122 ${}^circ.$ Найдите угол ACD. Ответ дайте в градусах.

Решение:

angle B и angle C – это внутренние односторонние углы при параллельных прямых.

и секущей BC, их сумма равна $180{}^circ .$

Значит, $angle C=180{}^circ -angle B=180{}^circ -122{}^circ =58{}^circ .$

ABCD – ромб, диагонали ромба делят его углы пополам.

Тогда $angle ACD=58div 2=29{}^circ .$

Ответ: 29.

Задача 5, ЕГЭ. Угол между стороной и диагональю ромба равен $54{}^circ .$ Найдите острый угол ромба.

Решение:

Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба. Поэтому один из углов ромба равен градусов, и это тупой угол ромба. Тогда острый угол ромба равен $180{}^circ -108{}^circ =72{}^circ .$

Ответ: 72.

Задача 6, ЕГЭ. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 ${}^circ.$ Найдите площадь трапеции.

Решение:

Пусть $angle D=150{}^circ ; AB=18; DC=6; AD=7.$

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними при и секущей BC. Их сумма равна $180{}^circ .$

Тогда $angle A=30{}^circ .$ Построим высоту из вершины Получим прямоугольный треугольник с острым углом в 30 ${}^circ .$

Высота трапеции DH – это катет, лежащий напротив угла в $30{}^circ$ и равный половине гипотенузы, т. е.

Отсюда $S_{ABCD}=displaystyle frac{DC+AB}{2}cdot h;$ $S_{ABCD}=displaystyle frac{6+18}{2}cdot 3.5=12cdot 3.5=42.$

Ответ: 42.

Задача 7, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

У равнобедренной трапеции углы при основании равны т.е.

По условию, $angle D-angle B=50{}^circ Rightarrow angle C-angle B=50{}^circ ;$

angle C и прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых
и и секущей BC. Их сумма равна $180{}^circ .$

$angle C+angle B=180{}^circ.$

Получили:

$left{ begin{array}{c}angle C-angle B=50{}^circ \angle C+angle B=180{}^circ end{array}right. .$

Сложив два уравнения, получим: $2angle C=230{}^circ ,$ тогда $angle C=115{}^circ.$

Ответ: 115.

Задания ЕГЭ Базового уровня, геометрия. Свойства углов при параллельных прямых и секущей.

Задание 1. Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол $150{}^circ .$ Найдите площадь трапеции.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных основаниях трапеции и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол трапеции равен 30 ${}^circ .$ Построив высоту, мы увидим, что она лежит против прямого угла в прямоугольном треугольнике. Значит, высота равна половине боковой стороны, т.е. h=4.

Отсюда

Ответ: 60.

Задание 2. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен $135{}^circ .$ Найдите меньшую боковую сторону.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $45{}^circ .$

Вторая высота отсекает равнобедренный прямоугольный треугольник с катетом, равным разности оснований. Значит, высота равна: 7–4=3.

Отсюда

Ответ: 16,5.

Задание 3. В трапеции ABCD известно, что AB = CD, $angle BDA=40{}^circ$ и $angle BDC=30{}^circ .$ Найдите угол ABD. Ответ дайте в градусах.

Решение:

$angle D=angle BDA+angle BDC=40{}^circ +30{}^circ =70{}^circ .$ Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $110{}^circ .$

Нам дана трапеция, в которой AB=CD. Очевидно, что это боковые стороны, и трапеция равнобедренная с основаниями и .

и параллельны, BD секущая, тогда $angle ADB=angle DBC=40{}^circ .$

$angle ABD=angle ABC-angle DBC=110{}^circ -40{}^circ =70{}^circ.$

Ответ: 70.

Задание 4. В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке K. Найдите KC, если AB = 4, а периметр параллелограмма равен 20.

Решение:

ABCD – параллелограмм, тогда AB = DC = 4.

AK – биссектриса угла А, значит,

как накрест лежащие углы при параллельных прямых и и секущей AK.

Получили, что – равнобедренный и

$P_{ABCD}=left(AB+ADright)cdot 2=20,$ значит

Ответ: 2.

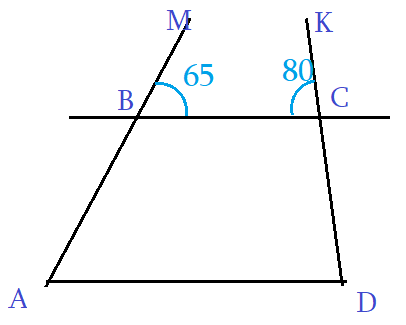
Задание 5. Прямые m и n параллельны (см. рисунок). Найдите если $angle 1=117{}^circ ,$ $angle 2=24{}^circ .$ Ответ дайте в градусах.

Решение:

$angle 2=angle 4=24{}^circ$ (как накрест лежащие углы).

$angle 1+angle 4+angle 3=180{}^circ$ (развернутый угол).

Тогда $angle 3=180{}^circ -left(angle 1+angle 4right)=180{}^circ -left(117{}^circ +24{}^circ right)=39{}^circ .$

Ответ: 39.

Задание 6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=104{}^circ .$ Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение:

Пусть диагонали пересекаются в точке О, т.е.

$AC=2ABRightarrow AB=displaystyle frac{1}{2}cdot ACRightarrow AB=AO=OC=CD.$

и параллельны, АС – секущая, $Rightarrow angle BAC=angle ACD=104{}^circ .$

– равнобедренный, отсюда угол между диагоналями равен:

$angle BOA=displaystyle frac{180{}^circ -104{}^circ }{2}=38{}^circ .$

Ответ: 38.

Если вам понравился наш материал на тему «Углы при параллельных прямых и секущей» — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Теоремы об углах, образованных двумя параллельными прямыми и секущей

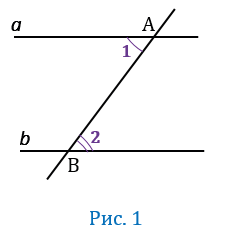
Теорема 1. Если две паралленльные прямые пересечены секущей, то накрест лежащие углы равны.

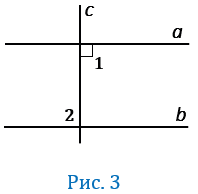
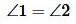
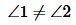
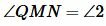
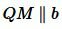
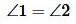
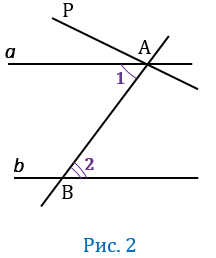
Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис. 1). Докажем,что . Предположим, что . Отложим от луча MN угол QMN, равной углу 2 так, чтобы углы QMN и 2 были накрест лежащие при пересечении прямых QM и b секущей MN. Поскольку , то . Получили, что через точку M проходят две прямые, параллельные прямой b, что противоречит аксиоме параллельных прямых (через точку не лежащую на данной прямой проходит только одна прямая, праллельная данной). Следовательно .

Следствие 1. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

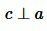
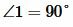
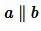
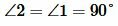
Доказательство. Пусть прямые a и b параллельны (Рис. 2) и пусть (т.е. ). Прямая a пересекает прямую b (поскольку ). Но углы 1 и 2 накрест лежащие, следовательно они равы. Т.е. . Следовательно прямые c и b перпендикулярны.

Теорема 2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Тогда по теореме 1 накрест лежащие углы равны: . Углы 2 и 3 вертикальные, т.е. . Из и имеем . То есть при пересечении параллельных прямых секущей соответственные углы равны.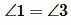

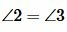
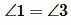
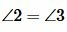
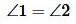
Теорема 3. Если две паралленльные прямые пересечены секущей, то сумма односторонних углов равна 180°.

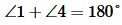
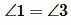
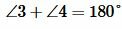
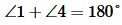
Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Покажем, что . Накрест лежащие углы равны: . Углы 3 и 4 смежные. Поэтому . Тогда .

Источник

Углы при пересечении двух прямых

Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.

При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.

На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).

Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:

Углы при пересечении параллельных прямых

Если секущая пересекает две параллельные прямые линии, то:

внутренние накрест лежащие углы равны;
сумма внутренних односторонних углов равна 180°;
соответственные углы равны;
внешние накрест лежащие углы равны;
сумма внешних односторонних углов равна 180°.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Геометрия. Урок 2. Углы

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Углы

Понятие угла

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .

Величину угла измеряют в градусах. ∠ A O B = 24 ° .

Виды углов:

Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.

∠ A O D = ∠ B O D = ∠ A O B 2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .

Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180 ° .

( 1 ) и ( 3 )
( 2 ) и ( 4 )

называются вертикальными .

По свойству вертикальных углов:

∠ C O D = ∠ A O B
∠ B O D = ∠ A O C

( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )

называются смежными .

По свойству смежных углов:

∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °

Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )

называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

( 3 ) и ( 5 )
( 4 ) и ( 6 )

называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

( 1 ) и ( 7 )
( 2 ) и ( 8 )

называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

( 3 ) и ( 6 )
( 4 ) и ( 5 )

называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

( 1 ) и ( 8 )
( 2 ) и ( 7 )

называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:

Соответственные углы равны.
Внутренние накрест лежащие углы равны.
Внешние накрест лежащие углы равны.
Сумма внутренних односторонних углов равна 180 ° .
Сумма внешних односторонних углов равна 180 ° .

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

S n = 180 ° ⋅ ( n − 2 )

где n – это количество углов в n -угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.

α n = 180 ° ⋅ ( n − 2 ) n

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с углами

источники:

http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/

Геометрия. Урок 2. Углы

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Параллельные прямые
Теорема о накрест лежащих углах

Теорема

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Дано: 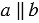, АВ — секущая, 1 и 2 — накрест лежащие (Рис.1).

Доказать: 1 =2.

Доказательство:

Предположим,что углы 1 и 2 не равны друг другу. Отложим от луча АВ угол РАВ, равный углу 2, так, чтобы РАВ и 2 были накрест лежащими углами при пересечении прямых АР и секущей АВ (Рис.2).

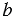
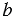
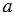
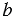
По построению накрест лежащие углы РАВ и 2 равны, значит АР (по признаку параллельности двух прямых). То есть мы получили, что через точку А проходят две прямые и АР, параллельные прямой . Но это противоречит аксиоме параллельных прямых. Значит наше предположение неверно и 1 = 2. Что и требовалось доказать.

Следствие

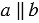
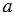
Дано: , (Рис.3).

Доказать: .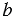

Доказательство:

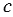
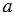
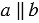
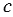
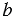
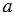
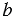
Прямая пересекает прямую , при этом , значит пересекает и прямую (смотри следствие 2⁰ из аксиомы параллельных прямых). При пересечении параллельных прямых и секущей образуются равные накрест лежащие углы: 1 =2 (по теореме о накрест лежащих углах). По условию , т.е. 1 = 90⁰, значит и 2 = 90⁰, т.е. . Что и требовалось доказать.

Советуем посмотреть:

Параллельные прямые

Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о соответственных углах

Теорема об односторонних углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Параллельные прямые

Правило встречается в следующих упражнениях:

7 класс

Задание 245,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 246,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 371,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 379,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 428,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 442,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 448,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 626*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1069,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Пересечение двух параллельных прямых секущей

Параллельными называются пара прямых, которые при продолжении не пересекаются.

Когда две паралелльные прямые $a$ и $b$ пересекаются секущей $c$ , то образуется много разнообразных углов.

Некоторые пары углов имеют свои имена — названия:

пара     накрест лежащие углы   :   ∠3   и   ∠5,         ∠4   и    ∠6;
пара     односторонние углы   :       ∠4    и   ∠5,         ∠3   и   ∠6;
пара     соответственные углы :      ∠1   и   ∠5,         ∠4   и   ∠8,      ∠2   и   ∠6,      ∠3   и   ∠7.

Свойства:

накрест лежащие углы равны: 3 = 5, 4 = 6.
соответственные углы равны: 1 = 5, 4 = 8, 2 = 6, 3 = 7.
сумма односторонних углов равна 180 градусов: 3 + 6 = 180 градусов, 4 + 5 = 180 градусов.

_____________________________________________________________________________________

Теорема    Если две параллельные линии пересекаются третьей (Секущей), тогда выполняется следующее:
ТеоремаТеорема    *      накрест лежащие углы равны   ;
ТеоремаТеорема    *      соответственные углы равны ;
ТеоремаТеорема    *      сумма односторонних углов 180 град. ;
ТеоремаТеорема    *      вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .

_____________________________________________________________________________________

Теорема Если две прямые перпендикулярны (обе одновременно) к третьей, то они параллельны друг другу.

_____________________________________________________________________________________

Теорема Если две прямые не параллельны друг другу, то равенства для сумм углов не выполняются: 3 + 6 < 180 ; 4 + 5 > 180 .

_____________________________________________________________________________________

Теорема Если одна прямая параллельна второй, а вторая параллельна третьей, то первая прямая так же параллельна третьей.

_____________________________________________________________________________________

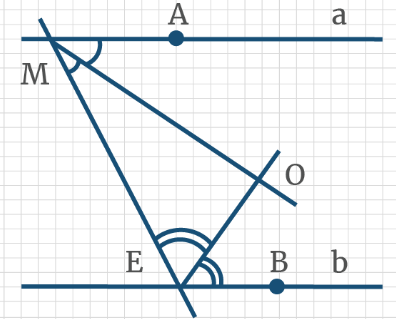
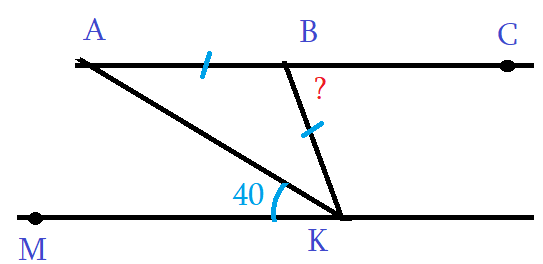
Задача 1: На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.

Решение: АС ║ МК параллельны, АК — секущая, $Rightarrow$ ∠АКМ и ∠КАВ накрест лежащие, $Rightarrow$ ∠КАВ = 40°.
∆АВК – равнобедренный, АВ = ВК $Rightarrow$ углы у основания ∠КАВ = ∠АКВ значит, $Rightarrow$ ∠АКВ = 40°.
Значит, углы ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность, ∠МКВ = ∠АКВ + ∠АКМ = 80°.
АС ║ МК параллельны, АК — секущая, $Rightarrow$ ∠ВКМ и ∠КВС накрест лежащие, $Rightarrow$ Ответ: ∠КВС = 80°.

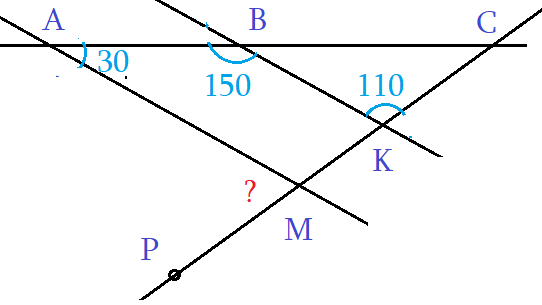
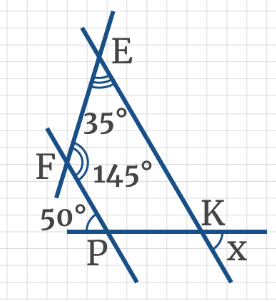
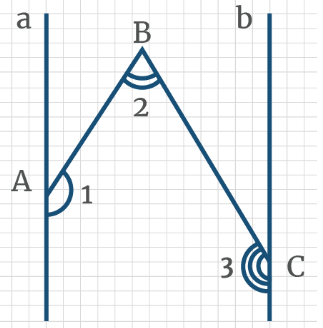
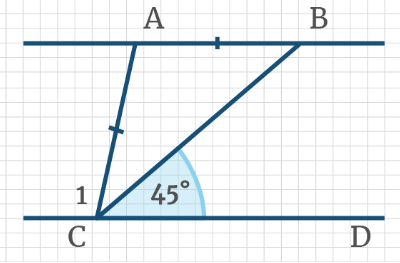
Задача 2: На рисунке, даны углы ∠ВАМ = 30°, ∠АВК = 150°, ∠ВКС = 110°. Найти ∠АМР.

Решение: Углы ∠ВАМ и ∠АВК — односторонные от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
Сумма односторонных 180°? … по теореме «о параллельных», прямые АМ и ВК должны быть параллельными. АМ ║ ВК.
Теперь: АМ ║ ВК, СР — секущая. Односторонные углы равные, ∠ВКС = ∠АМК. Значит, ∠АМК = 110°.
Наконец, углы ∠АМК и ∠АМР — смежные. Значит, ∠АМК + ∠АМР = 180°. $Rightarrow$ ∠АМР = 180° — ∠АМК = 70°.
Ответ: ∠АМР = 70°. Замечание: «надо видеть все секущие к параллельным, и углы к ним».

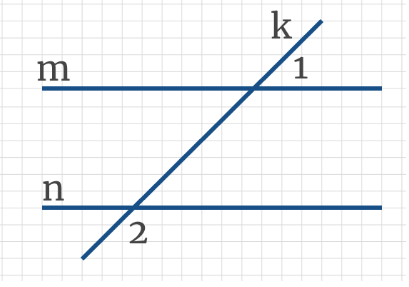
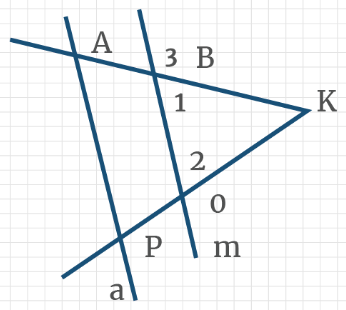
Задача 3: На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.

Решение: Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим: ∠САВ = 3∠РМК
Как связаны искомые углы по рисунку? ∠САВ и ∠МАВ — смежные, значит ∠МАВ = 180° — ∠САВ.
Углы ∠МАВ и ∠РМК односторонные углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
Из двух равенств получаем ∠РМК = 180° — ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим: ∠РМК = 180° — 3∠РМК
∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°. Ответ: 45°, 135°

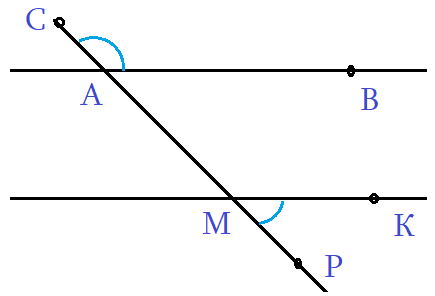
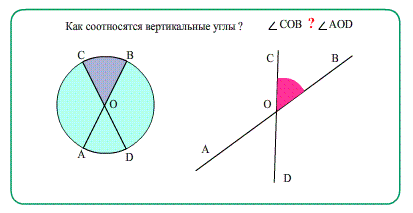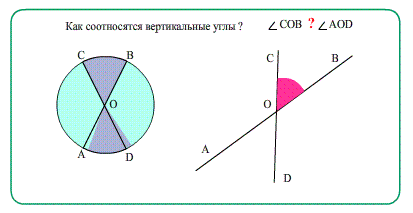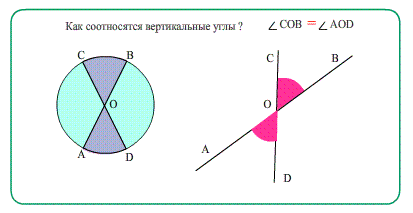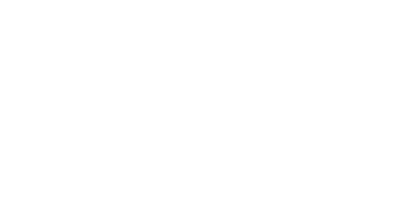
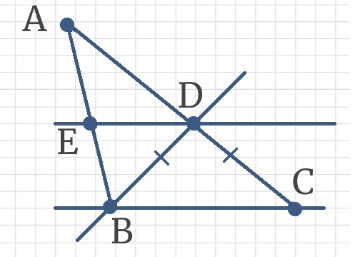
Задача 4: На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти четырехугольника АВСD.

Трапеция АВСD: Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
Решение: Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° — ∠МВС = 115°.
Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° — ∠ВСК = 100°.
АМ секущая к АD ║ ВС $Rightarrow$ ∠ВАD и ∠МВС соответственные, значит равные ∠ВАD = ∠МВС = 65°.
Аналогично, КD секущая к АD ║ ВС $Rightarrow$ ∠АDС и ∠ВСК соответственные, значит равные ∠АDС = ∠ВСК = 80°.
Ответ: Углы трапеции ∠ВАD = 65° ∠АВС = 115° ∠ВСD = 100° ∠АDС= 80°

Задача 4, продолжение, «углы в трапеции»: Пусть углы любые: ∠МВС = х, ∠ВСК = у.

Такими же рассуждениями о смежных и односторонных, получим: ∠А = х ∠В = 180° — х ∠С = 180° — у ∠D = у
Видно: ∠А + ∠В = 180° ∠С + ∠D = 180°. Сумма углов при боковой стороне трапеции 180° . Односторонные!
Видно: ∠А + ∠В + ∠С + ∠D = 180°. Сумма всех углов трапеции равна 360°. . Как у четырехугольника?

Факты, Следствия из теорем о углах при параллельных и секущей к ним:

В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
В паралеллограмме сумма углов у одной стороны равен 180 град. — внутренные односторонные. Что секущая?
В трапеции сумма углов у боковых сторон равен 180 град. — внутренные односторонные. Что секущая?
Еще о углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!

Интерактивные Упражнения:

Задачи из сайта https://resh.edu.ru :

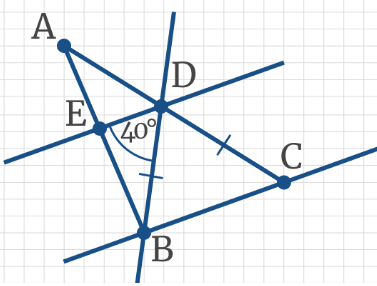
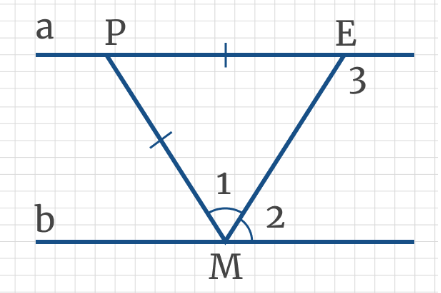
Задача 1: Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.

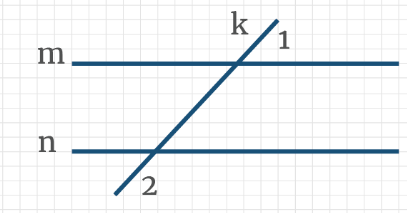
Задача 2: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.

Задача 3: По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.

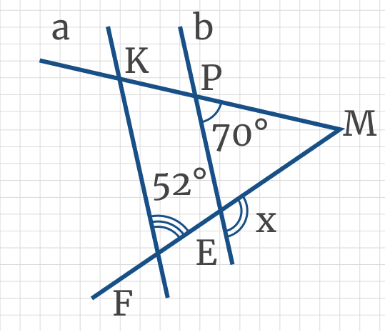
Задача 4: Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?

Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2

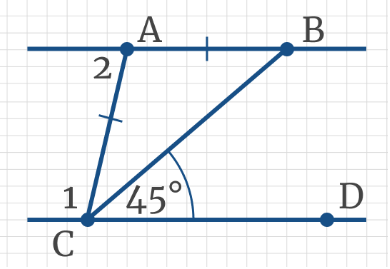
Задача 6: Прямые FP и EK параллельны, чему равна градусная мера угла x?

Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.

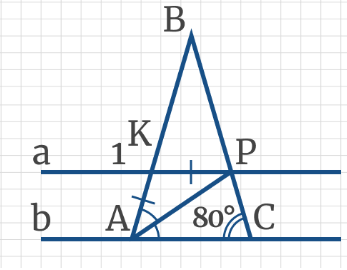
Задача 8: В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?

Задача 9: Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.

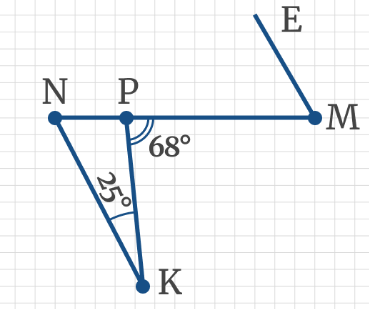
Задача 10: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.

Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.

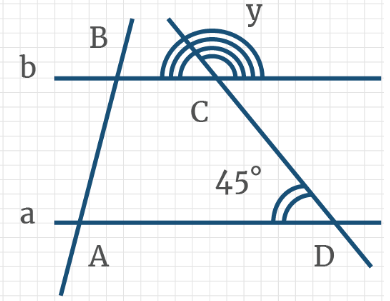
Задача 12: ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?

Задача 13: На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.

Задача 14: На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?

Задача 15: Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?

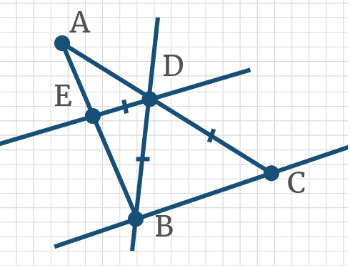
Задача 16: Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?

Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?

Задача 18: Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.

Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.

Задача 20: «углы в параллелограмме и трапеции»:

один из углов параллелограмма 40. найти остальные
найти углы параллелограмма, если известно, что сумма двух 80. (100, 160)
найти углы параллелограмма, если известно, что разность двух 70. (110, 130)
Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма
Углы параллелограмма относятся как 2:3 найти все углы
Чему равны углы равнобедренной трапеции, если разность противолежащих 40

Источник