Паскаль как найти наибольший общий делитель чисел

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var
  a, b, d: integer;

begin
  write('Введите два числа: ');
  readln(a, b);
  if a < b then d := a + 1 else d := b + 1; 
  {так как мы используем цикл с постусловием, 
  необходимо минимальное значение увеличить на один,
  иначе цикл repeat, в силу своих конструктивных особенностей,
  не учтет это минимальное число  
  и не сделает его кандидатом в НОД. Например, 5 и 25.}
  repeat d := d - 1
  until (a mod d = 0) and (b mod d = 0);
  write('NOD = ', d)
end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A,  B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

Доказательство:

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

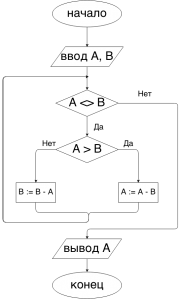
Блок — схема алгоритма Евклида «с вычитанием»

Программа

var
  a, b: integer;

begin
  write('a = '); 
  readln(a);
  write('b = ');
  readln(b);
  while a <> b do 
    if a > b then 
      a := a - b 
    else 
      b := b - a;
  writeln('NOD = ', a);
end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var
  a, b: integer;

begin
  write('a = ');
  readln(a);
  write('b = ');
  readln(b);
  while (a <> 0) and (b <> 0) do
    if a >= b 
    then 
      a := a mod b 
    else 
      b := b mod a;
  write(a + b)
end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Приведем 3 программы поиска наибольшего общего делителя двух натуральных чисел, основанных на:

• алгоритме Евклида
• перебора возможных делителей числа
• разложения чисел на простые множители

Что такое наибольший общий делитель двух натуральных чисел m и n, или НОД(m, n)

НОД двух натуральных чисел — это такое наибольшее натуральное число, которое одновременно делит без остатка оба этих числа.

Алгоритм Евклида

Евклид — древнегреческий математик, геометр, автор первого из дошедших до нас теоретических трактатов по математике.

Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Евклид впервые дал описание этого алгоритма в книгах «Начала». Изначально этот алгоритм назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль.

Сформулируем алгоритм

Пусть даны два натуральных числа m и n. Пока числа m и n не равны (или их разница не равна 0), большее число заменить их разницей. В качестве ответа взять любое из чисел.

Пример:

Пусть m = 12, n = 18

12<>18, n = 18 — 12 = 6

12<>6, m = 12 — 6 = 6

6<>6, НОД(12, 18) = 6

Программа на языке программирования Паскаль (алгоритм Евклида)

var m, n:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);  

  readln(m,n);

  while m<>n do

  begin

    if m>n then m:=m-n

           else n:=n-m;

  end;

  writeln(‘НОД(m,n): ‘,m);

end.

Результат запуска программы

Перебор возможных делителей числа

Будем использовать алгоритм, разобранный ранее в этом блоге.

Запустим цикл for с счетчиком k от 1 до n, будем проверять условие: если число n делится на значение счетчика k без остатка (n mod k = 0), то значение счетчика k — это делитель числа n, значение k можно вывести на экран или сохранить в отдельной переменной.

Поскольку нам нужен наибольший общий делитель чисел m и n, поэтому запустим цикл до минимального из чисел m и n (другое будет лишним), и будем проверять условие: если число m делится на значение счетчика цикла k без остатка и число n делится на значение счетчика цикла k без остатка одновременно (воспользуемся операцией and), это и будет их общий делитель.

Программа на языке программирования Паскаль (перебор возможных делителей числа)

var m, n, k, p:integer;

begin

  writeln(‘Введите два натуральных числа m и n:’);

  readln(m,n);

  for k:=1 to min(m,n) do 

  begin

    if (m mod k = 0) and (n mod k=0) then p:=k;

  end;

  writeln(‘НОД(m,n): ‘,p);

end.

Функция min будет работать в PascalABC.NET, в случае использования другой среды, нужно до цикла определить наибольшее число из m и n.

Разложение чисел на простые множители

Ранее мы разбирали алгоритм разложения натурального числа на простые множители. 

Как связаны простые множители числа и НОД. Приведем пример.

Пусть m = 18,  n = 12

Выполним разложение на простые множители.

Множители числа m: 2 3 3

Множители числа n: 2 2 3

Выделим их общие простые множители — это числа 2 и 3. В качестве наибольшего общего делителя нужно взять из произведение: 2 * 3 = 6. НОД(12, 18) = 6.

Пусть m = 36,  n = 48

Множители числа m: 2 2 3 3

Множители числа n: 2 2 2 2 3

Общие простые множители — это числа 2 2 3. Произведение этих множителей равно 12. НОД(36, 48) = 12.

Для нахождения НОД двух чисел нужно выполнить их разложение на простые множители и в качестве ответа взять произведение их общих множителей.

Как будем решать задачу

Для хранения множителей числа воспользуемся списком (PascalABC.NET), в него легко добавлять значение командой add.

Описание списка с именем nod в блоке var

var nod:List<integer>;

Создание нового пустого списка в теле программы

nod:=new List<integer>;

Добавление значения в конец списка

nod.add(значение);

Создадим два списка (s1 и s2) для хранения множителей числа m и n соответственно. С помощью конструкции вложенных циклов переберем все элементы списков и сравним на равенство, если множители равны, сохраним их в списке nod, а значения элементов списков сделаем равными -1 и -2 соответственно (чтобы далее их повторное сравнение на равенство было ложным) . В качестве ответа возьмем произведение элементов списка nod командой nod.Product.

Программа на языке программирования Паскаль (разложение чисел на простые множители)

var

  m, n, k1, k2: integer;      

  s1, s2, nod: List<integer>;

begin

  writeln(‘Введите два натуральных числа m и n:’);   

  readln(m, n);  

  s1 := new List<integer>; 

  s2 := new List<integer>; 

  nod := new List<integer>;

  k1 := 2; k2 := 2;  

  while (m > 1) or (n > 1) do   

  begin

    while m mod k1 = 0 do     

    begin

      m := m div k1;      

      s1.Add(k1); //добавить значение в список можно и так: s1+=k1;

    end;     

    k1 += 1;     

    while n mod k2 = 0 do    

    begin

      n := n div k2;       

      s2.Add(k2);     

    end;     

    k2 += 1;   

  end;   

  //writeln(s1, s2); 

  for k1:=0 to s1.Count-1 do //элементы списка нумеруются с 0, длина списка s1.count

    for k2:=0 to s2.Count-1 do

      if s1[k1]=s2[k2] then //s1[k1] — обращение к элементу списка по его номеру

        begin 

        nod.Add(s1[k1]);

        s1[k1]:=-1;

        s2[k2]:=-2;

        end;

  //println(s1,s2,nod);

  println(‘НОД(m,n): ‘,nod.Product);

end.

Это программа состоит из самого большого количества строк. Насколько она эффективна?

Задача на применение НОД

Даны числа: a = 2³ • 3¹⁰ • 5 • 7² , b = 2⁵ • 3 • 11. Чему равен  НОД (a,b)?

Вариант 1

var a,b:longint;
 
function NOD(x,y:longint):longint; { функция поиска наиб. общ. делителя }
begin
   if x<>0 then NOD:=NOD(y mod x,x) else NOD:=y;
end;
 
function NOK(x,y:longint):longint; { функция поиска наим. общ. кратного }
begin
   NOK:=( x div NOD(x,y) ) * y;
end;
 
begin { основная программа }
    readln(a,b);
    writeln( 'НОД этих чисел = ', NOD(a,b) );
    writeln( 'НОК этих чисел = ', NOK(a,b) );
end.

Вариант 2 Переборный алгоритм

var a, b, d: integer;
begin 
    write('Введите два числа: ');
    readln(a, b);
    if a < b then d := a + 1 else d := b + 1;
    {так как мы используем цикл с постусловием, необходимо минимальное значение увеличить на один, 
    иначе цикл repeat, в силу своих конструктивных 
    особенностей, не учтет это минимальное число и 
    не сделает его кандидатом в НОД. Например, 5 и 25.}
    repeat d := d - 1 
    until (a mod d = 0) and (b mod d = 0); 
write('NOD = ', d) 
end.

Вариант 3

var
m,n,r:integer;
label lb;
begin
write('Введите первое число:');readln(m);
write('Введите второе число:');readln(n);
lb:r:=m mod n;
if r=0 then writeln('НОД = ',n)
else
 begin
  m:=n;
  n:=r;
  goto lb;
 end;
end.

Вариант 4 Алгоритм Евклида с вычитанием

Пусть a и b — целые числа, тогда верны следующие утверждения:

Все общие делители пары a и b являются также общими делителями пары a — b, b;

И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b; НОД(A,  B) = НОД(A — B, B), если A > B; НОД(A, 0) = A.

Доказательство:

Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналогично предыдущему. Поэтому t — также общий делитель a и b. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а. Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

var a, b: integer;
begin 
    write('a = ');
    readln(a);
    write('b = ');
    readln(b);
    while a <> b 
        do if a > b then a := a - b else b := b - a;
    writeln('NOD = ', a);
end.

Вариант 5 Алгоритм Евклида с делением

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r). Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

var a, b: integer;
begin
    write('a = ');
    readln(a);
    write('b = ');
    readln(b);
    while (a <> 0) and (b <> 0) 
        do if a >= b then a := a mod b else b := b mod a;
    write(a + b)
end.

Вариант № 6

Program test2(input,output);
Const N = 5;
Var
       С: array[1..5] of integer;
       A,B:integer;
function HOК (A, В:integer):integer;
begin
        HOK:=A*B/ HOD(A,B);
end;
function НОD(А, В:integer):integer;
var
      X,Y:integer;
begin
X:= A; Y: = В;
1:IF X = Y THEN HOD:=X;
IF X > Y THEN begin
                           X:= X – Y;goto 1;
                           end;
IF Y > X THEN begin
                           Y:= Y – X;goto 1;
                           end;
end;
Begin
FOR i= 1 ТО N READ (C[i]);
A:= С ([l])
FOR i = 1 TO N–1 begin B:=С[i + 1];
                                          A:= HOK(A,B);
                               end;
writeln ("HOK="; A);
end.

Вариант 7

Program N_O_D (Input, Output); 
Var 
A, B: LongInt; 
NOD : LongInt; 
 
Begin
 
WriteLn ('PASCAL: Нахождение Н.О.Д. двух заданных чисел.');
Writeln ('Введите числа, для которых ищется НОД:'); 
Write('Первое число: ');ReadLn (A);
Write('Второе число: ');ReadLn (B); 
 
If (A < B)ThenNOD := A Else NOD := B;
 
While Not( (A mod NOD = 0) and (B mod NOD = 0) ) do 
NOD := NOD - 1;
 
WriteLn ('НОД = ',NOD);
 
ReadLn;
End. 

Program N_O_D (Input, Output); 
Var 
A, B: LongInt; 
NOK, NOD : LongInt; 
 
Begin
 
WriteLn ('PASCAL: Нахождение Н.О.К. двух заданных чисел.');
WriteLn ('Введите числа, для которых ищется НОК:'); 
Write ('Первое число: ');ReadLn (A); 
Write ('Второе число: ');ReadLn (B);
 
If (A < B)ThenNOD := A Else NOD := B;
 
While Not ( (A Mod NOD = 0) And (B Mod NOD = 0) ) Do 
NOD := NOD - 1;
 
A := A Div NOD;
B := B Div NOD; 
NOK := A * B * NOD; 
WriteLn ('НОК = ', NOK); 
 
ReadLn;
End. 

Алгоритм Евклида

Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).

Python

#!/usr/bin/env python
a = 18
b = 30
 
while a!=0 and b!=0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print (a+b)

Perl:

 sub nod
 {
 return  $_[0] != 0  ?  nod ( ( $_[1] % $_[0] ), $_[0] )  :  $_[1];
 }

C:

 int gcd(int a, int b) {
   int c;
   while (b) {
      c = a % b;
      a = b;
      b = c;        
   }
   return abs(a);
 }

Pascal:

  function nod( a, b: longint): longint; 
  begin
   while (a <> 0) and (b <> 0) do
     if a >= b then 
       a:= a mod b 
     else 
       b:= b mod a;
   nod:= a + b;
  end;

Java:

public class GCD {
    public static int gcd(int a,int b) {
        while (b !=0) {
            int tmp = a%b;
            a = b;
            b = tmp;
        }
        return a;
    }
}

C#:

int gcd(int a, int b)
{
    while (b != 0)
        b = a % (a = b);
    return a;
}