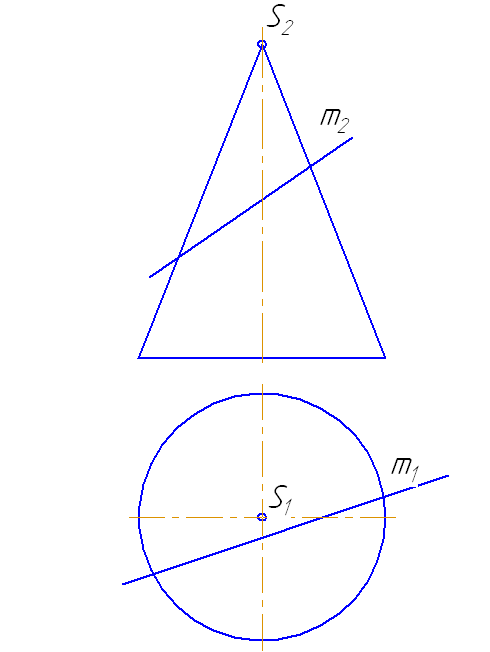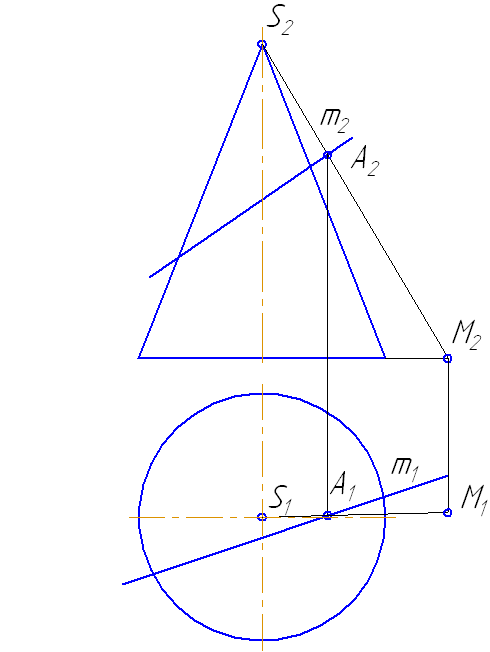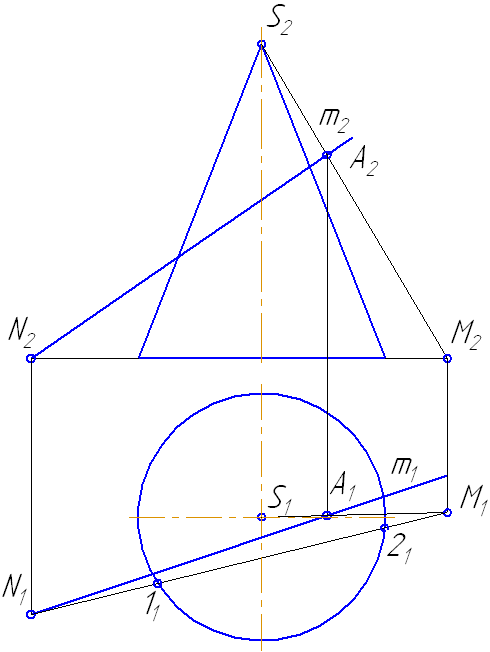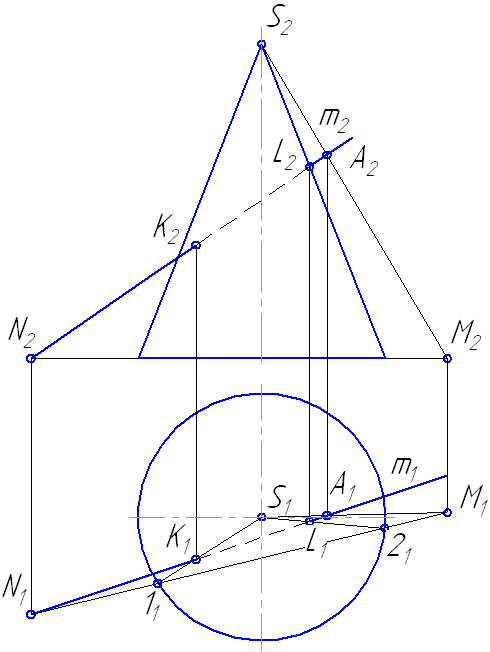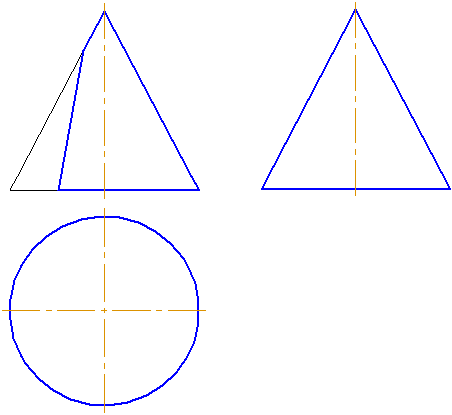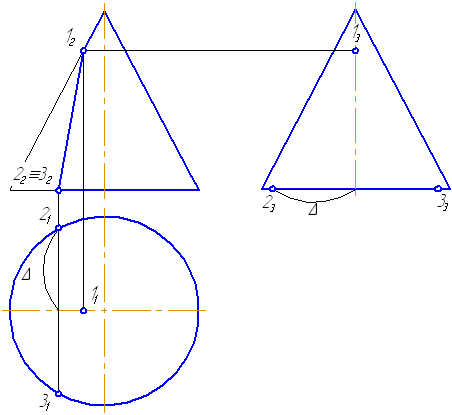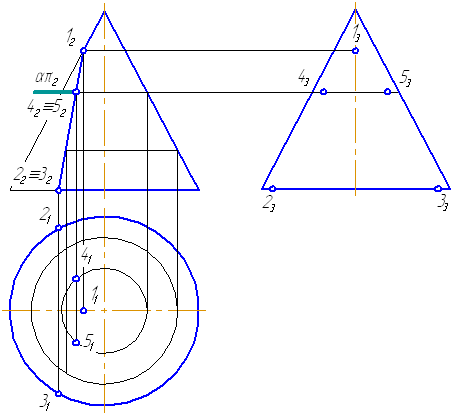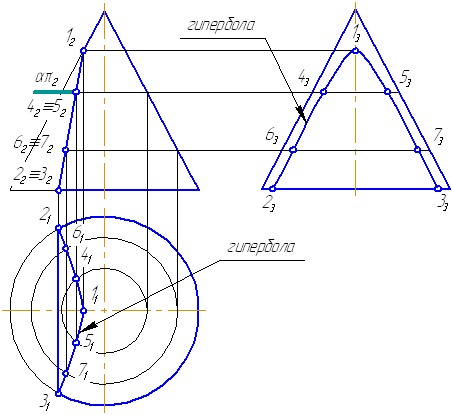Пересечение цилиндра плоскостью как найти

Содержание:

Пересечение поверхностей вращения плоскостью:

Линия пересечения кривой поверхности с плоскостью представляет собой плоскую кривую, которая может распадаться и на прямые линии в случае пересечения плоскости с линейчатой поверхностью по ее образующим.

Для построения этой кривой линии на чертеже находят проекции ее отдельных точек, соединяемых с помощью лекала.

Среди точек линии пересечения имеются точки, которые занимают особое расположение на кривой или выделяются своим местоположением относительно плоскостей проекций. Такие точки называют опорными или характерными. К ним относятся высшие и низшие, ближние и дальние, точки, расположенные на крайних образующих (точки видимости) и др.

Остальные точки называются промежуточными или случайными.

Для нахождения точек линии пересечения применяются вспомогательные секущие плоскости (проецирующие или плоскости уровня).

Вспомогательные плоскости выбираются так, чтобы в пересечении с кривой поверхностью получались простейшие линии — прямые и окружности.

Пересечение цилиндра плоскостью

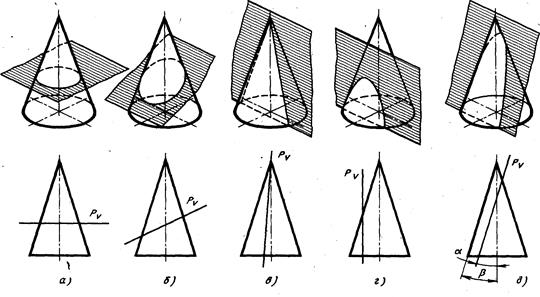
При пересечении цилиндра вращения плоскостью возможны случаи:

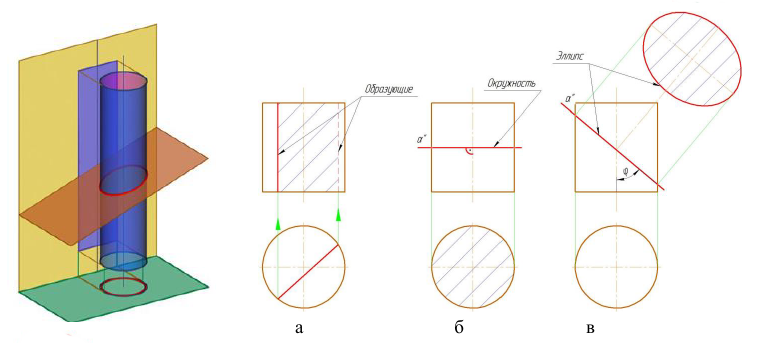
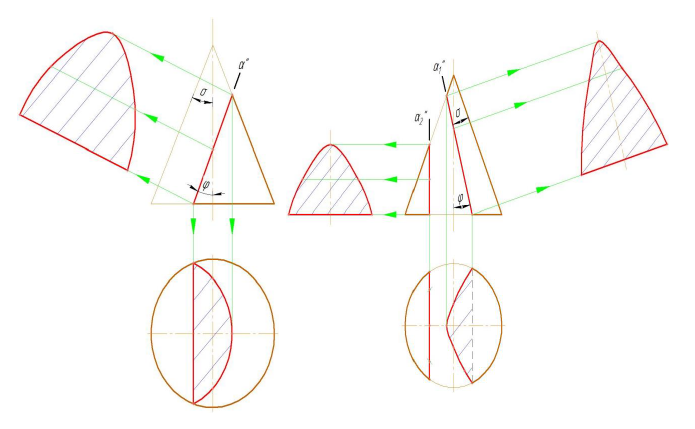
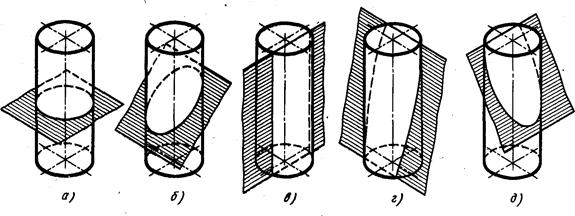
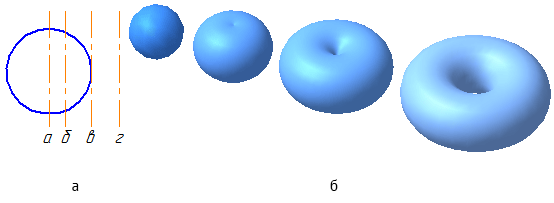
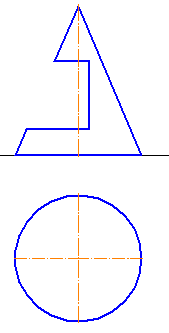
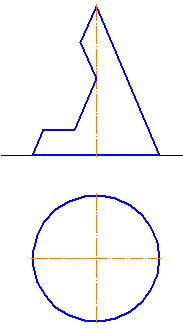
• секущая плоскость параллельна оси — в сечении цилиндрической поверхности полу-чаются две прямые (образующие) (рис. 8.1а);
• секущая плоскость перпендикулярна оси — в сечении получается окружность, равная окружностям оснований (рис. 8.1б);
• секущая плоскость наклонна к оси — в сечении получается эллипс, малая ось которого всегда равна диаметру цилиндра, а большая зависит от угла ϕ (рис. 8.1в).

Рисунок 8.1 — Пересечение цилиндра плоскостью

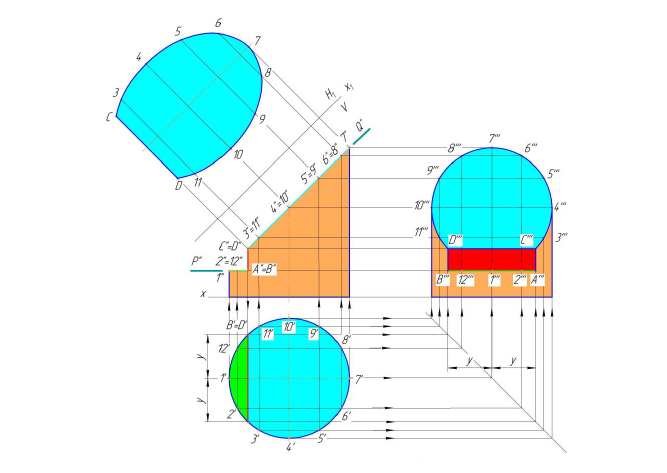
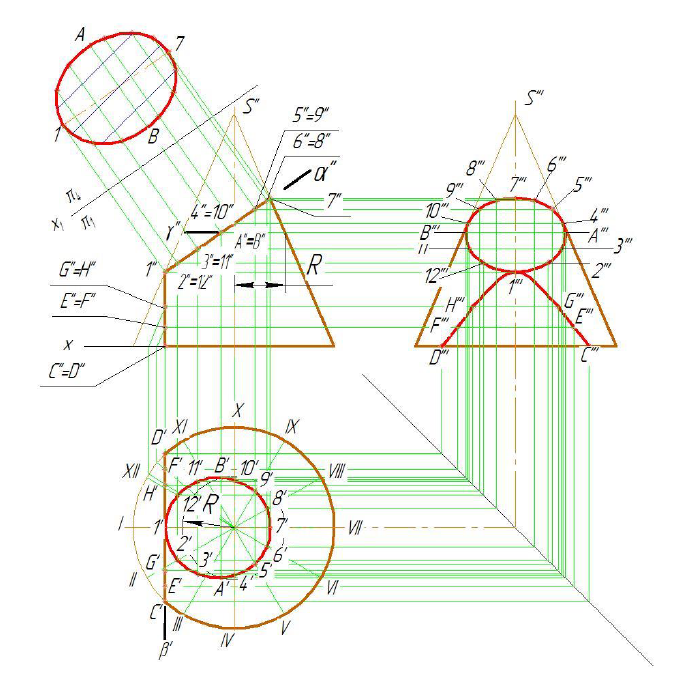
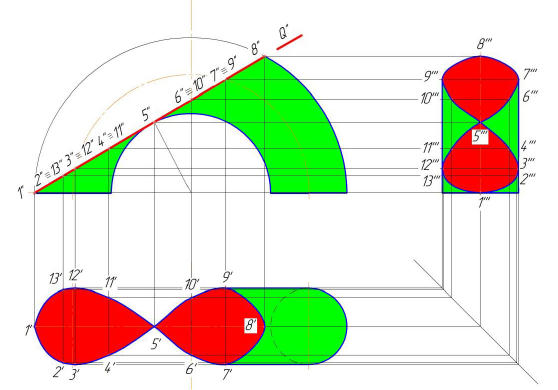
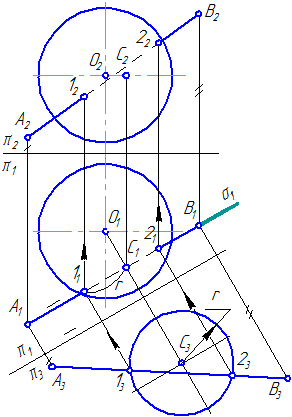
Горизонтальная плоскость Р (Р») пересекает поверхность цилиндра по части окружности, профильная плоскость T (T») по прямым АВ и CD (образующим цилиндра), фронтально-проецирующая плоскость Q (Q») — по части эллипса [5]. Фронтальная проекция линий пересечения совпадает со следами — проекциями секущих плоскостей (P «, T «, Q»), а горизонтальная — с окружностью оснований цилиндра (рис. 8.2).

Рисунок 8.2 — Построение проекций усеченной части цилиндра

Построение профильной проекции сводится к построению профильных проекций точек по двум заданным, направление построений линий связи указано стрелками). Вместо ломаных линий связи при построении профильных проекций точек можно использовать координаты y , которые откладываются на горизонтальных линиях связи по разные стороны оси цилиндра (см. построение точек А, В, С, D).

Обычно для построения точек линий сечения пользуются образующими, равноотстоящими друг от друга. Поэтому горизонтальная проекция цилиндра (окружность) разделена на 12 частей (точки 1, 2… 12). Этой равномерной «разметкой» удобно пользоваться не только для построения проекций сечений, но и для построения развертки.

Действительный вид фигуры сечения плоскостью Q построен способом перемены плоскостей проекций. Новая ось проекций х1 проведена параллельно следу — проекции Q». Выполнив соответствующие построения на плоскости H1, получим натуральную величину сечения цилиндра плоскостью Q.

Пересечение конуса плоскостью

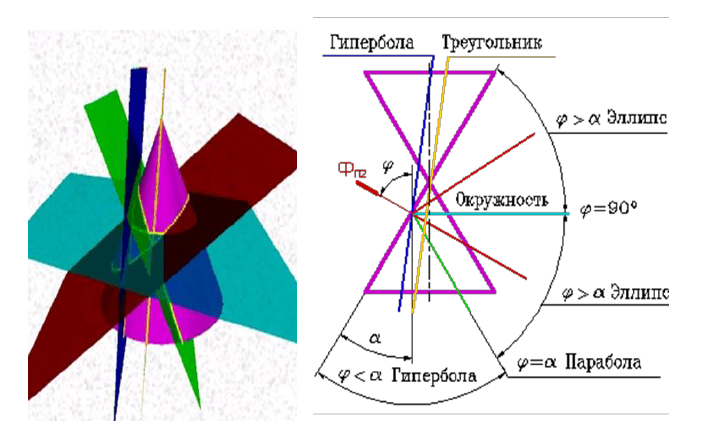
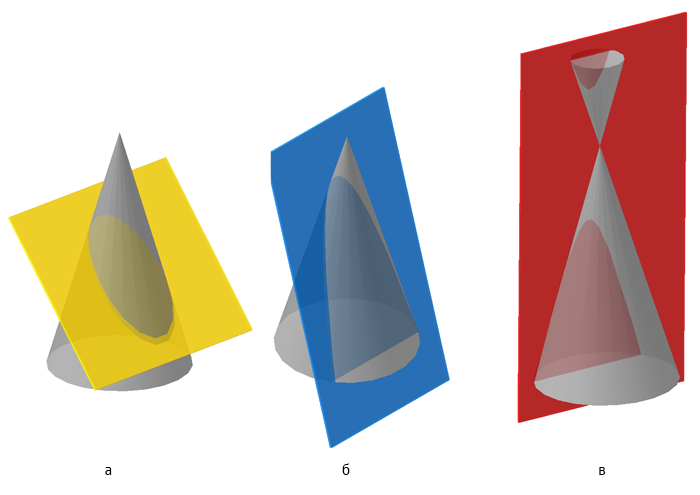
В зависимости от положения секущей плоскости линиями сечения конической поверхности (рис. 8.3) могут быть: эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка.

Рисунок 8.3 — Пересечение конуса плоскостью

Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс. В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.

В частном случае (φ=90) такая плоскость пересекает поверхность конуса по окружности; и сечение вырождается в точку, если плоскость проходит через вершину конуса.

Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ=α, то линией пересечения является парабола. В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую.

Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ<α, то линией сечения является гипербола. В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые.

При пересечении конуса вращения получаются различные виды кривых второго порядка (конические сечения) [5]. Рассмотрим возможные случаи пе-ресечения конуса фронтально-проецирующими плоскостями (угол между сле дом — проекцией и осью конуса — α , половина угла конуса при вершине –S.

Рисунок 8.4 — Конические сечения

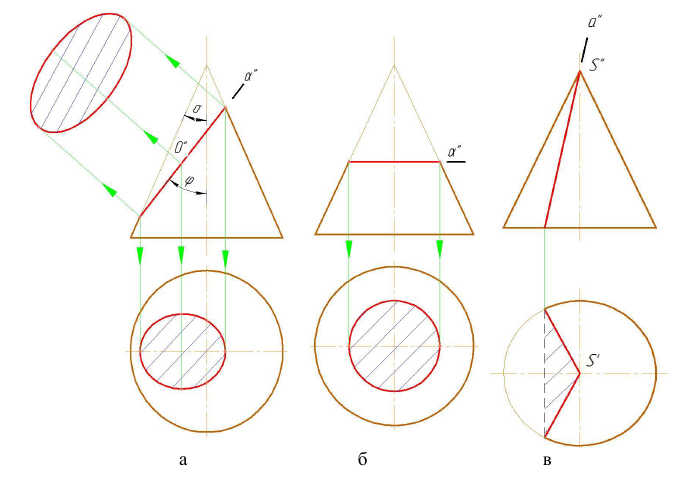
Секущая плоскость α (α») пересекает все образующие конуса ( не парал-лельные ни одной из образующих конуса) — в сечении получается эллипс ( φ> δ) (рис. 8.4 а).

В частности, если секущая плоскость перпендикулярна оси конуса, то получается окружность (рис. 8.4 б).

В частном случае, если секущая плоскость проходит через вершину конуса, то в сечении получается пара пересекающихся в вершине прямых (образующих) (рис. 8.4 в).

Секущая плоскость α (α») параллельная одной образующей конуса в сечении получается парабола (φ = φ) (рис. 8.5 а).

Секущая плоскость α1 (α1″) параллельна двум образующим конуса- в се-чении получается гипербола (φ < δ) (рис. 8.6 б). Профильная плоскость α2 (α2″) образует с осью конуса угол равный 0, что не противоречит вышеуказанному неравенству.

Рисунок 8.6 — Конические сечения

Если конус вращения пересекается плоскостью общего положения, то о линии пересечения можно судить, преобразовав плоскостью общего положения в проецирующую. Преобразование рационально выполнить переменой плоскостей проекций.

На рис. 8.7 показано построение проекций усеченной части конуса вращения плоскостями частного положения α и β.

Рисунок 8.7 — Построение проекций усеченной части конуса

• Заказать чертежи

Пересечение сферы и тора плоскостью

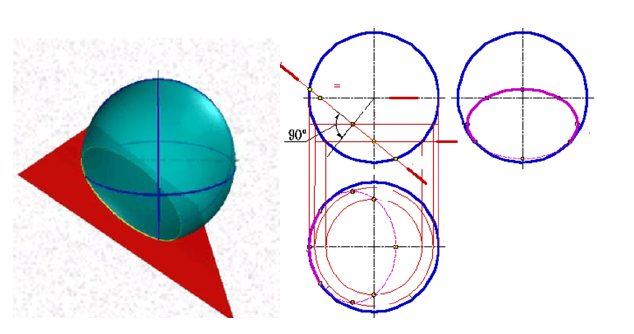
При пересечении сферы плоскостью всегда получается окружность, которая в зависимости от положения секущей плоскости по отношению к плоскостям проекций, проецируется в виде прямой, в виде эллипса или в виде окружности.

В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая. Рассмотрим решение задачи по определению линии пересечения сферы фронтально — проецирующей плоскостью.

Рисунок 8.8 — Пересечение сферы плоскостью

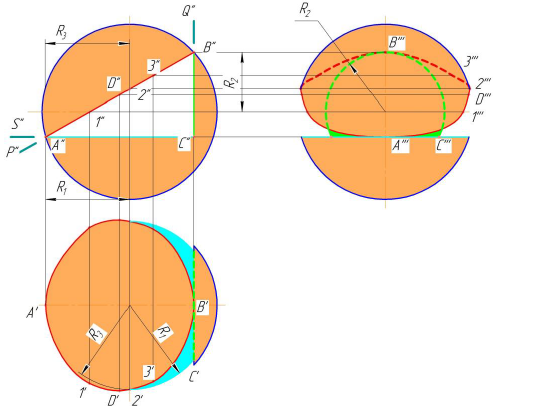
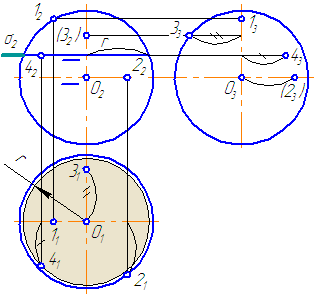
На рис. 8.9 показано построение проекций усеченной сферы плоско-стями частного положения S, P, Q [5]. Фронтальная проекция линий пересе-чения совпадает со следами — проекциями секущих плоскостей (S, P, Q ).

Рисунок 8.9 — Построение проекций сечения сферы плоскостями

Горизонтальная проекция сечения сферы плоскостью S — окружность радиуса R1, а профильная — прямая.

Профильная проекция сечения плоскостью Q — окружность радиуса R2, а горизонтальная — прямая.

Плоскость P пересекает сферу по окружности, которая на плоскости Н и W проецируется в виде эллипса. Две вершины этого эллипса (точки А и В) являются низшей и высшей точками сечения. Точки 1 и 2, лежащие на экваторе и профильном меридиане, определяют видимые части горизонтальной и профильной проекций от невидимой (точки обозначены только на одной симметричной части сечения). Вершина эллипса D (конец большой оси) определена при помощи горизонтальной секущей плоскости.

Дополнительная секущая плоскость пересекает заданную плоскость Р на фронтально проецирующей прямой, а сферу — по окружности радиуса R, проецирующейся на плоскость Н в натуральную величину. Профильная проекция D'» точки D строится по линиям связи. Аналогичным способом находят промежуточные точки 3, используя следующую вспомогательную секущую плоскость.

Видимость горизонтальной и профильной проекций линий сечений определяется в зависимости от расположения их относительно экватора и профильного меридиана сферы.

При пересечении тора плоскость в общем случае получается кривая 4-го порядка, в частных случаях она может распадаться на две кривые 2-го порядка.

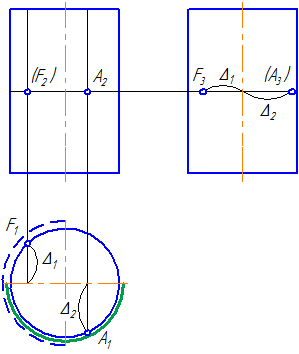
На рис. 8.9 показано построение проекций усеченной части открытого тора фронтально-проецирующей плоскостью Q (Qꞌꞌ).

Фронтальная проекция линии пересечения совпадает со следом – проекцией секущей плоскостью α.

Для построения кривой пересечения определены точки А, В, С, D, E и промежуточные 1, 2, 3, 4.

Рисунок 8.9 — Построение проекций сечения тора плоскостью

Точки А и В лежат на экваторе (наибольшей параллели) тора, точка С на горле (наименьшей параллели). Точка D и Е лежат на крайних параллелях (точки обозначены только на одной симметричной части сечения).

Промежуточные точки 1 и 2 расположены на параллелях m , точки 3.4 – на параллелях n. Построение горизонтальных проекций показано стрелками.

Профильные проекции точек кривой пересечения построены при помощи линий связи

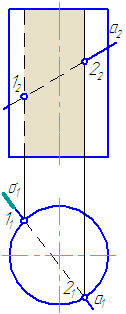
Для построения кривой линии, получаемой при пересечении
цилиндрической поверхности плоскостью, следует в общем случае находить
точки пересечения образующих с секущей плоскостью, как было сказано на
с. 170 в отношении линейчатых поверхностей вообще. Но это не исключает
возможности применять и вспомогательные плоскости, пересекающие каждый
раз поверхность и плоскость.

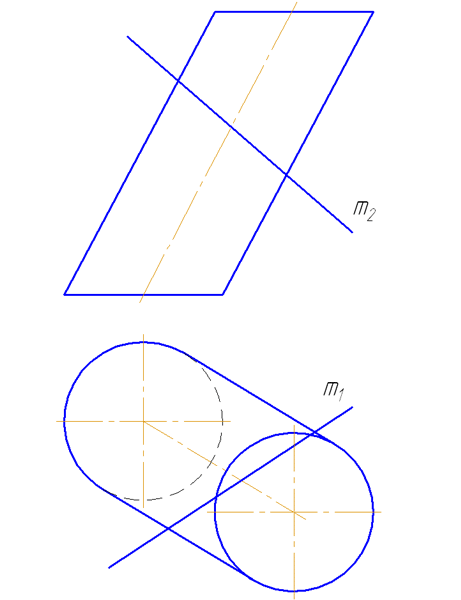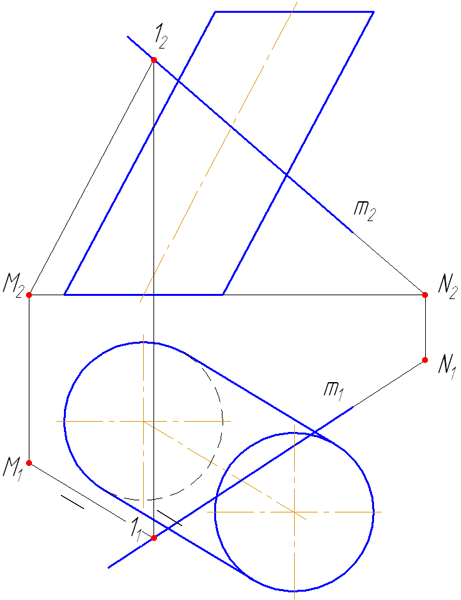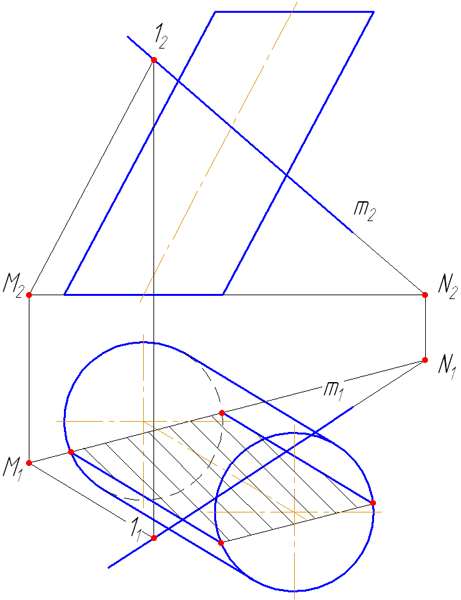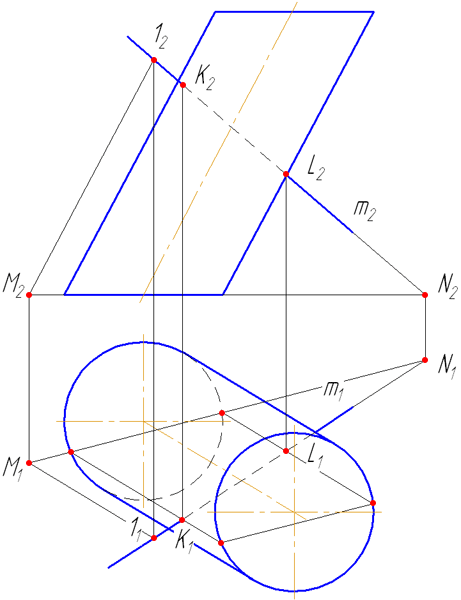
Прежде всего отметим, что любая цилиндрическая поверхность
пересекается плоскостью, расположенной параллельно образующей этой
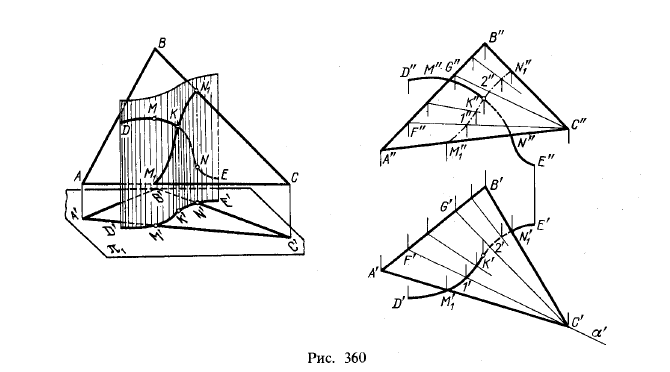
поверхности, по прямым линиям (образующим). На рис. 360 показано
пересечение цилиндрической поверхности плоскостью. В данном случае эта
поверхность является вспомогательным элементом при построении точки
пересечения кривой линии с плоскостью: через заданную кривую (см. рис.
360, слева) DMNE проведена цилиндрическая поверхность, проецирующая
кривую на пл. π₁. Далее, плоскость (на рис. 360 — треугольник) пересекает цилиндрическую поверхность по плоской кривой М₁ … N₁. Искомая точка пересечения кривой с плоскостью — точка К — получается в пересечении кривых — заданной и построенной.

Такая схема решения задачи на пересечение кривой линии с плоскостью
совпадает со схемой решения задач на пересечение прямой линии с
плоскостью (см. §§ 23

и 25); в обоих случаях через линию проводят вспомогательную поверхность, которая для прямой линии является плоскостью.

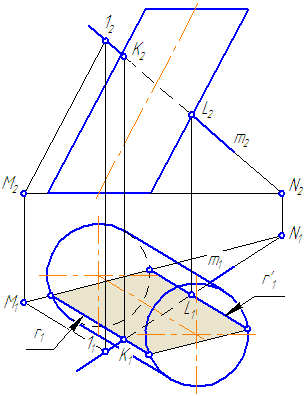
Горизонтальная проекция кривой M₁…N₁, по
которой цилиндрическая поверхность пересекается с плоскостью, совпадает с
горизонтальной проекцией кривой D … Е, так как эта кривая является
направляющей для цилиндрической поверхности при перпендикулярных к пл.
π₁, ее образующих. Поэтому по точке М’₁ на проекции А’С’ мы можем найти проекцию М»₁ на А»С» и по точке N’₁ — проекцию N»₁. Далее, на рис. 360 справа показана вспомогательная пл. α, пересекающая ABC по прямой CF, а цилиндрическую поверхность — по ее образующей с горизонтальной проекцией
в точке 1′. В пересечении этой образующей с прямой CF получается точка с
проекциями 1′ и 1″, принадлежащая кривой М₁ … N₁
Очевидно, можно не указывать следа плоскости, а просто провести прямую в
треугольнике, как это показано в отношении прямой CG, на которой
получена точка с проекциями 2′ и 2″.

В рассмотренных далее примерах будут показаны развертки.
Развертывание цилиндрической поверхности в общем случае может
производиться по схеме развертывания поверхности призмы. Цилиндрическая
поверхность как бы заменяется вписанной в нее или описанной
призматической, ребра которой соответствуют образующим цилиндрической поверхности. Само развертывание, подобно показанному на рис. 283, производится при помощи нормального сечения. Но вместо ломаной линии проводится плавная кривая.

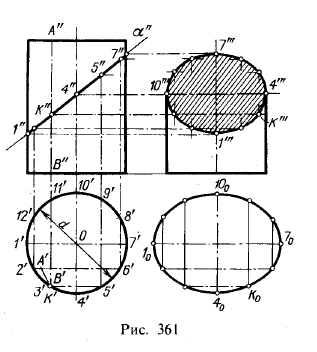
На рис. 361 показано пересечение прямого кругового цилиндра
фронтально-проецирующей плоскостью. Фигура сечения представляет собой
эллипс, малая ось которого равна диаметру основания цилиндра; величина
большой оси зависит от угла между секущей плоскостью и осью цилиндра.

Так как ось цилиндра перпендикулярна к пл. π₁ то горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией цилиндра.

Обычно для построения точек контура сечения проводят равномерно
расположенные образующие, т. е. такие, проекции которых на пл. π₁
являются точками, равноотстоящими друг от друга. Этой «разметкой» удобно
пользоваться не только для построения проекций сечения, но и развертки
боковой поверхности цилиндра, как это будет показано ниже.

Проекция фигуры сечения на пл. π₃ — эллипс, большая ось
которого в данном случае равна диаметру цилиндра, а малая представляет
собой проекцию отрезка 1″7″. На рис. 361 на пл. π₃ изображение построено так, как будто верхняя часть цилиндра снята после пересечения его плоскостью.

Если бы на рис. 361 плоскость α составляла с осью цилиндра угол 45°, то проекцией эллипса на π₃ была бы окружность. При этом отрезки 1″‘7″‘ и 4″’10″‘ оказались бы равными.

Если тот же цилиндр пересекать плоскостью общего положения, также
составляющей с осью цилиндра угол 45°, то проекцию фигуры сечения
(эллипса) в виде окружности можно получить на дополнительной плоскости
проекций, параллельной оси цилиндра и горизонталям секущей плоскости.

Очевидно, при увеличении угла наклона секущей плоскости к оси отрезок
1″‘7″‘ уменьшается; если же этот угол будет меньше 45°, отрезок 1′»7′»
увеличивается и становится большой осью эллипса на пл. π₃, малой же осью этого эллипса становится отрезок 4″’10″‘.

Натуральный вид сечения представляет собой, как уже сказано выше, эллипс. Его оси получаются на чертеже: большая — отрезок 1₀7₀ = 1″7″, малая — отрезок 4₀10₀, равный диаметру цилиндра. Эллипс может быть построен по этим осям.

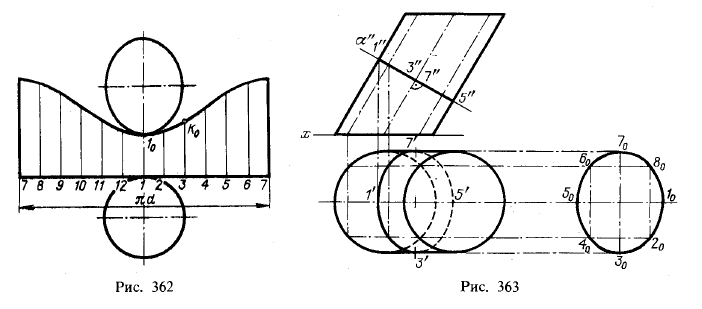
На рис. 362 показана полная развертка нижней части цилиндра.

Развернутая окружность основания цилиндра разделена на равные между
собой части соответственно делениям на рис. 361; отрезки образующих
отложены на перпендикулярах, проведенных в точках деления развернутой
окружности основания цилиндра. Концы этих отрезков соответствуют точкам
эллипса. Поэтому, проведя через них кривую линию, получаем развернутый
эллипс (эта линия представляет собой синусоиду) — верхнюю кромку
развертки боковой поверхности цилиндра.

К развертке боковой поверхности на рис. 362 присоединены круг
основания и эллипс — натуральный вид сечения, что дает возможность
сделать модель усеченного цилиндра.

На рис. 363 изображен эллиптический цилиндр с круговым основанием; его ось параллельна пл. π₂. Для определения нормального сечения этого цилиндра его надо рассечь
плоскостью, перпендикулярной к образующим, в данном случае
фронтально-проецирующей плоскостью. Фигура нормального сечения
представляет собой эллипс с большой осью, равной отрезку 3₀7₀, и с малой, равной 1₀5₀ = 1″5″.

Если надо будет развернуть боковую поверхность данного цилиндра, то,
имея нормальное сечение, развертывают ограничивающую его кривую в прямую
линию и в соответствующих точках этой прямой, перпендикулярно к ней,
откладывают отрезки образующих, беря их с фронтальной проекции. Для
разметки образующих делят окружность основания на равные части. При этом
и эллипс (нормальное сечение) разделится на такое же число частей, но
не все эти части получаются равной

длины. Развертывание эллипса в прямую можно произвести путем
последовательного откладывания на прямой достаточно малых частей
эллипса.

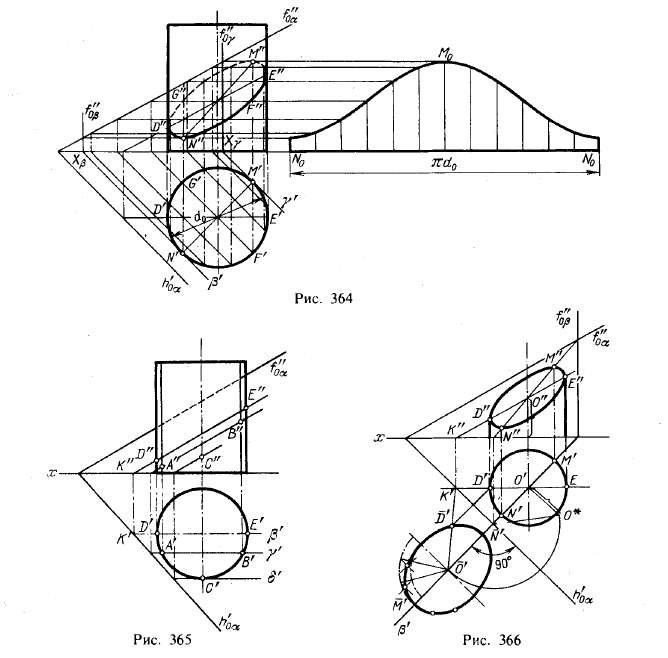
На рис. 364 показан прямой круговой цилиндр, пересеченный плоскостью
общего положения. В сечении получается эллипс: секущая плоскость
составляет с осью конуса некоторый острый угол.

Подобно тому, как это было на рис. 361, горизонтальная проекция
сечения совпадает с горизонтальной проекцией цилиндра. Поэтому положение
горизонтальной проекции точки пересечения любой из образующих цилиндра с
пл. α известно (например, точка А’ на рис. 365). Для нахождения
соответствующей фронтальной проекции можно ировести в пл. α горизонталь
или фронталь, на которой должна находиться искомая точка. На рис. 365
проведена фронталь; в том месте, где фронтальная проекция фронтали
пересекает фронтальную проекцию соответствующей образующей, лежит
проекция А». Одна и та же фронталь определяет две точки кривой, А и В
(рис. 365). Если же построить фронталь, соответствующую точке С, то

эта линия определит лишь одну точку кривой пересечения. Фронталь, построенная по точкам D и Е, определяет крайние точки D» и Е».

Продолжая аналогичные построения, можно найти достаточно точек для вычерчивания фронтальной проекции линии пересечения.

На рис. 366 верхняя часть цилиндра как бы срезана. Если же
фронтальную проекцию показывают полностью, то линию пересечения
вычерчивают так, как показано на рис. 364.

На рис. 365 показаны вспомогательные фронтальные плоскости β, γ, δ
пересекающие цилиндр по образующим, а пл. α по фронталям. Это
соответствует тому, что было сказано в начале параграфа. Вспомогательная
пл. δ лишь касается цилиндра, что дает возможность определить только
одну точку для кривой.

При построении фронтальной проекции линии пересечения, помимо точек
D» и Е» (рис. 365), следует найти еще две крайние точки, а именно М» и
N» — наивысшую и наинизшую точки проекции сечения на пл. π₂.
Для их построения надо выбрать вспомогательную плоскость,
перпендикулярную к следу h’_0α и проходящую через ось цилиндра (рис. 366).
Эта плоскость является общей плоскостью симметрии данных цилиндра и
секущей пл. а. Найдя линию пересечения плоскостей α и β, отметим точки
М» и N», построив их на фронтальной проекции по точкам М’ и N’.

Иной способ нахождения точек М» и N» заключается в проведении двух
плоскостей, касательных к цилиндру, горизонтальные следы которых
параллельны следу h’_0α. Эти плоскости пересекутся с пл. α по горизонталям последней (рис. 364, вспомогательные плоскости β и γ); отметив точки М’ и N’ построим точки М» и N» на фронтальных проекциях горизонталей.

Отрезок MN представляет собой большую ось эллипса — фигуры сечения
данного цилиндра пл. α. Это видно и на рис. 366, где построен в
совмещении с пл. π₁ эллипс — натуральный вид сечения. Но отрезок M»N» на
том же рисунке отнюдь не является большой осью эллипса — фронтальной
проекции фигуры сечения. Эту большую ось можно найти по сопряженным
диаметрам M»N» и F»G» (рис. 364) построением, указанным в § 21, или
специальным построением, приведенным в § 76.

Натуральный вид сечения может быть найден совмещением секущей плоскости с одной из плоскостей проекций, π₁ или π₂.

На рис. 366 эллипс в совмещенном положении построен по большой и малой осям (там же точка D’ получена совмещением фронтали).

Развертка боковой поверхности показана на рис. 364. Обратите внимание
на то, что разметка точек — горизонтальных проекций образующих — на
окружности основания производилась от точки N’. Этим построение
упрощалось, так как с помощью одной и той же горизонтали получаются две
точки на фронтальной проек

ции эллипса. Кроме того, фигура развертки имеет ось симметрии. Но при
этом точки D’ и Е’ не попали в число точек, размеченных на окружности.

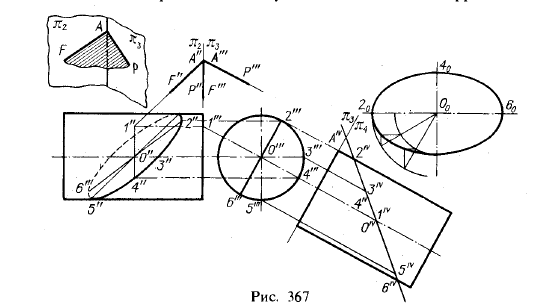
Еще один пример построения фигуры сечения цилиндра вращения
плоскостью дан на рис. 367. Это построение выполнено при помощи способа
перемены плоскостей проекций. Секущая плоскость задана пересекающимися
прямыми — фронталью (AF) и профильной прямой (АР). Так как профильная
проекция фронтали и фронтальная проекция профильной прямой лежат на
одной прямой А»≡A'», A»‘F»‘ = А»Р», то эти прямые лежат соответственно
в плоскостях π₂ и π₃, (см. рис. 367, слева вверху). Ось π₂/π₃ проходит через A'»F'»(A»P»).

Вводим новую пл. π₄ так, что π₄⊥π₃, и π₄⊥АР. Секущая плоскость оказывается перпендикулярной к π₄, и проекция на π₄ фигуры сечения получается в виде отрезка прямой 2 ^IV6^IV, равного большой оси эллипса — фигуры сечения. Положение прямой A^IV6^IV определяется построением проекций точек А и 1 на пл. π₄.

Проследим построение некоторых точек. Чтобы избежать излишних
построений, проекция 1″‘ была взята на продолжении перпендикуляра,
проведенного из О'» на π₃/ π₄. По точке 1″‘ была получена проекция 1″; отрезок 1″1″‘, отложенный от оси π₃/π₄, определил точку ^IV и совпадающую с ней точку О¹ — проекцию центра эллипса. Зная проекции 0^IV и О'», можно получить О» — центр эллипса — искомой фронтальной проекции фигуры сечения.

По точкам 2^IV и 2″‘ найдена точка 2″, наименее удаленная от π₃, а по точкам 6^IV и 6′» — точка 6″, наиболее удаленная от π₃.

По точке 5″‘ взяга точка 5^IV, и теперь по точкам 5^IV
и 5″‘ найдена точка 5″— одна из точек, определяющих разделение эллипса на фронтальной проекции цилиндра на «видимую» и «невидимую» части. Вторая точка расположена симметрично точке 5″ по отношению к О».

Остальное ясно из чертежа. Натуральный вид фигуры сечения (эллипс на рис. 367, справа) построен по осям — большой, равной 2^IV6^IV, и малой, равной диаметру цилиндра.

Вопросы к §§ 55 -56

1. Как строится кривая линия при пересечении кривой поверхности плоскостью?
2. По каким линиям пересекается цилиндрическая поверхность плоскостью, проведенной параллельно образующей этой поверхности?
3. Каким приемом пользуются в общем случае для нахождения точки пересечения кривой линии с плоскостью?
4. Какие линии получаются при пересечении цилиндра вращения плоскостями?
5. В каком случае эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π₁, фронтально-проецирующей плоскостью, спроецируется на пл. π₃ в виде окружности?
6. Как следует расположить дополнительную плоскость проекций, чтобы эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π₁, плоскостью общего положения, составляющей с осью цилиндра угол 45°, спроецировался на эту плоскость проекций в виде окружности?

Сечение цилиндра плоскостью

Цилиндр
является поверхностью проецирующей.
При пересечении цилиндра плоскостью,
параллельной основанию (рис.126 а),
в сечении получаем окружность. Плоскость,
параллельная двум образующим (рис.126
6),
в сечении дает прямоугольник. При
пересечении цилиндра плоскостью (рис126
в)
в сечении получаем эллипс.

Рис.126
а

Рис.126б

Рис.126в

Пересечение
цилиндра с фронтально-проецирующей
плоскостью показано на рис. 127.

Рис.127

Пересечение
прямой с поверхностью

При
пересечении прямой с поверхностью нужно
определить точки входа и выхода прямой
из данной поверхности.

Алгоритм
решения такой задачи сводится к
следующему:

1.заключить
прямую во вспомогательную плоскость;

2.
построить линию пересечения вспомогательной
плоскости с заданной поверхностью
(построить фигуру сечения);

3.найти
точки пересечения прямой с контуром
фигуры сечения;

4.определить
видимость прямой.

Пример
1. Конус (рис.128)

Рис.129

1. Заключаем
прямую l
в плоскость частного положения так,
чтобы при пересечении конуса с плоскостью
была простая линия пересечения –
окружность. В данной задаче α –
горизонтальная плоскость, f_оα
собирающий след, l»f_оα
(рис. 130).

2.
Строим линию пересечения конуса с
плоскостью α. Это окружность радиуса
R.

3.
На пересечении горизонтальной проекции
l’
и окружности радиуса R
отметим искомые горизонтальные проекции
M’
и N’.
M»
и N»
отмечаем на l».

4.
Определяем видимость прямой l.
Между получившимися точками M
и N
прямая всегда невидима. Горизонтальная
проекция прямая l’
видима (невидима только от M’
до N’).
Фронтальная проекция l»
до М»
видима, т.к. точка М
лежит на видимой части конуса относительно
π₂.
Точка N
лежит на невидимой части конуса
относительно π₂,
следовательно, фронтальная проекция
l»
от N»
до очерковой образующей невидима. За
очертаниями конуса прямая l
всегда видима (рис.130).

Рис.130

Рис.131

Пример
2. Гранная поверхность — призма (рис.131)

1.
Заключаем прямую l
во вспомогательную плоскость частного
положения. Линией пересечения плоскости
с гранной поверхностью будет ломаная
линия. Заключаем прямую l
во фронтально-проецирующую плоскость
απ₂,
l»f_oα,
f_oα
– собирающий след (рис.131).

2.
Строим линию пересечения плоскости α
с призмой. Отметим 1»,
2», 3»
на собирающем следе f_oα.

3.
Построим горизонтальные проекции 1′,
2′
и 3′
на соответствующих ребрах.

4.
Соединяем горизонтальные проекции
1′-2′-3′
ломаной линией с учетом видимости.

5.
На пересечении горизонтальной проекции
l’
с горизонтальной проекцией 1′-2′-3′
отметим горизонтальные проекции M’
и N’
искомых точек М
и N.

Рис.132Рис.133

6.
Построим фронтальные проекции M»
и N»
на l».

7.
Определяем видимость прямой l.
Между полученными точками M
и N
прямая невидима всегда. Горизонтальная
проекция l’
невидима между M’N’
и от M’
до горизонтальной проекции ребра В’,
т. к. горизонтальная проекция М’
принадлежит невидимой относительно π₁
грани ВС.
На π₂:
точка М
лежит на грани BС
видимой относительно π₂,
следовательно, М»
видима,
и фронтальная проекция l»
видима до М».
Точка N
принадлежит грани АC,
невидимой относительно π₂,
следовательно, фронтальная проекция
N»
не видима, и фронтальная проекция l»
от N»
невидима. За очертаниями призмы прямая
l
видима (рис.133).

Пример
3. Пересечение прямой со сферой показано
на рис. 134.
Рис.
134.

Соседние файлы в папке Компьютерная графика

• #
• #

  15.03.20153.99 Mб11Геометрическое черчение учебно-методическое пособие.wbk

• #

Разделы Уроки по теме Рекомендуем

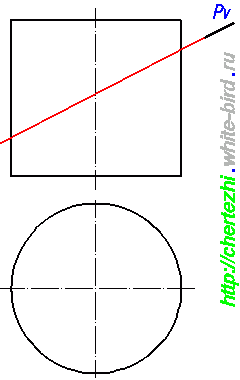
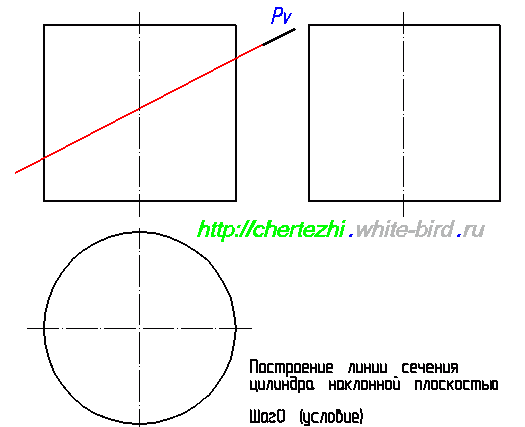
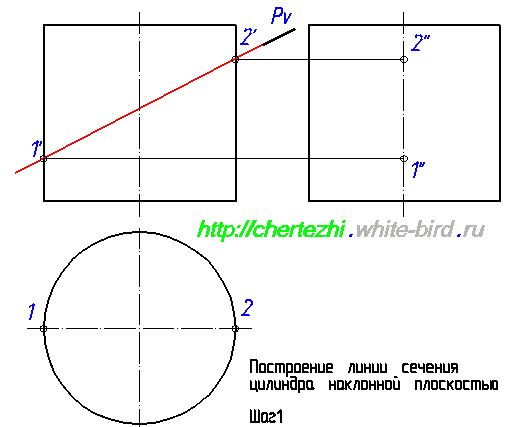
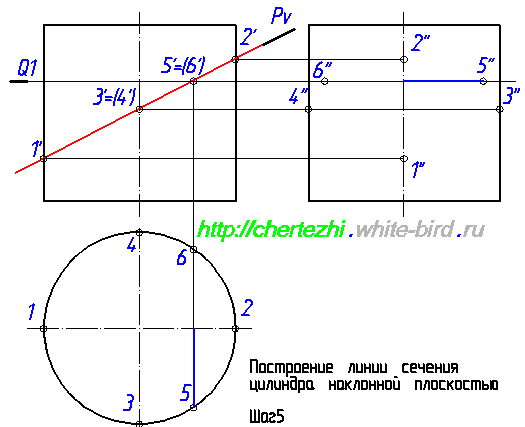
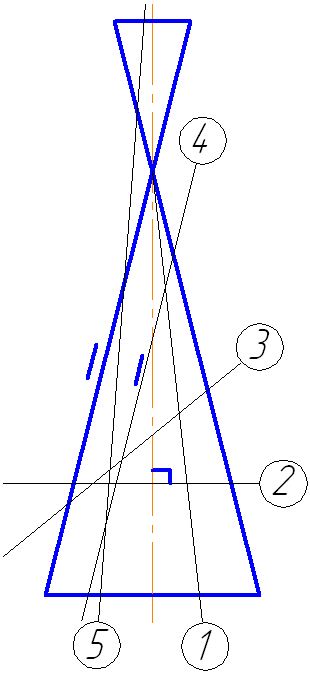
Сечение цилиндра наклонной плоскостью Автор: Moroz Дата: 2012-03-01     Этим уроком я открываю серию статей, посвященных построению линий пересечения простых тел вращения с наклонной плоскостью. Умение выполнять эти действия вам поможет не только решить одноименные задачи, но и будет серьезным подспорьем при нахождении натурального вида фигуры сечения сложных деталей. Ведь детали состоят из кусочков простых тел: конусов, цилиндров, параллелепипедов, сфер. Сегодня я научу вас строить линию пересечения плоскости с цилиндром. Исходное задание как правило имеет вид как на картинке слева от этого абзаца. Изображены два вида, дающие нам представление о том, что фигура является цилиндром вращения, а так же задается секущая плоскость, в моем случае это плоскость Pv.     Давайте попробуем предположить, что мы получим на каждом из трех видов? Определенно можно сказать, что вся линия пересечения на фронтальном виде сольется с прямой обозначающей секущую плоскость, а на горизонтальном виде, все точки пересечения будут лежать на окружности, которой задан цилиндр. Главный интерес данной задачи заключается в нахождении линии пересечения на третьем виде(на профильной проекции цилиндра). Вероятнее всего вы уже догадываетесь, что на третьем виде линия пересечения будет представлять собой эллипс. В частном случае, если секущая плоскость наклонена к цилиндру вращения под углом ровно 45 градусов, то в проекция сечения на третьем виде будет являться эллипсом с равными осями, т.е. эллипс выродится в окружность. Это был маленький кусочек теории, сейчас же предлагаю перейти к практическим построениям.     Итак, перед нами цилиндр с заданной фронтально-проецирующей секущей плоскостью. Начнем с подготовки третьего вида. 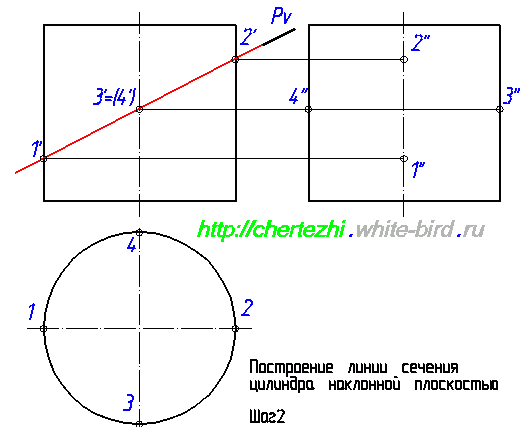Он будет точно такой же как и главный вид:     Первым делом давайте обозначим определяющие точки, которые можно найти сразу, без дополнительных построений. Определим точки 1′ и 2′. Горизонтальные проекции 1 и 2 лежат на пересечении образующей окружности с осью, а проекции 1» и 2» лежат на оси цилиндра. Это нужно либо понимать, либо поверить мне     Еще одна пара определяющих точек — точки 3 и 4. Определим их фронтальную проекцию, а потом найдем горизонтальную и профильную. 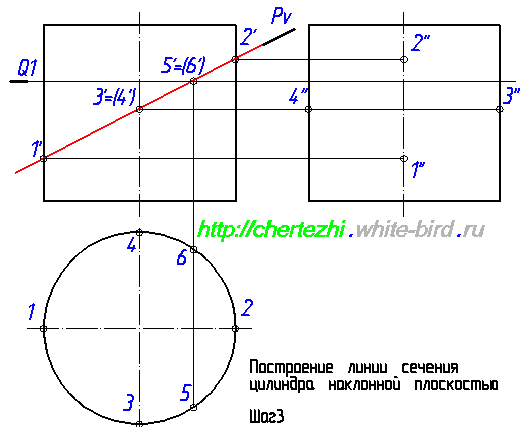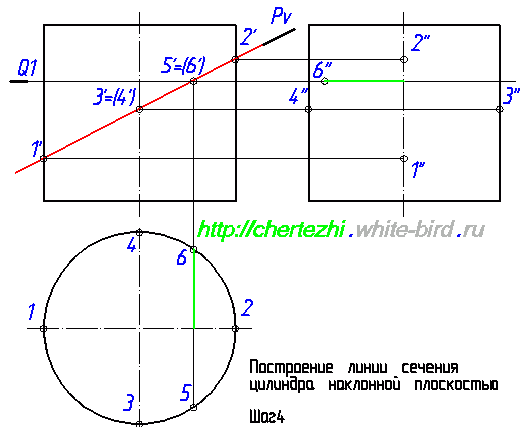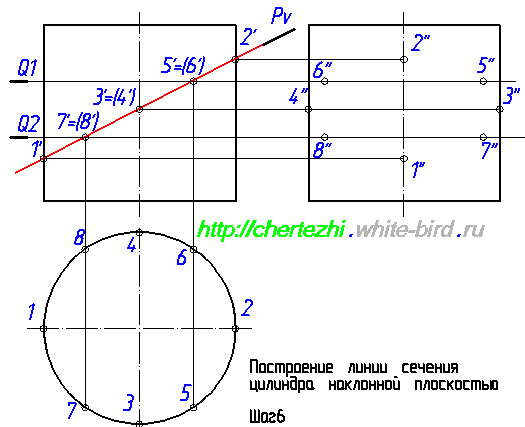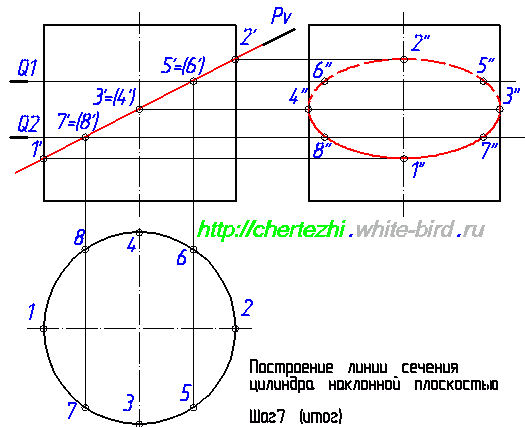Это не сложно:     Если бы наша задача была построить сечение в AutoCad, то на этом можно было бы остановиться, поскольку мы уже имеем 4 точки, определяющие оси эллипса. Но так как мы учимся чертить руками, то мы должны построить дополнительные точки, которые бы позволили нам с вами, не обладая точностью компьютера, максимально точно начертить линию пересечения.     Проведем вспомогательную секущую плоскость Q1. На фронтальной проекции в точке пересечения Q1 и Pv отметим точки 5′ и 6′. Снесем их по линии связи на горизонтальную проекцию, отметим там точки 5 и 6:     Теперь нужно построить профильные проекции 5» и 6». Отложим на фронтальной проекции влево от оси точку 6» на расстоянии равном удалению точки 6 от оси окружности на горизонтальной проекции. Эти соответствующие расстояния на рисунке ниже отмечены зелеными отрезками:     Чтобы построить точку 5» нужно выполнить ровно такие же действия. Нужно отложить аналогичное расстояние вправо от оси цилиндра. Соответствие размеров на профильной и горизонтальной проекции на рисунке ниже обозначено синими отрезками:     Проведем еще одну вспомогательную секущую плоскость — Q2. Мне нравится проводить вспомогательные плоскости симметрично относительно середины сечения — так во многих случаях удается сделать менее загруженный линиями чертеж. Т.е. я провел Q2 симметрично Q1 относительно точек 3′,4′. Полученные с ее помощью проекции точек 7 и 8 строим по аналогии с построениями проекций точек 5 и 6:     Мы ограничимся построением двух вспомогательных плоскостей и проведем эллипс по имеющимся точкам. Но на практике имеет смысл провести еще хотя бы по одной вспомогательной плоскости выше и ниже точки пересечения Pv с осью цилиндра. Особенно если вы не считаете себя мастером построения эллипса «от руки». Итак, завершающий этап: построение линии пересечения плоскости с цилиндром. Она имеет форму эллипса, строим его аккуратно соединяя точки. И последний штрих — на профильной проекции верхняя половина линии пересечения будет проходить за цилиндром, соответственно будет невидима. Что мы и обозначим штриховой линией.     В следующем уроке мы рассмотрим один из случаев построения линии пересечения конуса с плоскостью. Просмотров: 156539 Вы можете сказать «спасибо!» автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам» или или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение. А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны: Комментарии: Мне нужно вырезать эллипс в крыше для вывода металлической трубы, поэтому мне важнее начертить проекцию цилиндра на самой крыше. Спасибо. Михаил! Ваша задача сводится к продолжению задачи о сечении цилиндра плоскостью. Необходимо найти натуральную величину получившегося сечения. Имея его на руках — распечатываем на формате соответствующего размера, вырезаем трафарет и накладываем в нужном месте на крышу. Останется обвести и произвести вырезание по полученной линии. На сайте есть урок, связанный с нахождением натуральной величины сечений, но там не разобрано построение сечений циллиндрических поверхностей. Ну а в целом — спасибо за доброе слово! Вопрос к практическому применению, понятно как изготовить шаблон верхней проекции сечения, но мне, как сварщику, непонятно как изготовить шаблон для торцовки труб. Объясните, пожалуйста. Спасибо.     Сергей, попробую предложить вам способ. Сразу оговорюсь, что вряд ли он наиболее удобный, но зато качество разметки должно получиться хорошим. Метод потребует выполнить построение развертки цилиндра с нанесением на него линии пересечения с плоскостью. Т.е. я предлагаю вам на чем либо (рубероид, упаковочная бумага, лист обоев и т.д.) построить развертку цилиндра, нанести на нее линию пересечения цилиндра с наклонной плоскостью, отрезать лишнюю часть и, приложив ее к трубе, обвести по краю. Получиться должно просто замечательно.     Думаю, идею вы поняли. Ну а реализация построения линии пересечения на развертке цилиндра — либо найдете, либо дождетесь — планирую написать соответствующую статью.     Всего наилучшего! линия пунктир(пункт по немецки точка)не показывает невидимую линию. Линия невидимого контура называется штриховая. ГОСТ 2.303 Вот! Всегда есть шанс, что кто-то не поленится найти неточность и поправит! Спасибо за замечание, исправляю! Спасибо, это понятно по начерт.геометрии, но хотелось бы сделать построение математическим путём, т.к. шаблон, плаз, очень большой. Если дадите буду благодарен. спасибо огромноое очень помогло вспомнил Извиняюсь, Вы нарисовали бред, попробуйте построить по Вашему методу сечение цилиндра плоскостью с наклоном 45 и получите круг, а не эллипс )))) Приветствую Злого Енота! Зачем строить? Это и так известно, будет круг. У меня написано: эллипс с равными осями. Частный случай. Эллипс выродится в круг. Возможно, нужно было прочитать еще пару строк? Или попробовать построить эллипс с равными осями? спасибо очень пригодилось! Здравствуйте! Подскажите как выполните такое же задание при условии что цилиндр проецируется в виде круга на профильную плоскость? Зарание спасибо. Благлдарю!Много перелопатил информации,и в основном построенной на рекламе,а толком ничего путного,все вокруг да около,а вот зашел на Ваш сайт,сразу все стало на свои места.Ведь я где-то далеко помню,это было еще в школьные годы,и кого не спрашивал,никто дать толковую информацию так и не смог.С помощью Ваших уроков я вышел из положения,и теперь рекомендую Ваш сайт своим друзьям,знакомым.Ведь много людей занимаются строительством,и часто и густо выходят из того или иного положения методом втыка.Благодарю еще раз. Добавьте свой комментарий:

Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Ирина: Антон, спасибо за отлично выполненные чертежи!!! У меня единственная пятерка на курсе :))). Всем рекомендую обращаться только сюда! Работы выполнены безупречно! Сама рабатаю в комании, где есть конструкторский отдел и решила показать им чертежи Антона. Собрался целый консилиум, говорили где надо подправить, что-то вообще не так, но я решила сдать ничего не исправляя. И это было правильное решение :))). Еще раз спасибо, Антон!!! Ирина, я преклоняюсь перед вашим желанием оставить комментарий спустя 3 месяца после нашего сотрудничества. От этого он еще более ценен! И главное — в нем яркий пример того, насколько сильное значение имеет субъективность восприятия чертежа разными людьми. Мы делаем чертежи в соответствии с ГОСТами, но у каждого преподавателя может быть свое видение «более удачного варианта исполнения», и поэтому иногда студентам приходится что-то менять в наших работах.

Пересечение тел вращения проецирующей плоскостью

При пересечении тела вращения плоскостью контур пересечения будет представлять собой замкнутую кривую линию, форма которой зависит от формы тела вращения и положения секущей плоскости относительно оси вращения. Это может быть окружность, эллипс, парабола, гипербола, а также различные сложные сочета­ния кривых линий. Чтобы построить линию пересечения поверхности вращения с секущей плоскостью, необходимо построить ряд точек, которые будут принадлежать и поверхности тела вращения, и плоскости. Построение следу­ет начинать с характерных точек. К таким точкам относятся: габаритные точки, опреде­ляющие наибольшие размеры линии пересече­ния по высоте и ширине; точки, лежащие на крайних образующих и образующих, проекции которых совпадают с ‘осевыми линиями. По расположению этих точек можно представить характер искомой линии пересечения.

Построив характерные точки, строят проме­жуточные точки, используя для этого в качест­ве вспомогательных линий прямые — образую­щие или окружности (меридианы и паралле­ли). Строя линию пересечения, необходимо знать, по какой кривой пересекаются тела вра­щения — цилиндр, конус, шар и тор.

Пересечение цилиндра проецирующей плоскостью.Если прямой круговой цилиндр рассечь плос­костью, параллельной его основаниям, то линия пересечения боковой поверхности с этой плоскостью будет окружность (рис. 4, а).

Если цилиндр рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности с этой плоскостью будет эллипсом, величина и форма которого зависят от угла наклона секу­щей плоскости к плоскостям оснований ци­линдра (рис.4, б).

Если цилиндр рассечь плоскостью, перпенди­кулярной к его основаниям, линия пересечения боковой поверхности с этой плоскостью будет прямоугольником (рис. 4, в).

Если цилиндр рассечь наклонной плоско­стью так, что она пересечет основания и бо­ковую поверхность, то линия пересечения бу­дет частью эллипса, отсеченной двумя хордами оснований (рис. 4, г).

Если секущая плоскость пересечет одно ос­нование и часть боковой поверхности, то ли­ния пересечения боковой поверхности с этой плоскостью будет частью эллипса отсеченного одной хордой основания (рис.4, д).

Пересечение цилиндра проецирующей плоскостьюи построения сечения приведен на рис. В4 Вначале построили опорные точки A,B (наивысшая и самая низкая) и C,D (определяют границу видимости). Все остальные точки промежуточные, построены исходя из свойства принадлежности точки линии. Для их нахождения использовались горизонтали (дополнитель­ные образующие). На рис.В4 проведено 12 образующих. Для этого на профильной проек­ции, проекцию основания цилиндра делят на 12 равных частей и через точки деления строят фронтальные и горизонтальные проекции этих образующих. Прежде чем начать построение линии среза, надо представить себе эту ли­нию.

Развертка поверхности усеченного цилиндра. При построении развертки поверхности усе­ченного цилиндра сначала строят развертку боковой поверхности полного цилиндра, кото­рая представляет собой прямоугольник. Высота прямоугольника равна высоте цилиндра (в данном случае длине образующей, рис. B5). Длина пря­моугольника строится приближенно. Для этого на профильной проекции измеряют хорду между двумя любыми соседними точками деления ок­ружности основания и откладывают это рас­стояние 12 раз по нижней стороне развертки боковой поверхности цилиндра. Затем из всех полученных точек проводят образующие, на которых от нижней части развертки вверх от­кладывают расстояния, равные длинам усечен­ных образующих, взятых с фронтальной или горизонтальной проекций. Построенные на развертке боко­вой поверхности цилиндра точки соединяют от руки плавной кривой линией и обводят по лека­лу. Далее пристраивают полное основание к любой образующей боковой поверхности снизу, а сверху — часть основания, оставшуюся после рассечения цилиндра плоскостью, и натураль­ную величину среза.Развертка поверхности усеченного цилиндра приведена на рис. В5.

Пересечение конуса проецирующей плоскостью.На рис. 5 показаны примеры пересечения конуса плоскостями различного положения, где каждому наглядному изображению соответствует фронтальная проекция конуса со следом секущей плоскости.

Если прямой круговой конус рассечь плоско­стью, параллельной основанию, то линия пере­сечения боковой поверхности конуса с плоско­стью будет окружностью (рис. 5, а).

Если конус рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности конуса с плоскостью будет эллипсом (рис. 5, б).

Если конус рассечь плоскостью, проходящей через его вершину, то, будет ли плоскость пер­пендикулярна или наклонна к основанию, линия пересечения боковой поверхности конуса с пло­скостью будет треугольником (рис. 5, в).

Если на поверхности конуса можно провести две образующие параллельно пересекающей его плоскости, то такая плоскость пересечет боко­вую поверхность конуса по гиперболе (рис. 5, г).

Если плоскость пересекает конус параллельно одной образующей, то боковая поверхность конуса пересечется этой плоскостью по парабо­ле (рис. 5, д).

Пересечение шара проецирующей плоскостью.Шар представляет собой единственное гео­метрическое тело, поверхность которого пересе­кается плоскостью любого положения всегда по окружности.

Секущие плоскости, проходящие через верти­кальную ось шара, рассекают его по меридианам. Секущие плоскости, проходящие перпен­дикулярно к вертикальной оси шара, рассекают его по параллелям.

Пересечение тора проецирующей плоскостью.Если тор пересекать плоскостями, проходя­щими через ось тора, то линия пересечения по­верхности тора и плоскости в зависимости от формы образующей тора, будет либо окруж­ностью, либо дугой окружности.

Если тор пересекать плоскостями, перпенди­кулярными оси вращения, то его поверхность будет пересекаться всегда по окружности.

Если тор пересекать плоскостями, наклонны­ми к оси вращения или параллельно ей, то его поверхность будет пересекаться по кривым ли­ниям.

Еще раз обратим внимание на то что изображено на рисунках приложения В:

— рисунок В4- образец выполнение эпюра 3(построение сечения цилиндра);

— рисунок В5- образец выполнение эпюра 3(построение развертки цилиндра);

— рисунок В6- образец выполнение эпюра 3(построение сечения призмы);

— рисунок В.7- образец выполнение эпюра 3 (построение развертки призмы).

Контрольные вопросы при защите РГР 3

1 Чем можно задать поверхности вращения?

2 Как образуются поверхности вращения: сфера, тор, конус, цилиндр?

3 Какие линии на поверхности вращения называются параллелями и меридианами?

4 Как образуются цилиндрическая и коническая поверхности общего вида?

5 Как построить проекции произвольной точки, принадлежащей заданной поверхности?

6 Какие линии получаются при сечении прямого кругового цилиндра плоскостью?

7 Какие линии получаются при сечении конуса плоскостью?

8 Какие линии получаются при сечении сферы плоскостью и какими могут быть проекции этих линий?

9 Чему равна малая ось эллипса при сечении прямого кругового цилиндра плоскостью?

10 Как определить малую ось эллипса при сечении кругового конуса проецирующей плоскостью?

11 Какими способами можно найти натуральную величину сечения тела плоскостью?

12 Какое сечение цилиндра называется нормальным?

13 Каков алгоритм нахождения точек пересечения прямой с поверхностью?

14 Какие вспомогательные плоскости применяются при определении точек пересечения прямой и поверхности?

15 Как определяется видимость точек пересечения прямой с поверхностью геометрических тел различного вида?

16 В чем заключается способ посредников при построении точек, общих для двух пересекающихся поверхностей?

17 Как построить развертку поверхности конуса?

18 Как построить развертку поверхности цилиндра?

17 Как построить развертку поверхности пирамиды?

18 Как построить развертку поверхности призмы?

Пересечение поверхностей вращения плоскостью с примерами

Содержание:

Пересечение поверхностей вращения плоскостью:

Линия пересечения кривой поверхности с плоскостью представляет собой плоскую кривую, которая может распадаться и на прямые линии в случае пересечения плоскости с линейчатой поверхностью по ее образующим.

Для построения этой кривой линии на чертеже находят проекции ее отдельных точек, соединяемых с помощью лекала.

Среди точек линии пересечения имеются точки, которые занимают особое расположение на кривой или выделяются своим местоположением относительно плоскостей проекций. Такие точки называют опорными или характерными. К ним относятся высшие и низшие, ближние и дальние, точки, расположенные на крайних образующих (точки видимости) и др.

Остальные точки называются промежуточными или случайными.

Для нахождения точек линии пересечения применяются вспомогательные секущие плоскости (проецирующие или плоскости уровня).

Вспомогательные плоскости выбираются так, чтобы в пересечении с кривой поверхностью получались простейшие линии — прямые и окружности.

Пересечение цилиндра плоскостью

При пересечении цилиндра вращения плоскостью возможны случаи:

• секущая плоскость параллельна оси — в сечении цилиндрической поверхности полу-чаются две прямые (образующие) (рис. 8.1а);
• секущая плоскость перпендикулярна оси — в сечении получается окружность, равная окружностям оснований (рис. 8.1б);
• секущая плоскость наклонна к оси — в сечении получается эллипс, малая ось которого всегда равна диаметру цилиндра, а большая зависит от угла ϕ (рис. 8.1в).

Рисунок 8.1 — Пересечение цилиндра плоскостью

Горизонтальная плоскость Р (Р») пересекает поверхность цилиндра по части окружности, профильная плоскость T (T») по прямым АВ и CD (образующим цилиндра), фронтально-проецирующая плоскость Q (Q») — по части эллипса [5]. Фронтальная проекция линий пересечения совпадает со следами — проекциями секущих плоскостей (P «, T «, Q»), а горизонтальная — с окружностью оснований цилиндра (рис. 8.2).

Рисунок 8.2 — Построение проекций усеченной части цилиндра

Построение профильной проекции сводится к построению профильных проекций точек по двум заданным, направление построений линий связи указано стрелками). Вместо ломаных линий связи при построении профильных проекций точек можно использовать координаты y , которые откладываются на горизонтальных линиях связи по разные стороны оси цилиндра (см. построение точек А, В, С, D).

Обычно для построения точек линий сечения пользуются образующими, равноотстоящими друг от друга. Поэтому горизонтальная проекция цилиндра (окружность) разделена на 12 частей (точки 1, 2. 12). Этой равномерной «разметкой» удобно пользоваться не только для построения проекций сечений, но и для построения развертки.

Действительный вид фигуры сечения плоскостью Q построен способом перемены плоскостей проекций. Новая ось проекций х1 проведена параллельно следу — проекции Q». Выполнив соответствующие построения на плоскости H1, получим натуральную величину сечения цилиндра плоскостью Q.

Пересечение конуса плоскостью

В зависимости от положения секущей плоскости линиями сечения конической поверхности (рис. 8.3) могут быть: эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка.

Рисунок 8.3 — Пересечение конуса плоскостью

Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс. В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.

В частном случае (φ=90) такая плоскость пересекает поверхность конуса по окружности; и сечение вырождается в точку, если плоскость проходит через вершину конуса.

Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ=α, то линией пересечения является парабола. В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую.

Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ δ) (рис. 8.4 а).

В частности, если секущая плоскость перпендикулярна оси конуса, то получается окружность (рис. 8.4 б).

В частном случае, если секущая плоскость проходит через вершину конуса, то в сечении получается пара пересекающихся в вершине прямых (образующих) (рис. 8.4 в).

Секущая плоскость α (α») параллельная одной образующей конуса в сечении получается парабола (φ = φ) (рис. 8.5 а).

Секущая плоскость α1 (α1″) параллельна двум образующим конуса- в се-чении получается гипербола (φ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Лекция 7. Поверхности

7.1. Поверхности. Образование и задание поверхности на чертеже

Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

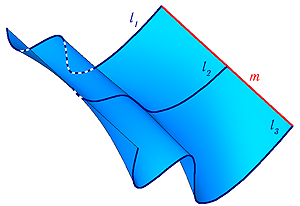
Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).

Подвижную линию принято называть образующей (l_i), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим .

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

Рисунок 7.1 — Кинематическая поверхность

По виду образующей различают поверхности линейчатые и нелинейчатые , образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на развертывающиеся , которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся .

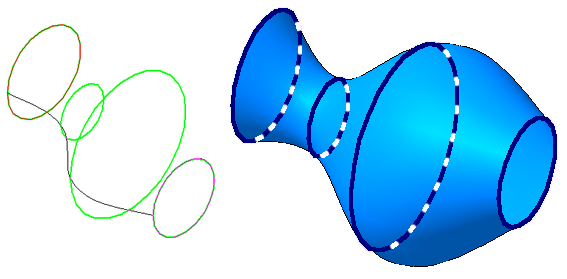
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).

Рисунок 7.2 — Циклическая поверхность

Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:

• поверхности вращения;
• винтовые поверхности;
• поверхности с плоскостью параллелизма;
• поверхности параллельного переноса.

Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).

Для графического изображения поверхности на чертеже используется её каркас.

Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности .

Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом .

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

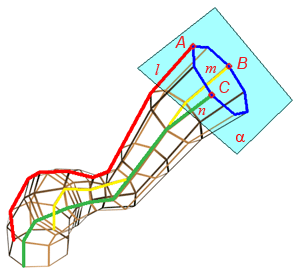
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:

• Геометрическая часть определителя: три направляющих l, m, n.

• Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение

Рисунок 7.3 –Образование циклической поверхности

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

Рисунок 7.4 – Образование поверхностей вращения

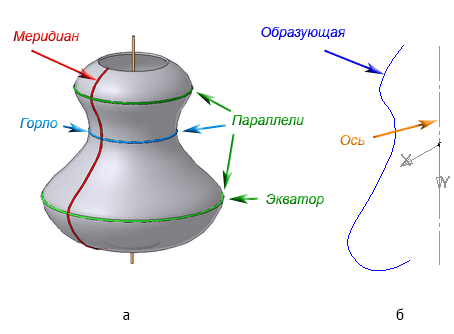
Рисунок 7.5 – Элементы поверхности вращения

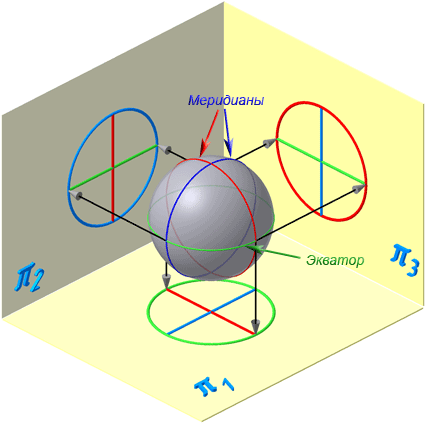
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).

Наименьшая параллель называется горлом , наибольшая – экватором .

Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом .

Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом .

7.3. Цилиндрическая поверхность

Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).

Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.

Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра .

Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой .

Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным .

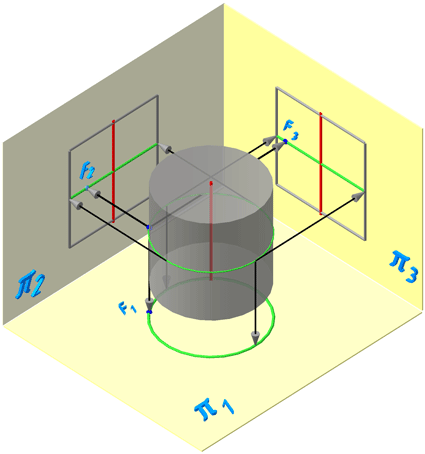
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.

Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).

Рисунок 7.6 – Проецирование цилиндра на плоскости проекций

Горизонтальная и профильная проекции точки F будут видимы.

При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π₁ сплошной зелёной линией – на плоскости проекции π₂ видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π₃.

Пусть точка А на π₂ видима (Рисунок 7.7). Тогда на π₁ она будет видима, а на π₃ невидима.

Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек

7.4. Пересечение прямой с поверхностью прямого кругового цилиндра

Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.

Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.

Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра

Упражнение

Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π₁ и прямая а общего положения (Рисунок 7.8).

Построить точки пересечения прямой а с поверхностью цилиндра.

Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

1. Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
2. Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π₂ условно заштрихован).
3. Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);

Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.

Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π₂ будет ещё невидим участок прямой от точки 1 до левой крайней образующей.

7.5. Пересечение прямой с поверхностью наклонного цилиндра

Упражнение

Заданы : наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π₁ и прямая mобщего положения (Рисунок 7.9).

Построить точки пересечения прямой mс поверхностью цилиндра.
Решение :

Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

Рисунок 7.9 – Пересечение прямой с наклонным цилиндром

1. Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
2. Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π₁) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π₁ (основания)) – (MN);
3. Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:

На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой .

Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

Упражнение

Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.

Необходимо построить горизонтальные и профильные проекции заданных точек.

• Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
• Точка 1 принадлежит главному меридиану (очерковой окружности на π₂), проекция которого на π₁ совпадает с проекцией горизонтальной оси, на π₃ – с проекцией вертикальной оси.
• Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
• Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π₁), проекции которого на π₂ и π₃ совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О₃ вправо. Профильная проекция точки 2 невидима.
• Точка 3 принадлежит очерковой окружности на π₃, которая также является меридианом, проекции которого на π₂ и π₁ совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π₃ двумя засечками, отложить на π₁ вверх от точки О₁. Горизонтальная и профильная проекции точки 3 видимы.
• Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π₁ и σ⊥π₂). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π₁ строим данное сечение и по линии проекционной связи находим 4₁. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π₃ вправо от оси. Все проекции точки 4 видимы.

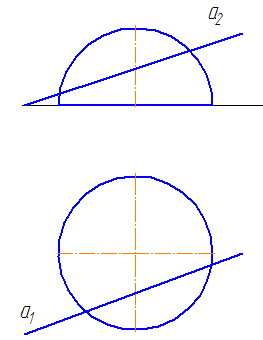
7.7. Пересечение прямой с поверхностью сферы

Упражнение

Заданы: сфера и прямая общего положения АВ.

Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).

Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:

1. Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
2. Построить фигуру пересечения сферы вспомогательной плоскостью;
3. Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).

• Через прямую проводим плоскость σ. Пусть σ⊥π₁ и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:

Рисунок 7.12 – Пересечение прямой с поверхностью сферы

• Введём π₃⊥π₁ и π₃//σ₁. Построим проекцию окружности сечения на π₃ и проекцию А₃В₃.
• Находим точки их пересечения 1₂ и 2₃.
• Определим видимость участков прямой.
• На π₁ точки 1 и 2 находятся на переднем полушарии, следовательно, на π₂ они видимы.

7.8. Коническая поверхность

Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).

Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом .

Плоская фигура, ограниченная конической поверхностью, называется основанием конуса .

Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса .

Если основание конуса является кругом, то конус называется круговым .

Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым .

Рисунок 7.13 – Принадлежность точки конической поверхности

Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).

1 способ . Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.

2 способ . Точка А лежит на параллели конуса радиусом r. На π₁ строим проекцию окружности (параллели) и по линии проекционной связи находим А₁. По двум проекциям точки строим третью.

7.9. Пересечение прямой с поверхностью конуса

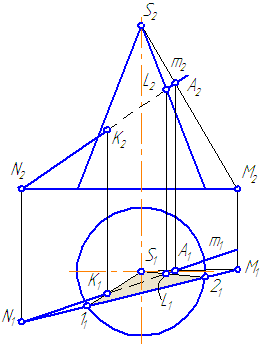
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.

1. Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
2. Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.

Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).

1. Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
2. Построим горизонтальные проекции этих объектов.
3. Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.

Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса

1. Построим её горизонтальную проекцию.
2. Соединим точки M₁N₁, на пересечении с окружностью основания получим точки 1 и 2.
3. Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
4. На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
5. Определим видимость прямой относительно поверхности конуса.

На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.

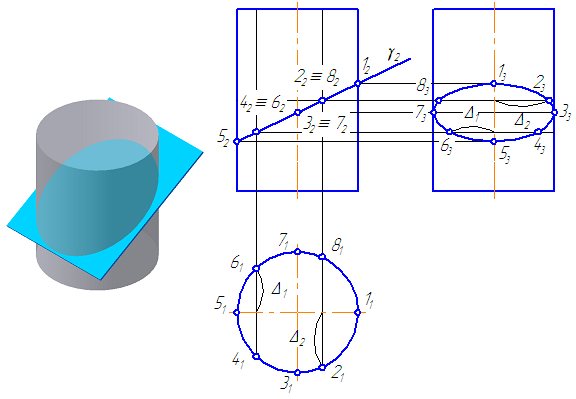
7.10. Пересечение цилиндра плоскостью

Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

1. Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
2. Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
3. Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

Рисунок 7.15 – пересечение цилиндра плоскостью

1. Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
2. Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π₁ произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
3. Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π₃. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ₁ и откладываем его по соответствующей линии связи на π₃. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.

7.11. Пересечение сферы плоскостью

Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).

7.12. Пересечение конуса плоскостью

Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

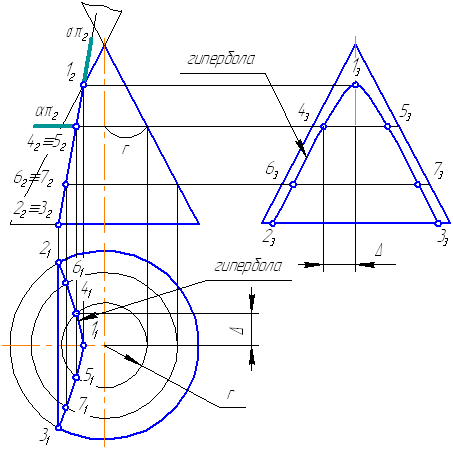
Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

7.13. Задачи для самостоятельной работы

1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).

Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).

Рисунок 7.21

Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).

Рисунок 7.23

источники:

http://www.evkova.org/peresechenie-poverhnostej-vrascheniya-ploskostyu

Лекция 7. Поверхности