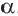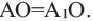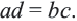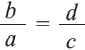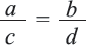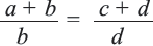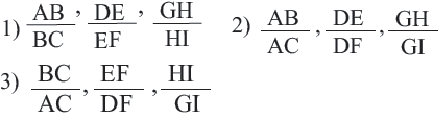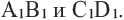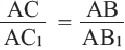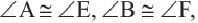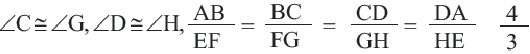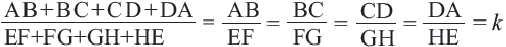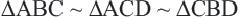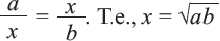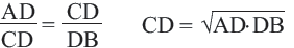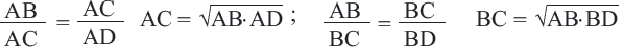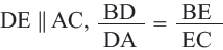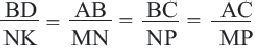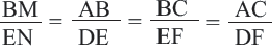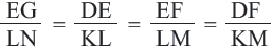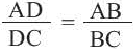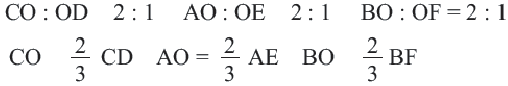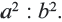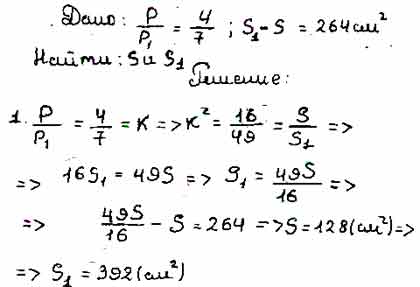Содержание
- Как узнать, похожи ли два многоугольника
- Пример 1: Определение длины и периметра с учетом масштабного коэффициента
- Пример 2: Определение длины соответствующих сторон похожих многоугольников
- Пример 3: Определение площади меньшего многоугольника по диагоналям и площадям
- Пример 4: Нахождение масштабных коэффициентов, длин сторон и периметров похожих многоугольников
- Пример 5: Нахождение масштабного коэффициента по периметрам подобных параллелограммов
- Пример 6: Решение проблемы похожих многоугольников с учетом соотношения площадей
- Пример 7: Определение площади большего треугольника с учетом периметров похожих многоугольников
- Пример 8: Подобные многоугольники с учетом суммы площадей и периметров
- Пример 9: Проблема с похожими многоугольниками
- Пример 10: Коэффициенты масштабирования и длины сторон похожих многоугольников
- Изучите другие статьи о геометрии
Похожие полигоны
АL = площадь большего многоугольника
Аs = площадь меньшего многоугольника
SL = длина более длинной соответствующей стороны
SS = длина более короткой соответствующей стороны
dL = длина более длинной соответствующей диагонали
dS = длина более короткой соответствующей диагонали
На показанных рисунках предполагается, что шестиугольник ABCDEF и PQRSTU подобны. Из определения подобных многоугольников можно сказать, что A P, B Q, C R, D S, E T и F U.
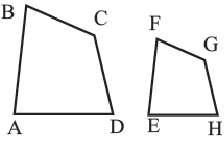
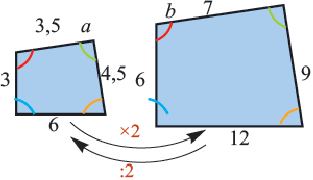
Например, рассмотрим следующие четырехугольники с учетом их сторон. Отметим, что A P, B Q, C R, D S. Находя отношения соответствующих сторон, получаем следующее.
Из приведенного выше решения следует, что AB / PQ = BC / QR = CD / RS = DA / SP = 5. По определению похожих многоугольников мы можем заключить, что четырехугольники ABCD и PQRS подобны. В символах ABCD ~ PQRS.
Как вы можете заметить, обычное отношение 5 — это масштабный коэффициент от ABCD до PQRS. Это означает, что все длины сторон PQRS должны быть умножены на масштабный коэффициент 5, чтобы получить размер сторон ABCD, поскольку ABCD — это больший четырехугольник.
Как узнать, похожи ли два многоугольника
Чтобы гарантировать, что n-сторонние многоугольники, n> 3, подобны, необходимо, чтобы выполнялись оба условия в определении похожих многоугольников. Даже если известно, что соответствующие углы двух многоугольников совпадают, из этого не следует, что многоугольники подобны. Итак, чтобы мы могли проверить, похожи ли два многоугольника, должны быть выполнены два условия.
- Соответствующие углы двух многоугольников совпадают.
- Длины соответствующих сторон пропорциональны.
Обратите внимание на рисунок A. Обратите внимание, что все соответствующие углы являются прямыми углами и, следовательно, конгруэнтны, но соответствующие стороны не пропорциональны. Кроме того, пропорциональность соответствующих сторон двух многоугольников не гарантирует схожести многоугольников. Также обратите внимание на рисунок B. Квадрат PQRS и ромб XYZW имеют пропорциональные стороны, но не идентичны.
Пример 1: Определение длины и периметра с учетом масштабного коэффициента
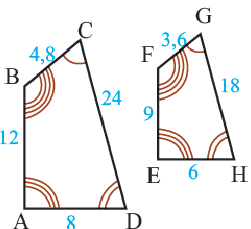
Четырехугольники ABCD и EFGH схожи с масштабным коэффициентом.
- Найдите длины a, b, c, d четырехугольника EFGH.
- Найдите отношение периметров четырехугольника ABCD и EFGH.
Решение
Учитывая масштабный коэффициент, вычислите значения a, b, c и d четырехугольника EFGH, умножив заданные длины сторон ABCD на масштабный коэффициент. Обратите внимание, что масштабный коэффициент равен делению большей длины на меньшую длину.
Масштабный коэффициент = большая длина / меньшая длина
= a / EF
= а / 5
а = 5 / ()
а = 5 х 3
а = 15
= b / BC
= b / 2
б = 2 / ()
б = 2 х 3
б = 6
= c / DC
= c / 3
с = 3 / ()
с = 3 х 3
с = 9
= d / AD
= d / 4
d = 4 / ()
г = 4 х 3
d = 12
Для отношения периметров ABCD и EFGH вычислите значение ребер.
P (ABCD) = 2 + 3 + 4 + 5
P (ABCD) = 14
P (EFGH) = 6 + 9 + 12 + 15
P (EFGH) = 42
Соотношение периметров = меньший периметр / больший периметр
Соотношение периметров = 14/42
Соотношение периметров =
Как видите, отношение периметра равно заданному коэффициенту масштабирования.
Окончательный ответ
Длины a, b, c, d четырехугольника EFGH равны 15, 6, 9 и 12 соответственно. Отношение периметров ABCD и EFGH равно заданному масштабному коэффициенту.
Пример 2: Определение длины соответствующих сторон похожих многоугольников
Площадь двух одинаковых многоугольников 120 см.2 и 30 см2. Если сторона меньшего многоугольника имеет длину 3 сантиметра, найдите длину соответствующей стороны большего многоугольника.
Решение
Пусть AL — площадь большего многоугольника, а AS — площадь меньшего многоугольника. Обратите внимание, что заданная длина стороны меньшего многоугольника SS составляет 3 сантиметра. Подставьте указанные величины в уравнение.
АL = 120 см2
АS = 30 см2
SS = 3 см
АL / АS = (SL/ SS)2
120/30 = (SL/3)2
4 = (SL/3)2
4 = SL2 / 9
SL2 = 9 х 4
SL2 = 36
SL2 = 36
SL = 6 см
Окончательный ответ
Длина соответствующей стороны большего многоугольника SL равен 6 сантиметрам.
Пример 3: Определение площади меньшего многоугольника по диагоналям и площадям
Соответствующие диагонали двух одинаковых многоугольников имеют длину 4 см и 7 см. Если площадь большего многоугольника составляет 147 квадратных сантиметров, найдите значение As.
Решение
Пусть dL — длина диагонали большего многоугольника, а dS соответствующей диагонали меньшего многоугольника. Учитывая, что AL = 147 см2, вычислите площадь меньшего многоугольника, используя упомянутые ранее формулы.
АL = 147 см2
ds = 4 см
dL = 7 см
АL / АS = (dL/ дS)2
147 / АS = (7/4)2
147 / АS = 49/16
АS = 147 (16) / (49)
АS = 48 см2
Окончательный ответ
Площадь меньшего многоугольника равна As = 48 см.2.
Пример 4: Нахождение масштабных коэффициентов, длин сторон и периметров похожих многоугольников
Учитывая, что PQRS ~ JKLM, найдите следующее.
- Коэффициент масштабирования от PQRS до JKLM
- Коэффициент масштабирования от JKLM до PQRS
- Значения x, y и w
- Периметр каждого многоугольника
- Отношение суммы граней PQRS к сумме сторон JKLM
Решение
При получении масштабного коэффициента от PQRS до JKLM постарайтесь найти длины сторон, указанные на рисунке. Разделите заданную длину PQRS на соответствующую длину стороны JKLM. С другой стороны, найдите коэффициент масштабирования JKLM в PQRS, изменив указанную процедуру в обратном порядке, разделив размер соответствующих сторон JKLM на размер PQRS.
PQ / JK = 15/12
PQ / JK = 4/3
JK / PQ = 12/15
JK / PQ = ¾
Поскольку мы получили масштабные коэффициенты JKLM в PQRS и PQRS в JKLM, теперь мы можем вычислить значения x, y и w.
х = KL х (4/3)
х = 10 х (4/3)
x = 40/3 единицы
у = LM x (4/3)
у = 16 х (4/3)
y = 64/3 единицы
w = PS x (¾)
ш = 25 х (¾)
w = 75/4 единицы
Теперь, когда все стороны одинаковых многоугольников завершены, определите периметр, просто добавив все стороны по отдельности. Затем получите отношение периметра PQRS к периметру JKLM.
P (PQRS) = 25 + 15 + 40/3 + 64/3
P (PQRS) = 224/3 = 74,6 единиц
P (JKLM) = 12 + 10 + 16 + 75/4
P (JKLM) = 227/4 = 56,75 единиц
Соотношение периметров = Периметр PQRS / Периметр JKLM
Соотношение периметров = 74,6 / 56,75
Соотношение периметров = 4/3
Окончательный ответ
Масштабные коэффициенты от PQRS до JKLM и от JKLM до PQRS составляют 4/3 и ¾ соответственно.
Значения x, y и w равны 40/3, 64/3 и 75/4 соответственно.
Периметр PQRS составляет 74,6 единицы.
Периметр JKLM составляет 56,75 единиц.
Отношение периметра PQRS к JKLM составляет 4/3, что равно масштабному коэффициенту PQRS к JKLM.
Пример 5: Нахождение масштабного коэффициента по периметрам подобных параллелограммов
Периметр параллелограммов PQRS и JKLM составляет 94 см и 18,8 см соответственно. Если два параллелограмма похожи, найдите масштабный коэффициент параллелограмма PQRS к параллелограмму JKLM.
Решение
Помните, что соотношение периметров двух одинаковых многоугольников равно их масштабному коэффициенту. Чтобы получить масштабный коэффициент параллелограмма от PQRS до JKLM, разделите периметр PQRS, равный 94 сантиметрам, на окружность JKLM, которая составляет 18,8 сантиметра.
Коэффициент масштабирования от PQRS до JKLM = P (PQRS) / P (JKLM)
Масштабный коэффициент от PQRS до JKLM = 94 / 18,8
Масштабный коэффициент от PQRS до JKLM = 5
Окончательный ответ
Коэффициент масштабирования параллелограмма PQRS на параллелограмм JKLM равен пяти.
Пример 6: Решение проблемы похожих многоугольников с учетом соотношения площадей
Площади двух одинаковых треугольников находятся в соотношении 25:16.
- Найдите длину стороны большего треугольника, если соответствующая сторона меньшего треугольника имеет длину 80 единиц.
- Найдите длину медианы большего треугольника, если соответствующая медиана меньшего треугольника имеет длину 10 единиц.
- Найдите длину биссектрисы меньшего треугольника, если соответствующая биссектриса большего треугольника имеет длину 15 единиц.
- Найдите периметр меньшего треугольника, если периметр большего треугольника равен 125.
Решение
Нам дано соотношение площадей двух одинаковых треугольников, которое составляет 25:16. При нахождении длины стороны большего треугольника по соответствующей стороне меньшего треугольника SS = 80 единиц, используйте формулу для соотношения площадей и соответствующих сторон.
АL / АS = (SL/ SS)2
25/16 = (SL/80)2
SL = 100 единиц
Относительно вопросов, касающихся медиан и биссектрис угла, помните, что два треугольника подобны, если отношение любых двух соответствующих сегментов (высоты, медианы или биссектрисы угла) равно доле любых двух соответствующих сторон. Теперь, когда мы получили значение более короткой стороны, создайте формулу пропорции для длин сторон и соответствующих сегментов, таких как медианы и биссектрисы.
SL / SS = ML / МS
100/80 = МL / 10
ML = 12,5 единиц
SL / SS = ABL / ABS
100/80 = 15 / ABS
ABS = 12 единиц
Наконец, решите периметр меньшего треугольника с учетом периметра большего треугольника PL = 125. Напомним, что отношение периметров двух одинаковых многоугольников равно отношению длин двух соответствующих сторон.
пL / ПS = SL / SS
125 / PS = 100 / 80
пS = 100 единиц
Окончательный ответ
Длина стороны большего треугольника равна 100 единицам.
Длина медиан большего треугольника равна 12,5 единицам.
Длина биссектрисы меньшего треугольника равна 12 единицам.
Периметр меньшего треугольника равен 100 единицам.
Пример 7: Определение площади большего треугольника с учетом периметров похожих многоугольников
Два одинаковых многоугольника имеют периметр 32 см и 24 см. Если площадь меньшего треугольника составляет 27 квадратных сантиметров, найдите площадь большего треугольника.
Решение
Учитывая периметры двух похожих многоугольников, вычислите отношение соответствующих сторон. Когда отношение соответствующих сторон станет доступным, вычислите площадь меньшего треугольника, используя формулу для отношения площадей и соответствующих сторон.
пL / ПS = SL / SS
32/24 = SL / SS
SL / SS = 4/3
АL / Аs = (SL/ SS)2
АL / 27 = (4/3)2
АL = 48 квадратных сантиметров
Окончательный ответ
Площадь большего треугольника равна 48 квадратным сантиметрам.
Пример 8: Подобные многоугольники с учетом суммы площадей и периметров
Сумма площадей двух одинаковых многоугольников составляет 65 квадратных единиц. Если их периметр равен 12 единицам и 18 единицам, найдите площадь большего многоугольника.
Решение
Составьте математическое уравнение, описывающее сумму площадей двух похожих многоугольников. Оттуда выразите площадь меньшего многоугольника через большой многоугольник.
АL + АS = 65 квадратных единиц
АS = 65 — АL
Вычислите пропорцию соответствующих длин двух похожих многоугольников, используя заданные периметры.
пL = 18 единиц
пS = 12 единиц
пL / ПS = SL / SS
18/12 = SL / SS
SL / SS = 3/2
Воспользуйтесь формулой соотношения площадей и соответствующих сторон. Подставьте полученное уравнение для площади меньшего многоугольника в уравнение.
АL / АS = (SL/ SS)2
АL / (65 — АL) = (3/2)2
АL = 45 квадратных единиц
Окончательный ответ
Площадь большего многоугольника составляет 45 квадратных единиц.
Пример 9: Проблема с похожими многоугольниками
Предположим, Альфред хочет, чтобы фотография размером с бумажник была похожа на фотографию 8 x 10. Если бы фотография размером с бумажник была шириной 2,5 дюйма, какой длины она была бы?
Решение
Больший многоугольник имеет размер 8 дюймов на 10 дюймов на основе данной фотографии размером с бумажник. Напомним, что похожие многоугольники подобны, если длины соответствующих сторон пропорциональны. Вычислите высоту фотографии размера бумажника, создав уравнение пропорций.
8 / 2,5 = 10 / год
y = 3,125 дюйма
Окончательный ответ
Размер фото кошелька составляет 2,5 дюйма и 3,125 дюйма.
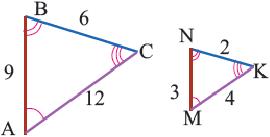
Пример 10: Коэффициенты масштабирования и длины сторон похожих многоугольников
Определите расширение и найдите его масштабный коэффициент. Затем найдите значения x, y и z.
Решение
Расширение — это состояние расширения, расширения или расширения. Следовательно, расширенные многоугольники можно рассматривать как аналогичные многоугольники. Вычислите масштабный коэффициент многоугольника и расширенного многоугольника, получив отношение двух соответствующих сторон. После вычисления вычислите значения x, y и z, найдя отношения соответствующих сторон.
Масштабный коэффициент = PQ / PQ
Масштабный коэффициент = 10/20
Масштабный коэффициент = ½
Масштабный коэффициент = 8 / x
½ = 8 / х
x = 16 единиц
Масштабный коэффициент = 10 / год
½ = 10 / год
y = 20 единиц
Масштабный коэффициент = 8 / z
½ = 8 / z
z = 16 единиц
Окончательный ответ
Значение масштабного коэффициента составляет ½. Полученные значения для x, y и z равны 16, 8 и 16 единиц.
Изучите другие статьи о геометрии
- Методы калькуляции многоугольников в плоской геометрии
Решение проблем, связанных с плоской геометрией, особенно с полигонами, можно легко решить с помощью калькулятора. Вот исчерпывающий набор задач о многоугольниках, решаемых с помощью калькуляторов. - Методы калькуляции четырехугольников в плоской геометрии
Узнайте, как решать задачи, связанные с четырехугольниками в плоской геометрии. Он содержит формулы, методы калькулятора, описания и свойства, необходимые для интерпретации и решения задач Четырехугольника. - Нахождение площади поверхности и объема створок пирамиды и конуса
Узнайте, как рассчитать площадь поверхности и объем усеченных углов правильного кругового конуса и пирамиды. В этой статье рассказывается о концепциях и формулах, необходимых для решения площади поверхности и объема усеченных твердых тел. - Определение площади поверхности и объема усеченных цилиндров и призм
Узнайте, как вычислить площадь поверхности и объем усеченных твердых тел. В этой статье рассматриваются концепции, формулы, проблемы и решения, касающиеся усеченных цилиндров и призм. - Полное руководство по треугольнику 30-60-90 (с формулами и примерами)
Эта статья представляет собой полное руководство по решению задач на 30-60-90 треугольниках. Он включает формулы паттернов и правила, необходимые для понимания концепции треугольников 30-60-90. Также приведены примеры, показывающие пошаговую процедуру, как это сделать. - Односторонние внутренние углы: теорема, доказательство и примеры
В этой статье вы можете изучить концепцию теоремы об односторонних внутренних углах в геометрии, решая различные приведенные примеры. В статье также содержится обращение к теореме о односторонних внутренних углах и ее доказательство.
Найди верный ответ на вопрос ✅ «Периметр подобных многоугольников относятся как 5:7 а разность площадей=864 см (квадратных). найдите площадь многоугольника. …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Периметр подобных многоугольников относятся как 5:7 а разность площадей=864 см (квадратных). найдите площадь многоугольника.
Отношение площадей двух подобных четырехугольников
Периметры двух подобных многоугольников относятся как 3 : 5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P1 и S1, периметр и площадь большего многоугольника соответственно равны P2 и S2. Поэтому
Преобразование фигур в геометрии с примерами решения
Содержание:
Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.
Поворот:
Пусть, заданы точка О и угол
1. Если точка А не совпадает с точкой О, то
2. Если точка А совпадает с точкой О, то точки 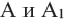
Пример 1. Угол поворота 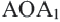
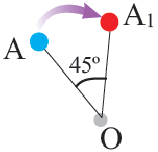
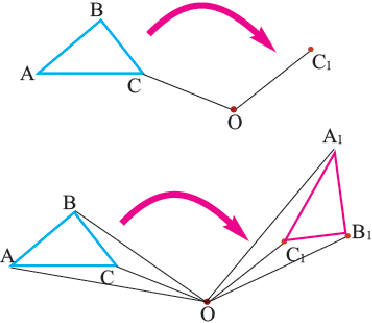
Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника 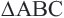
Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.
Исследуйте и начертите в тетради:
На рисунке показана последовательность шагов, которые выполняются при повороте треугольника 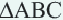
При повороте на угол 90″ в направлении по часовой стрелке координаты вершин изменяются следующим образом.
Отношения, пропорция
Свойства пропорции
Если 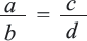
Если 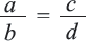
Если 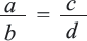
Если 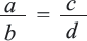
Пропорциональные отрезки
Практическая работа. Пропорциональные отрезки.
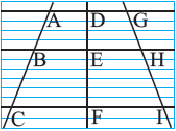
1. Начертите в тетради 3 параллельные прямые.
2. Проведите 3 секущие, которые пересекают эти прямые.
3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.
4. Запишите и вычислите следующие отношения
5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки
Если для отрезков АВ, CD, 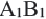
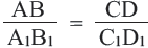
Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, 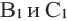
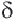
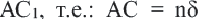
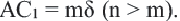
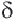
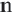
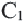
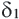
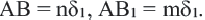
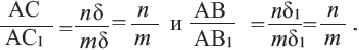
Подобные четырехугольники, подобные треугольники
Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.
Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как,
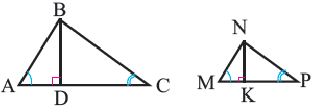
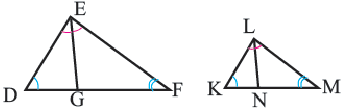
У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для 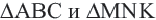
Так как 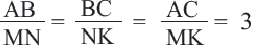
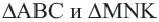
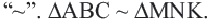
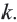
Периметр подобных многоугольников
Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)
Если 
Запишите доказательство теоремы, приняв коэффициент подобия за 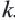
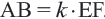
Признаки подобия треугольников
Признак подобия УУ (угол угол)
Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.
Признак подобия ССС
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.
Признак подобия СУС
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.
Подобие прямоугольных треугольников
Высота, проведенная к гипотенузе
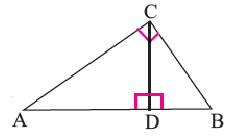
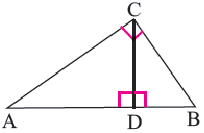
Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.
Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.
Среднее геометрическое
Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число 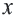
Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.
Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.
Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
Применение подобия треугольников
Пропорциональные отрезки
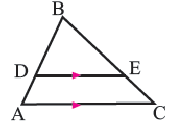
Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.
Если
Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.
Если 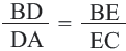
Высоты, медианы и биссектрисы подобных треугольников
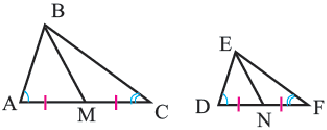
Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.
Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.
Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.
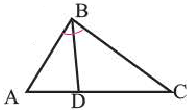
Свойство биссектрисы треугольника
Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.
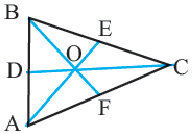
Теорема. Свойство медиан треугольника
Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.
Точка пересечения медиан называется центром тяжести треугольника.
Доказательство теоремы представлено в виде двухстолбчатой таблицы.
Дано: 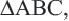
Доказательство: соединим точки O и E.
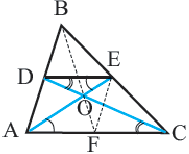
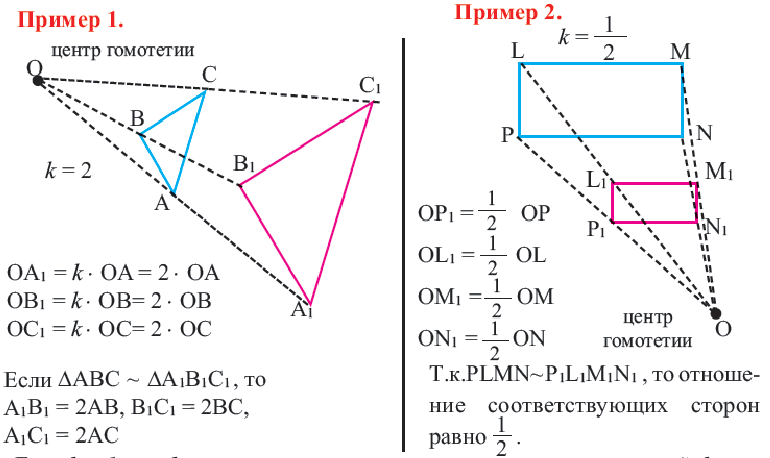
Преобразование подобия, гомотетия
Гомотетия
Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки 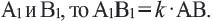
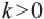
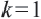
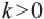
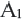
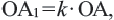
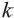
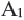
Если 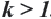
Если 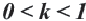
Если 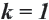
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно 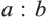
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многоугольник
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Подобие фигур
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
Для обозначения подобия фигур употребляется знак 



Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.
Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: 

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: 



Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
На рисунке 2.436 изображены два подобных пятиугольника 



Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).
Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
http://www.evkova.org/preobrazovanie-figur
http://natalibrilenova.ru/podobie-figur/

Valentina6799
+16
Решено
8 лет назад
Геометрия
5 — 9 классы
Периметры подобных многоугольников относятся как 5 : 7. Разница площадей =864 см2. Найти площади многоугольников
Смотреть ответ
1
Ответ проверен экспертом
3
(9 оценок)
8
LFP
8 лет назад
Светило науки — 7418 ответов — 43607 раз оказано помощи
периметры относятся как коэффициент подобия,
площади относятся как квадрат коэффициента подобия…
S1 / S2 = 25 / 49
S1 = 25*S2 / 49
S2 —большая площадь
S2 — S1 = 864
S2 — 25*S2 / 49 = 864
49*S2 — 25*S2 = 864*49
24*S2 = 24*36*49
S2 = 36*49 = 1764
S1 = 25*36*49 / 49 = 900
(9 оценок)
https://vashotvet.com/task/8767054
UCHEES.RU — помощь студентам и школьникам
В 3:09 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Периметры подобных многоугольников относятся как 4 : 7, а разность их площадей равна 264 см2. Найдите площади многоугольников.
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Периметры подобных многоугольников относятся как 4 : 7, а разность их площадей равна 264 см2. Найдите площади многоугольников.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Анисимова Нонна Ефимовна — автор студенческих работ, заработанная сумма за прошлый месяц 55 341 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 — 2023 — UCHEES.RU