Период обращения как найти астрономия

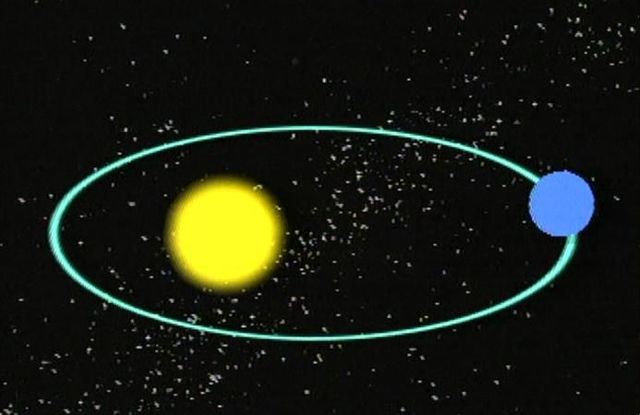
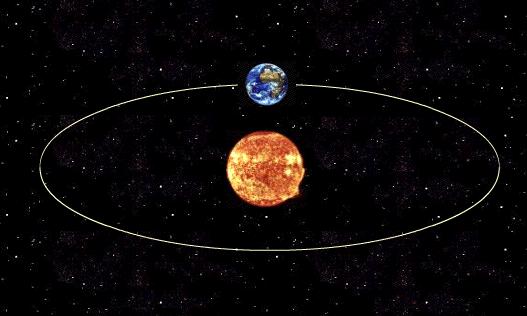
Синодическим периодом обращения(S) планеты называется промежуток времени
между ее двумя последовательными
одноименными конфигурациями.

Сидерическим или звездным периодом
обращения(Т) планеты называется
промежуток времени, в течение которого
планета совершает один полный оборот
вокруг Солнца по своей орбите.

Сидерический период обращения Земли
называется звездным годом (Т_☺).
Между этими тремя периодами можно
установить простую математическую
зависимость из следующих рассуждений.
Угловое перемещение по орбите за сутки
у планеты равно,
а у Земли.
Разность суточных угловых перемещений
планеты и Земли (или Земли и планеты)
есть видимое смещение планеты за сутки,
т.е..
Отсюда для нижних планет

(2.1)

для верхних планет

(2.2)

Эти равенства называются уравнениями
синодического движения.

Непосредственно из наблюдений могут
быть определены только синодические
периоды обращений планет S и сидерический
период обращения Земли, т.е. звездный
год Т_☺. Сидерические же периоды
обращений планет Т вычисляются по
соответствующему уравнению синодического
движения.

Продолжительность звездного года равна
365,26… средних солнечных суток.

7.4. Законы Кеплера

Кеплер был сторонником учения Коперника
и поставил перед собой задачу
усовершенствовать его систему по
наблюдениям Марса, которые на протяжении
двадцати лет производил датский астроном
Тихо Браге (1546-1601) и в течение нескольких
лет — сам Кеплер.

Вначале Кеплер разделял традиционное
убеждение, что небесные тела могут
двигаться только по кругам, и поэтому
он потратил много времени на то, чтобы
подобрать для Марса круговую орбиту.

После многолетних и очень трудоемких
вычислений, отказавшись от общего
заблуждения о кругообразности движений,
Кеплер открыл три закона планетных
движений, которые в настоящее время
формулируются следующим образом:

1. Все планеты движутся по эллипсам, в
одном из фокусов которых (общем для всех
планет) находится Солнце.

2. Радиус-вектор планеты в равные
промежутки времени описывает равновеликие
площади.

3. Квадраты сидерических периодов
обращений планет вокруг Солнца
пропорциональны кубам больших полуосей
их эллиптических орбит.

Как известно, у эллипса сумма расстояний
от какой-либо его точки до двух неподвижных
точек f₁и f₂, лежащих на его
оси АП и называемых фокусами, есть
величина постоянная, равная большой
оси АП (рис. 27). Расстояние ПО (или ОA), где
О — центр эллипса, называется большой
полуосью,
а отношение— эксцентриситетом эллипса. Последний
характеризует отклонение эллипса от
окружности, у которой е = 0.

Орбиты планет мало отличаются от
окружностей, т.е. их эксцентриситеты
невелики. Наименьший эксцентриситет
имеет орбита Венеры (е = 0,007), наибольший
— орбита Плутона (е = 0,247). Эксцентриситет
земной орбиты
е = 0,017.

Согласно первому закону Кеплера Солнце
находится в одном из фокусов эллиптической
орбиты планеты. Пусть на рис. 27,а это
будет фокус f₁(С — Солнце). Тогда
наиболее близкая к Солнцу точка орбиты
П называетсяперигелием, а наиболее
удаленная от Солнца точка A —афелием.
Большая ось орбиты АП называетсялинией
апсид, а линия f₂P, соединяющая
Солнце и планету Р на ее орбите, —радиусом-вектором планеты.

Расстояние планеты от Солнца в перигелии

q = а (1 — е), (2.3)

в афелии

Q = a (l + e). (2.4)

За среднее расстояние планеты от Солнца
принимается большая полуось орбиты

Согласно второму закону Кеплера площадь
СР₁Р₂, описанная радиусом-вектором
планеты за времяt
вблизи перигелия, равна площади СР₃Р₄, описанной им за то же времяt
вблизи афелия (рис. 27, б). Так как дуга
Р₁Р₂больше дуги Р₃Р₄, то, следовательно, планета вблизи
перигелия имеет скорость большую, чем
вблизи афелия. Иными словами, ее движение
вокруг Солнца неравномерно.

Скорость движения планеты в перигелии

(2.5)

в афелии

(2.6)

где v_c— средняя или круговая
скорость планеты при r = а. Круговая
скорость Земли равна 29,78 км/сек = 29,8
км/сек.

Третий закон Кеплера записывается так:

(2.7)

где Т₁и T₂— сидерические
периоды обращений планет, а₁и a₂— большие полуоси их орбит.

Если большие полуоси орбит планет
выражать в единицах среднего расстояния
Земли от Солнца (в астрономических
единицах), а периоды обращений планет
—
в годах, то для Земли а =1 и Т = 1 и
период обращения вокруг Солнца любой
планеты

(2.8)

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #

Как найти период обращения

Период обращения тела, которое движется по замкнутой траектории можно измерить при помощи часов. Если же обращение происходит слишком быстро, это делается после изменения некоторого числа полных обращений. Если тело вращается по окружности, и известна его линейная скорость, эта величина рассчитывается по формуле. Период обращения планеты рассчитывается по третьему закону Кеплера.

Вам понадобится

• — секундомер;
• — калькулятор;
• — справочные данные по орбитам планет.

Инструкция

Измерьте при помощи секундомера время, требующееся вращающемуся телу, чтобы прийти в исходную точку. Это и будет период его вращения. Если измерить вращения тела затруднительно, то измерьте время t, N полных обращений. Найдите отношение этих величин, это и будет период вращения данного тела T (T=t/N). Период измеряется в тех же величинах, что и время. В интернациональной системе измерения это секунда.

Если известна частота вращения тела, то найдите период, поделив число 1 на значение частоты ν (T=1/ν).

Если тело вращается по круговой траектории и известна его линейная скорость, рассчитайте период его вращения. Для этого измерьте радиус R траектории, по которой вращается тело. Убедитесь, что модуль скорости не изменяется со временем. Затем произведите расчет. Для этого поделите длину окружности, по которой движется тело, которая равна 2∙π∙R (π≈3,14), на скорость его вращения v. Результатом будет период вращения данного тела по окружности T=2∙π∙R/v.

Если нужно рассчитать период обращения планеты, которая движется вокруг звезды, используйте третий закон Кеплера. Если две планеты вращаются вокруг одной звезды, то квадраты периодов их обращения относятся как кубы больших полуосей их орбит. Если обозначить периоды обращения двух планет T1 и T2, большие полуоси орбит (они эллиптичные), соответственно, a1 и a2, то T1²/ T2²= a1³/a2³. Данные расчеты верны в том случае, если массы планет значительно уступают массе звезды.

Пример: Определите период обращения планеты Марс. Чтобы рассчитать эту величину, найдите длину большей полуоси орбиты Марса, a1 и Земли, a2 (как планеты, которая тоже вращается вокруг Солнца). Они равны a1=227,92∙10^6 км и a2=149,6∙10^6 км. Период вращения земли T2=365,25 суток (1 земной год). Тогда найдите период обращения марса, преобразовав формулу из третьего закона Кеплера, для определения периода вращения Марса Т1=√( T2²∙ a1³/a2³)=√( 365,25²∙ (227,92∙10^6)³/(149,6∙10^6)³)≈686,86 суток.

Источники:

• как найти обращения в тексте

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

From Wikipedia, the free encyclopedia

The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.

For celestial objects in general, the orbital period is determined by a 360° revolution of one body around its primary, e.g. Earth around the Sun.

Periods in astronomy are expressed in units of time, usually hours, days, or years.

Small body orbiting a central body[edit]

According to Kepler’s Third Law, the orbital period T of two point masses orbiting each other in a circular or elliptic orbit is:^[1]

where:

• a is the orbit’s semi-major axis
• G is the gravitational constant,
• M is the mass of the more massive body.

For all ellipses with a given semi-major axis the orbital period is the same, regardless of eccentricity.

Inversely, for calculating the distance where a body has to orbit in order to have a given orbital period T:

For instance, for completing an orbit every 24 hours around a mass of 100 kg, a small body has to orbit at a distance of 1.08 meters from the central body’s center of mass.

In the special case of perfectly circular orbits, the semimajor axis a is equal to the radius of the orbit, and the orbital velocity is constant and equal to

where:

• r is the circular orbit’s radius in meters,

This corresponds to 1⁄√2 times (≈ 0.707 times) the escape velocity.

Effect of central body’s density[edit]

For a perfect sphere of uniform density, it is possible to rewrite the first equation without measuring the mass as:

where:

• r is the sphere’s radius
• a is the orbit’s semi-major axis in metres,
• G is the gravitational constant,
• ρ is the density of the sphere in kilograms per cubic metre.

For instance, a small body in circular orbit 10.5 cm above the surface of a sphere of tungsten half a metre in radius would travel at slightly more than 1 mm/s, completing an orbit every hour. If the same sphere were made of lead the small body would need to orbit just 6.7 mm above the surface for sustaining the same orbital period.

When a very small body is in a circular orbit barely above the surface of a sphere of any radius and mean density ρ (in kg/m³), the above equation simplifies to (since M = Vρ = 4/3πa³ρ)

Thus the orbital period in low orbit depends only on the density of the central body, regardless of its size.

So, for the Earth as the central body (or any other spherically symmetric body with the same mean density, about 5,515 kg/m³,^[2] e.g. Mercury with 5,427 kg/m³ and Venus with 5,243 kg/m³) we get:

T = 1.41 hours

and for a body made of water (ρ ≈ 1,000 kg/m³),^[3] or bodies with a similar density, e.g. Saturn’s moons Iapetus with 1,088 kg/m³ and Tethys with 984 kg/m³ we get:

T = 3.30 hours

Thus, as an alternative for using a very small number like G, the strength of universal gravity can be described using some reference material, such as water: the orbital period for an orbit just above the surface of a spherical body of water is 3 hours and 18 minutes. Conversely, this can be used as a kind of «universal» unit of time if we have a unit of density.

Two bodies orbiting each other[edit]

In celestial mechanics, when both orbiting bodies’ masses have to be taken into account, the orbital period T can be calculated as follows:^[4]

where:

• a is the sum of the semi-major axes of the ellipses in which the centers of the bodies move, or equivalently, the semi-major axis of the ellipse in which one body moves, in the frame of reference with the other body at the origin (which is equal to their constant separation for circular orbits),
• M₁ + M₂ is the sum of the masses of the two bodies,
• G is the gravitational constant.

In a parabolic or hyperbolic trajectory, the motion is not periodic, and the duration of the full trajectory is infinite.

[edit]

For celestial objects in general, the orbital period typically refers to the sidereal period, determined by a 360° revolution of one body around its primary relative to the fixed stars projected in the sky. For the case of the Earth orbiting around the Sun, this period is referred to as the sidereal year. This is the orbital period in an inertial (non-rotating) frame of reference.

Orbital periods can be defined in several ways. The tropical period is more particularly about the position of the parent star. It is the basis for the solar year, and respectively the calendar year.

The synodic period refers to not the orbital relation to the parent star, but to other celestial objects, making it not a mere different approach to the orbit of an object around its parent, but a period of orbital relations with other objects, normally Earth, and their orbits around the Sun. It applies to the elapsed time where planets return to the same kind of phenomenon or location, such as when any planet returns between its consecutive observed conjunctions with or oppositions to the Sun. For example, Jupiter has a synodic period of 398.8 days from Earth; thus, Jupiter’s opposition occurs once roughly every 13 months.

There are many periods related to the orbits of objects, each of which are often used in the various fields of astronomy and astrophysics, particularly they must not be confused with other revolving periods like rotational periods. Examples of some of the common orbital ones include the following:

• The synodic period is the amount of time that it takes for an object to reappear at the same point in relation to two or more other objects. In common usage, these two objects are typically Earth and the Sun. The time between two successive oppositions or two successive conjunctions is also equal to the synodic period. For celestial bodies in the solar system, the synodic period (with respect to Earth and the Sun) differs from the tropical period owing to Earth’s motion around the Sun. For example, the synodic period of the Moon’s orbit as seen from Earth, relative to the Sun, is 29.5 mean solar days, since the Moon’s phase and position relative to the Sun and Earth repeats after this period. This is longer than the sidereal period of its orbit around Earth, which is 27.3 mean solar days, owing to the motion of Earth around the Sun.
• The draconitic period (also draconic period or nodal period), is the time that elapses between two passages of the object through its ascending node, the point of its orbit where it crosses the ecliptic from the southern to the northern hemisphere. This period differs from the sidereal period because both the orbital plane of the object and the plane of the ecliptic precess with respect to the fixed stars, so their intersection, the line of nodes, also precesses with respect to the fixed stars. Although the plane of the ecliptic is often held fixed at the position it occupied at a specific epoch, the orbital plane of the object still precesses, causing the draconitic period to differ from the sidereal period.^[5]
• The anomalistic period is the time that elapses between two passages of an object at its periapsis (in the case of the planets in the Solar System, called the perihelion), the point of its closest approach to the attracting body. It differs from the sidereal period because the object’s semi-major axis typically advances slowly.
• Also, the tropical period of Earth (a tropical year) is the interval between two alignments of its rotational axis with the Sun, also viewed as two passages of the object at a right ascension of 0 hr. One Earth year is slightly shorter than the period for the Sun to complete one circuit along the ecliptic (a sidereal year) because the inclined axis and equatorial plane slowly precess (rotate with respect to reference stars), realigning with the Sun before the orbit completes. This cycle of axial precession for Earth, known as precession of the equinoxes, recurs roughly every 25,772 years.^[6]

Periods can be also defined under different specific astronomical definitions that are mostly caused by the small complex external gravitational influences of other celestial objects. Such variations also include the true placement of the centre of gravity between two astronomical bodies (barycenter), perturbations by other planets or bodies, orbital resonance, general relativity, etc. Most are investigated by detailed complex astronomical theories using celestial mechanics using precise positional observations of celestial objects via astrometry.

Synodic period[edit]

One of the observable characteristics of two bodies which orbit a third body in different orbits, and thus have different orbital periods, is their synodic period, which is the time between conjunctions.

An example of this related period description is the repeated cycles for celestial bodies as observed from the Earth’s surface, the synodic period, applying to the elapsed time where planets return to the same kind of phenomenon or location. For example, when any planet returns between its consecutive observed conjunctions with or oppositions to the Sun. For example, Jupiter has a synodic period of 398.8 days from Earth; thus, Jupiter’s opposition occurs once roughly every 13 months.

If the orbital periods of the two bodies around the third are called T₁ and T₂, so that T₁ < T₂, their synodic period is given by:^[7]

Examples of sidereal and synodic periods[edit]

Table of synodic periods in the Solar System, relative to Earth:^{[citation needed]}

Object	Sidereal period	Synodic period
(yr)	(d)	(yr)	(d)[8]
Mercury	0.240846	87.9691 days	0.317	115.88
Venus	0.615	224.7 days[9]	1.599	583.9
Earth	1	365.25636 solar days	—
Mars	1.881	687.0[10]	2.135	779.9
Jupiter	11.86	4331[11]	1.092	398.9
Saturn	29.46	10,747[12]	1.035	378.1
Uranus	84.01	30,589[13]	1.012	369.7
Neptune	164.8	59,800[14]	1.006	367.5
134340 Pluto	248.1	90,560[15]	1.004	366.7
Moon	0.0748	27.32 days	0.0809	29.5306
99942 Apophis (near-Earth asteroid)	0.886		7.769	2,837.6
4 Vesta	3.629		1.380	504.0
1 Ceres	4.600		1.278	466.7
10 Hygiea	5.557		1.219	445.4
2060 Chiron	50.42		1.020	372.6
50000 Quaoar	287.5		1.003	366.5
136199 Eris	557		1.002	365.9
90377 Sedna	12050		1.0001	365.3[citation needed]

In the case of a planet’s moon, the synodic period usually means the Sun-synodic period, namely, the time it takes the moon to complete its illumination phases, completing the solar phases for an astronomer on the planet’s surface. The Earth’s motion does not determine this value for other planets because an Earth observer is not orbited by the moons in question. For example, Deimos’s synodic period is 1.2648 days, 0.18% longer than Deimos’s sidereal period of 1.2624 d.^{[citation needed]}

Synodic periods relative to other planets[edit]

The concept of synodic period applies not just to the Earth, but also to other planets as well, and the formula for computation is the same as the one given above. Here is a table which lists the synodic periods of some planets relative to each other:

Orbital period (years)

Relative to	Mars	Jupiter	Saturn	Chiron	Uranus	Neptune	Pluto	Quaoar	Eris
Sun	1.881	11.86	29.46	50.42	84.01	164.8	248.1	287.5	557.0
Mars		2.236	2.009	1.954	1.924	1.903	1.895	1.893	1.887
Jupiter			19.85	15.51	13.81	12.78	12.46	12.37	12.12
Saturn				70.87	45.37	35.87	33.43	32.82	31.11
2060 Chiron					126.1	72.65	63.28	61.14	55.44
Uranus						171.4	127.0	118.7	98.93
Neptune							490.8	386.1	234.0
Pluto								1810.4	447.4
50000 Quaoar									594.2

Example of orbital periods: binary stars[edit]

Binary star	Orbital period.
AM Canum Venaticorum	17.146 minutes
Beta Lyrae AB	12.9075 days
Alpha Centauri AB	79.91 years
Proxima Centauri – Alpha Centauri AB	500,000 years or more

See also[edit]

• Geosynchronous orbit derivation
• Rotation period – time that it takes to complete one revolution around its axis of rotation
• Satellite revisit period
• Sidereal time
• Sidereal year
• Opposition (astronomy)
• List of periodic comets

Notes[edit]

Bibliography[edit]

• Bate, Roger B.; Mueller, Donald D.; White, Jerry E. (1971), Fundamentals of Astrodynamics, Dover

External links[edit]

«Небесная механика», как было принято называть науку о звездах во времена Исаака Ньютона, подчиняется классическим законам движения тел. Одними из важных характеристик этого движения являются различные периоды обращения космических объектов по своим орбитам. В статье пойдет речь о сидерическом и синодическом периодах обращения звезд, планет и их естественных спутников.

Понятие о синодическом и сидерическом временных периодах

Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.

Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.

Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.

Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.

Главное отличие между сидерическим и синодическим периодами

Как уже было сказано, сидерический — это реальный период обращения, а синодический — это кажущийся, однако в чем же главная разница между этими понятиями?

Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие «сидерический период» принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период — это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.

Формула расчета сидерического периода

Для определения реального периода обращения планеты вокруг своей звезды или естественного спутника вокруг своей планеты, необходимо воспользоваться третьим законом Кеплера, который устанавливает взаимосвязь между реальным орбитальным периодом объекта и полудлиной его большой оси. В общем случае форма орбиты любого космического тела представляет собой эллипс.

Формула для определения сидерического периода имеет вид: T = 2*pi*√(a3/(G*M)), где pi = 3,14 — число пи, a — полудлина большой оси эллипса, G = 6,674*10-11 м3/(кг*с2) — универсальная гравитационная постоянная, M — масса объекта, вокруг которого осуществляется вращение.

Таким образом, зная параметры орбиты любого объекта, а также массу звезды, можно легко вычислить значение реального периода обращения этого объекта по своей орбите.

Расчет синодического временного периода

Как вычислить? Синодический период планеты или ее естественного спутника можно рассчитать, если знать значение реального ее периода обращения вокруг рассматриваемого объекта и реального периода обращения этого объекта вокруг своей звезды.

Формула, которая позволяет провести подобный расчет, имеет вид: 1/P = 1/T ± 1/S, здесь P — реальный период обращения рассматриваемого объекта, T — реальный период обращения объекта, относительно которого рассматривается движение, вокруг своей звезды, S — неизвестный синодический временной период.

Знаком «±» в формуле следует пользоваться так: если T > S, тогда формула используется со знаком «+», если же T < S, тогда нужно подставить знак «-«.

Использование формулы на примере Луны

Чтобы показать, как правильно пользоваться приведенным выражением, возьмем для примера вращение Луны вокруг Земли и синодический период обращения Луны рассчитаем.

Известно, что наша планета имеет реальный период обращения по орбите вокруг Солнца, равный T = 365,256363 дней. В свою очередь, из наблюдений можно установить, что на небосводе Луна появляется в рассматриваемой точке через каждые S = 29,530556 дня, то есть это ее синодический период. Поскольку S < T, то формулу, связывающую разные периоды, следует брать со знаком «+», получаем: 1/P = 1/365,256363 + 1/29,530556 = 0,0366, откуда P = 27,3216 дней. Как можно видеть, Луна на 2 дня быстрее совершает свой оборот вокруг Земли, чем земной наблюдатель снова может ее увидеть в отмеченном месте на небосводе.

Основные формулы школьного курса астрономии

1. Теоретическая разрешающая способность телескопа:

, где λ – средняя длина световой волны (5,5·10^-7 м), D – диаметр объектива телескопа, или , где D – диаметр объектива телескопа в миллиметрах.

2. Увеличение телескопа:

, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.

3. Высота светил в кульминации:

высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):

, где  – широта места наблюдения,  – склонение светила;

высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):

, где  – широта места наблюдения,  – склонение светила;

высота светил в нижней кульминации:

, где  – широта места наблюдения,  – склонение светила.

4. Астрономическая рефракция:

приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):

, где z – зенитное расстояние светила (для z

5. Время:

звездное время:

, где  – прямое восхождение какого-либо светила, t – его часовой угол;

среднее солнечное время (местное среднее время):

T_m=T_+, где T_ – истинное солнечное время,  – уравнение времени;

всемирное время:

, где  – долгота пункта с местным средним временем T_m, выраженная в часовой мере, T₀ – всемирное время в этот момент;

поясное время:

, где T₀ – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);

декретное время:

или

6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:

для верхних планет:

;

для нижних планет:

, где T_ – звездный период обращения Земли вокруг Солнца.

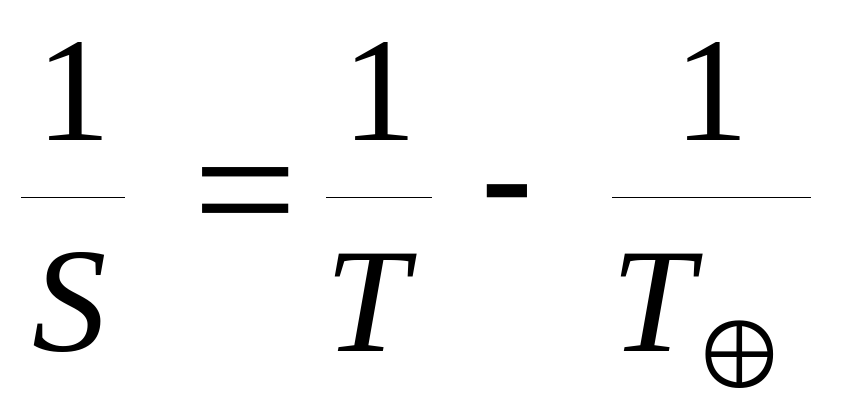
7. Третий закон Кеплера:

, где Т₁ и Т₂ – периоды обращения планет, a₁ и a₂ – большие полуоси их орбиты.

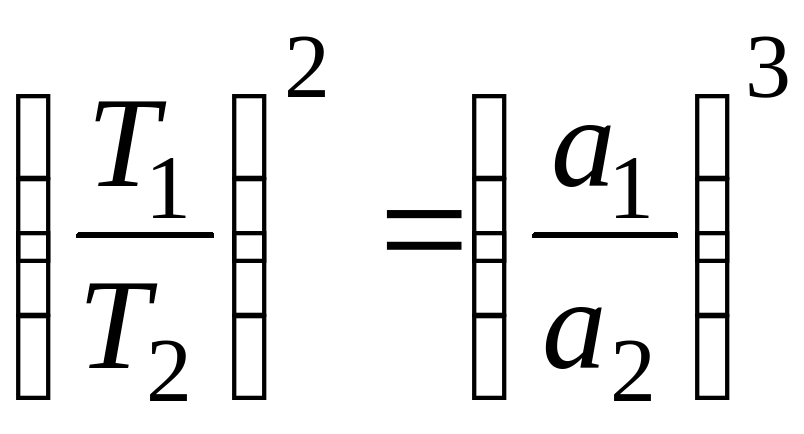
8. Закон всемирного тяготения:

, где m₁ и m₂ – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.

9. Третий обобщенный закон Кеплера:

, где m₁ и m₂ – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;

для системы Солнце и две планеты:

, где Т₁ и Т₂ – сидерические (звездные) периоды обращения планет, М – масса Солнца, m₁ и m₂ – массы планет, a₁ и a₂ –большие полуоси орбит планет;

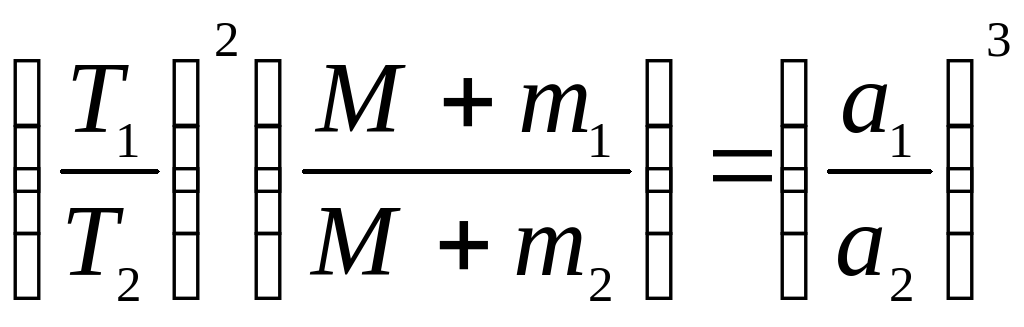
для систем Солнце и планета, планета и спутник:

, где M – масса Солнца; m₁ – масса планеты; m₂ – масса спутника планеты; Т₁ и a₁ – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т₂ и a₂ – период обращения спутника вокруг планеты и большая полуось его орбиты;

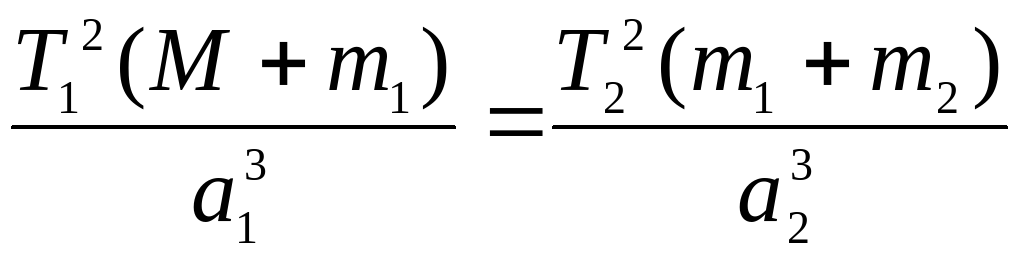
при M m₁, а m₁ m₂,

.

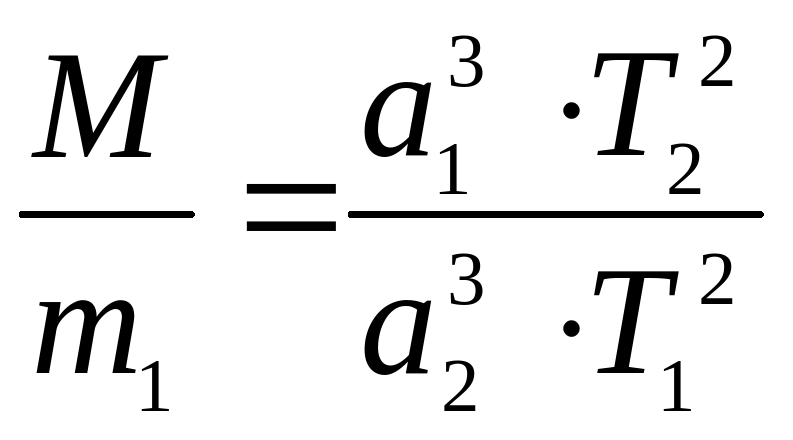
10. Линейная скорость движения тела по параболической орбите (параболическая скорость):

, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.

11. Линейная скорость движения тела по эллиптической орбите в избранной точке:

, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.

12. Линейная скорость движения тела по круговой орбите (круговая скорость):

, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, v_p – параболическая скорость.

13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:

, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.

14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:

, , , где r_П – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, r_А – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.

15. Расстояние до светила (в пределах Солнечной системы):

, где R_ – экваториальный радиус Земли, ρ₀– горизонтальный параллакс светила, выраженный в секундах дуги,

или , где D₁ и D₂ – расстояния до светил, ρ₁ и ρ₂ – их горизонтальные параллаксы.

16. Радиус светила:

, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R_ – экваториальный радиус Земли, ρ₀– горизонтальный параллакс светила.

17. Расстояние до звезд:

в парсеках: , где  – годичный параллакс звезды, выраженный в радианах;

в астрономических единицах: , где  – годичный параллакс звезды, выраженный в секундах дуги;

в километрах: , где  – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.

18. Связь блеска звезды и ее звездной величины (формула Погсона):

, где I₁ – освещенность, создаваемая звездой, звездная величина которой равна m₁, и I₂ – освещенность, создаваемая другой звездой, звездная величина которой равна m₂.

19. Абсолютная звездная величина:

, где m – видимая звездная величина, R – расстояние до звезды в парсеках.

20. Закон Стефана–Больцмана:

ε=σT⁴, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.

21. Закон Вина:

, где λ_max – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.

22. Закон Хаббла:

, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).

4