Площадь поперечного сечения для квадрата как найти

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.

Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

Математика ЕГЭ

Информатика ЕГЭ

Алексей Шевчук

• ведущий курсов и автор учебника ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — 18 лет;
• в 2021 году сдал ЕГЭ — 100 баллов (мат, физ) и 98 баллов (инф);
• рейтинг на Профи.ру — «4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Площадь поперечного сечения

В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.

Формулы для расчета площади основных фигур.

Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:

Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:

A=A1+A2+A3-A4

Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.

Площадь составного сечения

Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.

Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.

В результате сложив все составляющие профили, получим площадь всего сечения.

Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.

Сечение проводов в домах старой застройки и предельная нагрузка

В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.

При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.

Ток, А	Максимальная мощность, ВА	Диаметр кабеля, мм	Сечение кабеля, мм2
14	3000	1,6	2
16	3500	1,8	2,5
18	4000	2	3
21	4600	2,3	4
24	5300	2,5	5
26	5700	2,7	6
31	6800	3,2	8
38	8400	3,6	10

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d 2 — 2a 2 )]^(1/2) и P = 2b + [2 * (2d 2 — 2b 2 )]^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Формула площади треугольника по двум сторонам и углу между ними

S = 1 2 ⋅ b ⋅ c ⋅ sin ⁡ ( α ) S=frac{1}{2}cdot bcdot ccdotsin(alpha) S=21​⋅b⋅c⋅sin(α),

b , c b, c b,c — стороны треугольника;

α alpha α — угол между сторонами b b b и c c c.

Пример

Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.

Решение

b = 5 b=5 b=5 c = 6 c=6 c=6 α = 3 0 ∘ alpha=30^{circ} α=30∘

S = 1 2 ⋅ 5 ⋅ 6 ⋅ sin ⁡ ( 3 0 ∘ ) = 7.5 S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 S=21​⋅5⋅6⋅sin(30∘)=7.5 (см. кв.)

Ответ: 7.5 (см. кв.)

Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!

Приступаем к расчёту

Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:

• S = π (D/2 – N) 2 ;
• В этой записи D – внешний диаметр окружности;
• N – толщина стенки трубы.

Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).

D = 1 м.; N = 0,01 м.

Для упрощения возьмём π = 3,14. Подставляем значения в формулу:

S = π (D/2 – N) 2 = 3,14 (1/2 – 0,01) 2 = 0,754 м 2 .

Некоторые физические особенности

От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.

При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.

О чём стоит помнить?

Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.

Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.

Вычисление сечения провода для линии розеток

• материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
• особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
• использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
• система защиты – автомат, номинальный ток которого 10 А.

Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

, где — сторона.

Площадь равностороннего треугольника через высоту

, где — высота.

Формулы вычислений

При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.

Стандартная формула площади окружности такова:

S=π×R2, где

π – постоянное число, равное 3,14;

R – величина радиуса;

S – площадь сечения трубы, вычисленная для внутреннего диаметра.

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

Как найти площадь поперечного сечения прямоугольника?

Как найти площадь поперечного сечения прямоугольника?

Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.

Как считать площадь поперечного сечения?

Площадь сечения круга или шара можно найти по формуле:

1. S = πR2 …
2. c = S*q*r*t*(a2 + b2) …
3. S= c*h. …
4. S=a*b. …
5. S =2R*h. …
6. S =2а*h.

Как найти площадь поперечного сечения стержня?

S = π * d 2 / 4, где На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения стержня, если известен диаметр стержня.

Как найти длину трубы зная диаметр?

Внутренний и наружный диаметр, толщина стенки, радиус Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.

Как рассчитать объем трубы зная диаметр и длину?

Для расчета необходимо знать данные диаметра трубы. Его обозначают буквой D и рассчитывают по формуле R x 2. Определяется также длина окружности….Сама формула расчета, имеет следующий вид:

1. V = S x L.
2. Объем трубы – V;
3. Площадь сечения – S;
4. Длина – L.

Как рассчитать длину трубы по весу?

Расчет ведется по формуле m = ro / 7850 * 0.

Сколько весит 1 метр трубы?

Вес и сортамент стальных магистральных труб по ГОСТ’у /div>

Наружный диаметр трубы, мм	Толщина стенки, мм	Масса 1 метра погонного, кг
377	8,5	77,25
9	81,68
426	5	51,9
5,5	57,04

Сколько весит метр трубы таблица?

Вес трубы стальной

диаметр трубы, мм	Стенка, мм	Масса 1 метра, кг
Ø30	1,0 мм.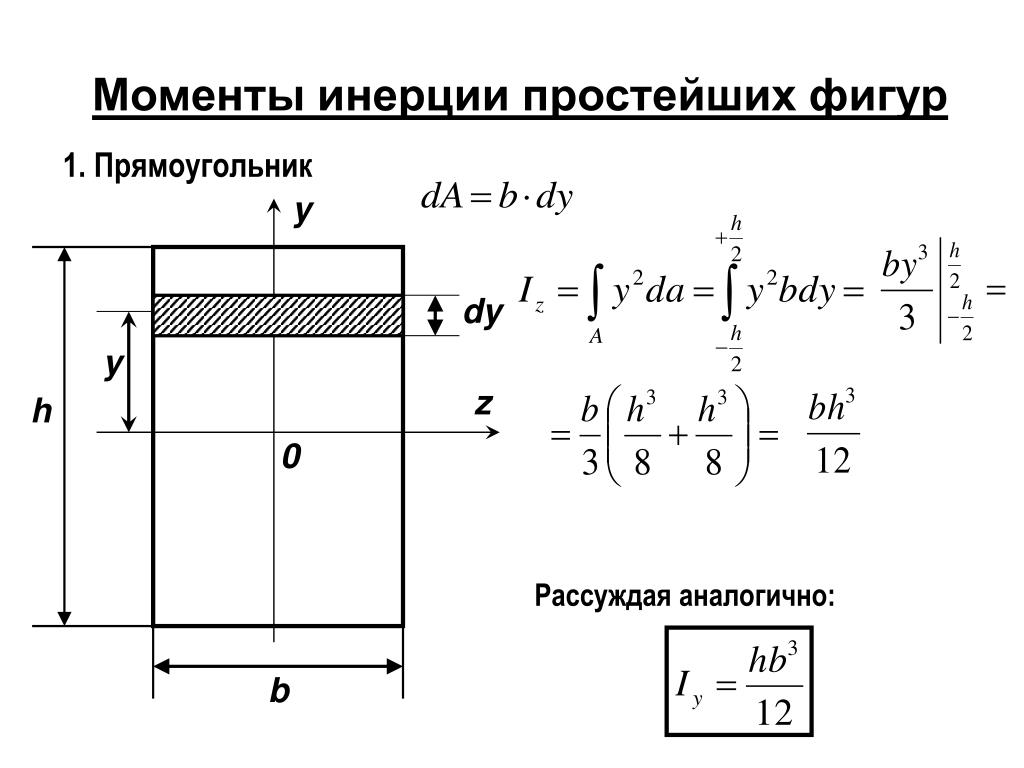	0,715кг
Ø30	1,2мм	0,852кг
Ø30	1,4мм	0,987кг
Ø30	(1,5)мм	1,165кг

Сколько весит метр трубы 57х3?

Теоретический вес труб стальных круглых

Наружный диаметр, мм	Толщина стенки, мм	Теоретический расчёт Массы 1м, кг
Труба 57	2,0	57х2 вес метра 2,713
Труба 57	2,5	57х2,5 вес метра 3,360
Труба 57	3,0	57 х3 вес метра 3,995
Труба 57	3,5	57х3,5 вес метра 4,618

Сколько весит 1 метр трубы диаметром 57 мм?

Вес метра трубы 57 с толщиной стенки 1.

Сколько стоит метр 57 трубы?

Труба электросварная 57 мм — от 100 руб/м купить в Сталь-Эксперт (цена)

Сколько метров в тонне трубы 57?

Теоретический вес горячедеформированных (г/д) бесшовных труб (ГОСТ 8732-78 и ГОСТ 8731-74)

Наружный диаметр, мм	Толщина стенки, мм	Метров в тонне
108	5	78,7
5,5	71,9
6	66,3
7	57,4

Сколько метров в тонне трубы?

Наружный диаметр, мм	Толщина стенки, мм	Ориентировочное количество метров в тонне
12	1,0	3690,04
1,2	3125,00
1,4	2732,24
1,5*	2577,32

Сколько метров профильной трубы в тонне?

Теоретический удельный вес квадратных профильных труб (ГОСТ 8639-82)

Размеры профильной трубы, мм	Толщина стенки профильной трубы, S, мм	Метров в тонне
25	1	1351,4
1,5	934,6
2	719,4
2,5	595,2

Как найти 1 погонный метр трубы?

Как посчитать погонный метр? Вам нужно точное значение плотности материала, из которого сделано изделие. Умножьте плотность на объем, чтобы получить значение массы погонного метра. Умножьте массу погонного метра на длину трубопровода.

Сколько будет 1 погонный метр?

Это очень упрощает учет. Погонный метр равен одному метру. Это единица измерения длины, без учёта ширины, или толщины. Можно взять в руки рулетку измерить длину в один метр, это и будет тот самый погонный метр.

Как рассчитать цену за погонный метр трубы?

Стоимость 1 погонного метра металлопроката можно определить по универсальной формуле: Цпм = Sпр х ρст х Цт / 1000, где

Как рассчитать цену погонного метра?

При необходимости можно перевести полученную площадь в погонные метры. Формула перевода такова – Pm = S/a, где a – это ширина линолеума. Например, имеется комната шириной 3 м и длиной 7 м.

Как рассчитать цену за квадратный метр?

Для расчета средней стоимости квадратного метра по абсолютному значению нам достаточно суммировать цены, суммировать метры и разделить суммированную цену на суммированную площадь. Рассчитаем стоимость квадратного метра для каждой квартиры и сопоставим результаты со средним значением.

Как считается погонный метр?

Погонный метр — это и есть метр, равный 100 см в длину. … Погонный метр — это величина, единица измерения длины или расстояния чего либо в метрах. Погонный метр = метр. В погонных метрах считают определенные отрезки поверхностей, для уточнения, измерения длинны, расстояния.

Расчет прямоугольного сечения балки по условию прочности

Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.

Задача

Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.

Соотношение сторон сечения h=2b (h – высота, b – ширина).

Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.

Другие примеры решений >
Помощь с решением задач >

Решение

Предыдущие пункты решения задачи:

1. Определение опорных реакций
2. Построение эпюр внутренних поперечных сил и изгибающих моментов
3. Расчет момента сопротивления сечения балки по условию прочности

Минимально необходимый расчетный момент сопротивления сечения балки составил

В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.

По справочнику находим формулу осевого момента сопротивления прямоугольного сечения

Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении

и запишем необходимое неравенство

откуда находим расчетную высоту прямоугольного сечения

Из заданного соотношения сторон определяем расчетную ширину сечения

Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.

При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).

По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.

Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.

После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.

Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

---

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)

Поиск формул и решений задач

Свойства прямоугольного сечения | Calcresource

Соглашение

-Геометрия

-Момент инерции

-Момент инерции и изгиба

-Полярный момент инерции

-Эластичный модуль

-Эластичные напряжения

-пластиковый модул

-около

-эластичные напряжения

-пластик

-около

-Эластичные напряжения

-пластик

-около

-Эластичные напряжения

-пластик

-около ось x

—  Вокруг оси y

—  Радиус вращения

—  Формулы прямоугольного сечения

—  Связанные страницы

93}{12}

Момент инерции и изгиб

Момент инерции (секундный момент или площадь) используется в теории балок для описания жесткости балки при изгибе.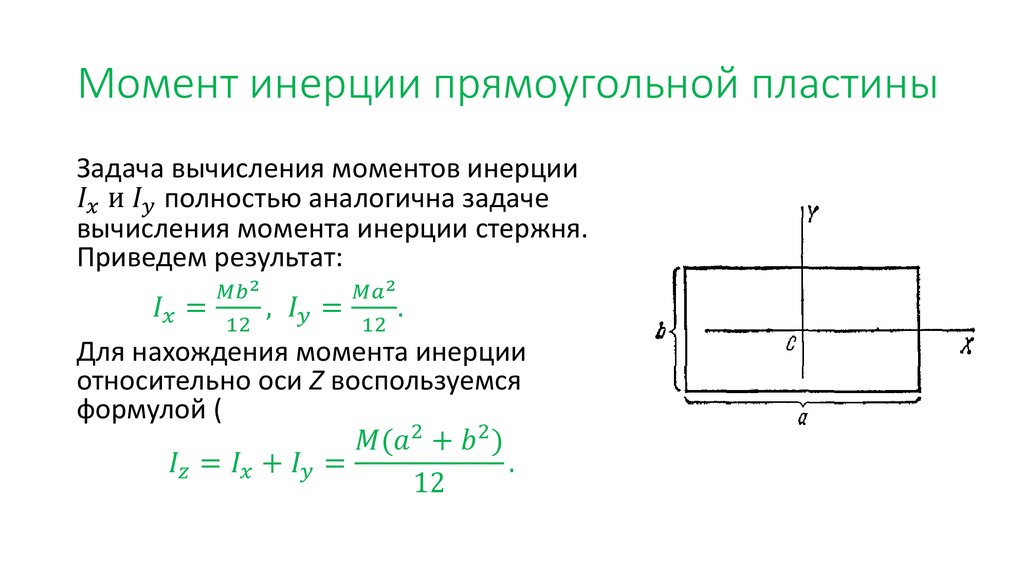 Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:

M = Etimes I times kappa

где E — модуль Юнга, свойство материала , а kappa — кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент М, результирующая кривизна обратно пропорциональна моменту инерции I.94 .

Полярный момент инерции

Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящим моментам, так же как описанные выше плоские моменты инерции связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (которая перпендикулярна плоскости сечения) можно выполнить с помощью теоремы о перпендикулярных осях:

I_z = I_x + I_y

, где I_x и I_y — моменты инерция вокруг осей x и y, которые взаимно перпендикулярны оси z и сходятся в одном начале координат.

Модуль упругости

Модуль упругости S_x любого поперечного сечения вокруг оси x (в центре) описывает реакцию сечения на упругий изгиб.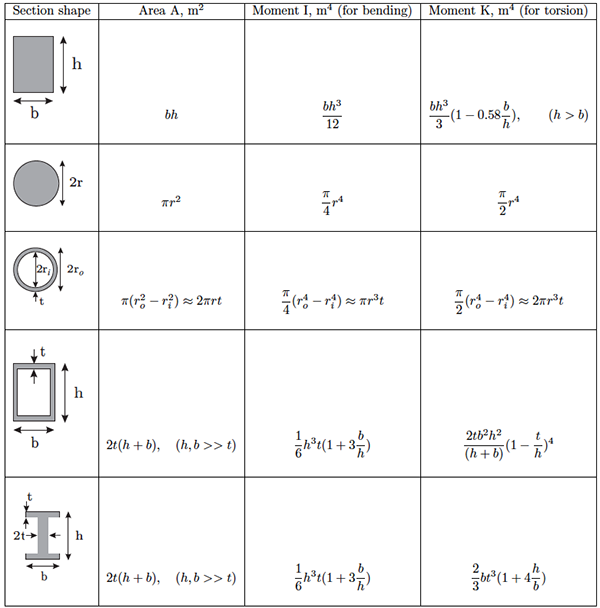 Он определяется как:

S_x = frac{I_x}{Y}

, где I_x — момент инерции секции вокруг оси x, а Y — расстояние от центра тяжести волокна секции, параллельное оси x и измеренное перпендикулярно от него. Как правило, представляют интерес более удаленные волокна. Для прямоугольника а наиболее удаленными от оси x волокнами являются волокна на верхнем и нижнем краях b на расстоянии, равном h/2. Таким образом, применение приведенной выше формулы для прямоугольного поперечного сечения приводит к следующему выражению для модуля упругого сечения вокруг оси x: 92}{6}

Можно заметить, что формула для S_y становится идентичной формуле для S_x, если заменить b на h и наоборот.

Упругие напряжения

Если к оси x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Над нейтральной осью напряжения равны нулю. Абсолютный максимум сигма будет иметь место на самом удаленном волокне, величина которого определяется формулой: 93 .

Модуль пластичности

Модуль пластичности аналогичен упругому модулю, но определяется с допущением полной пластической текучести поперечного сечения вследствие изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении, и A_c, при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, общая сжимающая сила по всей сжимаемой площади будет равна A_cf_y, если предположить условия пластичности (т. е. материал будет деформироваться везде) и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:

A_cf_y = A_t f_yRightarrow

A_c= A_t

Ось называется пластической нейтральной осью , а для несимметричных сечений она не совпадает с упругой нейтральной осью (которая снова является центроидальной). Однако прямоугольное сечение является симметричным (имеет две оси симметрии), поэтому его пластические нейтральные оси совпадают с упругими. Другими словами, пластические нейтральные оси проходят через центр тяжести прямоугольника.

Вокруг оси x

Модуль пластичности при изгибе вокруг оси x определяется по общей формуле:

Z = A_c Y_c + A_t Y_t

где Y_c, расстояние от центра масс области сжатия до пластика нейтральная ось и Y_t — соответствующее расстояние от центра тяжести области растяжения.

В случае прямоугольного поперечного сечения пластическая нейтральная ось проходит через центр тяжести, разделяя всю площадь на две равные части. Область сжатия будет прямоугольником с размерами b и h/2. Его центроид будет находиться на расстоянии, равном h/4, от оси x, как показано на следующем рисунке. То же самое относится и к области растяжения. Следовательно, модуль пластического сечения прямоугольного сечения при изгибе x-x находится следующим образом: 92}{4}

Еще раз, это последнее уравнение может быть получено из модуля пластичности Z_x, если мы заменим h на b и наоборот.

Радиус вращения

Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:

R_g = sqrt{frac{I}{A}}

где I момент инерции поперечного сечения вокруг той же оси и A его площади. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Для прямоугольного сечения замена приведенного выше выражения дает следующие радиусы вращения вокруг центральных осей x и y соответственно:

R_{gx} = frac{h}{2sqrt{3}}

R_{gy} = frac{b}{2sqrt{3}}

Круг – это фигура с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.

Формулы для прямоугольного сечения

В следующей таблице приведены формулы, которые можно использовать для расчета основных механических свойств прямоугольного сечения.

Свойства прямоугольного сечения
Количество 92}{4}
Радиус вращения	R_{gx} = frac{h}{2sqrt{3}} R_{gy} = frac{b}{2sqrt {3}}

Связанные страницы

Понравилась эта страница? Поделись с друзьями!

Площадь прямоугольника с калькулятором.

Определение и формула Площадь прямоугольника с калькулятором. Определение и формула — Открытый справочник по математике

Открытый математический справочник

Главная
Контакт
О
Предметный указатель

Количество квадратных единиц, необходимое для полного заполнения прямоугольника.

Формула: Ширина × Высота

Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер прямоугольника. По размеру прямоугольника
изменяется, площадь пересчитывается.

Формула площади

Площадь прямоугольника находится путем умножения ширины на высоту. Как формула:
где
w  это ширина
h  это высота

Калькулятор

Сторона 1		прозрачный
Сторона 2		прозрачный
Район:
Периметр:
Диагональ:

Используйте калькулятор выше, чтобы вычислить свойства прямоугольника.

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.

Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

Математика ЕГЭ

Информатика ЕГЭ

Алексей Шевчук

• ведущий курсов и автор учебника ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — 18 лет;
• в 2021 году сдал ЕГЭ — 100 баллов (мат, физ) и 98 баллов (инф);
• рейтинг на Профи.ру — «4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Площадь поперечного сечения

В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.

Формулы для расчета площади основных фигур.

Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:

Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:

A=A1+A2+A3-A4

Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.

Площадь составного сечения

Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.

Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.

В результате сложив все составляющие профили, получим площадь всего сечения.

Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.

Особенности электрических проводов

При всём многообразии кабельной продукции и огромном выборе проводов для прокладки электрических сетей существуют правила подбора. Не обязательно учить наизусть все марки кабелей и проводов, нужно уметь читать и расшифровывать их маркировку. Для начала стоит выяснить различие между проводом и кабелем.

Провод – проводник, используемый для соединения двух участков цепи. Может иметь одну или несколько токопроводящих жил. Жилы могут быть:

• голые;
• изолированные;
• одножильные;
• многожильные.

Голые линии применяются там, где прикосновение к токоведущим жилам невозможно. В большинстве случаев они используются для воздушных линий электропередач.

Изоляционное покрытие применяется однослойное или двухслойное. Провода, имеющие два или три проводника в двойной изоляции, путают с кабелем. Путаница происходит из-за того, что изоляция покрывает каждую жилу, а снаружи выполнено общее полимерное или иное покрытие. Такие проводники нашли применение внутри электрических устройств, щитов или шкафов. В быту они скрыты в стене или проложены в специальных каналах.

Изолированная продукция используется повсеместно. В зависимости от степени электробезопасности помещения и места прокладки, выбирается класс изоляции.

Многожильные проводники используются там, где необходимы изгибы малого радиуса при прокладке сложных трасс, где не могут пройти одножильные аналоги. Такой тип тоководов удобно монтировать в кабельных каналах. Одножильные провода в таких условиях изгибать труднее, нужно прикладывать силу, и существует опасность повреждения жилы.

К сведению. Маркировка АППВ 3*2,5 обозначает провод с алюминиевыми жилами, поливинилхлоридной изоляцией, плоский, имеющий разделительное основание. Расшифровку маркировки уточняют в справочной литературе.

По строению кабель – это сколько-то жил, имеющих индивидуальную изоляцию, помещённых в защитный внешний слой из диэлектрического материала. Пространство между сердечниками и оболочкой, для предотвращения слипания, заполняется бумажными лентами, пластмассовыми нитями или кабельной пряжей. Дополнительно изделие может быть усилено бронёй из лент или стальной оплёткой для защиты от механических повреждений.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

1. Найти квадрат диагонали (умножить диагональ на саму себя).
2. Найти половину этого квадрата – умножить его на 0,5.
3. Найти синус угла между диагоналями.
4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

1. Квадрат диагонали: 10*10 = 100 см.
2. Половина этого квадрата: 0,5*100 = 50 см.
3. Синус угла между диагоналями: sin 30 градусов = 0,5.
4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Приступаем к расчёту

Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:

• S = π (D/2 – N) 2 ;
• В этой записи D – внешний диаметр окружности;
• N – толщина стенки трубы.

Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).

D = 1 м.; N = 0,01 м.

Для упрощения возьмём π = 3,14. Подставляем значения в формулу:

S = π (D/2 – N) 2 = 3,14 (1/2 – 0,01) 2 = 0,754 м 2 .

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d 2 — 2a 2 )]^(1/2) и P = 2b + [2 * (2d 2 — 2b 2 )]^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

1. Найти квадрат радиуса (умножьте радиус на радиус).
2. Умножить квадрат радиуса на 4.
3. Найти квадрат известной стороны.
4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
5. Найти квадратный корень разности.
6. Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

1. Квадрат радиуса: 5*5=25 см.
2. Четыре квадрата радиуса: 4*25 = 100 см.
3. Квадрат стороны: 6*6 = 36 см.
4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
2. Найдите квадрат известной стороны.
3. Отнимите от квадрата диаметра квадрат стороны.
4. Найдите квадратный корень разности.
5. Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

1. Квадрат диаметра: 10*10 = 100 см.
2. Квадрат стороны: 8*8 = 64 см.
3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

1. Найти квадрат диагонали, то есть умножить ее на саму себя.
2. Найти квадрат известной стороны.
3. Из квадрата диагонали вычесть квадрат стороны.
4. Найти квадратный корень получившейся разности.
5. Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

1. Квадрат стороны = 3*3 = 9 см.
2. Квадрат диагонали = 5*5 = 25 см.
3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и периметру – 2 способ

Действия такие:

1. Умножьте периметр на сторону.
2. Найдите квадрат стороны.
3. Умножьте квадрат стороны на 2.
4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
5. Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

1. Умножаю периметр на сторону: 8*28 = 224 см.
2. Нахожу квадрат стороны: 8*8 = 64 см.
3. Умножаю квадрат стороны на два: 64*2 = 84 см.
4. Отнимаю из первого третье: 224-84 = 140 см.
5. Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

Как и чем измерить диаметр провода (проволоки)

Для измерения диаметра провода подойдет штангенциркуль или микрометр любого типа (механический или электронный). С электронными работать проще, но они есть не у всех. Измерять надо саму жилу без изоляции, потому предварительно ее отодвиньте или снимите небольшой кусок. Это можно делать, если продавец разрешит. Если нет — купите небольшой кусок для тестирования и проводите измерения на нем. На очищенном от изоляции проводнике замеряете диаметр, после чего можно определить реальное сечение провода по найденным размерам.

Какой измерительный прибор в данном случае лучше? Если говорить о механических моделях, то микрометр. У него точность измерений выше. Если говорить об электронных вариантов, то для наших целей они оба дают вполне достоверные результаты.

Если нет ни штангенциркуля, ни микрометра, захватите с собой отвертку и линейку. Придется зачищать довольно приличный кусок проводника, так что без покупки тестового образца на этот раз вряд ли обойдетесь. Итак, снимаете изоляцию с куска провода 5-10 см. Наматываете проволоку на цилиндрическую часть отвертки. Витки укладываете вплотную один к другому, без зазора. Все витки должны быть полными, то есть «хвосты» провода должны торчать в одном направлении — вверх или вниз, например.

Количество витков не важно — около 10. Можно больше или меньше, просто на 10 делить проще. Витки считаете, затем прикладываете полученную намотку к линейке, совместив начало первого витка с нулевой отметкой (как на фото). Измеряете длину участка, занятого проводом, потом его делите на количество витков. Получаете диаметр провода. Вот так все просто.

Например, посчитаем каков размер проволоки, изображенной на фото выше. Количество витков в данном случае — 11, занимают они 7,5 мм. Делим 7,5 на 11, получаем 0,68 мм. Это и будет диаметр данного провода. Далее можно искать сечение этого проводника.

Формулы вычислений

При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.

Стандартная формула площади окружности такова:

S=π×R 2 , где

π – постоянное число, равное 3,14;

R – величина радиуса;

S – площадь сечения трубы, вычисленная для внутреннего диаметра.