Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Газы являются основными объектами изучения в физике, поскольку они представляют собой одно из наиболее распространенных состояний вещества на Земле. Один из ключевых показателей газа — это работа, которую он может выполнить при изменении объема. Наиболее удобным способом определения работы газа является использование графика зависимости давления и объема, который представляет собой кривую на координатной плоскости.
График зависимости давления и объема является наглядным и наглядным способом отображения изменения объема и давления. Он содержит информацию о поведении газа при изменении условий, из которых главными являются давление и объем. В зависимости от конкретных характеристик графика, можно определить работу газа, произведенную при определенных условиях.
В данной статье мы рассмотрим основные методы определения работы газа на основе анализа графиков зависимости давления и объема. Также, мы рассмотрим некоторые из фундаментальных законов, лежащих в основе устройства газов и их поведения при изменении объема и давления. Наконец, мы рассмотрим некоторые из наиболее распространенных практических применений газов и методов работы с ними.
Основные понятия
Газ – это одно из четырех состояний вещества. Он отличается от твердого и жидкого состояний тем, что его молекулы движутся с большой скоростью и находятся на больших расстояния друг от друга.
Давление – это физическая величина, которая определяется силой, действующей на единицу площади поверхности. Давление газа зависит от его объема и температуры.
Объем – это количество места, занимаемого газом. Объем газа зависит от его давления и температуры.
Закон Бойля-Мариотта – это закон, который устанавливает обратную пропорциональность между давлением и объемом газа при постоянной температуре.
Изобарный процесс – это процесс, при котором давление газа остается постоянным, а его объем изменяется.
Изотермический процесс – это процесс, при котором температура газа остается постоянной, а его объем и давление изменяются.
Формула работы газа
Работа газа — это физическая величина, которая определяется произведением силы, приложенной газом к поверхности, на путь, который пройдет газ при этом.
Для расчета работы газа используется формула:
Где W — работа газа, F — сила, приложенная газом к поверхности, d — путь, который пройдет газ при этом, P — давление газа и S — площадь поверхности, на которую действует газ.
Для расчета работы газа по графику зависимости давления и объема, необходимо определить путь, который проходит газ и площадь поверхности, на которую оказывается давление. Эти параметры могут быть определены геометрически для конкретной системы.
Формула работы газа является основой для понимания тепловых и механических процессов, происходящих в газовых системах.
Как построить график зависимости давления от объема
Шаг 1: Задайте диапазон значений для объема. Для этого можно взять несколько значений объема и записать их в таблицу.
| Объем, м3 | Давление, Па |
|---|---|
| 0,1 | 20000 |
| 0,2 | 15000 |
| 0,3 | 12000 |
Шаг 2: Постройте координатную ось для объема по горизонтали и для давления по вертикали.
Шаг 3: Окрашивайте точки на графике для каждого значения объема. После того, как точки окрашены, соединяйте их линией.
Шаг 4: Проведите линию тренда через все точки на графике. Линия тренда показывает общий тренд в данных и облегчает оценку степени влияния объема на давление.
Шаг 5: Добавьте подписи к координатным осям и заголовок к графику. График готов, вы можете оценить отношение между объемом и давлением, а также проанализировать кривую линии тренда.
Определение работы газа по графику зависимости давления и объема
Изучение графика
Для определения работы газа наиболее эффективно использовать график зависимости давления и объема. График представляет собой кривую, которая отображает изменение давления газа в зависимости от объема при постоянной температуре.
Определение работы газа на графике происходит по площади, заключенной между кривой графика, осью абсцисс и отрезком, соединяющим начальную и конечную точки. Площадь, расположенная выше оси абсцисс, соответствует совершенной газом работы.
Расчет работы газа
Для расчета работы газа необходимо разделить процесс, изображенный на графике, на несколько малых частей. Затем каждую часть необходимо приблизительно вычислить, используя формулу площади прямоугольника или треугольника, зависимо от вида фрагмента кривой на графике. Полученные результаты необходимо сложить, чтобы получить общую работу газа.
Если процесс на графике представлен несколькими различными ступенями, то расчет может быть упрощен. В этом случае необходимо найти площадь каждой ступени и сложить все полученные значения.
Примеры расчета работы газа
Пример 1. На графике изображен процесс изотермического сжатия газа. Площадь, заключенная между кривой, осью абсцисс и отрезком, соединяющим начальную и конечную точки, соответствует работе газа. Для расчета работы газа необходимо разделить процесс на части и вычислить площадь каждой части.
| Объем, л | 10 | 5 |
|---|---|---|
| Давление, атм | 2 | 4 |
| Площадь, атм*л | 10 | 5 |
| Сумма площадей | 15 атм*л |
Таким образом, работа газа при изотермическом сжатии составила 15 атм*л.
Пример 2. График представляет собой процесс изотермического расширения газа с двумя ступенями. Расчет работы газа упрощается за счет того, что процесс можно разделить на две части, у каждой из которых площадь равна площади соответствующей ступени.
| Объем, л | 10 | 15 | 20 |
|---|---|---|---|
| Давление, атм | 2 | 1 | 0,5 |
| Площадь, атм*л | 20 | 7,5 | |
| Сумма площадей | 27,5 атм*л |
Таким образом, работа газа при расширении составила 27,5 атм*л.
Примеры расчета работы газа
Пример 1. Изобарный процесс
Рассмотрим случай, когда газ претерпевает изменения при постоянном давлении (изобарный процесс). На графике зависимости давления от объема это будет горизонтальная линия. Работа газа в таком случае вычисляется по формуле:
Работа = Давление * ΔОбъем
Где ΔОбъем — разность объемов между начальным и конечным состояниями газа.
Пример 2. Изотермический процесс
Рассмотрим случай, когда газ претерпевает изменения при постоянной температуре (изотермический процесс). На графике зависимости давления от объема это будет гипербола. Работа газа в таком случае вычисляется по формуле:
Работа = Площадь под гиперболой
Пример 3. Адиабатический процесс
Рассмотрим случай, когда газ претерпевает изменения без теплообмена с окружающей средой (адиабатический процесс). На графике зависимости давления от объема это будет кривая, близкая к гиперболе. Работа газа в таком случае вычисляется по формуле:
Работа = (Γ — 1) * ΔОбъем * Pср
Где Γ — показатель адиабаты, ΔОбъем — разность объемов между начальным и конечным состояниями газа, Pср — среднее значение давления в процессе.
Выводы
Определение работы газа по графику зависимости давления и объема является одной из важнейших задач в физике. Для решения этой задачи необходимо уметь работать с графиками и использовать соответствующие формулы.
Из графика зависимости давления и объема можно определить площадь фигуры под графиком, которая представляет собой меру работы газа при изохорном процессе. Также, площадь фигуры образованной под графиком при изобарном процессе, показывает работу газа в этом случае.
Для определения работы газа по графику, необходимо учитывать, что работа газа вычисляется как произведение изменения объема на изменение давления. При выполнении расчетов необходимо использовать соответствующие единицы измерения, например, Нм или Дж.
Важно также учитывать положение кривой на графике, так как это может влиять на знак работы газа. Если кривая на графике перемещается вверх, то работа газа будет положительной, если вниз — отрицательной.
Выводы о работе газа по графику можно сделать только при условии, что процесс является квазистатическим. В этом случае, процесс можно рассматривать как последовательность изохорных и изобарных процессов, что упрощает расчет работы газа.
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
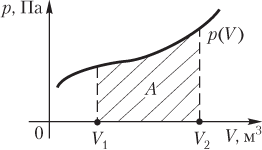
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1; объем газа в конечном состоянии V 2). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:
A = p∆V, или A = νR∆T,
где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V 2 − V 1; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T 2 − T 1; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе (V = const) не совершается:
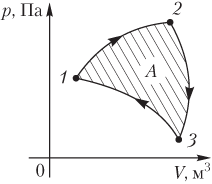
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
· положительной (прямой цикл);
· отрицательной (обратный цикл).
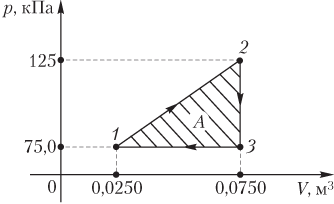
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
· парциальное давление водорода
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
· парциальное давление гелия
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
Преобразование данного уравнения к виду
позволяет выразить искомое отношение объемов
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Условие задачи:
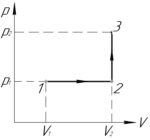
Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(V_1=2) л, (V_2=3) л, (p_1=400) кПа, (p_2=600) кПа, (A-?)
Решение задачи:
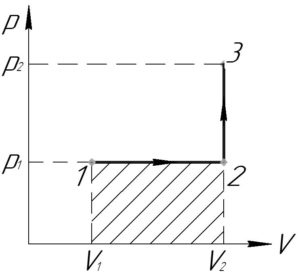
Процесс 1-2 — изобарный, поэтому работу газа (A_<1 — 2>) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению — заштриховано):
Процесс 2-3 — изохорный, работа газа (A_<2 — 3>) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).
В итоге формула (1) примет такой вид:
Переведём объемы газа (V_1) и (V_2) в систему СИ:
Ответ: 400 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода.
Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода. Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Поясните,почему умножение идет 2х10^5 ,когда газ совершает работу от 1 до 2, вроде должно быть 1х10^5,а по ответу получается от 0 до 2.
На участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется. Вся работа совершается на участке 2-3. Общее правило следующее, если процесс изображен на диаграмме , то работа равна площади под графиком со знаком плюс, если объем увеличивается, и со знаком минус, если уменьшается. Для тепловой машины, работающей по циклу, полезная работа равна площади ограниченной этим циклом, это укладывается в ранее озвученное правило. Когда мы идем по «верхней» части цикла, работа идет в +, потом возвращаемся по «нижней» в исходную точку, работа теперь идет в -, в результате остается только кусок внутри.
Алексей, вот Вы сказали, что «на участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется.»
а на участке 2-3 ведь не меняется давление.Так почему работа там совершается? Разве не A=pV ?
Не, не так. Давайте разбираться.
Будем выводить формулу, по которой можно посчитать работу совершенную газом. Когда газ работает? Когда он что-то перемешает. Для этого должен как-то меняться его объем. Например, газ расширяется и толкает поршень вверх, а с ним и какой-то груз, вот Вам и работа. То есть без изменения объема нет работы.
Чтобы вывести формулу, рассмотрим модельную задачу. Рассмотрим цилиндрический сосуд с газом. Пусть сосуд закрыт подвижным поршнем площади . Давление газа равно
. Определим, какую работу совершит газ, когда поршень сдвинется на малое расстояние
. Так как это работа на малом перемещении, то назовем ее элементарной работой и обозначим через
. Работа газа равна произведению силы, с которой он давит на поршень, на перемещение поршня (газ давит нормально, поэтому косинуса не возникает):
. Но сила, с которой газ давит на поршень связана с давлением газа соотношением:
. Если перемещение поршня мало, то можно считать, что давление газа не изменяется сильно и что оно остается постоянным. Тогда:
. Но
— это как раз изменение объема газа
. Окончательно имеем:
.
Получив эту формулу, можно забыть о том, как она выводилась (про сосуд и поршень), она оказывается верной для любого малого изменения объема.
Теперь, чтобы найти работу на конечном изменении объема нужно просуммировать работы по малым изменения, в математике это делается при помощи интеграла: Если внимательно приглядеться, то тут можно как раз увидеть площадь под линией процесса на диаграмме
. Вот почему говорят, что для поиска работы надо искать площадь под графиком на этой диаграмме.
Для частных случаев формула приобретает вид:
1) при изобарном процессе давление выносится за знак интеграла и получаем:
2) при изохорном объем не изменяется, поэтому пределы интегрирования совпадают, интеграл равен нулю, работа равна нулю.
3) при изотермическом процессе, давление уже изменяется с объемом, поэтому надо добавить в рассмотрение уравнение Клапейрона-Менделеева: . Следовательно,
. А значит работа при изотермическом процессе равна:
Пришло время поговорить об одной штуке, с которой постоянно сталкиваются студенты при изучении термодинамики. Она называется pV-диаграммой и представляет собой две взаимно перпендикулярные оси, на одной из которых отмечаются значения давления, а на другой – значения объема.
Чаще всего представленный график используют для изучения процессов, происходящих с газом, находящимся под поршнем в цилиндрическом сосуде.
Представим, что у нас как раз есть такой газ, и мы в какой-то момент заставили его перейти из некоего состояния 1 в состояние 2:
Получается, что мы уменьшили объем и увеличили давление, то есть просто передвинули поршень вниз. Но как именно протекал процесс? Как менялось давление с изменением объема? Вариантов очень много, все зависит от того, как именно мы перемещали поршень. Зависимость давления от объема могла бы выражаться совершенно разными кривыми.
Как бы там ни было, существуют процессы, для которых описание, данное pV-диаграммой, будет достаточно простым с математической точки зрения. Выделяют четыре таких процесса: изобарный, изотермический, изохорный и адиабатный. Мы начнем с самого первого из них.
Слово “изобарный” отсылает нас к барометру и редко используемым единицам измерения давления – барам. Действительно, изобарный процесс – это процесс, происходящий при постоянном давлении газа. Кроме того, предполагается, что и число молекул газа никак не меняется (нет никаких дырок и щелей в сосуде, это подразумевается для всех изучаемых нами сейчас процессов).
Если давление неизменно, на pV-диаграмме мы получим прямую, перпендикулярную вертикальной оси. Ее часто будут называть изобарой. Направление процесса будет определяться изменением объема. Если, например, поршень сдвинется вверх, будет наблюдаться увеличение объема газа, что можно продемонстрировать обычной стрелочкой.
Опыт подсказывает, что площадь под таким графиком чревата какой-то полезной информацией. Но какой именно? Что ж, речь идет о площади прямоугольника, одна из сторон которого соответствует значению давления, а другая – изменению объема:
Площадь=pvarDelta{V}
Вспомнив, что наблюдаемый процесс связан с перемещением поршня в сосуде с газом, и мы можем переписать представленное выше произведение в других физических терминах.
Давление – это отношение силы, под действием которой поршень перемещается вверх, к площади этого поршня, что соответствует и площади основания сосуда (обозначим ее как S):
Площадь=dfrac{F}{S}varDelta{V}
А чему равно изменение объема в данном случае? Используемый сосуд имеет форму цилиндра, поэтому нужный нам объем будет выражаться произведением площади основания S и расстояния d, на которое был смещен поршень:
Площадь=dfrac{F}{S}(Sd)
Площадь=dfrac{Fbcancel{S}}{bcancel{S}}d
Площадь=Fd
С правой стороны в этом выражении образовалась работа газа, и именно ей будет равна площадь под нашим графиком:
Площадь=Работа,газа
При этом нужно уделять большое внимание знакам, потому что можно легко допустить ошибку. Площадь под графиком в нашем случае равна работе, которую совершает газ. Если он расширяется, его работа считается положительной, а вот работа внешних сил в таком случае будет отрицательной. Если же объем газа, наоборот, уменьшается, перед работой газа, найденной по pV-диаграмме, нужно будет поставить знак минус, что будет означать положительную работу внешних сил.
Нам осталось обсудить последний вопрос. Каким образом изобарный процесс будет выглядеть в реальности? Ведь если мы начнем менять объем газа, это повлияет на его давление: оно либо уменьшится, либо возрастет в зависимости от наших манипуляций. Как же его сохранить постоянным?
Чтобы дать ответ на этот вопрос, нам стоит обратить внимание на третий фактор – температуру.
Если мы возьмем сосуд с газом, в который вставлен поршень, способный свободно перемещаться без каких-либо потерь энергий (то есть предполагается, что трением и сопротивлением воздуха можно пренебречь), и начнем медленно его нагревать, давление газа начнет увеличиваться. Но так как поршень может двигаться вверх, начнется увеличение объема, что будет означать уже уменьшение давления, которое в итоге никак меняться не будет.
Важно, чтобы нагрев газа и увеличение его объема происходили небольшими шажками. Именно тогда мы сможем говорить об изобарном процессе. Если нарушить это условие, если мгновенно сообщить газу большое количество теплоты, его давление резко вырастет, под действием чего поршень полетит вверх. Но когда он достигнет своего пика, он не остановится, как можно было бы предположить, а начнет совершать колебательное движение вверх и вниз, пока не придет наконец в равновесие с газом, находящимся под ним. Все это уже не будет изобарным процессом.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
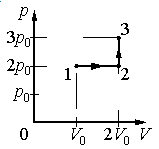
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k