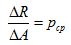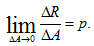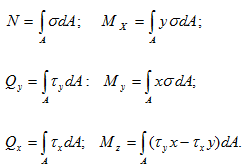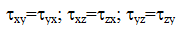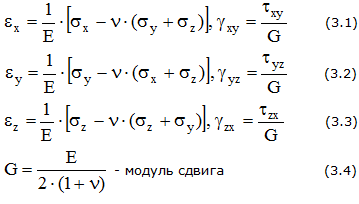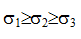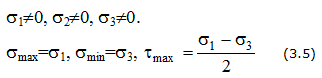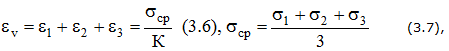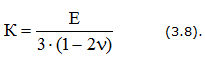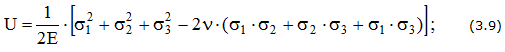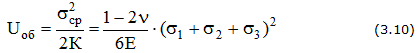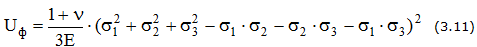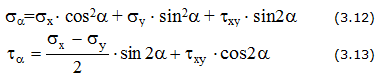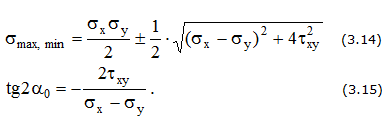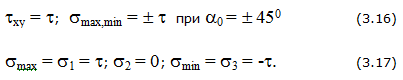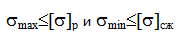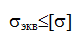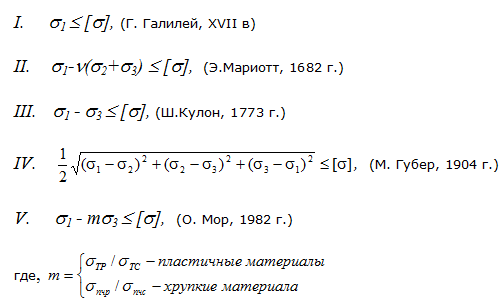Плоское напряженное состояние как найти напряжения

Линейное напряжённое
состояние имеет место в стержнях,
испытывающих растяжение или сжатие, а
также в некоторых точках стержня,
работающего на изгиб. Рассмотрим
растяжение стержня. Как указывалось в
главе 2, в поперечных сечениях, удалённых
от точек приложения внешних сил,
нормальные напряжения распределены
равномерно и равны (рис.3.5,а)

. (3.3)

Эти напряжения
являются главными, т.к. касательные
напряжения в поперечном сечении равны
нулю. Напряжённое состояние при растяжении
является однородным, поэтому размеры
выделяемых элементов не играют никакой
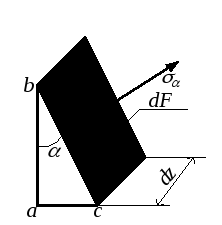
роли. Определим напряжения, действующие
по наклонной площадке. Наклон площадки
определяется острым углом α между
направлением оси стержня и нормалью n_α
к площадке. Условимся считать угол α
положительным, если он отсчитывается
против часовой стрелки (рис.3.5,а). Элемент,
находящийся в линейном напряжённом
состоянии, изображаем в виде плоской
фигуры, помня, однако, что в действительности
он имеет вид, показанный на рис.3.4,а.

Рассмотрим
равновесие нижней части стержня,
отсечённой наклонной площадкой
(рис.3.5,б). По наклонной площадке, площадь
которой равна F_α,
равномерно распределены напряжения
p_α,
параллельные осевой силе N
= P,
следовательно, результирующая этих
напряжений

p_αF_α
= N.

Отсюда найдём p_α,
подсчитав предварительно
,

.

Проектируя p_α
на нормаль n_α
и на плоскость сечения, получим выражения
для нормальных и касательных напряжений
по наклонной площадке:

σ_α
= p_αcos
α,
τ_α
= p_αsin
α

или

σ_α
= σ₁cos²α.
(3.4)

. (3.5)

а
б
в

Рис.3.5

Как
видно из формул (3.4) и (3.5), при α = 0 
τ_α
= 0 и σ_α
= σ₁,
при α = π/2 
σ_α
= 0 и τ_α
= 0. Таким образом, при растяжении
действительно имеет место линейное
напряжённое состояние: σ₁
= N/F,
σ₂
= σ₃
= 0. При сжатии σ₃
= – N/F,
σ₁
= σ₂
= 0.

Из выражения (3.5)
видно, что касательные напряжения
достигают своей наибольшей величины
при α = ± 45⁰,
причём

. (3.6)

Определим теперь
напряжения, действующие по площадке,
перпендикулярной заданной наклонной,
α₁
= α + 90⁰
(рис.3.5,в):

σ_α1
= σ₁ ∙
cos²
(α
+ 90) = σ₁sin²
α,

.

Итак

σ_α+90
= σ₁sin²
α. (3.7)

. (3.8)

3.3. Плоское напряжённое состояние

Плоское
напряжённое состояние встречается в
деталях машин и в строительных конструкциях
очень часто. Например, это стержень при
кручении (рис.3.6,а) и изгибе (рис.3.6,б),
тонкостенный сосуд под действием
внутреннего давления (рис.3.6,в).

а
б
в

Рис.3.6

Плоское напряжённое
состояние также имеет место в тонкой
пластине, нагруженной силами, параллельными
её плоскости и равномерно распределёнными
по толщине (рис.3.7): σ_х
≠ 0, σ_у
≠ 0, τ_ху
≠ 0, σ_z
= τ_zx
= τ_zy
= 0.

Рассмотрим два
аспекта задачи о плоском напряжённом
состоянии: найдём напряжения, действующие
по наклонной площадке (прямая задача),
и найдём величины и направления главных
напряжений (обратная задача).

Рис.3.7

3.3.1. Прямая задача

Дано: напряжения
σ_х,
σ_у,
τ_ху,
угол α
> 0 (рис.3.8,а).

Определить:
напряжения σ_α
и τ_α
(рис.3.8,б).

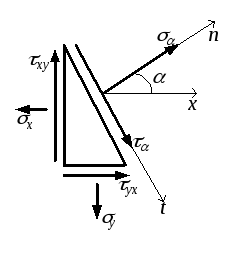
Рассмотрим
равновесие элемента abc. При записи
уравнений статики будем определять
силу как произведение напряжения на
площадь соответствующей грани:

площадь наклонной
грани bc
= dF;

площадь прямой
грани ab
= dF
∙ cos
α;

площадь прямой
грани ac
= dF
∙ sin
α.

а
б в

Рис.3.8

Теперь
запишем уравнения проекций всех сил,
действующих на элемент abc, на нормаль к
наклонной площадке и на ось, совпадающую
с этой площадкой (рис.3.8,в).

∑n
=
0:
σ_αdF
–
σ_x
dF
cos
α
∙
cos
α
–
σ_у
dF
sin
α
∙
sin
α
+
τ_xу
dF
cos
α
∙
sin
α
+
τ_ух
dF
sin
α
∙
cos
α
=
0,

∑t
=
0:
τ_αdF
+
σ_у
dF
sin
α
∙
cos
α
+
τ_уx
dF
sin
α
∙
sin
α
–
τ_xу
dF
cos
α
∙
cos
α
–
σ_х
dF
cos
α
∙
sin
α
=
0.

После несложных
преобразований и сокращения на dF получаем
следующие выражения:

σ_α
= σ_х cos²α
+ σ_y
sin²α
– τ_xy
sin
2α
, (3.9)

. (3.10)

Рис.3.9

Если исходные площадки являются главными (рис.3.9), то формулы (3.9) и (3.10) упрощаются: σα = σ1cos2α + σ2sin2, (3.11) . (3.12) Из формулы (3.12) следует, что наибольшее касательное напряжение

действует по
площадке, наклонённой под углом 45⁰
к главным
площадкам:

. (3.13)

Преобразуем формулу
(3.9), используя выражение для
тригонометрических функций

и
.

Получим

. (3.14)

Теперь
определим напряжения, действующие по
площадке, перпендикулярной к заданной:
α₁
= α + 90⁰.
Воспользуемся формулой (3.14), учитывая,
что cos
2α₁
= – cos
2α
и sin
2α₁
= – sin
2α.
Получим

. (3.15)

Сложим (3.14) и (3.15),
чтобы найти сумму нормальных напряжений,
действующих по взаимно перпендикулярным
площадкам.

Получим

σ_α
+ σ<sub>α
+ 90</sub>
= σ_х
+ σ_у
= const, (3.16)

т.е. сумма нормальных
напряжений по двум взаимно перпендикулярным
площадкам инвариантна по отношению к
наклону этих площадок.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.

Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.

Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение

представляет собой среднее напряжение на данной площадке.

Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке

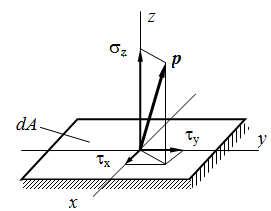
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.

Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.

Связь между напряжениями и внутренними силами

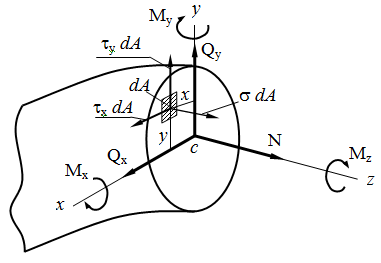
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τ_x dA, τ_y dA.

Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём;

Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.

Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.

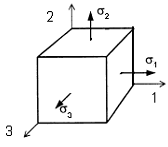
Объемное напряженное состояние

Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).

Рис. 3.1

Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:

Относительные деформации и напряжения связаны обобщенным законом Гука.

Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).

Обозначение главных напряжений:

Напряженное состояние называется объемным или трехосным, если

Рис. 3.2

Относительное изменение объема:

где К – модуль объемной упругости,

Удельная потенциальная энергия упругой деформации:

— полная

— изменение объема

— изменение формы

Плоское напряженное состояние

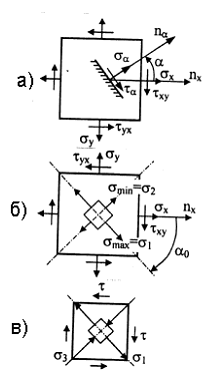
Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

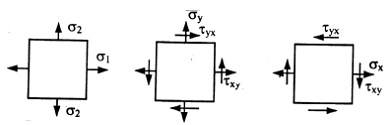
Рис.3.3

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Чистый сдвиг σ_x = σ_y = 0   (рис. 3.4,в)

Рис. 3.4

Линейное напряженное состояние

Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.

Проверка прочности при линейном напряженном состоянии проводится по условию прочности:

В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:

Величина σ_экв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.

Гипотезы прочности

Существует 5 гипотез прочности:

Примеры расчета напряжений >
Осевое растяжение-сжатие >

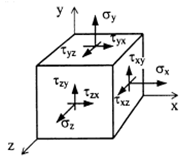
Если в некоторой точке напряжённого тела одно главное напряжение равно нулю – это случай плоского напряжённого состояния. Выделим элементарный кубик таким образом, чтобы фасадная и задняя грани совпадали с главной площадкой, главное напряжение на которой равно нулю. Покажем такой элемент и компоненты напряжённого состояния:

Ввиду того, что фасадная и задняя грани свободны от напряжений, ширину элемента в    направлении от Х обозначим через 1.

Необходимо иметь в виду:

1)   Параллелепипед бесконечно мал и все компоненты напряжения относятся к некоторой точке , а не к  трём разным точкам — центрам граней параллелепипеда, проходящим через эту точку .

2)   Напряжённое состояние считается однородным, то есть одноимённые напряжения на параллельных гранях параллелепипеда численно равны друг другу.

Индексы у касательных напряжений означают, к примеру, у касательного напряжения  :

индекс Z – данное касательное напряжение действует по площадке, перпендикулярной оси Z, а второй индекс Y касательного напряжения означает, что данное касательное напряжение действует параллельно оси Y. Знак касательных напряжений устанавливается в соответствии с правилом внешней нормали, согласно которому напряжение   положительно, когда оно совпадает по направлению с положительной осью. Если внешняя нормаль противоположна направлению оси, то касательное напряжение  положительно тогда, когда оно также противоположно своей координатной оси, причём последнее правило имеет чисто формальный смысл и зависит от того, как направлены оси.

Ввиду того, что мы рассматриваем однородное напряжённое состояние, нормальные напряжения на параллельных гранях взаимно уравновешены. Касательные напряжения образуют две пары сил    :

Тогда запишем:

Так как кубик находится в равновесии, то обязательно имеет место выражение 

Если сравнить выражения ,полученные для , то увидим следующее:

Эта запись выражает закон парности касательных напряжений: на двух взаимно перпендикулярных площадках, проходящих через напряжённую точку материала, действуют равные по величине касательные напряжения, причём под действием этих касательных напряжений кубик находится в равновесии.