Плотность электрическая как найти

Электрическим током называют направленное движение свободно заряженных частиц под действием электрического поля.

Как правило движение зарядов происходит в некоторой среде (веществе или вакууме), являющейся проводником для электрического тока. Движущимися в среде заряженными частицами могут быть электроны (в металлах, полупроводниках) или ионы (в жидкостях и газах).

Для возникновения и протекания электрического тока в любой токопроводящей среде необходимо выполнение двух условий:

1. Наличие в среде свободных носителей заряда;
2. Наличие электрического поля.

Для поддержания электрического поля, например в проводнике, к его концам необходимо подключить какой-либо источник электрической энергии (батарейку или аккумулятор). Поле в проводнике создается зарядами, которые накопились на электродах источника тока под действием сил (химических, механических и т.д.).

За направление тока условно принято принимать направление движения положительных зарядов. Следовательно, условно принятое направление тока обратно направлению движения электронов – основных отрицательных электрических носителей заряда в металлах и полупроводниках.

Понять явление электрического тока достаточно сложно так как его невозможно увидеть глазами. Для лучшего понимания процессов в электронике проведем аналогию между электрическим током в проводнике и водой в тонкой трубочке. В трубочке есть вода (носители заряда в проводнике), но она неподвижна, если трубочка лежит на горизонтальной поверхности и уровень высот ее концов (значения потенциалов электрического поля) одинаковый. Если трубочку наклонить так, что один конец станет выше другого (появится разность потенциалов), вода потечет по трубочке (электроны придут в движение).

Способность вещества проводить электрический ток под действием электрического поля называется электропроводностью. Каждому веществу соответствует определенная степень электропроводности. Ее значение зависит от концентрации в веществе носителей заряда – чем она выше, тем больше электропроводность. В зависимости от электропроводности все вещества делятся на три большие группы: проводники, полупроводники и диэлектрики.

Электрический ток может менять направление и величину во времени (переменный ток) или оставаться неизменным (постоянный) (рисунок 2).

Количественной мерой электрического тока служит сила тока I, которая определяется числом электронов (зарядов) q, проходящих через импровизированное поперечное сечение проводника в единицу времени t (рисунок 3).

Для постоянного тока представленное выше выражение можно записать в виде

Ток в системе СИ измеряется в амперах, [А]. Току в 1 А соответствует ток, при котором через поперечное сечение за 1 секунду проходит электрический заряд, равный 1 Кл.

1 A = 1 Кл/1 сек.

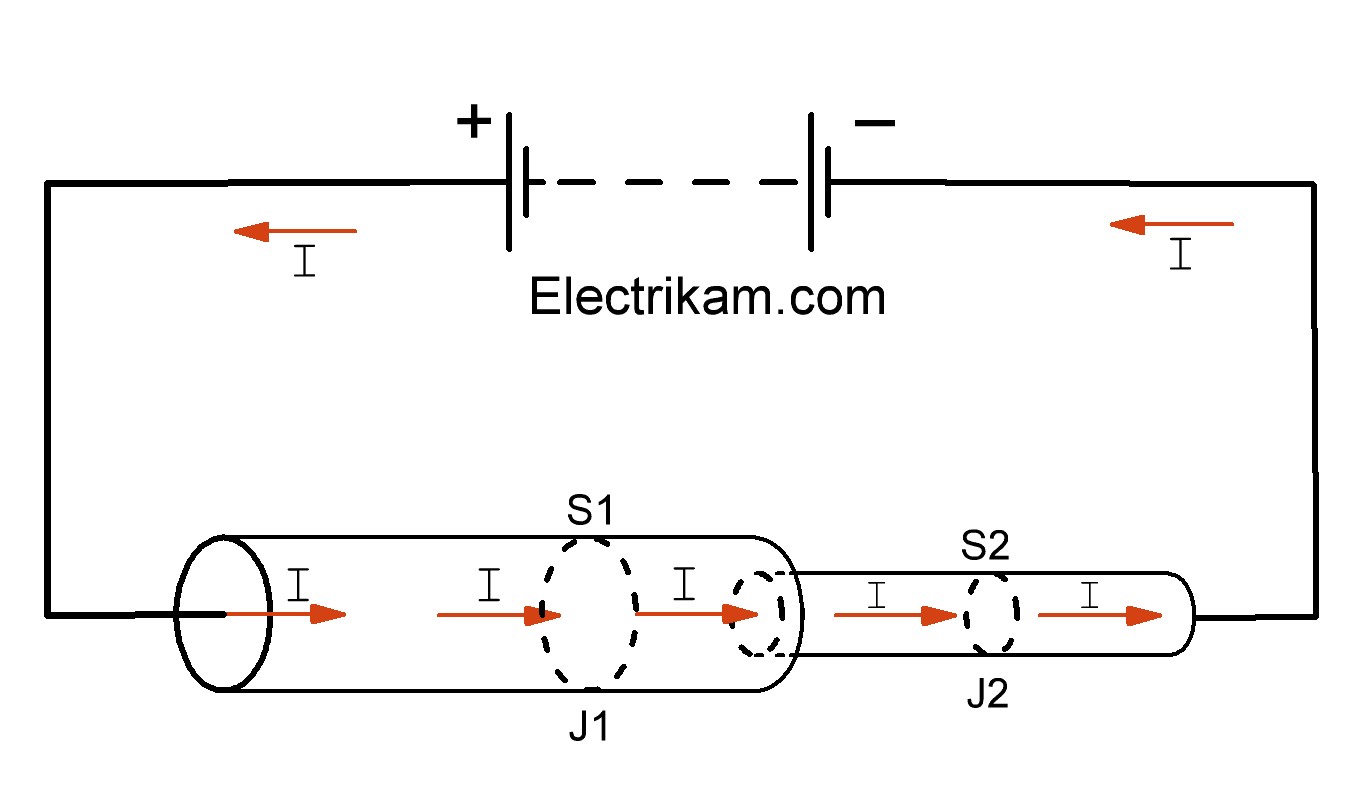
Плотность электрического тока

Под плотностью тока j понимается физическая величина, равная отношению тока I к площади поперечного сечения S проводника. При равномерном распределении тока по поперечному сечению проводника.

J = I/S 

Плотность тока в системе СИ измеряется в амперах на миллиметр квадратный, [А/мм²].

Рассмотрим плотность тока в проводнике с разным поперечным сечением. Например, соединены два проводника с различными сечениями: первый толстый провод с большим поперечным сечением S1 второй тонкий провод с сечением S2. К концам которых приложено постоянное напряжение (рисунок 5) в следствии чего через них протекает постоянный ток с одинаковой силой тока.

Предположим, что сила тока через поперечное сечение толстого проводника S1 и тонкого провода S2 различная. Из этого предположения вытекает, что за каждую единицу времени через сечения S1 и S2 протекают различные значения электрического заряда. Следовательно, в объёме провода, расположенного между двумя указанными сечениям происходит непрерывное скапливание зарядов, и напряженность электрического поля изменялась бы, чего не может быть, так как при изменении электрического поля ток был бы непостоянен. В проводах с различным сечением при одном и том же токе плотность тока обратно пропорциональна площади поперечного сечения.

I = J₁S₁ = J₂S₂

Плотность тока — векторная величина.

Направление вектора  совпадает с направлением положительно заряженных зарядов и, следовательно, с направлением самого тока I.

Если концентрация носителей тока равна n, каждый носитель имеет заряд e и скорость его движения в проводнике равна v (рисунок 3), то за время dt через поперечное сечение S проводника переносится заряд

В этом случае величину силы тока I можно представить в виде зависимости

а плотность тока

Сила тока через произвольную поверхность определяется через поток вектора плотности тока, как интеграл по произвольной (в общем случае) поверхности S (рисунок 6)

От величины плотности тока зависит важный показатель – качество электропередачи. Фактически этот показатель зависит от степени нагрузки проводника (хотя и не только от нее). В зависимости от значения плотности тока принято выбирать сечение проводов – это связано с наличием у проводников сопротивления, в результате которого происходит нагрев жил проводника вплоть до его расплавления и выхода из строя.

Для упрощения
математических расчетов электростатических
полей часто пренебрегают дискретной
структурой зарядов. Считают, что заряд
распределен непрерывно и вводят понятие
о плотности заряда.

Рассмотрим различные
случаи распределения зарядов.

1.Заряд
распределен вдоль линии.
Пусть на бесконечно малом участке
находится заряд.
Введем величину

.
(1.5)

Величина
называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.

2.Заряд
распределен по поверхности.
Введем поверхностную плотность заряда:

.
(1.6)

Её физический
смысл – заряд, приходящийся на единицу
площади.

3.Заряд
распределен по объёму.
Введем объёмную плотность заряда:

.
(1.7)

Её физический
смысл – заряд, сосредоточенный в единице
объёма.

Заряд,
сосредоточенный на бесконечно малом
участке линии, поверхности или в
бесконечно малом объёме можно считать
точечным. Напряжённость поля, создаваемого
им, определится формулой:

.
(1.8)

Для нахождения
напряжённости поля, создаваемого всем
заряженным телом, нужно применить
принцип суперпозиции полей:

.
(1.9)

В этом случае, как
правило, задача сводится к вычислению
интеграла.

1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца

Постановка
задачи.
Пусть имеется тонкое кольцо радиуса R,
заряженное с линейной плотностью заряда
τ.
Необходимо рассчитать напряжённость
электрического поля в произвольной
точке А,
расположенной на оси заряженного кольца
на расстоянии x
от плоскости кольца (рис. ).

Выберем
бесконечно малый элемент длины кольца
dl;
заряд dq,
находящийся на этом элементе равен dq=
τ·dl.
Этот заряд создает в точке А
электрическое поле напряжённостью
.
Модуль вектора напряжённости равен:

.
(1.10)

По
принципу суперпозиции полей напряжённость
электрического поля, создаваемого всем
заряженным телом, равна векторной сумме
всех векторов
:

.
(1.11)

Разложим
вектора
на составляющие: перпендикулярные оси
кольца ()
и параллельные оси кольца ().

.
(1.12)

Векторная
сумма перпендикулярных составляющих
равна нулю:
,
тогда.
Заменяя сумму интегралом, получим:

.
(1.13)

Из
треугольника (рис.1.2) следует:

=.
(1.14)

Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:

.
(1.15)

Так
как
,
то

.
(1.16)

С
учетом того, что
,
формулу (1.16) можно представить в виде:

.
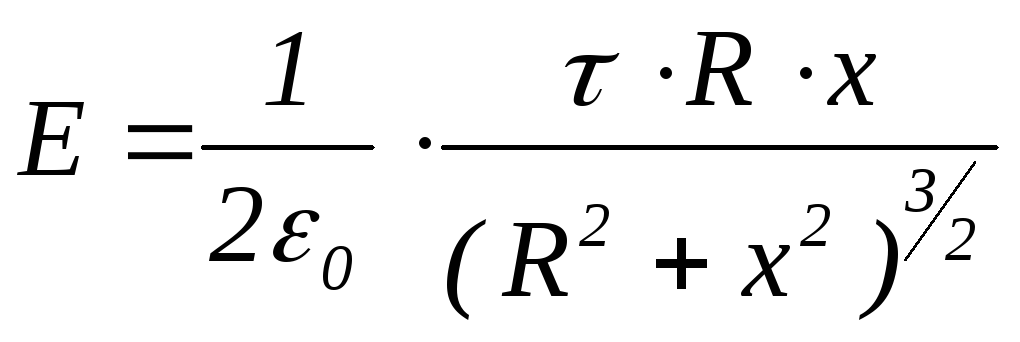
(1.17)

1.4.Геометрическое описание электрического поля. Поток вектора напряжённости

Для
математического описания электрического
поля нужно указать в каждой точке
величину и направление вектора

,
то есть задать векторную функцию.

Существует
наглядный (геометрический) способ
описания поля с помощью линий вектора
(силовых линий) (рис.13.).

Линии напряжённости
проводят следующим образом:

• касательная
  к линии в каждой точке должна совпадать
  с направлением поля;

• число
  линий пересекающих единичную площадку,
  перпендикулярную к ним, должно быть
  равно численному значению вектора
  .

Существует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.

На
рисунке 1.4 показано изображение
электростатического поля точечного
заряда с помощью линий вектора
,
а на рисунке 1.5 — изображение
электростатического поля диполя^.

1.5.
Поток
вектора напряжённости электростатического
поля

П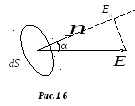оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь

— единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля

образует с нормалью

некоторый угол α.
Проекция вектора

на направление нормали равна E_n=E·cos
α .

Потоком вектора
через бесконечно малую площадку
называется скалярное произведение

,
(1.18)

или

.
(1.19)

Поток вектора
напряжённости электрического поля
является алгебраической величиной; его
знак зависит то взаимной ориентации
векторов
и
.

Поток
вектора
через произвольную поверхностьSконечной величины определится интегралом:

.
(1.20)

Если
поверхность замкнутая, интеграл отмечают
кружочком:

.
(1.21)

Для замкнутых
поверхностей нормаль берется наружу
(рис.1.7).

Поток
вектора напряжённости имеет наглядный
геометрический смысл: он численно равен
числу линий вектора
,
проходящих через поверхностьS.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.13 Энергия электрического поля. Плотность энергии.

Вернемся к обсуждению вопроса об энергии взаимодействия электрических зарядов. Ранее мы показали, что потенциальная энергия электростатического взаимодействия двух точечных зарядов q₁ и q₂, находящихся на расстоянии r друг от друга (рис. 212), рассчитывается по формуле

(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r}) . (1)

Придадим этой формуле несколько иной вид

(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r} = q_1 frac{1}{4 pi varepsilon_0} frac{q_2}{r} = q_1 varphi_1) ,

здесь (~varphi_1 = frac{1}{4 pi varepsilon_0} frac{q_2}{r}) — потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать

(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r} = q_2 frac{1}{4 pi varepsilon_0} frac{q_1}{r} = q_2 varphi_2) ,

где (~varphi_2 = frac{1}{4 pi varepsilon_0} frac{q_1}{r}) — потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь, перепишем выражение (1), в симметричной форме, легко допускающей обобщение

(~U(r) = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2)) . (2)

В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и появляется в формуле множитель 1/2.

Если система состоит из нескольких зарядов q₁, q₂, …, q_N , то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов (двойную сумму), можно заменить на суммирование по самим зарядам, то есть записать

(~U = sum_{pairs} {frac{1}{4 pi varepsilon_0} frac{q_i q_k}{r_{ik}}} = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2 + ldots + q_N varphi_N) = frac{1}{2} sum_{charges} {q_k varphi_k}) . (3)

В этой формуле φ_k — потенциал поля в точке, где находится заряд q_k, причем поля, создаваемого всеми зарядами, кроме самого заряда q_k (как говорят, исключая самовоздействие заряда на самого себя).

Использование понятия энергии взаимодействия требует чрезвычайной точности и внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны, предоставляет определенную свободу, а, с другой, требует четкого понимания о какой именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Если же требуется рассчитать работу поля при изменении положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от нулевого уровня потенциала.

Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим примеры расчета энергии электростатического взаимодействия.

Три точечных заряда.

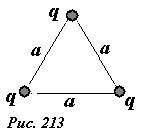
Пусть три одинаковых точечных заряда, величины которых равны между собой q₁ = q₂ = q₃ = q, расположены в вершинах правильного треугольника со стороной a (рис.213). Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен

(~varphi_1 = varphi_2 = varphi_3 = 2 frac{q}{4 pi varepsilon_0 a}) .

В соответствии с формулой (3) энергия взаимодействия зарядов равна

(~U_0 = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2 + q_3 varphi_3) = 3 frac{q^2}{4 pi varepsilon_0 a}) . (4)

Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное расстояние друг от друга.

Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной a₁ , то их энергия окажется равной

(~U_1 = 3 frac{q^2}{4 pi varepsilon_0 a_1}) .

При таком смещении работа электрического поля будет равна уменьшению энергии системы

(~A = U_0 — U_1 = 3 frac{q^2}{4 pi varepsilon_0} left ( frac{1}{a} — frac{1}{a_1} right)) .

Обратите внимание, при (~a_1 to infty) эта работа становится в точности равной начальной энергии U₀.

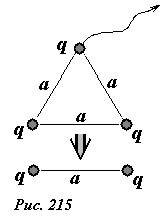
Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся (рис. 215), то энергия системы станет равной

(~U_1 = frac{q^2}{4 pi varepsilon_0 a}) .

При этом поле совершит работу

(~A = U_0 — U_1 = 3 frac{q^2}{4 pi varepsilon_0 a} — frac{q^2}{4 pi varepsilon_0 a} = 2 frac{q^2}{4 pi varepsilon_0 a}) .

Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу A₂ = U₁. В итоге начальная энергия полностью расходуется на совершение полной работы U₀ = A₁ + A₂ .

Задание для самостоятельной работы.

1. Проанализируйте изменение энергии и совершенные работы в рассмотренной системе, если один из зарядов отрицательный.

Энергия взаимодействия двух равномерно заряженных параллельных пластин.

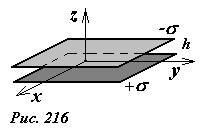
Найдем энергию взаимодействия двух равных по модулю зарядов противоположного знака, равномерно распределенными по двум параллельным пластинам. Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой —σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин, площадь каждой пластины обозначим S. Краевыми эффектами пренебрежем.

Для расчета энергии взаимодействия воспользуемся формулой U = qφ’, где φ’ — потенциал поля создаваемого всеми зарядами, кроме заряда q.

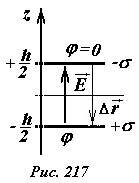
Напряженность поля между пластинами была вычислена нами ранее, она равна

(~E = frac{sigma}{varepsilon_0}) . (5)

Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен

(~varphi = -vec E cdot Delta vec r = Eh = frac{sigma h}{varepsilon_0}) . (6)

Здесь (~Delta vec r) — вектор перемещения от отрицательной пластины к положительной. Данная формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.

Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами (~E’ = frac{E}{2} = frac{sigma}{2 varepsilon_0}) , поэтому искомый потенциал будет равен (~varphi’ = E’h = frac{sigma h}{2 varepsilon_0}) . Таким образом, энергия взаимодействия зарядов оказывается равной

(~U = q varphi’ = (sigma S) frac{sigma h}{2 varepsilon_0} = frac{sigma^2}{2 varepsilon_0} Sh) , (7)

здесь σS — заряд положительно заряженной пластины.

Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.

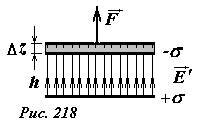
Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения (~F = q E’ = (sigma S) frac{sigma}{2 varepsilon_0} = frac{sigma^2}{2 varepsilon_0} S) , причем эта сила не зависит от расстояния между пластинами. Для того, чтобы раздвинуть пластины на расстояние h, необходимо приложить внешнюю силу, равную по модулю силе электрического притяжения (рис. 218). При этом эта сила совершит работу (равную увеличению энергии системы)

(~A = U = Fh = frac{sigma^2}{2 varepsilon_0} Sh) . (7′)

Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε₀E, выразим энергию взаимодействия через напряженность поля

(~U = frac{varepsilon_0^2 E}{2} Sh) . (8)

В процессе разнесения пластин создается электрическое поле во все большем объеме между пластинами, поэтому можно утверждать, что совершенная работа увеличивает энергию электрического поля, или работа расходуется на создание поля. Так при смещении пластины на расстояние Δz, объем занятый полем увеличивается на SΔz, если расстояние между пластинами увеличилось от нуля до некоторого значения h, то поле создается в объеме Sh. Таким образом, найденная энергия взаимодействия зарядов (7) есть энергия электрического поля — энергия «размазанная» по той области пространства, где создано поле. Косвенным подтверждением сделанного заключения, является тот факт, что энергия взаимодействия пропорциональна объему части пространства V = Sh, занятого полем и выражается через характеристику поля (его напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже благодаря своему существованию обладает энергией. В качестве энергетической характеристики поля следует рассматривать энергию, содержащуюся в единице объема, то есть объемную плотность энергии[~w = frac{W}{V}] . Из выражения (8) следует, что объемная плотность энергии электрического поля определяется формулой

(~w = frac{varepsilon_0 E^2}{2}) . (9)

Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю

(~w = frac{Delta U}{Delta V}) , при ΔV → 0 .

Энергия поля равномерно заряженной сферы.

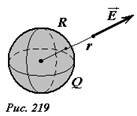
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна

(~E(r) = frac{Q}{4 pi varepsilon_0 r^2}) , (10)

в частности непосредственно у поверхности сферы напряженность поля равна

(~E_0 = frac{Q}{4 pi varepsilon_0 R^2}) . (11)

Обратим внимание, что произведение (~S = 4 pi R^2) есть площадь сферы, поэтому отношение (~frac{Q}{4 pi varepsilon_0} = sigma) является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе (~E_0 = frac{sigma}{varepsilon_0}). Потенциал поверхности сферы также был вычислен нами ранее

(~varphi_0 = frac{Q}{4 pi varepsilon_0 R}) . (12)

Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны (~delta Q_k = frac{Q}{N}) (k = 1,2…N). Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N-1) зарядами равен (~varphi_k = frac{(N-1) delta Q}{4 pi varepsilon_0 R}). С использованием симметричной формулы (~U = frac{1}{2} sum_{k} {q_k varphi_k}) , выражение для энергии взаимодействия приобретает вид

(~U = frac{1}{2} sum_{k} {q_k varphi_k} = frac{1}{2} sum_{k=1}^{N} {delta Q_k frac{(N-1) delta Q}{4 pi varepsilon_0 R}}) ,

данная сумма содержит N одинаковых слагаемых, поэтому равна

(~U = frac{1}{2} sum_{k=1}^{N} {delta Q_k frac{(N-1) delta Q}{4 pi varepsilon_0 R}} = frac{1}{2} N delta Q frac{(N-1) delta Q}{4 pi varepsilon_0 R} = frac{1}{2} N (N-1) frac{(delta Q)^2}{4 pi varepsilon_0 R} = frac{Q^2}{8 pi varepsilon_0 R} left ( 1 — frac{1}{N} right)) . (13)

Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе (~N to infty) слагаемое (~frac{1}{N}) исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид

(~U = frac{Q^2}{8 pi varepsilon_0 R}) . (14)

Заметим, что полученное выражение имеет вид (~U = frac{1}{2} Q varphi_0). Если сразу заявить, что уменьшение заряда на малую величину (~delta Q) пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.

Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда (~delta Q_k = frac{Q}{N}) (k = 1,2…N), которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k-1) порций заряда, то ее потенциал равен (~varphi_{(k-1)} = frac{(k-1) delta Q}{4 pi varepsilon_0 R}) . Поэтому для того, что бы перенести на сферу следующую порцию заряда необходимо совершить работу

(~A_k = delta Q varphi_{(k-1)} = (k-1) frac{(delta Q)^2}{4 pi varepsilon_0 R}) .

Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.

Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии

(~U = A = frac{1}{2} sum_{k=1}^{N} {A} = frac{(delta Q)^2}{4 pi varepsilon_0 R} sum_{k=1}^{N} {(k-1)} = frac{(delta Q)^2}{4 pi varepsilon_0 R} frac{N (N-1)}{2} = frac{Q^2}{8 pi varepsilon_0 R} left ( 1 — frac{1}{N} right)) . (15)

Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов ((~N to infty)) мы опять приходим к формуле (14).

В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.

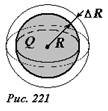
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя (~Delta V = 4 pi R^2 Delta R) . Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем запишем в виде

(~Delta U = w Delta V = 4 pi R^2 Delta R w) , (16)

где w — плотность энергии поля. С другой стороны эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы

(~Delta U = frac{Q^2}{8 pi varepsilon_0 R} — frac{Q^2}{8 pi varepsilon_0 (R + Delta R)} = frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R (R + Delta R)} approx frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R^2}) .

На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности (~Q = 4 pi varepsilon_0 R^2 E) :

(~Delta U = frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R^2} = frac{varepsilon_0 E^2}{2} 4 pi R^2 Delta R) .

Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой (~w = frac{varepsilon_0 E^2}{2}).

Следующая страница