Полиномиальные коэффициенты как найти - Исправление недочетов и поиск решений вместе с Examum.ru

From Wikipedia, the free encyclopedia

In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

Theorem[edit]

For any positive integer m and any non-negative integer n, the multinomial formula describes how a sum with m terms expands when raised to an arbitrary power n:

${displaystyle (x_{1}+x_{2}+cdots +x_{m})^{n}=sum _{k_{1}+k_{2}+cdots +k_{m}=n; k_{1},k_{2},cdots ,k_{m}geq 0}{n choose k_{1},k_{2},ldots ,k_{m}}prod _{t=1}^{m}x_{t}^{k_{t}},,}$

where

${n choose k_{1},k_{2},ldots ,k_{m}}={frac {n!}{k_{1}!,k_{2}!cdots k_{m}!}}$

is a multinomial coefficient. The sum is taken over all combinations of nonnegative integer indices k₁ through k_m such that the sum of all k_i is n. That is, for each term in the expansion, the exponents of the x_i must add up to n. Also, as with the binomial theorem, quantities of the form x⁰ that appear are taken to equal 1 (even when x equals zero).

In the case m = 2, this statement reduces to that of the binomial theorem.

Example[edit]

The third power of the trinomial a + b + c is given by

$(a+b+c)^{3}=a^{3}+b^{3}+c^{3}+3a^{2}b+3a^{2}c+3b^{2}a+3b^{2}c+3c^{2}a+3c^{2}b+6abc.$

This can be computed by hand using the distributive property of multiplication over addition, but it can also be done (perhaps more easily) with the multinomial theorem. It is possible to «read off» the multinomial coefficients from the terms by using the multinomial coefficient formula. For example:

$a^{2}b^{0}c^{1}$

has the coefficient ${displaystyle {3 choose 2,0,1}={frac {3!}{2!cdot 0!cdot 1!}}={frac {6}{2cdot 1cdot 1}}=3.}$

$a^{1}b^{1}c^{1}$

has the coefficient ${displaystyle {3 choose 1,1,1}={frac {3!}{1!cdot 1!cdot 1!}}={frac {6}{1cdot 1cdot 1}}=6.}$

Alternate expression[edit]

The statement of the theorem can be written concisely using multiindices:

$(x_{1}+cdots +x_{m})^{n}=sum _{{|alpha |=n}}{n choose alpha }x^{alpha }$

where

${displaystyle alpha =(alpha _{1},alpha _{2},dots ,alpha _{m})}$

and

${displaystyle x^{alpha }=x_{1}^{alpha _{1}}x_{2}^{alpha _{2}}cdots x_{m}^{alpha _{m}}}$

Proof[edit]

This proof of the multinomial theorem uses the binomial theorem and induction on m.

First, for m = 1, both sides equal x₁ⁿ since there is only one term k₁ = n in the sum. For the induction step, suppose the multinomial theorem holds for m. Then

${displaystyle {begin{aligned}&(x_{1}+x_{2}+cdots +x_{m}+x_{m+1})^{n}=(x_{1}+x_{2}+cdots +(x_{m}+x_{m+1}))^{n}\[6pt]={}&sum _{k_{1}+k_{2}+cdots +k_{m-1}+K=n}{n choose k_{1},k_{2},ldots ,k_{m-1},K}x_{1}^{k_{1}}x_{2}^{k_{2}}cdots x_{m-1}^{k_{m-1}}(x_{m}+x_{m+1})^{K}end{aligned}}}$

by the induction hypothesis. Applying the binomial theorem to the last factor,

$=sum _{{k_{1}+k_{2}+cdots +k_{{m-1}}+K=n}}{n choose k_{1},k_{2},ldots ,k_{{m-1}},K}x_{1}^{{k_{1}}}x_{2}^{{k_{2}}}cdots x_{{m-1}}^{{k_{{m-1}}}}sum _{{k_{m}+k_{{m+1}}=K}}{K choose k_{m},k_{{m+1}}}x_{m}^{{k_{m}}}x_{{m+1}}^{{k_{{m+1}}}}$

$=sum _{{k_{1}+k_{2}+cdots +k_{{m-1}}+k_{m}+k_{{m+1}}=n}}{n choose k_{1},k_{2},ldots ,k_{{m-1}},k_{m},k_{{m+1}}}x_{1}^{{k_{1}}}x_{2}^{{k_{2}}}cdots x_{{m-1}}^{{k_{{m-1}}}}x_{m}^{{k_{m}}}x_{{m+1}}^{{k_{{m+1}}}}$

which completes the induction. The last step follows because

${n choose k_{1},k_{2},ldots ,k_{{m-1}},K}{K choose k_{m},k_{{m+1}}}={n choose k_{1},k_{2},ldots ,k_{{m-1}},k_{m},k_{{m+1}}},$

as can easily be seen by writing the three coefficients using factorials as follows:

${frac {n!}{k_{1}!k_{2}!cdots k_{{m-1}}!K!}}{frac {K!}{k_{m}!k_{{m+1}}!}}={frac {n!}{k_{1}!k_{2}!cdots k_{{m+1}}!}}.$

Multinomial coefficients[edit]

The numbers

${displaystyle {n choose k_{1},k_{2},ldots ,k_{m}}}$

appearing in the theorem are the multinomial coefficients. They can be expressed in numerous ways, including as a product of binomial coefficients or of factorials:

${displaystyle {n choose k_{1},k_{2},ldots ,k_{m}}={frac {n!}{k_{1}!,k_{2}!cdots k_{m}!}}={k_{1} choose k_{1}}{k_{1}+k_{2} choose k_{2}}cdots {k_{1}+k_{2}+cdots +k_{m} choose k_{m}}}$

Sum of all multinomial coefficients[edit]

The substitution of x_i = 1 for all i into the multinomial theorem

${displaystyle sum _{k_{1}+k_{2}+cdots +k_{m}=n}{n choose k_{1},k_{2},ldots ,k_{m}}x_{1}^{k_{1}}x_{2}^{k_{2}}cdots x_{m}^{k_{m}}=(x_{1}+x_{2}+cdots +x_{m})^{n}}$

gives immediately that

${displaystyle sum _{k_{1}+k_{2}+cdots +k_{m}=n}{n choose k_{1},k_{2},ldots ,k_{m}}=m^{n}.}$

Number of multinomial coefficients[edit]

The number of terms in a multinomial sum, #_n,m, is equal to the number of monomials of degree n on the variables x₁, …, x_m:

${displaystyle #_{n,m}={n+m-1 choose m-1}.}$

The count can be performed easily using the method of stars and bars.

Valuation of multinomial coefficients[edit]

The largest power of a prime p that divides a multinomial coefficient may be computed using a generalization of Kummer’s theorem.

Interpretations[edit]

Ways to put objects into bins[edit]

The multinomial coefficients have a direct combinatorial interpretation, as the number of ways of depositing n distinct objects into m distinct bins, with k₁ objects in the first bin, k₂ objects in the second bin, and so on.^[1]

Number of ways to select according to a distribution[edit]

In statistical mechanics and combinatorics, if one has a number distribution of labels, then the multinomial coefficients naturally arise from the binomial coefficients. Given a number distribution {n_i} on a set of N total items, n_i represents the number of items to be given the label i. (In statistical mechanics i is the label of the energy state.)

The number of arrangements is found by

Multiplying the number of choices at each step results in:

${displaystyle {N choose n_{1}}{N-n_{1} choose n_{2}}{N-n_{1}-n_{2} choose n_{3}}cdots ={frac {N!}{(N-n_{1})!n_{1}!}}cdot {frac {(N-n_{1})!}{(N-n_{1}-n_{2})!n_{2}!}}cdot {frac {(N-n_{1}-n_{2})!}{(N-n_{1}-n_{2}-n_{3})!n_{3}!}}cdots .}$

Cancellation results in the formula given above.

Number of unique permutations of words[edit]

Multinomial coefficient as a product of binomial coefficients, counting the permutations of the letters of MISSISSIPPI.

The multinomial coefficient

${displaystyle {binom {n}{k_{1},ldots ,k_{m}}}}$

is also the number of distinct ways to permute a multiset of n elements, where k_i is the multiplicity of each of the ith element. For example, the number of distinct permutations of the letters of the word MISSISSIPPI, which has 1 M, 4 Is, 4 Ss, and 2 Ps, is

${11 choose 1,4,4,2}={frac {11!}{1!,4!,4!,2!}}=34650.$

Generalized Pascal’s triangle[edit]

One can use the multinomial theorem to generalize Pascal’s triangle or Pascal’s pyramid to Pascal’s simplex. This provides a quick way to generate a lookup table for multinomial coefficients.

References[edit]

^ National Institute of Standards and Technology (May 11, 2010). «NIST Digital Library of Mathematical Functions». Section 26.4. Retrieved August 30, 2010.

Источник

В математике , то полиномиальная теорема описывает , как расширить мощности на сумму в терминах степеней слагаемых в этой сумме. Это обобщение биномиальной теоремы от биномов к полиномам.

Теорема

Для любого положительного целого числа m и любого неотрицательного целого числа n полиномиальная формула описывает, как сумма с m членами расширяется при возведении в произвольную степень n :

${ displaystyle (x_ {1} + x_ {2} + cdots + x_ {m}) ^ {n} = sum _ {k_ {1} + k_ {2} + cdots + k_ {m} = n } {n выберите k_ {1}, k_ {2}, ldots, k_ {m}} prod _ {t = 1} ^ {m} x_ {t} ^ {k_ {t}} ,,}$

куда

${n select k_ {1}, k_ {2}, ldots, k_ {m}} = { frac {n!} {k_ {1}! , k_ {2}! cdots k_ {m}! }}$

— полиномиальный коэффициент . Сумма берется по всем комбинациям неотрицательных целочисленных индексов с k ₁ по k _m, таким образом, что сумма всех k _i равна n . То есть для каждого члена в разложении показатели степени x _i должны составлять в сумме n . Кроме того, как и в случае с биномиальной теоремой , появляющиеся количества вида x ⁰ принимаются равными 1 (даже если x равен нулю).

В случае m = 2 это утверждение сводится к утверждению биномиальной теоремы.

Пример

Третья степень трехчлена a + b + c равна

$(a + b + c) ^ {3} = a ^ {3} + b ^ {3} + c ^ {3} + 3a ^ {2} b + 3a ^ {2} c + 3b ^ {2} a + 3b ^ {2} c + 3c ^ {2} a + 3c ^ {2} b + 6abc.$

Это можно вычислить вручную, используя дистрибутивное свойство умножения над сложением, но это также можно сделать (возможно, более легко) с помощью полиномиальной теоремы. Можно «считать» полиномиальные коэффициенты из членов, используя формулу полиномиальных коэффициентов. Например:

$а ^ {2} б ^ {0} в ^ {1}$

имеет коэффициент ${ displaystyle {3 choose 2,0,1} = { frac {3!} {2! cdot 0! cdot 1!}} = { frac {6} {2 cdot 1 cdot 1} } = 3.}$

$а ^ {1} б ^ {1} в ^ {1}$

имеет коэффициент ${ displaystyle {3 choose 1,1,1} = { frac {3!} {1! cdot 1! cdot 1!}} = { frac {6} {1 cdot 1 cdot 1} } = 6.}$

Альтернативное выражение

Формулировку теоремы можно кратко записать с помощью мультииндексов :

$(x_ {1} + cdots + x_ {m}) ^ {n} = sum _ {{| alpha | = n}} {n choose alpha} x ^ { alpha}$

куда

${ Displaystyle альфа = ( альфа _ {1}, альфа _ {2}, точки, альфа _ {м})}$

а также

${ displaystyle x ^ { alpha} = x_ {1} ^ { alpha _ {1}} x_ {2} ^ { alpha _ {2}} cdots x_ {m} ^ { alpha _ {m} }}$

Доказательство

Это доказательство полиномиальной теоремы использует биномиальную теорему и индукцию по m .

Во-первых, при m = 1 обе стороны равны x ₁^n, поскольку в сумме есть только один член k ₁ = n . Для шага индукции предположим, что полиномиальная теорема верна для m . потом

${ displaystyle { begin {align} & (x_ {1} + x_ {2} + cdots + x_ {m} + x_ {m + 1}) ^ {n} = (x_ {1} + x_ {2 } + cdots + (x_ {m} + x_ {m + 1})) ^ {n} \ [6pt] = {} & sum _ {k_ {1} + k_ {2} + cdots + k_ {m-1} + K = n} {n выбрать k_ {1}, k_ {2}, ldots, k_ {m-1}, K} x_ {1} ^ {k_ {1}} x_ {2 } ^ {k_ {2}} cdots x_ {m-1} ^ {k_ {m-1}} (x_ {m} + x_ {m + 1}) ^ {K} end {выровнено}}}$

по предположению индукции. Применяя биномиальную теорему к последнему множителю,

$= sum _ {{k_ {1} + k_ {2} + cdots + k _ {{m-1}} + K = n}} {n выбрать k_ {1}, k_ {2}, ldots, k _ {{m-1}}, K} x_ {1} ^ {{k_ {1}}} x_ {2} ^ {{k_ {2}}} cdots x _ {{m-1}} ^ {{ k _ {{m-1}}}} sum _ {{k_ {m} + k _ {{m + 1}} = K}} {K выберите k_ {m}, k _ {{m + 1}}} x_ {m} ^ {{k_ {m}}} x _ {{m + 1}} ^ {{k _ {{m + 1}}}}$

$= sum _ {{k_ {1} + k_ {2} + cdots + k _ {{m-1}} + k_ {m} + k _ {{m + 1}} = n}} {n выбрать k_ {1}, k_ {2}, ldots, k _ {{m-1}}, k_ {m}, k _ {{m + 1}}} x_ {1} ^ {{k_ {1}}} x_ { 2} ^ {{k_ {2}}} cdots x _ {{m-1}} ^ {{k _ {{m-1}}}} x_ {m} ^ {{k_ {m}}} x _ {{ м + 1}} ^ {{к _ {{м + 1}}}}$

что завершает индукцию. Последний шаг следует, потому что

${n выбрать k_ {1}, k_ {2}, ldots, k _ {{m-1}}, K} {K выбрать k_ {m}, k _ {{m + 1}}} = {n выберите k_ {1}, k_ {2}, ldots, k _ {{m-1}}, k_ {m}, k _ {{m + 1}}},$

в этом легко убедиться, записав три коэффициента с использованием факториалов следующим образом:

${ frac {n!} {k_ {1}! k_ {2}! cdots k _ {{m-1}}! K!}} { frac {K!} {k_ {m}! k _ {m +1}}!}} = { Frac {n!} {K_ {1}! K_ {2}! Cdots k _ {{m + 1}}!}}.$

Полиномиальные коэффициенты

Цифры

${ displaystyle {n select k_ {1}, k_ {2}, ldots, k_ {m}}}$

в теореме фигурируют полиномиальные коэффициенты . Они могут быть выражены множеством способов, в том числе как произведение биномиальных коэффициентов или факториалов :

${ displaystyle {n select k_ {1}, k_ {2}, ldots, k_ {m}} = { frac {n!} {k_ {1}! , k_ {2}! cdots k_ { m}!}} = {k_ {1} choose k_ {1}} {k_ {1} + k_ {2} choose k_ {2}} cdots {k_ {1} + k_ {2} + cdots + k_ {m} выбрать k_ {m}}}$

Сумма всех полиномиальных коэффициентов

Подстановка x _i = 1 для всех i в полиномиальную теорему

${ displaystyle sum _ {k_ {1} + k_ {2} + cdots + k_ {m} = n} {n select k_ {1}, k_ {2}, ldots, k_ {m}} x_ {1} ^ {k_ {1}} x_ {2} ^ {k_ {2}} cdots x_ {m} ^ {k_ {m}} = (x_ {1} + x_ {2} + cdots + x_ {m}) ^ {n}}$

сразу дает, что

${ displaystyle sum _ {k_ {1} + k_ {2} + cdots + k_ {m} = n} {n select k_ {1}, k_ {2}, ldots, k_ {m}} = м ^ {п}.}$

Количество полиномиальных коэффициентов

Количество членов в полиномиальной сумме # _{n , m} равно количеству одночленов степени n от переменных x ₁ ,…, x _m :

${ displaystyle #_ {n, m} = {n + m-1 select m-1}.}$

Подсчет легко производится методом звездочек и столбиков .

Оценка полиномиальных коэффициентов

Наибольшая степень простого числа, которое делит полиномиальный коэффициент, может быть вычислена с использованием обобщения теоремы Куммера .

Интерпретации

Способы складывать предметы в мусорные ведра

Мультиномиальные коэффициенты имеют прямую комбинаторную интерпретацию, как количество способов размещения n различных объектов в m различных ячеек, где k ₁ объектов в первой ячейке, k ₂ объектов во второй ячейке и т. Д.

Количество способов выбора в зависимости от распределения

В статистической механике и комбинаторике, если имеется несколько распределений меток, то полиномиальные коэффициенты естественным образом возникают из биномиальных коэффициентов. Учитывая числовое распределение { n _i } в наборе из N общих элементов, n _i представляет количество элементов, которым должна быть присвоена метка i . (В статистической механике i — обозначение энергетического состояния.)

Количество аранжировок определяется по

Умножение количества вариантов на каждом этапе дает:

${ displaystyle {N choose n_ {1}} {N-n_ {1} choose n_ {2}} {N-n_ {1} -n_ {2} choose n_ {3}} cdots = { гидроразрыв {N!} {(N-n_ {1})! n_ {1}!}} cdot { frac {(N-n_ {1})!} {(N-n_ {1} -n_ {2 })! n_ {2}!}} cdot { frac {(N-n_ {1} -n_ {2})!} {(N-n_ {1} -n_ {2} -n_ {3}) ! n_ {3}!}} cdots.}$

Отмена приводит к формуле, приведенной выше.

Количество уникальных перестановок слов

Полиномиальный коэффициент как произведение биномиальных коэффициентов, считая перестановки букв MISSISSIPPI.

Мультиномиальный коэффициент также число различных способов переставить с мультимножеством из п элементов, где K _я это кратность каждых из I — го элемента. Например, количество различных перестановок букв слова MISSISSIPPI, которое имеет 1 M, 4 Is, 4 Ss и 2 Ps, равно
${ displaystyle { binom {n} {k_ {1}, ldots, k_ {m}}}}$

${11 choose 1,4,4,2} = { frac {11!} {1! , 4! , 4! , 2!}} = 34650.$

Обобщенный треугольник Паскаля

Можно использовать мультиномиальную теорему обобщать треугольник Паскаля или пирамиду Паскаля в симплекс Паскаля . Это обеспечивает быстрый способ создания таблицы поиска для полиномиальных коэффициентов.

Смотрите также

Полиномиальное распределение
Звезды и стержни (комбинаторика)

использованная литература

Источник

— полиномиальная
формула.
Суммирование в ней производится по всем
решениям уравнения n₁+n₂+…+n_k=n
в целых
неотрицательных числах.

Теорема
о полиномиальных коэффициентах.

Пример
5.

Определим
коэффициент с
в слагаемом

полинома (с приведенными подобными
членами), получаемого из выражения

.

В
силу теоремы о полиномиальных коэффициентах

3.2.3. Формула включений и исключений

Часто комбинаторная
конфигурация является объединением
других, число комбинаций в которых
вычислить проще. В таком случае требуется
уметь вычислять число комбинаций в
объединении.

Пусть А₁
и А₂
– 2 конечных множества. Тогда если
А₁А₂=,
то

.
Пусть теперь А₁А₂,
тогда в

каждый элемент из А₁А₂будет учтен
дважды. Поэтому

.
Последнюю формулу можно обобщить на
случай произвольного числа множеств:

.
(2)

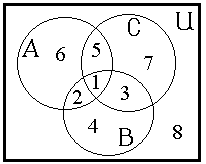
авенство (2) называется формулой
включений и исключений.
В частности, для трех множеств эта
формула имеет вид:

Доказывается
формула (1) методом математической
индукции.

Пример 6.

Сколько существует
натуральных чисел, меньших 1000, которые
не делятся ни на 3, ни на 5, ни на 7?

Всего чисел, меньших
тысячи, 999. Из них 999:3=333 делятся на 3,

999:5=199 (ост. 4) делятся
на 5,

999:7=142 (ост. 5) делятся
на 7,

999:(3х5)=66 (ост. 9)
делятся на 3 и на 5,

999:(3х7)=47 (ост. 12)
делятся на 3 и на 7,

999:(5х7)=28 (ост. 10)
делятся на 5 и на 7,

999:(3х5х7)=9 (ост. 45)
делятся на 3, на 5 и на 7.

В итоге искомых
чисел 999-(333+199+142-66-47-28+9)=457.

Следствие. Пусть
А –
конечное множество, А₁,
…, А_n
– его подмножества. Тогда

.
(3)

Доказательство.
Поскольку

,
а

,
то

.
Следовательно,

.
Применив для правой части последнего
равенства формулу включений и исключений,
получим искомый результат.

Пример 7.

Дано множество
А={0,
1, …, 10} и 3 его подмножества:

А₁={a
| a –
четное}, А₂={a
| a>6},
А₃={a
| 2<a<8}.
Сколько элементов множества А не
принадлежат ни одному из этих подмножеств?

тогда по формуле
(3)

.
Очевидно, что таким элементом является
1.

Вопросы для повторения

1.Что такое разбиение?

2.Запишите
полиномиальную формулу?

3.О чем говорится
в теореме о полиномиальных коэффициентах?

4.Как выглядит
формула включений и исключений?

5.Для чего необходима
формула включений и исключений?

Резюме по теме

Рассмотрено понятие
разбиения. Приведены необходимые теоремы
разбиения. Показана полиномиальная
формула, а так же приведена теорема о
полиномиальных коэффициентах. Рассмотрены
формулы включений и исключений.

Глава 4. Теория графов

Теория графов
— раздел дискретной
математики,
изучающий свойства графов.
В общем смысле граф представляется как
множество вершин (узлов), соединённых
рёбрами. В строгом определении графом
называется такая пара множеств G={R,V},
где V
есть подмножество любого счётного
множества, а R
— подмножество V×V.

Теория графов
находит применение, например, в
геоинформационных
системах
(ГИС). Существующие или вновь проектируемые
дома, сооружения, кварталы и т. п.
рассматриваются как вершины, а соединяющие
их дороги, инженерные сети, линии
электропередач и т. п. — как рёбра.
Применение различных вычислений,
производимых на таком графе, позволяет,
например, найти кратчайший объездной
путь или ближайший продуктовый магазин,
спланировать оптимальный маршрут.

Родоначальником
теории графов считается Леонард
Эйлер. В
1736 году в одном из своих писем он
формулирует и предлагает решение задачи
о семи
кёнигсбергских мостах,
ставшей впоследствии одной из классических
задач теории графов.

Терминология
теории графов
поныне не определена строго. В частности
в монографии Гудман, Хидетниеми, 1981
сказано «В программистском мире нет
единого мнения о том, какой из двух
терминов «граф» или «сеть».

При изображении
графов чаще всего используется следующая
система обозначений: каждой вершине
сопоставляется точка на плоскости, и
если между вершинами существует ребро,
то соответствующие точки соединяются
отрезком. В случаи ориентированного
графа отрезки заменяют стрелками.

Не следует путать
изображение графа с собственно графом
(абстрактной структурой), поскольку
одному графу можно сопоставить не одно
графическое представление. Изображение
призвано лишь показать какие пары вершин
соединены ребрами, а какие — нет. Часто
на практике бывает трудно ответить на
вопрос — являются ли два изображения
моделями одного и того же графа, или
нет. В зависимости от задачи, одни
изображения могут давать более наглядную
картину, чем другие.

Теория графов
решает такие задачи как: семь
мостов Кёнигсберга
— один из первых результатов в теории
графов, опубликован Эйлером
в 1736;
проблема
четырёх красок
— была сформулирована в 1852
году, но доказательство получено лишь
в 1976
году (достаточно 4-х красок для карты на
сфере (плоскости)); задача
коммивояжёра
— одна из наиболее известных NP-полных
задач; задача
о клике —
ещё одна NP-полная задача; нахождение
минимального стягивающего
дерева.

В
настоящее время на языке теории графов
формулируются и решаются многие задачи
управления, в том числе задачи сетевого
планирования и управления, анализа и
проектирования организационных структур
управления, анализа процессов
функционирования и целеполагания,
многие задачи принятия решений в условиях
неопределенности и др.

Гипотеза Улама
— а) всякий граф с более чем двумя вершинами
однозначно определяется набором графов,
где каждый граф из набора получен
удалением одной из вершин исходного
графа. б) всякий граф с более чем тремя
вершинами однозначно определяется
множеством графов, где каждый граф из
множества получен удалением одной из
вершин исходного графа. (Иными словами,
не существует таких двух различных
графов для которых бы эти наборы или
множества совпадали).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Мультиномиальный коэффициент: определение и примеры

17 авг. 2022 г.
читать 1 мин

Полиномиальный коэффициент описывает количество возможных разбиений n объектов на k групп размера n 1 , n 2 , …, n k .

Формула для расчета мультиномиального коэффициента:

Мультиномиальный коэффициент = n! / (n 1 ! * n 2 ! * … * n k !)

Следующие примеры иллюстрируют, как вычислить полиномиальный коэффициент на практике.

Пример 1: Буквы в слове

Сколько существует уникальных разделов слова ARKANSAS?

Решение. Мы можем просто подставить следующие значения в формулу для полиномиального коэффициента:

п (всего букв): 8

п 1 (буква «А»): 3

п 2 (буква «Р»): 1

п 3 (буква «К»): 1

п 4 (буква «Н»): 1

п 5 (буква «С»): 2

Мультиномиальный коэффициент = 8! / (3! * 1! * 1! * 1! * 2!) = 3360

Есть 3360 уникальных разделов слова ARKANSAS.

Пример 2: Учащиеся по классам

Группа из шести студентов состоит из 3 старших, 2 младших и 1 второкурсника. Сколько уникальных разделов этой группы учащихся существует по классам?

Решение. Мы можем просто подставить следующие значения в формулу для полиномиального коэффициента:

n (всего студентов): 6

n 1 (всего сеньоры): 3

n 2 (всего юниоров): 2

№ 3 (всего второкурсников): 1

Мультиномиальный коэффициент = 6! / (3! * 2! * 1!) = 60

Есть 60 уникальных разделов этих учеников по классам.

Пример 3: предпочтения политической партии

Из группы из десяти жителей определенного округа 3 — республиканцы, 5 — демократы и 2 — независимые. Сколько уникальных разделов этой группы жителей по политическим партиям?

Решение. Мы можем просто подставить следующие значения в формулу для полиномиального коэффициента:

n (всего жителей): 10

№ 1 (всего республиканцев): 3

n 2 (всего демократов): 5

n 3 (всего независимых): 2

Мультиномиальный коэффициент = 10! / (3! * 5! * 2!) = 2520

Существует 2520 уникальных разделов этих жителей по политическим партиям.

Дополнительные ресурсы

Полиномиальный коэффициент используется в части формулы полиномиального распределения , которая описывает вероятность получения определенного количества отсчетов для k различных исходов, когда каждый исход имеет фиксированную вероятность возникновения.

Бонус: вы можете использовать Калькулятор мультиномиальных коэффициентов, чтобы легко рассчитать полиномиальные коэффициенты.

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Комбинаторика

Иногда в задачах требуется подсчитать количество некоторых объектов, количество способов сделать что-то. При этом обычно это количество слишком велико, чтобы можно было перечислить все объекты в явном виде.

Например, можно посчитать количество перестановок из (n) различных элементов следующим образом. Понятно, что на первое место в перестановке мы можем поставить любой из (n) элементов, на второе — любой из (n — 1) оставшихся, и так далее. Для последнего места останется только 1 элемент. Значит, число перестановок (n) элементов равно (ncdot(n-1)cdotldotscdot2cdot1), что сокращенно обозначается как (n!)

Принято считать, что (0!=1)

Биномиальные коэффициенты

Посчитаем количество способов выбрать (k) элементов из (n) различных (называется числом сочетаний из (n) по (k) и обозначается (C_n^k)). Точно так же на первое место мы можем поставить любой из (n) элементов, на второе — любой из (n — 1) оставшихся, на (k)-е место останется (n — k + 1) вариант, то есть всего вариантов получится (ncdot(n-1)cdotldotscdot(n-k+1)=frac{n!}{(n-k)!}). Заметим, что так мы посчитали число упорядоченных наборов из (k) элементов и чтобы получить количество способов выбрать (k) элементов из (n) нужно поделить результат на (k!), ведь, как было установлено ранее, именно столько есть спобосов упорядочить (k) элементов. В итоге получается (C_n^k=frac{n!}{k!(n-k)!})

Есть и другой способ подсчета (C_n^k) для (0 < k < n). Посмотрим на первый элемент. Если он входит в набор, то осталось выбрать (k-1) из (n-1) оставшихся. Иначе нужно выбрать (k) из (n-1) оставшихся. Значит, (C_n^k=C_{n-1}^{k}+C_{n-1}^{k-1}). Так можно найти все (C_n^k) до какого-то (n) за (O(n^2)).

Таким образом, (C_n^k) легко представлять в виде бесконечного треугольника, где на сторонах стоят 1, а остальные числа равны сумме двух верхних. Легко видеть, что (C_n^k) это (k)-е число в строке номер (n). Это называют треугольником Паскаля.

Число путей черепашки

Пусть, в левом верхнем углу прямоугольного поля стоит черепашка, которая может ходить только на одну клетку вправо или вниз. Сколько у нее способов попасть в правый нижний угол?

Бином Ньютона

Рассмотрим разложение выражения ((a+b)^n). Докажем, что коэффициент при (a^kb^{n-k}) равен (C_n^k). Действительно ((a+b)^n=(a+b)(a+b)cdots(a+b)~)((n) раз). Чтобы получить член (a^kb^{n-k}) надо из (k) скобок выбрать (a), а из остальных (b). Как мы уже знаем, это можно сделать (C_n^k). Значит, ((a+b)^n=sumlimits_{k=0}^nC_n^ka^kb^{n-k}).

Из этого следует, что коэффициенты при разложении ((a+b)^n) являются строкой треугольника Паскаля.

Бином Ньютона часто используется для доказательства различных комбинаторных формул.

##Полиномиальные коэффициенты

Посчитаем теперь количество разбиений множества на (m) множеств размеров (k_1,k_2ldots,k_m). Это называется полиномиальные коэффициенты и обозначается (C(k_1,k_2,ldots,k_m)) Будем набирать эти множества по очереди. Количество способов выбрать первое подмножесто равно (C_n^{k_1}), второе (C_{n-k_1}^{k_2}) и так далее. Итоговая формула (C(k_1,k_2,ldots,k_m)=C_n^{k_1}cdot C_{n-k_1}^{k_2}cdots C_{k_m}^{k_m}=frac{n!}{k_1!k_2!cdots k_m!}).

Аналогично биному Ньютона, такие числа являются коэффициентами при членах (x_1^{k_1}x_2^{k_2}cdots x_m^{k_m}) выражения ((x_1+ldots+x_m)^n). Доказательство тоже аналогично доказательству из предыдущего раздела и оставляется в качестве упражнения.

Числа Каталана

Посчитаем количество правильных скобочных последовательностей (ПСП). Интуитивно понятно, что это, но формально они определятюся так: — Пустая последовательность является ПСП — Если (A) является ПСП, то ((A)) является ПСП — Если (A) и (B) являются ПСП, то (AB) является ПСП.

Теперь, посчитаем количество ПСП с (2n) скобками. Это называется числами Каталана и обозначается (C_n). Рассмотрим первое место, где разность количества открывающих и закрывающих скобок впервые становится равна 0 и часть ПСП до этого места обозначим ((A)), а часть после обозначим (B). Понятно, что (A) и (B) являются ПСП меньшего размера (возможно, пустыми).

Теперь (C_n) посчитать легко, перебирая размер (A).

(C_0=1)

(C_n=C_0C_{n-1}+C_1C_{n-2}+ldots+C_{n-1}C_0)

Полезные формулы

(C_n^k=C_n^{n-k})
(C_n^0+C_n^1+C_n^2+ldots+C_n^n=2^n)
(C_n^0-C_n^1+C_n^2-ldots+(-1)^nC_n^n=0)
(C_n=frac{1}{n+1}C_{2n}^n)

В качестве упражнения попробуйте их доказать.

Источник

Theorem[edit]

Example[edit]

Alternate expression[edit]

Proof[edit]

Multinomial coefficients[edit]

Sum of all multinomial coefficients[edit]

Number of multinomial coefficients[edit]

Valuation of multinomial coefficients[edit]

Interpretations[edit]

Ways to put objects into bins[edit]

Number of ways to select according to a distribution[edit]

Number of unique permutations of words[edit]

Generalized Pascal’s triangle[edit]

See also[edit]

References[edit]

Теорема

Пример

Альтернативное выражение

Доказательство

Полиномиальные коэффициенты

Сумма всех полиномиальных коэффициентов

Количество полиномиальных коэффициентов

Оценка полиномиальных коэффициентов

Интерпретации

Способы складывать предметы в мусорные ведра

Количество способов выбора в зависимости от распределения

Количество уникальных перестановок слов

Обобщенный треугольник Паскаля

Смотрите также

использованная литература

3.2.3. Формула включений и исключений

Вопросы для повторения

Резюме по теме

Глава 4. Теория графов

Мультиномиальный коэффициент: определение и примеры

Пример 1: Буквы в слове

Пример 2: Учащиеся по классам

Пример 3: предпочтения политической партии

Дополнительные ресурсы

Комбинаторика

Биномиальные коэффициенты

Число путей черепашки

Бином Ньютона

Числа Каталана

Полезные формулы